
图1 页岩压裂SRV形成机制
Fig. 1 The forming mechanism of the stimulated reservoir volume (SRV) in shale gas fracturing
任 岚 1 , 赵金洲 1 , 林 然 1 , 周长林 2
(1. 油气藏地质及开发工程国家重点实验室, 成都 610500;2. 中国石油天然气股份有限公司 西南油气田分公司工程技术研究院, 四川 广汉 618300)
摘要 : 页岩气藏开发实践表明,水平井分段压裂是实现页岩气藏经济有效开发的关键技术,其中增产改造体积(SRV)是控制页岩压后效果的核心参数,对SRV的准确计算和表征已成为页岩压裂研究领域的重点难点问题 . 基于目前SRV评价方法的局限性,考虑动态扩展裂缝与储层应力场和压力场的耦合作用,以及它们实时变化触发储层天然裂缝的破裂机制,建立了一种SRV动态演化计算模型,采用该模型可以计算和表征裂缝动态扩展形态、储层渗透率演化分布以及SRV的空间展布 . 由于模型与页岩压裂过程中储层SRV实际动态扩展物理机制较一致,采用该模型对SRV的评价计算更符合矿场实际 . 基于文中提出的计算方法,以威远页岩气开发示范区某压裂井段为例,验证了模型的可靠性,并计算分析了SRV随时间的动态演化过程及变化规律 . 该文研究对于提升页岩水平井分段分簇压裂SRV计算准确性,提高压裂优化设计以及压后效果评估具有重要的理论指导意义和矿场应用价值 .
关 键 词 : 页岩; 水平井; 水力压裂; 增产改造体积; 应力场; 压力场
页岩气藏储层基质渗透性极低,若不采取增产措施,基本不具备商业开发价值 . 但页岩由于其自身脆性,通常发育大量的天然裂缝 . 在原始地层条件下,这些天然裂缝处于未激活的闭合状态,但可通过大液量大排量实施水平井分段分簇水力压裂达到增产目的 . 压裂过程中,多条水力裂缝同时延伸,压裂液向地层发生滤失,使得地层应力和压力发生变化,促使延伸主裂缝附近大量天然裂缝发生破坏,被激活为相互交织的复杂裂缝网络 [1] ,其表观渗透率将提高几个数量级,形成的裂缝网络区域即被称为增产改造体积(SRV) [2] . 矿场数据表明,SRV与压裂井产气量有非常显著的正相关关系 [3] . 因此,如何准确、快速、高效、经济地获得SRV及其空间展布形态,对于压前设计、压裂实施和压后评价等环节都至关重要 .
目前页岩压裂对SRV的评估主要包括直接法和理论计算法,其中直接法包括微地震监测技术 [4] 、倾斜仪测量技术 [5] 和电磁感应成像技术 [6] 等 . 其中,微地震监测由于技术成熟和监测结果可靠应用最为广泛,但直接监测技术都存在应用成本较高和一定的作业工序,导致矿场推广和复制性差,因此,发展应用成本低、计算可靠的SRV理论计算方法及其重要 . Shapiro等 [7] 和Yu等 [8] 基于压裂过程流体扩散效应,考虑压力场变化对SRV的控制作用提出了一种SRV计算方法;随后Maulianda等 [9] 基于地应力和岩石力学特性对储层破裂的影响,提出了包含剪切和拉伸破裂的SRV计算方法,但它们都存在需要采用微地震监测数据进行校正的问题 . 任岚等 [10] 考虑裂缝扩展过程中压力场和应力场变化对天然裂缝的破坏影响,建立了一种SRV计算模型,但模型未考虑应力场变化和SRV动态演化区渗透率变化对裂缝扩展的反作用效应,属于一种半耦合模型 . 事实上,页岩压裂过程中,不但应力场变化会影响裂缝动态扩展 [11] ,SRV动态演化也会导致储层渗透率及压力场改变,影响裂缝延伸行为,为此,发展相互耦合作用的SRV动态演化模型计算结果与实际压裂改造形成的SRV更为一致 . 此外,近年来也发展了一些裂缝网络扩展模型用于表征SRV,通过在储层中预设正交天然裂缝或随机天然裂缝,建立了正交缝网延伸模型或随机缝网延伸模型 [12-13] ,上述模型主要用于模拟网络裂缝延伸区,但对延伸区外的天然裂缝激活状态没有进行表征 . 从本质上说,页岩压裂形成的SRV是由延伸主裂缝周围的天然裂缝破坏网络群构成,既包括相互连通也包括非连通的天然裂缝破坏网络群 [14] .
本文通过模拟页岩储层水平井分段分簇压裂的多裂缝动态扩展,以及扩展裂缝与储层应力场和压力场的相互作用,并结合页岩储层天然裂缝破坏过程,建立了一套SRV动态演化数值计算方法,以威远页岩气开发示范区某井段为例,在验证模型可靠性的基础上,对SRV随时间动态演化过程进行了计算分析 .
页岩压裂SRV形成机制如图1所示,其中, σ n , σ s , p nf 为天然裂缝受到原始正应力分量、剪应力分量和流体压力;Δ σ n ,Δ σ s ,Δ p nf 为天然裂缝受到诱导正应力分量、诱导剪应力分量和流体压力增量 . 页岩水平井分段分簇压裂过程中,多条水力裂缝同时从不同簇射孔点起裂并延伸(图1(a)) . 随着裂缝的扩展引发诱导应力;此外,大量低黏度压裂液从裂缝壁面向地层中滤失,导致储层流体压力抬升 . 因此,大量天然裂缝将受到来自水力裂缝引起的应力(Δ σ n ,Δ σ s )、压力(Δ p nf )双重干扰 . 当天然裂缝受到的有效剪切应力超过抗剪强度时,天然裂缝壁面将发生相互错动,造成剪切破坏(图1(c));当天然裂缝内净压力超过抗张强度时,天然裂缝将被撑开,造成张性破坏(图1(d)) . 根据天然裂缝的不同破坏类型,改造区域可以表征为剪切破坏SRV与张性破坏SRV .

图1 页岩压裂SRV形成机制
Fig. 1 The forming mechanism of the stimulated reservoir volume (SRV) in shale gas fracturing
与此同时,水力裂缝产生的诱导应力会改变原地应力分布,影响水力裂缝的扩展行为,延伸裂缝间出现相互干扰,造成中间裂缝延伸受限,外侧裂缝延伸转向的现象(图1(b));延伸裂缝周围发生破坏的天然裂缝其渗透率将显著增大,形成局部渗透率升高的储层改造区域,加剧压裂液的滤失,也会影响水力裂缝的扩展 . 为此,水力裂缝扩展与应力场和压力场的改变是相互作用影响 .
综上所述,建立页岩压裂水平井SRV数学模型过程中,需要准确描述4个关键物理过程:水力裂缝动态延伸、地层应力场变化、储层压力场抬升以及天然裂缝破坏 . 基于它们相互作用和影响,需要结合4个关键物理过程的数学描述方程进行耦合求解 .
数学模型包括裂缝延伸模型、应力场计算模型、压力场计算模型和天然裂缝破坏准则 .
2.1.1 物质平衡方程
根据物质平衡原理,注入压裂液量等于裂缝体积增量与压裂液滤失量之和,全局物质平衡方程为
(1)
式中, q T 为总流量,m 3 /min; L f, i 为第 i 条裂缝长度,m; h f 为裂缝高度,m; w f 为裂缝宽度,m; q L 为压裂液滤失量,m 2 /min; N 为裂缝条数,无因次; s 为裂缝长度方向坐标,m; t 为时间,min .
单条裂缝物质平衡方程为
(2)
式中, q 为单裂缝内流量,m 3 /min; A f 为裂缝横截面积,m 2 .
2.1.2 缝内压降方程
水力裂缝中流体压降方程为 [15]
(3)
式中, p 为缝内流体压力,MPa; μ 为液体黏度,mPa·s; q 为裂缝内流量,m 3 /min .
2.1.3 裂缝转向方程
根据最大周向应力理论,水力裂缝尖端延伸方向的转向角度 θ 满足方程 [16] :
K Ⅰ sin θ + K Ⅱ (3cos θ -1)=0,
(4)
式中, K Ⅰ , K Ⅱ 为第一、第二类应力强度因子,Pa·m 1/2 ; θ 为裂缝延伸转向角,(°) .
K Ⅰ , K Ⅱ 与裂缝缝尖单元的法向位移( D n )和切向位移( D s )相关 [17] :
(5)
(6)
式中, G 为储层岩石剪切模量,MPa; D n , D s 为裂缝尖端单元法向、切向位移,m; ν 为储层岩石Poisson(泊松)比,无因次; a 为不连续位移方法(DDM)模型离散裂缝单元长度的一半,m .
裂缝发生转向延伸且转向角度为 θ ,则转向后作用在裂缝壁面的正应力大小为
σ c = σ h cos 2 θ + σ H sin 2 θ ,
(7)
式中, σ c 为转向裂缝受到的正应力,MPa; σ h 为最小水平主应力( x 方向),MPa; σ H 为最大水平主应力( y 方向),MPa .
2.1.4 流量分配方程
压裂过程中,从水平井跟端至每条裂缝尖端沿程总压降为水平井筒内压降、射孔孔眼摩阻压降和裂缝内压降之和,流量和压降描述如图2所示,沿程压降方程如下 [18] :
(8)
其中
(9)
(10)
式中, p heel 为水平井跟端压力,MPa;Δ p pf, i 为第 i 条裂缝孔眼摩阻压降,MPa;Δ p w, j 为第 j 水平井段沿程压降,MPa; q pf, i 为第 i 条裂缝射孔处流量,m 3 /min; n pf 为射孔孔眼数量,个; d pf 为射孔孔眼直径,m; α pf 为孔眼流量系数,一般取0.8~0.85,无因次; ρ 为压裂液密度,kg/m 3 ; L w, j 为第 j 段水平井长度,m; d w 为水平井筒直径,m; q w, j 为第 j 段水平井流量,m 3 /min; δ 和 ε 为单位换算系数,无因次 .

图2 分簇压裂流量、压力平衡示意图
Fig. 2 Flow rate distribution and pressure equilibrium in the horizontal wellbore and hydraulic fractures
井筒中各段流量关系式如下:
(11)
式中, q w, j 为第 j 段水平井流量,m 3 /min; q T 为压裂液总流量,m 3 /min; q i 为第 i 条裂缝内总流量,m 3 /min .
根据物质平衡原理,列出1个方程:
(12)
根据沿程压降方程,列出 N 个方程:
(13)
联立上式,可得一组 N +1阶非线性方程组,可通过构造其Jacobi矩阵,利用Newton(牛顿)迭代法求解出 N +1个未知量,包括 q 1 , q 2 ,…, q N , p heel .
在裂缝扩展模型中, q L 需要结合流体场模型中式(33)计算;裂缝宽度 w f , D n 和 D s 需要结合应力场模型式(14)和式(15)求解 .
以三条裂缝同时延伸为例,建立如图3所示 xOy 二维直角坐标系,将水力裂缝离散为 N 段,每段长度2 a i . 分别以每段中心为原点建立该单元 ξO ′ ζ 局部坐标系,其中, ξ 沿离散裂缝单元切向方向, ζ 沿离散裂缝单元法向方向 . 根据DDM [19] ,建立离散裂缝 i 单元受到所有单元作用下的应力平衡方程组:
(14)
(15)
式中,( σ t ) i ,( σ n ) i 为 i 单元在局部坐标系内所受有效切应力和有效正应力, ![]() 为 j 单元在局部坐标系内的切向位移和法向位移,m;( A tt ) ij ,( A nt ) ij ,( A tn ) ij ,( A nn ) ij 为 j 单元切向位移和法向位移不连续量分别在 i 单元上引起的切向应力分量和法向应力分量;( D ) ij 为水力裂缝高度修正系数,无因次 . A tt , A nt , A tn , A nn , D 的表达式详见文献[19-20] .
为 j 单元在局部坐标系内的切向位移和法向位移,m;( A tt ) ij ,( A nt ) ij ,( A tn ) ij ,( A nn ) ij 为 j 单元切向位移和法向位移不连续量分别在 i 单元上引起的切向应力分量和法向应力分量;( D ) ij 为水力裂缝高度修正系数,无因次 . A tt , A nt , A tn , A nn , D 的表达式详见文献[19-20] .
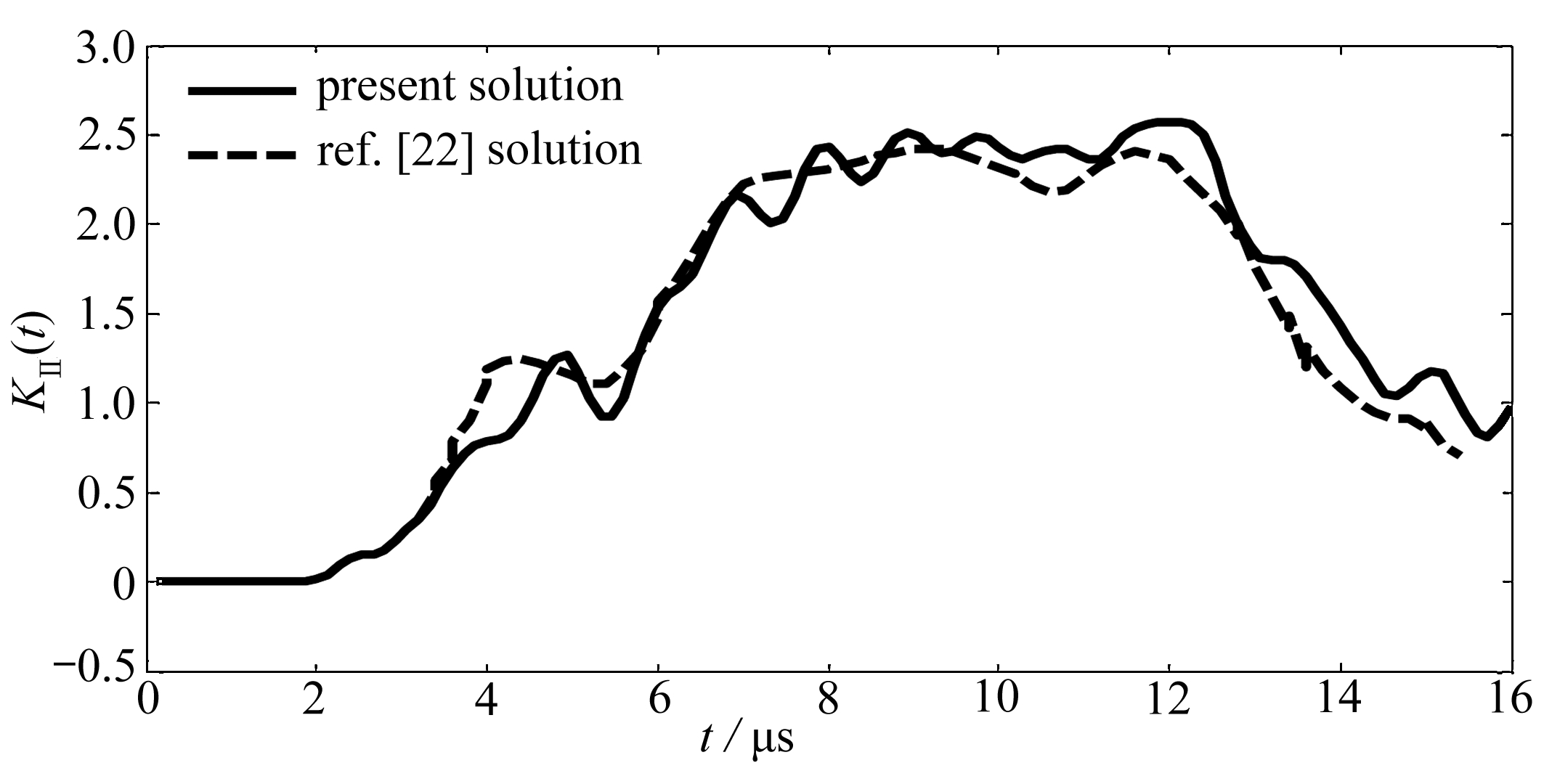
图3 非平面多裂缝离散单元示意图(xOy截面)
Fig. 3 Discretized elements of multiple non-planar hydraulic fractures (xOy plane)
水力裂缝处于张开状态,其任意 i 单元应力边界条件如下:
( σ t ) i =0,
(16)
( σ n ) i =-( p f - σ c ) i ,
(17)
式中, p f 为裂缝内流体压力,MPa .
根据裂缝离散单元应力边界条件,联立式(14)和式(15)进行求解 . 得出 ![]() 和
和 ![]() 后,代入以下方程中,即可计算出坐标平面域内任一点的诱导应力分量:
后,代入以下方程中,即可计算出坐标平面域内任一点的诱导应力分量:
(18)
(19)
(20)
Δ σ zz = ν (Δ σ xx +Δ σ yy ),
(21)
式中,Δ σ xx ,Δ σ yy ,Δ σ zz ,Δ σ xy 为地层诱导应力分量,MPa,局部坐标转换方程以及 F 3 ~ F 6 导数函数参见DDM文献[19] .
根据式(18)~(21)计算的诱导应力,利用叠加原理得到地层中任意点当前应力张量为
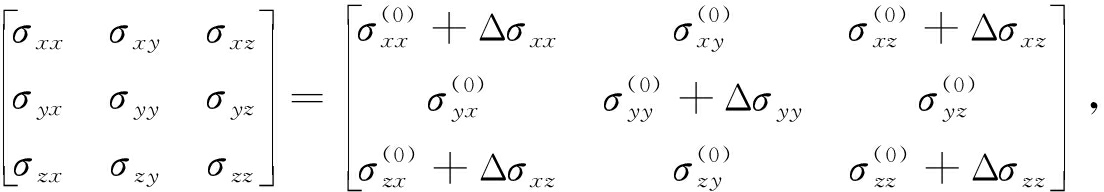
(22)
式中, ![]() 为原始地应力值分量,MPa; σ ij 为当前地应力值分量,MPa .
为原始地应力值分量,MPa; σ ij 为当前地应力值分量,MPa .
压裂过程中压裂液通过水力裂缝壁面向储层中滤失,压裂液在储层中流动的连续性方程为
(23)
式中, k x , k y 分别为沿 x , y 方向的渗透率,D(1 D=9.87×10 -13 m 2 ); p 为储层流体压力,MPa; φ 为孔隙度,无因次; C t 为地层综合压缩系数,MPa -1 ; t 为时间,min .
求解初始条件、内外边界条件分别为
p ( x , y ,0)= p i ,
(24)
p ( x i , y , t )= p f ( x i ), 0≤ y ≤ L f ,
(25)
p (+∞,+∞, t )= p i ,
(26)
式中, p i 为储层原始地层压力,MPa; L f 为裂缝长度,m; x i 为第 i 个射孔点位置 . 其中,在内边界处理时,内边界所在的网格为裂缝延伸路径上相遇的网格 .
由于渗透率 k x , k y 为时间变量,导致式(23)存在严重的非线性,选用差分法进行求解,差分方程为
(27)
式中, E , W , A , S , N , Q 为差分方程系数 [21] ;下标 i , j 分别为 x , y 方向网格序号 .
受储层压力和地应力的共同作用, 激活闭合的天然裂缝, 天然裂缝破坏后其等效渗透率 [22] 为
(28)
式中, a f 为天然裂缝开度,m; S f 为天然裂缝间距,m .
剪切破裂天然裂缝开度为 [23]
(29)
式中, K s 为天然裂缝剪切刚度,MPa/m;Δ τ 为天然裂缝受到的有效剪切力,MPa; φ dil 为天然裂缝剪切膨胀角,(°) .
张开破裂天然裂缝开度为 [24]
(30)
式中, K n 为天然裂缝正刚度,MPa/m; p nf 为天然裂缝内的流体压力,MPa; σ n 为天然裂缝受到的正应力,MPa .
由于天然裂缝的方向性,假设天然裂缝与最大水平主应力方向夹角为 α ,根据坐标转换原理,则天然裂缝破坏后的储层等效渗透率为
k x ( x , y , t )=sin 2 α · k nf + k m ,
(31)
k y ( x , y , t )=cos 2 α · k nf + k m ,
(32)
式中, k m 为储层初始渗透率,D .
基于压力场计算,可得到裂缝面的压裂液滤失速度:
(33)
本文基于Warpinski的二维准则 [25] ,通过张量运算 [26] ,推导出适用于任意产状天然裂缝的破坏判断准则 .
天然裂缝的单位法线向量为
(34)
其中
n x =sin( φ )·cos( α ), n y =sin( φ )·sin( α ), n z =cos( φ ),
式中, n 为天然裂缝单位法线向量,无因次; n i 为天然裂缝单位法线向量分量,无因次; e i 为坐标系单位向量,无因次; α 为天然裂缝与最大水平主应力方向( y 方向)夹角(逼近角),(°); φ 为天然裂缝与水平面夹角(倾角),(°) .
作用在天然裂缝面上的力为
F = σ · n = σ ij n j e i ,
(35)
式中, σ 为地应力二阶对称张量, σ ij 为应力张量分量,MPa; e 为标准正交基矢量; i , j 为坐标指标,取值 x , y , z .
当前天然裂缝壁面受到的正应力值为
(36)
当前天然裂缝壁面受到的切应力值为
(37)
天然裂缝张性破坏判别式为
(38)
式中, S t 为天然裂缝抗张强度,Pa .
天然裂缝剪切破坏判别式为
(39)
式中, K f 为天然裂缝摩擦因数,无因次; τ 0 为天然裂缝内聚力,MPa .
张性破坏储层改造体积(tensile-SRV)和剪切破坏储层改造体积(shear-SRV)分别为储层中天然裂缝发生张性破坏和剪切破坏的区域;总体储层改造体积(total-SRV)则为两者的空间并集 . 因此,可以通过对天然裂缝发生破坏的网格单元集合进行数值积分 [27] ,求得

(40)
式中, V tensile-SRV , V shear-SRV , V total-SRV 分别为张性破坏SRV、剪切破坏SRV、总体SRV,m 3 ; ε 为网格单元; ε tensile , ε shear 分别为发生张性破坏、剪切破坏的储层网格单元;Δ x ( ε ),Δ y ( ε ),Δ z ( ε )分别为 ε 网格单元 x , y , z 方向网格边长,m .
图4 SRV计算流程图
Fig. 4 The flowchart of the SRV calculation
综合上述各方程,SRV计算流程如图4所示 . 在该模型计算过程中,裂缝扩展延伸涉及4层迭代循环(裂缝内流体压力、单缝延伸长度、多缝延伸长度、滤失量)、3次耦合迭代(裂缝延伸模型+应力场模型、裂缝延伸模型+压力场模型、天然裂缝破坏准则+应力场模型+压力场模型),以及多个参数传递(裂缝内流体压力、裂缝长度、裂缝宽度、储层压力、地应力、滤失量等),其计算流程如下:
① 参数输入 地层参数、井筒参数、压裂施工参数等 .
② 水力裂缝延伸模型 分簇裂缝流量分配、裂缝延伸参数计算 . 其中,裂缝宽度与应力场模型耦合求解、滤失系数与压力场模型耦合求解,当两次迭代计算的缝内压力误差小于预定值时转到第⑤步 .
③ 应力场模型 诱导应力计算、 当前应力场计算、 裂缝转向角计算 . 其中, 裂缝压力、 裂缝位置由水力裂缝延伸模型计算得到 .
④ 压力场模型 天然裂缝破坏状态判断、储层渗透率场分布、储层压力场计算、水力裂缝滤失计算 . 其中,天然裂缝破坏状态由应力场和压力场共同决定 .
⑤ SRV计算 张性破坏SRV、剪切破坏SRV,总体SRV .
⑥ 数据输出 裂缝延伸数据、应力数据、压力数据、SRV数据 .
⑦ 图像输出 裂缝三维形态、SRV三维形态 .
⑧ 返回步骤②,进行下一时步计算 .
程序设计中,大型稀疏线性方程组求解选用复合共轭梯度法;非线性方程求解选用Newton迭代法;迭代循环选用Picard方法,迭代学习系数运用了自适应动态调整算法,根据每一步迭代循环的最大误差调整迭代学习系数(误差增大时,缩小学习系数,保证循环收敛;误差减小时,增大学习系数,加快收敛速度),这种针对学习系数的自适应动态调整算法能够大大减少循环计算量,缩短运算时间 .
利用上述SRV计算模型,对模型的可靠性和SRV演化规律进行计算讨论 .
针对四川威远页岩气藏的X1井,储层地质参数见表1所示,施工1~4段的施工参数分别见表2所示,模拟计算施工结束后的SRV展布状况,并与微地震监测数据进行对比,对模型的可靠性进行了验证 .
表1 储层地质及井眼射孔主要参数表
Table 1 Main parameters of geological condition and wellbore perforation
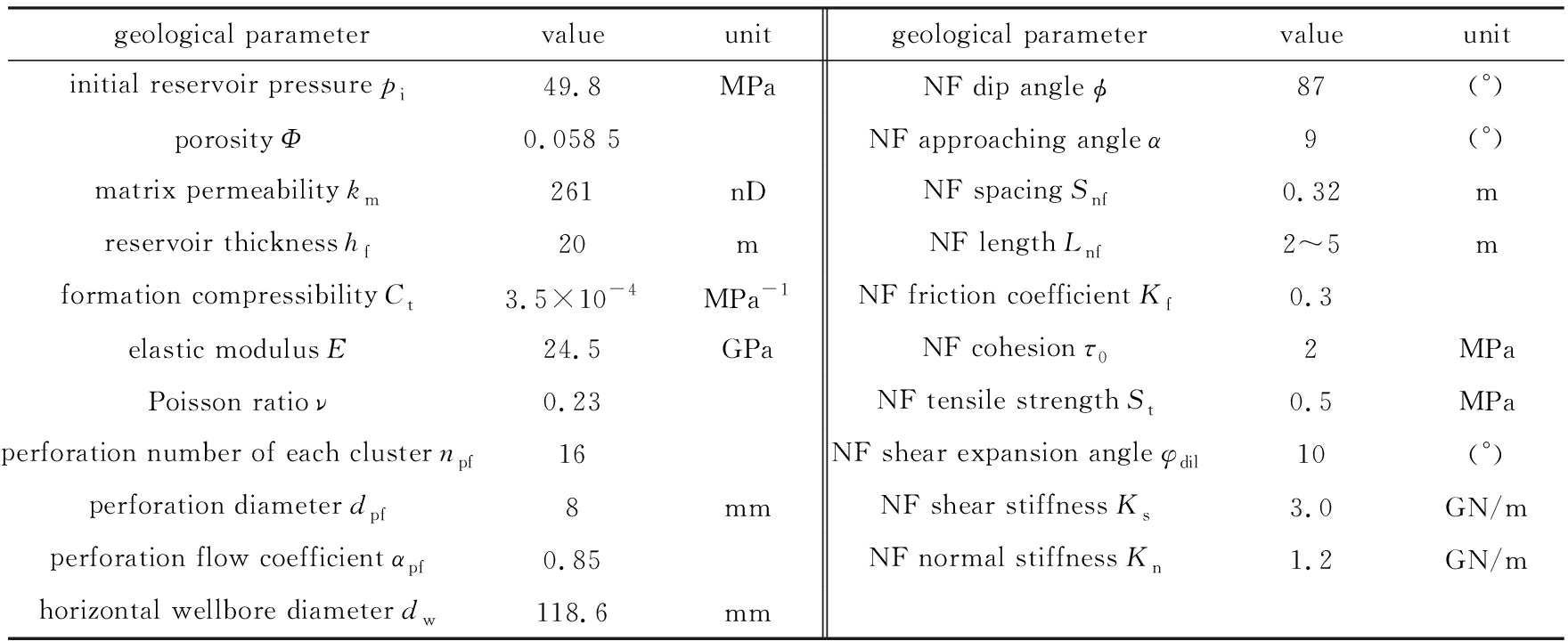
注 NF为天然裂缝
Note NF is the abbreviation of natural fracture
表2 威远X1水平井1~4段水力压裂施工主要参数表
Table 2 Fracturing parameters of fracturing stages 1~4 of the X1 horizontal well in the WY shale gas reservoir
将X1井模拟计算的SRV与实际压裂现场微地震监测信号进行对比,如图5所示,各段压裂形成的SRV展布存在较大差异 . 其中1、2段较3、4段的SRV展布不足,主要由于3、4段较1、2段的簇间距及水平应力差都小,导致3、4段主裂缝间的应力干扰效应较大,主裂缝延伸相互受限促使裂缝张开宽度不足,裂缝延伸长度得到强化,缝内流体净压力更高,诱导储层天然裂缝更易达到破裂条件 . 此外,3、4段较1、2段的注液总量要大,在储层条件和施工条件共同作用下,3、4段形成的SRV较大,各簇裂缝之间的区域得到了较为充分改造 .
(a) 三维图(b) xOy截面图
(a) The 3D diagram(b) The xOy plane
图5 威远X1水平井1~4段模拟计算剪切SRV与微地震监测SRV对比图
Fig. 5 Comparison between the calculated shear-SRV and the on-site microseismic monitoring signals of fracturing stages 1~4 of the X1 horizontal well in the WY shale gas reservoir
基于微地震监测信号来源为裂缝剪切破裂模式的原理 [28] ,通过X1井各段模拟计算的剪切破裂SRV与微地震解释SRV结果进行对比,如图6所示,相对误差范围在13%~19%,模型计算与微地震监测结果吻合程度较好 . 通过图中对比可知,微地震信号范围大于模型计算的SRV展布范围,这主要是受到理论模型规则性与储层非均质性的制约影响,压裂过程改造区远界天然裂缝存在随机破坏,导致微地震监测结果和理论模型的计算存在差异,理论计算的SRV较微地震监测的SRV偏小 .

图6 威远X1水平井1~4段微地震监测SRV体积与模拟计算剪切SRV体积对比图
Fig. 6 Comparison between calculated shear-SRV volume and the on-site microseismic monitored
volume of fracturing stages 1~4 of the X1 horizontal well in the WY shale gas reservoir

(a) t=10 min(b) t=30 min(c) t=60 min(d) t=135 min
图7 威远X1水平井第4段水力裂缝随时间动态延伸图
Fig. 7 Hydraulic fractures propagating during fracturing stage 4 of well X1 in the WY shale gas reservoir

(a) t=10 min(b) t=30 min(c) t=60 min(d) t=135 min
图8 威远X1水平井第4段压裂水平最小主应力场随时间动态分布图
Fig. 8 Minimum horizontal stresses changing during fracturing stage 4 of well X1 in the WY shale gas reservoir
(a) t=10 min(b) t=30 min(c) t=60 min(d) t=135 min
图9 威远X1水平井第4段压裂压力场随时间动态分布图
Fig. 9 Reservoir pressures varying during fracturing stage 4 of well X1 in the WY shale gas reservoir
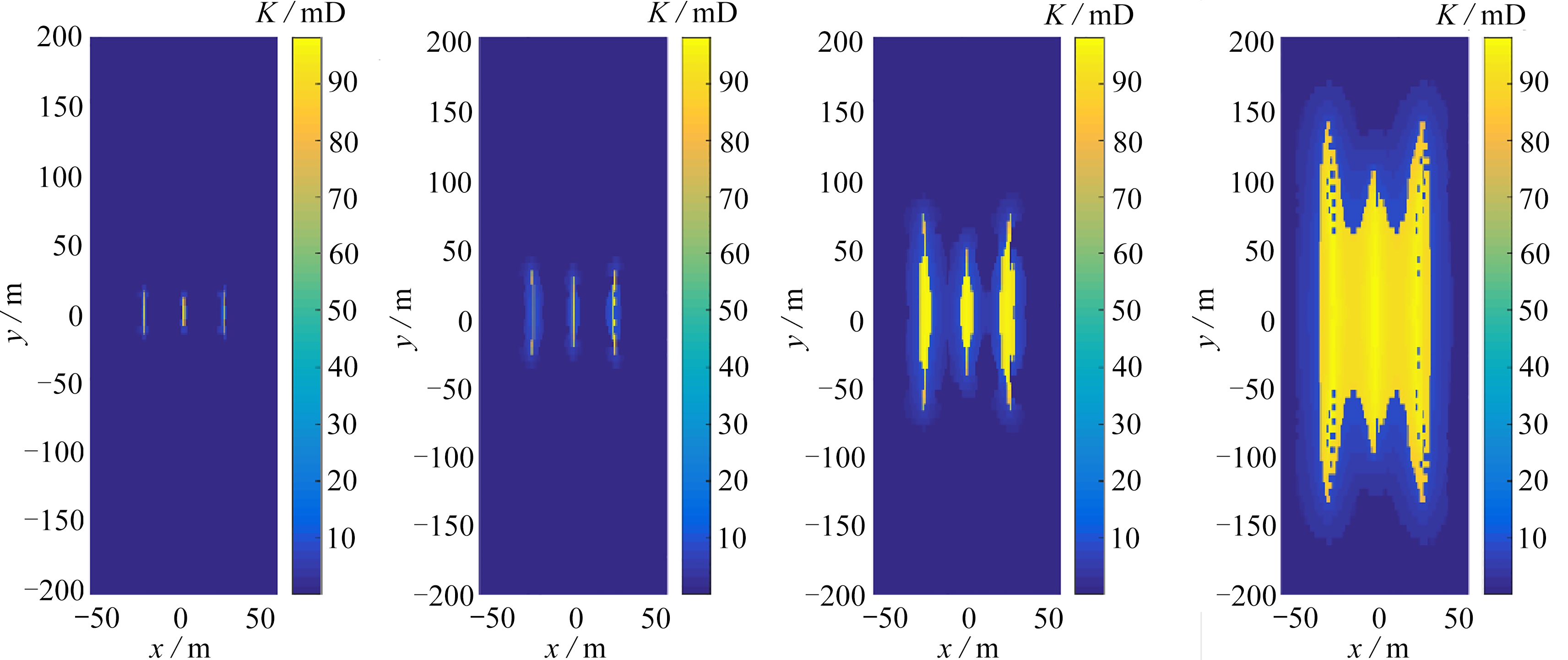
(a) t=10 min(b) t=30 min(c) t=60 min(d) t=135 min
图10 威远X1水平井第4段压裂渗透率场随时间动态分布图
Fig. 10 The reservoir permeability increasing during fracturing stage 4 of well X1 in the WY shale gas reservoir

(a) V SRV =3.1×10 3 m 3 , (b) V SRV =1.63×10 4 m 3 , (c) V SRV =8.96×10 4 m 3 , (d) V SRV =4.609×10 5 m 3 ,
t=10 min t=30 min t=60 min t=135 min
图11 威远X1水平井第4段压裂总体SRV随时间动态演化图
Fig. 11 The SRV expanding during fracturing stage 4 of well X1 in the WY shale gas reservoir
基于威远X1水平井第4段的压裂施工参数,计算分析了水力裂缝和SRV的动态演化过程 . 通过模拟计算,分别得到10,30,60,135 min(施工结束)时刻的水力裂缝延伸形态、储层应力场、储层压力场、储层渗透率变化、SRV展布形态,如图7~图11所示 . 根据模拟计算结果可知不同时间的动态演化特征 .
10 min时,各条裂缝均匀延伸约30 m,缝间干扰作用不明显,裂缝长度几乎相同,裂缝未发生转向 . 储层应力场在裂缝间都有干扰,但压力场影响范围小,储层天然裂缝以张性破坏为主,但范围很小,紧邻延伸裂缝 . 此时,改造区只在各条裂缝周围的很小区域内,这时候SRV仅为3.1×10 3 m 3 ,渗透率场无明显变化 .
30 min时,外侧裂缝延伸约80 m,中间裂缝长度约72 m,小于外侧裂缝,但裂缝仍未发生转向,此时裂缝间干扰作用初步显现 . 储层应力场影响范围扩大、强度增强,压力场也逐步向裂缝外围扩展,储层天然裂缝会发生张性破坏和剪切破坏,但范围仍然不大,紧邻延伸裂缝 . 此时,改造区仍然只分布在各条裂缝周围较小区域,SRV增至1.63×10 4 m 3 ,受SRV影响,渗透率场开始向裂缝外侧扩展 .
60 min时,外侧裂缝延伸约150 m,中间裂缝长度约94 m,此时裂缝间干扰作用进一步增大,中间裂缝延伸受到明显限制、外侧裂缝出现了转向延伸 . 储层应力场出现上下两翼增强的现象,压力场也逐步开始相互波及相连,储层天然裂缝发生张性破坏和剪切破坏,范围扩大,其中张性破坏区域紧邻裂缝,剪切破坏范围扩大至裂缝之间的区域,并发生相互交接 . 此时,裂缝之间部分区域成为改造区,SRV增至8.96×10 4 m 3 ,受SRV演化范围影响,裂缝间渗透率场改变区扩大到部分连接,离裂缝越近的天然裂缝张性破裂区渗透率提升幅度大,远离裂缝的天然裂缝剪切区渗透率提升幅度较小 .
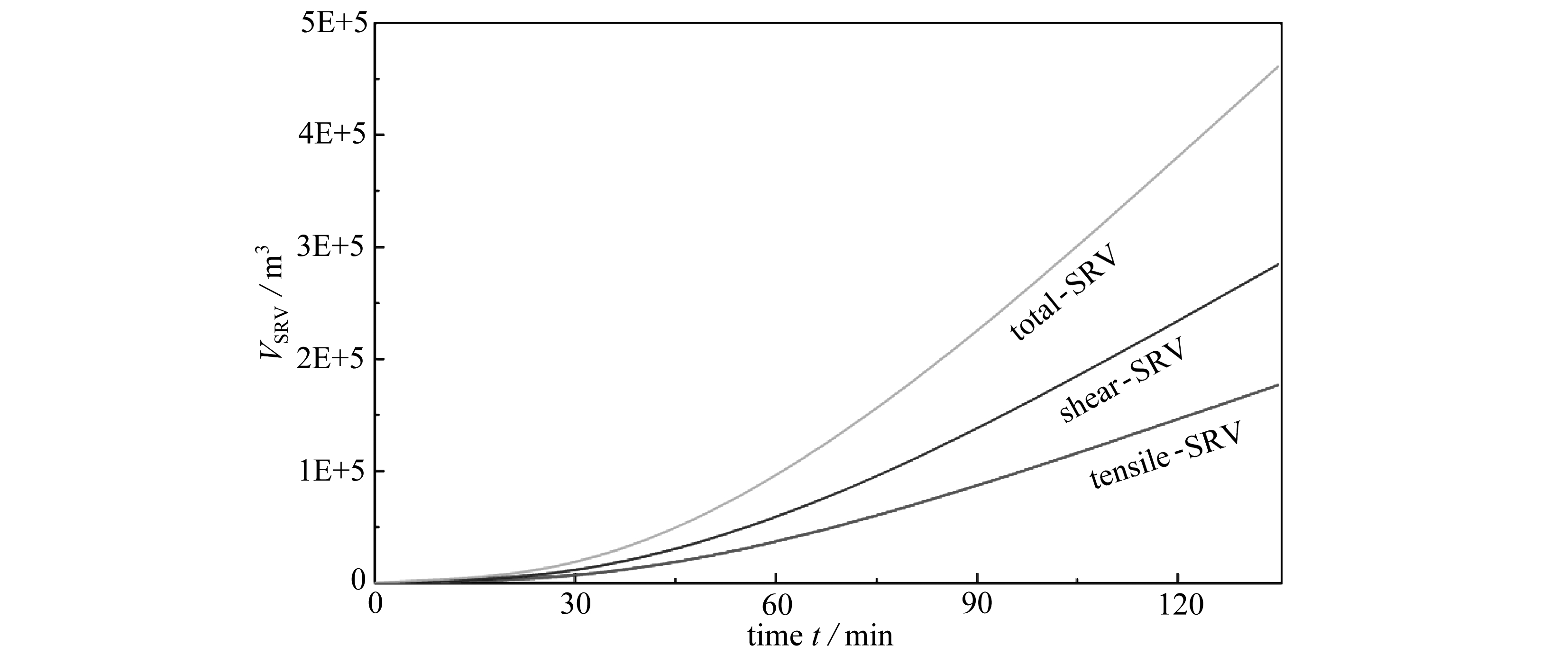
图12 威远X1水平井第4段压裂SRV随时间变化曲线
Fig. 12 The SRV volume increasing during fracturing stage 4 of well X1 in the WY shale gas reservoir
135 min时,外侧裂缝延伸约287 m,中间裂缝延伸至约190 m,随着外侧裂缝转向相互远离,缝间远端干扰效应有所减弱,外侧裂缝转向幅度减小 . 储层应力场影响范围和强度达到最大,压力场影响区域产生相互重叠,裂缝之间大范围内发生张性破坏和剪切破坏,且交接成为一个整体 . 此时,裂缝之间大部分区域成为改造区,SRV增至4.609×10 5 m 3 . 受SRV演化区域影响,裂缝中心位置的天然裂缝张性破裂区相互连接,其渗透率场提升范围和幅度较大且基本相等,外围天然裂缝剪切区渗透率提升幅度较小 .
由以上SRV动态演化分析可见,在SRV随时间增长过程中,储层流体压力上升和应力发生改变导致天然裂缝破坏,使得储层的渗透性逐步增加,有利于流体压力传播,进而加剧天然裂缝发生破坏的范围和程度 . 可见,天然裂缝的破坏与SRV的形成具有相互促进的作用效应,导致SRV在施工作业前期增加速率较小,而在施工作业后期上升速率较快,如图12所示 . 同时可见,SRV展布长度始终略大于水力裂缝延伸长度,这是由于裂缝尖端附近存在应力奇异区域,该区域内天然裂缝会发生破坏,形成SRV .
1) 基于分簇裂缝干扰延伸模型、裂缝诱导应力场模型、储层流体压力场模型和天然裂缝破坏准则,考虑延伸模型与诱导应力场和流体场的相互耦合作用,建立了一种计算页岩水平井分段分簇压裂的SRV动态演化模型 .
2) 实例计算表明,模拟计算的SRV与现场微地震监测解释结果较为吻合,证实模型的可靠性;SRV动态演化分析证实该模型可对页岩分簇压裂过程中分簇裂缝非平面扩展、储层天然裂缝破坏导致渗透率分布和动态SRV展布等物理过程进行表征 .
3) 文中提出的页岩水平井分段分簇SRV动态演化计算模型对完善页岩压裂理论,指导页岩气藏优化设计和压后评价具有重要理论价值和矿场实际意义,能有效提高目前水平井分段分簇SRV计算的准确性和可靠性 .
参考文献 ( References ):
[1] CIPOLLA C L, WARPINSKI N R, MAYERHOFER M J, et al. The relationship between fracture complexity, reservoir properties, and fracture treatment design: SPE 115769[R]. 2008.
[2] MAYERHOFER M J, LOLON E P, WARPINSKI N R, et al. What is stimulated reservoir volume?[J]. SPE Production & Operations , 2010, 25 (1): 89-98.
[3] ZHAO Y L, ZHANG L H, LUO J X, et al. Performance of fractured horizontal well with stimulated reservoir volume in unconventional gas reservoir[J]. Journal of Hydrology , 2014, 512 (10): 447-456.
[4] 刘尧文, 廖如刚, 张远, 等. 涪陵页岩气田井地联合微地震监测气藏实例及认识[J]. 天然气工业, 2016, 36 (10): 56-62.(LIU Yaowen, LIAO Rugang, ZHANG Yuan, et al. Application of surface-downhole combined microseismic monitoring technology in the fuling shale gas field and its enlightenment[J]. Natural Gas Industry , 2016, 36 (10): 56-62.(in Chinese))
[5] NANAYAKKARA A S, ROADARMEL W H, MARSIC S D. Characterizing the stimulated reservoir with a hydraulic deformation index using tiltmeter-based surface microdeformation: SPE 173381[R]. 2015.
[6] PALISCH T, Al-TAILJI W, BARTEL L, et al. Recent advancements in far-field proppant detection: SPE 179161[R]. 2016.
[7] SHAPIRO S A, DINSKE C. Fluid-induced seismicity: pressure diffusion and hydraulic fracturing[J]. Geophysical Prospecting , 2009, 57 (2): 301-310.
[8] YU G, AGUILERA R. 3D analytical modeling of hydraulic fracturing stimulated reservoir volume: SPE 153486[R]. 2012.
[9] MAULIANDA B T, HARELAND G, CHEN S. Geomechanical consideration in stimulated reservoir volume dimension models prediction during multi-stage hydraulic fractures in horizontal wells-glauconite tight formation in hoadley field[C]// The 48 th US Rock Mechanics / Geomechanics Symposium . Minneapolis, Minnesota, 2014.
[10] 任岚, 林然, 赵金洲, 等. 基于最优SRV的页岩气水平井压裂簇间距优化设计[J]. 天然气工业, 2017, 37 (4): 69-79.(REN Lan, LIN Ran, ZHAO Jinzhou, et al. Cluster spacing optimal design for staged fracturing in horizontal shale gas wells based on optimal SRV[J]. Natural Gas Industry , 2017, 37 (4): 69-79.(in Chinese))
[11] WU K, OLSON J E. Simultaneous multifracture treatments: fully coupled fluid flow and fracture mechanics for horizontal wells[J]. SPE Journal , 2015, 20 (2): 337-346.
[12] WENG X, KRESSE O, COHEN C E, et al. Modeling of hydraulic fracture network propagation in a naturally fractured formation[J]. SPE Production & Operations , 2011, 26 (4): 368-380.
[13] MEYER B R, BAZAN L W. A discrete fracture network model for hydraulically induced fractures-theory, parametric and case studies: SPE 140514[R]. 2011.
[14] WANG Y, LI X, ZHANG B, et al. Optimization of multiple hydraulically fractured factors to maximize the stimulated reservoir volume in silty laminated shale formation, Southeastern Ordos Basin, China[J]. Journal of Petroleum Science and Engineering , 2016, 145 : 370-381.
[15] VALK P, ECONOMIDES M J. Hydraulic Fracture Mechanics [M]. New York: Wiley,1995.
[16] ERDOGAN F, SIH G C. On the crack extension in plates under plane loading and transverse shear[J]. Journal of Basic Engineering , 1963, 85 (4): 519-525.
[17] OLSON J E. Fracture aperture, length and pattern geometry development under biaxial loading: a numerical study with applications to natural, cross-jointed systems[J]. Geological Society London Special Publications , 2007, 289 (1): 123-142.
[18] ELBEL J L, PIGGOTT A R, MACK M G. Numerical modeling of multilayer fracture treatments: SPE 23982[R]. 1992.
[19] CROUCH S. Solution of plane elasticity problems by the displacement discontinuity method I: infinite body solution[J]. International Journal for Numerical Methods in Engineering , 1976, 10 (2): 301-343.
[20] OLSON J E, WU K. Sequential vs. simultaneous multizone fracturing in horizontal wells: insights from a non-planar, multifrac numerical model: SPE 152602[R]. 2012.
[21] 张烈辉. 油气藏数值模拟基本原理[M]. 北京: 石油工业出版社, 2014.(ZHANG Liehui. Introduction for Numerical Simulation of Oil and Gas Reservoir [M]. Beijing: Petroleum Industry Press, 2014.(in Chinese))
[22] WENG X, SESETTY V, KRESSE O. Investigation ofshear-induced permeability in unconventional reservoirs[C]// The 49 th US Rock Mechanics / Geomechanics Symposium . San Francisco, California, USA, 2015.
[23] HOSSAIN M M, RAHMAN M K, RAHMAN S S. A shear dilation stimulation model for production enhancement from naturally fractured reservoirs[J]. SPE Journal , 2002, 7 (2): 183-195.
[24] GUO J, LIU Y. A comprehensive model for simulating fracturing fluid leakoff in natural fractures[J]. Journal of Natural Gas Science and Engineering , 2014, 21 : 977-985.
[25] WARPINSKI N R, TEUFEL L W. Influence of geologic discontinuities on hydraulic fracture propagation[J]. Journal of Petroleum Technology , 1987, 39 (2): 209-220.
[26] LASS H, WALKER M. Vector and Tensor Analysis [M]. McGraw-Hill, 1950.
[27] 吕同富, 康兆敏, 方秀男. 数值计算方法[M]. 北京: 清华大学出版社, 2008.(LÜ Tongfu, KANG Zhaomin, FANG Xiunan. Numerical Computation Method [M]. Beijing: Tsinghua University Press, 2008.(in Chinese))
[28] ITO Y, OBARA K. Very low frequency earthquakes within accretionary prisms are very low stress-drop earthquakes[J]. Geophysical Research Letters , 2006, 33 (9): 72-88.
REN Lan 1 , ZHAO Jinzhou 1 , LIN Ran 1 , ZHOU Changlin 2
(1. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation , Chengdu 610500, P . R . China ; 2. Engineering Technology Research Institute of Southwest Oil and Gasfield Company , CNPC , Guanghan , Sichuan 618300, P . R . China )
Abstract: For shale gas reservoir, hydraulic fracturing in horizontal well is the key technology to guarantee its commercial exploitation, and the stimulated reservoir volume (SRV) is a critical parameter deciding the post-fracturing performance. The SRV estimation plays an important role in shale gas fracturing design as well as post-fracturing evaluation, so it has become a hot topic in shale fracturing research. Based on the limitations of existing SRV estimation methods, a dynamic evolution model was built to simulate the forming process of the SRV, which coupled several vital processes during shale fracturing, including the formation stress changing, the reservoir pressure rising and the natural fracture failure mechanism. The real physical process of the SRV formation was fully considered in this model, e.g., the non-planar propagation of multiple hydraulic fractures and the SRV extending with the reservoir permeability, etc., so the model can yield more reliable results for field application. The model was firstly validated with calculated results compared with on-site micro-seismic monitored data for a fractured horizontal well in the Weiyuan shale gas field in southwest China, then it was applied to analyze the forming process and extending behavior of the SRV. The research can not only improve the SRV estimation reliability of multi-stage and multi-cluster fracturing in horizontal shale gas wells, but also provide theoretical guidelines and potential applications for fracturing design and post-fracturing evaluation.
Key words: shale; horizontal well; hydraulic fracturing; stimulated reservoir volume; stress field; pressure field
Foundation item: The National Natural Science Foundation of China(Major Program)(51490653); The National Science Fund for Young Scholars of China(51404204)
作者简介: 任岚(1979—),男,副教授,博士(E-mail: renlanswpu@163.com);林然(1989—),男,博士(通讯作者. E-mail: bob_home@126.com).
基金项目: 国家自然科学基金(重大项目)(51490653);国家自然科学基金青年科学基金(51404204)
修订日期: 2018-04-24
∗ 收稿日期: 2017-09-30;
ⓒ 应用数学和力学编委会,ISSN 1000-0887
文章编号 : 1000-0887(2018)10-1099-16
DOI: 10.21656/1000-0887.380268
文献标志码: A
中图分类号 : TE312
引用本文 / Cite this paper: 任岚, 赵金洲, 林然, 周长林. 页岩压裂水平井增产改造体积的动态演化模型[J]. 应用数学和力学, 2018, 39 (10): 1099-1114.REN Lan, ZHAO Jinzhou, LIN Ran, ZHOU Changlin. A dynamic evolution model for the stimulated reservoir volume of the staged fractured horizontal well in shale gas reservoir[J]. Applied Mathematics and Mechanics , 2018, 39 (10): 1099-1114.