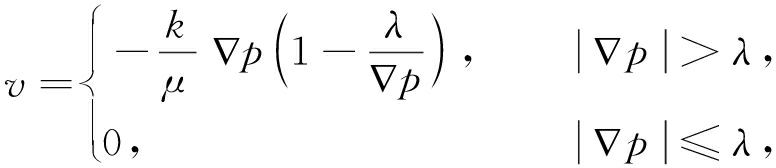
侯绍继 1,2 , 朱卫平 3 , 刘曰武 1,2 , 甄怀宾 3 , 高大鹏 1,2 , 李 奇 1
(1. 中国科学院 力学研究所, 北京 100190;2. 中国科学院大学, 北京 100049;3. 中联煤层气国家工程研究中心有限责任公司, 北京 100095)
摘要 : 低渗油藏渗流过程中普遍存在启动压力梯度(TPG) . 考虑低渗渗流特征,建立了平面径向低渗非Darcy渗流动边界数学模型,给出了计算动边界移动速度的公式,通过Laplace变换结合无穷级数方法求得了模型的半解析解,并进行了Stehfest数值反演 . 详细讨论与分析了动边界问题特性、动边界变化和传播情况,解释了启动压力梯度导致动边界不断向外扩展的现象 . 计算了启动压力梯度对井底压力、压力导数的影响,并给出不同条件下的地层压力分布曲线和Gringarten-Bourdet图版,同时给出了实例分析 . 研究发现:低渗渗流模型与常规渗流模型有着显著不同,低渗非Darcy渗流压力降是随时间扩展的,在动边界外的地层压力降为零,压力分布曲线呈现紧支性 . 针对具有动边界的低渗透问题,需充分考虑启动压力梯度与动边界的影响,该模型为低渗油藏渗流机理和开采动态、解释与数值模拟提供了一定的理论基础 .
关 键 词 : 低渗油藏; 启动压力梯度; 动边界; 半解析解; 数值反演
低渗储层中的渗流规律与高渗储层有着很明显的区别,由于低渗储层的渗透率小到一定程度,其渗流规律不符合Darcy渗流公式,这种渗流运动叫做非Darcy渗流,其最主要的特征就是存在启动压力梯度,当流体两端压差大于启动压力梯度时,流体才能克服黏性阻力开始流动 [1-6] . 存在启动压力梯度的非Darcy渗流模型属于强非线性动边界问题 [7] ,渗流力学中常见的数学求解方法,如Fourier变换、Laplace变换等不再适用 . 目前,动边界问题研究方法主要有积分近似解析方法 [7-10] 、Green函数的近似方法 [11-12] 、无网格方法 [13] 、基于空间坐标变换的有限差分方法 [14-15] 和精确解方法 [16] .
冯文光、葛家理 [17-18] 和程时清等 [19] 推导出了存在启动压力梯度,但没考虑流体动边界影响时的井底压力解;程林松等 [20] 针对流体动边界随时间变化的特点,通过数值离散化方法求得了模型的解;冯曦等 [21] 首先给出了恒定边界的级数解,然后通过用数值逼近的方法求得了动边界模型的解 . 程时清等 [10] 推导出非Darcy渗流动边界问题的积分解,该方法假设解的形式为非线性渗流稳态解的形式,通过待定系数法求解 . 刘启国等 [22] 采用源函数理论及Green函数方法在求解固定边界基础上,结合数值逼近的方法计算动边界模型 . Liu(刘文超)等 [23] 利用相似变量变换方法获得了一维低渗透非Darcy渗流动边界模型的解析解 .
郭永存等 [24] 采用无网格方法中的无单元Galerkin(伽辽金)方法对低渗透动边界问题进行数值分析给出了动边界变化情况与Gringarten-Bourdet图版 . 侯英敏、同登科 [25] 采用Ikoku-Ramey近似方法简化非低渗渗流方程,应用Douglas-Jones预估-校正法求得数值解,最后分析各参数的影响,给出动边界的传播规律 . 姚军等 [26] 通过坐标变换法将低渗透油藏非Darcy渗流的动边界数学模型转化为定边界数学模型,并采用全隐式有限差分法求得了该模型的数值解 .
在目前的求解方法中,近似解析求解法和数值法都分别有着不足之处 . 近似解析求解法:积分近似求解需要假设解的形式,理论依据不够充分;Green函数的近似方法得到的半解析解形式非常复杂不便于理论分析解的性质;此外,相似变量变换只能对一维低渗非Darcy动边界模型进行求解 . 数值求解法:无法直观地体现动边界与各参数之间的关系与定性分析动边界扩展速度等 .
为更好地研究低渗非Darcy渗流动边界特性与扩展规律,本文在前人研究的基础上,将通过Laplace变换结合无穷级数方法 [27] 和数值逼近思想,得出了考虑启动压力梯度径向低渗非Darcy动边界渗流模型的通解 . 创新性地提出了动边界扩展速度的公式,并详细研究了动边界扩展情况 . 然后进行了Laplace数值反演,对计算结果进行了动边界扩展分析,压力的分布分析及使用Gringarten-Bourdet图版进行井底压力曲线特性分析 . 本文的半解析方法对于径向低渗非Darcy渗流动边界的问题,具有求解方法简洁、计算结果准确、表达简洁等优越性,所得到的半解析解与动边界扩展公式比常规的近似处理方法更能直观且真实地反映动边界问题的渗流力学特征 .
笔者的研究内容在非常规油藏开发、非Newton(牛顿)Bingham流体流动规律、聚合物提高原油采收率等方面具有广泛的实际应用背景 . 为进一步解决低渗透油藏开发过程中遇到的非Darcy渗流力学问题提供了依据,为我国非常规油藏开发的渗流机理、开采动态与油藏数值模拟等奠定了一定的理论基础 .
本文研究对象为考虑启动压力梯度的径向低渗非Darcy渗流问题,采用如下假设条件 [28] :
1) 流体渗流是单相流动;
2) 多孔介质的渗透率为各向同性、均质且忽略温度带来的影响;
3) 不考虑重力的影响,假设地层的压力梯度很小;
4) 多孔介质和流体考虑为微可压缩的 .
低渗非Darcy渗流问题可以用以下运动方程来描述 [1-3] :
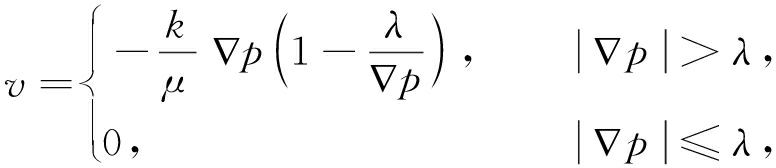
(1)
式中, k 为渗透率, μ 为流体黏度, λ 为启动压力梯度,  为梯度算子, v 为渗流速度 .
为梯度算子, v 为渗流速度 .
流体密度的状态方程为 [23]
ρ = ρ o exp(- C f ( p o - p )),
(2)
式中, ρ 为流体密度, ρ o 为流体的初始密度, p 为地层压力, p o 为地层初始压力, C f 为流体压缩系数 .
多孔介质的孔隙度的状态方程为 [8]
φ = φ o exp(- C φ ( p o - p )),
(3)
式中, φ 为孔隙度, φ o 为初始孔隙度, C φ 为孔隙压缩系数 .
平面径向多孔介质渗流的连续性方程为 [28]
(4)
考虑到动边界的影响,动边界的扩展示意图如图1所示,图中 x f 为动边界扩展位置, p o 为初始压力, p w 为井底压力,动边界距离随时间逐渐向外扩展 . 由于研究的问题是中心对称的,则方程(4)可化为
(5)

图1 动边界扩展示意图
Fig. 1 Diagram of boundary expansion
将状态方程式(2)、(3)和运动方程式(1)代入连续性方程式(5),可推得数学模型的控制方程为
(6)
式中, C t 为综合压缩系数,无量纲; r 为径向距离,m; s 为动边界距离,m .
考虑井储和表皮因子的影响, 引入有效井筒半径 r we = r w e - S , S 为表皮系数, 无量纲 . 引入有效井筒半径适用于井筒污染或射孔不足的堵塞井及酸化、 压裂的疏浚井 [6] , 定义下列无量纲量:
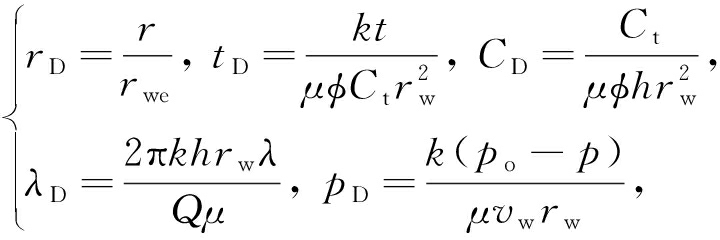
(7)
式中, r D 为无量纲径向距离; t D 为无量纲时间; C D 为无量纲井储系数; λ D 为无量纲启动压力梯度; p D 为无量纲地层压力; r w 为井筒半径,m; r we 为有效井筒半径,m; Q 为产量,m 3 /d .
根据以上无量纲量,对于平面径流低渗非Darcy流的控制方程为
(8)
初始条件为
p D ( r D ,0)=0;
(9)
内边界条件为
(10)
动边界条件为
p D r D = s ( t ) =0;
(11)
外边界条件为
① 无限大地层或者压力波动为传到真实边界之前(本质上是动边界条件)
(12)
② 压力波动传到真实封闭边界后
(13)
③ 压力波动传到真实定压边界后
p D r D = R D =0,
(14)
式中, R D 为无量纲真实边界距离 .
由式(11),可得
p D ( s ( t ), t D )=0 .
(15)
对式(15)两边关于时间 t D 求导,可得
(16)
将动边界条件即式(12)代入式(16),可得
(17)
式(8)两边取 r D = s ( t D ),可得
(18)
将条件(12)代入式(18)得
(19)
由式(19)可以看出,考虑启动压力梯度的平面径向流低渗透非Darcy渗流的动边界移动速度与无量纲启动压力梯度成反比,与动边界上无量纲压力关于径向距离的二次导数成正比 .
对考虑启动压力梯度的径向低渗透非Darcy渗流模型(8)及边界条件进行Laplace变换,可得
(20)
(21)
考虑压力扰动未传到真实边界之前某一时刻的情况,按固定边界处理 [19] :
(22)
方程(20)对应的齐次方程通解为
(23)
由边界条件(21)和(22)给出系数 A , B 为

(24)
式中I 0 ,K 0 为零阶修正Bessel(贝塞尔)函数,I 1 ,K 1 为一阶修正Bessel函数 .
压力扰动传到真实边界时候的情况,边界条件为:
封闭边界
(25)
定压边界
(26)
此时由真实边界条件给出系数 A , B 为
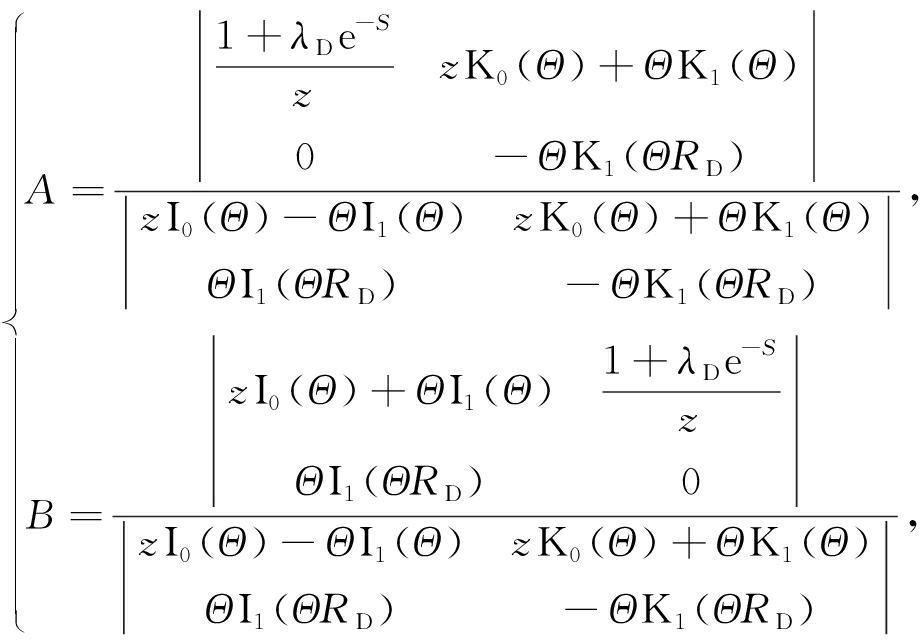
(27)
或

(28)
式(27)为封闭边界条件给出的系数 A , B ,式(28)为定压边界条件给出的系数 A , B .
因为 R D =0是方程(20)的正则奇点,因此可用幂级数解法求此非齐次方程的特解,设特解的表达式为 [18]
(29)
将上式代入方程(20),比较同类项的系数,得到
(30)
根据非齐次方程的特解和相应齐次方程的通解,构造出方程(8)的通解为
(31)
Laplace空间解有较多的数值反演方法,如Stehfest法 [29-31] 、Crump法 [32-33] 与Durbin法 [34] 等 . 针对本文所讨论的低渗非Darcy渗流问题,选用Stehfest数值反演法进行数值反演,计算步骤如下 .
1) 给定变换参数 α i ,按如下公式取值:
(32)
式中, k 为偶数,一般取20较好, t 为物理时间 .
2) 计算变换参数 V i ,按如下公式取值:
(33)
式中,[]为Gauss取整符号 .
3) 计算物理空间原函数,反演公式为
(34)
在上一小节中,得到了径向低渗透非Darcy渗流的拉氏解,那么通过上述反演变换计算可得到物理空间解 .
假设在无量纲时间 t D 时刻,扩展的无量纲动边界半径为 r D ,按照式(31)拉氏解通过Stehfest数值反演计算得到无量纲拟压力 p D ,如果所算值小于流体流动所需的无量纲启动拟压力 λ D ,减小 r D ;否则增大 r D ,直到解收敛到一定程度为止 . 具体步骤如图2所示 .

图2 计算流程图
Fig. 2 The flowchart for calculation
当计算的无量纲动边界半径 r D 扩大到与无量纲实际外边界半径 R D 相等时,则无量纲动边界半径不再扩大,直接令 r D = R D .
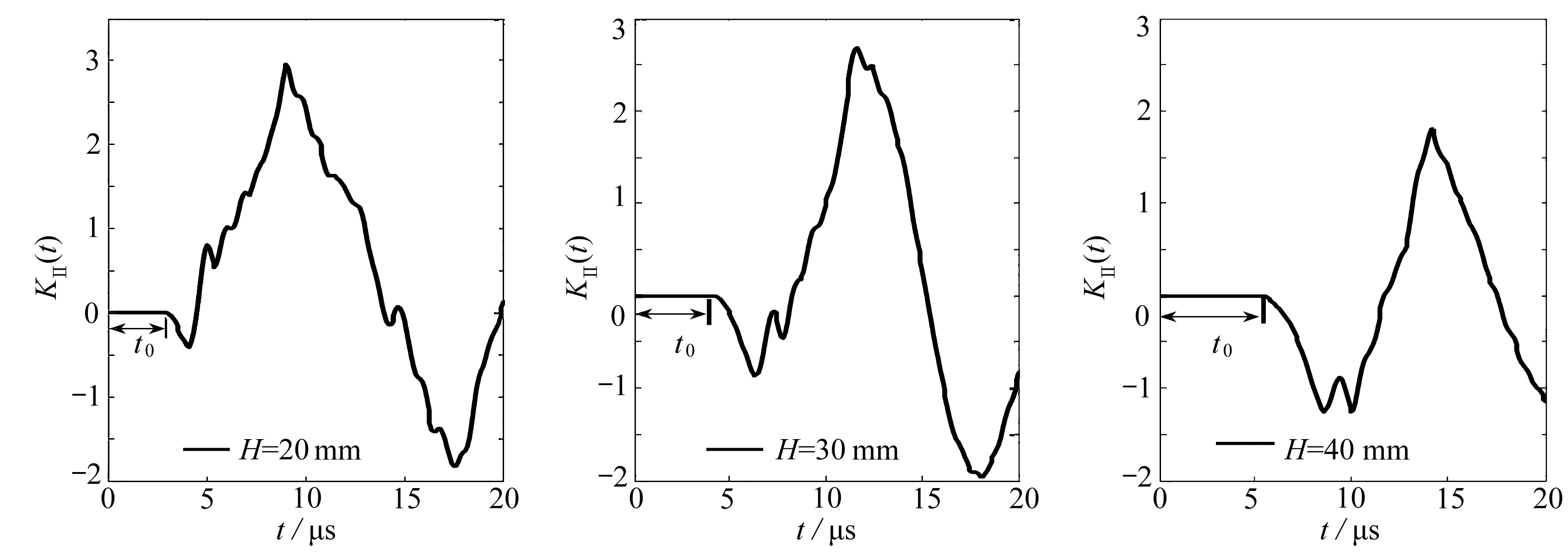
低渗非Darcy渗流问题最显著的特征就是存在动边界 . 由于启动压力梯度的存在,压力不能瞬时就传播到无限远处,而是随时间推移不断向外扩展 . 为了研究动边界 r D 相对于 λ D e - S 变化的特性,以无限大边界定流量生产情况为例 . C D e 2 S =1 000, λ D e - S 作为参数,以lg( t D / C D )为横坐标, r D 为纵坐标,用半对数坐标绘制图形,如图3所示,和姚军等 [26] 用数值计算出的图形趋势一样,证明了其正确性 . 启动压力梯度增大,动边界扩展的速度变慢,压力波动的传播速度也就越慢,且无量纲时间越长,启动压力梯度对动边界的影响也将越大 .
为了研究启动压力梯度对压力传播的影响,以无限大边界定流量生产情况为例给出压力径向分布图 . C D e 2 S =1 000, λ D e - S 作为参数,以 r D 为横坐标, p D 为纵坐标绘制图形,如图4所示 .
由图4可以看出,启动压力梯度越大,离井越远处压力分布越平缓,压力梯度越小,可推测远处流动并未发生 . 这与Darcy渗流对应的压力分布完全不同,Darcy渗流模型的压力降是瞬间传播到无穷远处,存在启动压力梯度的低渗非Darcy渗流模型的压力降是随时间不断扩展的,动边界外的地层压力降为零,压力分布曲线呈现紧支性 .
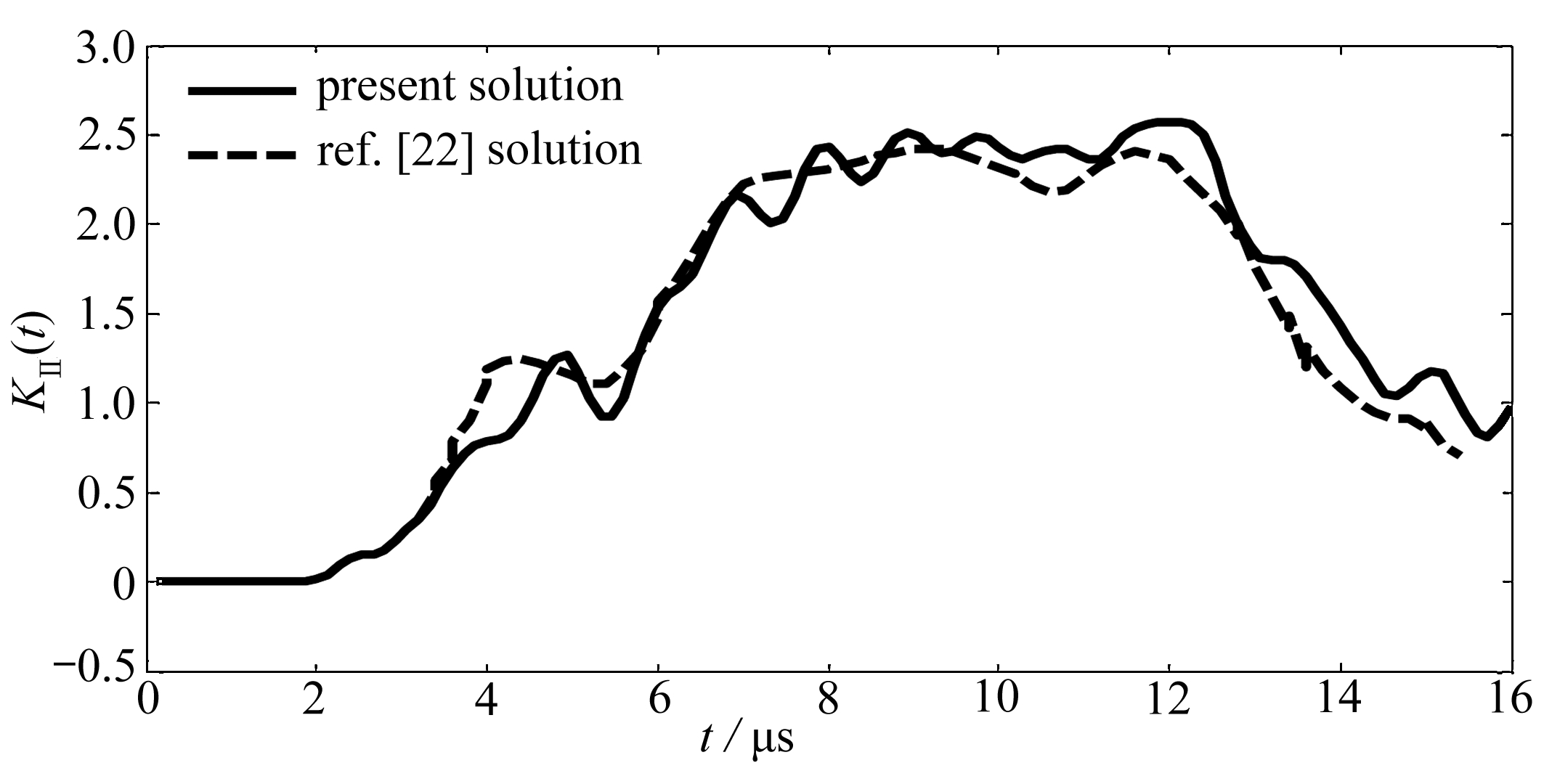
图3 无量纲动边界距离对比图图4 不同λ D e -S 条件压力分布
Fig. 3 Comparison of different TPGs to the dimensionless
Fig. 4 Comparison of different λ D e -S to moving boundary the pressure distribution
以圆形封闭外边界为例,研究了井底压力典型曲线的特性,即无量纲的井底压力 p D 和压力导数d p D /dln( t D / C D )相对于 t D / C D 的变化特性 . 以lg( t D / C D )为横坐标,lg p D ,lg( t D / C D ×d p D /d( t D / C D ))为纵坐标,以 C D e 2 S =1 000, λ D e - S 为参数,用双对数坐标绘制Gringarten-Bourdet图版 . 图5中上部分曲线代表无量纲压力,下部分曲线代表无量纲压力导数 .
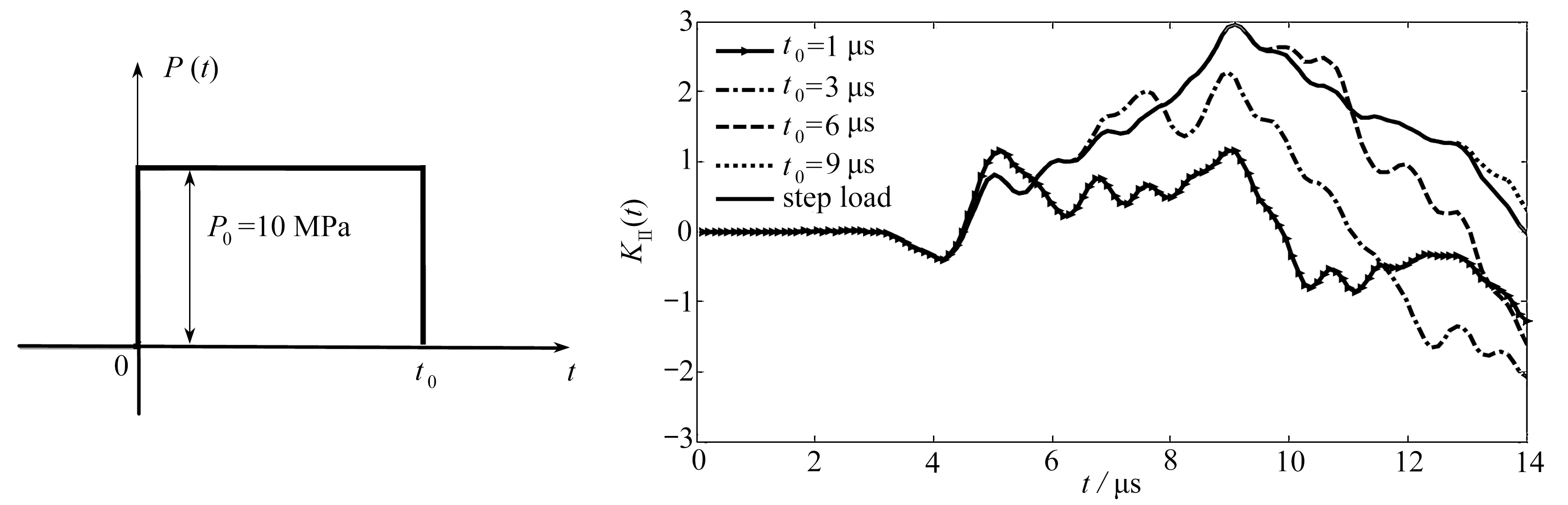
图5 不同λ D e -S 条件井底压力和压力导数
Fig. 5 Comparison of different λ D e -S to the bottom hole pressure and pressure derivative
从图5可以看出随着 λ D e - S 的增加,压力曲线增长变快,压力导数曲线的下降趋势减缓;在后期阶段,压力导数曲线的上翘段提前出现,此时的上翘不是边界影响,而是启动压力梯度较高使流体渗流性质发生了改变 .
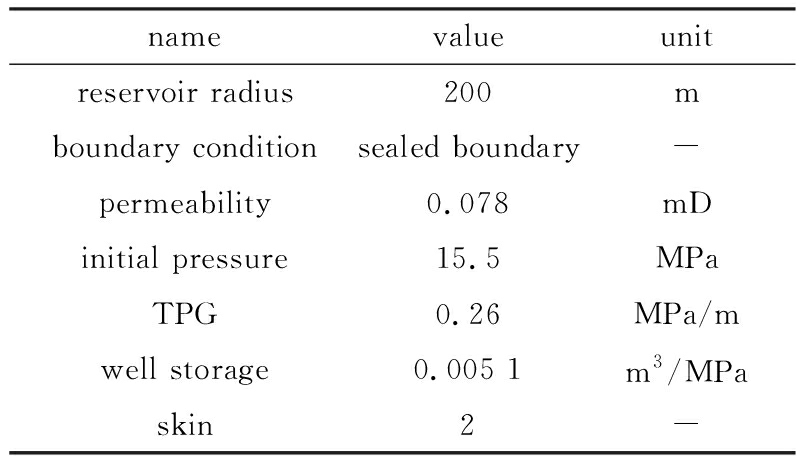
海拉尔油田是典型的低渗透储层, 黏度比较小范围为1.0~6.0 mPa·s, 取决于原油组成、 溶解气含量和油藏温度; 孔隙率的范围为10%~15%;该地层厚度范围为6~20 m;渗透范围为0.001~1.5 mD(1 mD=9.87×10 -16 m 2 );储层压缩系数为0.000 588 5 MPa -1 . 测试分为两个阶段:生产120天平均每天0.98 m 3 ,随后关闭15天 . 输入参数列于表1中,匹配参数列于表2 . 图6(a)给出了拟合的压力历史 . 图6(b)给出了压力和压力导数的双对数拟合曲线 . 结果表明解(31)考虑启动压力梯度和动边界效应可以较好地描述低渗透油藏的流动行为 .
(a) 压力历史拟合图 (b) 双对数曲线拟合图
(a) Pressure historical fitted data (b) Log-log curve fitting data
图6 压力历史拟合和双对数曲线拟合
Fig. 6 Pressure historical and log-log curve fitted data
表1 油藏输入参数表
Table 1 Reservoir input parameters
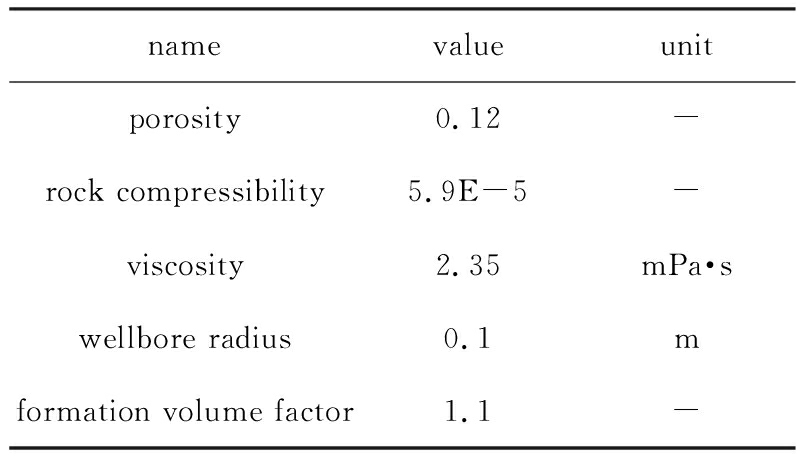
表2 油藏拟合参数表
Table 2 Reservoir fitting parameters
1) 考虑表皮效应和井筒,并引入有效井筒半径,建立了径向低渗非Darcy渗流动边界模型的控制方程、初始条件和各种边界条件,利用Laplace变换结合无穷级数法,对低渗非Darcy渗流动边界问题进行理论求解得到了半解析解,并结合实例验证了该解具有求解方法简洁、计算结果准确、表达简洁等优点 .
2) 给出了计算动边界扩展速度的公式与方法,动边界的扩展速度与无量纲启动压力梯度成反比,与动边界上无量纲压力关于径向距离的二次导数成正比 . 并计算了关键参数对动边界扩展产生的影响 . 计算结果表明,存在启动压力梯度的低渗非Darcy渗流中,压力扰动不能瞬时传递到无限远处,而是随时间逐渐向外扩展,并且对井底压力曲线产生影响 .
3) 给出了低渗非Darcy渗流存在启动压力梯度、井储和表皮效应的不稳定试井分析方法,计算并分析了无量纲启动压力梯度和表皮效应对Gringarten-Bourdet理论图版的影响,结合实例分析可以看出在低渗透油藏压力分析中,必须考虑启动压力梯度所产生的动边界的影响,才能得到较为正确的结果 .
参考文献 ( References ):
[1] 黄延章. 低渗透油层非线性渗流特征[J]. 特种油气藏, 1997, 4 (1): 9-14.(HUANG Yanzhang. Nonlinear percolation feature in low permeability reservoir[J]. Special Oil and Gas Reservoirs , 1997, 4 (1): 9-14.(in Chinese))
[2] PRADA A, CIVAN F. Modification of Darcy’s law for the threshold pressure gradient[J]. Journal of Petroleum Science and Engineering , 1999, 22 (4): 237-240.
[3] CAI J C. A fractal approach to low velocity non-Darcy flow in a low permeability porous medium[J]. Chinese Physics B , 2014, 23 (4): 385-389.
[4] ZHU W, SONG H, HUANG X, et al. Pressure characteristics and effective deployment in a water-bearing tight gas reservoir with low-velocity non-Darcy flow[J]. Energy & Fuels , 2011, 25 (3): 1111-1117.
[5] 姚同玉, 黄延章, 李继山. 孔隙介质中稠油流体非线性渗流方程[J]. 力学学报, 2012, 44 (1): 106-110.(YAO Tongyu, HUANG Yanzhang, LI Jishan. Nonlinear flow equations for heavy oil in porous media[J]. Chinese Journal of Theoretical and Applied Mechanics , 2012, 44 (1): 106-110.(in Chinese))
[6] 孔详言. 高等渗流力学[M]. 合肥: 中国科学技术大学出版社, 2010.(KONG Xiangyan. Advanced Mechanics of Fluids in Porous Media [M]. Hefei: China University of Science and Technology Press, 2010.(in Chinese))
[7] PASCAL H. Non steady flow through porous media in the presence of a threshold gradient[J]. Acta Mechanica , 1981, 39 (3/4): 207-224.
[8] WU Y S, PRUESS K, WITHERSPOON P A. Flow and displacement of Binghamnon-Newtonian fluids in porous media[J]. SPE Reservoir Engineering , 1993, 7 (3): 369-376.
[9] 祝春生, 程林松, 张淑娟. 低渗透油藏不稳定渗流的近似解法[J]. 西南石油大学学报(自然科学版), 2008, 30 (4): 69-72.(ZHU Chunsheng, CHEN Linsong, ZHANG Shujuan. Approximate solution for non-steady flow in low-permeability reservoir[J]. Journal of Southwest Petroleum University ( Science & Technology Edition ), 2008, 30 (4): 69-72.(in Chinese))
[10] 程时清, 张盛宗, 黄延章, 等. 低速非达西渗流动边界问题的积分解[J]. 力学与实践, 2002, 24 (3): 15-17.(CHEN Shiqing, ZHUANG Shenzong, HUANG Yanzhang, et al. An integal solution of free-boundary problem of non-Darcy flow behavior[J]. Mechanics in Engineering , 2002, 24 (3): 15-17.(in Chinese))
[11] SHAWKET G, JING L. Pressure behavior of vertical wells in low permeability reservoirs with threshold pressure gradient[J]. Special Topics and Reviews in Porous Media : An International Journal , 2011, 2 (3): 157-169.
[12] JING L. Pressure behavior of uniform-flux hydraulically fractured wells in low-permeability reservoirs with threshold pressure gradient[J]. Special Topics and Reviews in Porous Media : An International Journal , 2012, 3 (4): 307-320.
[13] GUO Y C, ZENG Q H, WANG Z X. Numerical simulation of low permeability flow with moving-boundary using meshless methods[J]. Engineering Mechanics , 2006, 23 (11): 188-192.
[14] 李凡华, 刘慈群. 含启动压力梯度的不定常渗流的压力动态分析[J]. 油气井测试, 1997, 6 (1): 1-4.(LI Fanhua, LIU Ciqun. Pressure transient analysis for unsteady porous flow with start-up pressure derivative[J]. Well Testing , 1997, 6 (1): 1-4.(in Chinese))
[15] SONG F Q, LIU C Q, LI F H. Transient pressure of percolation through one dimension porous media with threshold pressure gradient[J]. Applied Mathematics and Mechanics , 1999, 20 (1): 27-35.
[16] LIU W C, YAO J, CHEN Z X. Analytical solution of a double moving boundary problem for nonlinear flows in one-dimensional semi-infinite long porous media with low permeability[J]. Acta Mechanica Sinica , 2014, 30 (1): 50-58.
[17] 冯文光, 葛家理. 单一介质、双重介质非达西低速渗流的压力曲线动态特征[J]. 石油勘探与开发, 1986, 13 (5): 56-61.(FENG Wenguang, GE Jiali. The performance of the pressure curves with the non-Darcy low speed fluids flowing in the single and double porous media[J]. Petroleum Exploration and Development , 1986, 13 (5): 56-61.(in Chinese))
[18] 冯文光. 天然气非达西低速不稳定渗流[J]. 天然气工业, 1986, 6 (3): 41-48.(FENG Wenguang. Non-Darcy low-velocity unsteady-state seepage flow of natural gas[J]. Natural Gas Industry , 1986, 6 (3): 41-48.(in Chinese))
[19] 程时清, 李功权, 卢涛, 等. 双重介质油气藏低速非达西渗流试井有效井径数学模型及典型曲线[J]. 天然气工业, 1997, 17 (2): 35-37.(CHEN Shiqing, LI Gongquan, LU Tao, et al. Mathematical model and typical curve for calculating effective hole diameter in the low velocity non-Darcy flow testing of dual-media reservoirs[J]. Natural Gas Industry , 1997, 17 (2): 35-37.(in Chinese))
[20] 程林松, 任胜利, 廉培庆. 动边界双重介质油藏低速非达西渗流试井模型[J]. 计算力学学报,2011, 28 (6): 879-883.(CHENG Linsong, REN Shengli, LIAN Peiqing. Well test analysis on low velocity and non-Darcy flow in dual-porosity reservoir with dynamic boundary[J]. Chinese Journal of Computational Mechanics , 2011, 28 (6): 879-883.(in Chinese))
[21] 冯曦, 钟孚勋. 低渗透致密储层气井试井模型研究[J]. 天然气工业, 1998, 18 (1): 56-59.(FENG Xi, ZHONG Fuxun. Well test model study of the gas wells tight reservoir with low permeability[J]. Natural Gas Industry , 1998, 18 (1): 56-59.(in Chinese))
[22] 刘启国, 杨旭明, 魏红梅, 等. 动边界影响的低渗双重介质油气藏试井解释模型[J]. 西南石油学院学报, 2004, 26 (5): 30-33.(LIU Qiguo, YANG Xuming, WEI Hongmei, et al. Study of well-test model of low permeability dual-pore media with flowing boundary in oil and gas[J]. Journal of Southwest Petroleum Institute , 2004, 26 (5): 30-33.(in Chinese))
[23] LIU W C, YAO J, WANG Y Y. Exact analytical solutions of moving boundary problems of one-dimensional flow in semi-infinite long porous media with threshold pressure gradient[J]. International Journal of Heat and Mass Transfer , 2012, 55 (21/22): 6017-6022.
[24] 郭永存, 曾清红, 王仲勋. 动边界低渗透油藏的无网格方法数值模拟[J]. 工程力学, 2006, 23 (11): 188-192.(GUO Yongcun, ZENG Qinghong, WANG Zhongxun. Numerical simulation of low permeability flow with moving-boundary using meshless methods[J]. Engineering Mechanics , 2006, 23 (11): 188-192.(in Chinese))
[25] 侯英敏, 同登科. 动边界低渗透双重介质分形油藏中非牛顿幂律流体非稳态渗流[J]. 工程力学, 2009, 26 (8): 245-250.(HOU Yingming, TONG Dengke. Non steady flow of non-Newtonian power-law fluids of low permeability with moving-boundary in double porous media and fractal reservoir[J]. Engineering Mechanics , 2009, 26 (8): 245-250.(in Chinese))
[26] 姚军, 刘文超. 低渗透油藏非达西渗流动边界模型求解新方法[J]. 力学季刊, 2012, 33 (4): 597-601.(YAO Jun, LIU Wenchao. New method for solution of the model of non-Darcy seepage flow in low-permeability reservoir with moving boundary[J]. Chinese Quarterly of Mechanics , 2012, 33 (4): 597-601.(in Chinese))
[27] 冯曦, 钟孚勋. 低速非达西渗流试井模型的一种新的求解方法[J]. 油气井测试, 1997, 6 (3): 16-21.(FENG Xi, ZHONG Fuxun. A new solution for the well testing model of low velocity non-Darcy percolation[J]. Well Testing , 1997, 6 (3): 16-21.(in Chinese))
[28] 李顺初, 任丽, 郑鹏社, 等. 基于应力敏感的天然裂缝性页岩气藏双孔模型解的结构[J]. 应用数学和力学, 2017, 38 (2): 233-242.(LI Shunchu, REN Li, ZHENG Pengshe, et al. Similar structure of the solution to the dual-porosity model for naturally fractured shale gas reservoirs based on stress sensitivity[J]. Applied Mathematics and Mechanics , 2017, 38 (2): 233-242.(in Chinese))
[29] STEHFEST H. Numerical inversion of Laplace transforms[J]. Communications of the ACM , 1970, 13 (1): 47-49.
[30] JACQUOT R G, STEADMAN J W, RHODINE C N. The Gaver-Stehfest algorithm for approximate inversion of Laplace transforms[J]. IEEE Circuits & Systems Magazine , 1983, 5 (1): 4-8.
[31] CRUMP K S. Numericalinversion of Laplace transforms using a Fourier series approximation[J]. Journal of the ACM , 1976, 23 (1): 89-96.
[32] VALK  P P, VAJDA S. Inversion of noise-free Laplace transforms: towards a standardized set of test problems[J]. Inverse Problems in Engineering , 2002, 10 (5): 467-483.
P P, VAJDA S. Inversion of noise-free Laplace transforms: towards a standardized set of test problems[J]. Inverse Problems in Engineering , 2002, 10 (5): 467-483.
[33] BRANCIK L. Erroranalysis at numerical inversion of multidimensional Laplace transforms based on complex Fourier series approximation[J]. IEICE Transactions on Fundamentals of Electronics Communications & Computer Sciences , 2011, 94A (3): 999-1001.
[34] HONIG G, HIRDES U. A method for the numerical inversion of Laplace transforms[J]. Journal of Computational & Applied Mathematics , 1984, 10 (1): 113-132.
HOU Shaoji 1,2 , ZHU Weiping 3 , LIU Yuewu 1,2 ,ZHEN Huaibin 3 , GAO Dapeng 1,2 , LI Qi 1
(1. Institute of Mechanics , Chinese Academy of Sciences , Beijing 100190, P . R . China ; 2. University of Chinese Academy of Sciences , Beijing 100049, P . R . China ; 3. State Engineering Research Center , CUCBM Co . Ltd ., Beijing 100095, P . R . China )
Abstract: The threshold pressure gradient (TPG) generally exists in the seepage process of low permeability reservoir. In view of characteristics of low permeability seepage, the mathematical model for the moving boundary of non-Darcy flow was established, and the formula for calculating the moving speed of the boundary was given. The Laplace transform and the infinite series method were used to obtain the model’s general solution, and the Stehfest numerical inversion was conducted. The characteristics of moving boundary problems, the boundary change and propagation were discussed and explained in detail, and the phenomenon of TPG extending outward was explicated. The TPG effects on the bottom pressure and the pressure derivative were calculated, and the Gringarten-Bourdet charts under different conditions were given. The results show that, the low pressure percolation model is significantly different from the Darcy seepage model. For low permeability cases, the pressure drop expands with time and the pressure distribution curve is of compact support. The study on the low permeability problem with moving boundary, considering the influence of the TPG and the moving boundary, provides a theoretical basis for the seepage mechanism and production performance, interpretation and numerical simulation of low permeability oil reservoirs.
Key words: low permeability reservoir; threshold pressure gradient; moving boundary; semi-analytical model; numerical inversion
Foundation item: The National Science and Technology Major Project of China(2011ZX05038-003)
作者简介: 侯绍继(1992—),男,硕士(E-mail: houshaoji@imech.ac.cn);刘曰武(1965—),男,研究员,博士(通讯作者. E-mail: liuyuewulxs@126.com).
基金项目: 国家科技重大专项(2011ZX05038-003)
修订日期: 2018-04-19
∗ 收稿日期: 2017-12-19;
ⓒ 应用数学和力学编委会,ISSN 1000-0887
文章编号 : 1000-0887(2018)10-1115-13
DOI: 10.21656/1000-0887.380330
文献标志码: A
中图分类号 : TE312
引用本文 / Cite this paper: 侯绍继, 朱卫平, 刘曰武, 甄怀宾, 高大鹏, 李奇. 径向低渗非Darcy渗流动边界半解析模型[J]. 应用数学和力学, 2018, 39 (10): 1115-1127.HOU Shaoji, ZHU Weiping, LIU Yuewu, ZHEN Huaibin, GAO Dapeng, LI Qi. A semi-analytical model for moving boundary of radial non-Darcy flow in low permeability reservoir[J]. Applied Mathematics and Mechanics , 2018, 39 (10): 1115-1127.