毋晓妮 1 , 胡 存 2 , 李 晔 1
(1. 上海交通大学 船舶海洋与建筑工程学院, 上海 200240;2. 中国科学院 力学研究所, 北京 100190)
摘要 : 拖曳锚是海洋工程中一种常见的系泊基础,因造价低廉和高承载特性而得到广泛应用 . 其在海床中的安装轨迹和运动特性受到锚与土体之间复杂相互作用的影响,使得精确定位仍存在挑战 . 目前已有的塑性屈服面方法被广泛用于计算拖曳锚的运动特性,即假设整个拖曳过程为深埋板在不同深度的破坏过程 . 实际上,拖曳锚的安装是从浅埋到深埋的连续贯入,因此该方法不能考虑浅埋破坏对拖曳锚运动特性的影响,从而可能导致预测的轨迹不准确 . 通过有限元分析研究了锚板方位角及埋深比对单向承载和复合荷载下屈服面的影响,确定了锚板浅埋破坏时的屈服面,补充了塑性屈服面法对浅埋破坏效应的考虑;进一步地,考察了锚板方位角、承载系数、浅埋区域大小对拖曳锚轨迹预测和运动特性的影响,并与传统仅假设深埋破坏情况对比分析 . 结果表明:浅埋破坏时锚板方位角与浅埋区域大小决定了锚板的运动特性和轨迹;合理考虑浅埋破坏后,与纯假设深埋破坏情况比,锚板在达到稳定状态之前的预测埋深和锚链力要小,但极限嵌入深度一致 .
关 键 词 : 拖曳锚; 浅埋破坏; 塑性屈服面; 运动轨迹
作为深水系泊系统的重要组成部分,目前的系泊基础主要有重力锚、拖曳锚、吸力式板锚以及动力贯入锚(如OMNI-Max)等 . 拖曳锚因其高承载力特性和构造简单等特点而被广泛应用 . 传统的拖曳锚(DEA)多用于悬链线系泊 . 随着深水中对法向承载的需求和合成纤维系缆的应用,新型拖曳锚即法向承力锚(VLA)被广泛应用于深水浮式结构物的绷紧系泊系统中 [1] . DEA 与VLA有着相同的安装过程,即需拖船将其拖曳至目标深度 . 然而,无论是传统或者新型拖曳锚,其运动轨迹和锚链形态在拖曳中均不可见;并且,锚的贯入位置和方位角决定了锚的最终承载力 . 因此,对拖曳锚的运动轨迹的预测和运动特性的分析,对锚设计选择和现场安装有重要的意义 .
目前,国内外对拖曳锚轨迹的预测方法主要有基于设计表的经验法(Vryhof Anchors [2] 和Bruce Anchors [3] )、极限平衡法 [4-7] 、塑性极限法 [8-9] 、塑性屈服面法 [10-13] 、有限元大变形方法 [14-15] 以及实验测定法 [13,16-17] .
设计表法主要是采用拖曳锚供应商Vryhof Anchors和Bruce Anchors等所提供的设计表来确定锚的位置和拖曳距离,但其只适用于特定现场土体条件,并不能给出锚的实际运动轨迹 .
极限平衡法 [4-7] 和塑性极限法 [8-9] 的预测过程近似,均是将锚链和锚一起作为整体来分析其与土体的相互作用 . 结合锚链形态方程 [5,18-19] 通过对拖曳锚各部分土阻力进行求解,以保证在每一个运动状态其整体受力平衡,然后通过小位移增量步来实现锚的运动贯入过程 . 但该方法中计算土阻力需要的相关形状系数和角度参数,仍需要通过离心实验或现场试验来确定 . 塑性极限法不同于极限平衡法,其采用塑性上限法来计算土阻力 .
随着大变形有限元技术的发展, 耦合的Euler-Lagrange(CEL)法被用于拖曳锚安装过程分析 [14-15] ,但其模拟效率和可靠性仍需要进一步研究 . 现场试验和实验室试验对拖曳锚设计和使用有很好的指导意义, 考虑到其经济性和广泛使用性, 仍需要对数值和解析方法进行研究和发展 .
塑性屈服面法由Bransby 和 O’Neill [10] 提出并用于拖曳锚的运动特性分析 . 通过有限元计算得到锚在复合荷载下的承载特性并以屈服面表示,采用相关联流动法则,结合锚链力方程来进行拖曳锚轨迹和运动特性分析 [11-13] . 目前该方法亦逐渐被用于吸力式板锚(SEPLA)以及OMNI-Max锚的转动轨迹预测 [20-23] . 塑性屈服面方法相比其他方法使用更为简单,但因其采用的屈服面均基于深埋板的破坏模式,无法考虑锚板浅埋破坏对其运动特性的影响,可能会导致预测轨迹不合理 .
本文为了考虑浅埋破坏对拖曳锚运动特性的影响,将通过开展有限元分析研究锚板方位角及埋深对单向加载和复合加载下屈服面的影响,以期确定浅埋破坏时的屈服面;考察锚板方位角、埋深比、浅埋区域、锚链承载系数等对预测轨迹的影响 . 进一步地,由于塑性极限法亦逐渐用于其他新型锚(SEPLA 和OMNI-Max)的安装和承载特性分析,其中浅埋破坏效应仍然无法考虑 . 本文的研究内容对塑性极限分析法在其他锚中的应用也是一种补充 .
塑性屈服面最早被用于分析浅基础在复合荷载下的承载响应 [24-27] . 通过有限元或者塑性极限分析法,对基础施加不同的位移组合直至破坏以得到该基础在破坏时的复合荷载 . 因基础破坏时受到的复合荷载为在竖向(竖向荷载 V )、横向(横向荷载 H )和转动方向(转动矩 M )对应荷载下的多种荷载组合,因此称所得到的多种荷载组合形成的包络面为VHM屈服面 . 下式为Bransby和 O’Neill [10] 建议的VHM屈服面方程:
(1)
式中, V max , H max 和 M max 为锚板在单向荷载下的最大承载力,表征屈服面的大小; V , H 和 M 为锚板受到的复合荷载; m , n , p 和 q 为表征屈服面形状的参数,通过多组荷载组合进行最小二乘拟合后得到 .
采用相关联流动法则,屈服面的梯度决定了锚板周围土体破坏时的塑性位移比 . 如图1屈服面截面VH空间内的屈服线所示,在锚板的VH 屈服线上,其周围土的塑性应变增量的方向与屈服面外法线方向一致,对应竖向和水平向的位移比值( δ v / δ h )可以通过对应的屈服面梯度比值得到 . 其中 V max 和 H max 为最大承载力, B 为锚板长度 .
通过采用深埋破坏模式下的水平板锚的屈服面,Bransby和O’Neill [10-11] 给出了塑性屈服面法预测拖曳锚轨迹的步骤:
1) 假设锚板的初始位置,即锚板方位角 β 和系缆点的埋深 d c ,如图2所示 .
2) 计算锚胫上的法向力 F 1 和切向力 F 2 .
3) 假设系缆点的锚链力 T c .
4) 由锚链力方程 [5] 计算锚链角 θ c ,如式(2) .
5) 由锚整体受力平衡,计算 V , H 和 M .
6) 判断 V , H 和 M 是否满足屈服面方程 f =0;若是,则继续第7)步;若否,则重复步骤3)~6)直至满足 .
7) 使用屈服面确定在该荷载下对应的位移增量 δ v (竖向位移增量)、 δ h (横向位移增量)及 δ β (转角增量)之间的位移比,并对某方向假设一个小的位移增量值,进而求解其他位移增量值 .
8) 根据各方向的位移值调整锚板以及锚的位置,重复步骤1)~8) .
(2)
式中, θ c 为系缆点的锚链角; T c 为系缆点的锚链力; b c 为锚链有效宽度; N c 为承载力系数,一般取9; d a 为系缆点深度; S u0 为土面的不排水抗剪强度; S ug 为不排水抗剪强度梯度 .

图1 VH空间屈服线及对应塑性位移
Fig. 1 The yield locus in the VH space and the plastic displacement

图2 拖曳锚运动特性分析受力系统
Fig. 2 The force system of drag anchor kinematic analysis
如前所述,拖曳锚的贯入过程是将锚从浅埋拖曳至深埋的过程 . 而上述广泛内容被采用的传统塑性屈服面法将整个贯入过程,均看作是深埋板在不同深度的破坏过程 . 为了弥补该方法的不足,下文将通过有限元数值模拟,获得锚板在单向和复合荷载下的屈服面,考察锚板埋深和方位角对屈服面的影响,以期获得屈服面在浅埋破坏和深埋破坏的区别 . 而后,将基于锚板在不同荷载情况下的承载特性,针对深埋和浅埋板,采用相应的屈服面分析拖曳锚的运动特性,如锚链力和锚贯入深度以及拖曳距离 .
本部分使用有限元软件ABAQUS进行建模计算,开展预埋锚板位移控制的小应变分析,获得锚板在单向荷载和复合载荷下的承载屈服面 .
(a) 水平锚板 (b) 倾斜锚板
(a) The horizontal fluke (b) The inclined fluke
图3 水平锚板和倾斜锚板示意图
Fig. 3 Schematic of the horizontal and the inclined anchor flukes
图4 有限元模型
Fig. 4 The finite element model
拖曳锚锚板简化为长厚比 B / t (长度为 B ,厚度为 t )为7的板 [10-12] . 水平锚板( β =0°)和倾斜锚板( β ≠0°)如图3所示 . β 为锚板方位角, V , H 和 M 为锚板上所受载荷 . 锚板采用刚体模拟,为6节点平面应变三角形单元 . 本分析针对拖曳锚在饱和粘土中的安装过程,土体采用均质弹塑性Tresca材料,亦为6节点平面应变三角形单元 . 土体的弹性模量 E 和抗剪强度 S u 比值( E / S u )取值为10 000 . 研究证明 [28-29] , 该值的大小只影响达到破坏所需的位移值而不影响极限承载力 . 为了保证锚土之间的摩擦得到充分发挥, 上覆土压力值与抗剪强度 S u 的比值为10 . 土体的Poisson(泊松)比为0.495 . 本文所采用数值模型同Wu等 [30] 所采用的数值模型,其合理性已得到验证 .
锚与土之间接触面采用接触对,法向硬接触,切向为Coulomb(库伦)摩擦,接触面允许最大应力为1倍的 S u (完全粗糙) . 图4所示为埋深比 H D / B 为10的水平锚板有限元模型,其中 H D 为埋深 .
针对3组锚板单向承载分析中(仅有 V 或 H 或 M ),分别对6个锚板方位角 β 和6个不同埋深比 H D / B (涵盖深埋和浅埋)进行单向承载力考察,算例情况详见表1 .
针对4组锚板复合荷载下的分析中(不同埋深比和方位角),分别采用了75个算例予以拟合,详见表2~4 . 其中,表3中 d v , d h 及 d m 分别为屈服面分析中所采用的竖向位移,横向位移及转角 .
采用式(3)定义锚板的单向承载力系数:
(3)
式中, Q c v 和 Q c h 分别为在 V 和 H 下锚板破坏时的阻力, Q c m 为在 M 下锚板的破坏弯矩, A 为锚板面积(平面应变分析中等于锚长 B ) .
同样地,针对复合荷载情况,锚板的最大承载力通过无量纲形式承载力系数呈现,表示为 V max /( AS u ), H max /( AS u )和 M max /( ABS u ),而不同荷载组合对应的承载力以无量纲形式的承载力系数表示为 V /( AS u ), H /( AS u )和 M /( ABS u ) .
表1 单向承载算例
Table 1 Summary of the study cases of anchor behavior under unidirectional loading

表2 复合承载算例
Table 2 Summary of the study cases of anchor behavior under combined loading

表3 屈服面算例
Table 3 Summary of study cases of yield envelope

图5所示为锚板在 V 和 H 荷载下的单向承载系数 N c v , N c h 与埋深比 H D / B 和锚板方位角 β 的关系 .
(a) 竖向承载系数 (b) 横向承载系数
(a) The vertical bearing capacity factor (b) The horizontal bearing capacity factor
图5 埋深比和锚板方位角对单向承载系数的影响
Fig. 5 Influences of the anchor embedment depth ratio and the angle of anchor fluke on the unidirectional bearing capacity
可以看出:对任意 β 的锚板, H D / B 对 N c v 的影响主要在 H D / B <3的区域,且 N c v 随着 H D / B 而增加;当 H D / B >3时, N c v 为一常数12.1,不受 H D / B 和 β 的影响 . 对同一埋深比( H D / B <3), N c v 随 β 的增加而减小 . 结合Merifield等 [31] 和Wang等 [29] 的锚板抗拔承载分析可知:当 N c v 达到稳定值时,锚板周围土体的破坏呈现为不受土面影响的局部深埋破坏;否则即为受土面影响的浅埋破坏 .
此外可见, H D / B 对 N c h 的影响主要表现在 H D / B <2的区域, N c h 随 H D / B 增加至恒定值 . 对不同的 β ,该恒定值差别很小,如水平板为4.65而对倾斜锚板为4.61 .
再者,对转动承载的分析发现, N c m 不受 H D / B 和 β 的影响,均为恒定值1.66 .
综上所述,单向受力时深埋板和浅埋板的破坏模式和承载系数因埋深和锚板方位角的影响会不同 . 又因为单轴承载系数作为复合加载屈服面(方程(1))的特征参数,表征了屈服面的大小,其进一步反映了考虑浅埋效应的必要性 .
(a) VH屈服线
(a) The yield locus in the VH space
已有的研究 [11-13,21,32] 表明,锚板方位角的改变主要在浅埋深比的时候发生,且变化角度是从初始角到最终的稳定角 . 以O’Neill等 [11] 所分析的Stevpris锚为例,锚板方位角在40°到24°变化 . Liu等 [33] 针对砂土中锚的拖曳试验也发现有类似现象,锚板的角度由初始嵌入角很快减小至一稳定值 . 前文中的单轴承载分析亦表明,锚板方位角 β 的影响主要位于埋深比 H D / B <3的区域 . 因此本文将对表2中4种工况进行分析 . 其中工况1~3考虑浅埋破坏效应,工况4为仅考虑深埋情况(传统塑性屈服面法) .
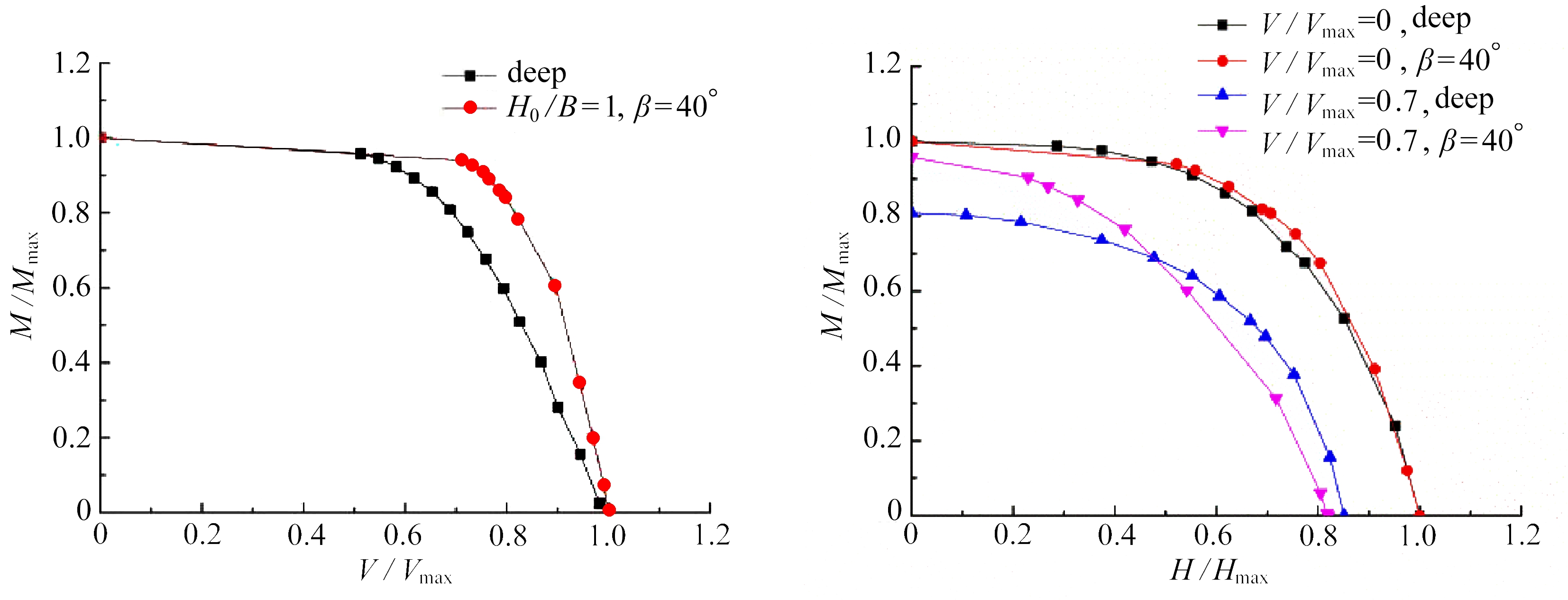
(b) VM屈服线 (c) HM屈服线
(b) The yield locus in the VM space (c) The yield locus in the HM space
图6 浅埋破坏和深埋破坏VH、VM和HM屈服线对比
Fig. 6 Comparison of the yield loci for shallow and deep anchor behaviors in the VH, VM and HM spaces
屈服面的求解方法同文献[12],即需获得VH( M =0)、VM( H =0) 和HM( V =0)空间的屈服线以及不同 V / V max (本文取值分别为0.3,0.5,0.7,0.8和0.9)对应的HM面 (见方程(1)) . 通过使用最小二乘法进行拟合屈服面的特征参数 m , n , p 和 q ,见表4 .
针对深埋时的屈服面,前文(3.1小节)发现,当埋深比 H D / B >3时, H D / B 和方位角 β 将不再影响单轴承载系数 . 因此,对于埋深比大于3的情况,可以采用任意埋深和任意方位角得到对应的屈服面 . 此处采用Wu等 [32] 针对埋深比为10,水平锚板求得的深埋屈服面 . 图6 所示为工况2( H D / B =1, β =40°)与工况4( H D / B =10, β =0°,对应图标为deep)在VH、VM和HM空间中的屈服线对比 . 由表4可见,浅埋破坏的屈服面不同于深埋情况,其不只表现在其大小特征参数 V max /( AS u ), H max /( AS u )和 M max /( ABS u )上, 同时也表现在其形状特征参数 m , n , p 和 q 上 .
表4 屈服面特征参数
Table 4 Summary of the yield envelope parameters

以上分析可知,与深埋不同,浅埋破坏的屈服面与锚板埋深和方位角均有关 . 采用塑性屈服面法预测拖曳锚贯入过程,最理想的方式即是在深埋区采用深埋屈服面,在浅埋区域采用能考虑锚板埋深和方位角连续变化的屈服面予以获得 . 这在理论上是可行的,但实际中则需要离散为一系列有限个屈服面予以计算 . 屈服面个数越多越趋于连续,同样工作量也增大 . 本部分旨在讨论浅埋效应的影响,因此在浅埋区仅采用1至2个屈服面,深埋区1个屈服面的方法予以预测,并与传统仅采用1个深埋屈服面的预侧结果进行对比 .
鉴于O’Neill等 [11] 使用深埋屈服面对Vryhof Anchors的Stevpris锚进行了轨迹预测,本文将采用同样的参数进行浅埋破坏的影响分析以便对比 . 拖曳锚和土体的参数如表5所示 .
表5 锚与土的特性参数
Table 5 Properties of the anchor and the soil

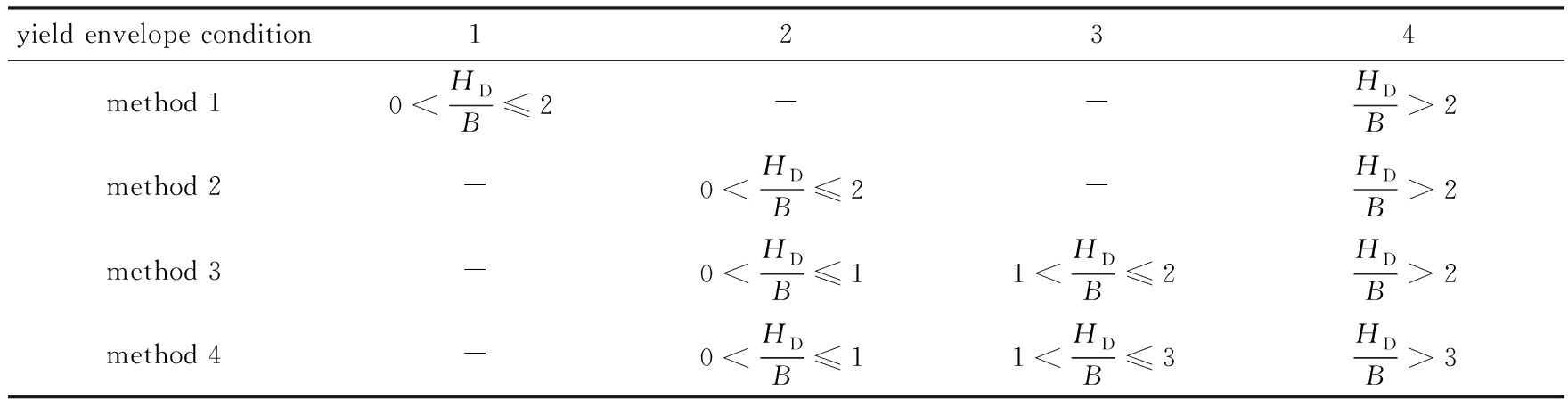
因为浅埋区屈服面受到方位角和埋深比的影响,本部分采用以下4种方法引入浅埋破坏屈服面,不同方法所使用的屈服面和控制区域总结如表6,其中“-”表示不使用对应工况得到的屈服面 .
表6 4种方法所用屈服面和控制区域
Table 6 Yield envelopes applied and the controlled embedment depth ratios of the 4 methods
(a) 锚板效率与拖曳距离关系
(a) Variation of the anchor efficiency with the drag length
方法1(method 1) 当0< H D / B ≤2时,采用工况1对应的屈服面计算受力;当 H D / B >2时,采用工况4的深埋屈服面 .
方法2(method 2) 当0< H D / B ≤2时,采用工况2对应的屈服面计算板锚受力;当 H D / B >2时,采用工况4的深埋屈服面 .
方法3(method 3) 当0< H D / B ≤1时,采用工况2对应的屈服面计算锚板受力;当1< H D / B ≤2时,采用工况3的屈服面;当 H D / B >2时,使用工况4的屈服面 .
方法4(method 4) 当0< H D / B ≤1时,采用工况2对应的屈服面计算锚板受力;当1< H D / B ≤3时,采用工况3的屈服面;当 H D / B >3时,使用工况4的屈服面 .
(b) 系缆点埋深与拖曳距离关系(c) 锚板中心点埋深与拖曳距离关系
(b) Variation of the shackle point depth (c) Variation of the fluke center depth with the drag length with the drag length
图7 考虑浅埋破坏的拖曳锚运动特性及对比
Fig. 7 Comparison the kinematic behavior of the drag anchor in view of the shallow anchor behavior
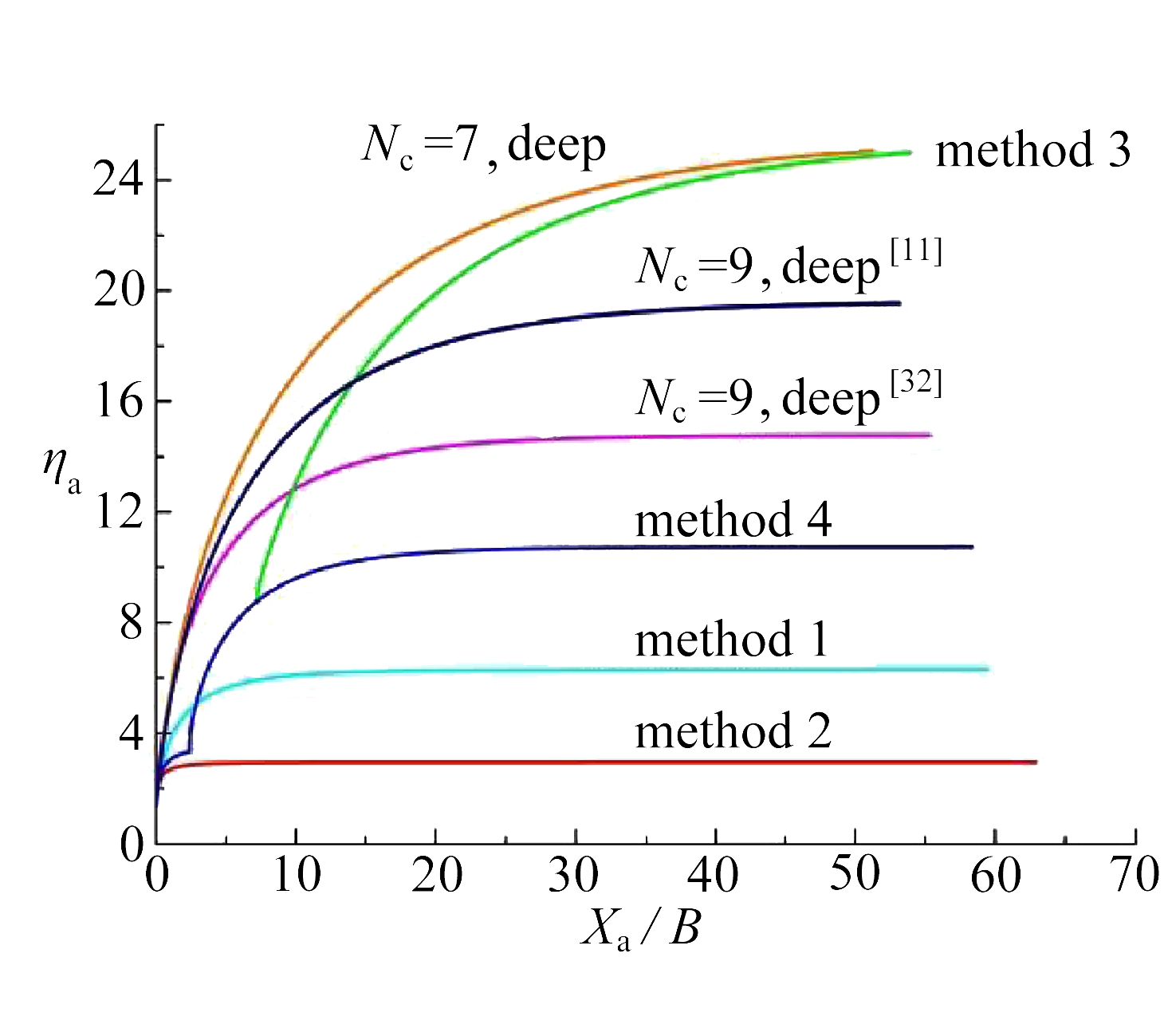
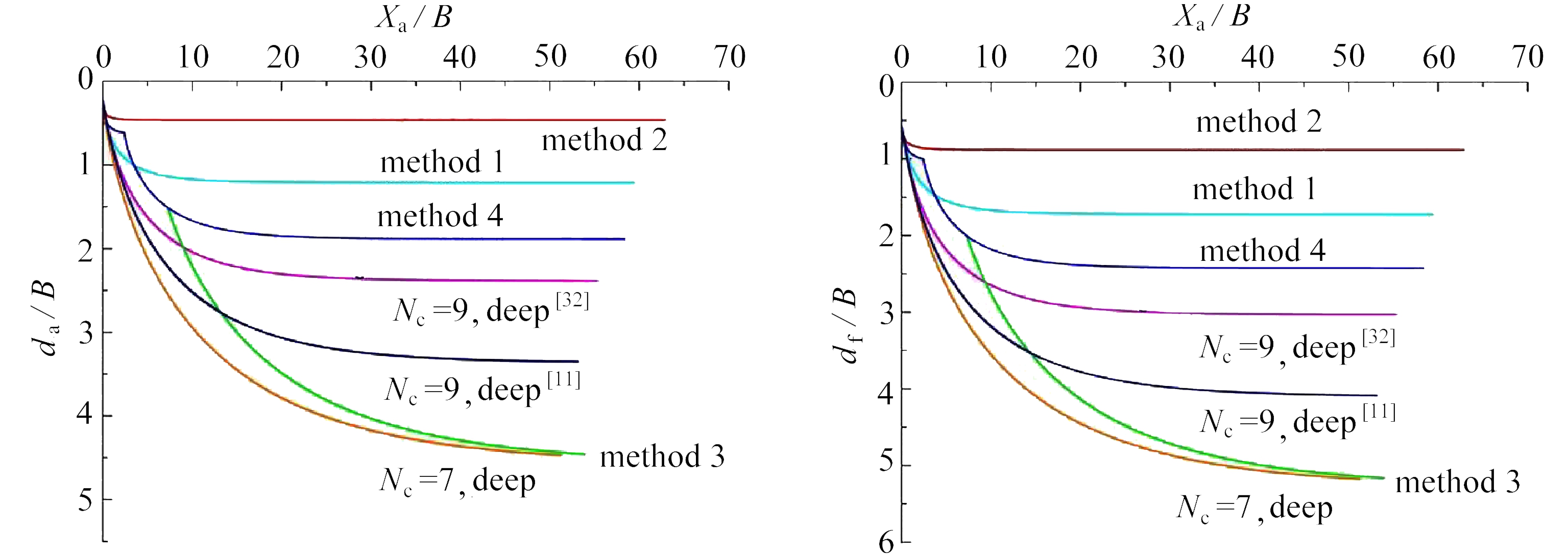
图7所示为使用4种不同引入浅埋破坏屈服面近似方法的预测结果与传统仅使用深埋破坏预测得到的结果(Wu等 [32] 和O’Neill 等 [11] )的对比 . 其中 η a 为拖曳锚效率,为锚链力 T a 与锚重的比值,反映了锚链力的变化 . X a 为锚板的拖曳距离,用系缆点的水平位移表示, d a 为系缆点的埋入深度, d f 为锚板中心点的埋入深度 . 埋深和拖曳距离均使用锚板长度 B 进行无量纲化 . 图7(a)为锚的承载效率与拖曳距离的关系,图7(b)为系缆点与拖曳距离的关系,图7(c)为锚板中心点与拖曳距离的关系, 其中deep用来标识使用仅考虑深埋破坏的屈服面预测法得到的相应变量结果 .
方法 1 和2仅采用1个浅埋屈服面予以控制整个浅埋区域 . 结果发现,使用这两种方法,锚板均未进入深埋破坏区域 . 对比方法1和2 ,可以发现采用不同方位角的浅埋屈服面,其预测的轨迹和极限嵌入深度相差甚大 . 方法1使用水平锚板的预测锚板埋深比 H D / B 为1.72,而采用锚板方位角40°的方法2预测得到的值约为0.88 . 这意味着浅埋板的轨迹预测中,方位角起到关键作用 . 仅使用水平锚板得到的屈服面会导致过大预测了埋深和锚链力 .
方法3的控制区域较方法1、2和4更为细化,即浅埋区采用了2个离散的屈服面 . 对比4种方法得到的结果,方法3得到的预测埋深比和锚链力均较其他方法大 . 其主要原因是只有方法3的锚板因为控制区域细化,锚板进入了深埋破坏控制区 . 尽管对方法1、2和4设置了使用深埋破坏屈服面的控制区域,但由于锚板在对应埋深比之前即达到稳定,因此未进入深埋比区域 . 通过这种对比,可以看出近似区域过于粗糙(浅埋区离散的屈服面个数少)会使得预测埋深和锚链力偏小(图7(b)和(c)) .
方法1~4的分析中,锚链承载系数为7 . 本分析同时给出了传统仅使用深埋破坏的结果( N c =7,deep) . 与Wu等 [32] 仅采用深埋破坏的预测结果对比,锚链承载系数 N c 从7增加到9,锚板的埋深比 d f / B 从5减小到3,相应的锚板承载效率 η a 从25减小到15(图7(b)和(c)) . 可见,锚链承载系数的增加会增加锚的贯入阻力,因此预测埋深和锚链力减小 .
对比方法 3 考虑浅埋破坏预测得到的结果与传统仅采用深埋破坏( N c =7,deep)的结果可以看出:浅埋破坏对运动特性的影响主要是在锚板达到稳定状态前(本例为拖曳距离50 B 处),预测埋深和锚链力均小于传统仅采用深埋破坏的预测结果 . 在0~50 B 拖曳距离区域内,考虑浅埋破坏和不考虑浅埋破坏得到的 η a , d f / B 及 d a / B 的差别先增加后减小 . 在2 B ~20 B 的拖曳距离内差别较大,最大的差值发生在拖曳距离7 B 附近,考虑浅埋破坏所得到的锚板埋深比 d f / B 比传统仅使用深埋破坏预测得到的结果小7%~43%, 而对应的系缆点的埋深比 d a / B 小8%~53%,比锚效率 η a 小7%~58% .
同时,由图7可以看出,在拖曳锚达到稳定的极限埋深前,考虑浅埋破坏的预测得到较小的埋深和锚链力 . 但是否考虑浅埋效应,对锚板的极限埋深和拖曳力并无影响 .
本文通过考察锚板埋深比和方位角对拖曳锚承载屈服面的影响,确定了浅埋屈服面,补充了传统塑性屈服面法对浅埋破坏考虑的不足;采用4种考虑浅埋破坏屈服面的方法对Stevpris锚进行了轨迹预测,分析了承载力系数、锚板方位角、浅埋破坏区域等对锚板运动特性的影响,并与传统仅考虑深埋破坏时的结果进行对比 . 主要结论如下:
1) 当埋深比小于3时,埋深比和方位角对屈服面的大小和形状均有影响;当埋深比大于3之后,屈服面将不再受其影响 .
2) 锚链力承载系数的增加会减小锚板的预测埋深;锚板方位角在预测浅埋轨迹时至关重要;与仅假设深埋破坏的传统塑性屈服面法预测结果比,考虑浅埋破坏时,在拖曳锚的嵌入达到稳定状态前,两者差别较大,预测埋深和拖曳力均较小 .
3) 当拖曳锚的嵌入趋于极限稳定状态时,是否考虑浅埋破坏对其极限嵌入深度和拖曳力并不影响 . 但工程中锚均难以达到极限状态,因而浅埋破坏的考虑对工程实际具有指导意义 .
4) 鉴于塑性屈服面方法亦逐渐用于对吸力板锚和OMNI-Max等的安装和承载特性分析,本文对拖曳锚贯入过程中浅埋破坏的考虑方法,对以上类型锚的分析起到一定参考作用 .
参考文献 ( References ):
[1] 岳艳召, 张炜, 刘海笑. 拖曳锚与安装缆绳相互作用力计算方法研究[J]. 岩土力学, 2013, 34 (11): 503-512.(YUE Yanzhao, ZHANG Wei, LIU Haixiao. Study of calculation for interactional force between drag anchor and installation cable[J]. Rock and Soil Mechanics , 2013, 34 (11): 503-512.(in Chinese))
[2] Vryhof Anchors. Anchor manual 2015: the guide to anchoring[Z]. Netherlands, 2015.
[3] Bruce Anchors. Brochure of Bruce FFTS MK 4[Z]. Douglas, England: Bruce Anchor Limited.
[4] STEWART W P. Drag embedment anchor performance prediction in soft soils[C]// Proceedings of the 24 th Annual Offshore Technology Conference . Houston, Texas, USA, 1992.
[5] NEUBECKER S R, RANDOLPH M F. The performance of drag anchor and chain systems in cohesive soil[J]. Marine Georesources and Geotechnology , 1996, 14 (2): 77-96.
[6] DAHLBERG R. Design procedures for deep water anchors in clay[C]// Proceedings of the 30 th Annual Offshore Technology Conference . Houston, Texas, USA, 1998.
[7] THORNE C P. Penetration and load capacity of marine drag anchors in softclay[J]. Journal of Geotechnical and Geoenvironmental Engineering , 1998, 124 (10): 945-953.
[8] KIM B M. Upper bound analysis for drag anchors in soft clay[D]. PhD Thesis. Texas: Texas A&M University, 2005.
[9] AUBENY C P, CHI C. Mechanics of drag embedment anchors in a soft seabed[J]. Journal of Geotechnical and Geoenvironmental Engineering , 2009, 136 (1): 57-68.
[10] BRANSBY M F, O’NEILL M P.Drag anchor fluke-soil interaction in clays[C]//PANDE G N, PIETRUSZCZAK S, SCHWEIGER H F, ed. Numerical Models in Geomechanics ( NUMOG VII ). Netherlands: CRC Press, 1999: 489-494.
[11] O’NEILL M P, BRANSBY M F, RANDLPH M F. Drag anchor fluke soil interaction in clays[J]. Canadian Geotechnical Journal , 2003, 40 (1): 78-94.
[12] ELKHATIB S,RANDOLPH M F. The effect of interface friction on the performance of drag-in plate anchors[C]// Proceedings of 1 st International Symposium on Frontiers in Offshore Geotechnics . Perth, Western Australia: Taylor & Francis, 2005.
[13] ELKHATIB S. The behaviour of drag-in plate anchors in soft cohesive soils[D]. PhD Thesis.Australia: University of Western Australia, 2006.
[14] ZHAO Y B, LIU H X. Numerical simulation of drag anchor installation by a large deformation finite element technique[C]// Proceedings of the ASEM 2014, 33 rd International Conference on Ocean , Offshore and Arctic Engineering . San Francisco, California, USA, 2014.
[15] 李培冬, 刘海笑, 赵燕兵. 拖曳锚在海床中运动特性的大变形有限元分析[J]. 海洋工程, 2016, 34 (2): 56-63.(LI Peidong, LIU Haiyan, ZHAO Yanbing. Large deformation finite element analysis on the kinematic behavior of drag anchors in the seabed[J]. Ocean Engineering , 2016, 34 (2): 56-63.(in Chinese))
[16] DUTTA A. A simple method of analyzing mooring chains with embedded anchor point[J]. Journal of Offshore Mechanics and Arctic Engineering , 1988, 110 (1): 71-73.
[17] 张炜, 刘海笑. 拖曳锚嵌入机理及运动特性实验研究[J]. 东南大学学报(自然科学版), 2010, 40 (3): 581-586.(ZHANG Wei, LIU Haixiao. Experimental research for embedment mechanism and kinematic characteristics of drag anchors[J]. Journal of Southeast University ( Natural Sciences ), 2010, 40 (3): 581-586.(in Chinese))
[18] GAULT J A, COX W R. Method for predicting geometry and load distribution in an anchor chain from a single point mooring buoy to a buried anchorage[C]// Proceeding of the 6 th Annual Offshore Technology Conference . Houston, Texas, USA, 1974.
[19] VIVATRAT V, VALENT P J, PONTERIO A A. The influence of chain friction on anchor pile design[C]// Proceedings of the 14 th Annual Offshore Technology Conference . Houston, Texas, USA, 1982.
[20] CASSIDY M J, GAUDIN C,RANDOLPH M F, et al. A plasticity model to assess the keying of plate anchors[J]. G é otechnique , 2012, 62 (9): 825-836.
[21] YANG M, MURFF J D, AUBENY C P. Undrained capacity of plate anchors under general loading[J]. Journal of Geotechnical and Geoenvironmental Engineering , 2010, 136 (10): 1383-1393.
[22] WEI Q, TIAN Y, CASSIDY M J,et al. Behaviour of OMNI-Max anchors under chain loading[C]// Proceedings of the 3 rd International Symposium Frontiers in Offshore Geotechnics ( ISFOG ). London, UK, 2015: 925-930.
[23] LIU J, LU L H, HU Y X. Keying behavior of gravity installed plate anchor in clay[J]. Ocean Engineering , 2016, 114 (1): 10-24.
[24] MURFF J D. Limit analysis of multi-footing foundation systems[C]// Proceedings 8 th International Conference on Computer Methods and Advances in Geomechanics , 1994: 223-244.
[25] TAN F S C. Centrifuge and theoretical modelling of conical footings on sand[D]. PhD Thesis.London: Cambridge University, 1990.
[26] MARTIN C M, HOULSBY G T. Combined loading of spudcan foundations on clay: numerical modelling[J]. G é otechnique , 2001, 51 (8): 687-699.
[27] BRANSBY M F, RANDOLPH M F. Combined loading of skirted foundations[J]. G é otechnique , 1998, 48 (5): 637-655.
[28] ZHANG Y, BIENEN B, CASSIDY M J,et al. Undrained bearing capacity of deeply buried flat circular footings under general loading[J]. Journal of Geotechnical and Geoenvironmental Engineering , 2012, 138 (3): 385-397.
[29] WANG D, HU Y, RANDOLPH M F. Three-dimensional large deformation finite-element analysis of plate anchors in uniform clay[J]. Journal of Geotechnical and Geoenvironmental Engineering , 2010, 136 (2): 355-365.
[30] WU X, CHOW Y K, LEUNG C F. Behavior of drag anchor under uni-directional loading and combined loading[J]. Ocean Engineering , 2017, 129 : 149-159.
[31] MERIFIELD R S, SLOAN S W, YU H S. Stability of plate anchors in undrained clay[J]. G é otechnique , 2001, 51 (2): 141-153.
[32] WU X N, CHOW Y K , LEUNG C F. Prediction of drag anchor trajectory with both shallow and deep anchor behavior[C]// Proceedings of the Offshore Technology Conference Asia . Kuala Lumpur, Malaysia, 2016.
[33] LIU H X, ZHANG W, ZHANG X, et al. Experimental investigation on the penetration mechanism and kinematic behavior of drag anchors[J]. Applied Ocean Research , 2010, 32 (4): 434-442.
WU Xiaoni 1 , HU Cun 2 , LI Ye 1
(1. School of Naval Architecture , Ocean and Civil Engineering , Shanghai Jiao Tong University , Shanghai 200240, P . R . China ;2. Institute of Mechanics , Chinese Academy of Sciences , Beijing 100190, P . R . China )
Abstract: The drag anchor is widely used in offshore engineering as a foundation for the mooring system due to high capacity and low cost. The prediction of kinematic behavior and trajectory is still challenging due to the complex interaction of the anchor fluke with soil. The existing plastic yield envelope method is generally used for the kinematic analysis, where the deep anchor failure is assumed to occur during the whole dragging process. In reality, the penetration is a process of anchor fluke being dragged into seabed soil continuously from shallow to deep depths. Obviously, the existing yield envelope method could not capture the effect of shallow anchor failure, which may lead to inaccurate prediction of the anchor trajectory. Finite element analyses were conducted firstly to obtain the influences of the anchor embedment depth and angle of the fluke on the drag anchor behaviors under unidirectional and combined loadings. The yield envelope for the shallow anchor failure was determined accordingly, with which the shallow failure effect can be taken into account for the yield envelop method. The effects of the fluke angle, the bearing capacity factor and the shallow zone size were investigated. The predicted trajectories with and without the shallow failure effect were compared. It is shown that the fluke angle and the shallow failure zone size influence significantly the kinematic behaviors and the trajectory of the drag anchor. The consideration of shallow failure results in a shallower predicted anchor embedment depth and a smaller anchor line force before the anchor penetration depth stabilizes, but hardly changes the ultimate embedment depth.
Key words: drag anchor; shallow anchor failure; plastic yield envelope; trajectory
Foundation item: The National Natural Science Foundation of China(51809165;51309213)
作者简介: 毋晓妮(1986—),女,博士(通讯作者. E-mail: wuxiaoni@sjtu.edu.cn).
基金项目: 国家自然科学基金(51809165;51309213)
修订日期: 2018-02-08
∗ 收稿日期: 2017-08-08;
DOI: 10.21656/1000-0887.380226
ⓒ 应用数学和力学编委会,ISSN 1000-0887
文章编号 : 1000-0887(2018)10-1137-12
文献标志码: A
中图分类号 : TU473
引用本文 / Cite this paper: 毋晓妮, 胡存, 李晔. 考虑浅埋破坏的拖曳锚在黏土中安装运动特性分析[J]. 应用数学和力学, 2018, 39 (10): 1137-1148.WU Xiaoni, HU Cun, LI Ye. Kinematic analysis on drag anchor installation in clay considering shallow failure effects[J]. Applied Mathematics and Mechanics , 2018, 39 (10): 1137-1148.