
图1 两自由度弹性双碰系统运动模型
Fig. 1 The dynamic model for a 2-DOF system under elastic symmetric impact
杜伟霞, 张思进, 殷 珊
(湖南大学 机械与运载工程学院, 长沙 410082)
摘要 : 研究了对称碰撞系统的间歇混沌控制方法,将Hopf分岔控制思想应用于该系统上,对该类系统的混沌控制提供一个新的控制方法 . 这里以两自由度弹性双碰系统为探究对象,首先,建立两自由度弹性双碰系统的力学模型,并根据其运动特点将其分成4个阶段,建立了合适的Poincaré映射;然后,取定一个合适的定相位面,施加间歇线性控制律,并构建施加控制后的映射,根据映射的稳定性判据得到该系统混沌控制的显式条件;最后,分别对原系统和控制系统进行了数值模拟 . 计算结果表明,该控制方法能够很好地控制原系统的混沌运动,实现了预期目的,验证了该控制方法在弹性系统上的有效应用 . 该控制方法有利于提高系统的运行稳定性和使用寿命,具有一定的实际意义 .
关 键 词 : 混沌控制; Poincaré映射; 间歇线性控制; 显式条件
从20世纪混沌被发现以来,至今对于混沌的控制还是没有给出严格的定义,基本上是通过对产生混沌运动的系统进行有目的的扰动,使得该系统达到被期望的运动状态 . 而关于混沌运动的控制方法也是层出不穷,最早的是20世纪90年代Ott、Grebogi和Yorke [1] 提出的OGY混沌控制方法,该方法通过对系统参数进行微调,以实现对不稳定的目标周期轨道的控制 . 文献[2]又对OGY混沌控制方法进行了改进及证明,此后又有很多混沌控制方法被提出,但大多都是在OGY方法上发展起来的 . 近年来有人提出了一些新的混沌控制方法,文献[3]基于线性可逆变换方法,将系统的部分状态变量在相应的子空间作变换来实现对混沌运动的控制 . 文献[4]的仿真结果表明,通过调节正弦外加驱动力,可将系统的概周期碰撞振动和混沌运动控制到稳定的周期运动上去 . 文献[5]通过对混沌控制因子更新策略进行改进,提出了基于改进自适应混沌控制的逆可靠度分析方法 . 而目前对非光滑动力学系统碰振控制的研究大部分集中在刚性碰撞系统上 . 文献[6]通过外加正弦力,抑制了小型打桩机的分岔和混沌运动 . 文献[7]应用OGY控制方法,对单自由度含双侧约束碰撞振动系统的混沌运动进行了控制分析 . 对于弹性碰撞系统的研究则涉及很少,文献[8]利用数值仿真方法,对一类两自由度含间隙弹性碰撞系统的动力学特性做了深入的研究,分析了系统周期运动及其参数存在区域,并揭示了系统的颤碰运动特性 . 文献[9]探究了一类两自由度含间隙和预紧弹簧的碰撞振动系统的动力学行为,用测试函数预测了系统发生擦边分岔的参数范围 . 以上研究主要是探究弹性系统的非线性动力学行为,对于其产生的非线性现象像混沌、分岔等行为并未进行过多的控制研究,也就少数论文涉及,而且方法有限 . 文献[10]通过线性增强方法控制冲击振荡器的共存吸引子;文献[11]利用非线性反馈方法来控制带有阻尼摆的一类振动系统的振动 . 因此,探究控制弹性系统中的非线性动力学行为的方法很有必要 .
本文尝试将文献[12]中提出的方法应用在非光滑弹性碰撞系统(即分段向量场系统)上,以一类两自由度弹性双碰系统为研究对象,对其动力学行为进行分析,选取合适的定相位面,并对其施加间歇线性反馈控制律,通过对受控系统的运动稳定性分析,得到该系统混沌控制的显式条件;采用数值模拟,给出了系统周期运动的控制参数分岔图,从控制参数分岔图中直接选取符合条件的控制参数便可以将原系统控制在周期运动范围内 . 而该模型可以应用在含间隙运动副 [13] 、车辆轮轨系统 [14] 、齿轮传动系统 [15] 等机械设备上,该方法可以用来提高这些设备的运行稳定性、工作效率和使用寿命,具有一定的实际工程意义 .
在文献[16]的基础上,本文基于Hertz接触力模型建立两自由度弹性对称碰撞运动模型(如图1) . M 1 和 M 2 分别是两振子的质量, C 1 , C 2 , C 3 , K 1 , K 2 , K 3 分别是系统的阻尼系数和弹簧刚度系数,两振子在外弦简谐激振力的作用下运动,当 M 1 向右运动与约束A接触时,系统的刚度与阻尼会随之发生改变;当其反向运动,会再次与A接触并改变系统的刚度与阻尼,如此反复运动 .

图1 两自由度弹性双碰系统运动模型
Fig. 1 The dynamic model for a 2-DOF system under elastic symmetric impact
设质块 M 1 与约束A右边接触后的瞬时为0时刻,且该模型里的阻尼是Rayleigh型比例阻尼 . 为了描述该系统的运动状态,这里定义一个边界函数:
则分界面为 ![]() 这里
这里 ![]() 这样就可以将运动状态空间分为3个部分,如图2所示 .
这样就可以将运动状态空间分为3个部分,如图2所示 .
为了方便讨论,这里使用时间段将运动过程分为4个阶段来考虑,分别是 t 0 ~ t 1 (表示区域Ⅰ)、 t 1 ~ t 2 与 t 3 ~ t 4 (表示区域Ⅱ)、 t 2 ~ t 3 (表示区域Ⅲ),其中 t 0 表示碰撞初始时刻( t 0 =0), t 4 表示一个周期 T ( T =2π/ ω ),每一阶段的运动微分方程为:
当 t 0 ≤ t ≤ t 1 或 t 2 ≤ t ≤ t 3 时
(1)
当 t 1 < t ≤ t 2 或 t 3 < t ≤ t 4 时
(2)
其中
μ m = M 2 / M 1 , μ c 2 = C 2 / C 1 , μ c 3 = C 3 / C 1 ,
x i = X i K 1 /( P 1 + P 2 ), i =1,2 .

图2 边界条件
Fig. 2 Boundary conditions
1) 通过模态叠加法可以求得以上各阶段方程所对应的通解,当 t 0 ≤ t ≤ t 1 或 t 2 ≤ t ≤ t 3 时,有
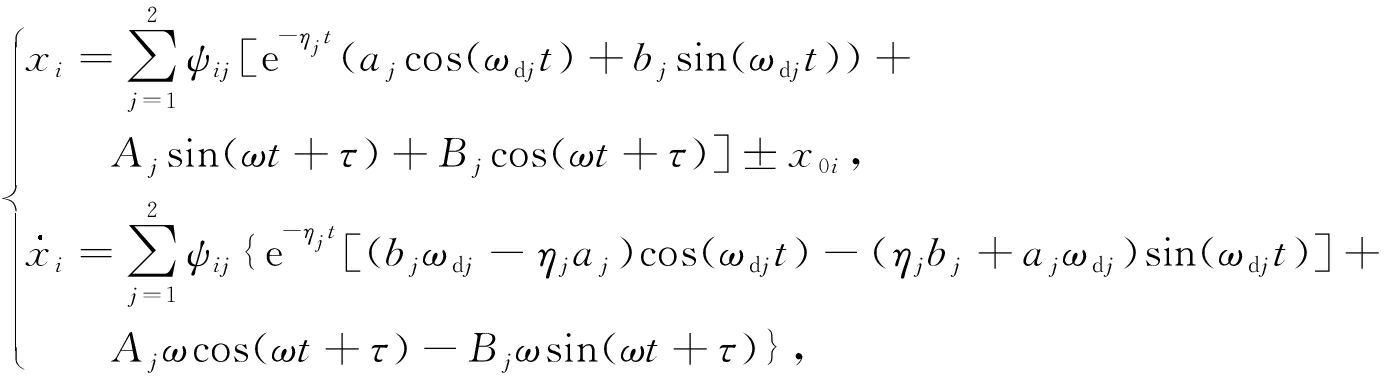
(3)
其中, i =1,2; ψ ij 是方程(1)的正则模态矩阵 Ψ 的元素; ![]() 为方程(1)的无阻尼固有频率; A j 和 B j 表示系统的振幅常数, a j 和 b j 是积分常数,由系统的初始条件
为方程(1)的无阻尼固有频率; A j 和 B j 表示系统的振幅常数, a j 和 b j 是积分常数,由系统的初始条件 ![]() 确定,
确定, ![]()
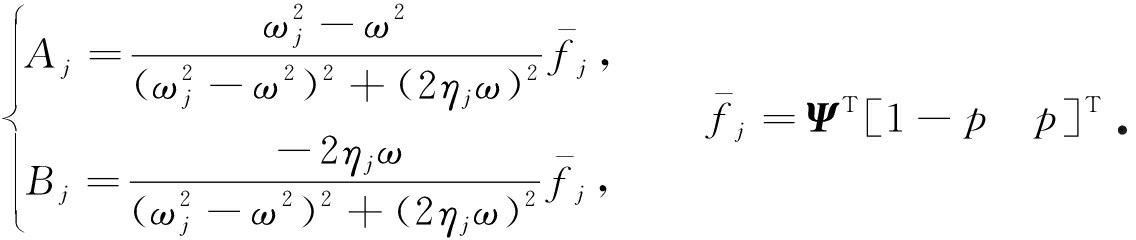
2) 当 t 1 < t ≤ t 2 或 t 3 < t ≤ t 4 时,有
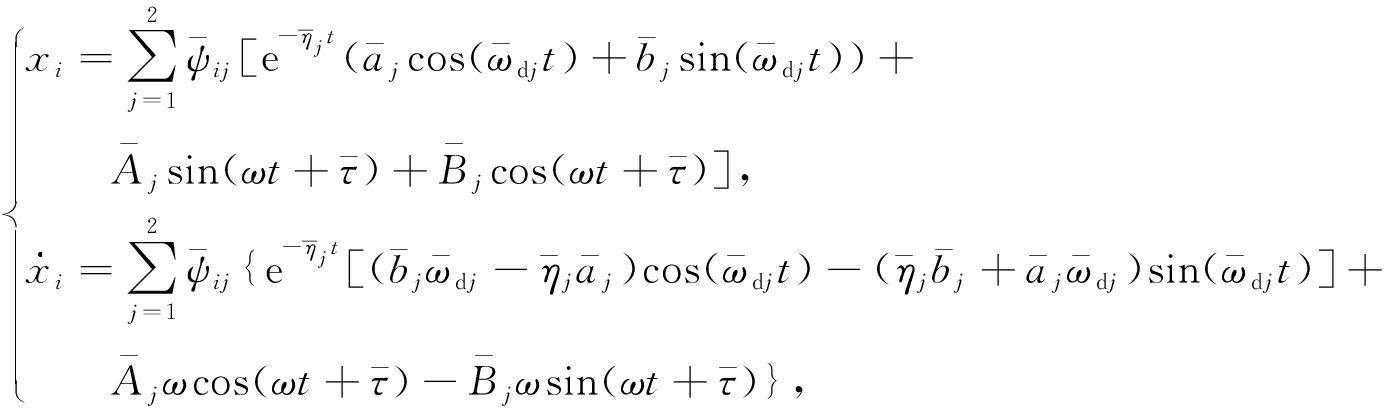
(4)
其中, ![]() 是方程(2)的正则模态矩阵
是方程(2)的正则模态矩阵 ![]() 的元素;
的元素; ![]() 为方程(2)系统的无阻尼固有频率;
为方程(2)系统的无阻尼固有频率; ![]() 和
和 ![]() 表示系统的振幅常数,
表示系统的振幅常数, ![]() 和
和 ![]() 是积分常数,由该阶段的初始条件确定,而各阶段的初始条件、积分常数以及积分时间 t i ( i =1,2,3)又可通过周期性条件求得 .
是积分常数,由该阶段的初始条件确定,而各阶段的初始条件、积分常数以及积分时间 t i ( i =1,2,3)又可通过周期性条件求得 .
为了研究两自由度双碰系统运动的稳定性情况,这里建立系统对应的Poincaré映射 P . 选择截面:
设 ![]() 表示系统在Poincaré截面上的周期 n -1不动点,将系统运动过程分为4个阶段,可分别建立相应的Poincaré映射:
表示系统在Poincaré截面上的周期 n -1不动点,将系统运动过程分为4个阶段,可分别建立相应的Poincaré映射:
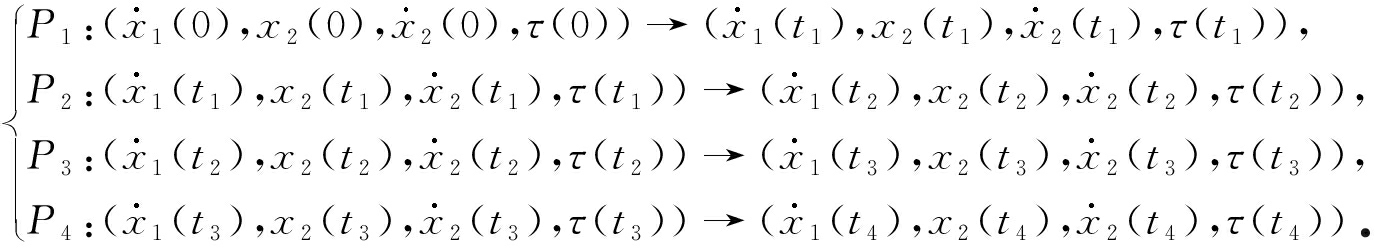
(5)
令 P 1 , P 2 , P 3 , P 4 分别代表 P 1 , P 2 , P 3 , P 4 映射所对应的矩阵,于是系统的Poincaré映射 P 可以表示为
(6)
可以通过Poincaré映射所对应的线性化矩阵 P 在不动点处的特征值情况来判断原系统的运动稳定性 .
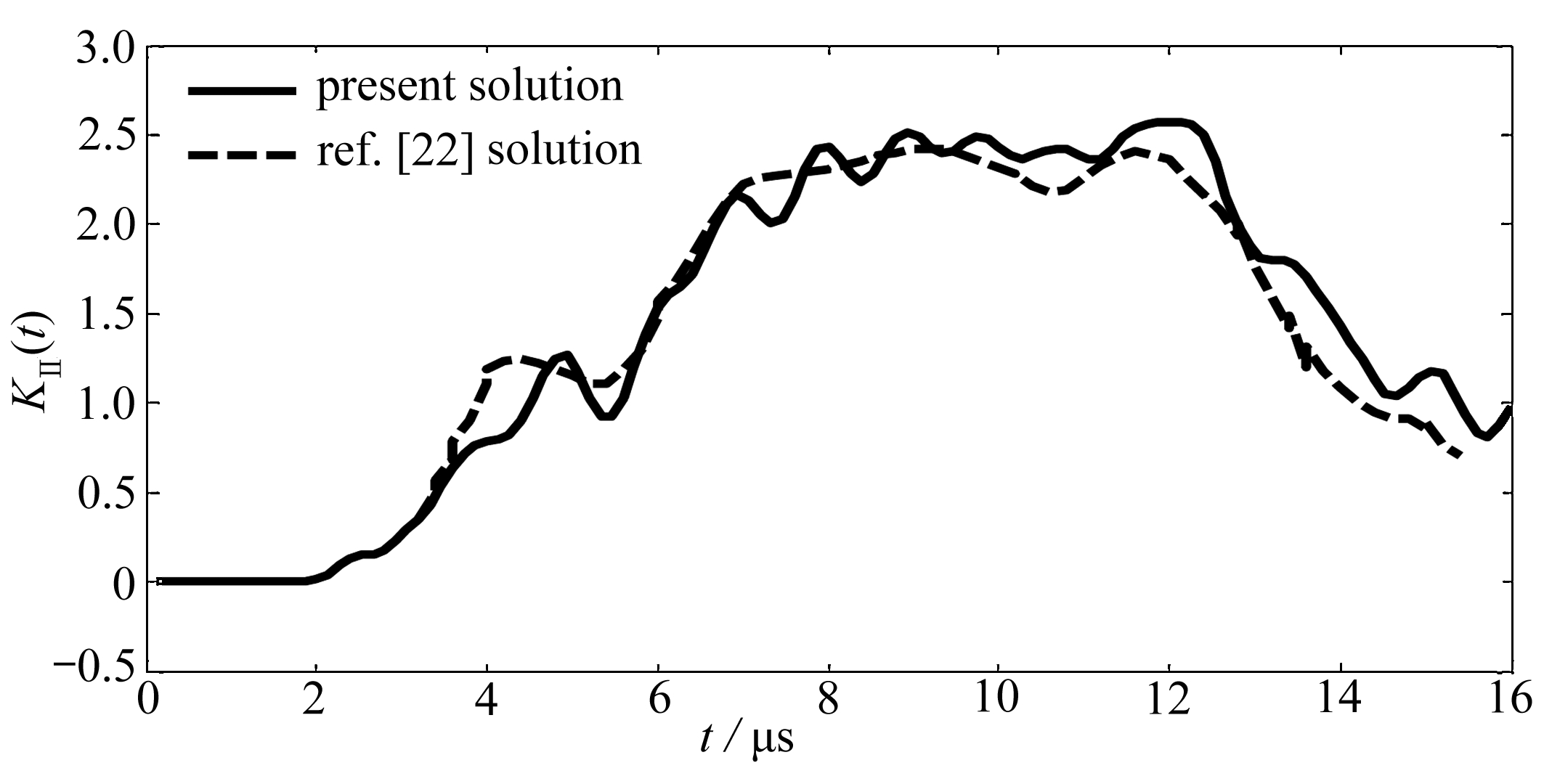
图3 加入控制的位置示意图
Fig. 3 The location diagram with the control
从原系统周期解的形式可以看出它是由非碰撞部分和碰撞部分组成,是一个不光滑的周期解,针对这种非光滑的周期解一般采用两种控制模式:一种是直接在非碰撞部分施加控制;另一种是在碰撞部分施加控制 . 本文采用的控制器是施加在非碰撞部分,也就是在不改变原平衡不动点的情况下对位移和速度两个向量施加了一个线性反馈控制,针对位移的控制器工程中可以理解为一个可调刚度的弹簧控制器,对速度的控制器工程中可以理解为一个可调阻尼的阻尼控制器 . 因为是在微分方程中施加的控制,激振力是输入,经过控制器反馈控制之后,输出系统的响应量,然后再将响应量反馈到微分系统中,起到闭环控制的效果 . 本文施加控制器的位置不同于文献[12],这里是取定一个合适的定相位面,通过在该位置处设置一个可调阻尼的阻尼控制器来对该截面上的速度施加控制,每隔一个周期 T 就会与阻尼控制器接触一次,以此来改变一次速度的大小(即状态间歇控制) . 控制器施加位置如图3所示 .
其控制系统运动方程如下:
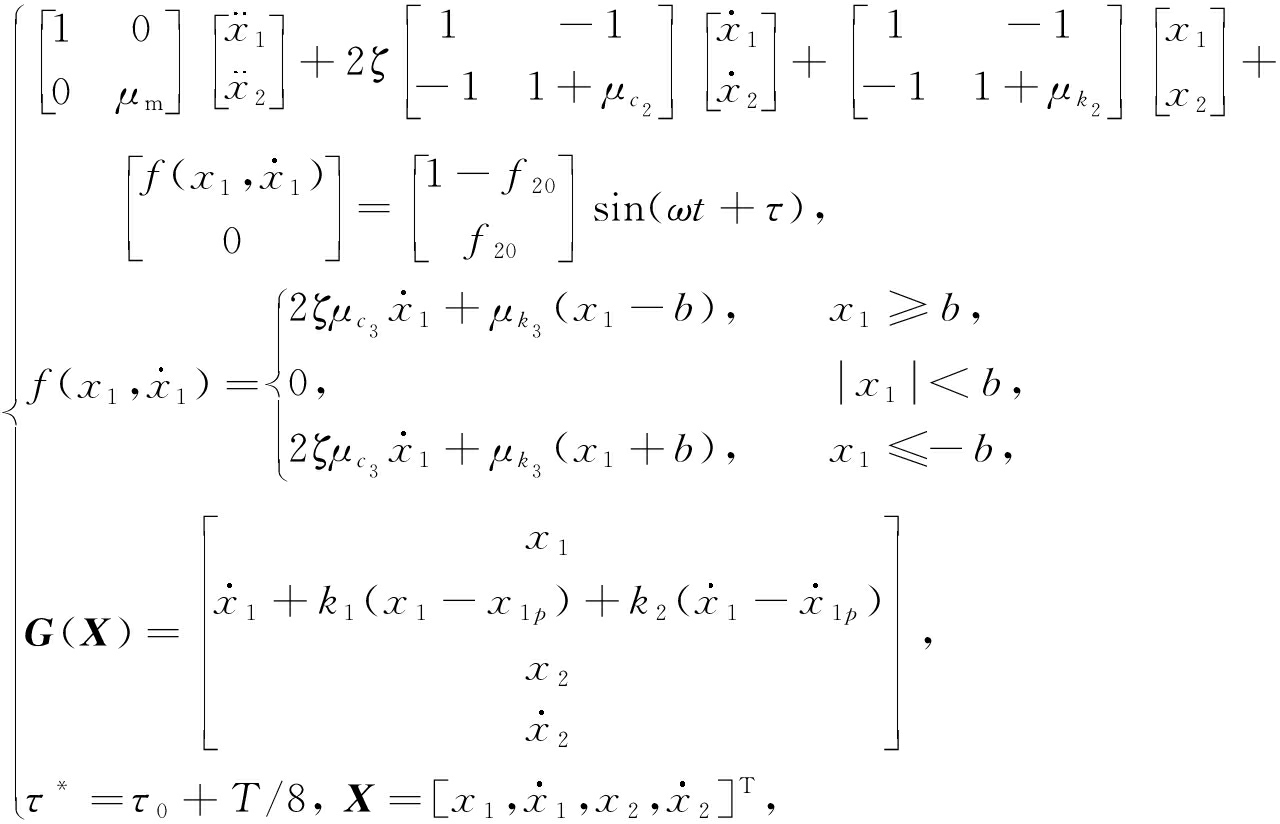
(7)
其中 k 1 , k 2 为控制参数, ![]() 为原系统的周期解位移和速度 . 可以看出该控制方法不改变原系统的周期解,通解形式和原系统也是一样的 . 在加入控制后,新的线性化复合映射为
为原系统的周期解位移和速度 . 可以看出该控制方法不改变原系统的周期解,通解形式和原系统也是一样的 . 在加入控制后,新的线性化复合映射为
P α = P 5 · P 4 · P 3 · G · P 2 · P 1 .
通常混沌控制的方法是在参数空间内逐点取值求出对应的特征值,并验证该特征值是否满足条件,这样的方法盲目、具有不确定性而且需要计算很长时间 . 本文通过应用Schur-Cohn稳定性判据,得到系统发生稳定性周期运动的不依赖于特征值的显式条件;并通过数值计算得到了符合条件的控制参数区域,在区域内选取控制参数即可将混沌运动控制到稳定的周期运动上 .
设映射 P α 在不动点 ![]() 处线性化矩阵所对应特征方程的一般形式为
处线性化矩阵所对应特征方程的一般形式为
P ( k 1 , k 2 ) ( λ )= m 0 ( k 1 , k 2 ) λ 4 + m 1 ( k 1 , k 2 ) λ 3 + m 2 ( k 1 , k 2 ) λ 2 + m 3 ( k 1 , k 2 ) λ +
m 4 ( k 1 , k 2 ), m n ( k 1 , k 2 )>0, m 0 ( k 1 , k 2 )=1, n =1,2,3,4 .
(8)
设
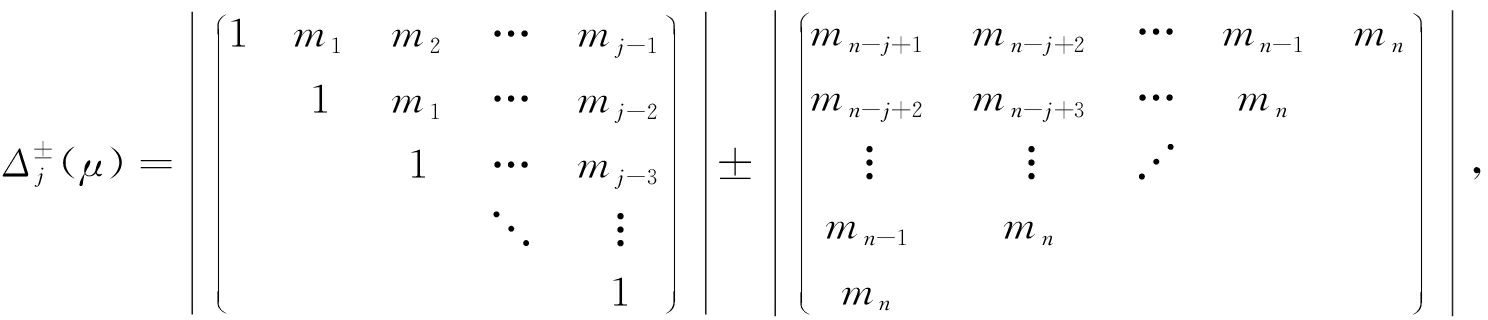
j =1,2,…, n .
(9)
由参考文献[17]所提出的定理(Schur-Cohn判据),特征多项式(8)的根全部位于复平面单位圆内部的充要条件为
(10)
将式(10)展开可得显式条件:
1+ m 1 + m 2 + m 3 + m 4 >0,
(11a)
1- m 1 + m 2 - m 3 + m 4 >0,
(11b)
(11c)
![]()
(11d)
1+ m 4 >0,
(11e)
1- m 4 >0 .
(11f)
首先对原系统进行数值模拟,选取一组无量纲系统参数:
μ m =2, μ k 2 =4, μ k 3 =6, μ c 2 =4, μ c 3 =6, p =0.01, ζ =0.01, b =0.1 .
系统随激励频率 ω 变化的分岔图如图4所示 . 图5给出了系统取不同的 ω 值时所对应的相图 .
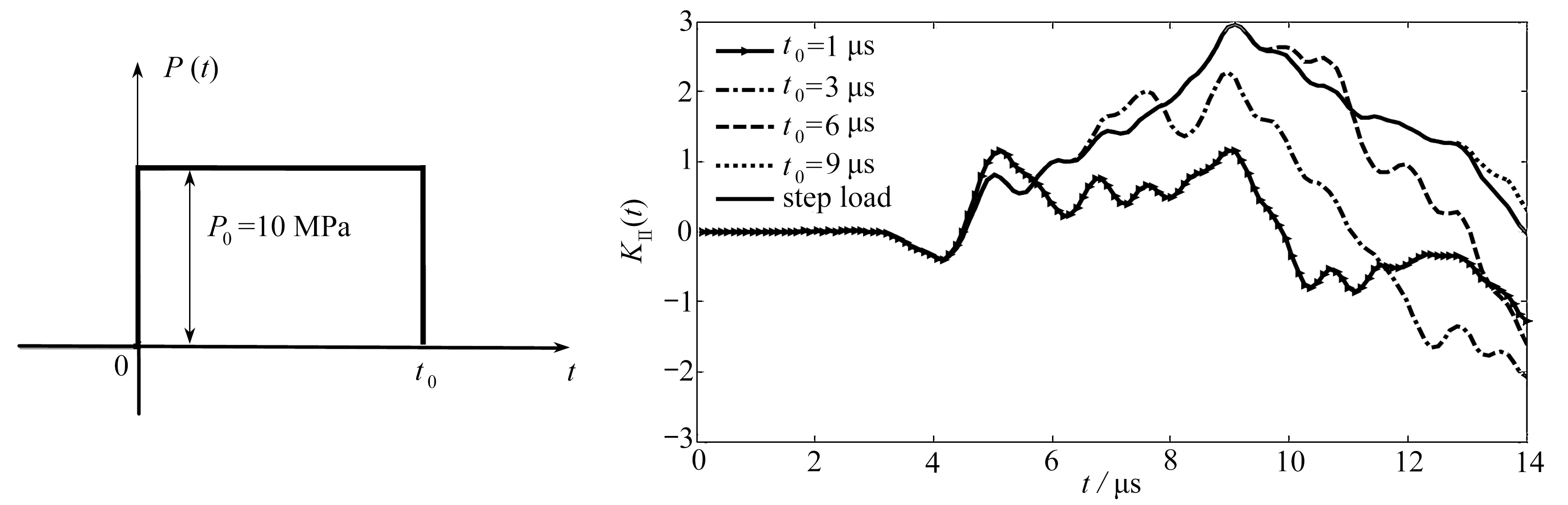
图4 原系统的全局分岔图
Fig. 4 Global bifurcations of the original system
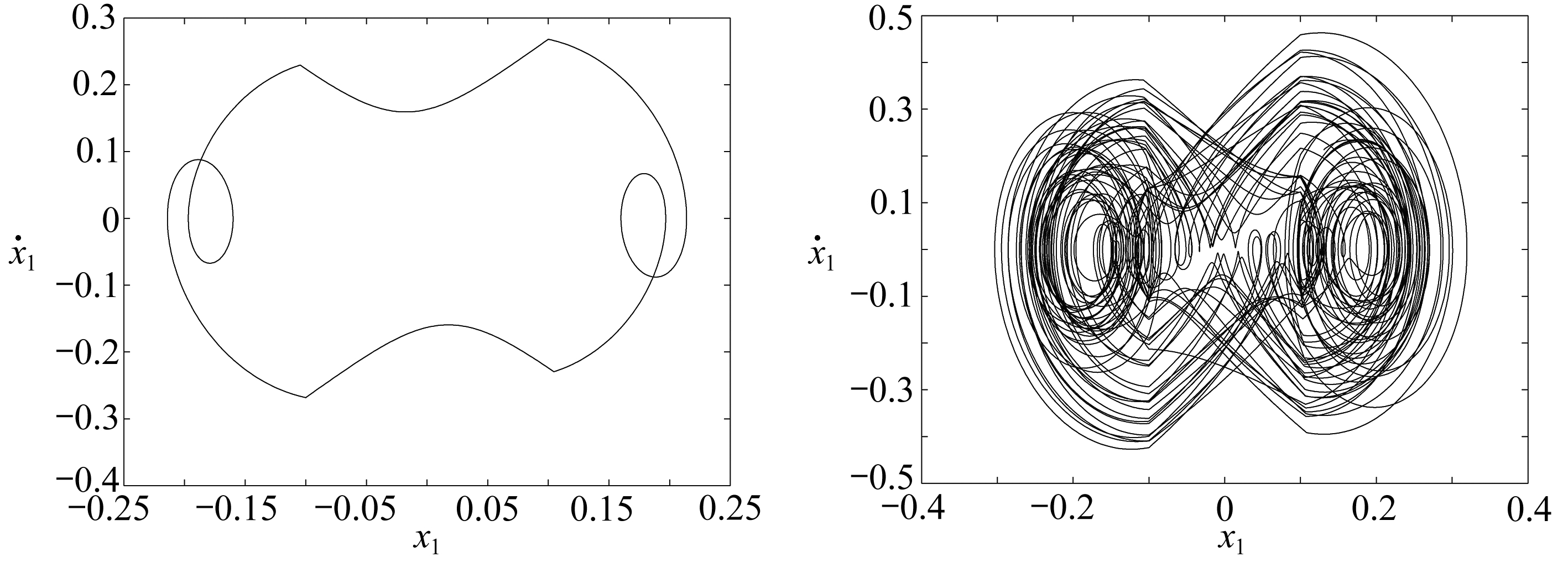
(a) 对称双碰周期二(ω=0.72)(b) 混沌(ω=0.57)
(a) Symmetric impact with 2 cycles(ω=0.72)(b) Chaos (ω=0.57)
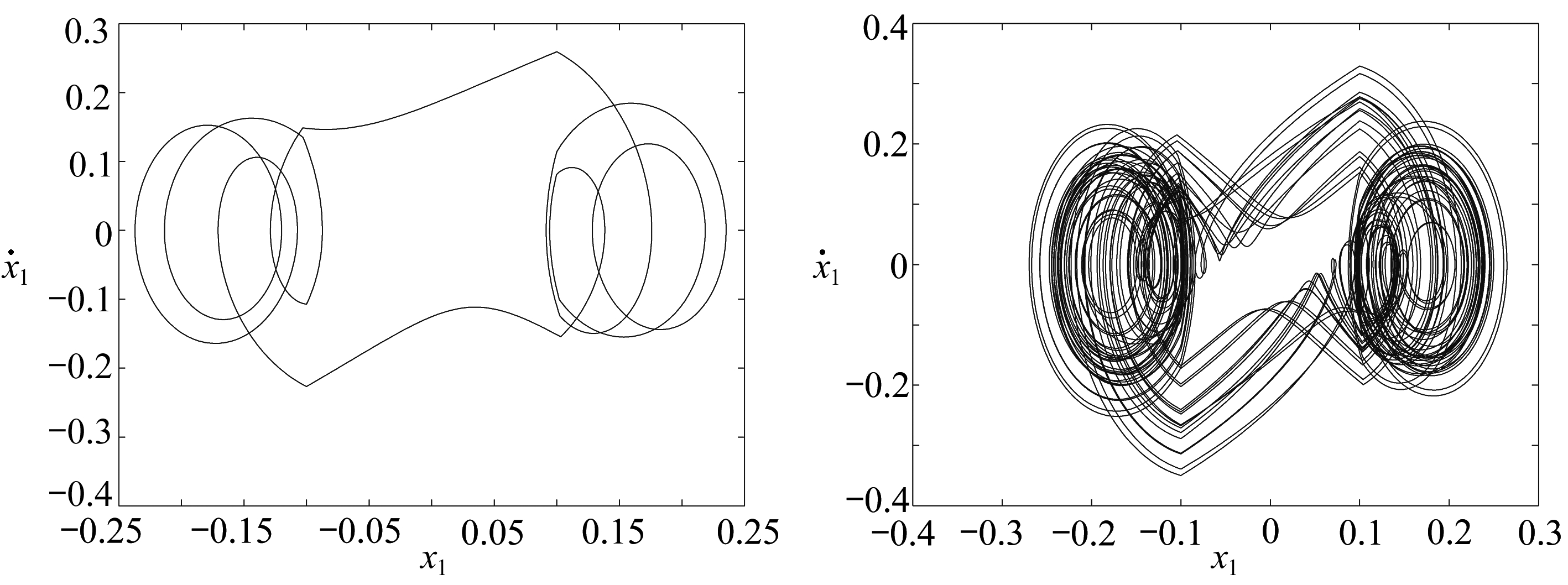
(c) 稳定的多周期(ω=0.37)(d) 混沌(ω=0.32)
(c) Stable multiple cycles (ω=0.37)(d) Chaos (ω=0.32)
图5 不同的ω值所对应的相图
Fig. 5 The phase diagrams corresponding to the differentωvalues
从以上各图可以观察到,系统随着 ω 的减小,其周期运动与混沌运动交替出现,这种现象对系统的工作效率和使用寿命可能产生较大的影响,因而对其混沌运动进行控制显得十分重要 .
作为算例,这里选取在激励频率为 ω =0.57时的运动状态作为控制目标,当 ω =0.57时,求得系统的特征值为
λ 1 =8.738 2, λ 2 =0.040 1,
λ 3,4 =-0.213 7±0.717 3i,
λ 1 =8.738 2, λ 2 =0.040 1,
λ 3,4 =0.748 5 .
有一个特征值在单位圆外,数值模拟结果显示该参数下系统做混沌运动 .
通过显式条件(11),可以得到控制参数分岔图,即稳定参数域,如图6所示 .
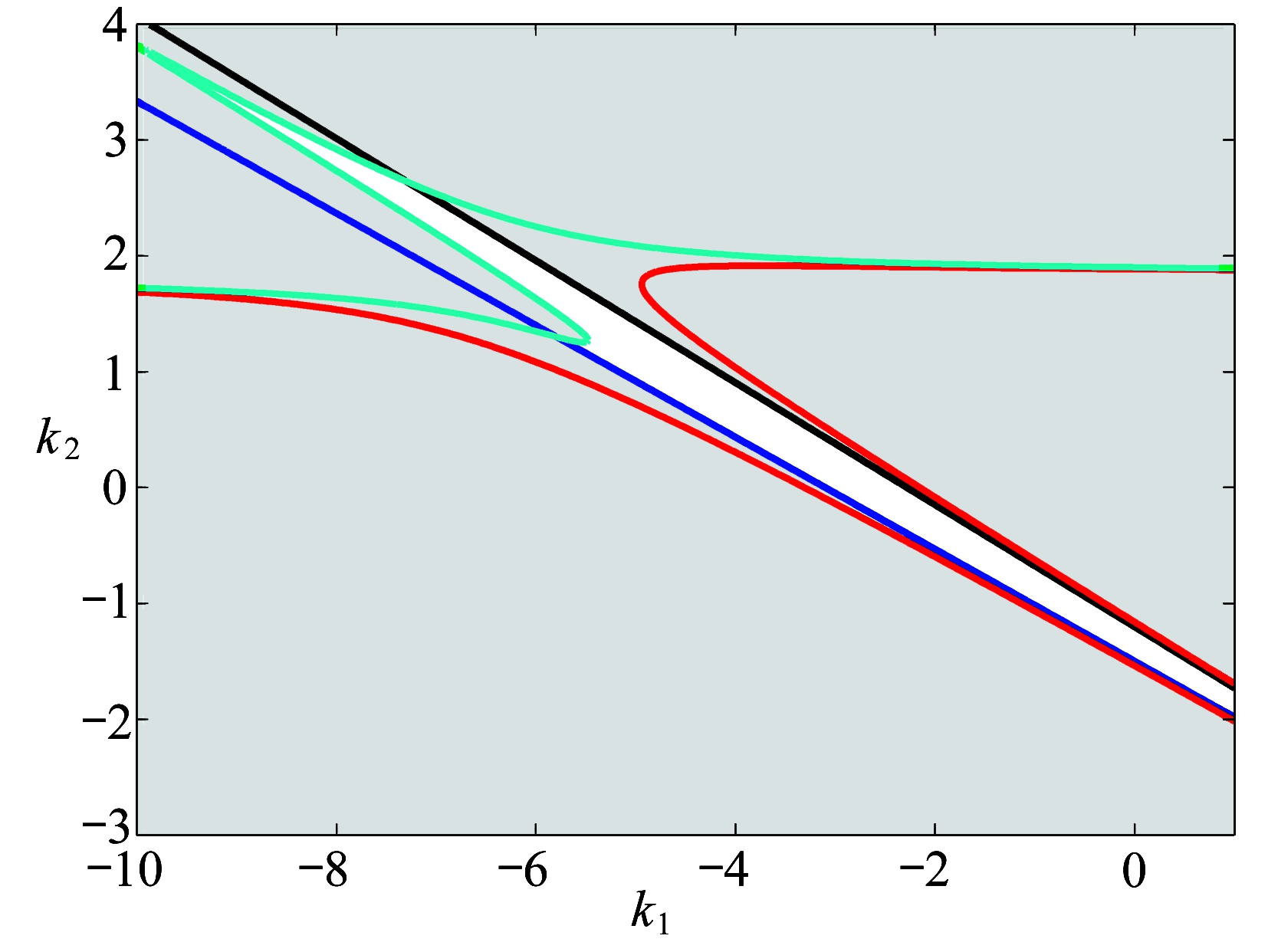
图6 控制参数分岔图
Fig. 6 The bifurcation diagram of control parameters
图中白色区域是由式(11a)、(11b)和(11d)围成,里面的参数符合式(11),任取其中一点(-2.108 4,-0.301 2),在该控制参数下可得控制之后的复合映射的特征值为
λ 1,2 =-0.031 75±0.483 69i, λ 3,4 =-0.205 69±0.735 88i,
λ 1,2 =0.484 74, λ 3,4 =0.764 08 .
特征值全部位于单位圆内,因而系统运动是稳定的周期运动 . 图7给出了该控制参数下的相图 .

(a) 控制前的混沌运动(b) 控制后的周期运动
(a) Chaotic motion without control (b) Controlled periodic motion
图7 控制前后的相图对比
Fig. 7 The phase diagrams without and with control
图8给出了该控制参数下被控制输入随时间变化的曲线图 .

图8 控制输入随时间变化的曲线
Fig. 8 The control input curve with time
图中的横坐标代表的是周期数,这里是将运动时间用周期数来代替,其中 ![]() 表示被控制输入 .
表示被控制输入 .
由以上两图对比可以发现该控制方法能够很好地将原系统的混动运动控制到周期运动上,从图8可以看出原周期解处于稳定状态,达到了预期目的 .
根据两自由度履带传动系统的运动特点得到该系统的运动方程,建立了系统的Poincaré映射,数值模拟发现该系统的动力学行为表现为混沌和周期运动交替出现,利用间歇控制方法对该系统的混沌运动施加控制 . 分析表明,该控制器不会改变原系统的周期解的形式 . 通过对受控系统Poincaré映射的稳定性分析,得到该系统混沌控制的显式条件,并用数值方法画出了控制参数分岔图,在符合条件的区域里面选取任一增益参数即可将混沌运动控制到周期运动上,进一步的数值模拟验证了该控制方法的有效性 .
参考文献 ( References ):
[1] OTT E, GREBOGI C, YORKE J. Controlling chaos[J]. Physical Review Letters , 1990, 64 (11): 1196-1199.
[2] 杨凌, 刘曾荣. OGY方法的改进及证明[J]. 应用数学和力学, 1998, 19 (1): 1-7.(YANG Ling, LIU Zengrong. An improvement and proof of OGY method[J]. Applied Mathematics and Mechanics , 1998, 19 (1): 1-7.(in Chinese))
[3] 张晓明, 彭建华, 张入元. 利用线性可逆变换增强延迟反馈方法控制混沌的有效性[J]. 物理学报, 2005, 54 (7): 3019-3026.(ZHANG Xiaoming, PENG Jianhua, ZHANG Ruyuan. Improving the efficiency of time-delayed feedback control of chaos through linear invertible transform[J]. Acta Physica Sinica , 2005, 54 (7): 3019-3026.(in Chinese))
[4] 马莉. 一类双自由度含间隙振动系统的混沌碰撞运动及控制[J]. 兰州交通大学学报(自然科学版), 2007, 26 (6): 136-139.(MA Li. Controlling chaotic motions for a two-degree-of-freedom vibratory system with a clearance[J]. Journal of Lanzhou Jiaotong University ( Natural Sciences ), 2007, 26 (6):136-139.(in Chinese))
[5] 李彬, 郝鹏, 孟增, 等. 基于改进自适应混沌控制的逆可靠度分析方法[J]. 应用数学和力学, 2017, 38 (9): 979-987.(LI Bin, HAO Peng, MENG Zeng, et al. An improved adaptive chaos control method for inverse reliability analysis[J]. Applied Mathematics and Mechanics , 2017, 38 (9):979-987.(in Chinese))
[6] 吕小红. 外加正弦力抑制小型打桩机的分岔与混沌[J]. 兰州交通大学学报, 2015, 34 (4): 146-150.(LÜ Xiaohong. Bifurcations and chaos of small pile driver controlled by external sine force[J]. Journal of Lanzhou Jiaotong University , 2015, 34 (4): 146-150.(in Chinese))
[7] 吕小红, 朱喜锋, 罗冠炜. 含双侧约束碰撞振动系统的OGY混沌控制[J]. 机械科学与技术, 2016, 35 (4):531-534.(LÜ Xiaohong, ZHU Xifeng, LUO Guanwei. Chaos control of a vibro-impact system with two-sided constraints based on OGY method[J]. Mechanical Science and Technology for Aerospace Engineering , 2016, 35 (4): 531-534.(in Chinese))
[8] 朱喜锋, 罗冠炜. 两自由度含间隙弹性碰撞系统的颤碰运动分析[J]. 振动与冲击, 2015, 34 (15): 195-200.(ZHU Xifeng, LUO Guanwei. Chattering-impact motion of a 2-DOF system with clearance and soft impacts[J]. Journal of Vibration and Shock , 2015, 34 (15): 195-200.(in Chinese))
[9] 张惠, 丁旺才, 李飞. 两自由度含间隙和预紧弹簧碰撞振动系统动力学分析[J]. 工程力学, 2011, 28 (3): 209-217.(ZHANG Hui, DING Wangcai, LI Fei. Dynamics of a two-degree-of-freedom impact system with clearance and pre-compressed spring[J]. Engineering Mechanics , 2011, 28 (3): 209-217.(in Chinese))
[10] LIU Yang, CHAVEZ J P. Controlling coexisting attractors of an impacting system via linear augmentation[J]. Physica D : Nonlinear Phenomena , 2017, 348 : 1-11.
[11] 张文娟, 俞建宁, 张建刚, 等. 利用非线性反馈控制一类振动系统的振动[J]. 重庆理工大学学报(自然科学), 2013, 27 (1): 27-31.(ZHANG Wenjuan, YU Jianning, ZHANG Jiangang, et al. Using nonlinear feedback control for the vibration of a nonlinear vibration system[J]. Journal of Chongqing University of Technology ( Natural Science ), 2013, 27 (1): 27-31.(in Chinese))
[12] WEN G L, CHEN S J, JIN Q T. A new criterion of period-doubling bifurcation in maps and its application to an inertial impact shaker[J]. Journal of Sound and Vibration , 2008, 311 (1): 212-223.
[13] 吴少培, 李国芳, 丁旺才. 含间隙运动副模型的机械动力学分析[J]. 兰州交通大学学报, 2016, 35 (4): 111-116.(WU Shaopei, LI Guofang, DING Wangcai. Dynamics analysis of mechanisms with joint clearance[J]. Journal of Lanzhou Jiaotong University , 2016, 35 (4): 111-116.(in Chinese))
[14] 郭树卓, 靳玲. 轮轨碰撞系统的分岔与混沌研究[J]. 兰州交通大学学报, 2012, 31 (1): 153-157.(GUO Shuzhuo, JIN Ling. Research on bifurcation and chaos of wheel-rail collision system[J]. Journal of Lanzhou Jiaotong University , 2012, 31 (1): 153-157.(in Chinese))
[15] 张晨旭, 杨晓东, 张伟. 含间隙齿轮传动系统的非线性动力学特性的研究[J]. 动力学与控制学报, 2016, 14 (2): 117-121.(ZHANG Chenxu, YANG Xiaodong, ZHANG Wei. Study on non-linear dynamics of gear transmission system with clearance[J]. Journal of Dynamics and Control , 2016, 14 (2): 117-121.(in Chinese))
[16] 周鹏. 非光滑系统的动力学及其在车辆工程中的应用[D]. 硕士学位论文. 兰州: 兰州交通大学, 2014.(ZHOU Peng. The dynamics of nonsmooth system and its application in vehicle engineering[D]. Master Thesis. Lanzhou: Lanzhou Jiaotong University, 2014.(in Chinese))
[17] LASALLE J P. The Stability and Control of Discrete Processes [M]. New York: Springer-Verlag, 1986.
DU Weixia, ZHANG Sijin, YIN Shan
( College of Mechanical and Vehicle Engineering , Hunan University , Changsha 410082, P . R . China )
Abstract: An intermittent chaos control method for symmetric impact systems was studied. The Hopf bifurcation control was applied to make a new control method for chaos control of such systems. The 2-DOF elastic double-impact system was considered. Firstly, the mechanical model for the 2-DOF system was built and its motion was divided into 4 stages according to the dynamic characteristics. Then, an appropriate Poincaré mapping was established; a suitable fixed phase plane was chosen, a linear controller was applied to the section to get the mapping with control, and the chaotic control explicit condition was obtained according to the stability criterion. Finally, numerical analyses of the original system and the controlled system were carried out respectively. The numerical results show that, the proposed method controls the chaos movement of the original system well, to achieve the desired goal and verify the correctness of the method. The method, with practical significance, is helpful to improve the stability, working efficiency and service life of the system.
Key words: chaos control; Poincaré mapping; intermittent linear control; explicit condition
Foundation item: The National Natural Science Foundation of China(11372101)
作者简介: 杜伟霞(1991—),女,硕士生(E-mail: weixia_du@hnu.edu.cn);张思进(1971—),男,教授(通讯作者. E-mail: sj_zh@sina.com).
基金项目: 国家自然科学基金(11372101)
修订日期: 2018-01-26
∗ 收稿日期: 2017-11-22;
ⓒ 应用数学和力学编委会,ISSN 1000-0887
文章编号 : 1000-0887(2018)10-1149-10
DOI: 10.21656/1000-0887.380292
文献标志码: A
中图分类号 : O322; TH113
引用本文 / Cite this paper: 杜伟霞, 张思进, 殷珊. 一类对称碰撞系统的间歇混沌控制方法[J]. 应用数学和力学, 2018, 39 (10): 1149-1158.DU Weixia, ZHANG Sijin, YIN Shan. An intermittent chaos control method for a class of symmetric impact systems[J]. Applied Mathematics and Mechanics , 2018, 39 (10): 1149-1158.