陈昌荣
(上海工程技术大学 飞行学院, 上海 201620)
摘要 : 用有裂纹与无裂纹时的远场 J 积分之差分析了无限大平面中心裂纹的能量释放率,材料形式分别为均匀和层状材料,裂纹垂直于拉伸方向,层状材料界面平行于拉伸方向 . 有裂纹与无裂纹 J 积分之差表示载荷作用下的无裂纹材料引入裂纹所导致的 J 积分变化 . 对于均匀材料无限大平面中心裂纹,能量释放率等于对称轴处应变能密度释放量沿对称轴的积分,其值等于无裂纹时的应变能密度乘以一个以裂纹半长为半径的圆周长 . 对于层状材料无限大平面中心裂纹,能量释放率等于对称轴处应变能密度释放量沿对称轴的积分减去界面 J 积分的改变量 .
关 键 词 : 能量释放率; J 积分; 材料非均匀性; 材料界面; Eshelby张量
裂纹驱动力的表征是断裂力学判据中的重要任务之一 [1] . 在裂纹驱动力的力学表征参数中,能量释放率是最根本的参数 [2] . 能量释放率具有坚实物理基础,定义清晰 . 以能量释放率为基础的Griffith断裂准则是-∂ U /∂ A = G c ,这里 U 是弹性应变能, A 是裂纹面积,-∂ U /∂ A 表示裂纹能量释放率, G c 是裂纹扩展单位面积所需能量 [3-4] . 然而,能量释放率的定义-∂ U /∂ A 在应用上存在数学困难, 因为-∂ U /∂ A 以无穷小理论为基础, 只适用于弹性应变能有解析解的情况, 不适用于以离散为基础的有限元计算 [5] . 在断裂问题的有限元分析中, 用 J 积分来取代-∂ U /∂ A 可避开直接计算能量释放率的数学困难, J 积分已成为一种计算能量释放率便捷且准确的方法 .
J 积分在能量释放率计算上的实用性得到广泛证实,但 J 积分的物理含义不易理解,尤其是 J 积分用于非均匀材料时 . 如果沿裂纹方向存在材料非均匀性,则 J 积分失去路径无关特性,也不能代表能量释放率 [6-7] . 例如:对于层状弹性材料中的裂纹,如果围绕裂尖的路径被限制在裂尖所在层内,则 J 积分是路径无关的而且等于能量释放率;如果围绕裂尖的路径包围了部分界面,则 J 积分就随路径所包围的界面数量和界面长度而变 [8-9] ,这是因为材料非均匀性在每个界面产生了 J 积分 [10] . 用构型力学可以分析裂纹 J 积分和界面 J 积分的产生原因和物理意义 [11-14] .
本文利用 J far( a ) - J far(0) 来分析能量释放率与无裂纹时应变能密度的关系,这里 J far( a ) 和 J far(0) 分别代表有裂纹和无裂纹时沿同一远场路径的 J 积分, J far( a ) - J far(0) 表示无裂纹材料引入裂纹时远场 J 积分发生的变化 . 裂纹形式为无限大平面中心裂纹,载荷为远处垂直于裂纹方向的拉伸应力,材料为均匀材料和层状材料 .
能量释放率定义为:在位移载荷保持不变的情况下,裂纹扩展单位面积所导致的系统应变能减小量 . 对于单位厚度平面中的裂纹,能量释放率为
(1)
这里 U 表示弹性应变能, a 表示裂纹长度,Δ a 表示裂纹长度增量 . 但用有限元方法分析断裂问题时,按式(1)计算能量释放率很不方便 [15] ,而用 J 积分取代式(1)可便捷和准确地计算出能量释放率 .
Rice的 J 积分公式是Eshelby的弹性体缺陷积分公式在断裂力学中的应用,而Eshelby的弹性体缺陷积分公式是静电学中的Maxwell(麦克斯韦)积分方程在弹性固体缺陷研究中的应用 [16] . 对于单位厚度均匀材料中的裂纹, J 积分的定义为 [17]
(2)
这里,路径 L 从裂纹下表面开始,逆时针围绕裂尖,终止在裂纹上表面; t i ( i =1,2)是路径 L 上的力 t 沿 x 1 和 x 2 方向的分量, t 与应力 σ 的关系是 t = σ · n , n 是路径 L 外法线方向单位向量, u 是位移向量; s 是沿路径 L 的长度; W 是应变能密度 .
J 积分也可表示为
(3)
这里 ![]() 表示沿 x 1 方向的Eshelby张量 [18] ,它是 J 积分的内核函数 . J 积分表示路径所包围缺陷沿 x 1 方向平移所引起的能量释放率 .
表示沿 x 1 方向的Eshelby张量 [18] ,它是 J 积分的内核函数 . J 积分表示路径所包围缺陷沿 x 1 方向平移所引起的能量释放率 .
图1是Rice给出的一个 J 积分算例 [17] : 无限长的长板条存在一个半无限长的裂纹,上边界 y =+ h /2和下边界 y =- h /2被夹持, 在上、下边界施加等位移载荷, J 积分的路径如虚线所示 . 在上、下边界,d y =0, ∂ u /∂ x = 0 ,所以上、下边界对 J 积分无贡献;左边 x =-∞处, W =0, t = 0 ,对 J 积分无贡献;只有右边 x =+∞对 J 积分有贡献 . 所以,
J = ![]() W +∞ d y = hW +∞ ,
W +∞ d y = hW +∞ ,
(4)
即能量释放率等于右边的应变能密度乘以板条高度 .

图1 高度为h的无限长板条含一条半无限长裂纹,板条上、下边界受等位移载荷作用
Fig. 1 A semi-infinite crack in an infinite strip of height h: the constant displacements are applied on the upper and lower boundaries
先假设图1的板条无裂纹,施加位移载荷,此时 J 积分 J (0) 为零,应变能密度为 W (0) ;保持上、下边界位移不变,引入裂纹,则右边 x =+∞的应变能密度不变,对 J ( a ) - J (0) 无贡献;上、下边界对 J ( a ) - J (0) 无贡献;左边 x =-∞的应变能密度由 W (0) 变为零,对 J ( a ) - J (0) 有贡献,
J = J ( a ) - J (0) =- ![]() ( W ( a ) - W (0) )d y = hW (0) ,
( W ( a ) - W (0) )d y = hW (0) ,
(5)
即,能量释放率等于板条左边的应变能密度释放量乘以板条高度 .
由于上、下边界和右边对 J ( a ) - J (0) 无贡献,由式(2)可知:沿任意一条从上边界到下边界的穿越裂纹的直线或曲线计算 F ( a ) - F (0) 的积分,结果就是裂纹扩展能量释放率, F ( a ) , F (0) 分别表示有裂纹和无裂纹时的Eshelby张量 .
无限大平面远处受 y 向拉应力 σ app 作用时,在平面应变条件下的应变能密度为
(6)
这里 E * = E /(1- ν 2 ) .
如图2所示, 无限大平面远场路径 L far 的上半部分由 L 1 , L 2 和 L 3 三段构成, L 1 和 L 2 远离裂尖位置, L 3 位于对称轴( y 轴) . 当裂纹被引入时, 由于 L 1 和 L 2 远离裂纹, L 1 和 L 2 处的应力没有变化, 对 J far( a ) - J far(0) 无贡献; 只有 L 3 靠近裂纹的部分发生应力释放, 对 J far( a ) - J far(0) 有贡献 . 所以, J far( a ) - J far(0) 转化为
J far( a ) - J far(0) =2( J L 3 ( a ) - J L 3 (0) ) .
(7)
在均匀材料中, J far(0) =0, 所以,
J far( a ) =2( J L 3 ( a ) - J L 3 (0) ) .
(8)
由于均匀材料裂纹 J 积分具有路径无关特性而且等于能量释放率,所以2( J L 3 ( a ) - J L 3 (0) )等于裂纹扩展能量释放率 . 根据式(3), J L 3 ( a ) - J L 3 (0) 可表示为
(9)
即, x 方向Eshelby张量的变化量 F ( a ) - F (0) 沿 L 3 积分的2倍就是裂纹扩展能量释放率,这里 F ( a ) 和 F (0) 分别表示有裂纹和无裂纹时 x 方向的Eshelby张量 .
当 L 3 位于 y 轴时,式(2)中的第二项为零,所以 x 方向Eshelby张量的变化量 F ( a ) - F (0) 可简化为应变能密度变化量 W ( a ) - W (0) ,这里 W ( a ) 和 W (0) 分别表示有裂纹和无裂纹时的应变能密度 . 所以,当 L 3 位于 y 轴时,
(10)
即,能量释放率等于应变能密度释放量 W (0) - W ( a ) 沿对称轴的积分, H y 表示 L 3 的 y 方向高度 .

图2 均匀材料无限大平面中心裂纹的远场积分路径L far 示意图
Fig. 2 Schematic of the far-field contour L far in a homogeneous infinite plane
在 y 轴的上半部分,发生应变能释放的区域为0≤ y ≤ fa ,这里 a 表示裂纹半长, f 是待求系数 . 从 y =0至 y = fa ,应变能密度释放量 W (0) - W ( a ) 逐渐由 W (0) 变为零 . 为计算 f 的最小值 f min ,假设在0≤ y < f min a 区间内 W (0) - W ( a ) = W (0) ,在 y ≥ f min a 区间 W (0) - W ( a ) =0 . 所以,
(11)
已知无限大平面中心裂纹的应力强度因子为
K Ⅰ ![]()
(12)
J far( a ) 与应力强度因子 K Ⅰ 的关系为
(13)
由式(8)、(11)、(12)、(13)可得
f min =π .
(14)
由式(8)、(11)、(14)可得
-∂ U /∂ a = J far( a ) =2π aW (0) .
(15)
所以,单位厚度均匀材料无限大平面中心裂纹的能量释放率-∂ U /∂ a 等于无裂纹时的应变能密度与圆周长2π a 的乘积,此圆以裂纹半长 a 为半径 .
如果沿 y 轴切开无限大平面, 则右半部分就变成含一条边裂纹的半无限大平面, 裂纹长度为 a , 其应力强度因子为 K Ⅰ ![]() 式(11)中的系数 f min 变为 f min =1.121 5 2 π=3.95≈4,能量释放率变为-∂ U /∂ a =7.9 aW (0) ≈8 aW (0) .
式(11)中的系数 f min 变为 f min =1.121 5 2 π=3.95≈4,能量释放率变为-∂ U /∂ a =7.9 aW (0) ≈8 aW (0) .
如图3所示,层状材料由 N 层A材料和 N +1层B材料构成,共2 N 个界面 . 假设 N 足够大,使对层状材料可以按无限大平面对待 . x 轴垂直于界面, y 轴平行于界面,裂纹位于 x 轴上,坐标原点位于裂纹中心 . 层状材料上下两端施加位移载荷 . 在没有裂纹时,层状材料中的应力由两部分组成:残余应力和两端位移载荷产生的应力 . A材料层和B材料层的 y 向应力分别为
(16)
这里 σ y AR , σ y BR 分别表示A,B材料层内的 y 向残余应力; σ y AE , σ y BE 分别表示由两端位移载荷在A,B材料层内产生的 y 向应力 .
图3 层状材料无限大平面中心裂纹的远场积分路径L far 示意图
Fig. 3 Schematic of the far-field contour L far for a central crack in an infinite plane of the layered material
无裂纹时,A材料层和B材料层内的应变能密度分别是
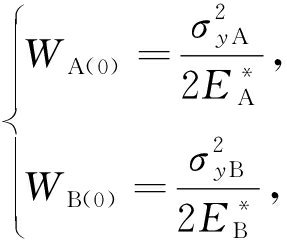
(17)
这里 ![]() 和
和 ![]() 分别表示A,B材料层在平面应变条件下的弹性模量,
分别表示A,B材料层在平面应变条件下的弹性模量, ![]() 界面两侧应变能密度差异产生界面 J 积分,界面 J 积分在引入裂纹前已存在 .
界面两侧应变能密度差异产生界面 J 积分,界面 J 积分在引入裂纹前已存在 .
如图3所示, L far 的上半部分由 L 1 , L 2 和 L 3 三段构成, L 1 和 L 2 远离裂尖位置, L 3 位于 y 轴 . 当裂纹被引入时,由于 L 1 和 L 2 远离裂纹, L 1 和 L 2 处的应力没有变化,对 J far( a ) - J far(0) 无贡献;只有 L 3 靠近裂纹的部分发生应力释放,对 J far( a ) - J far(0) 有贡献 . 所以, J far( a ) - J far(0) 可简化为
(18)
即, J far( a ) - J far(0) 等于 y 轴应变能密度释放量 W A(0) - W A( a ) 沿 y 轴的积分,这与均匀材料相同 .
第 i 个界面的 J 积分可表示为
J inf, i ( a ) - J inf, i (0) =
2 ![]() [( W (0) ( x i ,r , y )- W (0) ( x i ,l , y ))-( W ( a ) ( x i ,r , y )- W ( a ) ( x i ,l , y ))]d y ,
[( W (0) ( x i ,r , y )- W (0) ( x i ,l , y ))-( W ( a ) ( x i ,r , y )- W ( a ) ( x i ,l , y ))]d y ,
(19)
这里 x i ,r 和 x i ,l 分别表示第 i 个界面的右侧和左侧, x i ,r = x i ,l = x i , x i 表示第 i 个界面的 x 值 .
远场路径包围区域内所有界面 J 积分变化量之和为
(20)
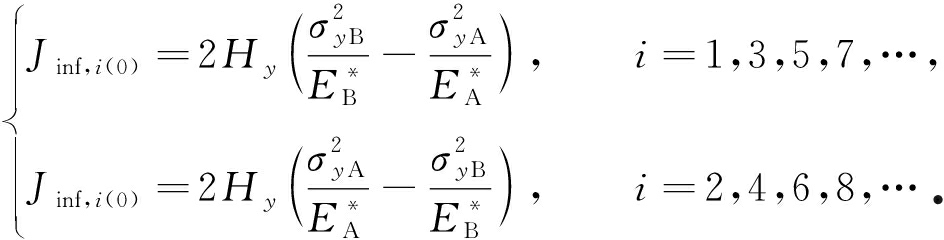
(21)
层状材料裂尖 J 积分与远场 J 积分、界面 J 积分的关系为
J tip = J far( a ) - J inf( a ) .
(22)
无裂纹时,远场 J 积分等于远场路径包围区域内的界面 J 积分之和,即
J far(0) = J inf(0) .
(23)
由式(22)、(23)可得
J tip =( J far( a ) - J far(0) )-( J inf( a ) - J inf(0) ),
(24)
J tip 是裂纹扩展能量释放率, J far( a ) - J far(0) 表示 y 轴处的应变能密度释放量沿 y 轴的积分 . 所以,与均匀材料不同,层状材料的能量释放率不等于应变能密度释放量沿 y 轴的积分,而等于应变能密度释放量沿 y 轴的积分减去界面 J 积分的改变量 .
远处载荷作用下的无限大平面引入裂纹只影响裂纹位置附近的应力应变场,远离裂纹处的应力应变不受裂纹的影响,所以引入裂纹导致的远场 J 积分变化量 J far( a ) - J far(0) 只与裂纹附近应力应变场的变化量有关 . 本文分析了均匀材料和层状材料无限大平面中心裂纹的 J far( a ) - J far(0) 转化为Eshelby张量变化量沿一条穿越裂纹的直线的积分 . 所得结论如下:
1) 对于均匀材料无限大平面中心裂纹, J far( a ) - J far(0) 等同于能量释放率,能量释放率等于Eshelby张量沿任意一条垂直穿越裂纹的直线的积分 . 能量释放率可用对称轴( y 轴)处的 W (0) - W ( a ) 沿 y 轴的积分表示,其值等于无裂纹时的应变能密度 W (0) 与2π a 的乘积,这里 a 是裂纹半长度, W (0) 和 W ( a ) 分别是无裂纹时和有裂纹时的应变能密度, W (0) - W ( a ) 表示引入裂纹所引起的应变能密度变化量 .
2) 对于含中心裂纹的均匀材料无限大平面,沿任一条垂直穿越裂纹的直线计算Eshelby张量的变化量 F (0) - F ( a ) 的积分就是能量释放率 .
3) 对于层状弹性材料无限大平面中的垂直于界面的裂纹, J far( a ) - J far(0) 等于对称轴处的 W (0) - W ( a ) 沿对称轴的积分,能量释放率等于对称轴处的 W (0) - W ( a ) 沿对称轴的积分减去界面 J 积分变化量 .
参考文献 ( References ):
[1] 嵇醒. 断裂力学判据的评述[J]. 力学学报, 2016, 48 (4): 741-753.(JI Xing. A critical review on criteria of fracture mechanics[J]. Chinese Journal of Theoretical and Applied Mechanics , 2016, 48 (4): 741-753.(in Chinese))
[2] WILLIAMS J G. The Griffith medal lecture: the fracture mechanics of soft solids[J]. Engineering Fracture Mechanics , 2015, 149 : 192-198.
[3] GRIFFITH A A. The phenomena of rupture and flow in solids[J]. Philosophical Transactions of the Royal Society of London , 1921, 221 (2): 163-198.
[4] IRWIN G R.Analysis of stresses and strains near the end of a crack traversing a plate[J]. Journal of Applied Mechanics , 1957, 24 : 361-364.
[5] 钟万勰. 力学与对称-离散: 祖冲之方法论[J]. 应用数学和力学, 2016, 37 (1): i-ii.(ZHONG Wanxie. Mechanics and symmetry-discretization: Zu-type methodology[J]. Applied Mathematics and Mechanics , 2016, 37 (1): i-ii.(in Chinese))
[6] GUO L C, KITAMURA T, YAN Y B, et al. Fracture mechanics investigation on crack propagation in the nano-multilayered materials[J]. International Journal of Solids and Structures , 2015, 64 / 65 : 208-220.
[7] YU H J, SUMIGAWA T, WU L Z, et al. Generalized domain-independent interaction integral for solving the stress intensity factors of nonhomogeneous materials[J]. International Journal of Solids and Structures , 2015, 67 / 68 : 151-168.
[8] 陈昌荣. 层状陶瓷的材料力和裂纹力评估方法[J]. 应用数学和力学, 2016, 37 (7): 748-755.(CHEN Changrong. A method for evaluating material forces and crack forces in ceramic laminates[J]. Applied Mathematics and Mechanics , 2016, 37 (7): 748-755.(in Chinese))
[9] CHEN C R, PASCUAL J, FISCHER F D, et al. Prediction of the fracture toughness of a ceramic multilayer composite: modeling and experiments[J]. Acta Materialia , 2007, 55 (2): 409-421.
[10] 陈昌荣. 层状弹性材料界面 J 积分的产生和特征[J]. 应用数学和力学, 2017, 38 (10): 1155-1165.(CHEN Changrong. Characteristics and generation of interface J -integrals in the layered elastic materials[J]. Applied Mathematics and Mechanics , 2017, 38 (10): 1155-1165.(in Chinese))
[11] 李群. 材料构型力学及其在复杂缺陷系统中的应用[J]. 力学学报, 2015, 47 (2): 197-214.(LI Qun. Material configurational mechanics with application to complex defects[J]. Chinese Journal of Theoretical and Applied Mechanics , 2015, 47 (2): 197-214.(in Chinese))
[12] 胡义锋, 胡翔, 师俊平. 含缺陷的弹塑性材料中构型体积力的研究[J]. 应用力学学报, 2015, 32 (4): 537-542.(HU Yifeng, HU Xiang, SHI Junping. Study on configurational volume force in defected elasto-plastic materials[J]. Chinese Journal of Applied Mechanics , 2015, 32 (4): 537-542.(in Chinese))
[13] 于宁宇, 李群. 基于数字散斑相关实验测量的材料构型力的计算方法[J]. 实验力学, 2014, 29 (5): 579-588.(YU Ningyu, LI Qun. On the algorithm of material configurational force based on digital image correlation measurement[J]. Journal of Experimental Mechanics , 2014, 29 (5): 579-588.(in Chinese))
[14] 古斌, 郭宇立, 李群. 基于构型力断裂准则的裂纹与夹杂干涉问题[J]. 力学学报, 2017, 49 (6): 1312-1321.(GU Bin, GUO Yuli, LI Qun. Crack interacting with an individual inclusion by the fracture criterion of configurational force[J]. Chinese Journal of Theoretical and Applied Mechanics , 2017, 49 (6): 1312-1321.(in Chinese))
[15] KUHN C, MULLER R. A discussion of fracture mechanism in heterogeneous materials by means of configurational forces in a phase field fracture model[J]. Computer Methods in Applied Mechanics and Engineering , 2016, 312 (1): 95-116.
[16] ESHELBY J D. The force on an elastic singularity[J]. Philosophical Transactions of the Royal Society of London , 1951, 244 (877): 87-112.
[17] RICE J R. A path independent integral and the approximate analysis of strain concentration by notches and cracks[J]. Journal of Applied Mechanics , 1968, 35 (2): 379-386.
[18] ESHELBY J D. The elastic energy-momentum tensor[J]. Journal of Elasticity , 1975, 5 (3/4): 321-335.
CHEN Changrong
( School of Air Transportation , Shanghai University of Engineering Science , Shanghai 201620, P . R . China )
Abstract: The difference between the J -integrals with and without a crack along a far-field contour was considered to analyze the energy release rate of the crack extension in an infinite plane. Two material cases were studied: a homogeneous material and a layered material. The constant displacement load was applied far from the crack, the crack was assumed to be perpendicular to the load, and the interfaces of the layered material were parallel to the load. The difference between the J -integrals with and without a crack represents the change of the far-field J -integral when a crack is introduced into the loaded material. For the central crack in a homogeneous infinite plane with a unit thickness, the energy release rate is the integral of the released strain energy density along the symmetry axis, and equals the product of the strain energy density without a crack and the perimeter of a circle, where the diameter of the circle is the crack length. For the central crack in an infinite plane of the layered material with a unit thickness, the energy release rate of crack extension equals the integral of the released strain energy density along the symmetry axis minus the change of the interface J -integral.
Key words: energy release rate; J -integral; material inhomogeneity; material interface; Eshelby tensor
Foundation item: The National Natural Science Foundation of China(51175321)
作者简介: 陈昌荣(1964—),男,教授,博士(E-mail: 13761742152@163.com).
基金项目: 国家自然科学基金(51175321)
修订日期: 2018-03-31
∗ 收稿日期: 2017-07-05;
ⓒ 应用数学和力学编委会,ISSN 1000-0887
文章编号 : 1000-0887(2018)10-1172-08
DOI: 10.21656/1000-0887.380191
文献标志码: A
中图分类号 : O346.1
引用本文 / Cite this paper: 陈昌荣. 利用有裂纹与无裂纹 J 积分之差分析裂纹扩展能量释放率[J]. 应用数学和力学, 2018, 39 (10): 1172-1179.CHEN Changrong. Analysis on the energy release rate considering the difference between J -integrals with and without a crack[J]. Applied Mathematics and Mechanics , 2018, 39 (10): 1172-1179.