马 晴, 王桂霞, 李联和
(内蒙古师范大学 数学科学学院, 呼和浩特 010022)
摘要 : 依据准晶弹性-流体动力学模型,采用有限差分方法,探讨了八次对称二维准晶Ⅱ型单边裂纹的动力学问题 . 首先分析了相同载荷的不同加载时间、不同的加载位置以及不同的试样尺寸对裂纹尖端处声子场应力强度因子的影响;其次分析了不同的声子场相位子场耦合弹性常数对相位子场位移分量的影响;最后分析了板端加载与裂纹面加载对动态应力强度因子的影响 . 计算结果表明:大小相同的脉冲载荷,加载的时间越长,无量纲化的应力强度因子越大,其曲线逐渐趋近于阶跃载荷下的曲线;试样宽度越宽,应力强度因子由零到非零需要的时间越长,无量纲化的应力强度因子值越小,说明应力强度因子与试样的尺寸有关系;声子场相位子场耦合弹性常数越大相位子场的位移分量也越大,这是因为相位子场的边界没有载荷,相位子场位移的作用力来自声子场,声子场起主导作用;而裂纹面加载和板端加载是不等价的,前者的无量纲化应力强度因子的变化幅度比后者大,这与板端加载更容易导致材料断裂的事实相一致 .
关 键 词 : 弹性-流体动力学模型; 有限差分格式; Ⅱ型裂纹; 应力强度因子
1984年准晶体的发现是凝聚态物理的一大突破 [1] . 此后,在国内外学者的努力之下,经过短短四十多年,有200多种准晶在不同的合金系中被发现 . 张泽等在Ti-V-Ni合金中发现了新的三维二十面准晶;冯国光等在急冷Al-Fe合金中发现了十次对称准晶;陈焕等在V-Ni-Si合金中发现了十二次对称准晶;王宁等在极冷凝固Cr-Ni-Si合金中发现了八次对称准晶;曹巍、周大顺等也分别在Mn-Si和Mn-Si-Fe中发现了八次对称准晶 [2] .
准晶体自发现以来,关于物理和力学性质的研究,引起了理论和实验工作者的极大兴趣 . 在研究过程中,人们发现准晶内部的裂纹会影响准晶材料的稳定性 . 为了解决准晶材料的不稳定性,其损伤机理和缺陷的研究成为人们关注的焦点 . 对于带裂纹的准晶静力学问题求解,尤其是分析解法的研究取得了大量有意义的成果 [2-9] ; 对于带裂纹的准晶动力学问题,相位子场动力学机理尚存在争议,Bak认为声子场和相位子场均为波动模式 [10-11] ,而Lubensky等认为相位子的运动模式应该是扩散模式 [12] . Fan(范天佑)等基于Lubensky等的观点提出了准晶弹性-流体动力学模型,得到了三维二十面体准晶反平面应变弹性动力学问题的控制方程,获得了位错动力学的近似分析解 [13] . Li(李显方)给出了十次对称准晶动力学问题的基本解 [14] . 张超华等研究了十次对称二维准晶材料的位错动力学问题 [15] .
对于准晶动力学的许多问题,即使做了很多限制,得到分析解仍然难度很大,或者只能把分析进行到某种程度 . 采用数值方法,对所研究的问题限制可以减少,能相对较好地模拟实际问题 . Zhu(祝爱玉)等利用有限差分方法研究了含裂纹的二维准晶的动力学问题 [16] ,Wang(王晓芳)等利用有限差分方法研究了点群10 mm二维准晶裂纹的起始扩展问题,讨论了相位子场在准晶动力学中的作用 [17] . Yin(尹志华)等 [18] 研究了五重对称准晶的裂纹起始问题和快速扩展问题 .
由于Ⅱ型裂纹八次对称二维准晶的复杂性,目前还没有关于其动力学问题解析解和数值解方面的研究 . 尹姝媛等发展了八次对称准晶材料的断裂理论,应用Fourier变换与对偶积分方程理论,得到了八次对称准晶材料Ⅱ型Griffith裂纹静力学问题的解析解 [19] . 李联和等通过引进新的应力势函数,获得八次对称二维准晶平面弹性问题的最终控制方程,采用发展了的Lekhnitskii方法,成功解决了椭圆缺口问题的位错问题 [2] . Zhu(祝爱玉)等采用Fourier变换方法求解了三维二十面体准晶的Ⅱ型裂纹问题 [20] ;郭玉翠等应用应力函数法,求解了二维十次对称准晶中的Ⅱ型Griffith裂纹问题 [21] .
依据范天佑等提出的弹性-流体动力学模型, 采用有限差分格式, 数值分析了有关八次对称二维准晶带Ⅱ型裂纹的动力学问题, 得到了声子场动态应力强度因子的数值解 . 通过加载不同时间的冲击载荷,对Ⅱ型裂纹尖端处的动态应力强度因子的动态响应进行了数值分析,讨论了试样尺寸对动态应力强度因子的影响以及声子场相位子场耦合弹性常数对相位子场位移分量的影响 .
本文选用的弹性-流体动力学方程为
(1)
对于八次对称二维准晶,讨论沿周期方向穿透整个材料的裂纹面的情况,在这种情况下有∂/∂ z =0 . 广义Hooke定律可简写为
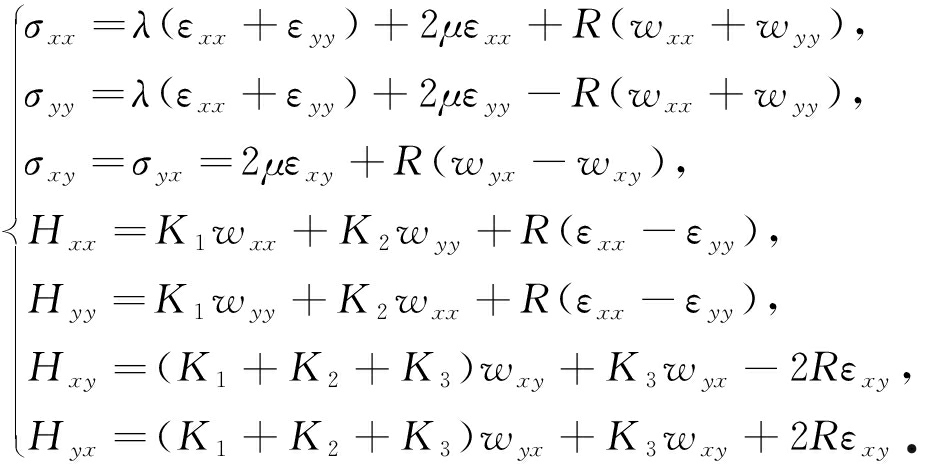
(2)
变形几何方程为
(3)
上式中, ρ 为准晶的密度, κ =1/ Γ w , Γ w 是相位子场动力学系数; σ ij 和 H ij 分别表示声子场和相位子场应力; u i 和 w i 分别是声子场和相位子场位移; ε ij 和 w ij 分别是声子场和相位子场应变; K 1 , K 2 和 K 3 是与相位子场相联系的3个非零独立弹性常数; R 是声子场相位子场耦合弹性常数 . μ =( C 11 - C 12 )/2, λ = C 12 是声子场弹性常数, C 11 , C 12 是两个与声子场有关的非零独立的弹性常数 .
将方程(2)和(3)代入方程(1), 有
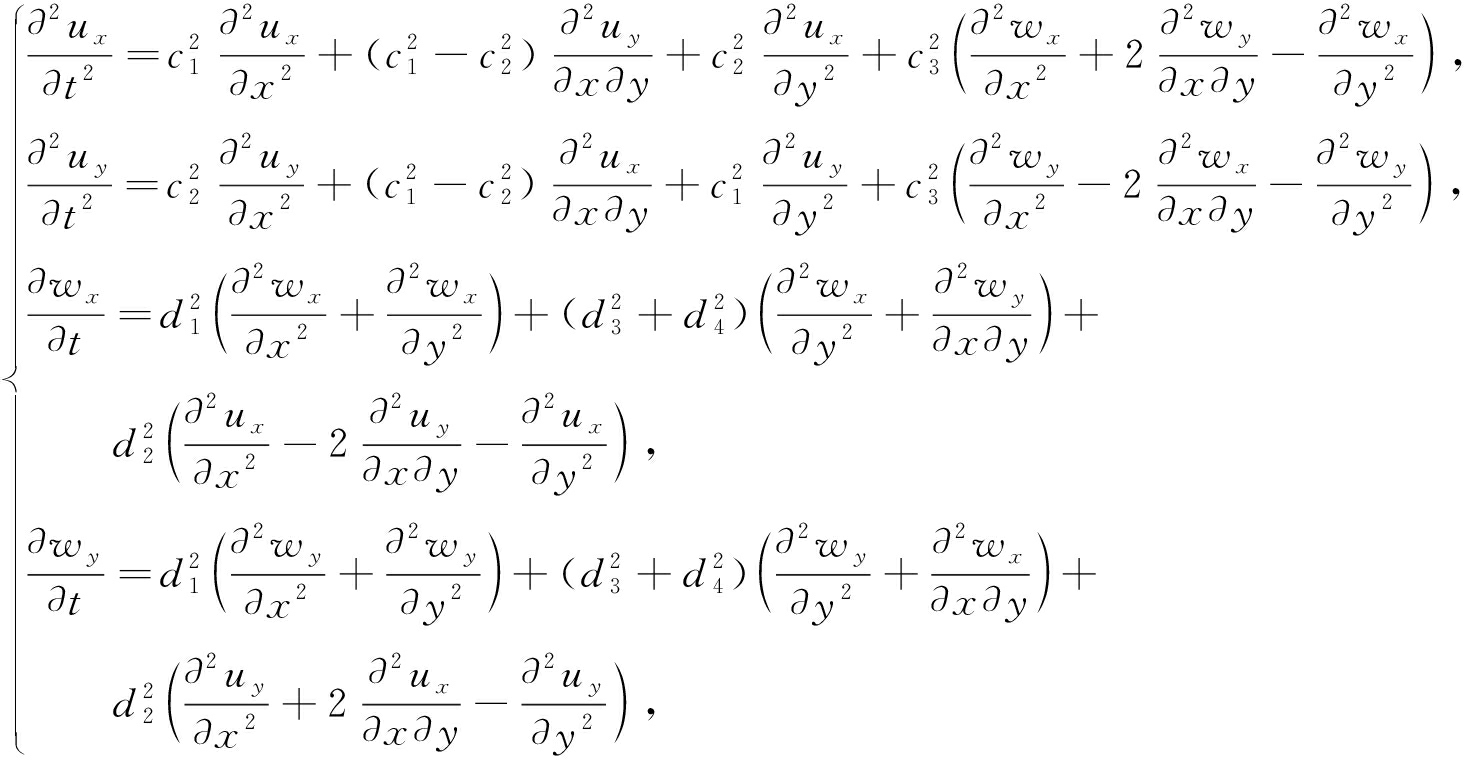
(4)
其中
设单边裂纹试样如图1所示 . 由于问题的反对称性,可以只研究其上半部分(如图2) .

图1 单边裂纹试样 图2 试样的上半部分
Fig. 1 The specimen with a unilateral crack Fig. 2 The upper part of the specimen
相应的边界条件为
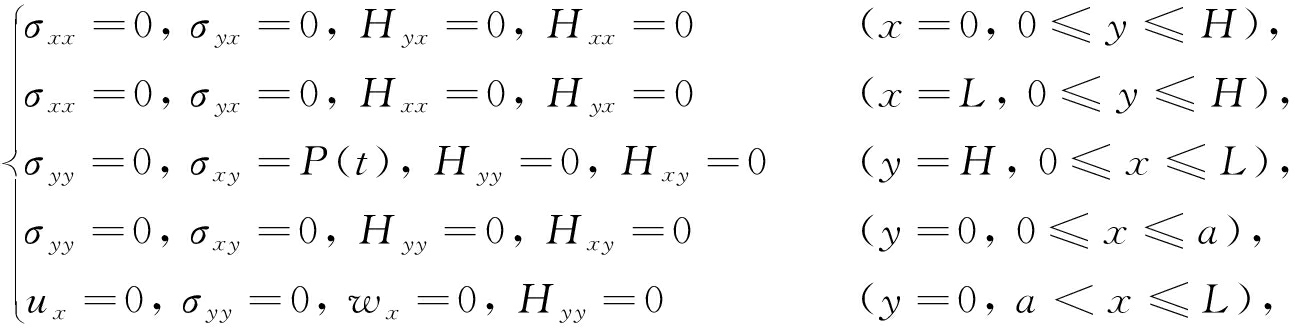
(5)
其中 P ( t )= P 0 ε( t )为动态加载函数,这里 P 0 是常数,ε( t )是Heaviside函数 .
对于瞬态动力学问题需要给出初始条件 . 本文仅研究零初始条件:
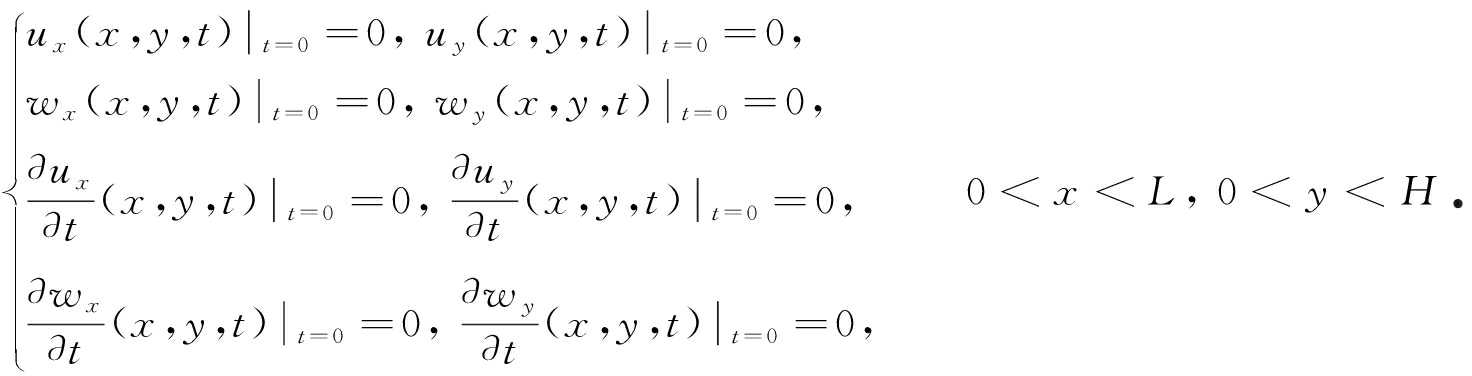
(6)
计算中, 空间步长Δ x 和Δ y 取值均为 h ,时间步长Δ t 记为 τ . 差分网格的划分如图3所示,裂纹尖端位于网格中点,稳定性条件是 c 1 τ / h =0.8 . 图中,板边界的4条网格线分别位于 x =- h /2, x = L + h /2, y =- h /2和 y = H + h /2处 . 在域内,采用了中心差分格式 .

图3 网格的划分 图4 阶跃载荷
Fig. 3 Scheme of the grid used Fig. 4 The step load
为了检验有限差分方法的可靠性和适用性,本文将八次准晶退化到晶体,在阶跃载荷(如图4所示)作用下,晶体的无量纲化应力强度因子的变化与文献[22]中的结果作了对比(见图5),数值结果与文献的结果基本一致 . 这说明了程序的正确性和适用性 .
Ⅱ型单边裂纹的无量纲化应力强度因子 K Ⅱ ![]() 其中
其中
(7)
目前,实验尚未测得八次二维对称准晶的密度、模量及声子场相位子场耦合弹性常数,所以文中选取了十次对称准晶中部分相关参数,取 a =12 mm, L =52 mm, P 0 =10 MPa, C 11 =2.343 0×10 12 dyn/cm 2 , C 12 =0.574 1×10 12 dyn/cm 2 , ρ =4.186×10 -3 g·mm -3 , K 1 =1.22 dyn/cm 2 , K 2 =0.24 dyn/cm 2 , K 3 =0.12 dyn/cm 2 , Γ w =4.8×10 -3 cm 3 ·μs/g .
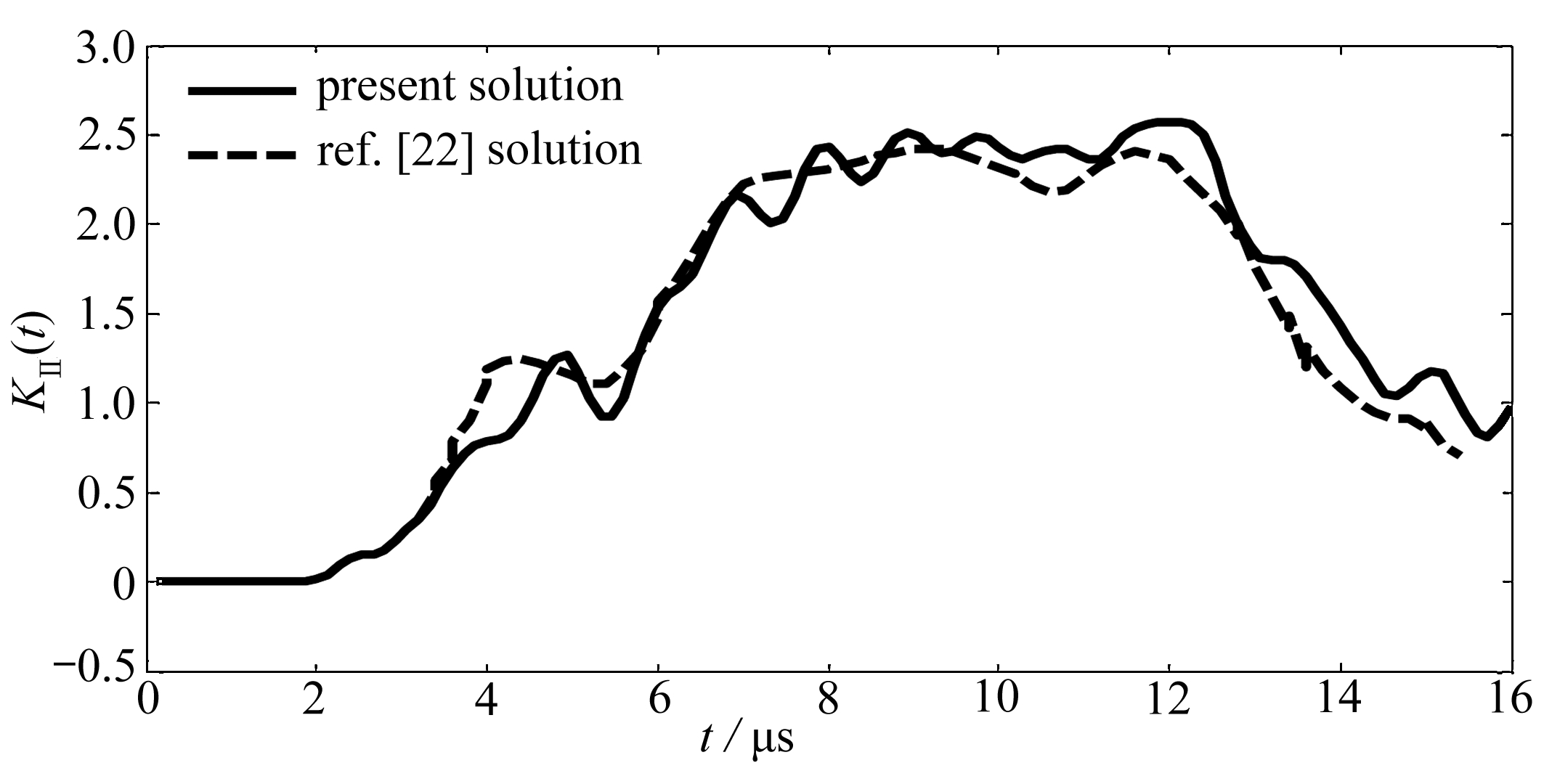
图5 晶体的无量纲化应力强度因子
Fig. 5 The normalized stress intensity factor of the crystal
2.3.1 载荷的不同加载时间对动态应力强度因子的影响
在实际情况中,外载多为脉冲载荷(如图6所示),因为和阶跃载荷(如图4所示)相比,脉冲载荷更接近实际情况 . 计算中假设 H =20 mm, R =0.01 μ . 在不同加载时间的矩形脉冲作用下,无量纲化动态应力强度因子的数值结果如图7所示 .
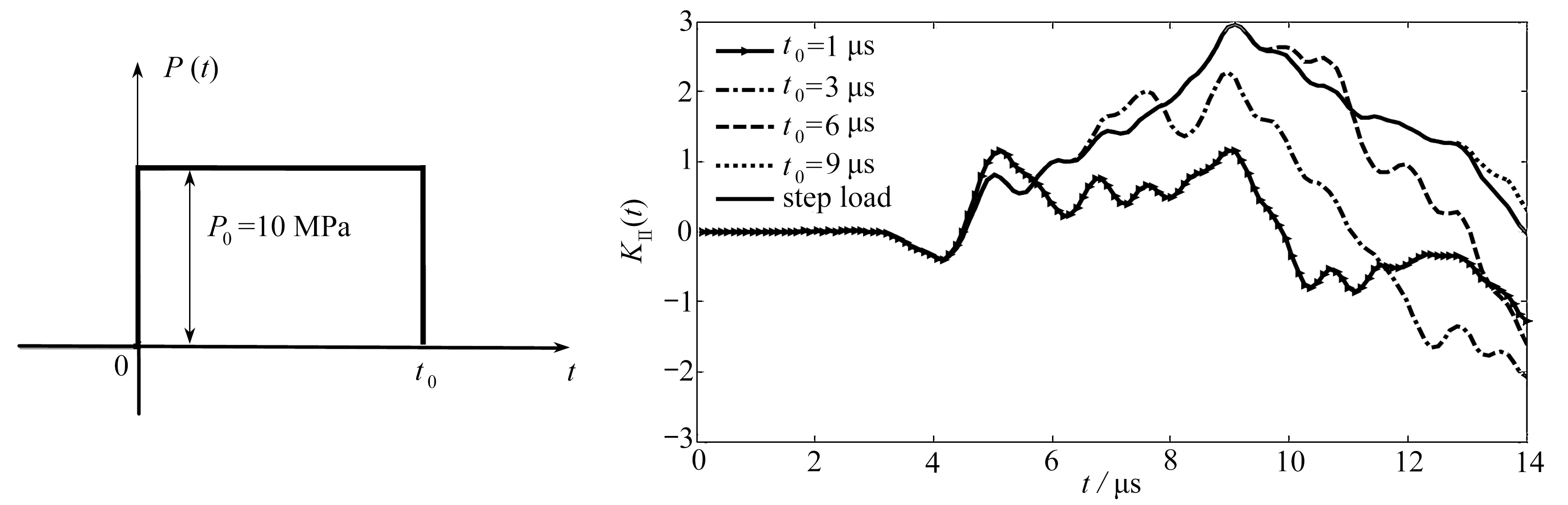
图6 矩形脉冲 图7 无量纲化动态应力强度因子
Fig. 6 The rectangular pulse Fig. 7 The normalized dynamic stress intensity factors
从图7中可以看出,随着加载时间 t 0 的增大,矩形脉冲作用下的无量纲化动态应力强度因子的峰值逐渐增大 . 动态应力强度因子的曲线逐渐趋近阶跃加载的曲线 . 其次,板端受载荷作用后,所产生的初始应力波从板端传播到裂纹尖端所需的时间大约为2.67 μs, 阶跃载荷在板内引起的应力波未到达裂纹表面时,应力强度因子为0, 则 H / t 0 =7.49 km/s,接近纵波的波速 ![]() 这说明了在相互耦合的复杂系统中, 声子场的波传播起主导作用, 这是因为相位子场的边界没有载荷 . 由于初始应力波与裂纹尖端相互作用, 使动态应力强度因子在2.67 μs处开始变化,先下降再上升 . 之后,对不同的加载时间 t 0 ,不同的曲线在不同的时间点达到局部峰值后,经过短暂的下降后开始上升,这是由初始应力波与尖端相互作用产生的纵波传播到最近的自由面后反射回到尖端并与尖端作用造成的 . 达到最大值后开始下降,这是由于初始应力波与裂纹发生作用而产生的横波从裂纹尖端传播到最近的自由面后,经反射再传到裂纹尖端造成的 .
这说明了在相互耦合的复杂系统中, 声子场的波传播起主导作用, 这是因为相位子场的边界没有载荷 . 由于初始应力波与裂纹尖端相互作用, 使动态应力强度因子在2.67 μs处开始变化,先下降再上升 . 之后,对不同的加载时间 t 0 ,不同的曲线在不同的时间点达到局部峰值后,经过短暂的下降后开始上升,这是由初始应力波与尖端相互作用产生的纵波传播到最近的自由面后反射回到尖端并与尖端作用造成的 . 达到最大值后开始下降,这是由于初始应力波与裂纹发生作用而产生的横波从裂纹尖端传播到最近的自由面后,经反射再传到裂纹尖端造成的 .
2.3.2 试样宽度对动态应力强度因子的影响
计算中,试样的宽度 H 分别取20,30,40 mm, R =0.01 μ . 无量纲化动态应力强度因子结果如图8所示 .
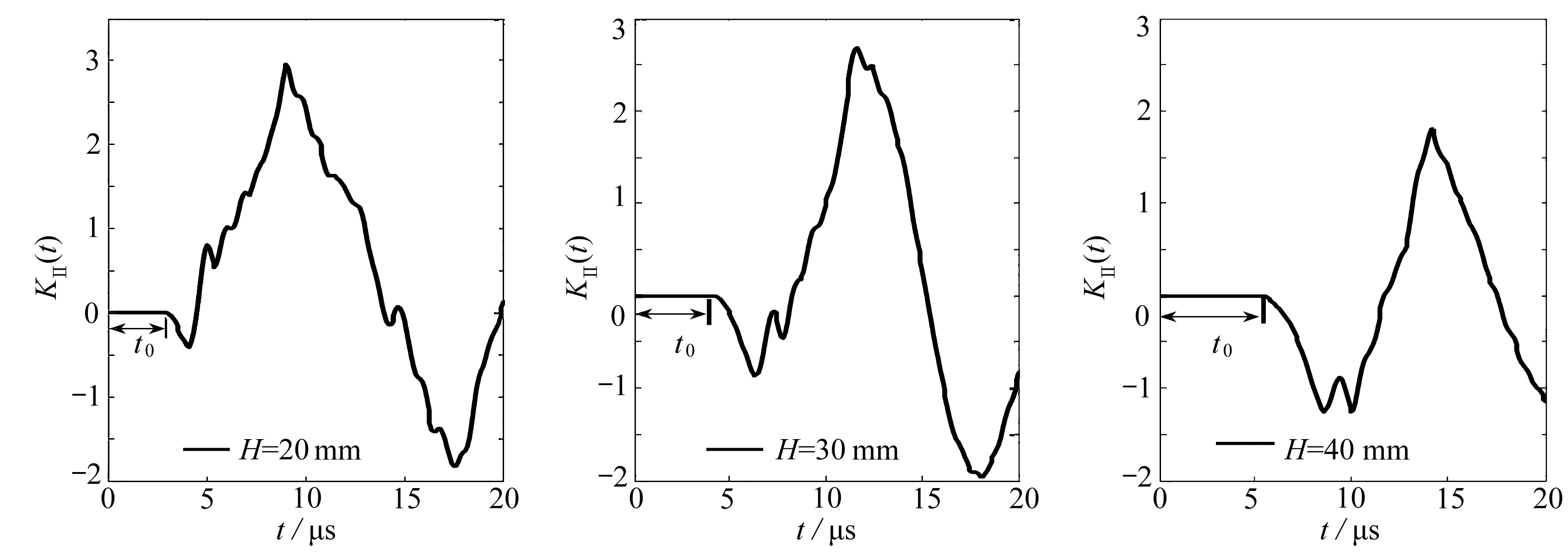
图8 应力强度因子对材料尺寸的响应
Fig. 8 The responses of normalized dynamic stress intensity factors to material sizes
显然,随着试样板宽的增大,应力波到达尖端的时间越来越长,可达到的峰值越来越小,达到峰值所需的时间越来越长 . 图8中反映了这种趋势,宽度 H =20 mm时,应力波到达裂纹尖端的时间 t 0 =2.67 μs; H =30 mm时, t 0 =4.03 μs; H =40 mm时, t 0 =5.34 μs . 曲线达到峰值的时间分别为9.09, 11.66, 14.11 μs,所对应的无量纲化后应力强度因子值为2.96,2.68,1.80 . 这说明,各种应力波与裂纹尖端相互作用的先后顺序与作用时间随试样宽度的变化而变化,从而影响应力强度因子的峰值 .
2.3.3 声子场相位子场耦合弹性常数的影响
计算中假设 H =20 mm . 对于不同的声子场相位子场耦合弹性常数 R ,相位子场位移随时间的变化如图9所示 .

图9 相位子场位移分量w x 随时间的变化
Fig. 9 The displacement component of phason field w x vs. time
当 R ≠0时,相位子场的位移分量 w x 有扩散趋势且与声子场相位子场耦合弹性常数 R 有关 . 在图9中,当 R =0时,相位子的位移分量是为0的,这是因为相位子场的边界没有载荷,相位子场位移分量的作用力来源于声子场,这说明了在耦合作用中,声子场起主导作用 . 对比 R =0.01 μ 及 R =0.02 μ 所对应的两条曲线,在 t =2.88 μs前,相位子场位移分量为0,之后相位子场位移分量均呈现扩散的趋势,且 R =0.02 μ 所对应的相位子场位移分量大于 R =0.01 μ 所对应的位移分量值 . 即,随着声子场相位子场耦合弹性常数 R 的增大,相位子场的位移分量 w x 也逐渐变大 .
2.3.4 板端加载与裂纹面加载对动态应力强度因子的影响
板端加载(图1)与裂纹面加载(图10)的动态应力强度因子数值结果如图11所示 .

图10 裂纹面加载 图11 动态应力强度因子
Fig. 10 Loading on the crack surface Fig. 11 Dynamic stress intensity factors
从图11中可见,不同位置上的加载会导致应力强度因子的结果明显不同,二者不能等价 . 对于板端加载,开始一段时间应力强度因子为0,表示阶跃载荷在板内引起的应力波并没有立刻到达裂纹表面 . 对于裂纹面加载,应力强度因子从加载开始就发生了变化,这是很容易理解的,因为初始应力波的传播时间与距离有关 . 其次,裂纹面加载的动态应力强度因子基本维持在初值附近做小的波动,板端加载比裂纹面加载的应力强度因子变化幅度大得多,所以板端加载更容易导致断裂 .
本文利用有限差分方法,研究了八次对称准晶Ⅱ型单边裂纹的动力学问题 . 对声子场应力强度因子以及相位子场的位移分量的影响因素进行了分析 . 结果表明,声子场应力强度因子与脉冲载荷的加载时间以及试样尺寸有关,而相位子场的位移分量与声子场相位子场耦合弹性常数有关 . 大小相同的脉冲载荷,加载的时间越长,无量纲化的应力强度因子越大,其曲线逐渐趋近于阶跃载荷下的曲线;试样宽度越宽,应力强度因子由零到非零需要的时间越长,无量纲化的应力强度因子值越小;声子场相位子场耦合弹性常数越大相位子场的位移分量也越大,这是因为相位子场的边界没有载荷,相位子场位移的作用力来自声子场,声子场起主导作用 . 本文分别在零初始条件下,计算了板端加载和裂纹面加载时的响应,由计算所得的无量纲化应力强度因子与时间 t 的关系图表明,裂纹面加载和板端加载是不等价的,前者的无量纲化应力强度因子的变化幅度比后者大,这与板端加载更容易导致材料断裂的事实相一致 .
致谢 本文作者衷心感谢内蒙古师范大学研究生科研创新基金(CXJJS16082)对本文研究的资助 .
参考文献 ( References ):
[1] SHECHTMAN D, BLECH I, GRATIAS D, et al. Metallic phase with long-range orientational order and no translational symmetry[J]. Physical Review Letters , 1984, 53 (20): 1951-1953.
[2] 李联和, 刘官厅. 准晶断裂力学的复变函数方法[M]. 北京: 科学出版社, 2013.(LI Lianhe, LIU Guanting. Quasicrystal Fracture Mechanics of Complex Variable Function Method [M]. Beijing: Science Press, 2013.(in Chinese))
[3] YANG W, FEUERBACHER M, TAMURA N, et al. Atomic model of dislocations in Al-Pd-Mn icosahedral quasicrytals[J]. Philosophical Magazine A , 1998, 77 (6): 1481-1497.
[4] WANG X. Green functions for a decagonal quasicrystalline material with a parabolice boundary[J]. Acta Mechanica Solida Sinica , 2005, 18 (1): 57-62.
[5] WANG X, ZHANG J Q. A steady line heat source in a decagonal quasicrystalline half-space[J]. Mechanics Research Communications , 2005, 32 (4): 420-428.
[6] CHEN W Q, MA Y L, DING H J. On three-dimensional elastic problems of one-dimensional hexagonal quasicrystal bodies[J]. Mechanics Research Communications , 2004, 31 (6): 633-641.
[7] GAO Y, XU S P, ZHAO B S. Boundary conditions for plate bending in one-dimensional hexagonal quasicrystals[J]. Journal of Elasticity , 2007, 86 (3): 221-233.
[8] 郭俊宏, 刘官厅. 一维六方准晶中具有不对称裂纹的圆形孔口问题的解析解[J]. 应用数学学报, 2007, 30 (6): 1066-1075.(GUO Junhong, LIU Guanting. Analytic solutions of the one-dimensional hexagonal quasicryst about problem of a circular hole with asymmetry cracks[J]. Acta Mathematicae Applicatae Sinica , 2007, 30 (6): 1066-1075.(in Chinese))
[9] LI X Y. Elastic field in an infinite medium of one-dimensional hexagonal quasicrystal with a planar crack[J]. International Journal of Solids & Structures , 2014, 51 (6): 1442-1455.
[10] BAK P. Phenomenological theory of icosahedral incommensurate (“quasiperiodic”) order in Mn-Al alloys[J]. Physical Review Letters , 1985, 54 (14): 1517-1519.
[11] BAK P. Symmetry, stability, and elastic properties of icosahedral incommensurate crystals[J]. Physical Review B : Condensed Matter , 1985, 32 (9): 5764-5772.
[12] LUBENSKY T C, RAMASWAMY S, TONER J. Hydrodynamics of icosahedral quasicrystals[J]. Physical Review B : Condensed Matter , 1985, 32 (11): 7444-7452.
[13] FAN T Y, WANG X F, LI W, et al. Elasto-hydrodynamics of quasicrystals[J]. Philosophical Magazine , 2009, 89 (6): 501-512.
[14] LI X F. Elastohydrodynamic problems in quasicrystal elasticity theory and wave propagation[J]. Philosophical Magazine , 2013, 93 (13): 1500-1519.
[15] 张超华, 李联和, 云国宏. 十次对称二维准晶材料的位错动力学问题[J]. 固体力学学报, 2017, 38 (2): 165-169.(ZHANG Chaohua, LI Lianhe,YUN Guohong. Study on moving dislocations in decagonal quasicrystals[J]. Chinese Journal of Solid Mechanics , 2017, 38 (2): 165-169.(in Chinese))
[16] ZHU A Y, FAN T Y. Dynamic crack propagation in decagonal Al-Ni-Co quasicrystal[J]. Journal of Physics Condensed Matter , 2008, 20 (20): 295217.
[17] WANG X F, FAN T Y, ZHU A Y. Dynamic behaviour of the icosahedral Al-Pd-Mn quasicarystal with a Griffith crack[J]. Chinese Physics B , 2009, 18 (2): 709-714.
[18] YIN Z H, FAN T Y, ZHU A Y. Dynanmic crack propagation in five-fold symmetry quasicrystals[J]. Modern Physics Letters B , 2009, 23 (12): 1509-1518.
[19] 尹姝媛, 周旺民, 范天佑. 八次对称准晶中的Ⅱ型裂纹[J]. 应用数学和力学, 2002, 23 (4): 376-380.(YIN Shuyuan, ZHOU Wangmin, FAN Tianyou. A model Ⅱ crack in a two-dimensional octagonal quasicrystals[J]. Applied Mathematics and Mechanics , 2002, 23 (4): 376-380.(in Chinese))
[20] ZHU A Y, FAN T Y. Elastic analysis of a mode Ⅱ crack in an icosahedral quasicrystal[J]. Chinese Physics , 2007, 16 (4): 1111-1118.
[21] 郭玉翠, 范天佑. 平面十次对称准晶中Ⅱ型中Griffith裂纹的求解[J]. 应用数学和力学, 2001, 22 (11): 1181-1186.(GUO Yucui, FAN Tianyou. A model-Ⅱ Griffith crack in decagonal quasicrytals[J]. Applied Mathematics and Mechanics , 2001, 22 (11): 1181-1186.(in Chinese))
[22] 郝莉. Ⅱ型动态裂纹的动态应力强度因子的数值分析[J]. 北京建筑工程学院学报, 1998, 14 (3): 72-84.(HAO Li. The numerical analysis about dynamic stress intensity factor of Ⅱ dynamic crack[J]. Journal of Beijing Institute of Civil Engineering and Architecture , 1989, 14 (13): 72-84.(in Chinese))
MA Qing, WANG Guixia, LI Lianhe
( College of Mathematics Science , Inner Mongolia Normal University , Hohhot 010022, P . R . China )
Abstract: Based on the elasto-hydrodynamic model, the dynamic problems of mode Ⅱ cracks in octagonal 2D quasicrystals were investigated with the finite difference scheme. The dynamic responses of stress intensity factors to different loading periods and different specimen sizes were analyzed, respectively. Then the influence of different phonon-phason coupling elastic constants on the displacement component of the phason field was demonstrated. The results indicate that, the stress intensity factor increases with the loading period, while the curve approaches the curve under the step load. The wider the specimen size is, the longer the time will be for the stress wave to reach the crack tip, and the smaller the stress intensity factor will be. The crack loading is different from the board loading, for the change of the stress intensity factor under the former is greater than that under the latter. With the increasing phonon-phason coupling constant, the displacement component of the phason field rises. Because of the influence of the phonon and phonon-phason coupling effect, the displacement component of the phason field equals zero when the phonon-phason coupling constant is zero.
Key words: elasto-hydrodynamic model; finite difference method; mode Ⅱ crack; stress intensity factor
Foundation item: The National Key R&D Program of China(2017YFC1405600);The National Natural Science Foundation of China(11462020;11361039)
ⓒ 应用数学和力学编委会,ISSN 1000-0887
文章编号 : 1000-0887(2018)10-1180-09
作者简介: 马晴(1989—),女,硕士生(E-mail: 940972965@qq.com);王桂霞(1968—),女,教授,博士(通讯作者. E-mail: nsdwgx@126.com).
基金项目: 国家重点研发计划(2017YFC1405600);国家自然科学基金(11462020;11361039);内蒙古自然科学基金(2017MS0104;2017MS0124;2017MS0125);内蒙古自治区高等学校科学研究项目(NJZY17045)
修订日期: 2018-02-26
∗ 收稿日期: 2017-10-27;
DOI: 10.21656/1000-0887.380272
文献标志码: A
中图分类号 : O346.1; O242.1; O343
引用本文 / Cite this paper: 马晴, 王桂霞, 李联和. 八次对称二维准晶Ⅱ型单边裂纹的动力学问题[J]. 应用数学和力学, 2018, 39 (10): 1180-1188.MA Qing, WANG Guixia, LI Lianhe. Dynamic problems of mode Ⅱ cracks in 2D octagonal quasicrystals[J]. Applied Mathematics and Mechanics , 2018, 39 (10): 1180-1188.