杨 娜, 陈龙伟, 熊 梅
(云南财经大学 统计与数学学院, 昆明 650221)
摘要 : 利用动力系统方法,针对广义带导数的非线性Schrödinger方程的精确解问题进行研究分析 . 采用行波变换,将其化为常微分方程动力系统;计算出该方程动力系统的首次积分,讨论了系统在不同参数条件下的奇点与相图,得到对应的精确解,包括孤立波解、周期波解、扭结波解和反扭结波解 . 运用数值模拟的方法,对方程的光滑孤立波解和周期波解等进行了数值模拟 . 分析计算获得的结果完善了相关文献已有的研究成果 .
关 键 词 : 非线性Schrödinger方程; 动力系统; 孤立波解
非线性偏微分方程是现代数学一个重要的分支组成 . 近些年来,众多研究者在研究分析中得到了许多可行的求解非线性偏微分方程精确解的方法,如:tanh函数法 [1-2] 、首次积分法 [3] 、 G ′/ G 展开法 [4] 、Jacobi椭圆函数展开法 [5] 等 . 文献[6-8]详细研究了偏微分方程的行波精确解及其分支 . 而用动力系统的方法 [9] 来求解偏微分方程精确解也颇受研究者们重视 . 在文献[10-12]中,利用动力系统的方法求解了偏微分方程 .
广义带导数的非线性Schrödinger方程是一个非常重要的非线性偏微分方程,关于此方程的研究,已经吸引了很多的数学和物理研究学者的注意 . 文献[13]运用齐次平衡法对此方程进行分析研究 . 文献[14]运用Hirota方法对此类方程进行研究 . 本文将对下面的广义带导数的非线性Schrödinger方程,应用动力系统方法来求解这个模型的精确解 . 目前为止,尚未有研究者用动力系统方法对下面的方程进行研究:
i u x = u tt +2 ![]() u +i α (
u +i α ( ![]() u ) t +i β (
u ) t +i β ( ![]() ) t u + γ
) t u + γ ![]() u ,
u ,
(1)
在这里 α , β , γ 为实常数,而 u 是一个复函数 .
为了得到方程(1)的精确解,假设
(2)
其中, c , k , w 为实参数 . 将式(2)代入式(1)中,并分离实部和虚部,可得到一个常微分方程组:
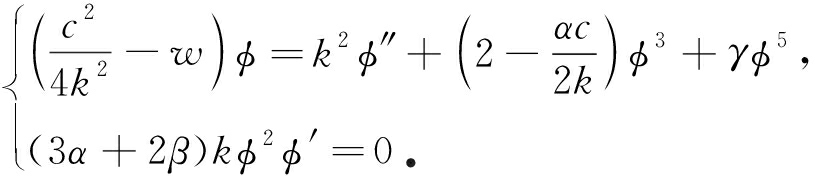
(3)
为了得到方程(1)的非平凡解,需假设3 α +2 β =0且 k ≠0,那么
(4)
为了方便计算,令
则
φ ″= Aφ 5 + Bφ 3 + Cφ .
(5)
假设d φ /d ξ = y ,于是式(5)等价于下面的二维平面系统:
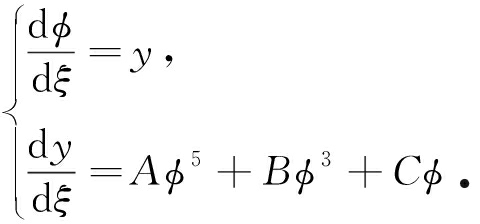
(6)
该系统有如下首次积分:
(7)
系统(6)对应的奇点( φ , y )需满足
则该系统有奇点 E 0 (0,0), E 1 ( φ 1 ,0), E 2 ( φ 2 ,0), E 3 ( φ 3 ,0), E 4 ( φ 4 ,0),其中
且 φ 1 ≠ φ 2 , φ 3 ≠ φ 4 . 本文只讨论坐标为实数的奇点,而奇点个数取决于对应的参数空间 . 只有一个奇点 E (0,0)的情况较为简单,本文不做具体分析 .
接下来,借助线性系统(6)的系数矩阵
的Jacobi行列式,来判定奇点类型 . 从而可知
J (0,0)=det M (0,0)=- C ,
J ( φ 1,2 ,0)=det M ( φ 1,2 ,0)=-5 A ( φ 1,2 ) 4 -3 B ( φ 1,2 ) 2 - C ,
J ( φ 3,4 ,0)=det M ( φ 3,4 ,0)=-5 A ( φ 3,4 ) 4 -3 B ( φ 3,4 ) 2 - C .
根据Hamilton(哈密尔顿)量 H 等于动能加势能 [15] . 势能为
势能的极大值为鞍点,极小值为中心,拐点为尖点(退化) . 又根据平面动力系统定理,对于平面可积系统的奇点, 若 J <0,那么该奇点为鞍点; 若 J >0且(tr M ) 2 -4 J <0(或>0),那么该奇点为中心(或结点) . 下面划分参数空间,用Jacobi行列式来判断奇点的类型,并对应于不同的参数空间,利用MAPLE软件画出相图(如图1) . 从图中可以看出:
情况1 A >0, B <0, C >0时,如图1(a)中,系统(6)有5个奇点,其中 E (0,0)是鞍点, E ( φ 1,2 ,0)是鞍点, E ( φ 3,4 ,0)是中心 .
情况2 A >0, C <0时,如图1(b)、1(c)中,系统(6)有3个奇点,其中 E (0,0)是中心, E ( φ 1,2 ,0)是鞍点 .
情况3 A <0, C >0时,如图1(d)、1(e)中,系统(6)有3个奇点,其中 E (0,0)是鞍点, E ( φ 3,4 ,0)是中心 .
情况4 A <0, B >0, C <0时,如图1(f)中,系统(6)有5个奇点,其中 E (0,0)是中心, E ( φ 1,2 ,0)是鞍点, E ( φ 3,4 ,0)是中心 .

(a) A>0, B<0, C>0(b) A>0, B<0, C<0(c) A>0, B>0, C<0
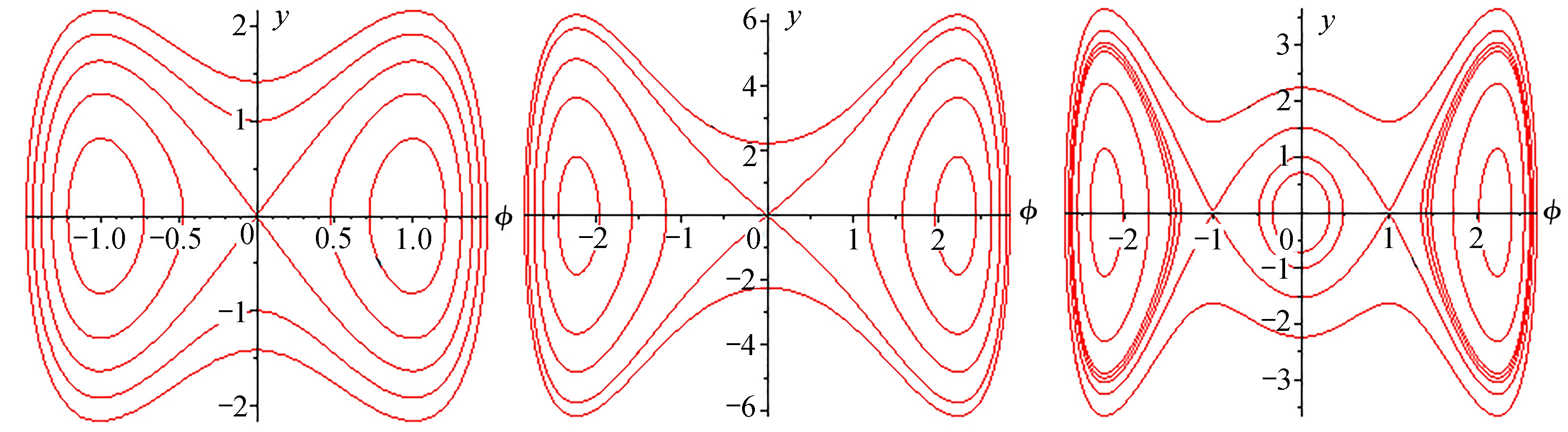
(d) A<0, B<0, C>0(e) A<0, B>0, C>0(f) A<0, B>0, C<0
图1 系统(6)的相图分支
Fig. 1 Bifurcations of phase portraits of system (6)
在这一部分,将根据上一部分中给出的相图轨道,通过定性分析结合三角函数和Jacobi椭圆函数等,讨论方程(1)的行波解 .
由式(7),可以得出
(8)
为方便计算,引入中间变量 φ = φ 2 ,于是 φ 1 =( φ 1,2 ) 2 , φ 2 =( φ 3,4 ) 2 ,则
那么,式(8)变为
令 Y =d φ /d ξ ,上式可写成
(9)
对情况1,当 A >0, B <0, C >0时,如图1(a),0< φ 2 < φ 1 ,记 h 1 = H ( φ 1 ,0), h 2 = H ( φ 2 ,0),那么此时 h 1 <0< h 2 .
① 当 h = h 1 时,系统(6)存在着两个被 H ( φ , Y )= h = h 1 定义的异宿轨道 . 此时 Y 2 =(4/3) A ( φ 1 - φ ) 2 φ ( φ - φ l ),系统(6)存在扭结波解和反扭结波解:
(10)
其中
0< φ 0 < φ 1 , A 1 = φ 1 ( φ 1 - φ l ), B 1 =-(2 φ 1 - φ l ),
由式(10)得方程(1)有如下精确扭结波解:
(11)
② 当 h ∈( h 1 ,0)时,系统(6)存在着一族围绕着 E 0 , E 3 , E 4 的周期轨道 . 此时 ![]() 系统(6)存在周期波解:
系统(6)存在周期波解:
(12)
其中
由式(12)得方程(1)有如下精确周期波解:
(13)
③ 当 h =0时,系统(6)存在着两个被 H ( φ , Y )= h =0定义的同宿轨道 . 此时 Y 2 =(4/3) Aφ 2 ( φ - φ M )( φ - φ m ),系统(6)存在孤立行波解:
(14)
(15)
其中, ![]() 由式(14)和(15)得方程(1)有如下精确孤立波解:
由式(14)和(15)得方程(1)有如下精确孤立波解:
(16)
(17)
④ 当 h ∈(0, h 2 )时, 系统(6)存在着两族分别围绕着 E 3 , E 4 的周期轨道 . 此时 Y 2 =(4/3) A ( φ - r 1 )( r 2 - φ ) φ ( r 3 - φ ), Y 2 =(4/3) A ( φ - r 1 )( φ - r 2 ) φ ( φ - r 3 ),系统(6)的左边的周期轨道对应如下表达式:
(18)
系统(6)的右边的周期轨道对应如下表达式:
(19)
其中
由式(18)和(19)得方程(1)有如下精确周期波解:
(20)
(21)
对情况2,当 A >0, C <0时,如图1(b)、1(c), φ 1 >0,那么此时 h 1 <0 .
① 当 h = h 1 时, 系统(6)存在着两个被 H ( φ , Y )= h = h 1 定义的异宿轨道 . 此时 Y 2 =(4/3) A ( φ 1 - φ ) 2 φ ( φ - φ n ),系统(6)存在扭结波解和反扭结波解:
(22)
其中
0< φ 0 < φ 1 , A 2 = φ 1 ( φ 1 - φ n ), B 2 =-(2 φ 1 - φ n ),
由式(22)得方程(1)有如下精确扭结波解:
(23)
② 当 h ∈( h 1 ,0)时,系统(6)存在着一族围绕着 E 0 的周期轨道 . 此时 Y 2 =(4/3) A ( φ - s 1 )( φ - s 2 ) φ ( φ - s 3 ),系统(6)存在周期波解:
(24)
其中
由式(24)得方程(1)有如下精确周期波解:
(25)
③ 当 h ∈(0,∞)时,系统(6)存在着被 H ( φ , Y )= h ∈(0,∞)定义的一系列有界开轨道 . 此时 Y 2 =(4/3) Aφ 2 ( φ - φ N )( φ - φ n ),系统(6)存在如下行波解:
(26)
(27)
其中, ![]() 注意到 φ N φ n =3 C / A <0 . 由式(26)和(27)得方程(1)有如下精确孤立波解:
注意到 φ N φ n =3 C / A <0 . 由式(26)和(27)得方程(1)有如下精确孤立波解:
(28)
(29)
对情况3,当 A <0, C >0时,如图1(d)、1(e), φ 2 >0,此时 h 2 >0 .
① 当 h ∈(-∞,0)时,系统(6)存在着一族围绕着平衡点 E 0 , E 3 , E 4 的周期轨道 . 那么此时, H ( φ , Y )= h 的表达式与情况1中的②相同,所以可以得到与式(13)相同的周期波解 .
② 当 h =0时,系统(6)有着两个被 H ( φ , Y )= h =0定义的同宿轨道 . 此时, H ( φ , Y )= h 的表达式与情况1中的③相同,所以可以得到分别与式(16)和(17)相同的孤立行波解 .
③ 当 h ∈(0, h 2 )时,系统(6)有着两族分别围绕着 E 3 , E 4 的周期轨道 . 此时, H ( φ , Y )=0的表达式与情况1中的④相同,所以可以得到分别与式(20)和(21)相同的周期波解 .
对情况4,当 A <0, B >0, C <0时,如图1(f),0< φ 1 < φ 2 ,此时 h 1 <0< h 2 .
① 当 h ∈(-∞, h 1 )时,系统(6)有着围绕着平衡点 E 1 , E 2 , E 3 , E 4 的一族周期轨道 . 此时, H ( φ , Y )= h 的表达式与情况1中的②相同,所以可以得到与式(13)相同的周期波解 .
② 当 h = h 1 时,系统(6)有着两个被 H ( φ , Y )= h = h 1 定义的异宿轨道 . 此时 Y 2 =(4/3) A ( φ - φ 1 ) 3 φ ,系统(6)存在扭结波解和反扭结波解:
(30)
由式(23)得方程(1)有如下精确扭结波解:
(31)
③ 当 h ∈( h 1 ,0)时,系统(6)有着一族围绕着 E 0 的周期轨道 . H ( φ , Y )= h 的表达式与情况2中的②相同,所以可以得到与式(25)相同的周期波解 .
④ 当 h ∈(0, h 2 )时,系统(6)有着两族分别围绕着 E 3 , E 4 的周期轨道 . 此时, H ( φ , Y )= h 的表达式与情况1中的④相同,所以可以得到分别与式(20)和(21)相同的周期波解 .
本文主要采用动力系统方法,对广义带导数的非线性Schrödinger方程进行动态分析,并求得精确行波解 . 动力系统方法不仅可以得到非线性偏微分方程的精确解,而且有利于研究学者对非线性行波方程的动态分析 . 本文对广义带导数的非线性Schrödinger方程动态分析的结果,体现了行波结构的多样性,具有一定的研究意义 .
参考文献 ( References ):
[1] WAZWAZ A M. The extended tanh method for new compact and noncompact solutions for the KP-BBM and the ZK-BBM equations[J]. Chaos , Solitons and Fractals , 2008, 38 (5): 1505-1516.
[2] 徐振民, 李柱. 推广的tanh-函数法及其应用[J]. 广西民族大学学报(自然科学版), 2009, 15 (3): 54-56.(XU Zhenmin, LI Zhu. Extended tanh-function method and its applications[J]. Journal of Guangxi University for Nationalities ( Natural Science Edition ), 2009, 15 (3): 54-56.(in Chinese))
[3] ABBASBANDY S, SHIRZADI A. The first integral method for modified Benjamin-Bona-Mahony equation[J]. Communications in Nonlinear Science and Numerical Simulation , 2010, 15 (7): 1759-1764.
[4] BILIGE S, CHAOLU T. A generalized ( G ′/ G )-expansion method and its applications[J]. Journal of Inner Mongolia University ( Natural Science Edition ), 2011, 42 (1): 12-20.
[5] CHEN Y, WANG Q. Extended Jacobi elliptic funtion rational expansion method and abundant families of Jacobi elliptic functions solutions to (1+1)-dimensional dispersive long wave equation[J]. Chaos , Solitons and Fractals , 2005, 24 (3): 745-757.
[6] LIU Z R, TANG H. Explicit periodic wave solutions and their bifurcations for generalized Camassa-Holm equation[J]. International Journal of Bifurcation and Chaos , 2010, 20 (8): 2507-2519.
[7] LIU Q, ZHOU Y Q, ZHANG W N. Bifurcation of travelling wave solutions for the modified dispersive water wave equation[J]. Nonlinear Analysis , 2008, 69 (1): 151-166.
[8] ZHOU Y Q, LIU Q, ZHANG W N. Bounded traveling waves of the Burgers-Huxley equation[J]. Nonlinear Analysis , 2011, 74 (4): 1047-1060.
[9] LI J B. Singular Nonlinear Traveling Wave Equations [M]. Beijing: Science Press, 2013: 1-70.
[10] WANG H, CHEN L W, LIU H J. Bifurcation analysis and exact traveling wave solutions of the (2+1)-dimensional Zoomeron equation[J]. Pioneer Journal of Advances in Applied Mathematics , 2015, 14 (1/2): 13-19.
[11] LIU H Z, LI J B. Symmetry reductiongs, dynamical behavior and exact explicit solutions to the gordon types of equations[J]. Journal of Computational and Applied Mathematics , 2014, 257 (1): 144-156.
[12] 王恒, 王汉权, 陈龙伟, 等. 耦合Higgs方程和Maccari系统的行波解分支[J]. 应用数学和力学, 2016, 37 (4): 434-440.(WANG Heng, WANG Hanquan, CHEN Longwei, et al. Bifurcations of exact travelling wave solutions to coupled Higgs equations and Maccari systems[J]. Applied Mathematics and Mechanics , 2016, 37 (4): 434-440.(in Chinese))
[13] WANG M L, ZHANG J L, LI X Z. Solitary wave solutions of a generalized derivative nonlinear Schrödinger equation[J]. Communications in Theoretical Physics , 2008, 50 (1): 39-42.
[14] ZHAI W, CHEN D Y. N -soliton solutions of the general nonlinear Schrödinger equation with derivative[J]. Communications in Theoretical Physics , 2008, 49 (5): 1101-1104.
[15] 张伟年, 杜正东, 徐冰. 常微分方程[M]. 北京: 高等教育出版社, 2006.(ZHANG Weinian, DU Zhengdong, XU Bing. Ordinary Differential Equation [M]. Beijing: Higher Education Press, 2006.(in Chinese))
YANG Na, CHEN Longwei, XIONG Mei
( School of Statistics and Mathematics , Yunnan University of Finance and Economics , Kunming 650221, P . R . China )
Abstract: With the dynamic system method, the qualitative performance and the exact solution of the general nonlinear Schrödinger equation with derivative were studied. Through the traveling wave transformation, the corresponding ordinary differential equation was deduced and the first integral was calculated. Under different parameter space conditions, the bifurcations of the general nonlinear Schrödinger equation with derivative were investigated, and the exact traveling wave solutions were obtained, such as solitary solutions, periodic solutions as well as kink and anti-kink solutions. The solitary wave solutions were considered through numerical simulation. The results show that the present findings improve the related previous conclusions.
Key words: nonlinear Schrödinger equation; dynamic system; solitary wave solution
Foundation item: The National Natural Science Foundation of China(11761075)
作者简介: 杨娜(1991—),女,硕士(E-mail: 513327775@qq.com);陈龙伟(1967—),男,博士(通讯作者. E-mail: tc715@sina.com).
基金项目: 国家自然科学基金(11761075)
修订日期: 2018-01-17
∗ 收稿日期: 2017-12-05;
ⓒ 应用数学和力学编委会,ISSN 1000-0887
文章编号 : 1000-0887(2018)10-1198-08
DOI: 10.21656/1000-0887.380302
文献标志码: A
中图分类号 : O357.41
引用本文 / Cite this paper: 杨娜, 陈龙伟, 熊梅. 广义带导数的非线性Schrödinger方程的动态分析和精确解[J]. 应用数学和力学, 2018, 39 (10): 1198-1205.YANG Na, CHEN Longwei, XIONG Mei. Dynamic analysis and exact solution of the general nonlinear Schrödinger equation with derivative[J]. Applied Mathematics and Mechanics , 2018, 39 (10): 1198-1205.