含参广义向量均衡问题近似解集的连通性 ∗

巨兴兴 1 , 陈加伟 1 , 张俊容 1 , 李高西 2

(1. 西南大学 数学与统计学院, 重庆 400715; 2. 重庆工商大学 数学与统计学院, 重庆 400067)

摘要 ： 主要研究了含参广义向量均衡问题的几类近似解 ． 在 C -次似凸性的条件下, 建立了该类含参广义向量均衡问题 ε -弱近似解的标量化特征, 并得到该类含参广义向量均衡问题两类近似解集的连通性 ． 通过举例说明了所得结果的正确性 ．

关 键 词 ： 广义向量均衡问题; 近似解; 连通性

引 言

向量均衡问题作为均衡问题的推广, 为向量优化问题、鞍点问题、向量互补问题和向量变分不等式等问题的研究提供了统一框架 ． 研究向量均衡问题最重要的问题之一是研究解的性质, 如解的存在性、 连续性、 适定性、 连通性、稳定性等 ． 在这些性质当中, 连通性被学者们广泛研究 [1-4] ． Peng等 [5] 通过标量化方法, 在适当的条件下, 得到了含参弱向量均衡问题近似解映射下半连续性的充分性条件 ． Chen等 [3] 提出了 ε -弱有效解和 ε -有效解的概念, 并且研究了向量均衡问题近似解集的连通性 ． Li等 [6] 通过标量化方法, 研究了含参向量均衡问题近似解映射的Berge上、下半连续性 ． Han等 [4] 研究了广义向量均衡问题近似解集的连通性以及含参广义向量均衡问题近似解映射的上、下半连续性 ． Wang等 [7] 在不包含任何解映射的条件下, 通过标量化方法, 研究了一类广义含参向量均衡问题解映射的下半连续性 ． Sadeqi等 [8] 通过使用标量化方法, 在不使用映射有界的条件下, 研究了向量均衡问题解集的紧性和凸性, 并且研究了含参均衡问题近似解映射的Lipschitz连续性 ． 韩瑜等 [9] 在不需要映射的单调性和解映射信息的条件下, 讨论了一类含参广义向量均衡问题有效解映射的下半连续性和Hausdorff上半连续性 ． 受以上文献的启发, 本文主要研究在不需要假设映射的单调和紧性条件下, 借助函数的 C -次似凸性, 建立了该类含参广义向量均衡问题 ε -弱近似解的标量化特征, 并借助这个标量化结果研究了含参广义向量均衡问题近似解集的连通性 ．

1 预 备 知 识

在本文中, X , Y 和 Z 是三个赋范空间 ． 假设 C 是 Y 的一个闭凸点锥, 并且int C ≠∅ ． 设 Y * 是 Y 的对偶空间, C 的对偶锥 C * 定义为 C * = f ∈ Y * : f ( y )≥0,∀ y ∈ C ,并且定义 C * 的拟内部为 C # = f ∈ Y * : f ( y )>0,∀ y ∈ C\ 0 ． D 是 Y 的子集, 记 D 的闭包为cl( D ), D 的内部为int D ． 凸锥 C 的非空凸子集 B 称为 C 的一个基, 若 C =cone( B )且0∉cl( B ) ． 容易得到, C # ≠∅，当且仅当 C 具有基 [2] ． 设 ω ∈int C , 令 B * = f ∈ C * : f ( ω )=1, B # = f ∈ C # : f ( ω )=1 ． B * 是 C * 的弱*紧基, B # 是 C # 的基且关于弱*拓扑有 B * =cl( B # ) [10] ．

设 A 是 X 的非空闭凸子集, F : A × A →2 Z 是集值映射 ． Sadeqi等 [8] 考虑了如下形式的广义向量均衡问题：

找 x ∈ A ,使得

F ( x , y )∩(-int C )=∅, ∀ y ∈ A ．

(1)

由于在实际问题中, 得到问题(1)的精确解并不容易 ． 正因为如此, 许多学者考虑问题(1)的近似问题: 设 ε >0, f ∈ B * \ 0,找 x ∈ A ,使得

( F ( x , y )+ εω )∩(-int C )=∅, ∀ y ∈ A ;

找 x ∈ A ,使得

f ( F ( x , y ))+ ε ⊆ R + , ∀ y ∈ A ．

设 A 是 X 的非空闭凸子集, u ∈ M , M ⊂ Z 并且 F : A × A × M →2 Z 是集值映射 ． Li等 [6] 考虑了如下形式的含参向量均衡问题：找 x ∈ A ,使得

F ( x , y , u )∉-int C , ∀ y ∈ A ．

(2)

类似地, 问题(2)的近似问题是: 设 ε >0, f ∈ B * \ 0,找 x ∈ A ,使得

F ( x , y , u )+ εω ∉-int C , ∀ y ∈ A ；

找 x ∈ A ,使得

f ( F ( x , y , u ))+ ε ⊆ R + , ∀ y ∈ A ．

当集合 A 与映射 F 被参数 λ 扰动时，其中 λ ∈ Λ ⊆ Y ，考虑如下含参广义向量均衡问题：找 x ∈ A ( λ ),使得

F ( x , y , λ )∩(- Δ )=∅, ∀ y ∈ A ( λ )，

(3)

其中， Δ ∪0是 Z 中的凸锥, A : Λ →2 X \ ∅以及 F : X × X × Λ →2 Z \ ∅是两个集值映射 ． 用 A ( Λ )表示 A 的像, 即 A ( Λ ) ∪ λ ∈ Λ A ( λ ) ． 本文主要讨论 Δ 的两种特殊情形, 即 Δ =int C 和 Δ = C\ 0 ．

定义1 设 ε >0, λ ∈ Λ , Λ ⊂ Y , f ∈ B * \ 0并且 A : Λ →2 X \ ∅以及 F : X × X × Λ →2 Z \ ∅是两个集值映射 ．

x ∈ A ( λ )称为含参广义向量均衡问题(3)的 ε -弱近似解, 如果

( F ( x , y , λ )+ εω )∩(-int C )=∅, ∀ y ∈ A ( λ ) ．

x ∈ A ( λ )称为含参广义向量均衡问题(3)的 ε -近似解, 如果

( F ( x , y , λ )+ εω )∩(- C\ 0)=∅, ∀ y ∈ A ( λ ) ．

x ∈ A ( λ )称为含参广义向量均衡问题(3)的 εf -近似解, 如果

f ( F ( x , y , λ ))+ ε ⊆ R + , ∀ y ∈ A ( λ ) ．

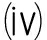x ∈ A ( λ )称为含参广义向量均衡问题(3)的强有效解, 如果

F ( x , y , λ )⊂ C , ∀ y ∈ A ( λ ) ．

特别地, 含参广义向量均衡问题(3)的 ε -弱近似解集, ε -近似解集, εf -近似解集和强有效解集分别记为 S εW ( λ ), S ε ( λ ), S εf ( λ )和 Ω ( λ ) ．

设 A : Λ →2 X \ ∅与 F : X × X × Λ →2 Z \ ∅是两个集值映射 ． 如果 S ε 1 W ( λ )和 S ε 2 W ( λ )是非空的并且0≤ ε 1 < ε 2 , 则 S ε 1 f ( λ )⊂ S ε 2 f ( λ )(见文献[8]中的引理2.1) ． 如果 S ε 1 ( λ )和 S ε 2 ( λ )是非空的并且0≤ ε 1 < ε 2 , 则 S ε 1 ( λ )⊂ S ε 2 ( λ ) ．

下面, 通过例1说明存在含参广义向量均衡问题的 ε -近似解, ε -弱近似解和强有效解 ．

例1 令 并且 F : X × X × Λ →2 Z \ ∅定义如下：

F ( x , y , λ )=[ x - λ 2 +1,10]×[1+ y 2 - λ ,50], ∀ y ∈ A ( λ ) ．

首先，求解 Ω ( λ ) ． 当-5≤ y ≤ λ 2 +6, λ ∈ Λ =[0,1]时，显然有1+ y 2 - λ ≥0恒成立 ． 下面只需 x - λ 2 +1≥0, 即 x ≥ λ 2 -1 ． 因此, Ω ( λ )=[ λ 2 -1,6+ λ 2 ] ．

然后, 求解 S εW ( λ ), S ε ( λ ) ． 由例子条件得, F ( x , y , λ )+ εω =[ x - λ 2 +1,10]×[1+ y 2 - λ ,50]+(2,4) ． 由于1+ y 2 - λ +4>0,50+4=54>0，故对∀ x ∈[-5,6+ λ 2 ], 有( F ( x , y , λ )+ εω )∩(-int C )=∅, 以及( F ( x , y , λ )+ εω )∩(- C\ 0)=∅ ．

定义2 设 E 是 X 的非空闭凸子集, ε >0, λ ∈ Λ , Λ ⊂ Y , 并且 A : Λ →2 X \ ∅与 Ψ : X × X × Λ →2 Z \ ∅是两个集值映射 ．

λ ∈ Λ , y ∈ E , x Ψ ( x , y , λ )称为 C -凸的，如果∀ x 1 , x 2 ∈ E , t ∈[0,1]使得

tΨ ( x 1 , y , λ )+(1- t ) Ψ ( x 2 , y , λ )- Ψ ( tx 1 +(1- t ) x 2 , y , λ )⊆ C ．

λ ∈ Λ , x ∈ E , y Ψ ( x , y , λ )称为 C -凹的，如果∀ y 1 , y 2 ∈ E , t ∈[0,1]使得

Ψ ( x , ty 1 +(1- t ) y 2 , λ )-( tΨ ( x , y 1 , λ )+(1- t ) Ψ ( x , y 2 , λ ))⊆ C ．

λ ∈ Λ , y ∈ E , x Ψ ( x , y , λ )称为 C -次似凸的, 存在 θ ∈int C , 如果∀ x 1 , x 2 ∈ E , t ∈[0,1], ε >0,使得

εθ + tΨ ( x 1 , y , λ )+(1- t ) Ψ ( x 2 , y , λ )- Ψ ( E , y , λ )⊆ C ．

定义3 [11] 设 X 1 和 X 2 是两个Hausdorff拓扑向量空间, u 0 ∈ X 1 并且 T : X 1 →2 X 2 ．

如果对于 T ( u 0 )的任意邻域 V , 存在 u 0 的邻域 U ( u 0 )，使得对任意 u ∈ U ( u 0 ), 有 T ( u )⊆ V , 称映射 T 在点 u 0 处是上半连续的 ．

如果对于任意 x ∈ T ( u 0 )以及 x 任意邻域 V , 存在 u 0 的邻域 U ( u 0 )，使得对任意 u ∈ U ( u 0 ), 有 T ( u )∩ V ≠∅, 称映射 T 在点 u 0 处是下半连续的 ．

如果 T 在 X 1 的每一点都是上半连续的(下半连续的), 则称 T 在 X 1 上是上半连续的(下半连续的) ． 如果 T 在 X 1 上同时是上半连续和下半连续的,则称 T 在 X 1 上是连续的 ．

引理1 [11] 集值映射 T : X 1 →2 X 2 在点 u 0 ∈ X 1 是下半连续的，当且仅当任意序列 u n ⊆ X 1 满足 u n → u 0 以及任意 x 0 ∈ T ( u 0 ), 存在 x n ∈ T ( u n )使得 x n → x 0 ．

引理2 [4] 假设 A γ : γ ∈ Γ 是拓扑空间 Z 中的连通集族 ． 如果∩ γ ∈ Γ A γ ≠∅, 则∪ γ ∈ Γ A γ 是拓扑向量空间 Z 的连通集 ．

引理3 [7] X 和 Z 是两个赋范空间, E 是 X 的非空闭凸子集, F : E →2 Z 是一个集值映射, 则 F 在 E 上是 C -次似凸的⟺ F ( E )+int C 是凸的⟹cl cone( F ( E )+ C )是凸的 ．

2 含参广义向量均衡问题近似解集的标量化性质

本节主要利用映射 F 关于第2个变量是 C -次似凸的, 研究 ε -弱近似解的标量化结果 ．

定理1 设 ε >0, λ ∈ Λ , Λ ⊂ Y 并且 A : Λ →2 X \ ∅以及 F : X × X × Λ →2 Z \ ∅是两个集值映射 ． 假设 S εW ( λ )≠∅, 并且 λ ∈ Λ , x ∈ A ( λ ), y F ( x , y , λ )是 C -次似凸的，则有

(4)

证明 先证明∪ f ∈ B * S εf ( λ )⊂ S εW ( λ ) ． 令 x 0 ∈∪ f ∈ B * S εf ( λ ), 则存在 f ∈ B * 使得

f ( F ( x 0 , y , λ ))+ ε ⊆ R + , ∀ y ∈ A ( λ ) ．

(5)

假设 x 0 ∉ S εW ( λ ), 则存在一个 y 0 ∈ A ( λ )使得( F ( x 0 , y 0 , λ )+ εω )∩(-int C )≠∅ ． 因此, 存在一个 z 0 ∈( F ( x 0 , y 0 , λ )+ εω )∩(-int C ),使得 f ( z 0 )<0 ． 又因为 z 0 ∈( F ( x 0 , y 0 , λ )+ εω ), 故存在 ξ 0 ∈ F ( x 0 , y 0 , λ ), 使得 z 0 = ξ 0 + εω ． 于是有0> f ( z 0 )= f ( ξ 0 + εω )= f ( ξ 0 )+ εf ( ω )= f ( ξ 0 )+ ε ,即 f ( ξ 0 )+ ε <0,与式(5)矛盾 ． 所以∪ f ∈ B * S εf ( λ )⊂ S εW ( λ ) ．

下面证明 S εW ( λ )⊂∪ f ∈ B * S εf ( λ ) ． 令 x 0 ∈ S εW ( λ ),则

( F ( x 0 , y , λ )+ εω )∩(-int C )=∅, ∀ y ∈ A ( λ ) ．

所以( F ( x 0 , A ( λ ), λ )+ C + εω )∩(-int C )=∅,从而

cl cone( F ( x 0 , A ( λ ), λ )+ C + εω )∩(-int C )=∅ ．

因为 λ ∈ Λ , x ∈ A ( λ ), y F ( x , y , λ )是 C -次似凸的,由引理3可得cl cone( F ( x , A ( λ ), λ )+ C + εω )是一个凸集 ． 由凸集分离定理可知,存在一个连续线性函数 h ∈ Y * \ 0,使得

inf h ( z ): z ∈cl cone( F ( x 0 , y , λ )+ c 1 + εω ), c 1 ∈ C ≥

sup h ( c ): c ∈-int C ．

(6)

因为0∈cl cone( F ( x 0 , y , λ )+ c 1 + εω ),从而

inf h ( z ): z ∈cl cone( F ( x 0 , y , λ )+ c 1 + εω ), c 1 ∈ C ≤ h (0)=0 ．

结合式(6)有sup h ( c ): c ∈-int C ≤0, 于是有 h ( c )≥0,∀ c ∈int C ． 因为 h 是连续线性泛函, 则有 h ( c )≥0,∀ c ∈ C ． 根据对偶锥的定义知, h ∈ C * , 从而 h ∈ C * \ 0 ． 由于0∈ C , 则有 F ( x 0 , y , λ )+ εω ⊆ F ( x 0 , y , λ )+ εω + C ． 因此对任意的 y ∈ A ( λ ), 有 h ( F ( x 0 , y , λ )+ εω )= h ( F ( x 0 , y , λ ))+ εh ( ω )⊆ R + ． 又因为 ω ∈int C 并且 h ∈ C * \ 0, 所以 h ( ω )>0 ． 令 f = h / h ( ω ), 则有 f ∈ B * , f ( F ( x 0 , y , λ ))+ ε ⊆ R + , ∀ y ∈ A ( λ ),也即是 x 0 ∈ S εf ( λ ), 这表明 x 0 ∈∪ f ∈ B * S εf ( λ ) ． 所以 S εW ( λ )⊂∪ f ∈ B * S εf ( λ ) ．

注1 假设映射 F 在 C -凸的条件下, 可得到不同定义的近似解的标量化结果, 即文献[3]中的引理3.1, 文献[6]中的引理4.1和文献[10]中的引理2.1 ． 假设映射 F 在 C -似凸的条件下, 也可以得到不同定义的近似解的标量化结果, 即文献[4]中的定理3.3、文献[5]中的定理4.1和文献[9]中的引理3.1 ． 当 ε =0, 映射 F 关于第2个变量在 C -次似凸的条件下, 定理1退化为文献[7]中的引理3.2 ． 由文献[12] 中的式(4)可知, C -次似凸的条件比 C -凸与 C -似凸更弱, 故定理1推广了文献[3-7,9-10]的相关结果 ．

3 含参广义向量均衡问题近似解集的连通性

定理2 令 Ω ( λ )≠∅, f ∈ B * , λ ∈ Λ ，假设下面条件成立:

1) A ( λ )是非空闭凸集;

2) λ ∈ Λ , y ∈ A ( λ ), x F ( x , y , λ )在 A ( λ )上是 C -凹的;

3) λ ∈ Λ , x ∈ A ( λ ), y F ( x , y , λ )在 A ( λ )上是 C -凸的 ．

则 S εf ( λ )是一个凸集，并且 S εW ( λ )也是一个连通集 ．

证明 令 x 1 ∈ S εf ( λ ), x 2 ∈ S εf ( λ )以及 t ∈[0,1], 则有 x t = tx 1 +(1- t ) x 2 ∈ A ( λ ) ． 由 S εf 的定义可知, f ( F ( x 1 , y , λ ))+ ε ⊆ R + , f ( F ( x 2 , y , λ ))+ ε ⊆ R + ． 进而, t f ( F ( x 1 , y , λ ))+ tε ⊆ R + ,(1- t ) f ( F ( x 2 , y , λ ))+(1- t ) ε ⊆ R + ． 于是有

tf ( F ( x 1 , y , λ ))+(1- t ) f ( F ( x 2 , y , λ ))+ ε ⊆ R + ．

(7)

由条件2)可得

F ( tx 1 +(1- t ) x 2 , y , λ )⊆ C + tF ( x 1 , y , λ )+(1- t ) F ( x 2 , y , λ ) ．

又因为 f ∈ B * ,则

f ( F ( x t , y , λ ))⊆ R + + tf ( F ( x 1 , y , λ ))+(1- t ) f ( F ( x 2 , y , λ )) ．

(8)

由式(7)、(8)可得

f ( F ( z t , y , λ ))+ ε ⊆ R + + tf ( F ( x 1 , y , λ ))+

(1- t ) f ( F ( x 2 , y , λ ))+ ε ⊆ R + + R + ⊆ R + ．

所以 x t = tx 1 +(1- t ) x 2 ∈ S εf ( λ ), 即 S εf ( λ )是凸集, 并且是一个连通集 ．

下证 S εW ( λ )是一个连通集, 只需证明∩ f ∈ B * S εf ( λ )≠∅ ． 由条件知 Ω ( λ )≠∅, 显然有 Ω ( λ )⊆ S εf ( λ )≠∅, 所以∩ f ∈ B * S εf ( λ )≠∅ ． 结合引理2和定理1可知, S εW ( λ )是一个连通集 ．

注2 当映射 F : X × X × Λ → R 时, 含参广义向量均衡问题(3)退化为文献[6]所讨论的含参均衡问题, 并且当 F 关于第1个变量 x 是凹函数时, 定理2即为文献[6]中的引理3.3 ．

下面, 通过一个例子说明 S εW ( λ )是一个连通集 ．

例2 令 并且 F : X × X × Λ →2 Z \ ∅定义如下：

F ( x , y , λ )=( x - y + λ -2, x - y -5), ∀ y ∈ A ( λ ) ．

由例子中已知条件可知 F 满足定理2的条件,并且 F ( x , y , λ )+ εω =( x - y + λ , x - y +1) ． 因此, 为了使得( F ( x , y , λ )+ εω )∩(-int C )=∅,只需 x - y + λ ≥0或 x - y +1≥0, 即 x ≥( y -1) max =4或者 x ≥( y - λ ) max =4, 因此只需 x ≥4 ． 故 S εW ( λ )=[4,4+ λ 2 ], 从而 S εW ( λ )是一个连通集 ．

定理3 设 f ∈ B * , λ ∈ Λ ,且下面条件成立：

1) A ( λ )是非空闭凸集;

2) 对 λ ∈ Λ , y ∈ A ( λ ), x F ( x , y , λ )在 A ( λ )× A ( λ )× Λ 上是下半连续的 ．

则 S εf ( λ )是闭的 ．

证明 令 x n ⊆ S εf ( λ ), 并且 x n → x 0 ,则有

f ( F ( x n , y , λ ))+ ε ⊆ R + , ∀ y ∈ A ( λ ) ．

(9)

因为 A ( λ )是闭的并且 x n ⊆ A ( λ ), 所以 x 0 ∈ A ( λ ) ． 对任意的 z ∈ F ( x 0 , y , λ ), 由于 λ ∈ Λ , y ∈ A ( λ ), x F ( x , y , λ )在 A ( λ )× A ( λ )× Λ 上是下半连续的, 所以由引理1可得, 存在 z n ∈ F ( x n , y , λ )使得 z n → z ． 由式(9)可得

f ( z n )+ ε ⊆ R + ．

(10)

对式(10)的左端取极限, 于是有 f ( z )+ ε ⊆ R + ． 因此 x 0 ∈ S εf ( λ ) ． 故 S εf ( λ )是闭的 ．

□

下面，讨论 S εf ( λ ), S ε ( λ ), S εW ( λ )之间的关系 ．

定理4 令 ε >0, Ω ( λ )≠∅, λ ∈ Λ ,假设下面条件成立:

1) λ ∈ Λ , x ∈ A ( λ ), y F ( x , y , λ )在 A ( λ )上是 C -次似凸的;

2) S εf ( λ )在 B * 上关于 f 是下半连续的 ．

则

⊆ S ε ( λ )⊆ ⊆

(11)

证明 由定义知∪ f ∈ B # S εf ( λ )⊆ S ε ( λ )⊆ S εW ( λ ) ． 由定理1得

(12)

所以∪ f ∈ B # S εf ( λ )⊆ S ε ( λ )⊆ S εW ( λ )=∪ f ∈ B * S εf ( λ ) ．

下证∪ f ∈ B * S εf ( λ )⊆cl(∪ f ∈ B # S εf ( λ )) ． 设 则存在 使得 令 h ∈ B # 并且 所以 f n ∈ B # ． 显然当 n → +∞时 注意到 S εf ( λ )在 B * 上关于 f 是下半连续的,通过引理1可得,存在 x n ∈ S εf n ( λ )⊆∪ f ∈ B # S εf ( λ ),使得 即 结合式(12),可得式(11)成立 ．

注3 当 ε =0, 映射 A 和映射 F 不受参数 λ 扰动影响时, 在适当条件下, 可以得到∪ f ∈ B # S εf ( λ )⊆ S ε ( λ )⊆ S εW ( λ )=∪ f ∈ B * S εf ( λ )⊆cl(∪ f ∈ B # S εf ( λ )),即文献[3]中的引理5.3、文献[4]中的定理3.5、文献[9]中的定理3.2以及文献[10]中的引理2.2 ．

4 结 论

本文主要研究了含参广义向量均衡问题的几类近似解, 通过举例说明了几类近似解的存在性 ． 借助函数的 C -次似凸性, 建立了该类含参广义向量均衡问题 ε -弱近似解的标量化特征, 并借助这个标量化结果研究了含参广义向量均衡问题近似解集的连通性 ． 通过举例说明所得结果的正确性,主要推广了文献[3,6-7,9,13-15]的相关结果 ．

参考文献 ( References )：

[1] LUC D T. Connectedness of the efficient point sets in quasiconcave vector maximization[J]. Journal of Mathematical Analysis and Applications , 1987, 122 (2): 346-354.

[2] GONG X H. Connectedness of efficient solution sets for set-valued maps in normed spaces[J]. Journal of Optimization Theory and Applications , 1994, 83 (1): 83-96.

[3] CHEN B, LIU Q Y, LIU Z B, et al. Connectedness of approximate solutions set for vector equilibrium problems in Hausdorff topological vector spaces[J]. Fixed Point Theory and Applications , 2011, 2011 (1): 1-11.

[4] HAN Y, HUANG N J. Some characterizations of the approximate solutions to generalized vector equilibrium problems[J]. Journal of Industrial and Management Optimization , 2016, 12 (3): 1135-1151.

[5] PENG Z Y, ZHAO Y, YANG X M. Semicontinuity of approximate solution mappings to parametric set-valued weak vector equilibrium problems[J]. Numerical Functional Analysis and Optimization , 2015, 36 (4): 481-500.

[6] LI X B, LI S J. Continuity of approximate solution mappings for parametric equilibrium problems[J]. Journal of Global Optimization , 2011, 51 (3): 541-548.

[7] WANG Q L, LI S J. Lower semicontinuity of the solution mapping to a parametric generalized vector equilibrium problem[J]. Journal of Industrial and Management Optimization , 2014, 10 (4): 1225-1234.

[8] SADEQI I, PAYDAR M S. Lipschitz continuity of an approximate solution mapping for parametric set-valued vector equilibrium problems[J]. Optimization , 2016, 65 (5): 1003-1021.

[9] 韩瑜, 黄南京. 含参广义向量均衡问题有效解的稳定性[J]. 中国科学: 数学, 2017, 47 (3): 397-408.(HAN Yu, HUANG Nanjing. Stability of efficient solutions to parametric generalized vector equilibrium problems[J]. Scientia Sinica : Mathematica , 2017, 47 (3): 397-408.(in Chinese))

[10] GONG X H. Efficiency and henig efficiency for vector equilibrium problems[J]. Journal of Optimization Theory and Applications , 2001, 108 (1): 139-154.

[11] GÖPFERT A, RIAHI H, TAMMER C, et al. Variational Methods in Partially Ordered Spaces [M]. New York: Springer, 2003.

[12] LI Z F, CHEN G Y. Lagrangian multipliers, saddle points, and duality in vector optimization of set-valued maps[J]. Journal of Mathematical Analysis and Applications , 1997, 215 (2): 297-316.

[13] 杨丽, 李军. Hilbert空间中分裂可行性问题的改进Halpern迭代和黏性逼近算法[J]. 应用数学和力学, 2017, 38 (9): 1072-1080.(YANG Li, LI Jun. Modified Halpern iteration and viscosity approximation methods for the split feasibility problems in Hilbert spaces[J]. Applied Mathematics and Mechanics , 2017, 38 (9): 1072-1080.(in Chinese))

[14] 彭再云, 李科科, 张石生. 向量 D - η - E -半预不变凸映射与向量优化[J]. 应用数学和力学, 2014, 35 (9): 1020-1032.(PENG Zaiyun, LI Keke, ZHANG Shisheng. D - η - E -semipreinvex vector mapping and vector optimization[J]. Applied Mathematics and Mechanics , 2014, 35 (9): 1020-1032.(in Chinese))

[15] 赵勇, 彭再云, 张石生. 向量优化问题有效点集的稳定性[J]. 应用数学和力学, 2013, 34 (6): 643-650.(ZHAO Yong, PENG Zaiyun, ZHANG Shisheng. Stability of the sets of effective points of vector-valued optimization problems[J]. Applied Mathematics and Mechanics , 2013, 34 (6): 643-650.(in Chinese))

Connectedness of Approximate Solution Sets to Parametric Generalized Vector Equilibrium Problems

JU Xingxing 1 , CHEN Jiawei 1 , ZHANG Junrong 1 , LI Gaoxi 2

(1. School of Mathematics and Statistics , Southwest University , Chongqing 400715, P . R . China ; 2. College of Mathematics and Statistics , Chongqing Technology and Business University , Chongqing 400067, P . R . China )

Abstract: Several approximate solution sets to generalized vector equilibrium problems were studied. The scalarization characterization of ε -approximate solutions to parametric generalized vector equilibrium problems was established by means of the C -subconvexlike property of the involved mappings. Further, the connectedness of the 2 types of approximate solution sets was derived with the scalarization methods. Finally, the relationships among these approximate solution sets were obtained under some typical conditions.

Key words: generalized vector equilibrium problem; approximate solution; connectedness

Foundation item: The National Natural Science Foundation of China(11401487)

ⓒ 应用数学和力学编委会，ISSN 1000-0887

文章编号 ： 1000-0887(2018)10-1206-07

作者简介： 巨兴兴(1993—)，男，硕士生(E-mail: juxxmath@163.com)；陈加伟(1984—)，男，副教授，博士(通讯作者. E-mail: J.W.Chen713@163.com).

基金项目： 国家自然科学基金(11401487)；重庆市基础与前沿研究计划项目(cstc2016jcyjA0239)

修订日期： 2018-01-11

∗ 收稿日期： 2017-11-01；

DOI: 10.21656/1000-0887.380279

文献标志码： A

中图分类号 ： O357.41

引用本文 / Cite this paper: 巨兴兴, 陈加伟, 张俊容, 李高西. 含参广义向量均衡问题近似解集的连通性[J]. 应用数学和力学, 2018, 39 (10): 1206-1212.JU Xingxing, CHEN Jiawei, ZHANG Junrong, LI Gaoxi. Connectedness of approximate solution sets to parametric generalized vector equilibrium problems[J]. Applied Mathematics and Mechanics , 2018, 39 (10): 1206-1212.