杨 旭,梁英杰,孙洪广,陈 文
(河海大学 力学与材料学院,南京 211100)
(我刊编委陈文来稿)
摘要:对非Newton流体的本构及流动规律进行研究是分析、预测和控制非Newton流体在管道中流动的关键.实验表明非Newton流体在流动过程中具有历史记忆性,基于空间分数阶微积分方法,建立了分数阶非Newton流体本构模型;并推导了该模型在圆管中的流速分布、流量、平均流速、压降、平均Reynolds数等管道流动参数;提出了分数阶非Newton流体圆管流态判别准则.研究表明非Newton流体的圆管流层间的切应力可以通过流速的轴向分布大小来描述.对于不含屈服切应力的分数阶非Newton流体,分数阶的阶数越大,断面流速分布越均匀,记忆能力越强.分数阶的阶数大小反映了流体对全域空间的记忆性强弱;而对于含有屈服切应力的分数阶非Newton流体,分数阶的阶数越大,速梯区流速分布越均匀,流核区速度越小.分数阶的阶数大小反映了局部空间记忆性强弱.该研究为非Newton流体的记忆特征提供了一种新的建模方法.
关键词:分数阶算子; 圆管流动; 流态判别; 数学力学建模
石油、钻井液、流态软黏土、生物流体、液晶高分子、泥石流、高分子聚合物溶液、润滑油、流质食品等复杂流体是能源、土建、生物医药、材料、交通、环境、化工、食品工程等领域的主要研究对象并得到了广泛应用[1-5].大量的实验研究表明,以上复杂流体的剪切应力与剪切应变率之间并不满足标准的Newton内摩擦定律,因此也被称为非Newton流体或非线性流体[6].
已有研究表明,非Newton流体具有明显的时间记忆性(如触变性流体与震凝性流体)或空间剪切记忆性(如伪塑性流体、膨胀型流体、Bingham(宾汉姆)流体等)[7-8].建立在经验或半经验基础上的非Newton流体本构模型(如幂律模型、Bingham模型、Casson(卡森)模型、Herschel-Bulkley(赫巴)模型等)并不能很好地描述这些特性,且通过拟合实验数据所得到的相关参数的物理意义并不明确[9].相应的物理参数,如表观黏度等,其与剪切时间拟合得到的函数常表现为幂率形式[10].因此,建立简单有效的非Newton流体本构关系,长期以来是非Newton流体研究的一个重要课题.
从工程角度讲,非Newton流体的本构关系及在圆管中的流动规律研究具有重要的理论与应用价值.近年来,国内外学者在这方面开展了大量的研究工作.Pinho等[11]研究了剪切稀化流体在管道中的流动特征,量化了由剪切稀化引起的从层流到湍流的过渡延迟问题.Cho等[12]研究了黏弹性流体在湍流管道中的传热行为.Fetecau[13]推导了管状域下非Newton流体的解析解.Zheng等[14]对现场尺度下的管道中蜡沉积现象进行了建模,开发出了一种利用墙法定律并考虑蜡质油的非Newton特性的增强蜡沉积模型.Azhdari等[15]运用数值方法对处于螺旋管中的非Newton流体快速瞬态流参数进行了研究,并取得了良好的效果.Shaikh等[16]运用有限元方法对非弹性的非Newton流体在扩展管中的流动进行了建模,并提出了一种有限元Taylor-Galerkin压力校正方案.李孝军等[17]综述了国内外非Newton流体石油管流研究现状.张钧波等[18]运用有限体积法,对幂率流体在偏心圆环通道中的层流进行了研究.王旭东等[19]针对聚合物溶液的非Newton性和海上注聚管柱的特性,提出了油管注聚和环空注聚情况下聚合物溶液摩阻计算方法,对注聚管的精细化管理提供了参考.然而,以上的研究并没有从力学本构关系角度对非Newton流体在圆管中的流动记忆性进行分析和讨论.另一方面,目前各种非Newton流体本构模型繁多,通用性不强.
分数阶微积分作为一种强有力的数学力学建模工具,因其定义中含有卷积积分,能够较好地反映非局部空间相关性和历史记忆特征,近几十年来取得了长足的进步和发展[20-22].目前已被成功运用于反常扩散建模[23-24]、黏弹性材料建模[25-27]、信号处理[28]、流变学[29-30]等领域.近年来,时间分数阶导数在非Newton流体本构建模方面得到了一定的发展[31].相比之下,空间分数阶非Newton流体的本构关系及流动规律的研究却鲜有报道.
本文工作采用分数阶微积分建模的方法,推导了分数阶非Newton流体本构关系以及在圆管中的流动参数,包括轴向流速分布、流量、平均流速、压降、平均Reynolds数.并讨论了分数阶的阶数与流速分布之间的关系,提出了一种新的非Newton流体流态判别准则,以期为非Newton流体的理论研究及工程应用提供参考依据.
分数阶微积分是传统整数阶微积分的推广,是微分和积分在阶数上的插值.式(1)~(4)给出了本文建模过程中所需要的分数阶算子的定义及部分性质[32].
Riemann-Liouville分数阶导数定义:
(1)
其中![]() 代表Riemann-Liouville分数阶导数,0代表积分下限,x表示积分上限,α表示分数阶求导阶数,Γ表示Gamma函数.
代表Riemann-Liouville分数阶导数,0代表积分下限,x表示积分上限,α表示分数阶求导阶数,Γ表示Gamma函数.
1) 积分微分性质,设n<α≤n-1,f(x)可积,存在α>0,使得
(2)
其中![]() 表示分数阶左侧积分.
表示分数阶左侧积分.
2) 幂函数求导性质,设f(x)=(x-a)ν,则有
(3)
3) 线性性质,即
(4)
为表征非Newton流体的空间非局部记忆效应,Sun(孙洪广)等[33]提出了如下本构方程:
(5)
其中τ为切应力,τ0为剪切屈服应力,μα为分数阶黏性系数,![]() 为剪切速率.
为剪切速率.
不同阶数下分数阶非Newton流体流动曲线如图1所示.
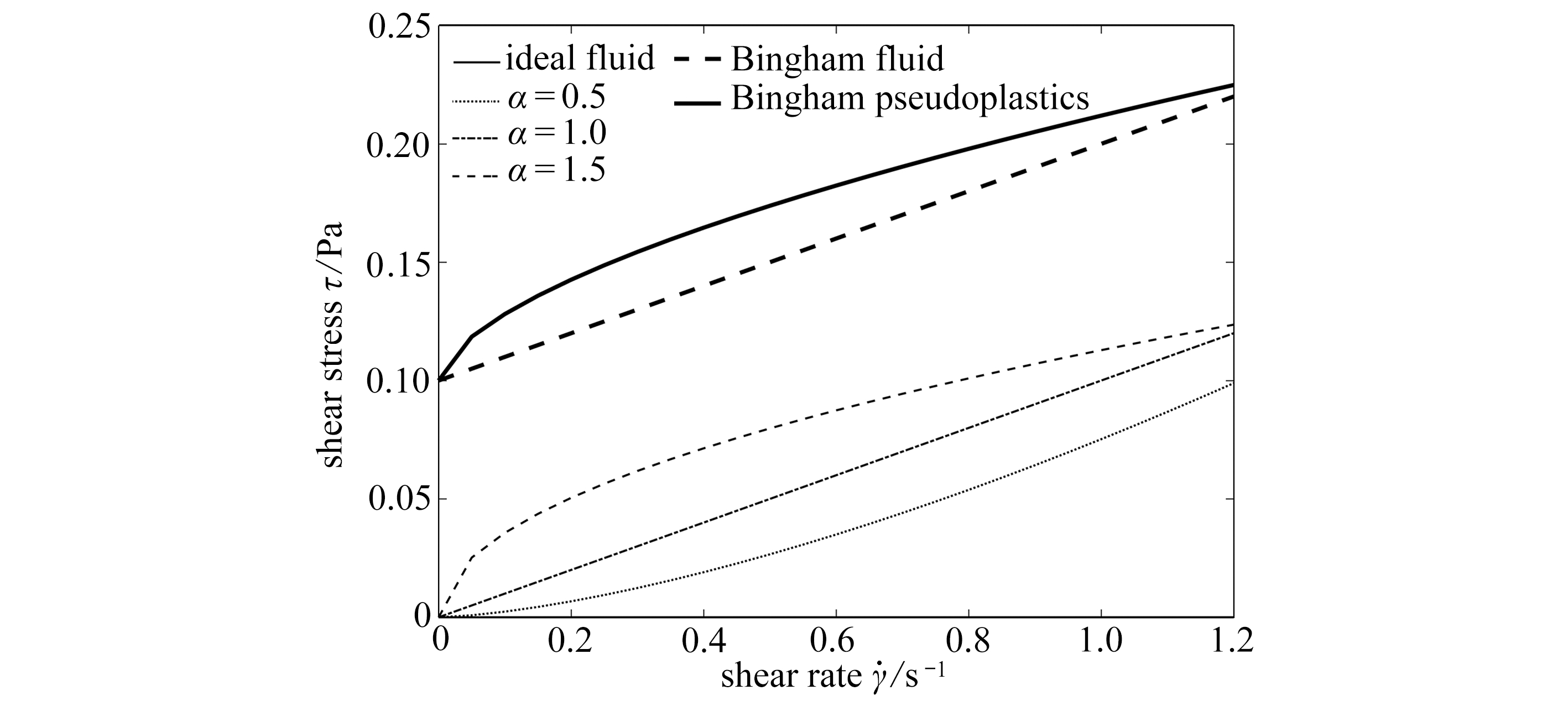
图1 不同阶数下分数阶非Newton流体流动曲线(μα=0.001 Pa·s,τ0=0,0.1 N/m2)
Fig.1 The flow curves of the fractional non-Newtonian fluid with different fractional derivative orders (μα=0.001 Pa·s,τ0=0,0.1 N/m2)
当τ>τ0时,图1显示了τ0=0和τ0=0.1 N/m2时,不同阶数下分数阶非Newton流体流动曲线.当μα=0时,表示理想流体.当0<α<1时,可以刻画膨胀型流体流动;当α=1时,表示Newton流体;当1<α<2时,可以表示伪塑性流体.此外,当τ0≠0,且α=1时,可以表示Bingham流体;当τ0≠0,且α≠1时,可以表示Bingham假塑性体.由此,不同种类的非Newton流体均可通过不同的分数阶的阶数和屈服切应力的取值反映在式(5)中.式(5)可以作为更广泛意义上的非Newton流体本构方程使用.
由圆管均匀流分析可知,圆管中切应力与压降的关系如下:
(6)
则半径为r0处的切应力为
(7)
管壁处切应力为
(8)
图2为圆管流动示意图,其中Δp为圆管压降,L为圆管长度,R为圆管半径.
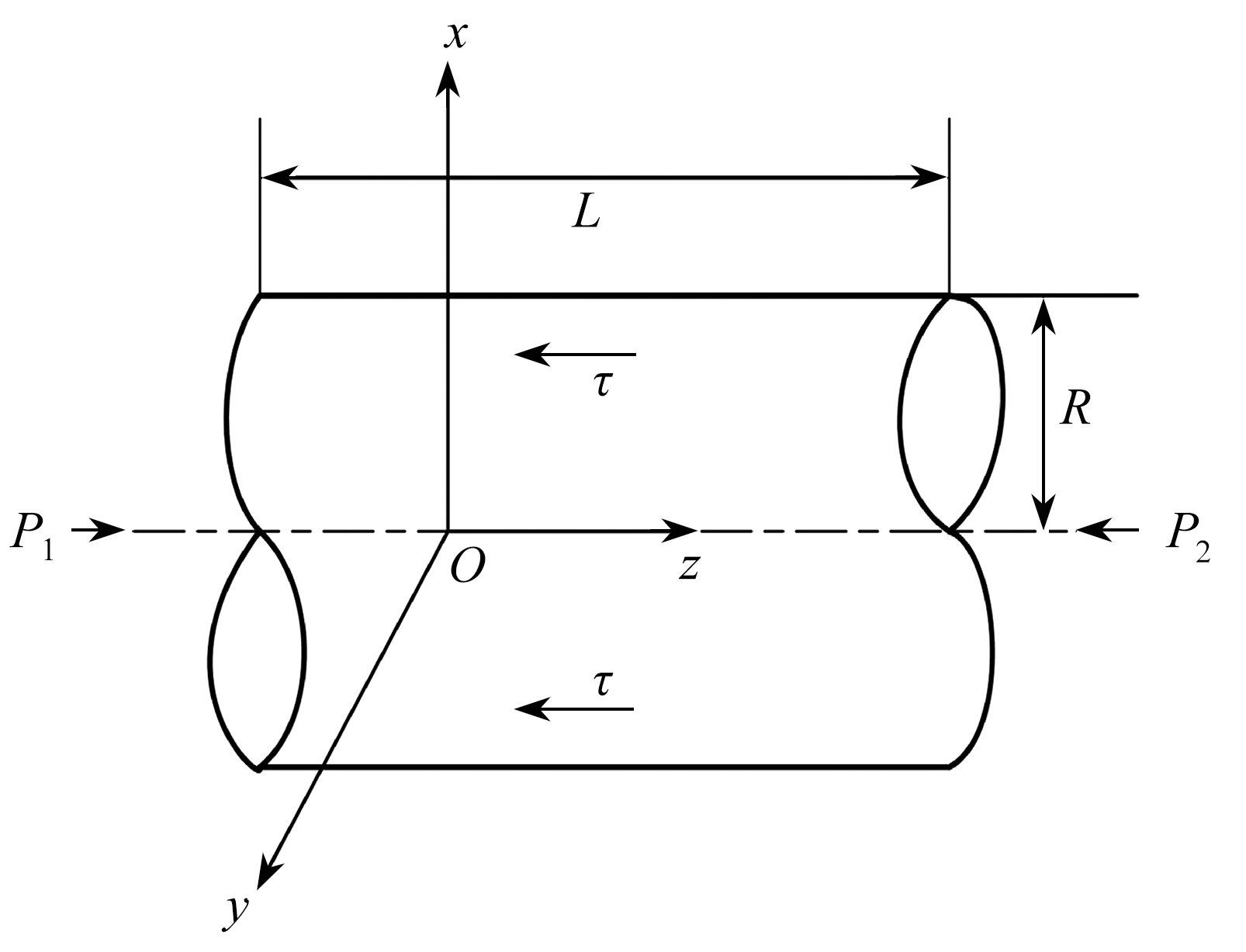
图2 圆管层流示意图
Fig.2 The diagram for laminar flow in a circular pipe
将式(6)、(7)代入式(5),并结合式(2)可得
(9)
又由式(3)和(4),可得分数阶非Newton流体本构方程:
(10)
当τ<τ0时,流体在圆管内部不产生运动,即![]() 综上所述:
综上所述:
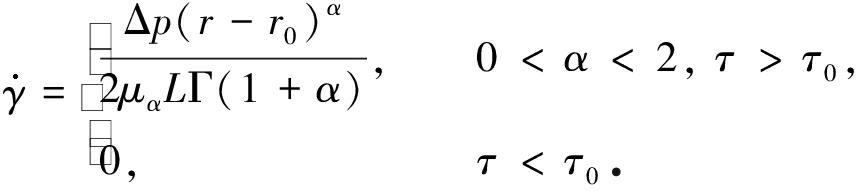
(11)
本文根据是否存在屈服切应力将分数阶非Newton流体分为两类,即不含屈服切应力的分数阶非Newton流体和含有屈服切应力的分数阶非Newton流体,推导各自的相关流动参数.
令τ0=0,根据式(7)、(10),则有
(12)
1) 流速分布
由非Newton流体圆管层流理论[34]可知,非Newton流体圆管层流流速分布可由下式得到:
(13)
将式(12)代入式(13),由边界条件(u(R)=0)可得
(14)
由式(14)可得流速最大值(r=0)为
(15)
不同阶数下分数阶非Newton流体流速分布图如图3所示.
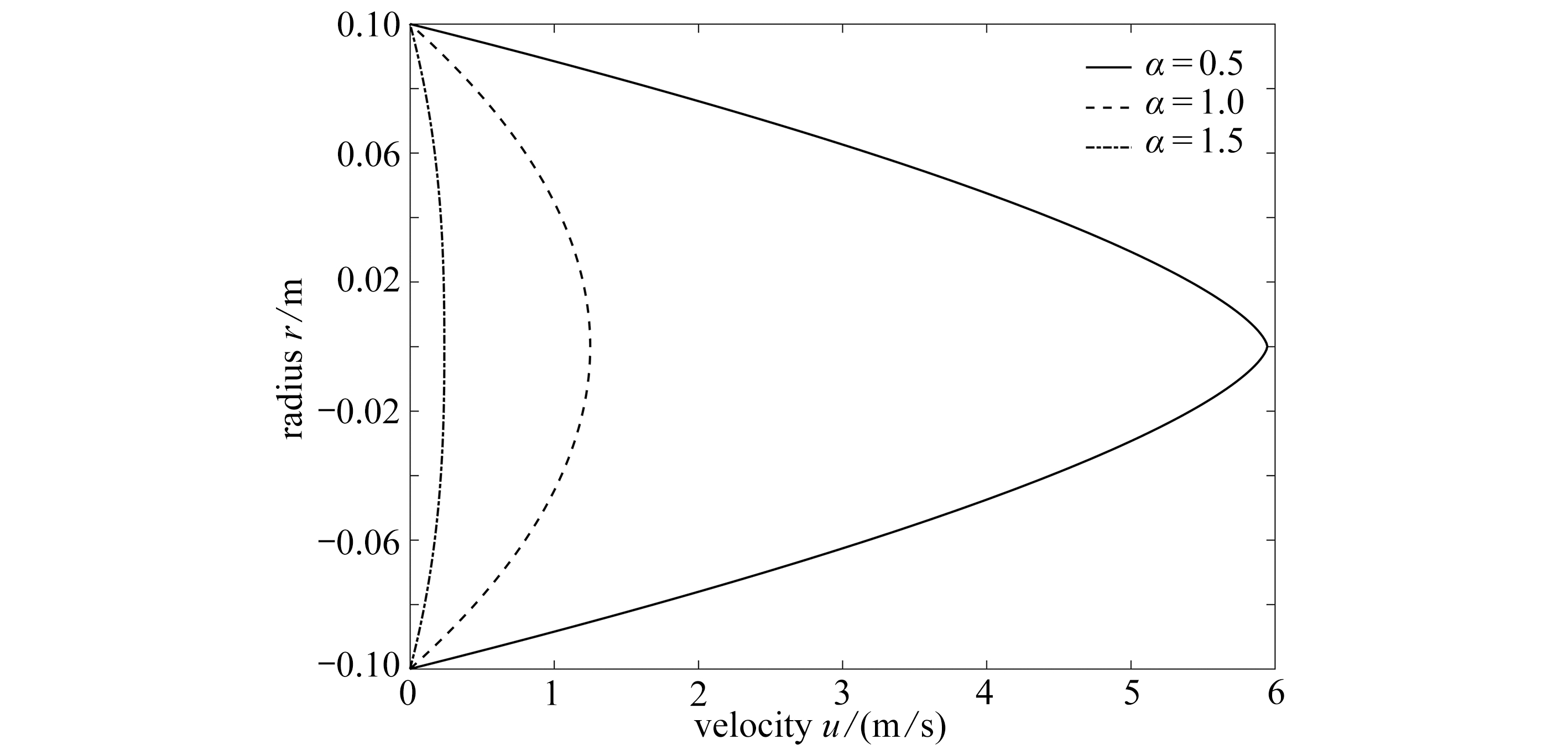
图3 不同阶数下分数阶非Newton流体流速分布图(τ=0,Δp=250 Pa,L=50 m,R=0.1 m,μα=0.01 Pa·s)
Fig.3 The velocity profiles of fractional non-Newtonian fluid with different fractional derivative orders (τ=0,Δp=250 Pa,L=50 m,R=0.1 m,μα=0.01 Pa·s)
2) 流量
由非Newton流体圆管层流理论,非Newton流体圆管层流流量表达式为
Q=![]() 2πru(r)dr.
2πru(r)dr.
(16)
将式(14)代入式(16)可得
(17)
Newton流体流量公式为
(18)
对比式(17)和式(18),当α=1时,两者一致.当α≠1时,其他条件不变,Newton流体的流量与圆管半径成四次方关系.而基于分数阶理论建立的非Newton流量公式,其流量大小与半径的3+α次方有关.
3) 平均流速
由平均流速的定义![]() 和式(17)可得
和式(17)可得
(19)
由式(15)和式(19)可得最大流速与平均流速的比值为
(20)
由此,断面上的流速轮廓与分数阶阶数的关系可以通过式(20)反映出来.图4是根据式(20)所得到的流速分布比值图.
当α=1时,最大流速为平均流速的2倍,这与Newton流体圆管层流的结论一致[34].当0<α<1时,为膨胀型流体.由图4不难发现:相比于Newton流体,膨胀型流体流速梯度更大,速度分布陡峭,非Newton流体流层间的切应力大于Newton流体.当1<α<2时,为伪塑性流体,与Newton流体相比,其断面流速分布较均匀,流速梯度小,非Newton流体流层间的切应力小于Newton流体.因此,圆管内非Newton流体流层间的切应力可通过断面流速分布形态得以记忆,不同流体记忆能力可以通过分数阶阶数α的大小反映,即α的值越大,记忆能力越强.

图4 流速分布比值图![]()
Fig.4 The velocity profiles of![]()
4) 压降
由式(17)经过整理可得
(21)
5) 平均Reynolds数
由Darcy(达西)公式:
(22)
(其中λ=64/Re,D为圆管直径,ρ为流体密度)可得
(23)
由式(19)、(23)经整理可得
(24)
设![]() 则平均Reynolds数可表示为
则平均Reynolds数可表示为
(25)
本小节对不含屈服切应力的分数阶非Newton流体的流速、流量、压降以及平均Reynolds数进行了推导和讨论.因为没有考虑屈服切应力,因此流速等参数可以进行整体分析,下一小节将对含屈服切应力的分数阶非Newton流体进行分析和讨论.
对于含有屈服切应力的分数阶非Newton流体,由式(11)可知,本构方程为分段函数.因此,流体是否在圆管中产生流动需要根据τ0与τw两者的大小关系判断.
1) 流速分布
当τ0≥τw时,即![]() 因此,
因此,
u(r)=0.
(26)
当τ0<τw时,即τ0<ΔpR/(2L),管内流动分为两个区域:流核区(因切应力小于屈服切应力而造成流层之间无法产生相对运动的区域)和速梯区(流核区以外的部分)[34],见图5.
图5 含屈服应力的分数阶非Newton流体流速分布
Fig.5 The diagram of the fractional non-Newtonian fluid velocity profile with yield shear stress
对于速梯区,由式(10)、(13)整理可得
(27)
对于流核区,令r=r0,代入式(27),得
(28)
综上所述,可以得到

(29)
不同阶数下,含屈服应力的分数阶非Newton流体流速分布如图6所示.
由图6可知,随着分数阶阶数α的增大,速梯区的流速分布越均匀,流核区的速度越小.反映出对应阶数下的非Newton流体速度分布形态越平缓,记忆能力越强.相比较而言,阶数α大小能更直观地反映出靠近管壁的局部空间区域速度变化.
2) 流量
当τ0≥τw时,即τ0≥ΔpR/(2L),由式(26)可知u(r)=0,故
Q=0.
(30)
当τ0<τw时,即τ0<ΔpR/(2L),将式(27)和(28)代入以下表达式:
(31)
取ζ=r0/R,经整理可得
(32)
其中![]()
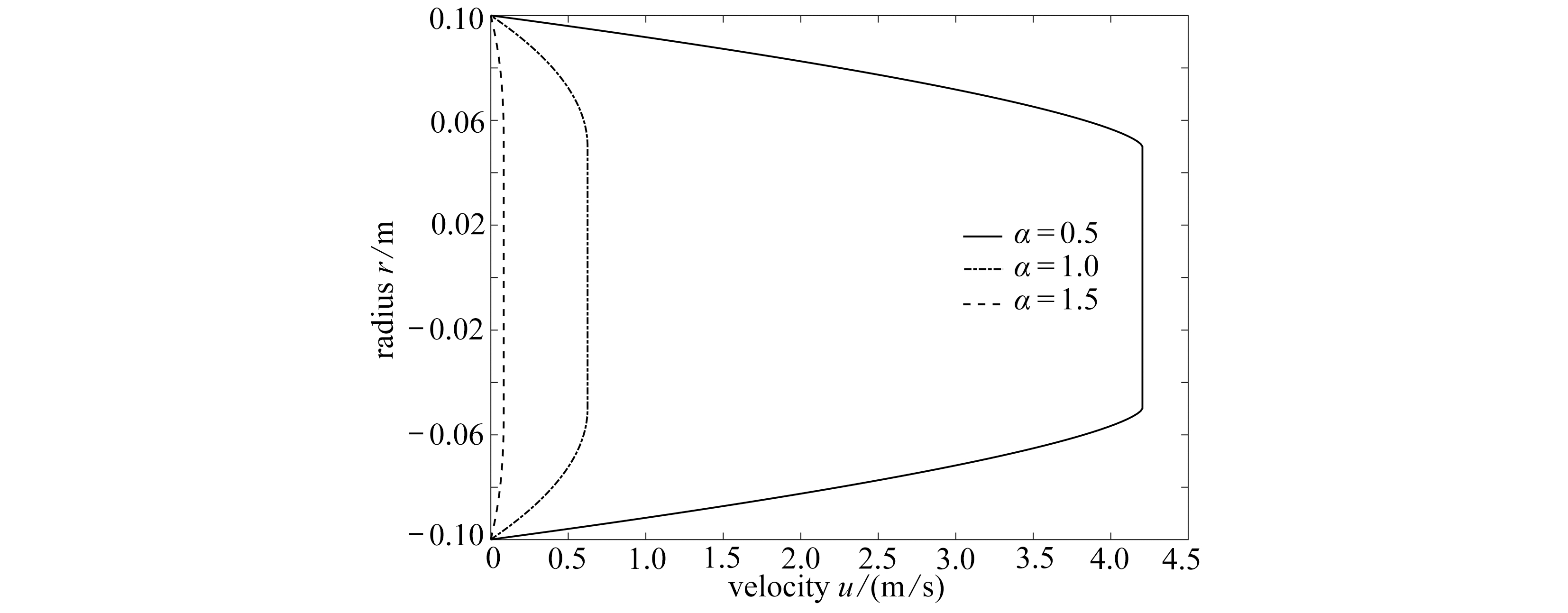
图6 不同阶数下分数阶非Newton流体流速分布图(τ0≠0, r0=0.05 m,Δp=250 Pa,L=25 m,μα=0.01 Pa·s)
Fig.6 The velocity profiles of fractional non-Newtonian fluid with different fractional derivative ordersτ0≠0(r0=0.05 m,Δp=250 Pa,L=25 m,μα=0.01 Pa·s)
综上所述,可以得到

(33)
3) 平均流速
由平均流速的定义![]() 以及式(32),可得
以及式(32),可得
(34)
4) 压降
由式(32)经整理可得
(35)
5) 平均Reynolds数
由式(23)、(34)可得
(36)
设![]() 故
故
(37)
含有屈服切应力的分数阶非Newton流体流动状态与屈服切应力大小有关.当屈服值大于0且小于管壁切应力时,圆管中的流场需要分区讨论.处于流核区的分数阶非Newton流体因为切应力小于屈服值,并不发生流层间的相对运动,类似于固体滑动,速度相同;而速梯区的速度分布与不含屈服切应力的非Newton流体流速分布形态类似.两种流体的流场区别主要在于流核区不同.从另一个角度讲,对于不含屈服切应力的分数阶非Newton流体,分数阶的阶数更接近反映流体对空间的整体记忆性.而含有屈服切应力的分数阶非Newton流体,分数阶的阶数反映的是流体对空间的局部记忆性.
圆管中流体的流态判别主要基于确定流体从层流过渡至湍流所对应的临界流速,本文以首先发生湍流的半径为r的某层为参考,以该层Reynolds数Rer为流态判别准则.以Rer的最大值(Rer)max为临界Reynolds数,有
(38)
其中ηa为表观黏度.Rer在管轴处(r=0)和在管壁处(u(R)=0)均为零,因此,Rer最大值处于两者之间.当流速大于临界流速即为湍流,当流速小于临界流速即为层流.
由表观黏度的定义[34]:
(39)
令τ0=0代入式(7),结合式(6)和(10),可得
ηa=μαΓ(1+α)r1-α.
(40)
将式(14)、(40)代入式(38)并整理,可得
(41)
为求得(Rer)max,令
(42)
可得
(43)
将式(43)代入式(41),则有

(44)
取
且由式(8)和(19)整理后可得
(45)
将式(8)、(19)代入式(45)化简可得临界Reynolds数的表达式为
(46)
由剪切实验和圆管实验测得分数阶阶数α和平均流速![]() 再由式(46)计算可得该流体的临界Reynolds数,从而求得临界流速.
再由式(46)计算可得该流体的临界Reynolds数,从而求得临界流速.
对于含有屈服切应力的分数阶非Newton流体,研究人员通常从广义Reynolds数的角度计算临界流速.本文亦采用此方法.
由式(8)和(10)可得管壁处的剪切速率:
(47)
由式(8)和(47)可得表观黏度表达式如下:
(48)
故含屈服切应力的分数阶非Newton流体临界Reynolds数为
(49)
由实验确定分数阶阶数α和平均流速![]() 再由式(49)计算出该流体的临界Reynolds数,最后求得临界流速.
再由式(49)计算出该流体的临界Reynolds数,最后求得临界流速.
非Newton流体的流态判别比Newton流体更复杂,因此,非Newton流体的流态判别式并不统一,且多为近似估计.本节仍以Newton流体的临界Reynolds数为参考,分别推导了含有和不含有屈服切应力的分数阶非Newton流体临界Reynolds数.
非Newton流体的流动问题具有多尺度、长程相关性等特点[35],从工程角度讲,一维圆管非Newton流体流动问题研究是探索非Newton流体输运问题的重要切入口[36].
从研究对象角度分析:多组分、传热传质、化学反应等过程耦合于流场是难以进行非Newton流体精确建模和仿真的主要障碍.基于实验或野外数据拟合得到的经验公式往往因研究对象、实验条件等客观因素而具有一定的局限性.分数阶非Newton流体模型的建立可以为复杂流体输运问题的研究提供新的研究思路.
从载体角度分析:管径变化、弯转、圆管的粗糙度分布等同样会对非Newton流体在圆管中的流动产生影响.微观上,近壁面处,流体质点在粗糙壁面摩擦、碰撞易产生脉动,形成大小不一漩涡,造成局部流速分布不均和能量损失.对于不含屈服切应力的非Newton流体,这种相互作用会沿程累积,又由于流层间的内摩擦力,两种因素共同作用产生圆管断面的流速分布不均和能量损失.流体对于外部作用的记忆性可以通过本构方程中分数阶导数的阶数表征.对于含有屈服切应力的非Newton流体,因为屈服切应力的存在,流核区的流体流层间不产生相对运动,因此流体对于壁面粗糙度和内摩擦作用的记忆性主要通过速梯区的流速分布反映.从这个层面讲,分数阶导数阶数反映的是局部空间记忆性.目前,大粗糙度的圆管层流可以通过收缩半径预测,但紊流问题仍然难以做到准确预测[37].
基于实验或者理论,用来判别非Newton流体流态的Reynolds数较多[38].由于过渡区的存在,使得Reynolds数的选取有较大的不确定性[39].本文基于分数阶非Newton流体本构方程提出了一种新的流态判别准则,不仅考虑了流体本身记忆特性同时也考虑了载体的物理特征,具有一定的参考价值.通过实验数据探索分数阶导数阶数和临界Reynolds数的定量关系,并探讨其中内在的物理机理是笔者进一步的工作内容之一.
本文基于分数阶微积分理论,采用空间分数阶导数,建立了分数阶非Newton流体本构模型.现有的模型均可通过是否含有屈服切应力和不同的分数阶导数阶数来表示,且非Newton流体的空间依赖特征可以通过分数阶导数阶数的大小来表征.此外,本文还推导了圆管内分数阶非Newton流体流动参数.这对于管道设计和非Newton流体的分析、控制以及测量相关参数,均可提供较好的理论参考.笔者下一步将研究如何将此模型扩展至高维,并结合实际问题进行数值计算及仿真.
参考文献:
[1] 刘海燕, 庞明军, 魏进家.非牛顿流体研究进展及发展趋势[J].应用化工, 2010,39(5): 740-746.(LIU Haiyan, PANG Mingjun, WEI Jinjia.A progress and trend of the non-Newtonian fluids[J].AppliedChemicalIndustry, 2010,39(5): 740-746.(in Chinese))
[2] 姜楠, 田砚.舌尖上的非牛顿流体[J].力学与实践, 2017,39(1): 89-92.(JIANG Nan, TIAN Yan.The non-Newtonian fluid on the tongue tip[J].MechanicsandEngineering, 2017,39(1): 89-92.(in Chinese))
[3] 彭岩, 吕冰海, 纪宏波, 等.非牛顿流体材料在工业领域的应用与展望[J].轻工机械, 2014,32(1): 109-114.(PENG Yan, LÜ Binghai, JI Hongbo, et al.Application and prospect of non-Newtonian fluid in the industrial field[J].LightIndustryMachinery, 2014,32(1): 109-114.(in Chinese))
[4] 董正远.含蜡原油管输的通用速度分布与温度分布[J].西安石油大学学报(自然科学版), 2005,20(6): 37-40.(DONG Zhengyuan.Velocity and temperature distributions of the circular pipe flow of waxy crude oil[J].JournalofXi’anShiyouUniversity(NaturalScienceEdition), 2005,20(6): 37-40.(in Chinese))
[5] 朱克勤.非牛顿流体力学研究的若干进展[J].力学与实践, 2006,28(4): 1-8.(ZHU Keqin.Some advances in non-Newtonian fluid mechanics[J].MechanicsandEngineering, 2006,28(4): 1-8.(in Chinese))
[6] 李勇, 柳文琴.非牛顿流体流动的格子Boltzmann方法研究进展[J].力学与实践, 2014,36(4): 383-395.(LI Yong, LIU Wenqin.The research progress of lattice Boltzmann method in non-Newtonian fluid flow[J].MechanicsandEngineering, 2014,36(4): 383-395.(in Chinese))
[7] MEWIS J, WAGNER N J.Thixotropy[J].AdvancesinColloid&InterfaceScience, 2009,147: 214-227.
[8] NGUYEN Q H, NGUYEN N D.Incompressible non-Newtonian fluid flows[C]//ContinuumMechanics-ProgressinFundamentalsandEngineeringApplications.Rijeka: InTech, 2012.
[9] DEALY J M.Weissenberg and Deborah numbers-their definition and use[J].RheolBull, 2010,79(2): 14-18.
[10] YANG X, CHEN W, XIAO R, et al.A fractional model for time-variant non-Newtonian flow[J].ThermalScience, 2017,21(1A): 61-68.
[11] PINHO F T, WHITELAW J H.Flow of non-Newtonian fluids in a pipe[J].JournalofNon-NewtonianFluidMechanics, 1990,34(2): 129-144.
[12] CHO Y I, HARNETT J P.Non-Newtonian fluids in circular pipe flow[J].AdvancesinHeatTransfer, 1982,15: 59-141.
[13] FETECAU C.Analytical solutions for non-Newtonian fluid flows in pipe-like domains[J].InternationalJournalofNon-LinearMechanics, 2004,39(2): 225-231.
[14] ZHENG S, SAIDOUN M, MATEEN K, et al.Wax deposition modeling with considerations of non-Newtonian fluid characteristics[C]//OffshoreTechnologyConference.Houston, USA, 2016.
[15] AZHDARI M, RIASI A, TAZRAEI P.Numerical study of non-Newtonian effects on fast transient flows in helical pipes[R].cn.arXiv.org, ArXiv: 1703.06877.
[16] SHAIKH H, SHAH S B, MEMON R A, et al.Finite element modeling of shear-thinning flow of inelastic non-Newtonian fluid past expansion pipe[J].SindhUniversityResearchJournal(ScienceSeries), 2017,49(1): 69-74.
[17] 李孝军, 刘永刚, 林凯, 等.非牛顿流体石油管流动研究进展及建议[J].石油管材与仪器, 2016,2(3): 8-14.(LI Xiaojun, LIU Yonggang, LIN Kai, et al.Study advances and suggestions on non-Newtonian fluid in oil tubular flow[J].PetroleumInstruments, 2016,2(3): 8-14.(in Chinese))
[18] 张钧波, 张敏.幂律非牛顿流体在偏心圆环通道中的流动特性[J].南京工业大学学报(自科版), 2015,37(6): 114-118.(ZHANG Junbo, ZHANG Min.Characteristics of power-law non-Newtonian fluid flows in eccentric annular channel[J].JournalofNanjingTechUniversity(NaturalScienceEdition), 2015,37(6): 114-118.(in Chinese))
[19] 王旭东, 张健, 康晓东, 等.基于幂律流体模型的渤海油田注聚管柱注入能力分析[J].中国海上油气, 2017,29(2): 87-92.(WANG Xudong, ZHANG Jian, KANG Xiaodong, et al.Injection capacity analysis of downhole polymer injection pipe string in Bohai oilfield based on power law fluid model[J].ChinaOffshoreOilandGas, 2017,29(2): 87-92.(in Chinese))
[20] 庞国飞, 陈文, 张晓棣, 等.复杂介质中扩散和耗散行为的分数阶导数唯象建模[J].应用数学和力学, 2015,36(11): 1117-1134.(PANG Guofei, CHEN Wen, ZHANG Xiaodi, et al.Fractional differential phenomenological modeling for diffusion and dissipation behaviors of complex media[J].AppliedMathematicsandMechanics, 2015,36(11): 1117-1134.(in Chinese))
[21] 陈文, 孙洪广, 李西成.力学与工程问题的分数阶导数建模[M].北京: 科学出版社, 2010.(CHEN Wen, SUN Hongguang, LI Xicheng.FractionalDerivativeModelinginMechanicalandEngineeringProblems[M].Beijing: Science Press, 2010.(in Chinese))
[22] HILFER R.ApplicationsofFractionalCalculusinPhysics[M].World Scientific, 2000.
[23] METZLER R, KLAFTER J.The random walk’s guide to anomalous diffusion: a fractional dynamics approach[J].PhysicsReports, 2000,339(1): 1-77.
[24] SUN H G, CHEN W, CHEN Y Q.Variable-order fractional differential operators in anomalous diffusion modeling[J].PhysicaA:StatisticalMechanics&ItsApplications, 2009,388(21): 4586-4592.
[25] SCHIESSEL H, METZLER R, BLUMEN A, et al.Generalized viscoelastic models: their fractional equations with solutions[J].JournalofPhysicsA:Mathematical&General, 1995,28(552): 6567-6584.
[26] 刘林超, 杨骁.竖向集中力作用下分数导数型半无限体粘弹性地基变形分析[J].工程力学, 2009,26(1): 13-17.(LIU Linchao, YANG Xiao.Analysis on settlement of semi-infinite viscoelastic ground based on fractional derivative model[J].EngineeringMechanics, 2009,26(1): 13-17.(in Chinese))
[27] 吴杰, 上官文斌.采用粘弹性分数导数模型的橡胶隔振器动态特性的建模及应用[J].工程力学, 2008,25(1): 161-166.(WU Jie, SHANGGUAN Wenbin.Modeling and applications of dynamic characteristics for rubber isolators using viscoelastic fractional derivative model[J].EngineeringMechanics, 2008,25(1): 161-166.(in Chinese))
[28] MONJE C A, CHEN Y Q, VINAGRE B M, et al.Fractional-OrderSystemsandControls[M].London: Springer, 2010.
[29] MAINARDI F, SPADA G.Creep, relaxation and viscosity properties for basic fractional models in rheology[J].EuropeanPhysicalJournalSpecialTopics, 2011,193(1): 133-160.
[30] 肖世武, 周雄, 胡小玲, 等.分数阶导数线性流变固体模型及其应用[J].工程力学, 2012,29(10): 354-358.(XIAO Shiwu, ZHOU Xiong, HU Xiaoling, et al.Linear rheological solid model with fractional derivative and its application[J].EngineeringMechanics, 2012,29(10): 354-358.(in Chinese))
[31] EZZAT M A.Thermoelectric MHD non-Newtonian fluid with fractional derivative heat transfer[J].PhysicaB:PhysicsofCondensedMatter, 2010,405(19): 4188-4194.
[32] 刘发旺, 庄平辉, 刘青霞.分数阶偏微分方程数值方法及其应用[M].北京: 科学出版社, 2015.(LIU Fawang, ZHUANG Pinghui, LIU Qingxia.NumericalMethodsofFractionalPartialDifferentialEquationsandApplications[M].Beijing: Science Press, 2015.(in Chinese))
[33] SUN H G, ZHANG Y, WEI S, et al.A space fractional constitutive equation model for non-Newtonian fluid flow[J].CommunicationsinNonlinearScience&NumericalSimulation, 2018,62: 409-417.
[34] 沈仲棠, 刘鹤年.非牛顿流体力学及其应用[M].北京: 高等教育出版社, 1989: 41-66.(SHENG Zhongtang, LIU Henian.Non-NewtonianFluidMechanicsandItsApplication[M].Beijing: Higher Education Press, 1989: 41-66.(in Chinese))
[35] CHHABRA R P.Non-Newtonian fluids: an introduction[C]//RheologyofComplexFluids.New York: Springer, 2010.
[36] 韩式方.非牛顿流体本构方程和计算解析理论[M].北京: 科学出版社, 2000.(HAN Shifang.ConstitutiveEquationandComputationalAnalyticalTheoryofNon-NewtonianFluids[M].Beijing: Science Press, 2000.(in Chinese))
[37] GRAHAM L J W, PULLUM L, WU J.Flow of non-Newtonian fluids in pipes with large roughness[J].CanadianJournalofChemicalEngineering, 2016,94(6): 1102-1107.
[38] CRESPI-LIORENS D, VICENTE P, VIEDMA A.Generalized Reynolds number and viscosity definitions for non-Newtonian fluid flow in ducts of non-uniform cross-section[J].ExperimentalThermal&FluidScience, 2015,64: 125-133.
[39] PATEL Y, SANYAL A, SHARMA D, et al.Dimensionless Reynolds number as a dimension for fluid mechanics in rheology[J].JournalofDrugDiscoveryandTherapeutics, 2017,5(1): 25-30.
YANG Xu, LIANG Yingjie, SUN Hongguang, CHEN Wen
(CollegeofMechanicsandMaterials,HohaiUniversity,Nanjing211100,P.R.China)
(Contributed by CHEN Wen, M.AMM Editorial Board)
Abstract:A thorough understanding of the flow behavior of non-Newtonian fluid is the first step for analyzing, predicting and controlling of pipe flow.Experiments indicate that non-Newtonian fluid is historically dependent on the procedure of shear flow.The constitutive model for fractional non-Newtonian fluid was established via the spatial fractional calculus approach.The velocity profile, the flux, the mean velocity, the pressure drop and the mean Reynolds number of the proposed model were also derived.In addition, a novel criterion for the flow state of fractional non-Newtonian fluid was proposed.The results show that, the shear stress of the non-Newtonian fluid can be described by the axial velocity distribution.For the fractional non-Newtonian fluid without yield shear stress, the larger the fractional order is, the more uniform the velocity distribution will be and the stronger the memory of the fluid will be.The magnitude of the fractional order reflects the memory of the fluid with respect to the global space.For the fractional non-Newtonian fluid with yield shear stress, the larger the fractional order is, the more uniform the velocity distribution in the velocity gradient region will be, and the smaller of the velocity in the core region will be.In this case, the magnitude of the fractional order reflects the memory of the fluid with respect to the local region.This study offers a new method for the modeling of memory characteristics of non-Newtonian fluid.
Key words:fractional operator; pipe flow; criterion for flow state; mathematical and physical modeling
Foundation item:The National Science Fund for Distinguished Young Scholars of China(11125208);The National Natural Science Foundation of China(11572112; 41628202; 11528205)
作者简介:杨旭(1990—),男,博士生(E-mail: darrenyang366@gmail.com);梁英杰(1989—),男,讲师(E-mail: liangyj@hhu.edu.cn);孙洪广(1982—),男,教授,博士生导师(E-mail: shg@hhu.edu.cn);陈文(1967—)男,教授,博士生导师(通讯作者.E-mail: chenwen@hhu.edu.cn).
基金项目:国家杰出青年科学基金(11125208); 国家自然科学基金(11572112;41628202;11528205);111引智计划(B12032);中央高校基本科研业务费(2018B687X14);江苏省研究生科研与实践创新计划(KYCX18_0532)
修订日期:2018-09-26
*收稿日期:2018-05-25;
文章编号:1000-0887(2018)11-1213-14
文献标志码:A DOI: 10.21656/1000-0887.390153
中图分类号:O232; O172; O373
① 引用本文/Citethispaper:
杨旭,梁英杰,孙洪广,陈文.空间分数阶非Newton流体本构及圆管流动规律研究[J].应用数学和力学, 2018,39(11): 1213-1226.
YANG Xu, LIANG Yingjie, SUN Hongguang, CHEN Wen.A study on the constitutive relation and the flow of spatial fractional non-Newtonian fluid in circular pipes[J].AppliedMathematicsandMechanics, 2018,39(11): 1213-1226.