
图1 输流管道模型的示意图
Fig.1 The diagram of a pipe conveying fluid
张凯凯1,谭 霞1,丁 虎1,陈立群1,2
(1.上海大学 上海市应用数学和力学研究所,上海 200072;2.上海大学 力学系,上海 200444)
(我刊编委陈立群来稿)
摘要:研究了3∶1内共振下输流管道在超临界领域的参激稳态响应.基于输流管道的非平凡静平衡位形,通过坐标代换得到超临界输流管道非线性振动的偏微分-积分控制方程.运用直接多尺度法,分析得到3∶1内共振下输流管道参激振动响应的近似解析解,并用Galerkin截断法数值验证近似解析结果的可靠性.数值算例表明,内共振条件下输流管道系统不同模态间存在能量转移.通过近似解析结果预测了参激幅值对内共振条件下幅频响应曲线的影响.
关键词:输流管道; 内共振; 多尺度法; 参激振动; 超临界
工程中存在许多输流管道系统,如天然气供应、自来水供应和干热岩开采等.流体的流动会引起管道振动,流速越大,振动越剧烈.当流速超过一定值时,管道将发生屈曲变形[1],并在新的平衡位形附近振动,因此对输流管道系统动力学特性的研究进入了超临界领域.
在研究输流管道系统的振动特性时,国内外学者发现了许多有趣的现象[2-4].席红敏、张伟等研究了参数激励和外激励联合作用下变速输液管的周期及混沌运动[5].孟丹、郭海燕等研究了输流管道的流体诱发振动稳定性[6].Liang和Yang等研究了两端简支的旋转输液管的自由振动和稳定性[7-8].Liu等研究了悬臂式输液管的非线性受迫振动[9].徐鉴、杨前彪研究了水平悬臂输液管的内共振现象和模态转换,发现了鞍结分岔以及Hopf分岔[10-11].黄慧春、张艳雷等研究了两端简支的超临界输液管2∶1内共振特性[12-13].毛晓晔、丁虎等分析了超临界输液管3∶1内共振下的受迫振动响应[14].目前对超临界输液管3∶1内共振下的参激振动特性还没有相关研究.由于参激振动引起的疲劳破坏会对生产和生活造成严重危害,因此,对该系统的研究有着十分重要的理论意义和工程实际意义.
本文利用多尺度方法研究两端简支的输流管道在超临界3∶1内共振下的幅频特性;然后将近似解析方法得到的结果与数值仿真结果进行对比,并在近似解析方法的基础上研究了参激扰动幅值对输流管道不同位置幅频响应的影响.
弹性输流管道模型如图1所示,L为管道长度,U表示流体速度,v(x,t)为输流管道y方向上的位移量,即横向位移,x是轴向坐标,t为时间.

图1 输流管道模型的示意图
Fig.1 The diagram of a pipe conveying fluid
由于管道截面为圆环,根据对称性进行降维处理,假设管道的振动发生在纸平面内,并且轴向位移远小于横向位移,故忽略轴向位移,只考虑管道的横向位移.可以由Newton第二定律得到控制方程及边界条件[15].
无量纲化系数如下:
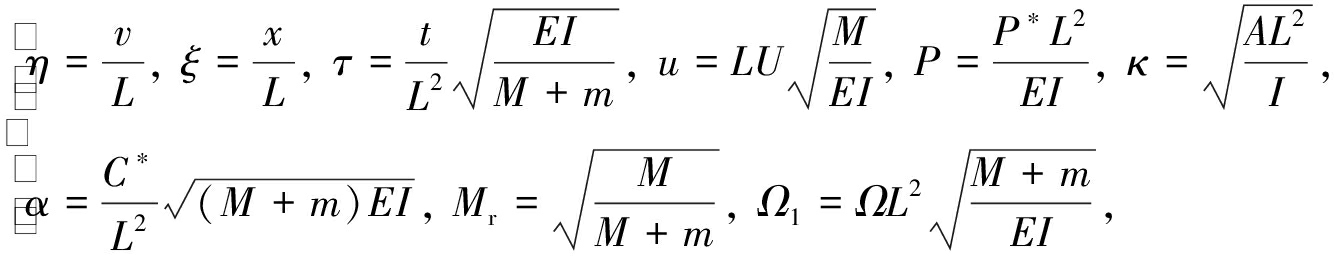
(1)
其中,M为单位长度管道内流体质量,m为单位长度管道质量,P*为管道轴力,A是管道可通过流体的截面面积,E表示管道的弹性模量,I为管道惯性矩.将能量耗散集中处理为线性阻尼项,C*为阻尼系数,Ω为流体扰动频率.
无量纲控制方程及边界条件为
αη,τ+η,ξξξξ=0,
(2)
(3)
其中,u=u0[1+μsin(Ω1τ)],u0为流体平均速度,μ为流体速度扰动系数,Ω1为流体扰动频率.忽略方程(2)中的非线性项以及与时间有关的项,可得到静态平衡方程:
(4)
结合简支边界条件,推导得到输流管道的非平凡静平衡位形:
(5)
引入坐标变换
η(ξ,τ)↔![]()
推导得到超临界下输流管道的参激振动方程:
(6)
按照多尺度法过程[14],引入时间尺度,并对控制方程进行如下重刻度:
(7)
引入三阶摄动解:
η(ξ,T0,T1,T2)=η0(ξ,T0,T1,T2)+εη1(ξ,T0,T1,T2)+ε2η2(ξ,T0,T1,T2).
(8)
将式(7)和(8)代入方程(6)中,按照小参数ε展开,并提取前3阶系数项,得到如下系数方程.
ε0项系数
(9)
ε1项系数
(10)
ε2项系数
(11)
观察发现方程(9)为偏微分齐次线性方程,该方程的解可以写为
(12)
式中cc为前面各项的共轭复数,其中pkn可用待定系数法确定.通过将式(12)代入线性微分方程式(9),提取eiωnT0的系数可得到频率方程,从而确定固有频率ωn.
将方程(9)的解代入方程(10)中,可得
(13)
其中,RNST表示产生长期项的项,cc表示前面项的共轭复数.消去长期项,得到(∂/∂T1)A(T1,T2)=0,即有A(T1,T2)=A(T2).假设方程(13)的解为
η1=B1(ξ,T2)e2iω1T0+B2(ξ,T2)e2iω2T0+B3(ξ,T2)ei(ω1+ω2)T0+
B4(ξ,T2)ei(ω1-ω2)T0+B5(ξ,T2)eiΩ1T0+cc+B6(ξ,T2).
(14)
该解中也只涉及到前两阶模态,式中cc为前面各项共轭复数,其中
(15)
同样地,Snk(T2)用待定系数法确定.将方程(9)和(10)的解代入方程(11)中,为了找出长期项,仅假设η2的齐次解部分如下:
(16)
引入解谐因子σ1和σ2,用以衡量前两阶固有频率的接近程度以及参激频率与第一阶固有频率的接近程度,将解谐关系
ω2=3ω1+ε2σ1,Ω1=2ω1+ε2σ2
代入方程(11),做内积,可得
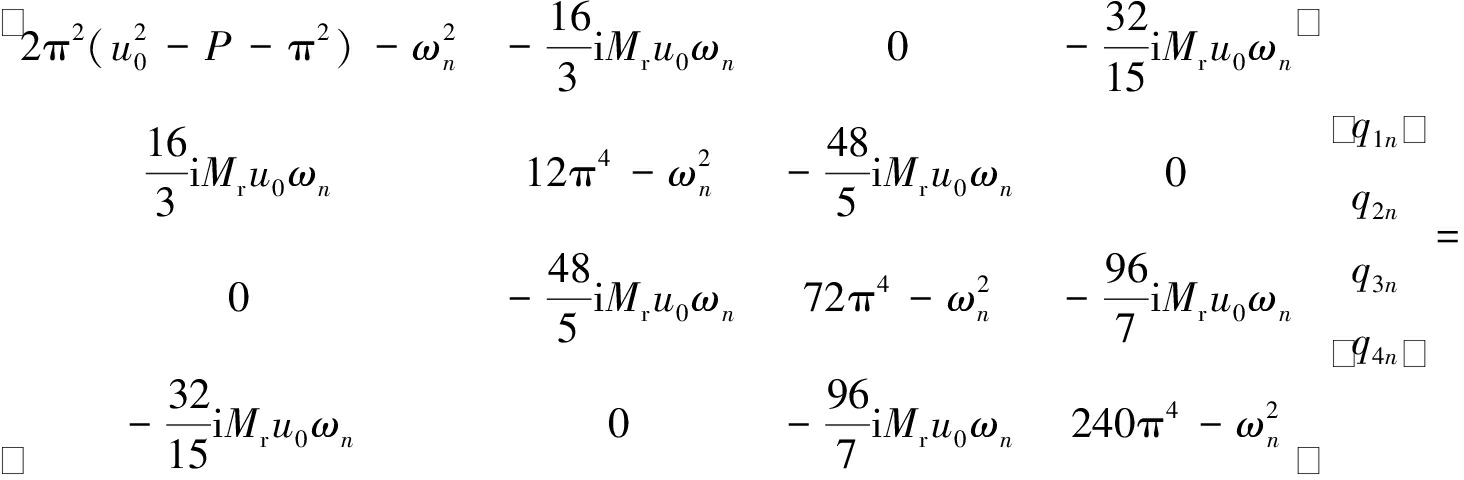
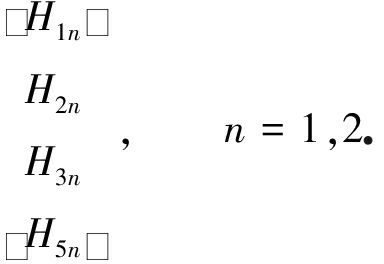
(17)
用方程(17)中等式右边的列向量代替等式左边系数矩阵中的任一列,令行列式值等于0,即为可解性条件.将An(T2)=(an1+ian2)eiΛnT2(n=1,2)代入可解性条件,可得
并分离实部和虚部可得4个方程.代入具体数据可得ɑ11,ɑ12,ɑ21,ɑ22的值,再回代至式(8),即可得近似解析结果.
对方程(6)进行Galerkin截断[16],假设方程有如下形式解:
(18)
将式(18)与近似解析结果对比可以发现:
qn(τ)=pn1A1(T2)eiω1T0+pn2A2(T2)eiω2T0+S1n(T2)e2iω1T0+S2n(T2)e2iω2T0+
S3n(T2)ei(ω1+ω2)T0+S4n(T2)ei(ω1-ω2)T0+S5n(T2)eiΩ1T0+cc+S6n(T2).
(19)
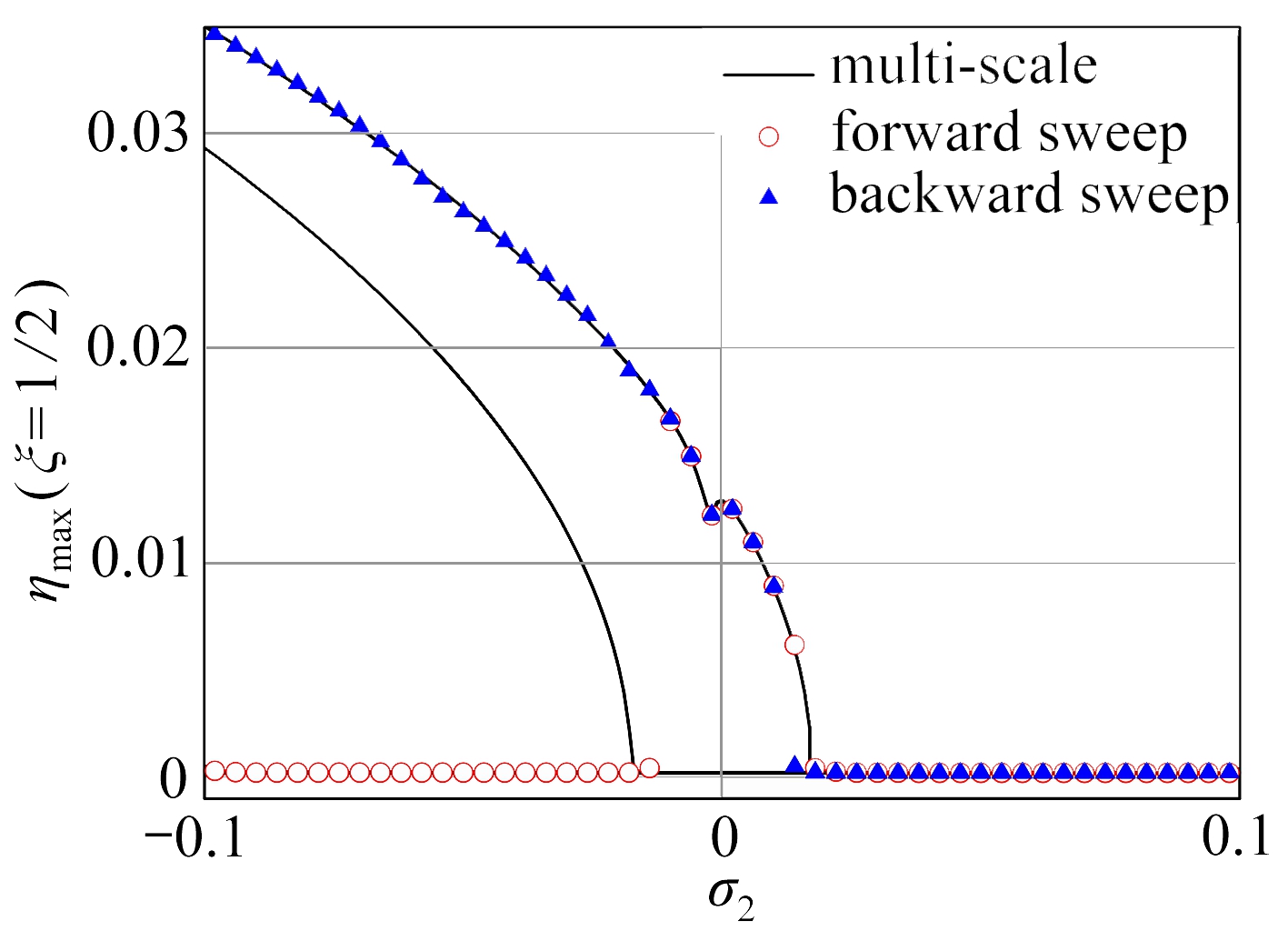
(a) ξ=1/2
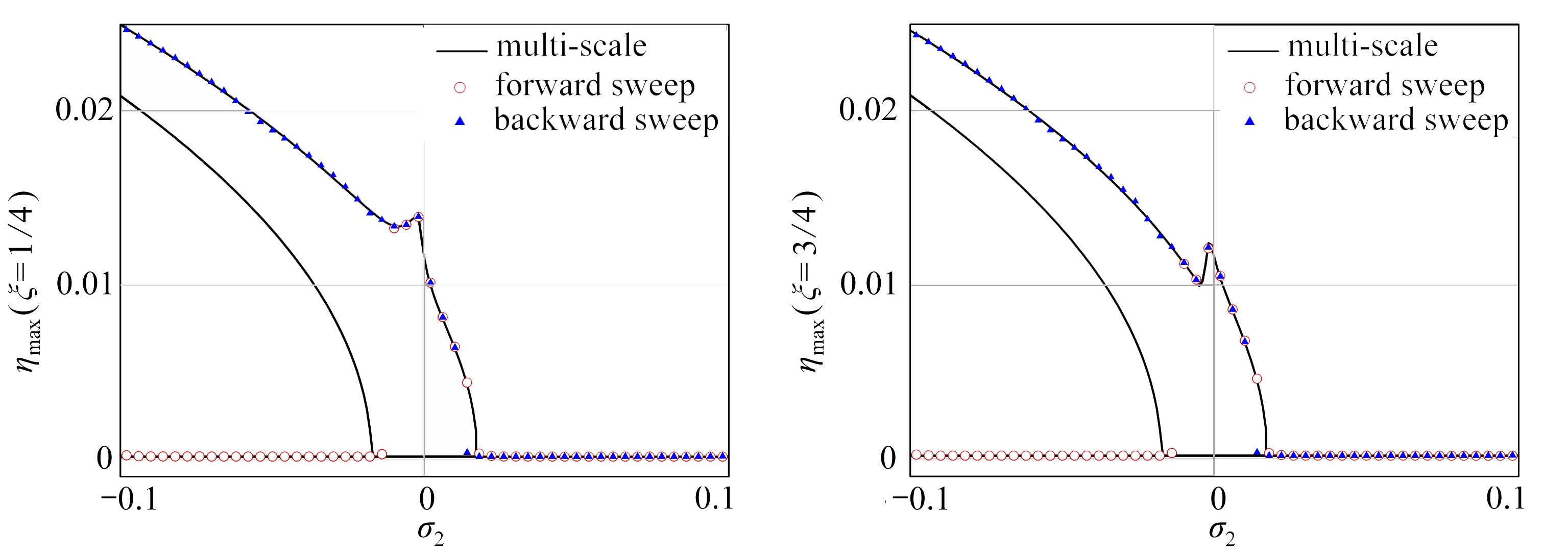
(b) ξ=1/4 (c) ξ=3/4
图2 输流管道不同位置的幅频响应曲线(ξ=1/2, 1/4, 3/4)
Fig.2 Amplitude-frequency curves of the pipe conveying fluid(ξ=1/2, 1/4, 3/4)
输流管道参数取值为P=-5,Mr=0.447,α=0.005,κ=4,此时产生3∶1内共振的流速及前两阶固有频率为u0=3.475 6,ω1=11.549 115,ω2=34.647 345.当σ1=0,μ=0.000 8时,管道不同位置的近似解析结果和数值仿真结果可见图2.
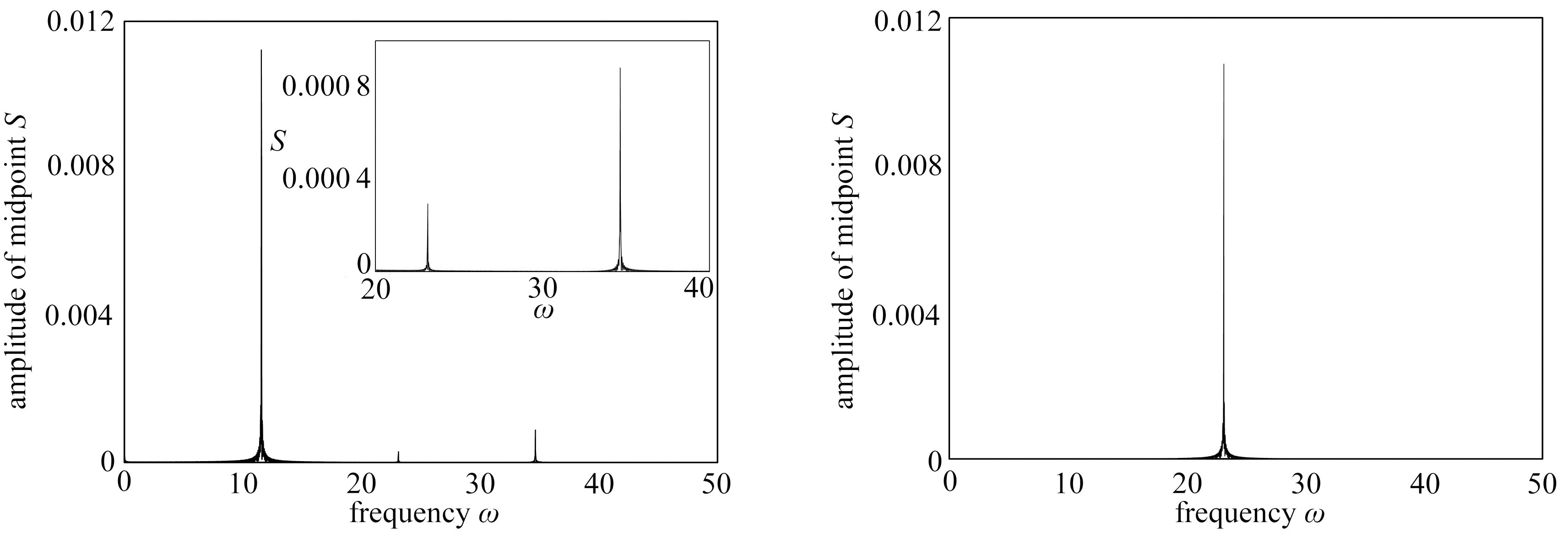
(a) σ2=-0.004时管道中点频谱分析 (b) σ2=0.04时管道中点频谱分析
(a) The frequency spectrum analysis at the pipeline midpoint, σ2=-0.004 (b) The frequency spectrum analysis at the pipeline midpoint, σ2=0.04
图3 频谱分析
Fig.3 Frequency spectrum analysis
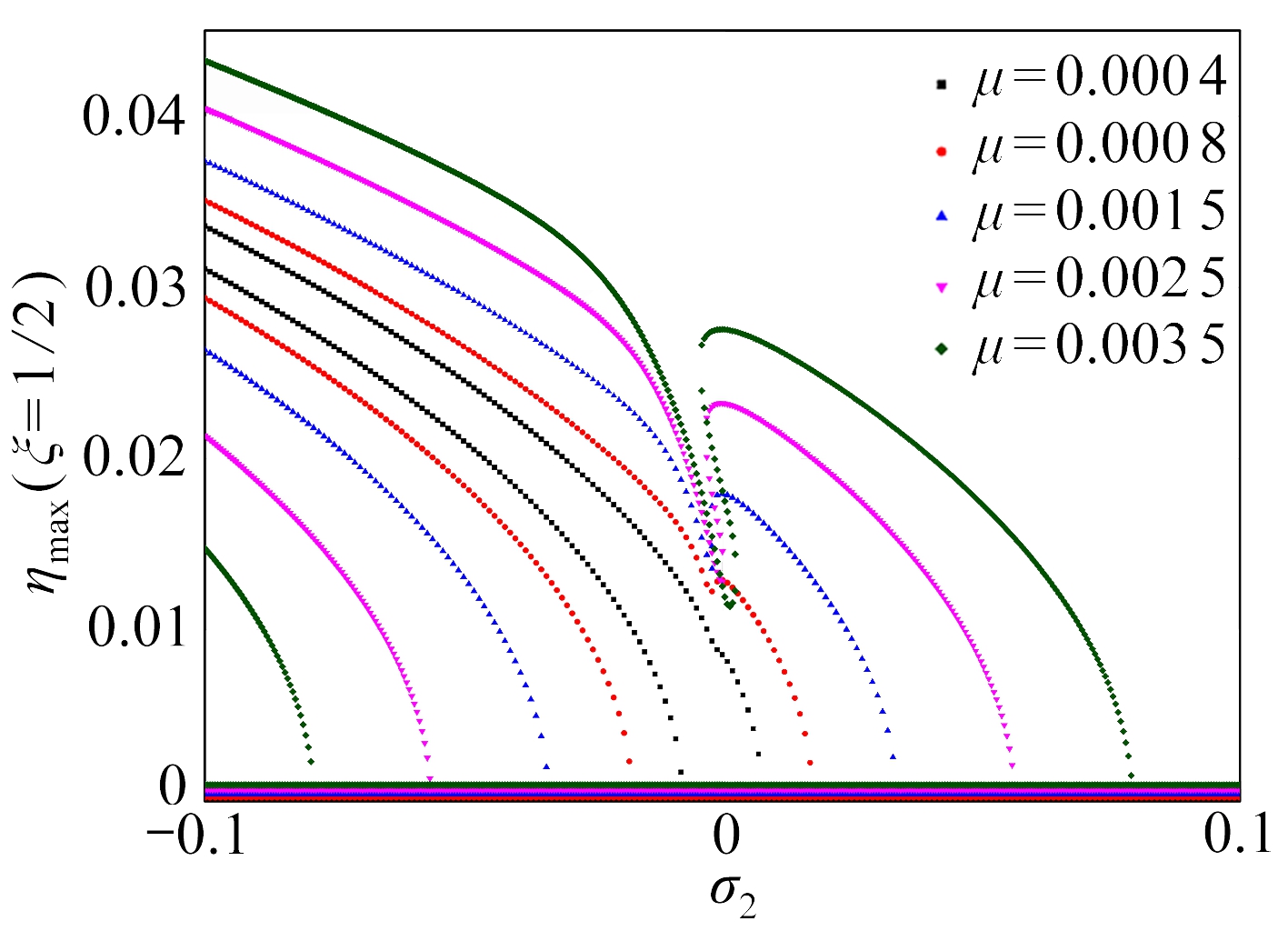
(a) ξ=1/2
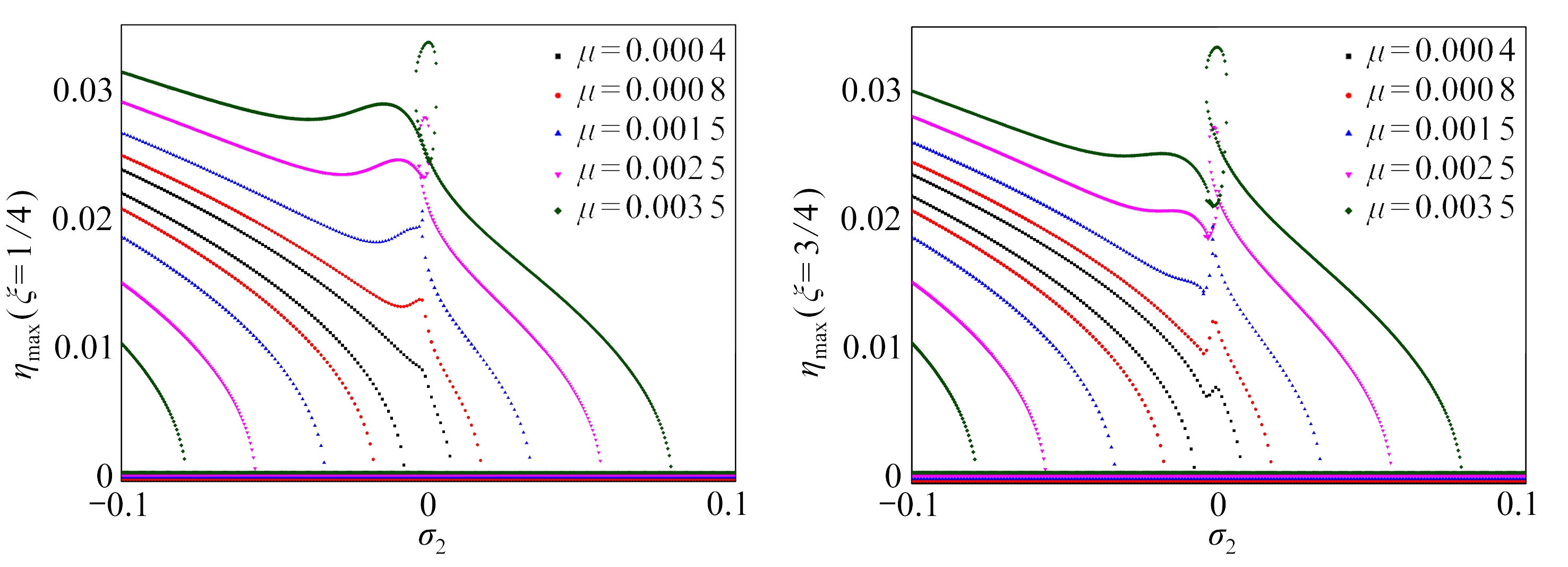
(b) ξ=1/4 (c) ξ=3/4
图4 不同扰动幅值下的幅频响应图
Fig.4 Amplitude-frequency curves under different disturbance amplitudes
图2中实线代表近似解析结果,圆圈和三角形分别代表数值仿真得到的正向和反向扫频的结果.从图中可以看出:数值结果和近似解析解吻合得很好,从而验证了近似解析解的正确性;输流管道幅频响应曲线向左弯曲,具有软特性;对比图2(b)和2(c),发现在ξ=1/4和ξ=3/4处除了激起输流管道的第一阶模态外,还激起了第二阶模态;并且二阶模态上的响应在σ2=0附近表现得尤为明显.
数值计算时,取σ1=0,μ=0.000 8.管道中点振动情况的频谱分析如图3所示,观察图3(a)发现σ2=-0.004时输流管道频率成分包含第一阶固有频率,参激频率和第二阶固有频率,说明内共振条件下,能量在模态间发生了转移.图3(b)中σ2=0.04时,远离共振区域,故管道仅有参激频率的振动.
图4描述了扰动幅值变化对幅频响应的影响.近似解析结果表明:跳跃范围随着扰动幅值增大而变宽;图4(a)中随着扰动幅值增大,固有频率左侧产生一个凹陷,且凹陷最低点的幅值基本不变;图4(b)和4(c)中随着扰动幅值的增大幅频曲线均出现了一个环,这是由于输流管道结构的对称性导致其在对称位置上出现了响应的近似对称,这种近似对称不仅体现了输流管道与两端简支静态梁振动的相似性,也体现了由于流体流动引起的二者之间的差异.
本文推导了超临界输流管道的偏微分-积分控制方程,利用直接多尺度法分析,得到了超临界输流管道3∶1内共振下参激振动的近似解析解,通过Galerkin截断法数值验证了近似解析结果的正确性.研究了参数对参激振动的影响,发现幅频曲线发生跳跃的范围随着参激幅值的增大而增大;在主共振附近,输流管道中点的幅频曲线随着扰动幅值增大会出现下凹现象,而在ξ=1/4和ξ=3/4处则会出现一个封闭的环.频谱分析表明:由于非平凡静平衡位形的存在,超临界速度下的振动一直存在参激频率成分;内共振条件下,输流管道系统的能量会在前两阶模态间发生转移,在主共振附近,能量转移更加明显.
参考文献:
[1] PAÏDOUSSIS M P, ISSID N T.Dynamic stability of pipes conveying fluid[J].JournalofSoundandVibration, 1974,33(3): 267-294.
[2] 任建亭, 姜节胜.输流管道系统振动研究进展[J].力学进展, 2003,33(3): 313-324.(REN Jianting, JIAGN Jiesheng.Advances and trends on vibration of pipes conveying fluid[J].AdvancesinMechanics, 2003,33(3): 313-324.(in Chinese))
[3] 黄玉盈, 邹时智, 钱勤, 等.输液管的非线性振动、分叉与混沌: 现状与展望[J].力学进展, 1998,28(1): 30-42.(HUANG Yuying, ZOU Shizhi, QIAN Qin, et al.Advances and trends of nonlinear dynamics of pipes conveying fluid[J].AdvancesinMechanics, 1998,28(1): 30-42.(in Chinese))
[4] 徐鉴, 杨前彪.输液管模型及其非线性动力学近期研究进展[J].力学进展, 2004,34(2): 182-194.(XU Jian, YANG Qianbiao.Recent development on models and nonlinear dynamics of pipes conveying fluid[J].AdvancesinMechanics, 2004,34(2): 182-194.(in Chinese))
[5] 席红敏, 张伟, 姚明辉.变流速输液管的周期和混沌运动[J].动力学与控制学报, 2008,6(3): 243-246.(XI Hongmin, ZHANG Wei, YAO Minghui.Periodic and chaotic oscillations of the fluid conveying pipes with pulse fluid[J].JournalofDynamicsandControl, 2008,6(3): 243-246.(in Chinese))
[6] 孟丹, 郭海燕, 徐思朋.输流管道的流体诱发振动稳定性分析[J].振动与冲击, 2010,29(6): 80-83.(MENG Dan, GUO Haiyan, XU Sipeng.Stability analysis on flow-induced vibration of fluid-conveying pipes[J].JournalofVibrationandShock, 2010,29(6): 80-83.(in Chinese))
[7] LIANG F, YANG X D, QIAN Y J, et al.Transverse free vibration and stability analysis of spinning pipes conveying fluid[J].InternationalJournalofMechanicalSciences, 2018,137: 195-204.
[8] LIANG F, YANG X D, ZHANG W, et al.Dynamical modeling and free vibration analysis of spinning pipes conveying fluid with axial deployment[J].JournalofSoundandVibration, 2018,417: 65-79.
[9] LIU Z Y, WANG L, SUN X P.Nonlinear forced vibration of cantilevered pipes conveying fluid[J].ActaMechanicaSolidaSinica, 2018,31(1): 32-50.
[10] 徐鉴, 杨前彪.流体诱发水平悬臂输液管的内共振和模态转换(Ⅰ)[J].应用数学和力学, 2006,27(7): 819-824.(XU Jian, YANG Qianbiao.Flow-induced internal resonances and mode exchange in horizontal cantilevered pipe conveying fluid(Ⅰ)[J].AppliedMathematicsandMechanics, 2006,27(7): 819-824.(in Chinese))
[11] 徐鉴, 杨前彪.流体诱发水平悬臂输液管的内共振和模态转换(Ⅱ)[J].应用数学和力学, 2006,27(7): 825-832.(XU Jian, YANG Qianbiao.Flow-induced internal resonances and mode exchange in horizontal cantilevered pipe conveying fluid(Ⅱ)[J].AppliedMathematicsandMechanics, 2006,27(7): 825-832.(in Chinese))
[12] 黄慧春, 张艳雷, 陈立群.受迫振动的超临界输液管Galerkin数值模拟[J].应用数学和力学, 2014,35(10): 1100-1106.(HUANG Huichun, ZHAN Yanlei, CHEN Liqun.A Galerkin numerical method for the pipe conveying supercritical fluid under forced vibration[J].AppliedMathematicsandMechanics, 2014,35(10): 1100-1106.(in Chinese))
[13] ZHANG Y L, CHEN L Q.Internal resonance of pipes conveying fluid in the supercritical regime[J].NonlinearDynamics, 2012,67(2): 1505-1514.
[14] 毛晓晔, 丁虎, 陈立群.3∶1内共振下超临界输液管受迫振动响应[J].应用数学和力学, 2016,37(4): 345-351.(MAO Xiaoye, DING Hu, CHEN Liqun.Forced vibration responses of supercritical fluid-conveying pipes in 3∶1 internal resonance[J].AppliedMathematicsandMechanics, 2016,37(4): 345-351.(in Chinese))
[15] SEMLIER C, LI G X, PAÏDOUSSIS M P.The non-linear equations of motion of pipes conveying fluid[J].JournalofSoundandVibration, 1994,169(5): 577-599.
[16] 张国策, 丁虎, 陈立群.复模态分析超临界轴向运动梁横向非线性振动[J].动力学与控制学报, 2015,13(4): 283-285.(ZHANG Guoce, DING Hu, CHEN Liqun.Complex modal analysis of transversally non-linear vibration for supercritically axially moving beams[J].JournalofDynamicsandControl, 2015,13(4): 283-285.(in Chinese))
ZHANG Kaikai1, TAN Xia1, DING Hu1, CHEN Liqun1,2
(1.ShanghaiInstituteofAppliedMathematicsandMechanics,ShanghaiUniversity,Shanghai200072,P.R.China;2.DepartmentofMechanics,ShanghaiUniversity,Shanghai200444,P.R.China)
(Contributed by CHEN Liqun, M.AMM Editorial Board)
Abstract:The parametric vibration responses were studied in the supercritical fluid-conveying pipes in the 3∶1 internal resonance condition.In the control equation, the non-normal static configuration of the pipe at the supercritical velocity was introduced, and the partial differential-integral control equation was obtained.The approximate analytic solution was deduced with the direct multiscale method, and the reliability of the approximate analytic results was verified with the Galerkin truncation method.Numerical examples show that, there exists energy transfer between different modes of the pipeline system in internal resonance.The influence of the parameter amplitude on the amplitude-frequency response was predicted based on approximate analytical results.
Key words:fluid-conveying pipe; internal resonance; multiscale method; parametric vibration; supercritical
Foundation item:The National Natural Science Foundation of China(11772181)
作者简介:张凯凯(1993—),男,硕士生(E-mail: 2294360286@qq.com);谭霞(1992—),女,博士生(通讯作者.E-mail: tanxiadyx0108@163.com).
基金项目:国家自然科学基金(11772181);上海市教育委员会“曙光”计划(17SG38);上海市教育委员会创新计划(2017-01-07-00-09-e00019)
修订日期:2018-09-14
*收稿日期:2018-04-16;
文章编号:1000-0887(2018)11-1227-09
文献标志码:A DOI: 10.21656/1000-0887.390121
中图分类号:O32
① 引用本文/Citethispaper:
张凯凯, 谭霞, 丁虎, 陈立群.超临界输流管道3∶1内共振下参激振动响应[J].应用数学和力学, 2018,39(11): 1227-1235.
ZHANG Kaikai, TAN Xia, DING Hu, CHEN Liqun.Parametric vibration responses of supercritical fluid-conveying pipes in 3∶1 internal resonance[J].AppliedMathematicsandMechanics, 2018,39(11): 1227-1235.