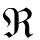 (ω),用以描述基础振动位移与外力关系,以此表征土与基础的动力相互作用效应.基础阻抗函数
(ω),用以描述基础振动位移与外力关系,以此表征土与基础的动力相互作用效应.基础阻抗函数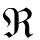 (ω)是一个依赖于外荷载激振频率ω的复变函数,可表示为
(ω)是一个依赖于外荷载激振频率ω的复变函数,可表示为王 珏1,2,周 叮3
(1.河海大学 机电工程学院,江苏 常州 213022;2.河海大学 土木与交通学院,南京 210098;3.南京工业大学 土木工程学院,南京 211816)
摘要:利用Chebyshev复多项式在数值拟合中的优越性以及递归函数理论,将风机基础的频域阻抗函数等效为可直接用于结构时域分析的Chebyshev递归集总参数模型.并根据d’Alembert(达朗伯尔)原理和时域逐步积分法,利用模型的递归特性编制了地震作用下求解土-基础-风机支撑结构时程响应的通用程序,通过对比算例验证了程序的有效性和优越性.最后对一个长桩群基础上的风机支撑结构进行了数值计算,研究表明本模型解决了集总参数模型高阶数值震荡的问题,并在求解风机支撑结构地震响应分析中具有稳定性好、通用性强的优点.
关键词:土-结构相互作用; 风机; 集总参数模型; Chebyshev多项式; 地震响应
近海风机支撑结构长径比大、侧向刚度小,属于典型的长周期结构,土-基础动力相互作用效应对风机支撑结构的动力行为有着显著的影响.以有限元和边界元为代表的数值法虽可以对土-基础-风机结构建立精细化的整体分析模型,但巨大的计算量难以通过参数化分析得到土与结构动力相互作用(soil-structure interaction,以下简称SSI)效应的影响规律.Chopra等[1]在研究大坝与基础地震相互作用时提出的子结构法,可对每个子系统(结构、基础、地基)采用其合适的方法进行独立分析,因而广泛应用于SSI问题的研究[2].利用子结构法分析SSI问题时,土与基础动力相互作用通过阻抗函数来反映[3-5].它是一个与外激振频率相关的复变函数,其实部和虚部分别表示振动过程中土对基础的弹簧刚度和辐射阻尼.由于阻抗函数具有频率依赖性,考虑SSI效应的上部结构动力分析只能通过Fourier(傅里叶)变换在频域内求解,无法直接用于结构地震时程分析[6-8].
为了实现阻抗函数的时域化分析,研究者们提出了用由多个与频率无关的质量元、阻尼器、弹簧按某种形式组合起来的多自由度集总参数模型来等效地基土对结构的动力作用.栾茂田和林皋[9]提出了双自由度八参数集总参数模型;王满生等[10]利用EKF滤波技术改进了上述集总参数模型中的参数识别方法,进而计算了上部结构的地震响应;Wang等[11]利用上述双自由度八参数集总参数模型进行了不带土箱的土-结构动力相互作用实时耦联模拟地震试验.杜修力等[12]基于六阶并联集总参数模型计算了考虑SSI效应的圆盘基础上多层结构地震响应.以上模型是基于“半经验法”提出的,虽可通过最小二乘拟合来识别模型参数,但无法根据进度要求进行扩展.为此,Wolf[13-14]、Wu和Lee[15-16]、Saitoh[17]等学者使用一般多项式对阻抗函数进行数学处理,发展出了形式多样的集总参数模型,用以描述土与基础动力相互作用效应.Wu和Chen[18]基于可扩展的弹簧-阻尼器-质点串联集总参数模型,分析了地震作用下考虑SSI效应的矩形筏板基础上的多层结构振动问题.但上述模型在采用普通多项式拟合复杂阻抗时,存在由于使用高阶多项式引起的数值振荡问题,尤其是对复杂基础阻抗函数的拟合.Du(杜修力)和Zhao(赵密)[19]提出了有理近似稳定的判别准则,并提出了能预先保证稳定性的参数识别方法.刘伟庆等[20]为了利用Chebyshev复多项式在数值拟合中的优越性,建立了群桩基础的集总参数模型,但由于该方法需将比值形式的复数多项式展开成多项分式,易造成数值不稳定.赵宏和高广运等[21]则通过矢量匹配法将群桩阻抗函数直接拟合成两类多项分式的形式,并采用Routh理论对高频阻抗进行了降阶处理.但文献[20-21]中并没有将其提出的理论模型应用于上部结构的时域动力分析,进而分析相应模型在结构时域分析中的稳定性.
集总参数模型研究的最终目的是为了将考虑SSI效应的计算方法纳入到风机结构设计体系中去,通过开发等效模型的通用程序从而实现土-基础-风机支撑结构地震响应的计算分析.Chebyshev多项式是以递归方式定义的一系列正交多项式,它可以避免插值时由于使用高次多项式插值时出现Gibbs(吉布斯)震荡这一现象[22].为此本文利用Chebyshev复多项式实现连续函数最佳一致逼近的优点,将基础阻抗函数等效为一个由弹簧-阻尼器组成的Chebyshev递归集总参数模型.在此基础上编制了地震作用下求解时程响应的通用程序,并将其应用于土-基础-风机支撑结构地震响应的计算.
研究者们已经通过不同的理论方法得到了各种基础在不同地质条件下的阻抗函数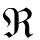 (ω),用以描述基础振动位移与外力关系,以此表征土与基础的动力相互作用效应.基础阻抗函数
(ω),用以描述基础振动位移与外力关系,以此表征土与基础的动力相互作用效应.基础阻抗函数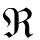 (ω)是一个依赖于外荷载激振频率ω的复变函数,可表示为
(ω)是一个依赖于外荷载激振频率ω的复变函数,可表示为
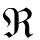 (ω)=
(ω)=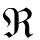 (a0)=Ks[K(a0)+ia0C(a0)],
(a0)=Ks[K(a0)+ia0C(a0)],
(1)
其中,Ks为基础的静刚度,K(a0)和C(a0)为规格化的刚度和几何阻尼,![]() 为虚数单位.无量纲频率a0=ωd/Vs,其中Vs为土体剪切波速,d为基础的特征长度.
为虚数单位.无量纲频率a0=ωd/Vs,其中Vs为土体剪切波速,d为基础的特征长度.
根据Wu和Lee的研究[15],采用基础动柔度拟合可以在不使用任何权函数的情况下使得低频范围占拟合过程的支配地位.当不考虑耦合阻抗时,动柔度为阻抗函数的倒数;当考虑耦合阻抗时,动柔度矩阵则为阻抗函数矩阵的逆矩阵.与阻抗函数类似,其动柔度可采用相应的静柔度Fs进行格式化:
F(a0)=Fs×Fd(a0).
(2)
由于Chebyshev复多项式的插值多项式能最大限度地降低Gibbs震荡现象,提供多项式在连续函数的最佳一致逼近,因此本文采用N阶Chebyshev复多项式对动柔度进行函数拟合,目标函数可以表示为
(3)
式中,φn和φn为各阶Chebyshev复多项式的待定系数,均为实数.s=ia0/a0max,a0max为需要拟合的最大频率.各项Chebyshev复多项式Tn(ix)的表达式如下:
T0(ix)=1,T1(ix)=ix,
(4a)
Tn(ix)=(-1)n-12ixTn-1(ix)-Tn-2(ix),n=2,3,….
(4b)
式(3)中系数C和κ的引入是为确保双精度拟合,使函数Fd(a0)满足以下两个条件:
① 当外荷载激振频率趋于零时(a0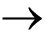 0),满足
0),满足
Fd(a0)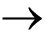 0;
0;
(5a)
② 当外荷载激振频率趋于最大值时(a0 a0max),满足
a0max),满足
Fd(a0) 1/(iσa0),
1/(iσa0),
(5b)
式中,σ为激振频率趋于最大值时的阻尼系数.
由式(5)的两个条件可确定式(3)中系数κ和C的取值为
(6)
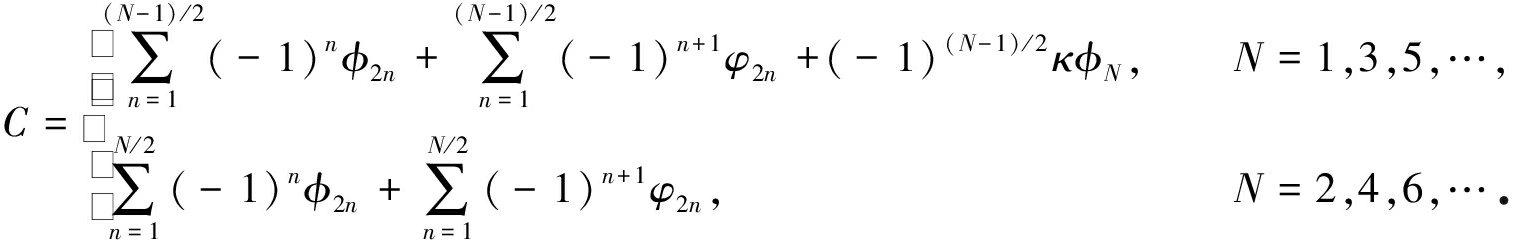
(7)
式(3)中各阶Chebyshev复多项式的未知系数φn和φn可以通过最小二乘法拟合得到,将得到的系数代入式(3)后重新整理可得
(8)
根据递归算法理论,式(8)可以写成如下形式:
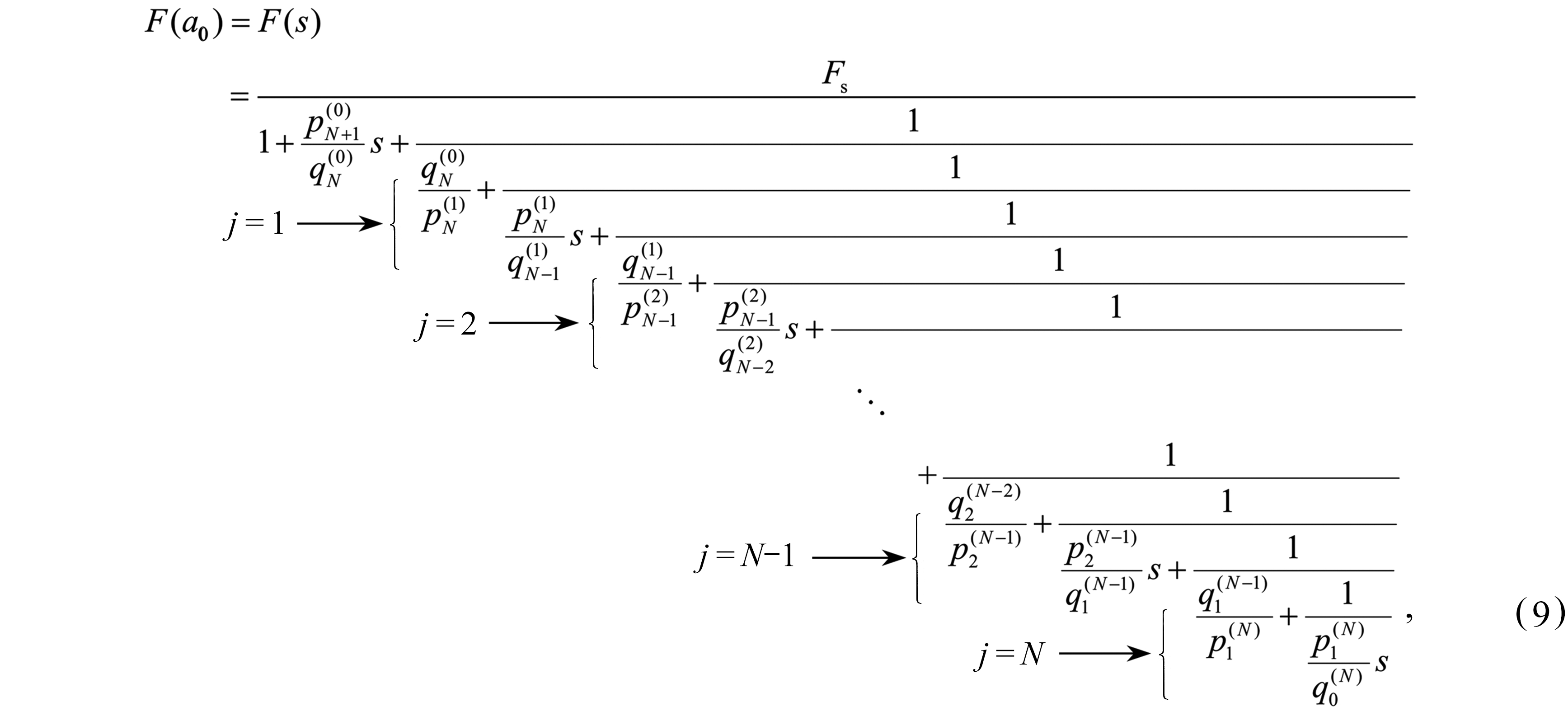
其中
![]()
j=0,1,…,N;n=1,2,…,N-j.
上述基于Chebyshev复多项式拟合得到的动柔度函数,可以用如图1所示的含有待定系数的离散化弹簧-阻尼器模型来等效.图1所示模型的柔度函数可表示为

式中,P0和U0分别为作用在基础顶部的荷载及其引起的变形.将通过Chebyshev复多项式及递归函数理论得到的式(9)与式(10)对比,可识别出图1中的所有力学元件的待定系数λj和γj,从而得到Chebyshev递归集总参数模型:
(11)
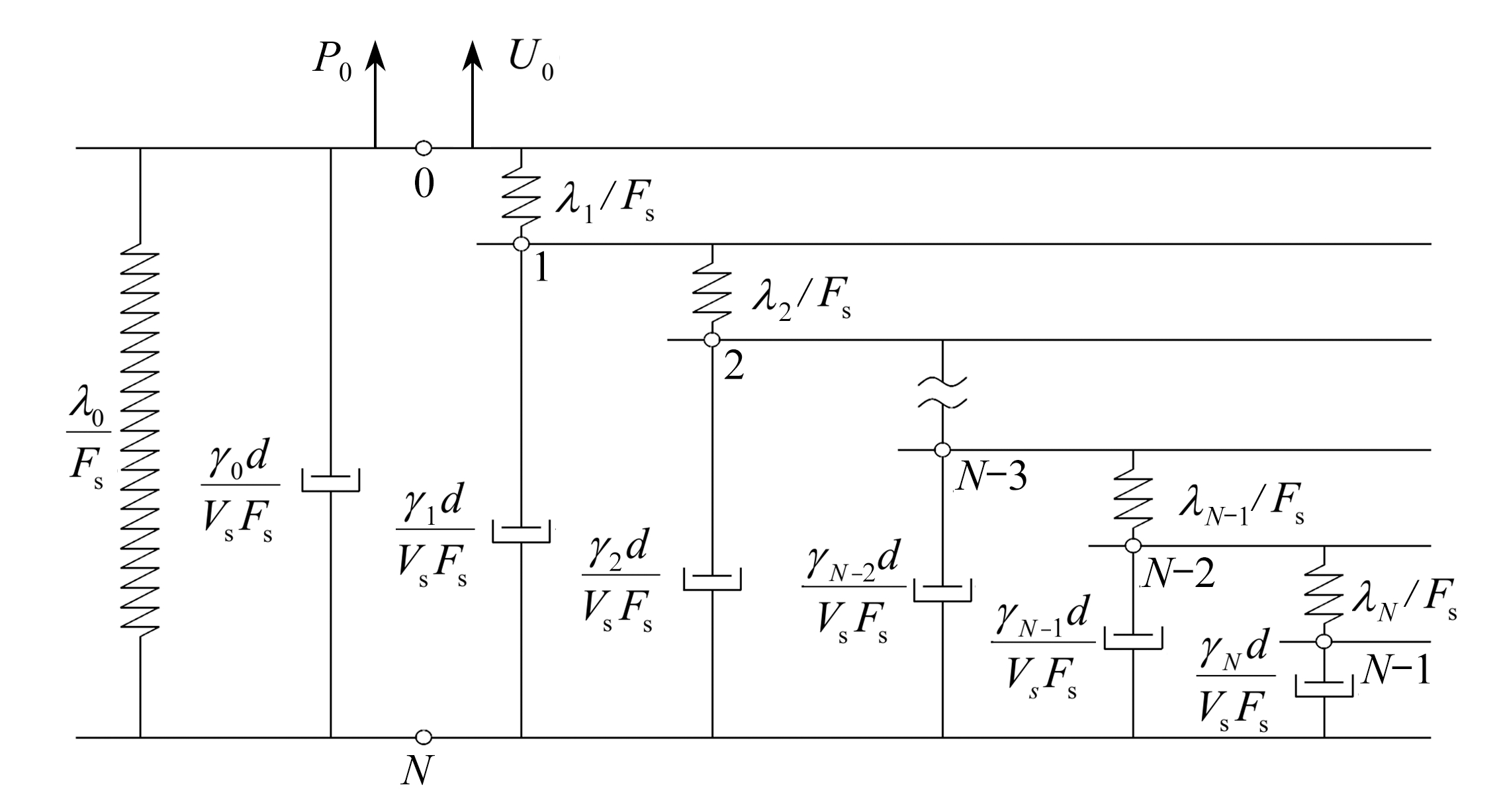
图1 Chebyshev递归集总参数模型
Fig.1 The nested Chebyshev lumped-parameter model(LPM)
如图2所示将风机支撑结构离散为Ns段,并将分布质量向每段节点集中,将各节点集中质量和质量惯性矩用msi和Isi表示,各层剪切刚度和阻尼分别用ksi和csi表示,各层楼板到基础的高度用hi表示.m0和I0分别为基础的质量和惯性矩.基础的水平和摇摆阻抗分别采用含有Nh和Nr个自由度的Chebyshev递归集总参数模型来表示.在地震作用下,第i层与基础间的水平相对位移用usi表示,基础的绝对水平位移和转角用uf和φf表示,集总参数模型中第i个自由度的绝对水平位移和转角用uhi和φri表示.根据d’Alembert原理,对上部结构以及Chebyshev递归集总参数模型的动力平衡条件建立地震作用下土-基础-风机支撑结构系统的时域运动控制方程:
(12)
式中,M,K,C分别为系统的广义质量矩阵、刚度矩阵和阻尼矩阵,u为系统各质点的位移列向量,M*为系统广义质量列向量,![]() 为地震波水平地面加速度.矩阵M,K,C以及列向量u,M*的具体表达式见附录.
为地震波水平地面加速度.矩阵M,K,C以及列向量u,M*的具体表达式见附录.
上式运动方程可采用经典的时域逐步积分Wilson-θ法求解[23],该方法是基于线性加速的基础上提出的一种无条件收敛的计算方法.数值计算中当θ取大于等于1.37时,即可无条件收敛,由此即可得到地震作用下土-基础-风机支撑结构动力相互作用体系的位移、速度和加速度时域动力响应.
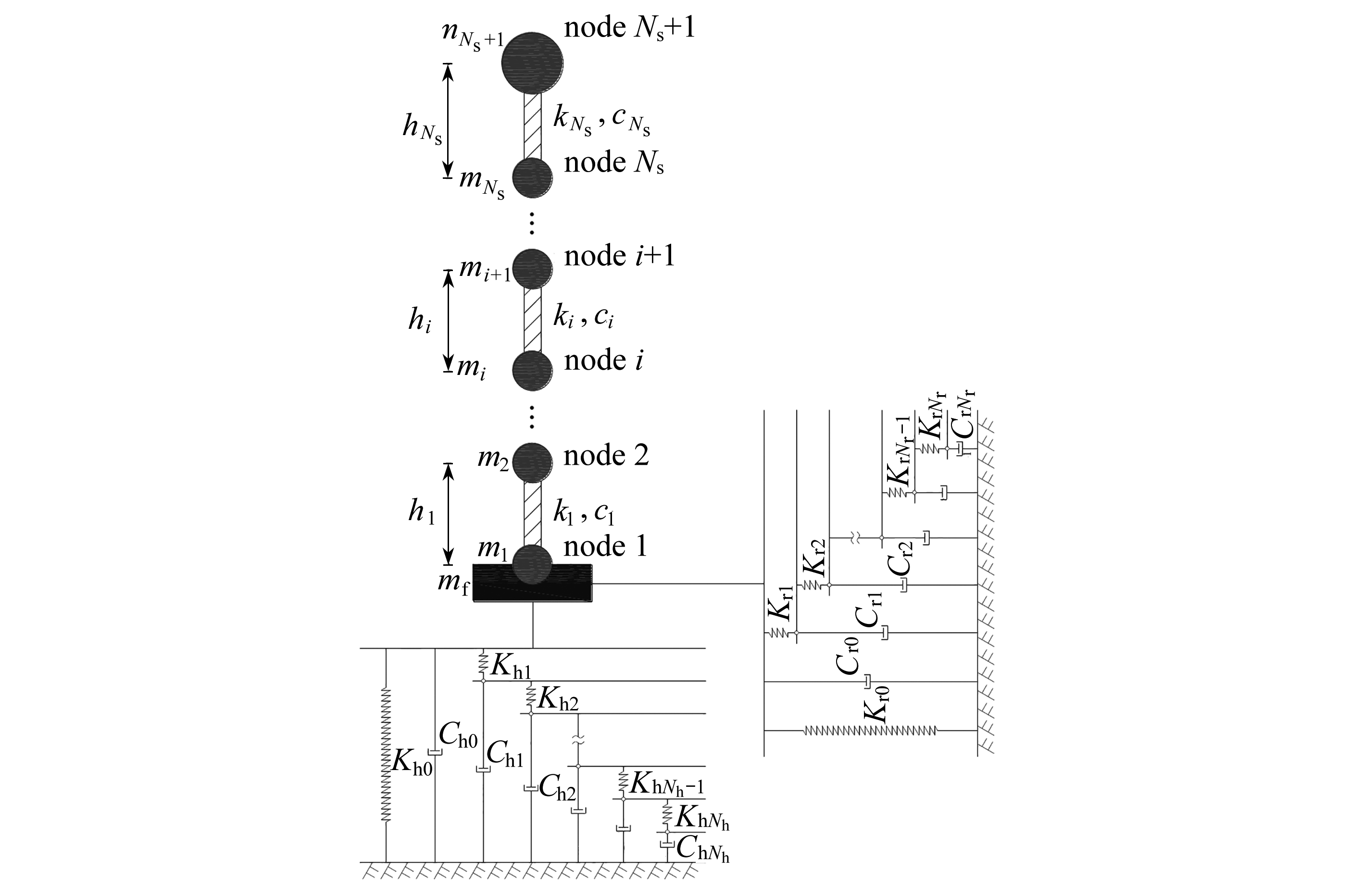
图2 土-基础-风机支撑结构动力相互作用体系的计算模型
Fig.2 The calculation model for the soil-foundation-wind turbine supporting system
为验证Chebyshev递归集总参数模型的有效性及优越性,本算例对一矩形筏板基础上的结构进行了考虑SSI效应的时域分析,得到了其在200 gal(1 gal=1 cm/s2)的El-Centro地震波下的时程响应,并与基于同一阻抗函数的Wu和Chen模型[18]计算结果进行了对比.El-Centro波的加速度及其反应谱如图3所示.结构、基础和地基土的计算参数如表1所示.图4为采用Chebyshev递归集总参数模型表示的规格化基础阻抗函数与基于弹性半空间理论得到的频域解对比.从图4中可以看出,当多项式阶数N为1时,Chebyshev递归集总参数模型即可反映出该矩形基础的水平阻抗函数随频率的变化;而当多项式阶数N为2时,Chebyshev递归集总参数模型即可反映出该矩形基础的摇摆阻抗函数随频率的变化.对应的水平、摇摆递归集总参数模型中的弹簧-阻尼器系数列于表2.
图5为地震作用下结构顶部相对于矩形基础的加速度时程,并与Wu和Chen提出的集总参数模型的计算结果进行了对比.这里需要注意的是,由于本算例与Wu和Chen文献[18]采用了同样的基础阻抗函数表征土与基础间的动力相互作用,因此结构顶部的响应与参数模型的计算结果具有非常好的一致性.但是,对于同一个矩形筏板基础的阻抗函数,Wu和Chen[18]基于一般多项式拟合,则需要在水平和摇摆方向分别采用6个和9个质量-弹簧-阻尼器元件表征土与基础间的动力相互作用效应.而相比之下,本文利用Chebyshev复多项式拟合,则仅采用4个和6个弹簧-阻尼器元件就能很好地表征土与基础间的水平和摇摆动力相互作用效应.此外,由于本文提出的集总参数模型不含有质量元,因此无需对输入基础的地震波进行修正,使得该模型在实际工程中的应用更方便.
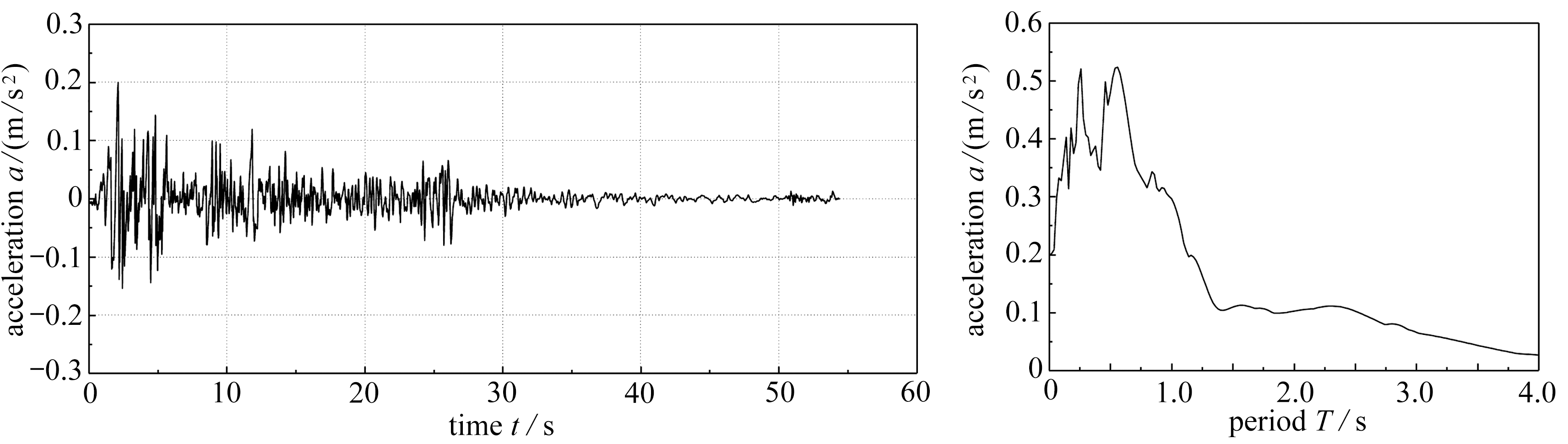
图3 El-Centro波的加速度时程及其反应谱
Fig.3 The time history and the response spectrum of the El-Centro ground motion acceleration
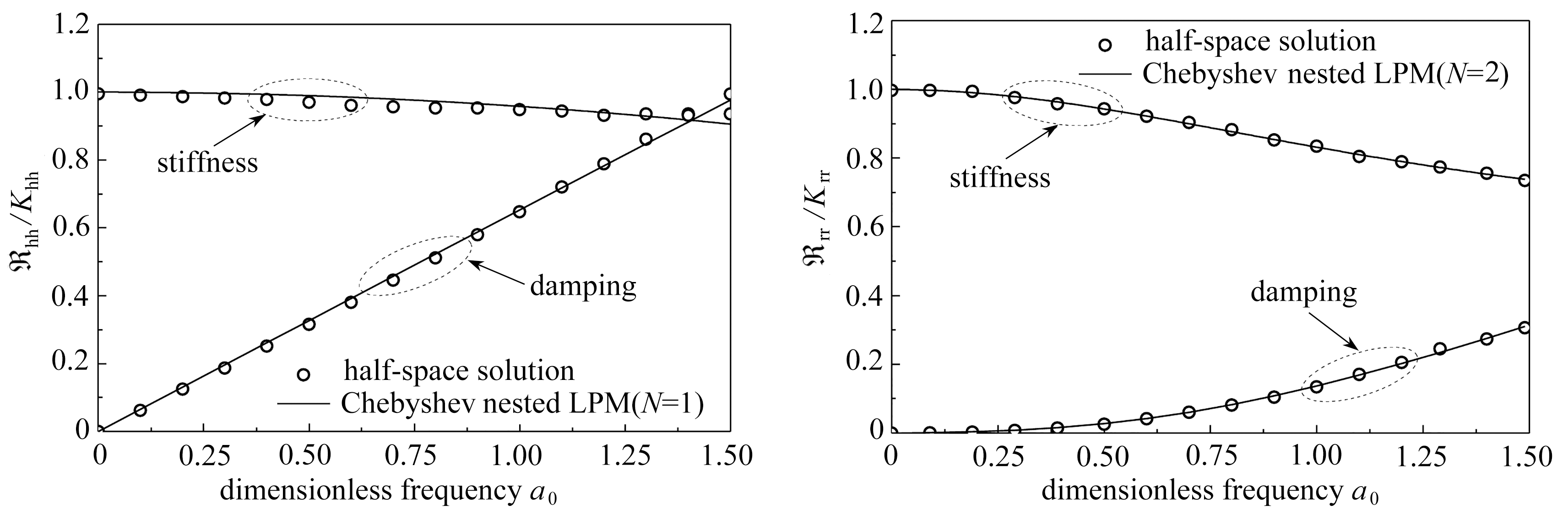
(a)水平 (b)摇摆
(a) Lateral (b) Rocking
图4 矩形筏板基础规格化的阻抗函数
Fig.4 Normalized impedances of the square raft foundation
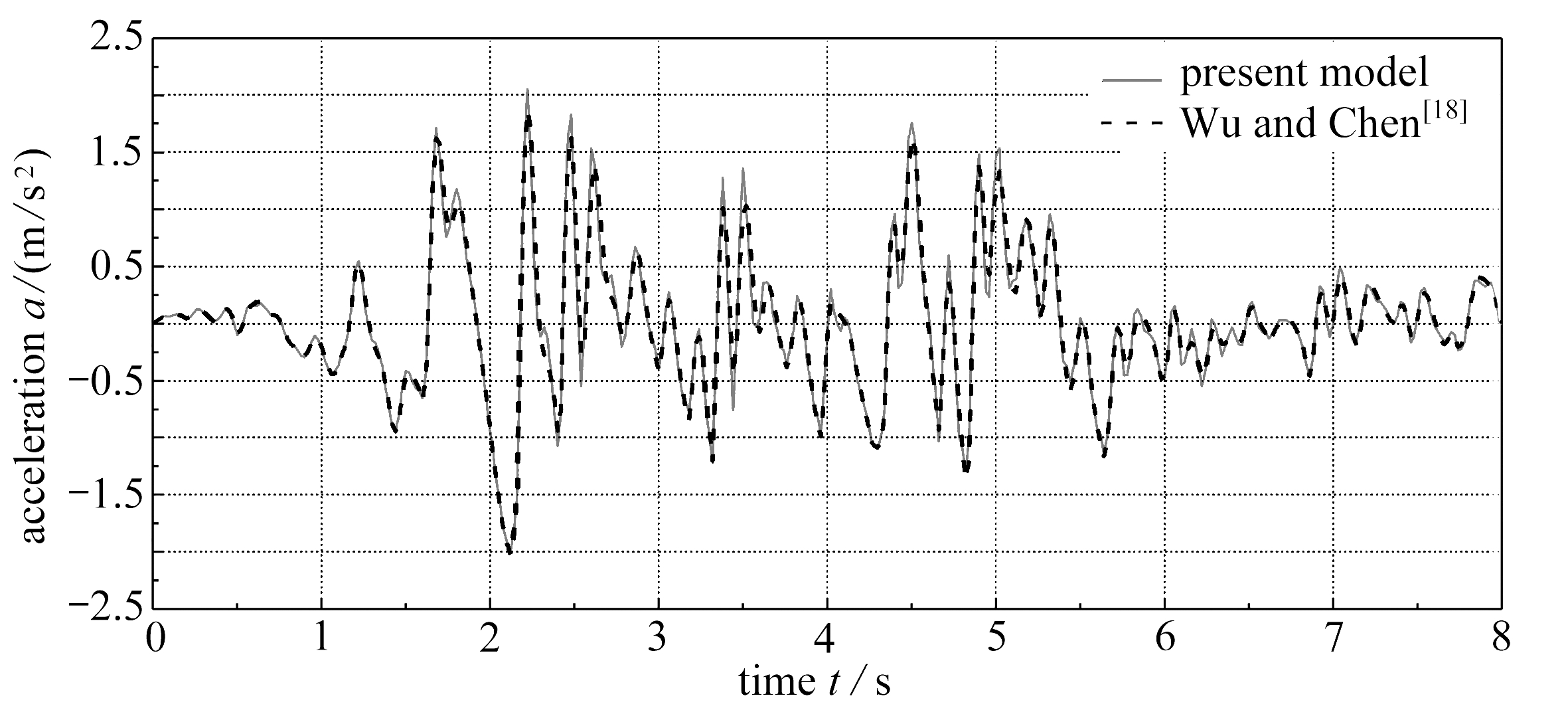
图5 结构顶部加速度时程对比
Fig.5 Comparison of the acceleration history at the top of the superstructure
表1土-筏板基础-结构计算参数
Table 1 Calculation parameters of the soil-raft foundation-structure system

表2筏板基础递归集总参数模型的弹簧阻尼器系数
Table 2 The coefficients of springs and dashpots in the Chebyshev nested LPM for the raft foundation

利用本文的通用程序计算了由3×3长桩群基础支承的风机支撑结构在200 gal的Taft地震波作用下其顶部的时程响应.Taft波的加速度及其反应谱如图6所示.结构自身阻尼比取为5%,各离散节点等效质量为25 000 kg,节点间剪切刚度为5×107N/m,间距为3.5 m,质量惯性矩为1 500 000 kg·m2.桩基础参数如下:桩长20 m,直径1 m,桩间距5 m,密度2 000 kg/m3,弹性模量3.92×109N/m2,Poisson比0.25.地基参数如下:土密度1 400 kg/m3,Poisson比0.4,阻尼比0.05,剪切波速100 m/s.
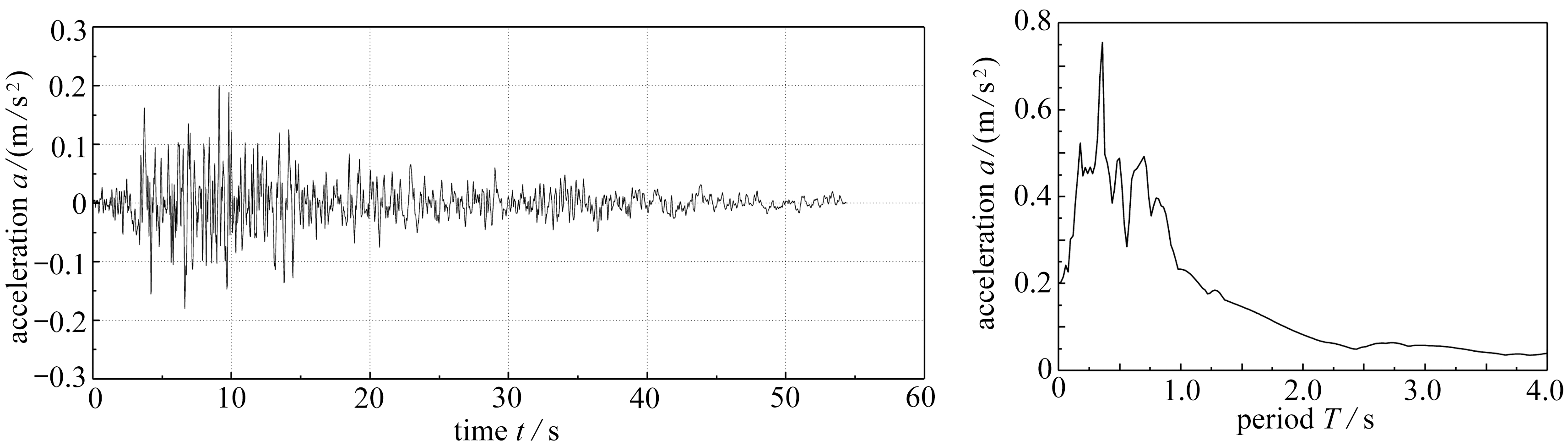
图6 Taft波的加速度时程及其反应谱
Fig.6 The time history and the response spectrum of the Taft ground motion acceleration
算例基于薄层法理论[3]得到的长桩群基础频域内的水平、摇摆阻抗函数,建立了Chebyshev递归集总参数模型来模拟长桩群基础与地基土间的动力相互作用的频率依赖性.图8为采用Chebyshev递归集总参数模型表示的规格化基础阻抗函数与薄层法理论得到的频域解的对比.从图7中可以看出:当拟合阶数N=4时可以很好地反映出长桩群基础水平阻抗函数随频率的变化;当拟合阶数N=12时,Chebyshev递归集总参数模型可以很好地反映出长桩群基础摇摆阻抗函数随频率的变化.对应的水平、摇摆递归集总参数模型中的弹簧-阻尼器系数列于表3.图8为风机支撑结构顶部的加速度时程.从图中可以看出,与刚性地基下的情况相比,考虑土与长桩群基础动力相互作用后风机支撑结构顶部的速度峰值减小.
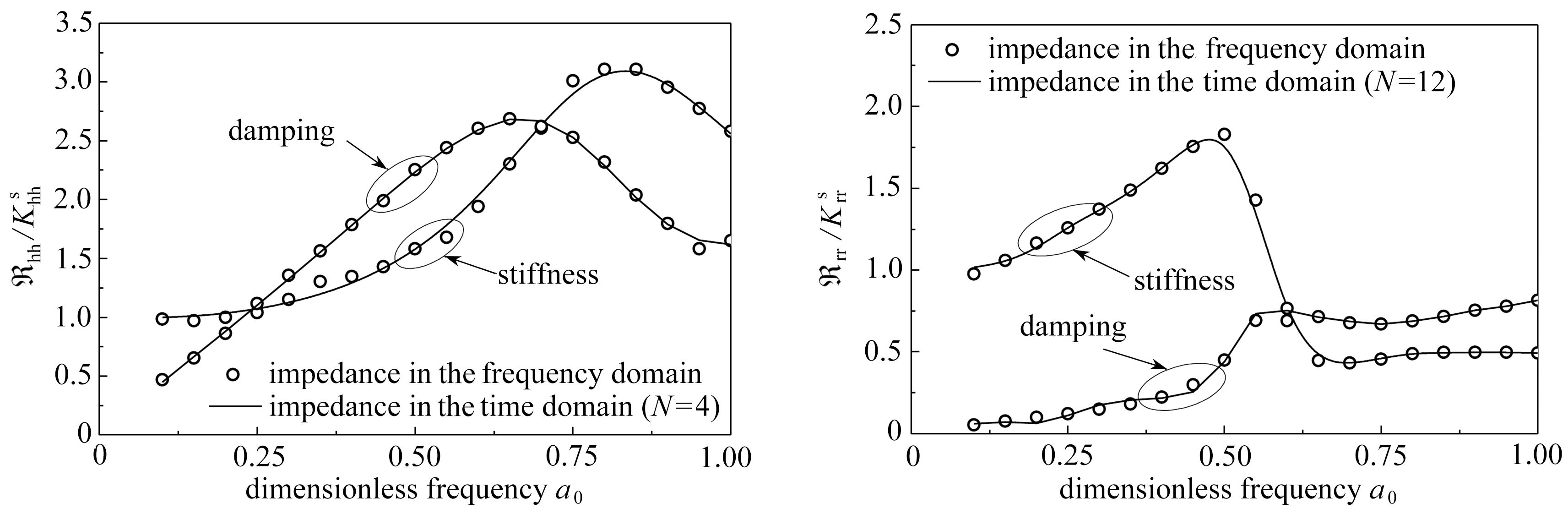
(a) 水平 (b) 摇摆
(a) Lateral (b) Rocking
图7 长桩群基础的规格化的阻抗函数
Fig.7 Normalized impedances of the 3×3 pile group foundation
表33×3长桩群基础Chebyshev递归集总参数模型的弹簧阻尼器系数
Table 3 The coefficients of springs and dashpots in the nested LPM for the 3×3 pile group foundation
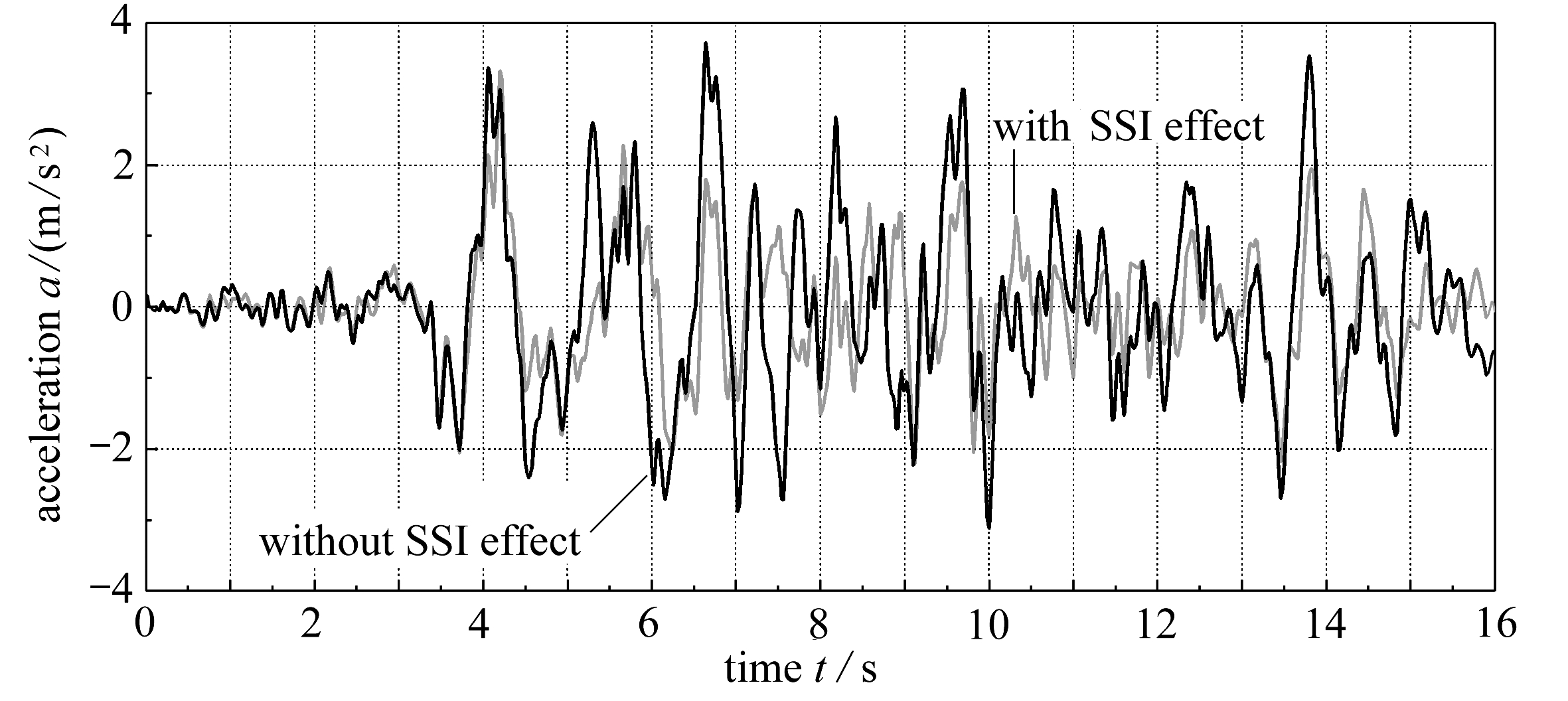
图8 风机支撑结构顶部加速度时程
Fig.8 Acceleration responses at the top of the wind turbine
本文对已有的集总参数模型进行改进,提出了可以将描述土与基础动力相互作用效应的基础频域阻抗函数等效为由一系列与频率无关的弹簧-阻尼器组成的时域递归集总参数模型,并利用递归特性,编制了计算地震作用下土-基础-风机支撑结构动力相互作用时程分析的通用程序.通过数值算例的对比及分析体现了Chebyshev递归集总参数模型在考虑SSI效应的结构地震响应时域计算中的有效应及优越性,具体如下:
1) Chebyshev复多项式拟合的目标函数能很好地描述阻抗函数的频率相关性,避免了传统集总参数模型在采用普通多项式拟合复杂函数时因阶次较高所产生的数值振荡问题,从而提高了计算的稳定性.
2) 递归形式的集总参数模型不仅避免了在函数展开成多项分式的过程中因出现共轭复数而引发数值计算不稳定的情况,而且在根据拟合精度的要求进行扩展运算时,递归特性有助于通用程序的编制.此外,由于该模型中未引入质量元,因此无需对输入基础的地震波进行修正,提高了本方法在工程中的实用性.
3) 验证算例表明与基于一般多项式得到的集总参数模型模型相比,Chebyshev递归集总参数模型模型可以使用较少的参数模拟桩土相互作用效应.基于该模型计算的长桩群基础支承的风机支撑结构地震响应算例表明:与刚性地基上风机支撑结构地震响应相比,考虑土与长桩群基础动力相互作用后风机支撑结构顶部的速度峰值减小.
附录
运动控制方程式(12)中的质量矩阵M表达式如下:
M(Ns+Nh+Nr+2)×(Ns+Nh+Nr+2)=
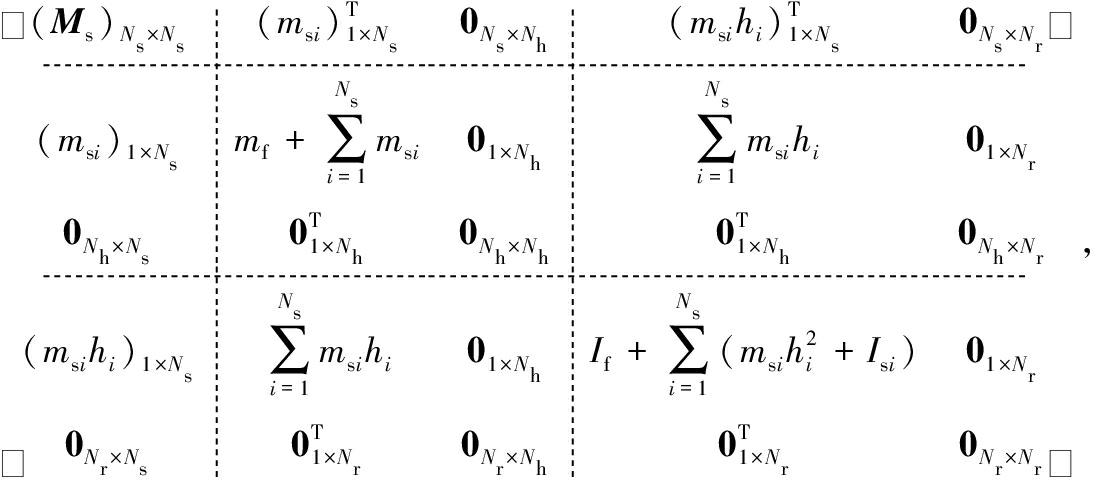
其中下标表示矩阵的大小,子矩阵Ms为(Ms)Ns×Ns=diag(msNsms(Ns-1)…ms1).
运动控制方程式(12)中的刚度矩阵K表达式如下:
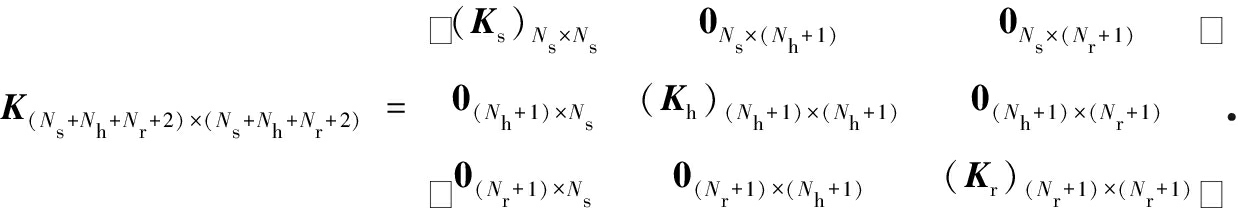
其中各子矩阵为

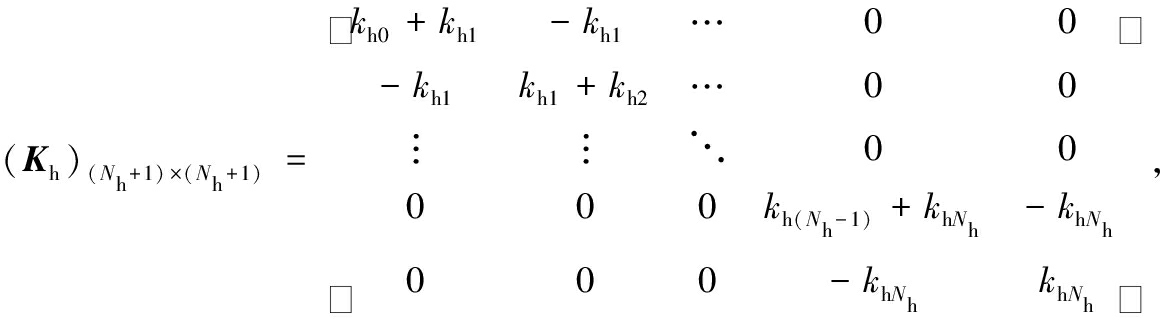
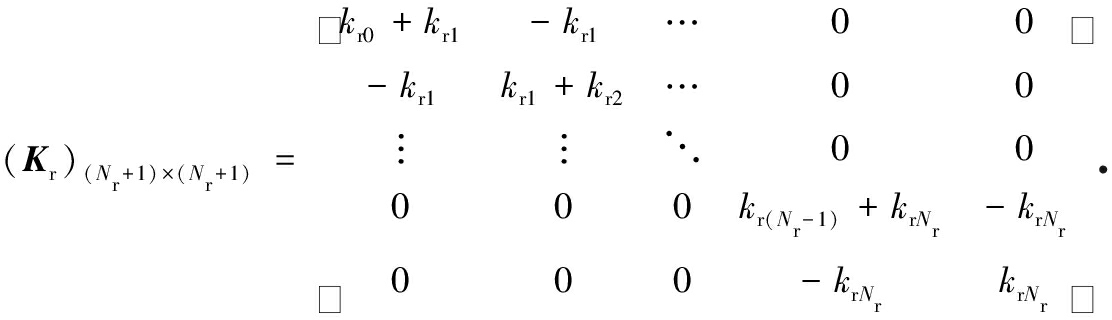
运动控制方程式(12)中的阻尼矩阵C表达式如下:
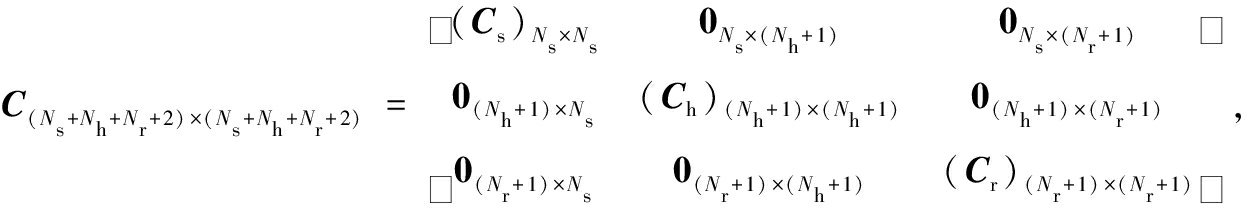
其中
(Ch)(Nh+1)×(Nh+1)=diag(Ch0Ch1…CNh),
(Cr)(Nr+1)×(Nr+1)=diag(Cr0Cr1…CNr),
(Cs)Ns×Ns=αKs+βMs,
α和β为Rayleigh(瑞利)阻尼系数,由结构前两阶阵型阻尼比决定.
运动控制方程式(12)中的系统广义位移向量u为
u(Ns+Nh+Nr+2)×1={(usi)Ns×1,uf,(uhi)Nh×1,φf,(φri)Nr×1}.
运动控制方程式(12)中列向量M*为
参考文献:
[1] CHOPRA A K, PERUMALSWAMI P R.Dam foundation interaction during earthquakes[C]//Proceedingsofthe4thWCEE.Santiago, Chile, 1969.
[2] DOBRY R.Simplified methods in soil dynamics[J].SoilDynamicsandEarthquakeEngineering, 2014,61(2): 246-268.
[3] 蒋通, 田治见宏.地基-结构动力相互作用分析方法: 薄层法原理及应用[M].上海: 同济大学出版社, 2009.(JIANG Tong, TAJIMI H.Soil-StructureInteraction:TheoryandApplicationofThinLayeredMethod[M].Shanghai: Tongji University Press, 2009.(in Chinese))
[4] 王珏, 周叮, 刘伟庆, 等.相邻明置刚性条形基础的水平-摇摆耦合阻抗研究[J].振动工程学报, 2016,29(2): 253-260.(WANG Jue, ZHOU Ding, LIU Weiqing, et al.Coupled lateral-rocking impedances of adjacent rigid strip foundations rested on elastic half-space[J].JournalofVibrationEngineering, 2016,29(2): 253-260.(in Chinese))
[5] WANG J, ZHOU D, LIU W.Horizontal impedance of pile groups considering shear behavior of multilayered soils[J].SoilsandFoundations, 2014,54(5): 927-937.
[6] 易伟建, 马文丽, 刘光栋.土-结构动力相互作用的振型分解法[J].湖南大学学报(自然科学版), 2004,31(3): 68-71.(YI Weijian, MA Wenli, LIU Guangdong.Modal analysis of soil-structure dynamic interaction[J].JournalofHunanUniversity(NaturalSciences), 2004,31(3): 68-71.(in Chinese))
[7] 黄茂松, 钟锐.海上风机部分埋入群桩水平-摇摆振动与结构共振分析[J].岩土工程学报, 2014,36(2): 286-294.(HUANG Maosong, ZHONG Rui.Coupled horizontal-rocking vibration of partially embedded pile groups and its effect on resonance of offshore wind turbine structures[J].ChineseJournalofGeotechnicalEngineering, 2014,36(2): 286-294.(in Chinese))
[8] 赵岩, 贾甜, 周瑞鹏.地震作用下管道-土耦合结构非平稳随机振动分析[J].应用数学和力学, 2018,39(5): 394-505.(ZHAO Yan, JIA Tian, ZHOU Ruipeng.Non-stationary radom vibration analysis of coupled pipeline-soil systems under earthquake[J].AppliedMathematicsandMechanics, 2018,39(5): 394-505.(in Chinese))
[9] 栾茂田, 林皋.地基动力阻抗的双自由度集总参数模型[J].大连理工大学学报, 1996,36(4): 477-481.(LUAN Maotian, LIN Gao.2-DOF lumped-parameter model of dynamic impedances of foundation soils[J].JournalofDalianUniversityofTechnology, 1996,36(4): 477-481.(in Chinese))
[10] 王满生, 胡聿贤, 周锡元.利用改进的EKF滤波技术识别成层土集总参数模型的参数[J].振动工程学报, 2006,19(2): 252-257.(WANG Mansheng, HU Yuxian, ZHOU Xiyuan.Identification of parameters in lumped-parameter model of layered-soil by using improved EKF method[J].JournalofVibrationEngineering, 2006,19(2): 252-257.(in Chinese))
[11] WANG Q, WANG J T, JIN F, et al.Real-time dynamic hybrid testing for soil-structure interaction analysis[J].SoilDynamicsandEarthquakeEngineering, 2011,31(12): 1690-1702.
[12] 杜修力, 赵建锋.考虑土-结构相互作用效应的结构地震响应时域子结构分析法[J].北京工业大学学报, 2007,33(5): 517-523.(DU Xiuli, ZHAO Jianfeng.A time-domain substructure method for seismic response analysis with soil-structure interaction effect[J].JournalofBeijingUniversityofTechnology, 2007,33(5): 517-523.(in Chinese))
[13] WOLF J P.Consistent lumped-parameter models for unbounded soil: physical representation[J].EarthquakeEngineering&StructuralDynamics, 1991,20(1): 11-32.
[14] WOLF J P.Consistent lumped-parameter models for unbounded soil:frequency-independent stiffness, damping and mass matrices[J].EarthquakeEngineering&StructuralDynamics, 1991,20(1): 33-41.
[15] WU W H, LEE W H.Systematic lumped-parameter models for foundations based on polynomial-fraction approximation[J].EarthquakeEngineering&StructuralDynamics, 2002,31(7): 1383-1412.
[16] WU W H, LEE W H.Nested lumped-parameter models for foundation vibrations[J].EarthquakeEngineering&StructuralDynamics, 2004,33(9): 1051-1058.
[17] SAITOH M.On the performance of lumped parameter models with gyro-mass elements for the impedance function of a pile-group supporting a single-degree-of-freedom system[J].EarthquakeEngineering&StructuralDynamics, 2012,41(4): 623-641.
[18] WU W, CHEN C.Simplified soil-structure interaction analysis using efficient lumped-parameter models for soil[J].JournaloftheJapaneseGeotechnicalSociety, 2002,42(6): 41-52.
[19] DU X L, ZHAO M.Stability and identification for rational approximation of frequency response function of unbounded soil[J].EarthquakeEngineering&StructuralDynamics, 2010,39(2): 165-186.
[20] 刘伟庆, 王海, 王曙光, 等.群桩基础阻抗函数的集总参数模型研究[J].振动与冲击, 2011,30(11): 249-253.(LIU Weiqing, WANG Hai, WANG Shuguang, et al.Lumped-parameter model of pile group impedance function[J].JournalofVibrationandShock, 2011,30(11): 249-253.(in Chinese))
[21] 赵宏, 高广运, 姜洲.基于矢量匹配-劳斯法的群桩阻抗改进模型[J].岩土力学, 2014,35(9): 2448-2463.(ZHAO Hong, GAO Guangyun, JIANG Zhou.An improved model for dynamic impedance of pile groups based on vector fitting-Routh method[J].RockingandSoilMechanics, 2014,35(9): 2448-2463.(in Chinese))
[22] MASON J C, HANDSCOMB D C.ChebyshevPolynomials[M].USA: CRC Press, 2002.
[23] 刘晶波, 杜修力.结构动力学[M].北京: 机械工业出版社, 2005.(LIU Jingbo, DU Xiuli.DynamicsofStructures[M].Beijing: China Machine Press, 2005.(in Chinese))
WANG Jue1,2, ZHOU Ding3
(1.CollegeofMechanicalandElectricalEngineering,HohaiUniversity,Changzhou,Jiangsu213022,P.R.China;2.CollegeofCivilandTransportationEngineering,HohaiUniversity,Nanjing210098,P.R.China;3.CollegeofCivilEngineering,NanjingTechUniversity,Nanjing211816,P.R.China)
Abstract:A Chebyshev nested lumped-parameter model (LPM) was proposed to incorporate the frequency-dependent impedances into the time history analysis of soil-foundation-wind turbine systems.The complex Chebyshev polynomials were introduced to approximate the foundation impedances with the least squares curve-fitting technique.The computational program for seismic analysis of the system was developed based on the direct integration of the governing equation in the time domain.The validity and efficiency of the computational program were verified through the comparison examples.The time history analysis of a wind turbine supported by a pile group foundation under seismic excitation shows the universality and stability of the computational program.The advantage of the Chebyshev nested LPM is that it can express the frequency-dependent impedance accurately in the time domain and avoid the high-order numerical oscillation.The nested form of the model enables wider application to different kinds of foundations.In addition, as the present model adopts no mass unit, it avoids the problem of modifying the seismic loading at the node of the foundation and makes the analysis of practical engineering more convenient.
Key words:soil-structure interaction; wind turbine; lumped-parameter model; Chebyshev polynomial; seismic response
Foundation item:The National Natural Science Foundation of China(51708179);China Postdoctoral Science Foundation(2018M632216)
作者简介:王珏(1988—),女,讲师,博士(通讯作者.E-mail: juewang@hhu.edu.cn).
基金项目:国家自然科学基金(51708179);江苏省自然科学基金(BK20170299);中国博士后科学基金(2018M632216); 中央高校基本科研业务费(2016B15014)
修订日期:2018-05-16
*收稿日期:2018-04-11;
文章编号:1000-0887(2018)11-1246-12
文献标志码:A DOI: 10.21656/1000-0887.390114
中图分类号:O32; TU435
① 引用本文/Citethispaper:
王珏, 周叮.基于阻抗函数的土-基础-风机支撑结构地震响应建模方法[J].应用数学和力学, 2018,39(11): 1246-1257.
WANG Jue, ZHOU Ding.A modeling method for soil-foundation-wind turbine seismic analysis based on foundation impedance[J].AppliedMathematicsandMechanics, 2018,39(11): 1246-1257.