基于4变量精确平板理论的剪切效应分析*
周 涛,宋彦琦
(中国矿业大学(北京) 力学与建筑工程学院,北京 100083)
摘要:由于中厚板壳结构或者复合材料板壳结构中横向剪切模量与面内伸缩模量之比较低,剪切效应对其结构力学行为的影响较为严重.该文基于4变量精确平板理论(refined plate theory,RPT),对平板弯曲过程中的剪切效应进行了分析和讨论.首先对RPT进行了简要的介绍,然后以受横向均布载荷的四边简支矩形板为例,进行了无量纲的数值计算,着重讨论了平板的几何尺寸和性质对其剪切效应的影响:剪切效应随着厚度增加而加强,尤其是当宽厚比小于10以后,剪切效应会迅速加强;剪切效应随横向剪切模量与面内伸缩模量的比值减小而增强;在同种条件下,“剪切”挠度在正交各向异性板中的比重始终大于其在各向同性板中的比重,并且平板越厚或者长宽比越大,两种板的剪切效应差异性越大;各向同性板中的剪切效应受长宽比的变化表现得更加敏感,其“剪切”挠度比重随长宽比的增大而持续减小,而正交各向异性板中的“剪切”挠度比重则呈现出先减小后增大的趋势.研究结果可为提高板壳结构弯曲分析的准确性提供参考.
关键词:剪切效应; 剪切变形理论; 矩形板; 各向同性; 正交各向异性
引 言
对于薄板小挠度弯曲问题,我们可以忽略横向剪切效应,进而采用经典平板理论(classical plate theory,CPT)就可以得到合理的结果.但是对于中厚板结构,横向剪切效应对其结果的精确性影响很大.另外,随着复合材料等新材料的不断出现,横向剪切应力和应变对其力学行为影响很大[1].因此,在对中厚板尤其是复合材料组成的中厚板结构的弯曲分析中,横向剪切效应是需要被慎重考虑的一个因素.
到目前为止,已经出现了多种不同形式的考虑横向剪切变形的板壳理论.Reissner[2]和 Mindlin[3]假设横向剪切应力是沿厚度方向的一个常量,从而考虑横向剪切效应,提出了一阶剪切变形理论(first-order shear deformation theory,FSDT);一部分学者将位移函数展开成高阶项的Taylor(泰勒)级数,提出高阶剪切变形理论(higher-order shear deformation theory,HSDT),这其中包括Librescu[4]、 Lewis-Duarte等[5]、Reddy[6-7]等;还有一部分学者将平板沿厚度方向的位移分解成两部分,一部分是由弯曲变形引起的位移,另一部分是由剪切变形引起的位移,并且将这两种变形引起的位移视为两个独立的物理量(本文将这种观点的理论统称为精确平板理论,RPT).这种方法最早是由Timoshenko[8]提出来的,随后相继由Donnell[9]、Davidson和Meier[10]、Anderson[11]、Jacobsen[12]、Huffington[13]、Allen等[14]、Murty[15]、Senthilnathan等[16]、 Zenkert[17]、Han等[18]采用.近十几年来又有 等[20-21]、Vo和Thai[22-23]分别采用.Endo和Kimura[24]、Shimpi等[25]、Thai和Choi[26-27]、Ko
等[20-21]、Vo和Thai[22-23]分别采用.Endo和Kimura[24]、Shimpi等[25]、Thai和Choi[26-27]、Ko akowski和Królak[28]基于这种观点提出新的一阶剪切变形理论.Endo[29-31]对RPT和FSDT做了详尽的对比分析和讨论.例如Endo在文献[29]中给出了由两种理论计算得到的固有频率,RPT的计算值始终大于FSDT的计算值,并且其差异性会随着平板厚度的增加而变大,并且最后解释了其差异性的出现是因为RPT相对于FSDT具有更严格的变形自由度.Endo[31]还给出这样的结论:FSDT可以完整地考虑横向弯曲和面内弯曲效应,而RPT能考虑完整的横向剪切和部分的面内剪切.换句话说,不同的剪切变形理论对于剪切效应的考虑程度是不同的,这势必会导致最终结果的差异,而且这种差异性在剪切效应严重的平板中(例如中厚板或者复合材料板)将变得尤为明显.因此,对平板弯曲过程中的剪切效应进行系统的分析和讨论,不仅可以为工程中板壳结构分析准确性的提高提供必要的理论支持和帮助,而且也能为剪切变形板壳理论的完善提供一定的帮助.
akowski和Królak[28]基于这种观点提出新的一阶剪切变形理论.Endo[29-31]对RPT和FSDT做了详尽的对比分析和讨论.例如Endo在文献[29]中给出了由两种理论计算得到的固有频率,RPT的计算值始终大于FSDT的计算值,并且其差异性会随着平板厚度的增加而变大,并且最后解释了其差异性的出现是因为RPT相对于FSDT具有更严格的变形自由度.Endo[31]还给出这样的结论:FSDT可以完整地考虑横向弯曲和面内弯曲效应,而RPT能考虑完整的横向剪切和部分的面内剪切.换句话说,不同的剪切变形理论对于剪切效应的考虑程度是不同的,这势必会导致最终结果的差异,而且这种差异性在剪切效应严重的平板中(例如中厚板或者复合材料板)将变得尤为明显.因此,对平板弯曲过程中的剪切效应进行系统的分析和讨论,不仅可以为工程中板壳结构分析准确性的提高提供必要的理论支持和帮助,而且也能为剪切变形板壳理论的完善提供一定的帮助.
本文采用4变量RPT[32],对平板弯曲过程中的剪切效应进行了分析和讨论.同FSDT相比,RPT在计算过程中不需要引入剪切修正因子,且用于建立有限元板单元时不会出现剪切自锁现象[30];同HSDT相比,RPT的未知变量较少;更主要的是RPT将挠度分解成“弯曲挠度”和“剪切挠度”独立的两部分,因此可以很容易地对剪切变形效应的大小进行分析和讨论.这也是本文采用RPT来进行平板剪切效应讨论的依据和原因.本文首先对RPT进行了简要的介绍,呈现了其控制方程的推导.然后,以受横向均布载荷的四边简支矩形板为例,采用Navier解析解.最后,进行了无量纲的数值计算,着重讨论了平板的几何尺寸和性质对其剪切效应的影响.
1 4变量RPT
图1为矩形板示意图,长度为b,宽度为a,厚度为h,三边满足关系h<a≤b,以中面xOy为坐标面建立直角坐标系.
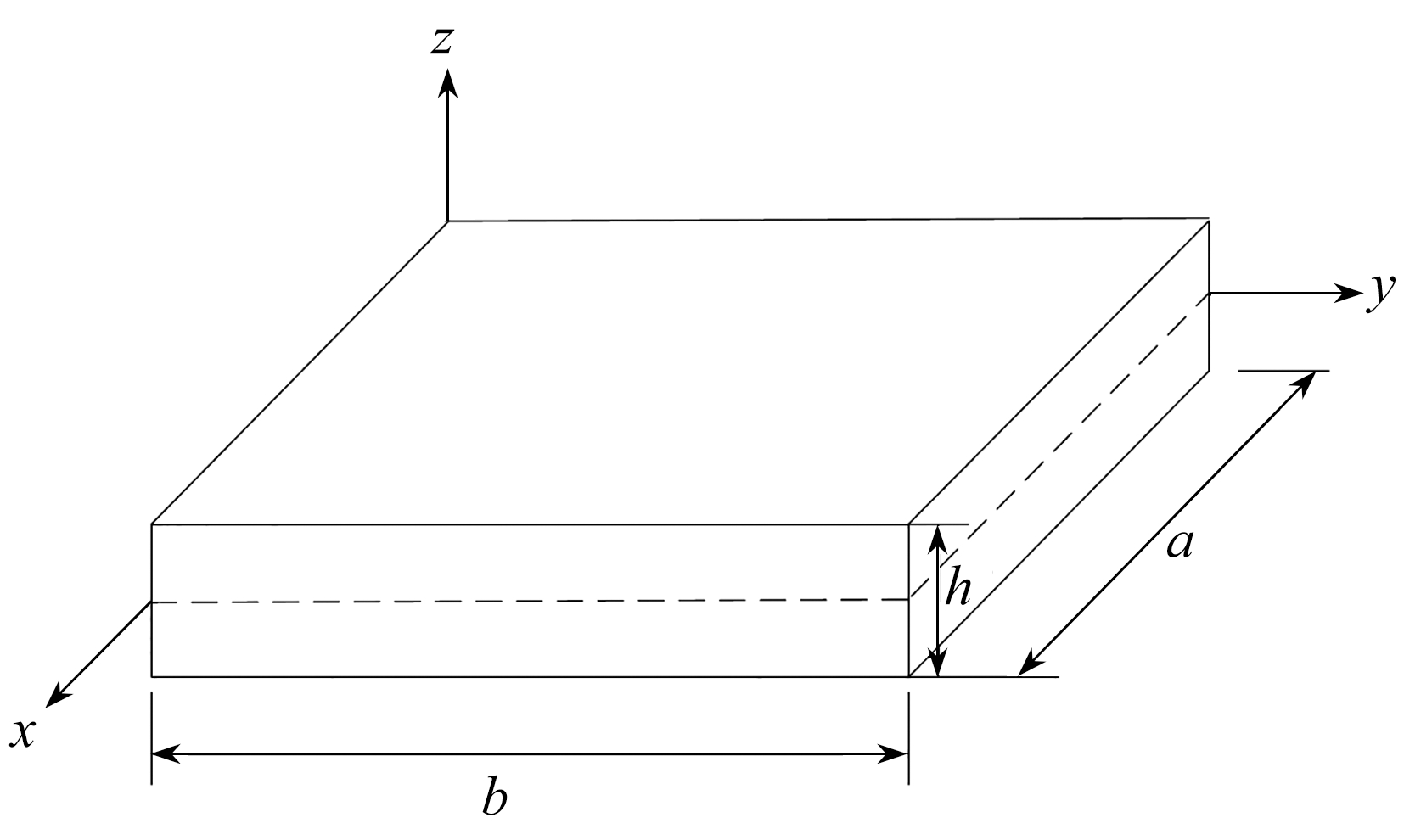
图1 矩形板结构示意图
Fig.1 Configuration of a rectangular plate
1.1基本方程
本文采用的4变量RPT[32-33]是在Shimpi[19]的2变量RPT基础上推广而来,Shimpi的2变量RPT有如下假设:① 平板中各点的位移相对于板厚很小,因此所涉及的应变是无穷小的;② 面内和横向位移都包括弯曲和剪切部分;③ 面内位移的弯曲部分与经典平板理论相似;④ 由面内位移的剪切部分导出的剪切变形表现为抛物线形.基于以上假设,4变量RPT给出的位移场为
(1)
其中f(z)=-z/4+5z3/(3h2),U,V,W分别为平板内任意一点沿坐标轴x,y,z方向的位移;u,v为平板中面内一点沿坐标轴x,y方向的位移;wb和ws分别为横向位移的弯曲部分和剪切部分;h是平板厚度.很显然,RPT同样认为横向位移沿厚度方向不变,即同样不考虑厚度的变化.可以清楚地发现,RPT的位移场和CPT 的位移场根本区别就是RPT多了ws部分,如果把ws去掉,则二者将完全一样.
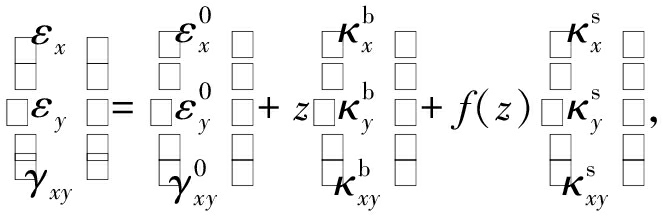
应用小变形理论,可以得到位移几何关系:
(2)
(3)
其中
(4a)
(4b)
(5)
本文将对各向同性板和正交各向异性板进行讨论,采用线弹性本构关系:
(6)
对于各向同性板:
(7)
其中,E和μ分别为各向同性板的弹性模量和Poisson(泊松)比.
对于正交各向异性板,其弹性对称面平行于xOy平面:
(8)
其中,E11,E22是弹性模量,G12,G13,G23是剪切模量,μ12,μ21是Poisson比.本文中假设G12=G13=G23.
由虚功原理可以推导出由位移变量表示的控制方程[34]
(9)
(10)
(11)
(12)
其中,Aij,Bij等为平板的刚度系数,定义如下:
(13)
控制方程的详细推导可以参考文献[34].
1.2RPT理论的Navier解
本文中,矩形板的四边均为简支,则有
(14)
(15)
(16)
(17)
(18)
(19)
将位移u,v,wb,ws展开成三角级数:
(20)
其中Umn,Vmn,Wbmn和Wsmn为待求系数,λ=mπ/a,μ=nπ/b.
同样外力可以展开成三角级数:
(21)
对于正弦分布力:
m=n=1,q11=q0,
(22)
其中q0为作用在板中心的载荷集度.
对于载荷集度q0为均布力:
(23)
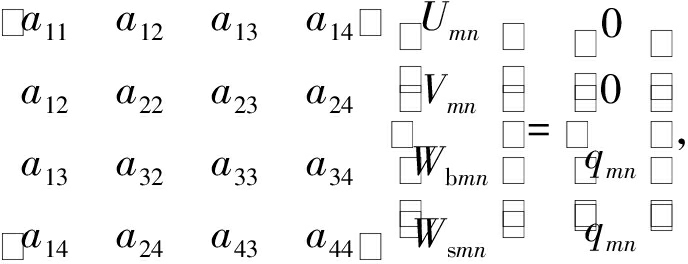
将式(14)~(23)中的对应项代入式(6)~(12)中,得到
(24)
其中
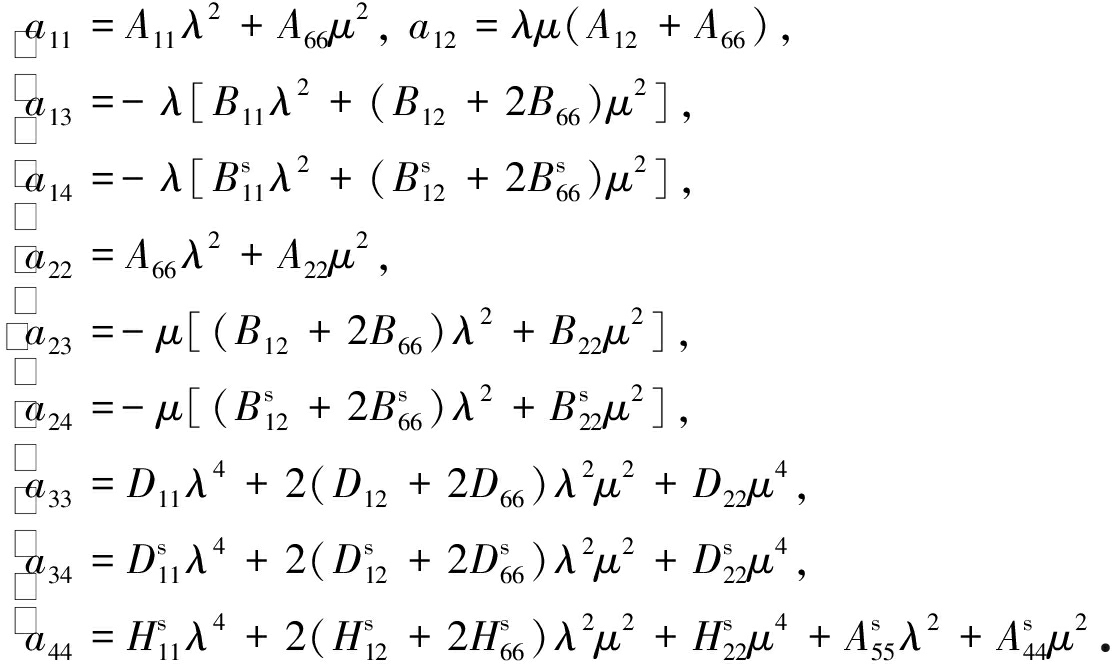
(25)
2 数值结果及其讨论
2.1RPT理论合理性的验证
本小节首先对RPT的合理性进行简要的讨论,以各向同性矩形板(μ=0.3)为例,其四边为简支约束,所受外力为垂直于板面的均布载荷q0,将所得挠度和应力结果与经典理论CPT、剪切变形理论FSDT和HSDT以及有限元(ABAQUS)计算结果进行比较.其中CPT、FSDT、HSDT的结果均采用Reddy[6]的计算结果,有限元结果参考Thai等[35]的计算结果,见表1.为了便于分析和讨论,所有结果均采用无量纲化,定义如下:
(26)
若给定长宽比b/a,采用式(26)的无量纲形式,则由CPT得到的挠度和应力将为一常数.当b/a=1时,由CPT计算得到的无量纲挠度恒为0.044 4,当b/a=2时,则恒为0.110 6.而在中厚板情况下,如a/h=5或a/h=10,由剪切变形理论FSDT、HSDT以及RPT计算得到的挠度值都大于CPT的理论值,这充分说明了这3种剪切变形理论都考虑了板在弯曲过程的剪切变形.并且RPT的计算值与另外两种剪切平板理论FSDT、HSDT的计算值以及有限元结果都相当吻合,这也就说明了RPT理论的合理性.
表1均布载荷作用下四边简支各向同性矩形板的无量纲挠度和应力(b=a,μ=0.3)
Table 1 Non-dimensional deflections and stresses of the simply supported isotropic rectangular plate subjected to uniformly distributed load (b=a,μ=0.3)
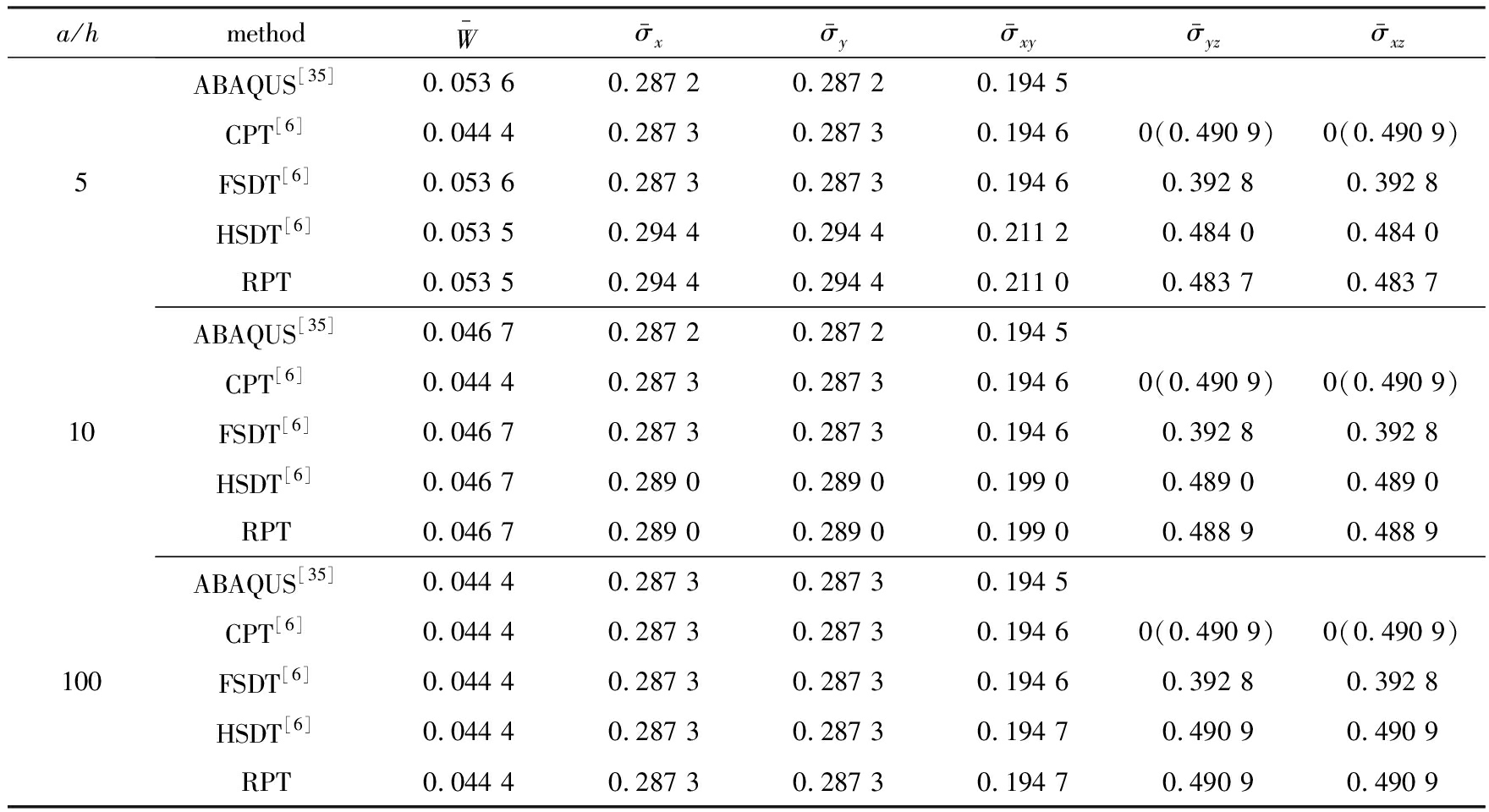
a/hmethodW-σ-xσ-yσ-xyσ-yzσ-xz5ABAQUS[35]0.053 60.287 20.287 20.194 5CPT[6]0.044 40.287 30.287 30.194 60(0.490 9)0(0.490 9)FSDT[6]0.053 60.287 30.287 30.194 60.392 80.392 8HSDT[6]0.053 50.294 40.294 40.211 20.484 00.484 0RPT0.053 50.294 40.294 40.211 00.483 70.483 710ABAQUS[35]0.046 70.287 20.287 20.194 5CPT[6]0.044 40.287 30.287 30.194 60(0.490 9)0(0.490 9)FSDT[6]0.046 70.287 30.287 30.194 60.392 80.392 8HSDT[6]0.046 70.289 00.289 00.199 00.489 00.489 0RPT0.046 70.289 00.289 00.199 00.488 90.488 9100ABAQUS[35]0.044 40.287 30.287 30.194 5CPT[6]0.044 40.287 30.287 30.194 60(0.490 9)0(0.490 9)FSDT[6]0.044 40.287 30.287 30.194 60.392 80.392 8HSDT[6]0.044 40.287 30.287 30.194 70.490 90.490 9RPT0.044 40.287 30.287 30.194 70.490 90.490 9
通过对比观察几种不同方法计算得到的应力值,也会发现类似的规律.不过这里需要注意的是平板的横向剪应力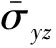 和
和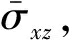 表1中的这两种应力都是由本构方程计算得到的.但是我们知道,由于经典理论CPT中假设条件的限制,
表1中的这两种应力都是由本构方程计算得到的.但是我们知道,由于经典理论CPT中假设条件的限制,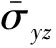 和
和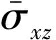 不能直接由本构方程计算得到,只能通过平衡方程计算得到,所以表1中对应CPT的无量纲剪应力
不能直接由本构方程计算得到,只能通过平衡方程计算得到,所以表1中对应CPT的无量纲剪应力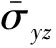 和
和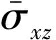 为0.为了对比,表1中括号里给出了由CPT理论平衡方程计算得到的横向剪应力值.由于Shimpi等已经对RPT的合理性、有效性作了详尽的分析和讨论,本文就不再过多的对其讨论,对于正交各向异性板的结果可以参考文献[1].
为0.为了对比,表1中括号里给出了由CPT理论平衡方程计算得到的横向剪应力值.由于Shimpi等已经对RPT的合理性、有效性作了详尽的分析和讨论,本文就不再过多的对其讨论,对于正交各向异性板的结果可以参考文献[1].
2.2剪切变形效应的讨论
2.2.1 各向同性板
表2给出了基于RPT理论,四边简支的各向同性板(μ=0.3)在均布载荷作用下,“弯曲”挠度和“剪切”挠度占总挠度比例的分布情况,并且同样给出了CPT的计算结果以便于进行对比.为了更直观地展示其特性,将表中的数据以曲线的形式展现出来,如图2、3.
表2均布载荷作用下“弯曲”挠度和“剪切”挠度在总挠度中的比例(各向同性板,μ=0.3)
Table 2 The proportions of the “bending” deflection and the “shear” deflection in the total deflection under uniformly distributed load (an isotropic plate,μ=0.3)

b/aa/hCPTW-RPTW-w-b(w-b/W-)/%w-s(w-s/W-)/%120.044 40.100 80.044 443.990.056 556.0140.044 40.058 70.044 475.620.014 324.3860.044 40.050 70.044 487.440.006 412.5680.044 40.047 90.044 492.520.003 67.48100.044 40.046 70.044 495.080.002 34.92120.044 40.046 00.044 496.530.001 63.47140.044 40.045 50.044 497.430.001 22.57180.044 40.045 10.044 498.430.000 71.57260.044 40.044 70.044 499.240.000 30.76500.044 40.044 50.044 499.790.000 10.21220.110 60.198 60.110 655.700.088 044.3040.110 60.132 80.110 683.320.022 116.6860.110 60.120 50.110 691.820.009 98.1880.110 60.116 20.110 695.220.005 54.78100.110 60.114 20.110 696.890.003 63.11120.110 60.113 10.110 697.820.002 52.18140.110 60.112 40.110 698.390.001 81.61180.110 60.111 70.110 699.020.001 10.98260.110 60.111 10.110 699.530.000 50.47500.110 60.110 70.110 699.870.000 10.13
由表中的数据可以明显地看出:弯曲变形引起的挠度wb和CPT计算得到的挠度总是相等的,这说明RPT中的“弯曲”挠度wb完全等效于CPT,也进一步说明了RPT是通过加入“剪切”挠度项ws来对CPT进行修正,因此来考虑弯曲变形效应;当b=a,a/h≥26或者b=2a,a/h≥18时,弯曲变形引起的挠度占据了总挠度的99%以上,而剪切变形引起的挠度不足1%;当b=a,a/h≥8或者b=2a,a/h≥6时,“弯曲”挠度依然能够达到90%以上,“剪切”挠度却不足10%;当a/h=2时,对于两种长宽比,“弯曲”挠度和“剪切”挠度两者在总挠度的比重相当;但是当宽厚比(a/h)一定,长宽比(b/a)不同时,两种挠度在总挠度中的比例表现出一些差异性,具体表现为,b=a的“剪切”挠度比重始终大于b=2a的“剪切”挠度比重,当a/h=2时,b=a中“剪切”挠度比重甚至大于“弯曲”挠度比重.从曲线图2、3可以发现:当2<a/h<10,两种挠度在总挠度中的比例随长厚比的变化而剧烈变化,具体表现在随着a/h变大,“弯曲”挠度比重快速增大,“剪切”挠度比重迅速减小;当a/h≥20,两种挠度的比重都几乎处于一种稳定的趋势.
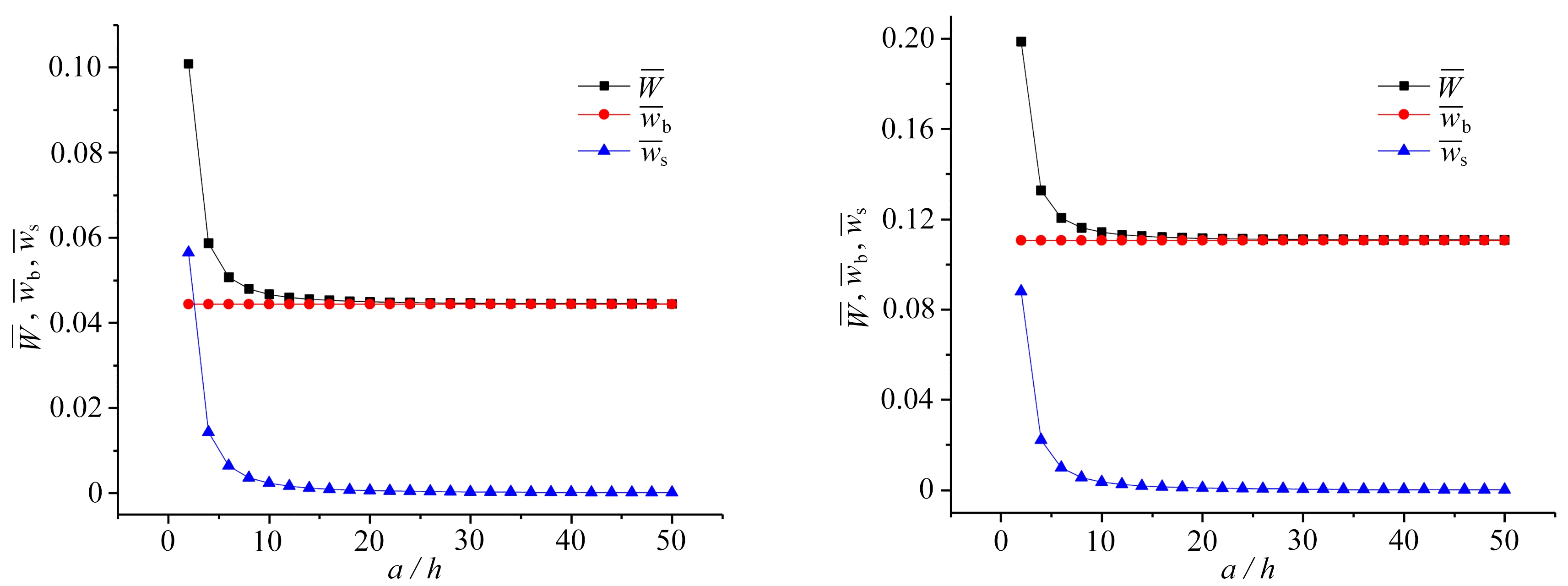
(a) b=a (b) b=2a
图2 四边简支各向同性矩形板(μ=0.3)受横向均布载荷:无量纲挠度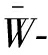 宽厚比(a/h)曲线
宽厚比(a/h)曲线
Fig.2 Effects of the width-to-thickness ratio on the non-dimensional deflection for the simply supported isotropic rectangular plate (μ=0.3) subjected to uniformly distributed load
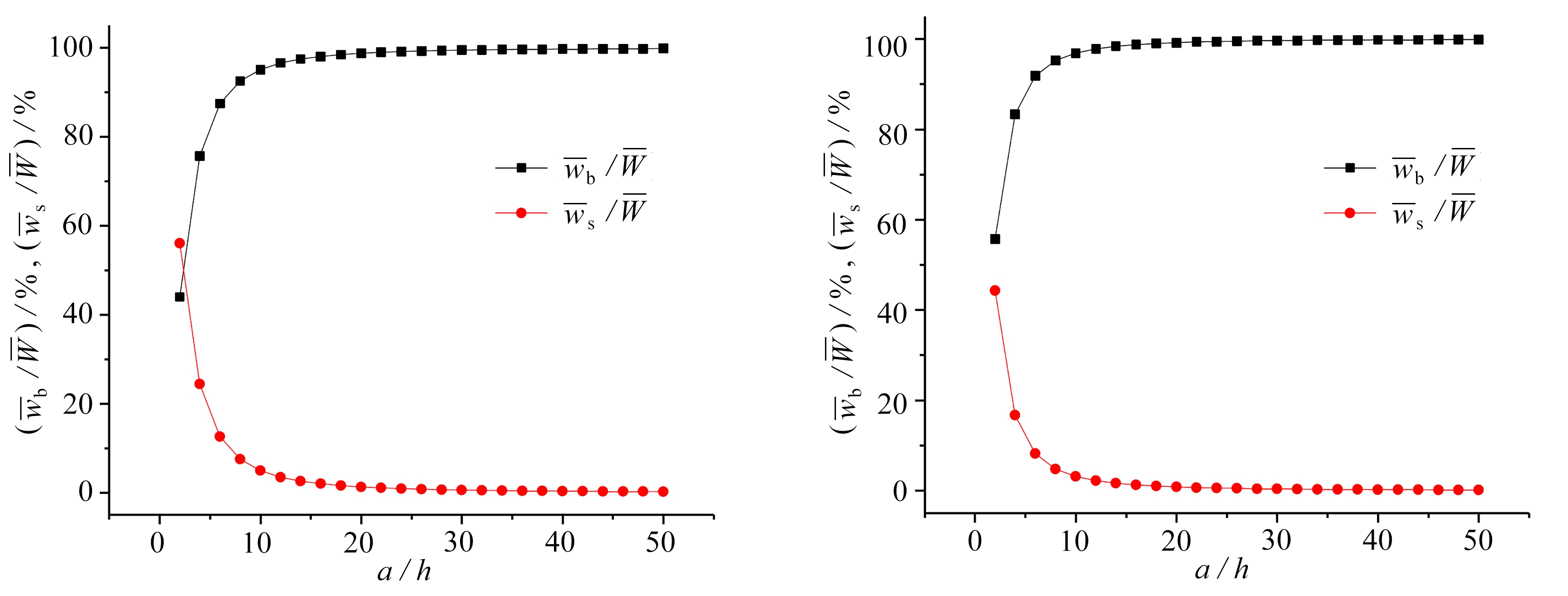
(a) b=a (b) b=2a
图3 四边简支各向同性矩形板(μ=0.3)受横向均布载荷:无量纲挠度比重-宽厚比(a/h)曲线
Fig.3 Effects of the width-to-thickness ratio on the non-dimensional deflection proportions for the simply supported rectangular plate (μ=0.3) subjected to uniformly distributed load
我们知道,板壳结构理论和工程中以宽厚比来为板进行分类:a/h>100为薄膜,20<a/h<100为薄板,a/h<20为厚板.通过以上讨论可以发现:在大多数薄板(20<a/h<100)的弯曲问题中,其挠度主要还是由弯曲变形控制,其剪切变形效应作用很小,故由CPT得到的结果不会存在太大误差,即便CPT忽略了剪切变形.但是对于厚板(a/h<20),弯曲过程中的剪切变形效应会随着板厚增加逐渐加强,尤其是当达到a/h<10以后,剪切变形效应会随板厚增加快速加强,此时再由CPT来进行求解将会产生很大误差.其实对于宽厚比为a/h<10的厚板结构,随着该比值的增大,厚板结构越来越接近三维立方体实体结构,剪切效应随着板厚的增加而快速加强与这种结构形状的变化有密切关系.通过以上对两种长宽比的各向同性简支板在均布载荷作用下的剪切变形效应的讨论和分析,也再一次验证了CPT理论在求解厚板问题的不足,看到了发展和完善剪切变形平板理论的必要性,也看到了对板进行如此分类的合理性.
2.2.2 正交各向异性板
本文采用的正交各向异性矩形板的弹性常数为[31]
E2/E1=0.525,G12/E1=0.269 3,G13/E1=0.159 91,G23/E1=0.268 81,
μ12=0.440 46,μ21=0.231 24,
其中下标1,2,3分别对应于x,y,z.
从正交各向异性板的结果(如表3所示)可以发现,许多规律与各向同性板中的结果一致,这里就不再赘述.但是值得注意的是,相同条件下,剪切效应在各向同性板和正交各向异性板中的表现是有区别的,其差异性可通过图4~6反映出来.
表3均布载荷作用下“弯曲”挠度和“剪切”挠度在总挠度中的比例(正交各向异性板)
Table 3 The proportions of the “bending” deflection and the “shear” deflection in the total deflection under uniformly distributed load (an orthotropic plate)
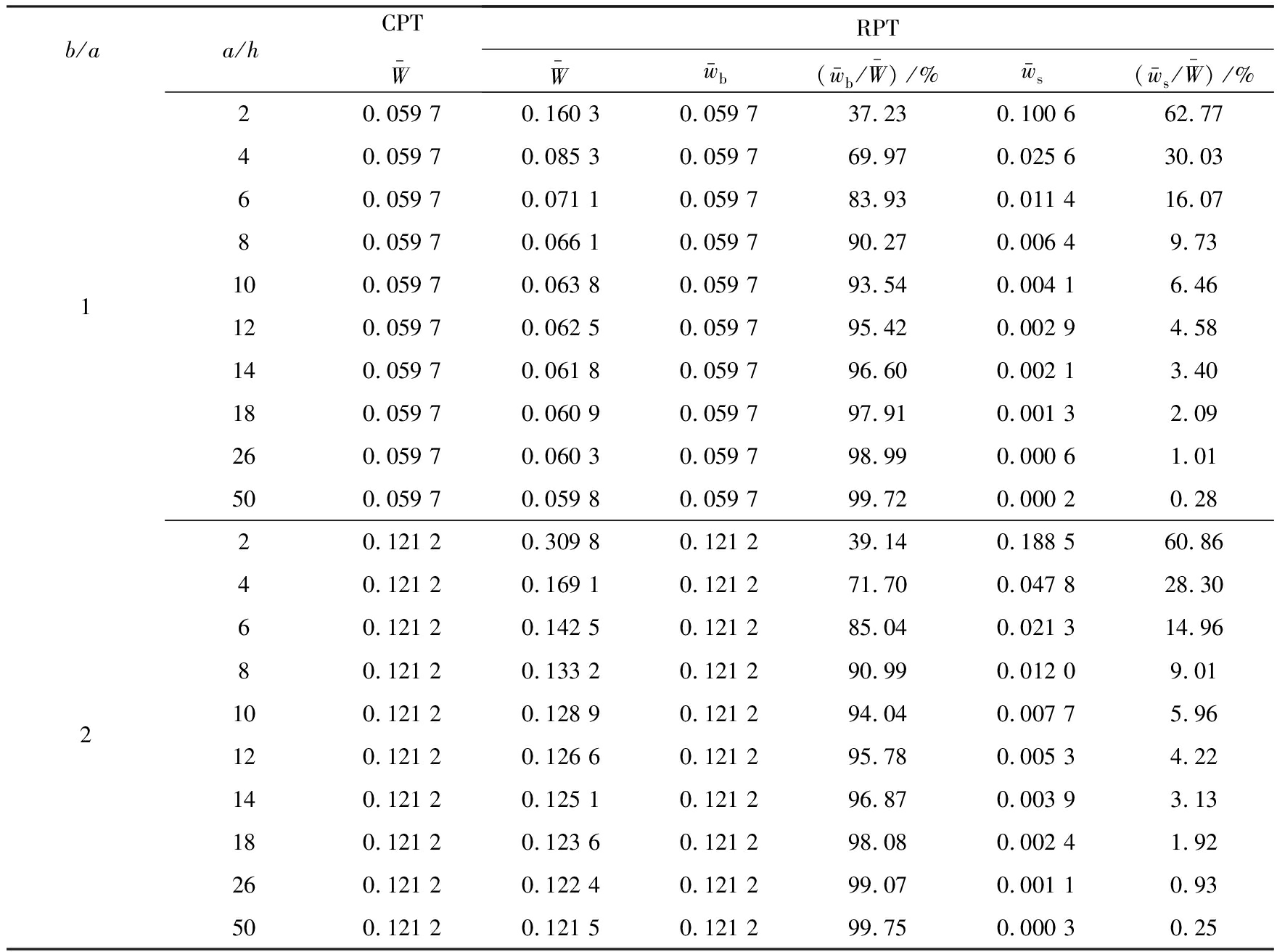
b/aa/hCPTW-RPTW-w-b(w-b/W-)/%w-s(w-s/W-)/%120.059 70.160 30.059 737.230.100 662.7740.059 70.085 30.059 769.970.025 630.0360.059 70.071 10.059 783.930.011 416.0780.059 70.066 10.059 790.270.006 49.73100.059 70.063 80.059 793.540.004 16.46120.059 70.062 50.059 795.42 0.002 94.58140.059 70.061 80.059 796.600.002 13.40180.059 70.060 90.059 797.910.001 32.09260.059 70.060 30.059 798.990.000 61.01500.059 70.059 80.059 799.720.000 20.28220.121 20.309 80.121 239.140.188 560.8640.121 20.169 10.121 271.700.047 828.3060.121 20.142 50.121 285.040.021 314.9680.121 20.133 20.121 290.990.012 09.01100.121 20.128 90.121 294.040.007 75.96120.121 20.126 60.121 295.780.005 34.22140.121 20.125 10.121 296.870.003 93.13180.121 20.123 60.121 298.080.002 41.92260.121 20.122 40.121 299.070.001 10.93500.121 20.121 50.121 299.750.000 30.25
图4为两种矩形板中的“剪切”挠度比重随宽厚比(a/h)变化的曲线图,可以发现平板的宽厚比(a/h)越小,两种板的剪切效应差异性越大,反之,越小.图5为两种矩形板的“剪切”挠度比重随长宽比(b/a)变化的曲线图.
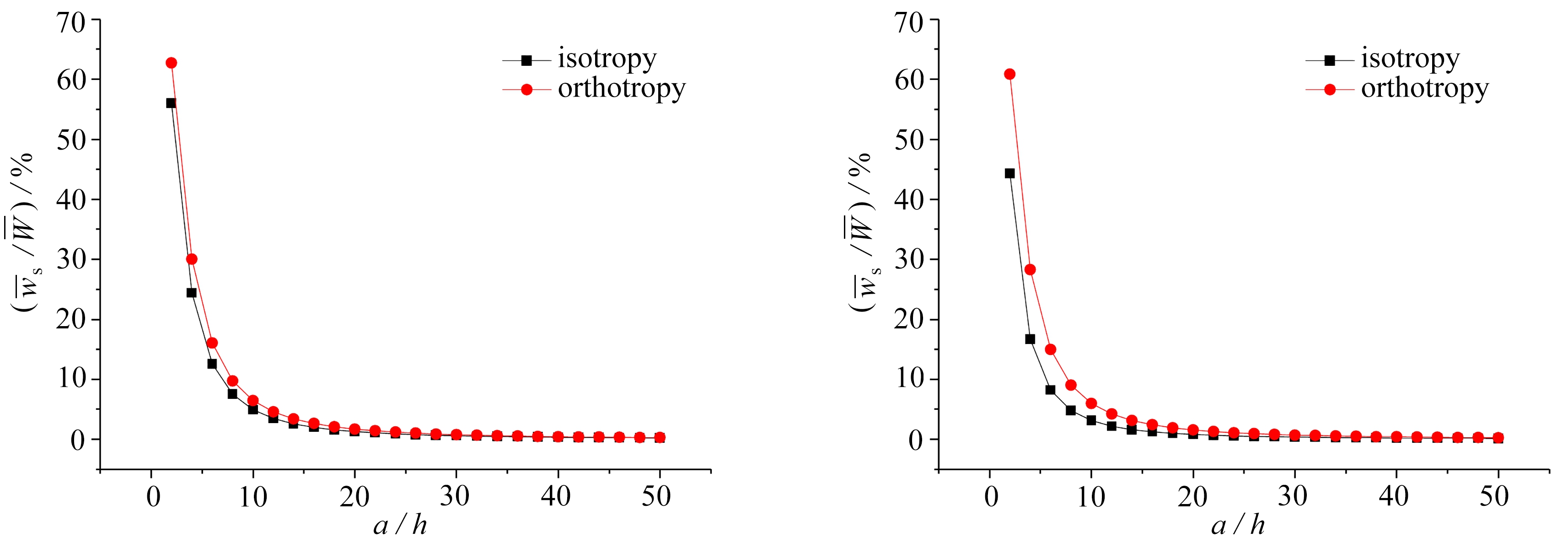
(a) b=a (b) b=2a
图4 四边简支矩形板受横向均布载荷:剪切挠度比重-宽厚比(a/h)曲线
Fig.4 Effects of the width-to-thickness ratio on the shear deflection proportions for the simply supported rectangular plate subjected to uniformly distributed load

(a) a=10h (b) a=20h
图5 四边简支矩形板受横向均布载荷:剪切挠度比重-长宽比(b/a)曲线
Fig.5 Effects of the aspect ratio on the shear deflection proportions for the simply supported rectangular plate subjected to uniformly distributed load
可以发现长宽比(b/a)对平板剪切效应的影响明显没有宽厚比(a/h)对其的影响那样强烈;各向同性板中的“剪切”挠度比重随长宽比(b/a)的增大而减小,而正交各向异性板中的“剪切”挠度比重则呈现出先减小后增大的趋势,且各向同性板对长宽比的变化表现得更加敏感,两板的差异性随着长宽比的增大而越大;另外特别重要的一点,图4、5都显示出“剪切”挠度在正交各向异性板中的比重始终大于其在各向同性板中的比重,所以在同种条件下,本文所用的正交各向异性板的剪切效应强于各向同性板.Endo[31]指出由于中厚板壳结构或者复合材料板壳结构中横向剪切模量与面内伸缩模量之比较低,导致剪切效应对其结构力学行为的影响较为严重.这里可以很容易看出本文中各向同性板的横向剪切模量与面内伸缩模量之比,G/E=0.277 78,而正交各向异性板中该比值为G13/E1=0.159 91,后者小于前者.由此笔者推断横向剪切模量与面内伸缩模量比值越小,剪切效应越强.为了验证该观点的正确性,做如下分析:各向同性材料的弹性常数满足G=E/[2(1+μ)],横向剪切模量与面内伸缩模量之比则为G/E=1/[2(1+μ)],只要找出剪切挠度比重与Poisson比之间的关系,就能知道剪切效应随G/E的变化规律.同样以四边简支各向同性矩形板受均布荷载为例(b/a=1或b/a=2,a/h=10或a/h=20,0<μ<1),得到剪切挠度比重随Poisson比的变化曲线,见图6.可以看出,剪切挠度比重随Poisson比的增大而增大,而G/E与Poisson比是成反比的,所以可以说明剪切效应随横向剪切模量与面内伸缩模量的比值减小而增强.一般情况下,非各向同性材料(例如复合材料)的横向剪切模量与面内伸缩模量的比值都比较小,所以这类平板中的剪切效应都比较严重.
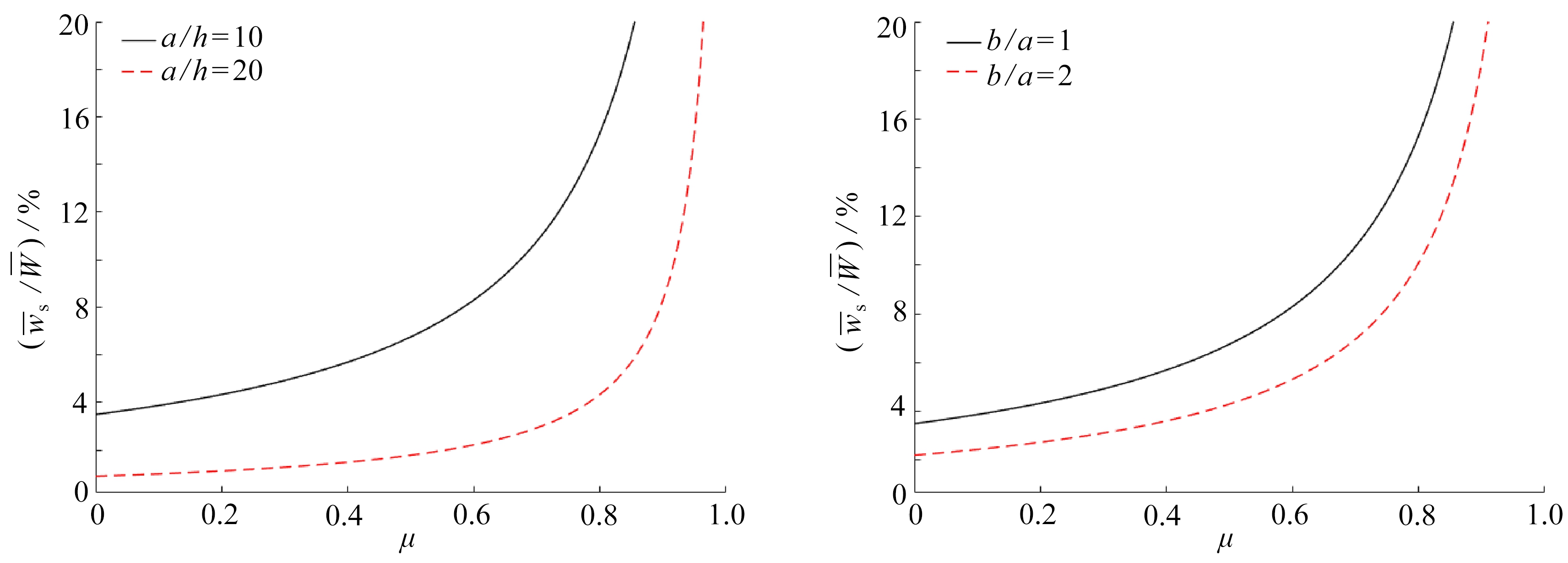
(a) b=a (b) a=10h
图6 四边简支矩形板受横向均布载荷:剪切挠度比重-Poisson比μ曲线
Fig.6 Effects of the Poisson’s ratio on the shear deflection proportions for the simply supported rectangular plate subjected to uniformly distributed load
3 结 论
本文基于4变量RPT,对平板弯曲过程中的剪切效应进行了分析和讨论,可以为板壳结构弯曲分析准确性的提高和剪切变形板壳理论的完善提供参考和帮助.以受均布载荷的四边简支矩形板(各向同性和正交各向异性)为例,分析和讨论了影响剪切效应的不同因素.
1) 平板几何尺寸的影响:宽厚比对平板剪切效应产生的影响比长宽比对其产生的影响更加明显;剪切效应随着厚度增加而加强,尤其是当宽厚比小于10以后,剪切效应会迅速加强.
2) 平板材料性质的影响:剪切效应随横向剪切模量与面内伸缩模量比值减小而增强;在本文中,同种条件下,“剪切”挠度在正交各向异性板中的比重始终大于其在各向同性板中的比重,并且平板越厚或者长宽比越大,两种板的剪切效应差异性越大;各向同性板中的剪切效应对长宽比的变化表现得更加敏感,其“剪切”挠度比重随长宽比的增大而减小,而正交各向异性板中的“剪切”挠度比重则呈现出先减小后增大的趋势.
致谢本文作者衷心感谢中国矿业大学(北京)深部岩土力学与地下工程国家重点实验室开放基金(SKLGDUEK1728)对本文的资助.
参考文献:
[1] SHIMPI R P, PATEL H G.A two variable refined plate theory for orthotropic plate analysis[J].InternationalJournalofSolids&Structures, 2006,43(22): 6783-6799.
[2] REISSNER E.The effect of transverse shear deformation on the bending of elastic plates[J].JournalofAppliedMechanics, 1945,12(3): 69-77.
[3] MINDLIN R D.Influence of rotary inertia and shear on flexural motions of isotropic, elastic plates[J].JournalofAppliedMechanics, 1951,18(1): 31-38.
[4] LIBRESCU L.On the theory of anisotropic elastic shells and plates[J].InternationalJournalofSolids&Structures, 1967,3(1): 53-68.
[5] LEWIS-DUARTE M, BLIGH M C.An accurate, simple theory of the statics and dynamics of elastic plates[J].MechanicsResearchCommunications, 1980,7(6): 343-350.
[6] REDDY J N.A refined nonlinear theory of plates with transverse shear deformation[J].InternationalJournalofSolids&Structures, 1984,20(9): 881-896.
[7] REDDY J N.A general non-linear third-order theory of plates with moderate thickness[J].InternationalJournalofNon-LinearMechanics, 1990,25(6): 677-686.
[8] TIMOSHENKO S P.StrengthofMaterials,PartI:ElementaryTheoryandProblems[M].New York: Van Nostrand, 1940.
[9] DONNELL L H.Discussion of paper by Reissner E: the effect of transverse shear deformation on the bending of elastic plates[J].JournalofAppliedMechanics-TransactionsoftheAsme, 1946,68: 249-252.
[10] DAVIDSON T, MEIER J H.Impact on prismatic bars[J].ProcSESA, 1946,4: 88-111.
[11] ANDERSON R A.Flexural vibrations in uniform beams according to the Timoshenko theory[J].JournalofAppliedMechanics-TransactionsoftheAsme, 1953,20(4): 504-510.
[12] JACOBSEN L S.EngineeringVibrations:WithApplicationstoStructuresandMachinery[M].Mcgraw-Hall Book Company, Inc, 1958.
[13] HUFFINGTON N J.Response of elastic columns to axial pulse loading[J].AIAAJournal, 1963,1(9): 2099-2104.
[14] ALLEN H G, NEAL B G.AnalysisandDesignofStructuralSandwichPanels[M].Berlin: Pergamon Press, 1969.
[15] MURTY A V K.Flexure of composite plates[J].CompositeStructures, 1987,7(3): 161-177.
[16] SENTHILNATHAN N R, LIM S P, LEE K H, et al.Buckling of shear-deformable plates[J].AIAAJournal, 1987,25(9): 1268-1271.
[17] ZENKERT D.AnIntroductiontoSandwichConstruction[M].London: Chamelon Press, 1995.
[18] HAN S C, YOON S H, CHANG S Y.Bending and dynamic characteristics of antisymmetric laminated composite plates considering a simplified higherorder shear deformation[J].JKSSC, 1997,9(4): 601-609.(in Korean).
[19] SHIMPI R P.Refined plate theory and its variants[J].AIAAJournal, 2002,40(1): 137-146.
[20] I,
I, I, TOMA
I, TOMA
 S.Coupled flexural and torsional vibrations of ship-like girders[J].Thin-WalledStructures, 2007,45(12): 1002-1021.
S.Coupled flexural and torsional vibrations of ship-like girders[J].Thin-WalledStructures, 2007,45(12): 1002-1021.
[21] I, TOMA
I, TOMA
 S, VLADIMIR N.An advanced theory of thin-walled girders with application to ship vibrations[J].MarineStructures, 2009,22(3): 387-437.
S, VLADIMIR N.An advanced theory of thin-walled girders with application to ship vibrations[J].MarineStructures, 2009,22(3): 387-437.
[22] VO T P, THAI H T.Static behavior of composite beams using various refined shear deformation theories[J].CompositeStructures, 2012,94(8): 2513-2522.
[23] THAI H T, VO T P.A new sinusoidal shear deformation theory for bending, buckling, and vibration of functionally graded plates[J].AppliedMathematicalModelling, 2013,37(5): 3269-3281.
[24] ENDO M, KIMURA N.An alternative formulation of the boundary value problem for the Timoshenko beam and Mindlin plate[J].JournalofSound&Vibration, 2007,301(1): 355-373.
[25] SHIMPI R P, PATEL H G, ARYA H.New first-order shear deformation plate theories[J].JournalofAppliedMechanics, 2007,74(3): 523-533.
[26] THAI H T, CHOI D H.A simple first-order shear deformation theory for the bending and free vibration analysis of functionally graded plates[J].CompositeStructures, 2013,101(15): 332-340.
[27] THAI H T, CHOI D H.A simple first-order shear deformation theory for laminated composite plates[J].CompositeStructures, 2013,106(12): 754-763.
[28] KO AKOWSKI Z, KR
AKOWSKI Z, KR LAK M.Modified continuity conditions of plates in beam-column using the Mindlin plate theory[J].Thin-WalledStructures, 2014,74(1): 261-268.
LAK M.Modified continuity conditions of plates in beam-column using the Mindlin plate theory[J].Thin-WalledStructures, 2014,74(1): 261-268.
[29] ENDO M.An alternative first-order shear deformation concept and its application to beam, plate and cylindrical shell models[J].CompositeStructures, 2016,146: 50-61.
[30] ENDO M.Study on an alternative deformation concept for the Timoshenko beam and Mindlin plate models[J].InternationalJournalofEngineeringScience, 2015,87: 32-46.
[31] ENDO M.“One-half order shear deformation theory” as a new naming for the transverse, but not in-plane rotational, shear deformable structural models[J].InternationalJournalofMechanicalSciences, 2017,122: 384-391.
[32] HAN S C, PARK W T, JUNG W Y.A four-variable refined plate theory for dynamic stability analysis of S-FGM plates based on physical neutral surface[J].CompositeStructures, 2015,131:1081-1089.
[33] 哈吉 L, 艾特阿特曼 H A, 杜尼斯 A, 等.应用4变量精确平板理论分析FG复合板的自由振动[J].应用数学和力学, 2011,32(7): 866-882.(HADJI L, ATMANE H A, TOUNSI A, et al.Free vibration of functionally graded sandwich plates using four-variable refined plate theory[J].AppliedMathematicsandMechanics, 2011,32(7): 866-882.(in Chinese))
[34] MECHAB I, ATMANE H A, TOUNSI A, et al.A two variable refined plate theory for the bending analysis of functionally graded plates[J].ActaMechanicaSinica, 2010,26(6): 941-949.
[35] THAI H T, NGUYEN T K, VO T P, et al.A new simple shear deformation plate theory[J].CompositeStructures, 2017,171: 277-285.
Shear Effect Analysis on Plates Based on the4-Variable Refined Plate Theory①
ZHOU Tao, SONG Yanqi
(SchoolofMechanicsandCivilEngineering,ChinaUniversityofMining&Technology,Beijing,Beijing100083,P.R.China)
Abstract:For moderately thick plates or composite plates, due to the low ratio of the transverse shear modulus to the in-plane extension modulus, the shear effects signify much to the mechanical behavior of structures.Based on the 2-variable refined plate theory (RPT), the discussion about the shear effects on the bending of plates was carried out.The RPT was introduced briefly at first, then numerical examples of simply supported rectangular plates subjected to uniformly distributed load were given, with a focus on the geometry and property effects on the shear effects.The shear effects increase with the plate thickness, especially dramatically when the width-thickness ratio is less than 10; the shear effects increase with the ratio of the transverse shear modulus to the in-plane extension modulus; under the same condition, the proportion of the “shear” deflection in the orthotropic plate is always larger than that in the isotropic plate, and the difference of shear effects between these 2 kinds of plates becomes more significant with the increase of the thickness or the aspect ratio; the shear effects in the isotropic plates are more sensitive to the aspect ratios, and the proportion of the “shear” deflection in the isotropic plate decreases with the aspect ratio, but decreases first and increases later in the orthotropic plate.
Key words:shear effect; shear deformation theory; rectangular plate; isotropy; orthotropy
Foundation item:The National Natural Science Foundation of China(Key Program)(41430640)
作者简介:周涛(1989—),男,博士生(通讯作者.E-mail: tzhou5@qq.com);宋彦琦(1969—),女,教授,博士,博士生导师(E-mail: songyq@cumtb.edu.cn).
基金项目:国家自然科学基金(重点项目)(41430640)
修订日期:2018-04-13
*收稿日期:2018-03-01;
文章编号:1000-0887(2018)11-1268-14
文献标志码:A DOI: 10.21656/1000-0887.390066
中图分类号:O341
① 引用本文/Citethispaper:
周涛,宋彦琦.基于4变量精确平板理论的剪切效应分析[J].应用数学和力学, 2018,39(11): 1268-1281.
ZHOU Tao, SONG Yanqi.Shear effect analysis on plates based on the 4-variable refined plate theory[J].AppliedMathematicsandMechanics, 2018,39(11): 1268-1281.
 akowski和Królak[28]基于这种观点提出新的一阶剪切变形理论.Endo[29-31]对RPT和FSDT做了详尽的对比分析和讨论.例如Endo在文献[29]中给出了由两种理论计算得到的固有频率,RPT的计算值始终大于FSDT的计算值,并且其差异性会随着平板厚度的增加而变大,并且最后解释了其差异性的出现是因为RPT相对于FSDT具有更严格的变形自由度.Endo[31]还给出这样的结论:FSDT可以完整地考虑横向弯曲和面内弯曲效应,而RPT能考虑完整的横向剪切和部分的面内剪切.换句话说,不同的剪切变形理论对于剪切效应的考虑程度是不同的,这势必会导致最终结果的差异,而且这种差异性在剪切效应严重的平板中(例如中厚板或者复合材料板)将变得尤为明显.因此,对平板弯曲过程中的剪切效应进行系统的分析和讨论,不仅可以为工程中板壳结构分析准确性的提高提供必要的理论支持和帮助,而且也能为剪切变形板壳理论的完善提供一定的帮助.
akowski和Królak[28]基于这种观点提出新的一阶剪切变形理论.Endo[29-31]对RPT和FSDT做了详尽的对比分析和讨论.例如Endo在文献[29]中给出了由两种理论计算得到的固有频率,RPT的计算值始终大于FSDT的计算值,并且其差异性会随着平板厚度的增加而变大,并且最后解释了其差异性的出现是因为RPT相对于FSDT具有更严格的变形自由度.Endo[31]还给出这样的结论:FSDT可以完整地考虑横向弯曲和面内弯曲效应,而RPT能考虑完整的横向剪切和部分的面内剪切.换句话说,不同的剪切变形理论对于剪切效应的考虑程度是不同的,这势必会导致最终结果的差异,而且这种差异性在剪切效应严重的平板中(例如中厚板或者复合材料板)将变得尤为明显.因此,对平板弯曲过程中的剪切效应进行系统的分析和讨论,不仅可以为工程中板壳结构分析准确性的提高提供必要的理论支持和帮助,而且也能为剪切变形板壳理论的完善提供一定的帮助.
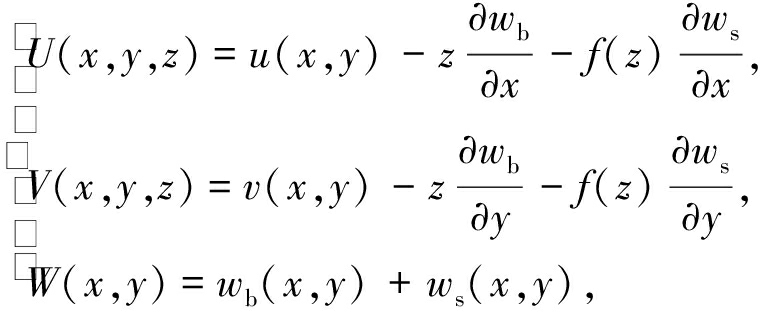

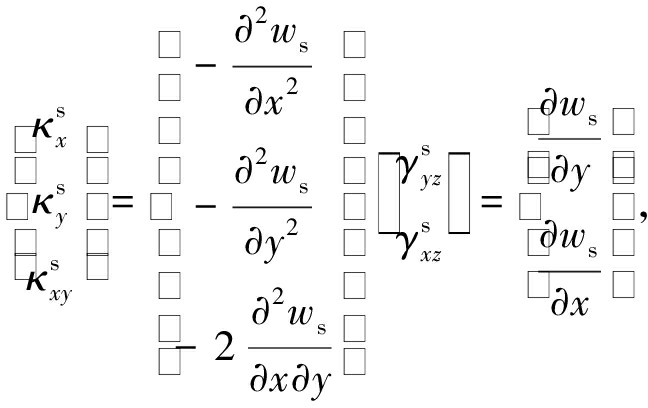
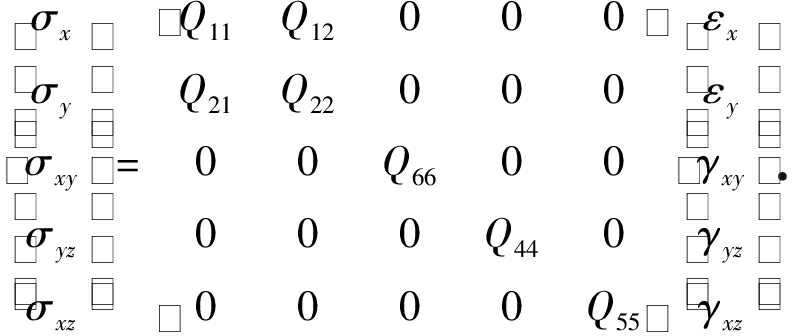
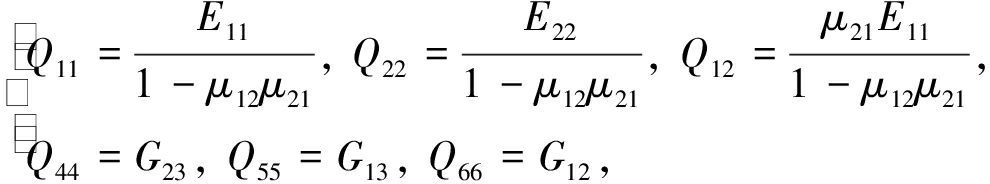
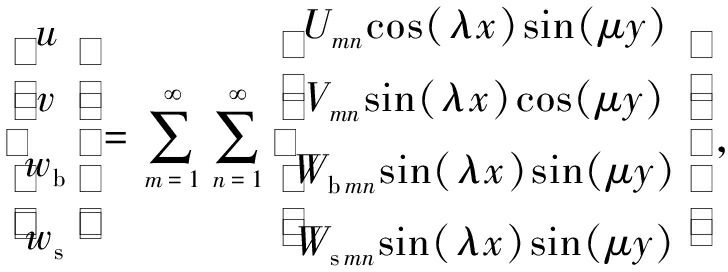
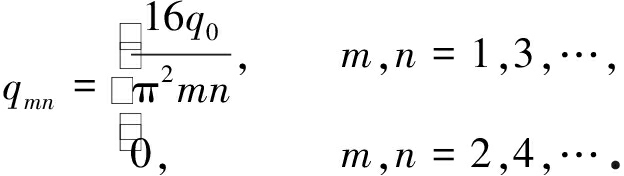
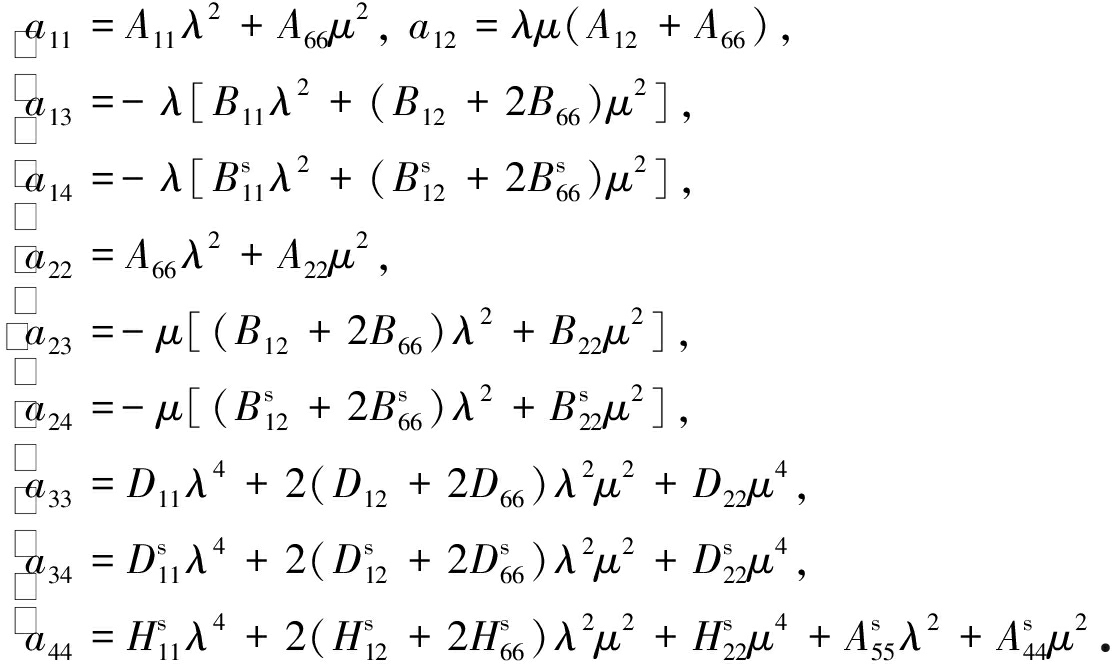









 AKOWSKI Z, KR
AKOWSKI Z, KR LAK M.Modified continuity conditions of plates in beam-column using the Mindlin plate theory[J].
LAK M.Modified continuity conditions of plates in beam-column using the Mindlin plate theory[J].