
江 林,孙峪怀,张 雪,洪 韵
(四川师范大学 数学与软件科学学院,成都 610068)
摘要:通过分数阶复杂变换将(2+1)维时空分数阶Nizhnik-Novikov-Veslov方程组转化为一个常微分方程;再利用动力系统分支方法得到系统的Hamilton量和分支相图;并根据相图轨道构建出该方程的孤立波解、爆破波解、周期波解、周期爆破波解;最后讨论了这些解之间的联系.
关键词:时空分数阶Nizhnik-Novikov-Veslov方程; 动力系统分支方法; 分支相图;精确行波解
近年来, 分数阶非线性偏微分方程广泛应用于流体力学、量子力学、通信工程、系统识别、生物医学等众多科学及工程领域[1-3], 相关研究人员对此提出了许多行之有效的方法来构建方程的精确解, 例如: 函数展开法[4-7]、(G′/G)-展开法[8-9]、Adomian分解方法[10]、Hirota双线性方法[11]、Backlund变换法[12]等.
考虑如下(2+1)维时空分数阶Nizhnik-Novikov-Veslov方程[13-14]:

(1)
其中a,b,d,f,α,β,γ是任意常数,且![]() 表示α阶Riemann-Liouville分数阶导数,定义为[15]
表示α阶Riemann-Liouville分数阶导数,定义为[15]

(2)
其中f:R→R,x→f(x)表示连续但不一定可微函数.方程(1)可以描述多孔介质中一般的热和流体流动.
文献[14]利用(G′/G)-展开法获得了方程(1)的精确解, 这些解包括双曲函数解、三角函数解和有理函数解; 文献[16]采用指数函数法构建出方程(1)的新精确解; 文献[17]运用扩展的Jacobi椭圆函数展开法得到了方程(1)的一些精确解; 文献[18]应用分数(DαG/G)方法[19]发现了方程(1)的一些新形式的行波解.然而,文献[14,16-18]都只是对此方程的解进行了研究, 而对于其解的性态及全局相图还没有系统的研究.为此, 本文拟先通过复合变换将分数阶偏微分方程转化为常微分方程, 再利用动力系统分支方法[20-23]对该方程的解性态及演化过程进行分析, 得到系统的分支相图, 并根据相图轨道构建出精确解, 其方法、过程及结果如后文所述.
引入如下分数阶复杂变换[24-25]:
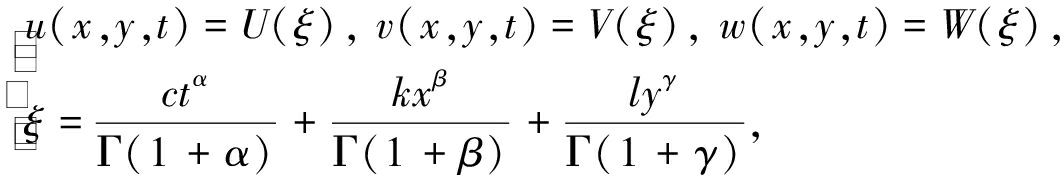
(3)
其中k,l,c是行波参数,c表示波速.将其代入方程(1), 并且对其中每个方程分别积分一次, 可得
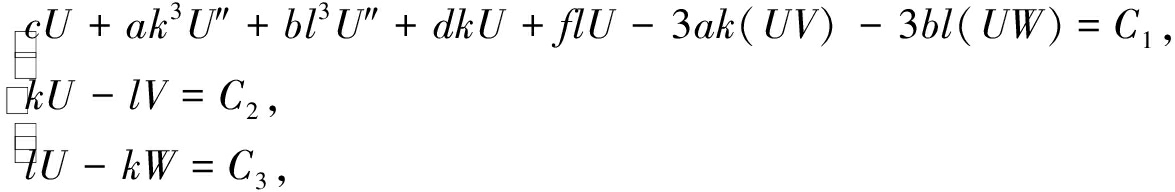
(4)
其中C1,C2和C3是积分常数.
由方程(4)可得
(5)
令U′=y,则方程(5)等价于平面动力系统:
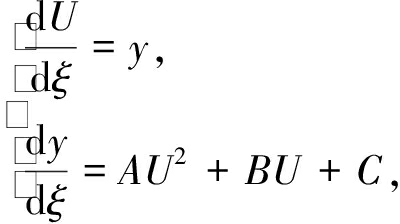
(6)
其中
显然, 系统(6)有如下首次积分:
(7)
其中h是Hamilton常量.
下面, 本文将研究系统(6)的相图分支.为了研究系统(6)的平衡点分布情况, 设
f(U)=AU2+BU+C.
(8)
令Δ=B2-4AC,显然, 当Δ>0时, 系统(6)有两个平衡点S1(U1,0)和S2(U2,0),其中
当Δ=0时, 系统(6)有唯一的平衡点S3(U3,0),其中U3=-B/(2A);
当Δ<0时, 系统(6)没有平衡点.
由式(8)可得
f′(U)=2AU+B.
(9)
假设Si(Ui,0)(i=1,2,3)是系统(6)的任一平衡点, 则系统(6)在此点处的特征值为
(10)
由微分方程定性理论[23], 可知
1) 若f′(Ui)>0,则平衡点Si(Ui,0)是鞍点;
2) 若f′(Ui)=0,则平衡点Si(Ui,0)是退化鞍点;
3) 若f′(Ui)<0,则平衡点Si(Ui,0)是中心.
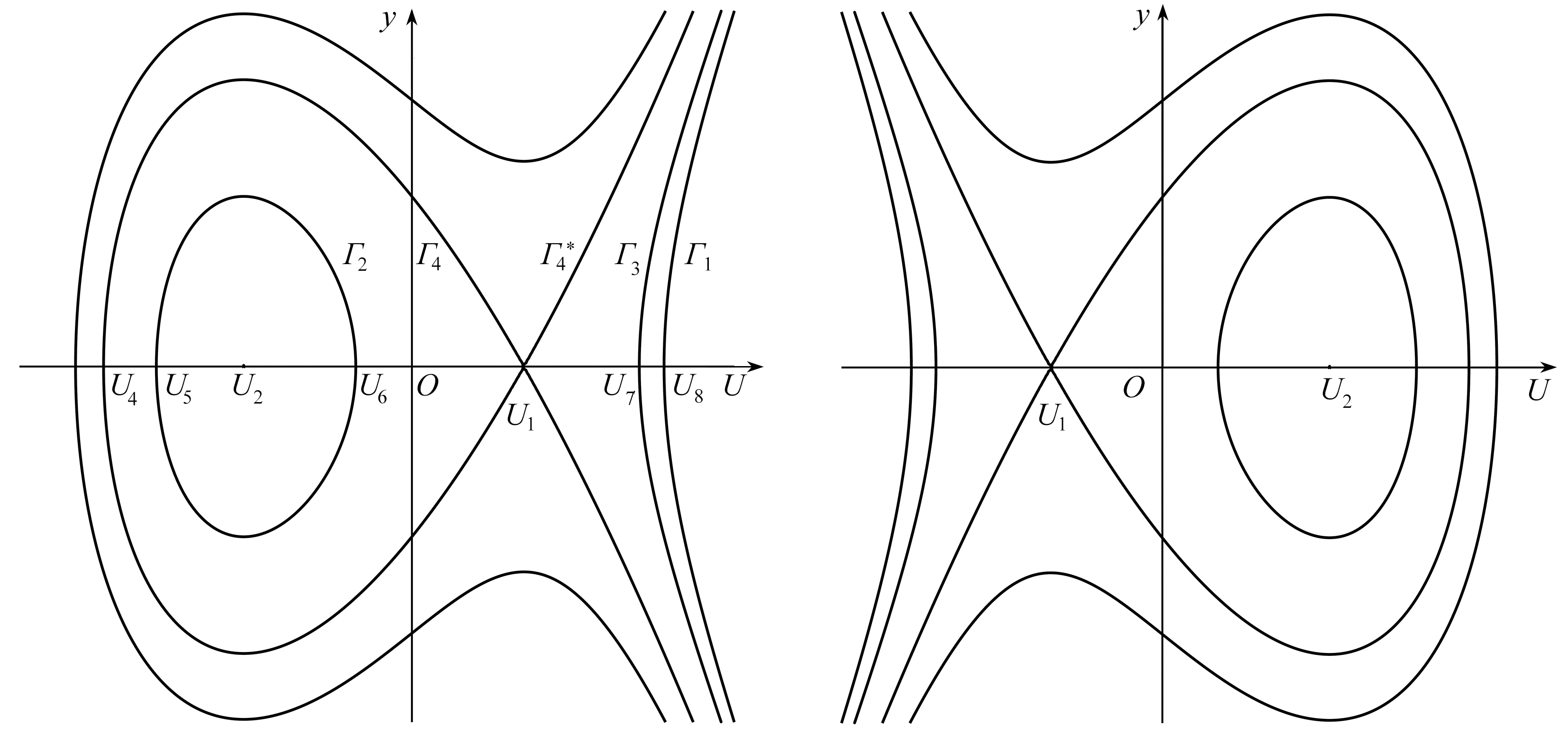
图1 当A>0, C<B2/(4A)时, 系统(6)的相图 图2 当A<0, C>B2/(4A)时, 系统(6)的相图
Fig.1 The bifurcations of the phase portrait for system (6), A>0 and C<B2/(4A) Fig.2 The bifurcations of the phase portrait for system (6), A<0 and C>B2/(4A)

图3 当A>0, C=B2/(4A)时, 系统(6)的相图 图4 当A<0, C=B2/(4A)时, 系统(6)的相图
Fig.3 The bifurcations of the phase portrait for system (6), A>0 and C=B2/(4A) Fig.4 The bifurcations of the phase portrait for system (6), A<0 and C=B2/(4A)
根据以上结论, 借助数学软件MAPLE可得系统(6)随不同参数A,B,C变化的分支相图如图1~4所示.
下面考虑系统(6)的轨道和Hamilton量之间的联系, 对于Hamilton量
记

(11)
根据平面动力系统分支理论[22-23], 得到下面的结论.
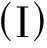 当A>0,C<B2/(4A)时, 有下面的结论:
当A>0,C<B2/(4A)时, 有下面的结论:
1) 当h<h2或h>h1时, 系统(6)没有任何闭轨;
2) 当h=h2时, 系统(6)有一条开轨道Γ1;
3) 当h2<h<h1时, 系统(6)有一条周期轨Γ2和一条开轨道Γ3;
4) 当h=h1时, 系统(6)有一条同宿轨Γ4和一条特殊轨道![]()
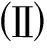 当A>0,C=B2/(4A)时,有下面的结论:
当A>0,C=B2/(4A)时,有下面的结论:
1) 当h≠h3时, 系统(6)没有任何闭轨;
2) 当h=h3时, 系统(6)有一条特殊轨道Γ5.
利用平面动力系统分支理论可知, 在偏微分系统中, 一个孤立波解在行波系统中对应着同宿轨道, 一个周期波解在行波系统中对应着周期轨道, 一个扭波解在行波系统中对应着异宿轨道.根据以上的分析, 可得下面的结论.
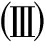 当A>0,C<B2/(4A)时, 有下面的结论:
当A>0,C<B2/(4A)时, 有下面的结论:
1) 当h=h2时, 系统(6)有一个周期奇异波解(对应于图1中的轨道Γ1);
2) 当h2<h<h1时, 系统(6)有一个周期波解和一个奇异波解(分别对应于图1中的轨道Γ2和Γ3);
3) 当h=h1时, 系统(6)有一个孤立波解和一个奇异孤立波解(分别对应于图1中的轨道Γ4和![]()
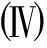 当A>0,C=B2/(4A)时, 系统(6)有一个奇异波解(对应于图3中的轨道Γ5).
当A>0,C=B2/(4A)时, 系统(6)有一个奇异波解(对应于图3中的轨道Γ5).
根据第1节的结论, 首先, 研究当A>0,C<B2/(4A)时方程(1)的显示行波解.
 从分支相图1中注意到有一条开轨道Γ1,它与中心(U2,0)有相同的Hamilton量, 其在(U,y)平面的表达式为
从分支相图1中注意到有一条开轨道Γ1,它与中心(U2,0)有相同的Hamilton量, 其在(U,y)平面的表达式为
(12)
其中![]()
把上式代入dU/dξ=y并沿轨道Γ1积分可得
(13)
完成上面的积分可得方程(1)的如下周期爆破波解:
(14)
其中
 从分支相图1中注意到有一条过点(U5,0)和(U6,0)的周期轨道Γ2和一条过点(U7,0)的开轨道Γ3,它们在(U,y)平面的表达式为
从分支相图1中注意到有一条过点(U5,0)和(U6,0)的周期轨道Γ2和一条过点(U7,0)的开轨道Γ3,它们在(U,y)平面的表达式为
(15)
和
(16)
把以上两式分别代入dU/dξ=y并分别沿轨道Γ2积分可得
(17)
沿轨道Γ3积分可得
(18)
完成上面的积分可得方程(1)的周期波解为
u2(x,y,t)=U5+(U6-U5)sn2(Φ,m);
(19)
周期爆破波解为
(20)
其中
 从分支相图1中注意到有一条过鞍点(U1,0)的同宿轨道Γ4和一条特殊轨道
从分支相图1中注意到有一条过鞍点(U1,0)的同宿轨道Γ4和一条特殊轨道![]() 它们在(U,y)平面的表达式为
它们在(U,y)平面的表达式为
(21)
和
(22)
其中![]()
把以上两式分别代入dU/dξ=y并分别沿轨道Γ4积分可得
(23)
沿轨道![]() 积分可得
积分可得
(24)
完成上面的积分可得方程(1)的孤立波解为
(25)
爆破波解为
(26)
其中
其次,研究当A>0,C=B2/(4A)时, 方程(1)的显示行波解.
从分支相图3中注意到有一条开轨道Γ5,它与退化鞍点(U3,0)有相同的Hamilton量,其在(U,y)平面的表达式为
(27)
其中![]()
把上式代入dU/dξ=y并沿轨道Γ5积分可得
(28)
完成上面的积分可得方程(1)的如下周期爆破波解:
(29)
其中
再次,研究方程(1)的行波解之间的联系.
 令
令![]() 从而有
从而有
进一步可得
(30)
(31)
其中

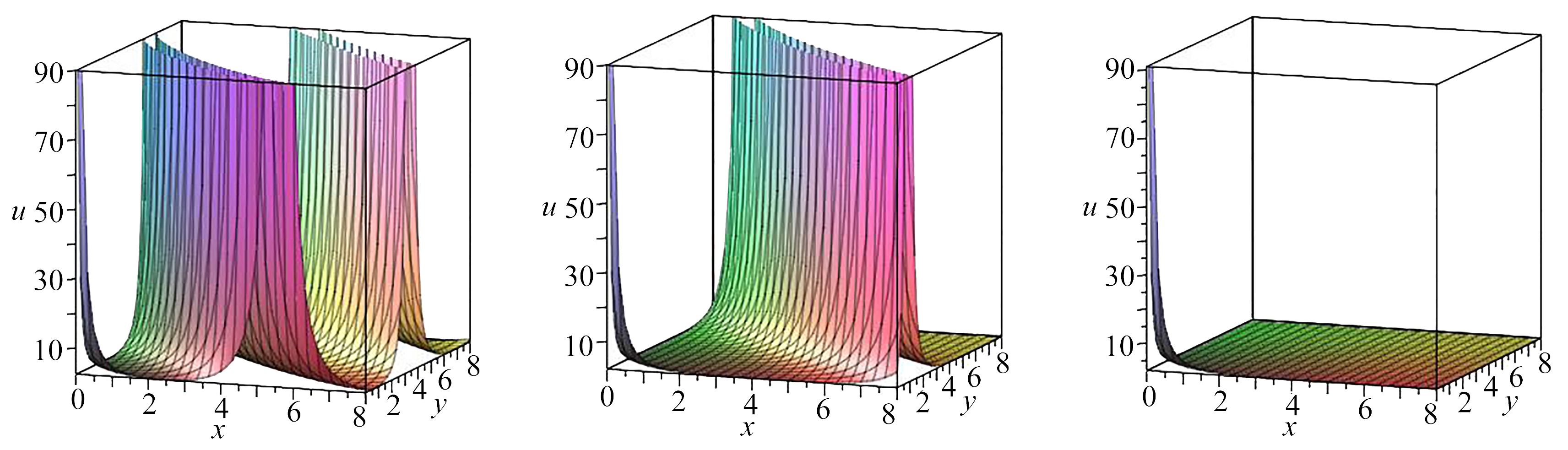
(a) h=20/3 (b) h=21.99/3 (c) h=22/3
图5 周期波解u2(x,y,t)趋于孤立波解u4(x,y,t)的极限过程
Fig.5 The limit process of periodic wave solution u2(x,y,t) approchingsolitary wave solution u4(x,y,t)
(a) h=20/3 (b) h=21.99/3 (c) h=22/3
图6 周期爆破波解u3(x,y,t)趋于爆破波解u5(x,y,t)的极限过程
Fig.6 The limit process of periodic blow-up wave solution u3(x,y,t) approchingblow-up wave solution u5(x,y,t)
由式(30)可得, 当U5趋于![]() 时, 有周期波解u2(x,y,t)趋于孤立波解u4(x,y,t),其极限过程如图5所示; 由式(31)可得, 周期爆破波解u3(x,y,t)趋于爆破波解u5(x,y,t),其极限过程如图6所示.从图1也可看到, 在这个过程中, 周期轨道Γ2和开轨道Γ3分别逼近于同宿轨道Γ4和特殊轨道
时, 有周期波解u2(x,y,t)趋于孤立波解u4(x,y,t),其极限过程如图5所示; 由式(31)可得, 周期爆破波解u3(x,y,t)趋于爆破波解u5(x,y,t),其极限过程如图6所示.从图1也可看到, 在这个过程中, 周期轨道Γ2和开轨道Γ3分别逼近于同宿轨道Γ4和特殊轨道![]()
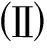 令
令![]() 从而有
从而有
进一步可得
(32)
其中
由式(32)可得, 当U5趋于![]() 时, 有周期爆破波解u3(x,y,t)趋于周期爆破波解u1(x,y,t),其极限过程与图5和图6 类似.从图1也可看到, 在这个过程中, 开轨道Γ3逼近于开轨道Γ1.
时, 有周期爆破波解u3(x,y,t)趋于周期爆破波解u1(x,y,t),其极限过程与图5和图6 类似.从图1也可看到, 在这个过程中, 开轨道Γ3逼近于开轨道Γ1.
特别说明, 本节中选取的一组参数为A=1,B=1,C=-6,α=0.8,β=0.8,γ=0.8,c=1,k=1,l=1.
本文利用动力系统分支方法, 通过分数阶复杂变换, 将(2+1)维时空分数阶Nizhnik-Novikov-Veslov方程组化为平面动力系统, 得到了在不同参数条件下系统对应的分支相图.通过分析相图的不同轨道, 获得了相应的孤立波解、爆破波解、周期波解和周期爆破波解, 并研究了它们之间的联系.需要说明的是, 通过将本文第2节研究得到的8个解ui(x,y,t),i=1,2,…,8,及式(3)代入式(4)的第2个和第3个方程可分别得到vi(x,y,t)和wi(x,y,t),具体结果在此不一一赘述.另外, 当参数满足条件A<0,C>B2/(4A),即图2, 所得结果与图1一致, 当参数满足条件A<0,C=B2/(4A),即图4, 所得结果与图3一致.
参考文献:
[1] MILLER K S, ROSS B.AnIntroductiontotheFractionalCalculusandFractionalDifferentialEquations[M].New York: Wiley, 1993.
[2] PODLUBNY I.FractionalDifferentialEquations[M].San Diego: Academic Press, 1999.
[3] KILBAS A A, SRIVASTAVA H M, TRUJILLO J J.TheoryandApplicationsofFractionalDifferentialEquations[M].San Diego: Elsevier, 2006.
[4] ZHOU Y B, WANG M L, WANG Y M.Periodic wave solution to a coupled KdV equations with variable coefficients[J].PhysicsLettersA, 2003,308(1): 31-36.
[5] FAN E G.Extended tanh-function method and its applications to nonlinear equations[J].PhysicsLettersA, 2000,277(4): 212-218.
[6] HE J H.Exp-function method for fractional differential equations[J].InternationalJournalofNonlinearSciencesandNumericalSimulation, 2013,14(6): 363-366.
[7] FENG Q, MENG F.Explicit solutions for space-time fractional partial differential equations in mathematical physics by a new generalized fractional Jacobi elliptic equation-based sub-equation method[J].Optik-InternationalJournalforLightandElectronOptics, 2016,127(19): 7450-7458.
[8] WANG M L, LI X Z, ZHANG J L.TheG′/G-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics[J].PhysicsLettersA, 2007,372(4): 417-423.
[9] 石兰芳, 聂子文.应用全新G′/(G+G′)-展开方法求解广义非线性Schrödinger方程和耦合非线性Schrödinger方程组[J].应用数学和力学, 2017,38(5): 539-552.(SHI Lanfang, NIE Ziwen.Solutions to the nonlinear Schrödinger equation and coupled nonlinear Schrödinger equations with a newG′/(G+G′)-expansion method[J].AppliedMathematicsandMechanics, 2017,38(5): 539-552.(in Chinese)).
[10] 冯再勇, 陈宁.解分数阶微分代数系统的Adomian分解方法[J].应用数学和力学, 2015,36(11): 1211-1218.(FENG Zaiyong, CHEN Ning.On the solution of fractional differential-algebraic systems with the Adomian decomposition method[J].AppliedMathematicsandMechanics, 2015,36(11): 1211-1218.(in Chinese)).
[11] HIROTA R, SATSUMA J.Soliton solution of a coupled KdV equation[J].PhysicsLettersA, 1981,85: 407-408.
[12] LI B, CHEN Y, ZHANG H Q.Auto-backlund transformations and exact solutions for the generalized two-dimensional Korteweg-de Vries-Burgers-type equations and Burgers-type equations[J].ZeischriftfurNaturforschungA, 2003,58(7/8): 464-472.
[13] YANG X J, BALEANU D.Fractal heat conduction problem solved by local fractional variation iteration method[J].ThermalScience, 2013,17(2): 625-628.
[14] ZHENG B.Exact solutions for some fractional partial differential equations by theG′/Gmethod[J].MathematicalProblemsinEngineering, 2013,43(3): 114-136.
[15] JUMARIE G.Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results[J].ComputersandMathematicsWithApplications, 2006,51(9): 1367-1376.
[16] JIA S M, HU M S, CHEN Q L, et al.Exact solution of fractional Nizhnik-Novikov-Veselov equation[J].ThermalScience, 2014,18(5): 1716-1717.
[17] MIRZAZADEH M, EKICI M, SONMEZOGLU A, et al.Soliton solutions to a few fractional nonlinear evolution equations in shallow water wave dynamics[J].EuropeanPhysicalJournalPlus, 2016,131(5): 1-11.
[18] FENG Q.A new analytical method for seeking traveling wave solutions of space-time fractional partial differential equations arising in mathematical physics[J].Optik-InternationalJournalforLightandElectronOptics, 2017,130: 310-323.
[19] ZHENG B, WEN C.Exact solutions for fractional partial differential equations by a new fractional sub-equation method[J].AdvancesinDifferenceEquations, 2013,2013(1): 199-211.
[20] LI J B, LIU Z R.Smooth and non-smooth traveling waves in a nonlinearly dispersive equation[J].AppliedMathematicalModelling, 2000,25(1): 41-56.
[21] 冯大河, 李继彬.Jaulent-Miodek方程的行波解分支[J].应用数学和力学, 2007,28(8): 894-900.(FENG Dahe, LI Jibin.Bifurcations of travelling wave solutions for Jaulent-Miodek equaions[J].AppliedMathematicsandMechanics, 2007,28(8): 894-900.(in Chinese))
[22] LI J B.SingularNonlinearTravellingWaveEquations:BifurcationsandExactSolutions[M].Beijing: Science Press, 2013.
[23] 刘正荣.微分方程定性方法和数值模拟[M].广州: 华南理工大学出版社, 2013.(LIU Zhengrong.TheQualitativeMethodsandNumericalSimulationsofDifferentialEquations[M].Guangzhou: South China University of Technology Press, 2013.(in Chinese))
[24] HE J H, LI Z B.Converting fractional differential equations into partial differential equations[J].ThermalScience, 2012,16(2): 331-334.
[25] LI Z B, ZHU W H, HE J H.Exact solutions of time-fractional heat conduction equation by the fractional complex transform[J].ThermalScience, 2012,16(2): 335-338.
JIANG Lin, SUN Yuhuai, ZHANG Xue, HONG Yun
(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,
Chengdu610068,P.R.China)
Abstract:The (2+1)-dimensional space-time fractional-order Nizhnik-Novikov-Veslov equations were transformed into ordinary differential equations through the fractional complex transform, then the Hamiltonian and the bifurcation phase portraits for the corresponding plane system to the equations were got with the bifurcation method for dynamical systems.According to the tracks in the phase portraits, solitary wave solutions, blow-up wave solutions, periodic wave solutions and periodic blow-up wave solutions to the equations were obtained.Relations between the traveling wave solutions were also discussed.
Key words:space-time fractional-order Nizhnik-Novikov-Veslov equation; bifurcation method for dynamical systems; bifurcation phase portrait; exact traveling wave solution
Foundation item:The National Natural Science Foundation of China(11371267)
作者简介:江林(1992—), 男, 硕士生(E-mail: 184196138@qq.com);孙峪怀(1963—), 男, 教授, 博士, 硕士生导师(通讯作者.E-mail: sunyuhuai63@163.com).
基金项目:国家自然科学基金(11371267)
修订日期:2018-05-13
*收稿日期:2017-12-05;
文章编号:1000-0887(2018)11-1313-10
文献标志码:A DOI: 10.21656/1000-0887.380299
中图分类号:O175.29
① 引用本文/Citethispaper:
江林,孙峪怀,张雪,洪韵.(2+1)维时空分数阶Nizhnik-Novikov-Veslov方程的精确行波解及其分支[J].应用数学和力学, 2018,39(11): 1313-1322.
JIANG Lin, SUN Yuhuai, ZHANG Xue, HONG Yun.Exact traveling wave solutions and bifurcations of (2+1)-dimensional space-time fractional-order Nizhnik-Novikov-Veslov equations[J].AppliedMathematicsandMechanics, 2018,39(11): 1313-1322.