图1 《郭永怀文集》[1]
Fig. 1Collected Works of GUO Yonghuai[1]
纪念郭永怀先生壮烈殉国50载特稿
识别一个人，当从其一言一行量度．识别一个科学家，其青壮年时期所撰写的数十篇代表性论文以至于自成一统的论文集无疑是其治学理念、品味、风格之集大成的最好度量，即文如其人其声其貌了．一本汇总郭永怀(1909—1968)34～48岁年龄段(1943—1957)的18篇论文于一体的《郭永怀文集》(图1)[1]，又即如是了(郭永怀生平简介见文后附录)．
世上唯一先后同Einstein(爱因斯坦)、Bohr(玻尔)两大科学泰斗共过事、也是研究他们其人其事的无可争辩的科学家、科学史家的Pais(派斯)就在其为Einstein撰写的一部最具权威性传记的第一章《目标与计划》里这样坦言道：“研究科学论文的重要性是其他任何事情都无可比拟的．”[2]
再读《郭永怀文集》，诚哉斯言！
认识郭永怀，学习郭永怀，就从《郭永怀文集》入手而再好不过了．
正是在那段岁月里与郭永怀“最相知”[1] (第331～332页)的钱学森在一别《写在〈郭永怀文集〉的后面》[1] (第331～332页)8年后再度回看郭永怀而凝注于其笔尖下的寥寥话语还是那般“初心不改”——《冷与热、科学态度与献身精神的结合》[3]．至此，可历史性地定格郭永怀其风其范的基调了．
何谓冷？何谓热？
冷，即指科学实在或科学态度吧；热，即指献身精神或义无反顾吧．于是，郭永怀终于以其59年的冷热华光盛年融为一炉了．
细细读来，《郭永怀文集》[1]就显现出郭永怀以下至少3条主要的治学印迹、特征：应用数学、流体力学和气体动力学．从中又折射出郭永怀怎样的一派精神风貌呢？
图1 《郭永怀文集》[1]
Fig. 1Collected Works of GUO Yonghuai[1]
通观《郭永怀文集》[1]，将数学应用于力学的“问题导向、条件假设、符号设置、方程推演、图表陈列”的大多数篇幅疏密有致、条目井然地布局其中．以“Blasius定理的推广[1](第4～6页，或文献[4])、寻找一个解而非定解[1] (第7～21页，或文献[5])、解析延拓、收敛性、存在性、相容性[1] (第22～99页及第112～165页，或文献[6-7])、高阶线性非齐次偏微分方程[1](第100～101页，或文献[8])、伸缩坐标 [1] (第199～211页及第276～295页，或文献[9-10])、对称性[1] (第102～111页，或文献[11])、映射[1] (第168～190页，或文献[12])”等等为求解特征，一派应用数学家的谨严和铺陈跃然纸上．“我们也许见不到他的是他刻苦的功夫，呕心沥血的劳动[1] (第331～332页)．”
数学物理，可称为数学的十大分支之一[13]．假如将其作为物理的一大分支，当也可行．若将其断为应用数学的领地，那么它所覆盖的疆域会有多大呢？Einstein为此早已有言在先：“应用数学的范围相应地可以定义为我们全部知识中能够用数学语言表达出来的那个部分．”[14]
也正是在郭永怀所处的那个黄金年龄段里，数学和物理以至于力学已经彼此渐行渐远、到了后来相当地不再相干往来了． “时势造英雄”．郭永怀却能“敢为天下先”、就以破解航空界多年困境的“跨声速流动的不连续性之声障大问题”为自我博士选题而连续奋战、克艰攻难4年方达成[15]，并进而与钱学森一起经过一整套的“方程变换-特解叠加-解析延拓-数值算例”等应用数学步骤而最终发表了他二人一生最长的一篇天作之合论文[1] (第22～99页，或文献[6])——从中提出了划时代的应用数学概念：“上临界Mach数而不是以前大家所注意的下临界Mach数”[1] (第331～332页)，不能不说是数学与力学相适宜的又一杰作．无独有偶，却难上加难——郭永怀独自提出并独自开战的“连数学方法都得另辟蹊径的超出上临界Mach数而引发的激波与边界层的相互作用”课题[1] (第331～332页)就最终催生出重要的应用数学之PLK方法[1] (第199～211页及第276～295页，或文献[9,10,16-18])，以至其获得了积极的拓展和应用价值[17-21]．其中的“K”，就源自于郭永怀．
一个人能以上述两大贡献载入史册，敢不以应用数学家相称？近450余年以来那些为数不多、举世公认的大应用数学家或大数学物理家[2，13，22-24]又有哪一位不是“思探物理幽幽深，视通数学绵绵长”的呢？郭永怀早年一路走南闯北去国离乡的求学生涯就与应用数学和数学物理有着固有的师承渊源，以至于后来自我大力扩展而源远流长了[25-26]．很难想象，一石激起千层浪的“钱学森之问”的“为什么我们的学校总是培养不出杰出人才？”不可能没有感念首当其冲的如他、如郭永怀一般的杰出应用数学家．
中国科学最基础的纯粹数学或应用数学或数学物理将往何处去？
往何处去，其人才也必将往何处去．
“六四，中行独复．‘象’曰：“中行独复”，以从道也．”[27]我中华应用数学复兴应大力思忖、借鉴此一溯流求源的古训[28]．
两位先生虽都已故去， 但“向钱学森和郭永怀学习”与“纪念钱学森和郭永怀”将常在常新．其最大意义无非就是何时破解钱学森之问并继而杰出人才鸿儒源源不断了， 尤其在当下时下．
钱学森和郭永怀先后师承于堪称为一代应用数学和力学大师的Von K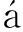
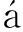rmn(冯·卡门)．为推荐钱学森升任麻省理工学院终身教授，Von K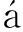rm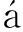n这样作道[29]：“在应用数学和数学物理解决空气动力学和结构弹性方面的问题时，钱学森博士是这一领域当之无愧的佼佼者……”
假如需要推荐郭永怀呢？Von K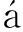rm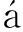n也必如此这般．
能在“两弹一星”上三者并举多有贡献者，究竟有无其人？有，郭永怀是也，且在23位两弹一星功勋奖章获得者里“三方面都涉及的只有郭先生一个人”(中科院院士俞鸿儒语)．可见其发端于应用数学和数学物理的积淀深厚、源源不竭的创新活力、动力了．
举世闻名的两大数学物理学家Courant(柯朗)和Hilbert(希尔伯特)之不朽经典名著《数学物理方法》[30]，势必早已烂熟于郭永怀的心头，并且常备于郭永怀的案头．那就随手将其作为1篇参考文献吧[1](第102～111页，或文献[11])．
由应用数学转而流体力学，后者的哪一种“流场、流动、流速”图案不是构筑于《郭永怀文集》的框架体系之中呢？郭永怀从应用数学里剑走偏锋，偏的就是于时运命运国运息息相关的流体力学从而成就了个流体力学家[25-26]． 这就又与出身于同一师门Von K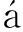rm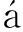n麾下的钱伟长的名言“国家的需要就是我的专业”心心相印了．且看郭永怀对一系列“可压缩与不可压缩、黏性与无黏、有旋与无旋的流体、等熵运动、Mach数、Reynolds数、环量、边界层、稳定性、激波”等等流体概念、场景的“体察解读、缜密分析、穷理尽性” [1]吧．
细究起来，郭永怀的每一篇论文都显得“刚健质朴、力透纸背”．借助Blasius定理的推广，郭永怀表达流体动力的结果与钱学森的表述相一致且更为简要[1](第4～6页，或文献[4])．以此述说郭永怀与钱学森在初次以文会友时就一见如故了．面对“可压缩黏性流体在直管中的流动”，郭永怀就欲要从数学上给出非同于以往“实验、粗略的水力学”之结果的一个精致描述 [1](第7～21页，或文献[5])． 作为“一个重大发现的上临界Mach数” [1] (第331页)又是如何得到的呢？钱学森和郭永怀该是首次强强联手“采用速度图方法” [1] (第22～99页，或文献[6])．即要以时空要素之速度坐标取代空间坐标，使得可以线性微分方程取代非线性微分方程．如此这般究竟蕴含了何种力学深层妙理？势必相应的就是“相空间对决构型空间”，或曰“Hamilton力学对决Lagrange力学 ．”[31]对此，钱学森、郭永怀两位力学先驱大家可否点头称许或笑而不答呢？并不满足发现上临界Mach数的方法，郭永怀紧接着独自“对其作了一些改进并推广到包含有环量的流动” [1] (第112～165页，或文献[7])．当两位著名应用数学家和流体力学家Lighthill和Cherry怀疑“钱-郭解”的正确性时，郭永怀就从对方的两步数学论证里入手而明察秋毫地指出了他们“显然忽视了一些基本事实”而给予“澄清”[1] (第166～167页，或文献[32])．至于PLK里的K是怎样与PL成鼎足之势的，郭永怀就以“非PLK之L原先处理的范畴”、又非“小、大”Reynolds数、而是以深具数学物理内涵的“中等Reynolds数下的不可压缩黏性流体绕平板的流动”为试解平台，在奇点邻域处作自变量摄动展开而达到在整个或全局求解区域上一致有效，就使得“各节的结果都指向正确、且具有唯一性[1] (第199～211页，或文献[9])”．照样无独有偶．由PLK里的K之“不可压黏性流体”过度到“可压黏性流体”又将如何呢？在高超声速时解的特征应该是“从黏性边界层解到无黏性场解的更为广义的光滑衔接，以至少会给出高超声速黏性流的最主要特性”．为此，郭永怀再一次却更为细致入微地运用了PLK方法 [1] (第276～295页，或文献[10])．到了此刻，已是“奔腾急，万马战犹酣”(毛泽东《十六字令》)，要“无独有三”了．郭永怀便“再下一城”——以3个图将前面所得理论模型的计算值 [1] (第276～295页，或文献[10])与“一组非常有意义的数据”做了进一步的定量比较 [1] (第296～298页，或文献[33])．其结果各有所表又丝丝入扣：“前半段理论曲线与数据点很是符合，但后半段存在偏差，目前还不能肯定地说什么；整体上只是定性的一致；无论如何，边界曲线还是十分接近 [1] (第296～298页，或文献[33])．”
就这样，郭永怀将数学运用于流体运动，便“呕心沥血”成就了一本《郭永怀文集》[1]．假若施展于其他领域，别样般的《郭永怀文集》照样是其风采如故吧．
由流体力学进而可压缩流体的气体动力学，继而将《郭永怀文集》[1]翻转成《郭永怀气体动力学文集》，那实在是郭永怀对一门学科精当处置、毅然抉择的“浓缩聚焦、狂飙突进”之生活工作场景的集中再现．前面之所述，实则是郭永怀之气体动力学的浓墨重彩．这也表明，将“应用数学、流体力学、气体动力学”的“精气神”集于一身的郭永怀怎能不处处大放异彩呢？
于是，“亚音速、跨音速、超音速、高超音速、激波、上下临界Mach数、尖端流场、高温气流的冷凝、高温气体”等等一整套“依速而上、高处不胜热”的气体动力学概念就进入郭永怀宽广的学术视野而自始至终贯穿于《郭永怀文集》[1]了．刚刚回国半年多就请“钱学森先生读过”而发表、且是《郭永怀文集》[1]里最后一篇“垫底压舱石”论文而要“介绍一下近十几年来空气动力学在这方面存在的一些问题……指出这些问题今后发展的方向”的《现代空气动力学的问题》[1](第321～330页，或文献[34])，到了今天，实际上就是“现代气体动力学的问题”，依旧是“报国心切、高瞻远瞩”．于此中，应用数学的“描写二次偏微分方程不同性格的亚声速椭圆型和超声速双曲线型”、流体力学的“固体在无旋、连续的流场里所受的力为零”、气体动力学的“N-S方程在高超声速极尖端流场点处解的特性”等等不一而足而融会贯通了．在这里，就不得不触及“7个悬赏一百万美元的千年数学难题”[35]的之一难题的“如何求解N-S方程？”这究竟是纯粹数学还是应用数学抑或流体力学再或直接就是气体动力学的问题呢？无论哪一种或“合四为一”，郭永怀“矢志不移、一往无前、血战到底”的品性总是要“涓涓流淌”而要注入其求解过程之中的．
流体力学“一路上扬”的空气动力学或气体动力学学无止境，“将来的发展是无限的”[1](第321～330页，或文献[34])．但是，一路追踪的研究者生命却短暂有年且飘忽无常．于是，在回国短短的却是最后的12年间里，郭永怀只争朝夕的“冷与热”[1] (第331～332页,或文献[3])淬火特性在其身体力行倡导[36] 或“尽量地充实自己……作些贡献” [1](第321～330页，或文献[34])的“高速空气动力学、磁流体力学、爆炸力学”等新兴学科[36]上交相辉映了，直至那最是璀璨夺目、惊心动魄的最后“十秒钟”[1] (第331～332页)！
独独1卷18篇的《郭永怀文集》，不可谓之皇皇巨著．但却其中哪一篇不是“挥笔有声、煌煌照人”呢？又是独独1卷的全部“纯粹数学、应用数学、数学物理学”成果之《Riemann全集》“据说应该用金子来装订” [37]．那么，《郭永怀文集》呢？
所谓“道路自信、理论自信、制度自信、文化自信”,其最根本的自信只能是“文化自信”．无根无须，漂泊不定，自信何来？所以，“六四，中行独复”．[27]所以，《郭永怀文集》就是一种生发于中华民族根须血脉的当代“数学、物理、力学”文化自信而光芒四射了．读其文，终究还在于识其人得其道．
从一本《郭永怀文集》里而于今距郭永怀壮烈殉国50周年之时果真识得郭永怀吗？在其牺牲后的若干时段节点上的纪念文章、文集、活动已经愈来愈清晰地描画了郭永怀一生追求真理正义、无私无畏、无怨无悔的品貌本色吗？
本文也许是首次以《郭永怀文集》为本而大致勾勒出3条郭永怀主要治学路线．它们应该是郭永怀最基本的学术特征进而精神风貌蕴涵其中就有所阐发和感悟了．正因为郭永怀的“冷与热”秉性[1] (第331～332页,或文献[3])，本文即以“冷与热”相认相识相知于他．
可以推断，郭永怀既然英年西去，那就必然在上述3条主打方向上抱憾终身——他所未竟的“应用数学、流体力学、气体动力学”宏图伟志大业究竟要伸展得多广多高多远呢？正所谓“红日初升，其道大光”(梁启超《少年中国说》)．
无论过去，现在，将来，《郭永怀文集》永不退色，郭永怀一生追求、奋斗的本源初心、伟业航标已昭昭其上、跃然纸面了．郭永怀是一部大书、奇书、天书，就值得一代代细读、慢品、体味，尤其是老家与郭永怀同一抔荣成乡亲故土的笔者．
致谢 本文作者衷心感谢海洋工程国家重点实验室开放课题基金(1503)对本文的资助．
附录 郭永怀简介[1,38]
郭永怀(1909年4月4日—1968年12月5日)，男，山东荣成人，中国共产党党员．著名力学家、应用数学家、空气动力学家、中国科学院学部委员(即中国科学院院士)、中国科学技术大学化学物理系首任系主任、近代力学事业的奠基人之一．
郭永怀长期从事航空工程研究，发现了上临界Mach数，发展了奇异摄动理论中的变形坐标法，即国际上公认的PLK方法，倡导了中国的高超声速流、电磁流体力学、爆炸力学的研究，培养了优秀的力学人才．担负了国防科学研究的业务领导工作，为发展导弹、核弹与卫星事业作出了重要贡献．
1968年12月5日，郭永怀因飞机失事以身殉国．1999年，郭永怀被授予“两弹一星功勋奖章”，是该群体中获得“烈士”称号的科学家．2018年7月，国际小行星中心已正式向国际社会发布公告，编号为212796号的小行星被永久命名为“郭永怀星”．
[1] 中国力学学会, 中国科学院力学研究所. 郭永怀文集[C]. 北京: 科学出版社, 1982.(The Chinese Society of Theoretical and Applied Mechanics, Institute of Mechanics, Chinese Academy of Sciences.Collected Works of GUO Yonghuai[C]. Beijing: Science Press, 1982.(in Chinese))
[2] 亚伯拉罕·派斯. 上帝难以捉摸: 爱因斯坦的科学与生平[M]. 方在庆, 李勇, 译. 北京: 商务印书馆, 2017.(PAIS A.Subtle is the Lord:the Science and the Life of Albert Einstein[M]. FANG Zaiqing, LI Yong, transl. Beijing: The Commercial Press, 2017.(Chinese version))
[3] 钱学森. 冷与热、科学态度与献身精神的结合[C]//郭永怀纪念文集. 北京: 科学出版社, 1990.(QIAN Xuesen. A combination of heat and cold, the scientific attitude of mind and the spirit of selfless devotion[C]//GUO Yonghuai Memorial Corpus. Beijing: Science Press, 1990.(in Chinese))
[4] KUO Y H. On the force and moment acting on a body in shear flow[J].Quarterly of Applied Mathematics, 1943,1: 273-275.
[5] KUO Y H. The flow of a compressible viscous fluid through a straight pipe[J].Journal of Mathematical Physics, 1943,22(1/4): 13-30.
[6] TSIEN H S, KUO Y H. Two-dimensional irrotational mixed subsonic and supersonic flow of a compressible fluid and the upper critical Mach number[Z]. NACA technical note: 995, 1946.
[7] KUO Y H. Two-dimensional irrotational transonic flows of a compressible fluid[Z]. NACA technical note: 1445, 1948.
[8] KUO Y H. On the stability of transonic flows[J].Proceedings of Symposia in Applied Mathematics, 1949,1: 72-73.
[9] KUO Y H. On the flow of an incompressible viscous fluid past a flat plate at moderate Reynolds numbers[J].Journal of Mathematical Physics, 1953,32(1/4): 83-101.
[10] KUO Y H. Viscous flow along a flat plate moving at high supersonic speeds[J].Journal of the Aeronautical Sciences, 1956,23(2): 125-136.
[11] KUO Y H. The propagation of a spherical or a cylindrical wave of finite amplitude and the production of shock waves[J].Quarterly of Applied Mathematics, 1947,4(4): 349-360.
[12] KUO Y H. Two-dimensional transonic flow past airfoils[Z]. NACA technical note: 2356, 1951.
[13] GOWERS T. 普林斯顿数学指南[M]. 齐民友, 译. 北京: 科学出版社, 2014.(GOWERS T.The Princeton Companion to Mathematics[M]. QI Minyou, transl. Beijing: Science Press, 2014.(Chinese version))
[14] 林家翘, 西格尔 L A. 自然科学中确定性问题的应用数学[M]. 赵国英， 朱保如， 周忠民， 译. 北京: 科学出版社, 1986.(LIN Jiaqiao, SEGEL L A.Mathematics Applied to Deterministic Problems in the Natural Sciences[M]. ZHAO Guoying, ZHU Baoru, ZHOU Zhongmin, transl. Beijing: Science Press, 1986.(Chinese version))
[15] 樊洪业. 院士故事[M]. 杭州: 浙江科学技术出版社, 1996.(FAN Hongye.Chinese Academician Story[M]. Hangzhou: Zhejiang Science and Technology Publishing House, 1996.(in Chinese))
[16] TSIEN H S. The Poincaré-Lighthill-Kuo method[J].Advances in Applied Mechanics, 1956,4(2): 281-349.
[17] 戴世强. PLK方法[C]//钱伟长. 奇异摄动理论及其在力学中的应用. 北京: 科学出版社, 1981.(DAI Shiqiang. PLK methods[C]//CHIEN Weizang.Singular Perturbation Theory and Its Applications in Mechanics. Beijing: Science Press, 1981.(in Chinese))
[18] 戴世强. PLK方法与符号运算[J]. 应用数学和力学, 2001,22(3): 221-227.(DAI Shiqiang. Poincare-Lighthill-Kuo method and symbolic computation[J].Applied Mathematics and Mechanics, 2001,22(3): 221-227.(in Chinese))
[19] HUANG Hu.Dynamics of Surface Waves in Coastal Waters:Wave-Current-Bottom Interactions[M]. Beijing: Higher Education Press, 2009.
[20] 黄虎. 直立堤前部分反射短峰波演变的三个无穷序列[J]. 物理学报, 2011,60(7): 463-466.(HUANG Hu. Three infinite sequences for evolution of partially reflected short-crested waves by a vertical wall breakwater[J].Acta Physica Sinica, 2011,60(7): 463-466.(in Chinese))
[21] 黄虎, 刘国梁. 五阶双色双向海洋表面波理论[J]. 应用数学和力学, 2016,37(5): 472-482.(HUANG Hu, LIU Guoliang. A 5th-order theory for bichromatic and bidirectional ocean surface waves[J].Applied Mathematics and Mechanics, 2016,37(5): 472-482.(in Chinese))
[22] 罗德里·埃文斯, 布莱恩·克莱格. 十大物理学家[M]. 向梦龙, 译. 重庆: 重庆出版社, 2017.(EVANS R, CLEGG B.Ten Physicists[M]. XIANG Menglong, transl. Chongqing: Chongqing Publishing House, 2017.(Chinese version))
[23] 格雷姆·法米罗. 量子怪杰: 保罗·狄拉克传[M]. 蓝梅, 译. 重庆: 重庆大学出版社, 2015.(FARMELO G.The Strangest Man:The Hidden Life of Paul Dirac,Mystic of the Atom[M]. LAN Mei, transl. Chongqing: Chongqing University Press, 2015.(Chinese version))
[24] 外尔. 对称[M]. 冯承天, 陆继宗, 译. 北京: 北京大学出版社, 2018.(WEYL H.Symmetry[M]. FENG Chengtian, LU Jizong, transl. Beijing: Beijing University Press, 2018.(Chinese version))
[25] 吴承康. 郭永怀光辉的一生[J]. 力学学报, 1999,31(4): 385-388.(WU Chengkang. In memory of professor GUO Yonghuai[J].Acta Mechnica Sinica, 1999,31(4): 385-388.(in Chinese))
[26] 李家春. 高山仰止、大爱无疆: 我们心目中的郭永怀和李佩先生[M]. 北京: 科学出版社, 2013.(LI Jiachun.Great Admiration and Great Love:Mr GUO Yonghuai and Mr LI Pei in Our Minds[M]. Beijing: Science Press, 2013.(in Chinese))
[27] 周易[M]. 杨天才, 张善文, 译. 北京: 中华书局, 2011.(The Book of Changes[M]. YANG Tiancai, ZHANG Shanwen, transl. Beijing: Zhonghua Book Company, 2011.(in Chinese))
[28] 钟万勰. 中国应用数学的发展思路[J]. 应用数学和力学, 2016,37(3): i-ii.(ZHONG Wanxie. A thought about the development of applied mathematics in China[J].Applied Mathematics and Mechanics, 2016,37(3): i-ii.(in Chinese))
[29] 张纯如. 蚕丝: 钱学森传[M]. 鲁伊, 译. 北京: 中信出版社, 2011.(CHANG I.Thread of the Silkworm[M]. LU Yi, transl. Beijing: China CITIC Press, 2011.(Chinese version))
[30] COURANT R, HILBERT D.Methoden der Math Physik[M]. Vol2. Berlin: Springer, 1937.
[31] ARNOLD V I.Mathematical Methods of Classical Mechanics[M]. Berlin: Springer-Verlag, 1978.
[32] KUO Y H. On the hodograph method[J].Journal of the Aeronautical Science, 1949,16(3): 189.
[33] KUO Y H. Viscous flow along a flat plate moving at high supersonic speeds[J].Journal of the Aeronautical Science, 1956,23(2): 977.
[34] 郭永怀. 现代空气动力学的问题[J]. 科学通报, 1957(10): 289-295.(GUO Yonghuai. Problems of modern aerodynamics[J].Chinese Science Bulletin, 1957(10): 289-295.(in Chinese))
[35] 基思·德夫林. 千年难题: 七个悬赏1 000 000美元的数学问题[M]. 沈崇圣, 译. 上海: 上海科技教育出版社, 2006.(DEVLIN K.The Millennium Problems:The Seven Greatest Unsolved Mathematical Puzzles of Our Time[M]. SHEN Chongsheng, transl. Shanghai: Shanghai Scientific & Technological Education Publishing House, 2006.(Chinese version))
[36] 李家春, 崔尔杰, 樊菁. 序[J]. 力学进展, 2009,39(4): 385-386.(LI Jiachun, CUI Erjie, FAN Jing. Preface[J].Advances in Mechanics, 2009,39(4): 385-386.(in Chinese))
[37] 埃里克·坦普尔·贝尔. 数学大师: 从芝诺到庞加莱[M]. 徐源, 译. 上海: 上海科技教育出版社, 2004.(BELL E T.Men of Mathematics:The Lives and Achievements of the Great Mathematicians From Zero to Poincaré[M]. XU Yuan, transl. Shanghai: Shanghai Scientific & Technological Education Publishing House, 2004.(Chinese version))
[38] 百度百科. 郭永怀[EB/OL]. [2018-11-22]. https://baike.baidu.com/item/%E9%83%AD%E6%B0%B8%E6%80%80/926351?fr=aladdin.(Baidu Encyclopedia. GUO Yonghuai[EB/OL]. [2018-11-22]. https://baike.baidu.com/item/%E9%83%AD%E6%B0%B8%E6%80%80/926351?fr=aladdin.(in Chinese))