结构动力特性是结构动力响应分析和动力设计的基础, 因此结构动力特性非常重要.结构动力特性主要取决于结构系统刚度、质量分布以及边界条件等因素, 对于结构的抗震抗风设计、振动分析等均有重要意义, 如用来防止共振现象和减隔震设置等[1].然而结构参数的真实值很难或者不可能准确获得, 引起结构参数不确定性来源主要包括材料特性的不确定性、几何尺寸的不确定性、结构边界条件的不确定性以及结构物理性质的不确定性等[2].结构参数不确定性必将会导致结构动力特性具有不确定性(变异性), 因此有必要量化参数不确定性传递给动力特性不确定性的大小, 为结构动力分析提供更为准确的动力信息.
统计矩(比如均值和方差)是表征结构动力特性不确定性非常重要的统计量, 反映了结构动力特性变化的统计特性.高阶统计矩可用来逼近动力特性的的概率密度函数, 可为表征动力特性不确定提供更全面的信息.MCS(Monte-Carlo simulation)方法是结构动力特性不确定性量化最基本的方法, 它主要是对结构进行大量的有限元分析, 然后对得到的动力特性进行统计, 进而得到动力特性的统计矩和概率密度函数等.MCS方法[3-5]虽然简单且便于实施, 但其涉及到大量次数的模型计算, 计算成本很高.摄动法[6-8]在动力特性不确定性量化也得到广泛的应用, 但是当随机参数较多且模型非线性程度较高时, 其计算结果不够理想.与此同时, 区间分析法[9-12]也在结构动力特性确定性量化中得到广泛应用.上述摄动法和区间分析法均需要得到结构的系统矩阵(质量、刚度和阻尼矩阵), 然而复杂结构的有限元模型往往是借助商用有限元软件建立的, 因此提取结构的系统矩阵并进行后续的迭代计算是非常困难的.
为了克服MCS等方法的不足, 本文提出采用多项式混沌展开(polynomial chaos expansion, PCE)替代模型取代原复杂的有限元模型.多项式混沌展开建立的思想是响应可以表示成随机参数的正交多项式形式, 可很好地近似随机参数与目标量的输入输出关系.本文提出的多项式混沌展开方法适用于随机参数服从任意概率分布, 且可用来计算动力特性的高阶统计矩.该方法的具体实施流程是:不确定参数为自变量和目标变量结构动力特性为因变量, 将结构动力特性的统计矩分解为单随机变量统计特征与多项式混沌展开系数的组合形式, 然后进行简单运算即可得到结构动力特性的统计矩.多项式混沌展开法在结构动力特性高阶统计矩计算的有效性通过一平板结构进行验算, 计算结果与MCS法进行对比.除此之外, 本文还探究了结构随机变量变异系数对结构动力特性统计矩的影响.
将任意多项式混沌展开应用于不确定性量化时,组成多项式混沌展开模型的最优基底取决于各个随机变量的概率密度函数.对于正交多项式序列φl(x)![]() ,φl(x)是第l阶多项式,ω(x)为该多项式的正测度(positive measure), 则该正交多项式序列满足以下关系:
,φl(x)是第l阶多项式,ω(x)为该多项式的正测度(positive measure), 则该正交多项式序列满足以下关系:
(1)
其中,S为满足正测度ω(x)的积分区域,γl=〈φl(x),φl(x)〉为标准化常量,x为单变量; δlj为Kronecker(克罗内克)符号.
正交多项式序列满足下面的3项递推关系[13]:
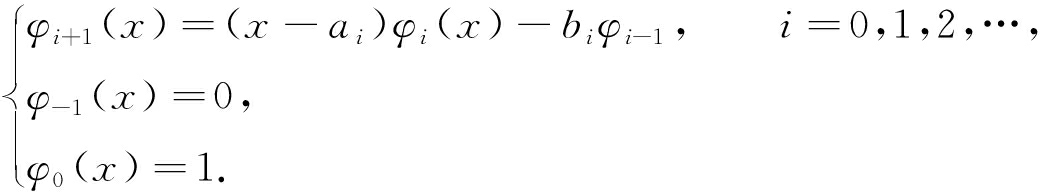
(2)
递推系数如下:
(3)
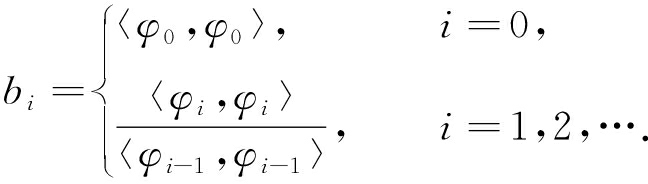
(4)
由上式可知递推系数由正测度ω(x)唯一确定, 由此能够确定出与单随机变量任意概率密度函数相匹配的正交多项式基底.多维的多项式混沌展开式为多个单变量正交多项式连乘再相加形式, 如下所示:
(5)
式中,ψi1…iq(x)=φi1(x1)φi2(x2)…φiq(xq),φik(xk)为单变量xk所保留正交多项式的ik次项,βi1…iq为多项式混沌展开系数,Nk是单变量xk的正交多项式的阶数.
在实际应用中,多项式混沌展开达到一定阶数时即可满足所要求的模拟精度, 故在使用多项式混沌展开模型时可以进行截断.对于d个随机参数, 每个参数的最高阶次均设定为p时, 则多项式混沌展开的待定系数个数为
(6)
此时多项式混沌展开为
(7)
如当d=3,取多项式混沌展开阶次p=2,设单变量的前两阶一维多项式基底为φi,0(xi)=1,φi,1(xi),φi,2(xi),i=1,2,3,则对应的三参数二阶多项式混沌展开为
y=β0+β1φ1,1(x1)+β2φ2,1(x2)+β3φ3,1(x3)+
β1,2φ1,1(x1)φ2,1(x2)+β1,3φ1,1(x1)φ3,1(x3)+
β2,3φ2,1(x2)φ3,1(x3)+β1,1φ1,2(x1)+β2,2φ2,2(x2)+β3,3φ3,2(x3).
(8)
接下来介绍几种标准的多项式混沌展开例子, 即对应于概率密度为正态分布、beta分布和均匀分布.关于其他概率分布(即任意概率分布)的多项式混沌展开的推导请查阅文献[14].
1.2.1 Hermite 多项式
Hermite多项式是一类经常使用的经典多项式.对应于随机变量服从正态分布的情况, 其概率密度函数为
(9)
递推系数为
(10)
表1中列出了对应标准正态分布(μ=0,σ2=1)的前5项一维Hermite多项式,如图1所示.
表1 前5项Hermite多项式
Table 1 The 1st 5 Hermite polynomials
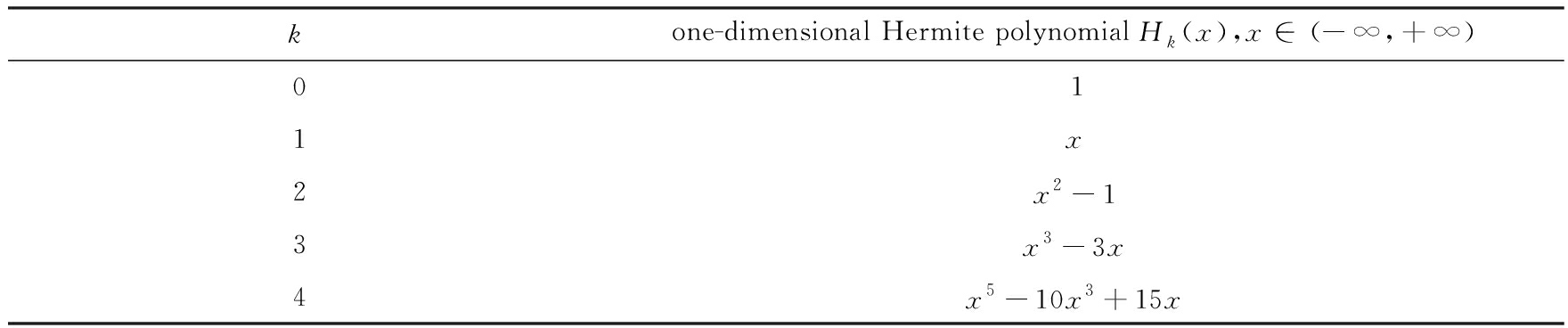
kone-dimensional Hermite polynomial Hk(x),x∈(-∞,+∞)011x2x2-13x3-3x4x5-10x3+15x
1.2.2 Jacobi 多项式
Jacobi多项式混沌展开对应于概率密度分布为beta分布, beta分布的概率密度函数为
p(x)=(1-x)α(1+x)β,α>-1,β>-1.
(11)
递推系数为
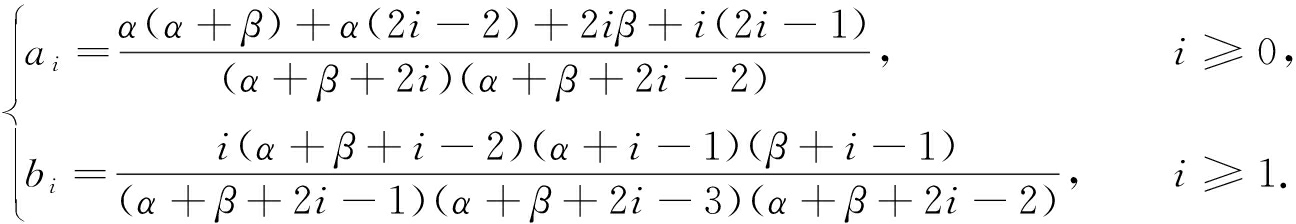
(12)
取α=1,β=2时, 表2列出了前5项一维Jacobi多项式,如图2所示.
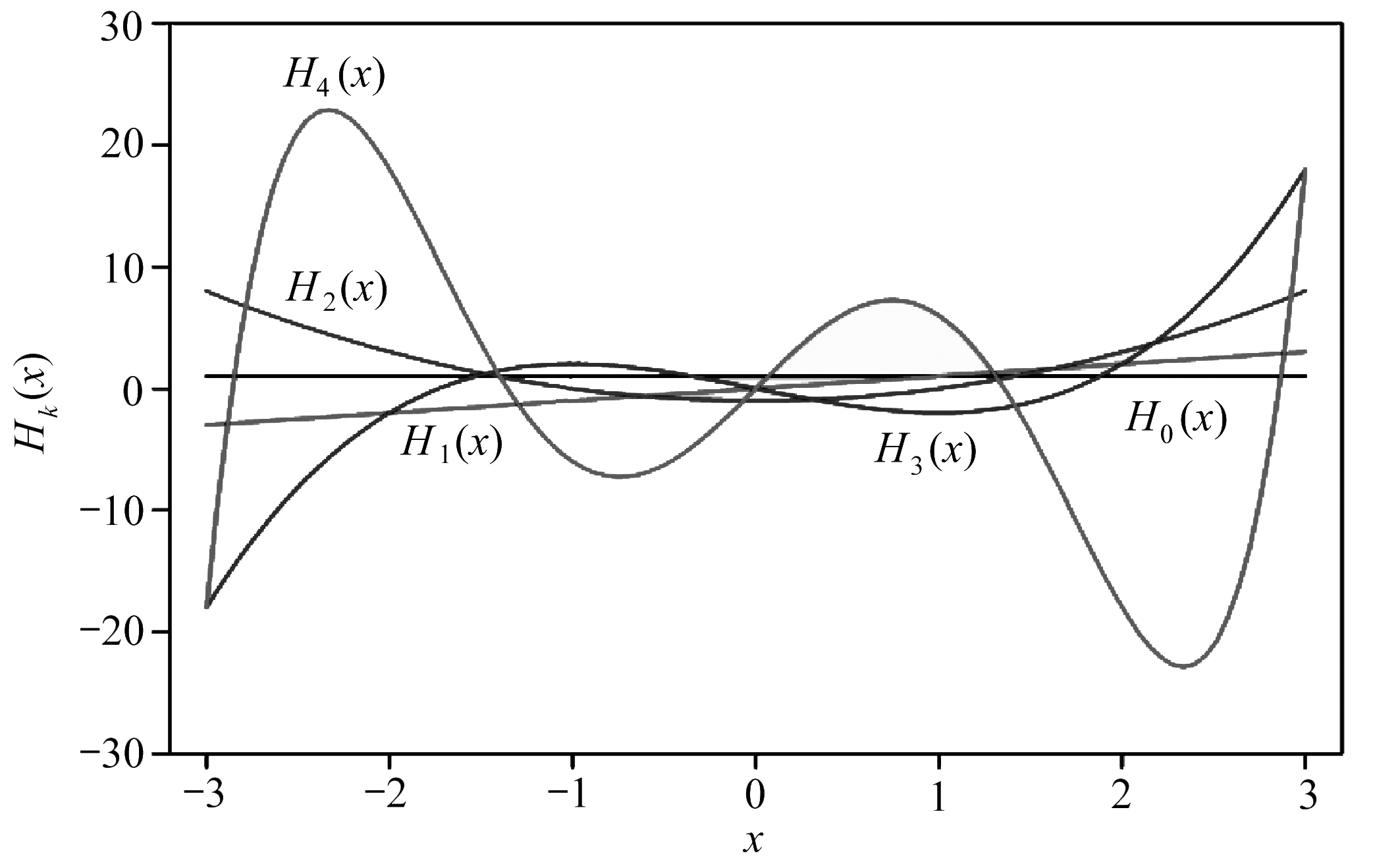
图1 前5项Hermite多项式曲线图
Fig. 1 The 1st 5 Hermite polynomial curves
表2 前5项Jacobi多项式
Table 2 The 1st 5 Jacobi polynomials

kone-dimensional Jacobi polynomial Jk(x),x∈(0,1)011x-132110(10x2-8x+1)3135(35x3-45x2+15x-1)41126(126x4-224x3+126x2-24x+1)
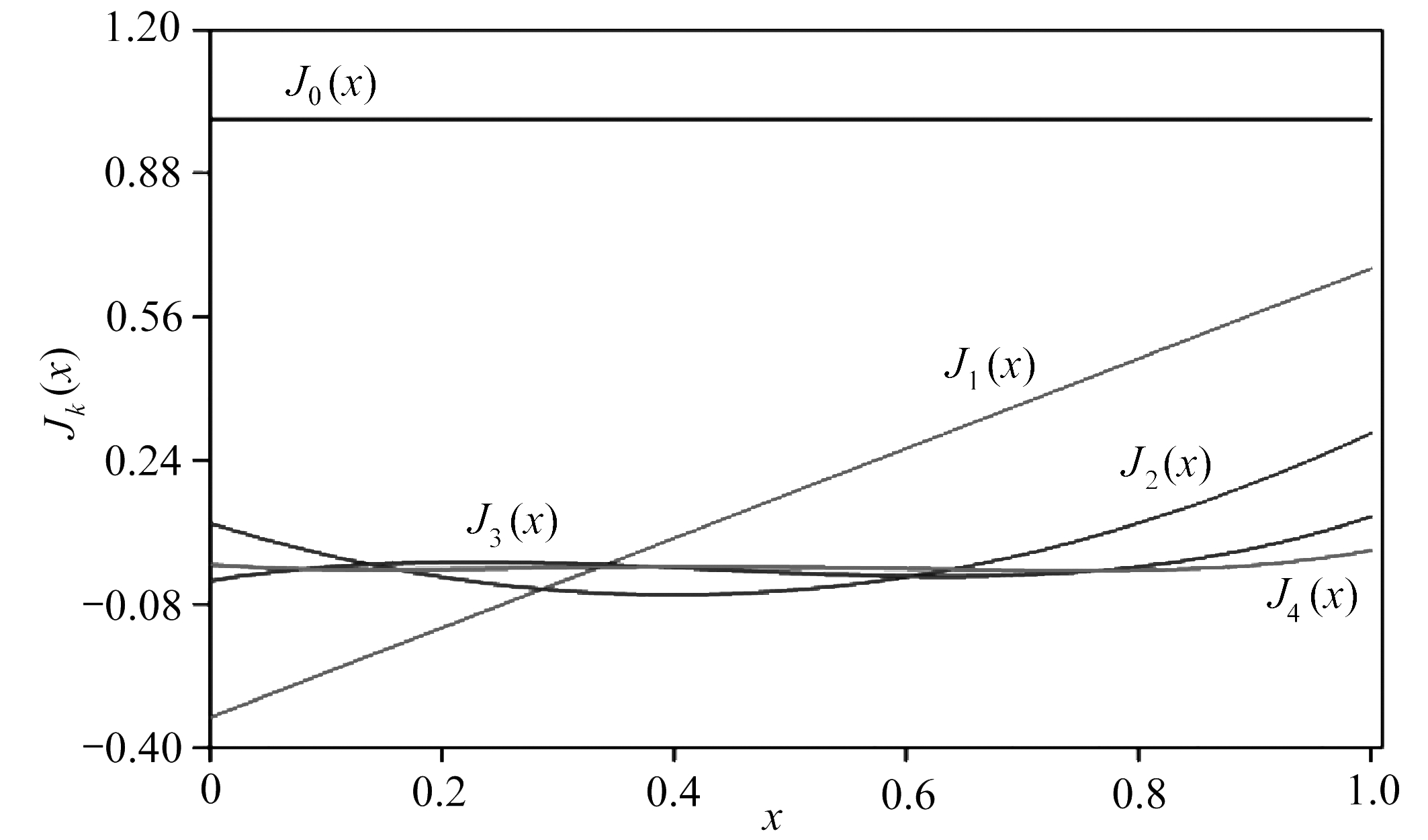
图2 前5项Jacobi多项式曲线图
Fig. 2 The 1st 5 Jacobi polynomial curves
1.2.3 Legendre 多项式
Legendre多项式混沌展开对应于概率密度分布为均匀分布.很显然均匀分布是beta分布的一个特例, 当α=β=0时beta分布退化为均匀分布如下:
(13)
因此令式(12)的α=β=0,可得到Legendre的递推系数:

(14)
表3列出了前5项一维Legendre多项式, 如图3所示.
表3 前5项Legendre多项式
Table 3 The 1st 5 Legendre polynomials

kone-dimensional Legendre polynomial Lk(x),x∈[-1,1]011x212(3x2-1)312(5x3-3x)418(35x4-30x2+3)

图3 前5项Legendre多项式曲线图
Fig. 3 The 1st 5 Legendre polynomial curves
多项式混沌展开完全由其系数决定, 本文采用回归方法来估计多项式混沌展开系数, 即最小二乘法拟合方法.假设共有n组样本,y=yi是每组样本所获得的系统输出向量, 截断的K+1个多项式混沌展开系数表示为βα,则系数最优值估计为求解下式最小化问题y:
(15)
设定符号如下:

(16)
则式(15)的最优解为
(17)
一旦多项式混沌展开被确定, 接下来就可以在多项式混沌展开替代模型框架下求解动力特性的统计矩.为了描述方便, 多项式混沌展开写成如下形式:
y(x)=β0+β1ψ1(x)+…+βKψK(x).
(18)
则动力特性的k阶统计矩可由下式计算:
(19)
由于y(x)为多项式混沌展开形式, 因此其k次方也为多项式形式.注意到多项式为多个变量不同次方乘积连加形式, 因此式(19)最后转化为求解单变量原点矩问题.比如动力特性的一阶统计矩可表示如下:
μ=β0+β1E(ψ1(x))+…+βKE(ψK(x))=β0,
(20)
式中E(·)表示求均值运算.
由式(18)和(20)可知, 采用多项式混沌展开替代模型使结构动力特性的高阶统计矩的高维积分问题转变为一维积分问题,使问题变得非常简单.因此,利用多项式混沌展开替代模型可从根本上解决复杂结构动力特性的统计矩计算耗时巨大的问题.
采用一块长为0.55 m、宽为0.1 m的平铝板(图4)算例来验证多项式混沌展开方法的有效性.
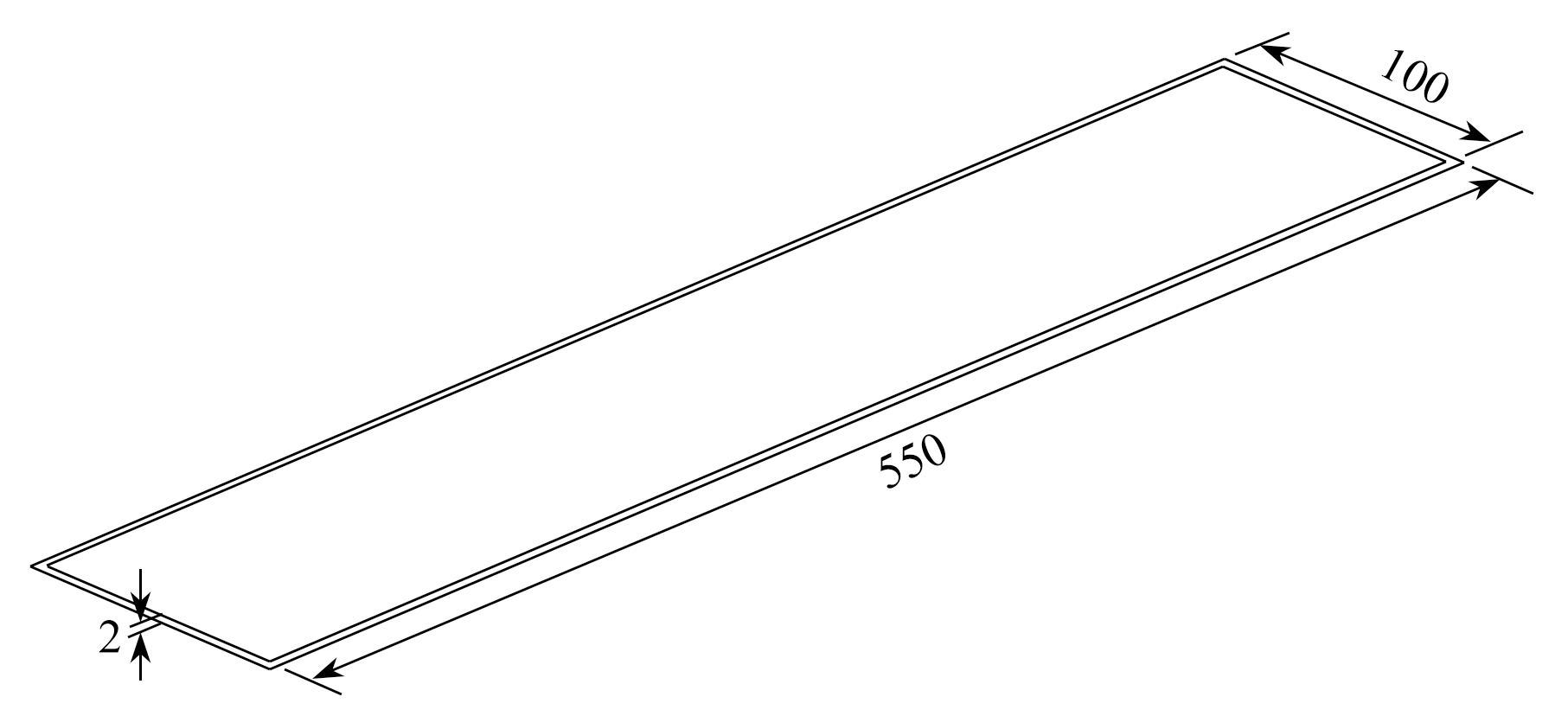
图4 平铝板尺寸示意图(单位:mm)
Fig. 4 Schematic diagram of the aluminum plate(unit: mm)
平铝板在制作过程中存在物理材料和结构几何尺寸等不确定性,为此假设弹性模量服从正态分布,均值为E=7.0×1010 Pa, 变异系数ρcov为0.1; 质量密度服从均匀分布,均值为D=2.7×103 kg/m3, 变异系数ρcov为0.1; 厚度服从正态分布,均值为T=2×10-3 m, 变异系数ρcov为0.15.剪切模量G视为确定性参数G=2.6×1010 Pa.该平板的有限元模型在ANSYS有限元软件平台上建立.整块平板采用壳单元(Shell63)模拟, 有限元模型共有561个节点和500个单元.平铝板的有限元模型及前四阶模态如图5所示.

(a) 有限元模型
(a) The finite element model

(b) 一阶竖弯(c) 二阶竖弯
(b) The 1st vertical mode(c) The 2nd vertical mode

(d) 一阶扭转(e) 三阶竖弯
(d) The 1st torsional mode(e) The 3rd vertical mode
图5 平铝板有限元模型及前四阶模态
Fig. 5 The finite element model and the 1st 4 modes of the aluminum plate
表4 一阶竖弯固有频率高阶统计矩计算
Table 4 Calculation of high order statistical moments of the 1st vertical mode natural frequency
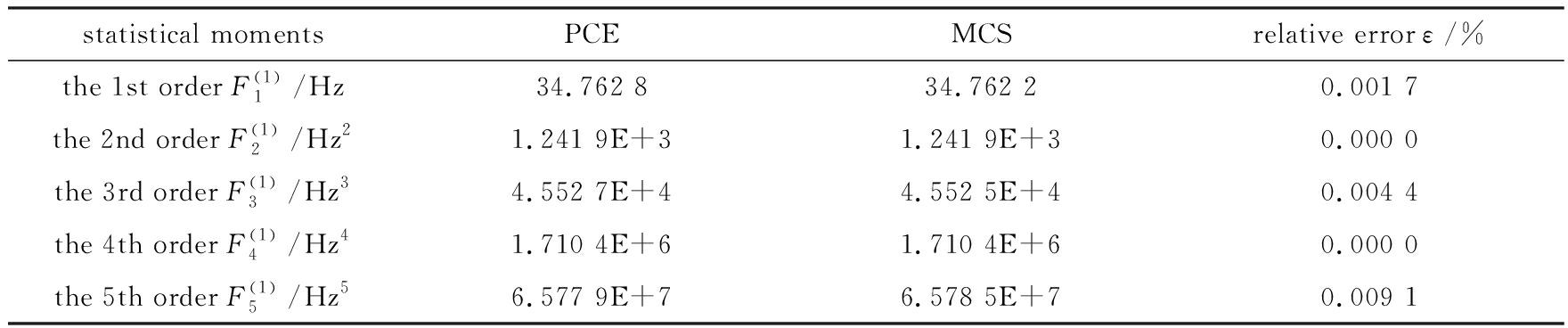
statistical momentsPCEMCSrelative error ε/%the 1st order F(1)1/Hz34.762 834.762 20.001 7the 2nd order F(1)2/Hz21.241 9E+31.241 9E+30.000 0the 3rd order F(1)3/Hz34.552 7E+44.552 5E+40.004 4the 4th order F(1)4/Hz41.710 4E+61.710 4E+60.000 0the 5th order F(1)5/Hz56.577 9E+76.578 5E+70.009 1
首先采用Sobol实验设计方法[15]用来产生训练样本,然后对每个训练样本执行有限元分析,得到训练样本对应的目标量,即固有频率.接着根据训练样本点来构建多项式混沌展开替代模型,最后基于替代模型来计算固有频率的统计矩.本文提出的方法可以计算任意高阶统计矩,限于篇幅仅列出前五阶统计矩.与此同时,MCS方法用来验证本文方法的精度,对比结果如表4~7所示.由表4~7可以看到,多项式混沌展开方法与MCS方法的结果非常接近,最大相对误差仅为0.009 4%,表明本文提出的基于多项式混沌展开的统计矩计算方法的准确性.
表5 二阶竖弯固有频率高阶统计矩计算
Table 5 Calculation of high order statistical moments of the 2nd vertical mode natural frequency

statistical momentsPCEMCSrelative error ε/%the 1st order F(2)1/Hz96.257 396.255 60.001 8the 2nd order F(2)2/Hz29.521 7E+39.521 3E+30.004 2the 3rd order F(2)3/Hz39.664 7E+59.664 4E+50.003 1the 4th order F(2)4/Hz41.005 3E+81.005 3E+80.000 0the 5th order F(2)5/Hz51.070 4E+101.070 5E+100.009 3
表6 一阶扭转固有频率高阶统计矩计算
Table 6 Calculation of high order statistical moments of the 1st torsional mode natural frequency
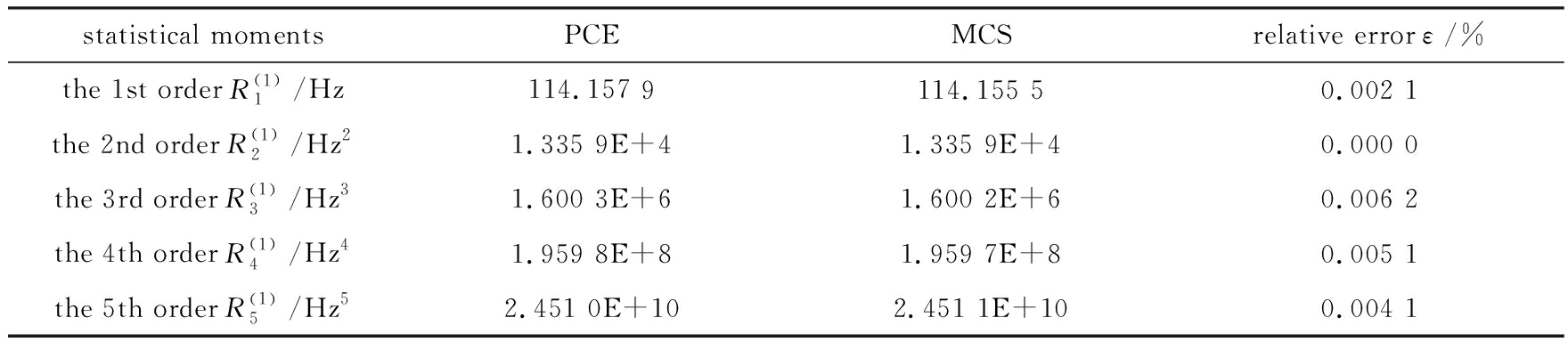
statistical momentsPCEMCSrelative error ε/%the 1st order R(1)1/Hz114.157 9114.155 50.002 1the 2nd order R(1)2/Hz21.335 9E+41.335 9E+40.000 0the 3rd order R(1)3/Hz31.600 3E+61.600 2E+60.006 2the 4th order R(1)4/Hz41.959 8E+81.959 7E+80.005 1the 5th order R(1)5/Hz52.451 0E+102.451 1E+100.004 1
表7 三阶竖弯固有频率高阶统计矩计算
Table 7 Calculation of high order statistical moments of the 3rd vertical mode natural frequency
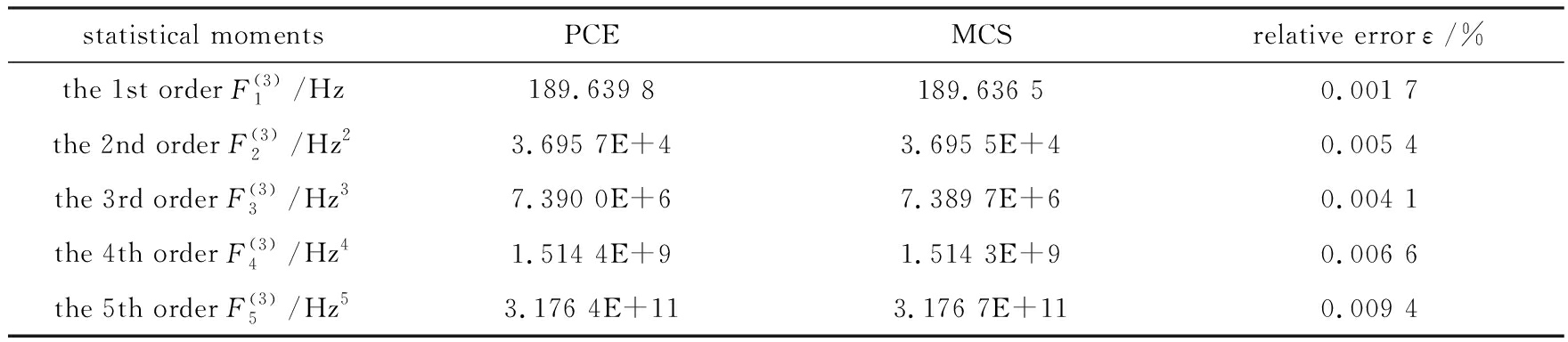
statistical momentsPCEMCSrelative error ε/%the 1st order F(3)1/Hz189.639 8189.636 50.001 7the 2nd order F(3)2/Hz23.695 7E+43.695 5E+40.005 4the 3rd order F(3)3/Hz37.390 0E+67.389 7E+60.004 1the 4th order F(3)4/Hz41.514 4E+91.514 3E+90.006 6the 5th order F(3)5/Hz53.176 4E+113.176 7E+110.009 4
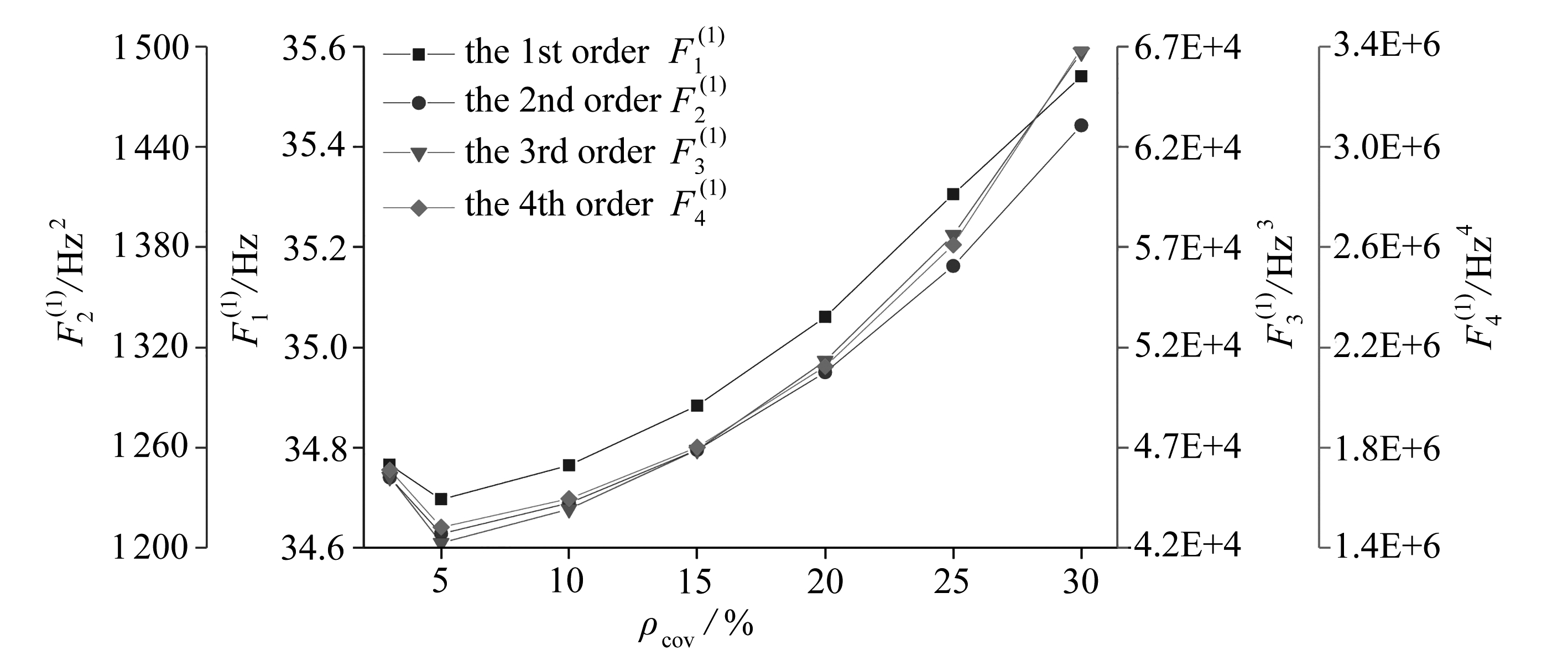
(a) 一阶竖弯频率
(a) The 1st vertical frequency
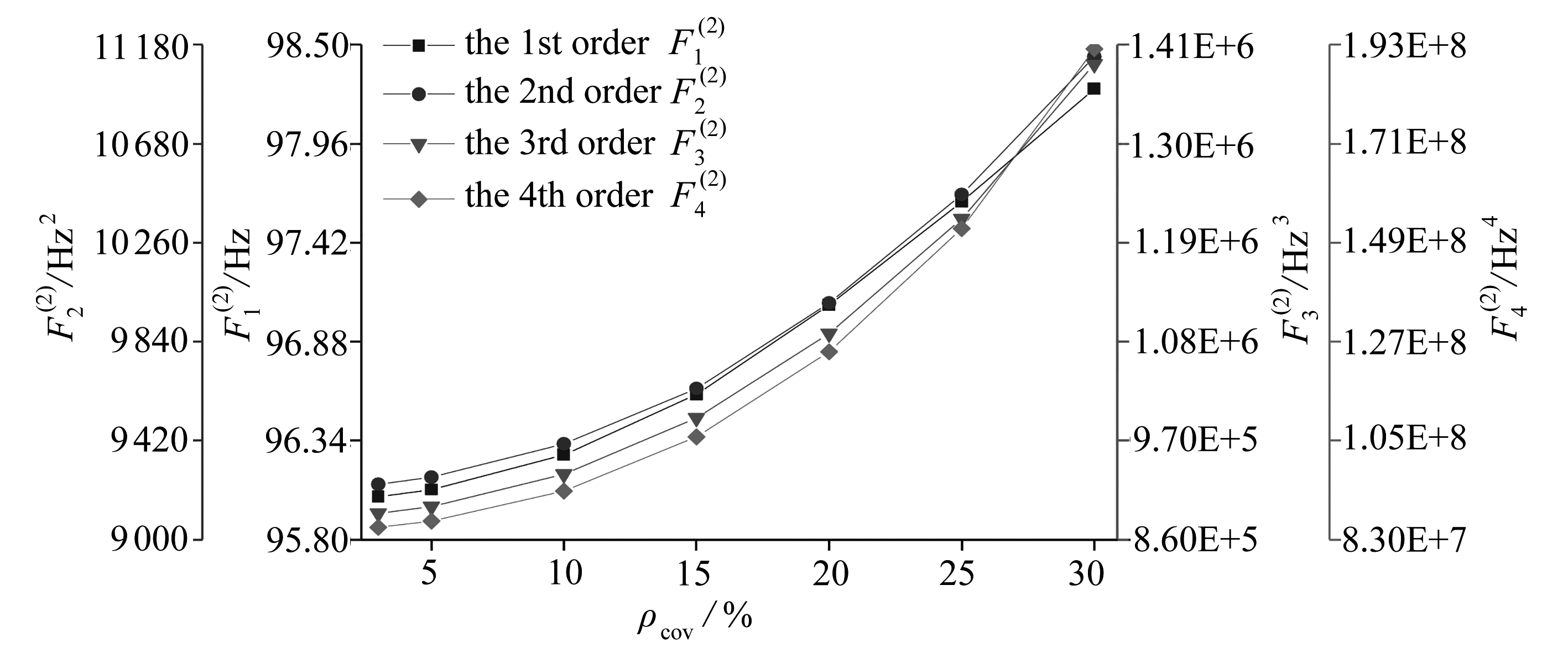
(b) 二阶竖弯频率
(b) The 2nd vertical frequency

(c) 一阶扭转频率
(c) The 1st torsional frequency
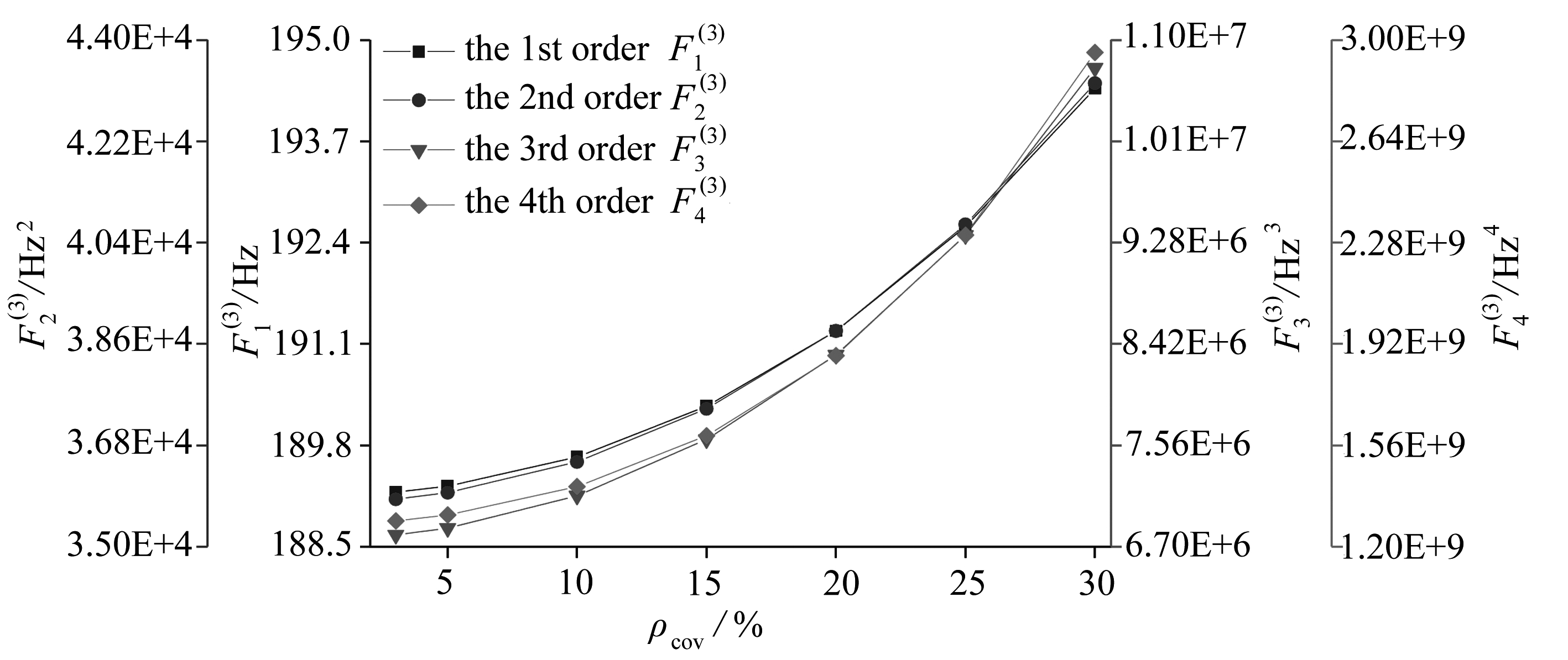
(d) 三阶竖弯频率
(d) The 3rd vertical frequency
图6 前四阶固有频率统计矩与变异系数变化关系
Fig. 6 Statistical moments of the 1st 4 natural frequencies against the coefficient of variation
在验证本文方法的有效性后, 接下来探究参数变异性系数大小对平板结构的固有频率统计矩的影响.为此将随机变量的变异系数分别设定为3%,5%,10%,15%,20%,25%和30%, 然后采用多项式混沌展开方法来计算固有频率的统计矩.绘制统计矩随参数变异系数变化的关系曲线, 结果如图6所示(注意为了展示方便, 在此只给出了前四阶统计矩的结果).由图6(a)可以看出,随着随机变量变异系数的增大, 一阶竖弯固有频率统计矩在开始时有轻微下降, 随后随着变异系数的增大而随之增大; 由图6(b)、(c)和(d)可知, 对应的固有频率统计矩均随着变异系数的增大而随之增大.总体上说, 平板结构的固有频率的统计矩随着随机参数变异系数的增大而增大.
本文提出了基于多项式混沌展开的结构固有频率的高阶统计矩计算方法,适用于任意分布的随机变量.该方法实现是根据结构单随机变量的概率密度函数选择相应的正交多项式,由各随机变量的正交多项式连乘再相加得到多维度的多项式混沌展开式.多项式混沌展开来表征不确定性参数与结构固有频率之间的映射关系,接着在替代模型基础上计算固有频率的统计矩.利用多项式混沌展开系数与单个随机变量统计特征之间的组合关系可快速地计算出结构固有频率的统计矩.本文方法不涉及复杂的积分运算,达到了高效快速计算固有频率高阶统计矩的目的.文中采用平铝板为例来验证多项式混沌展开的有效性,计算结果与MCS方法结果相对比.结果表明本文方法与MCS方法的结果非常接近,最大相对误差仅为0.009 4%,表明了本文方法用于结构固有频率的高阶统计矩计算的精度高.最后本文还探讨了结构随机变量变异系数对结构动力特性统计矩的影响, 结果表明结构固有频率的统计矩随着随机变量变异系数的增大而增大.
[1] 万华平, 任伟新, 颜王吉. 桥梁结构动力特性不确定性的全局灵敏度分析的解析方法[J]. 振动工程学报, 2016,29(3): 429-435.(WAN Huaping, REN Weixin, YAN Wangji. Analytical global sensitivity analysis for uncertainty in structural dynamic properties of bridges[J].Journal of Vibration Engineering, 2016,29(3): 429-435.(in Chinese))
[2] 万华平, 任伟新, 钟剑. 桥梁结构固有频率不确定性量化的高斯过程模型方法[J]. 中国科学: 技术科学, 2016,46(9): 919-925.(WAN Huaping, REN Weixin, ZHONG Jian. Gaussian process model-based approach for uncertainty quantification of natural frequencies of bridge[J].Scientia Sinica:Technologica, 2016,46(9): 919-925.(in Chinese))
[3] SHINOZUKA M, ASTILL C J. Random eigenvalue problems in structural analysis[J].AIAA Journal, 1972,10(4): 456-462.
[4] SZEKELY G S, SCHUELLER G I. Computational procedure for a fast calculation of eigenvectors and eigenvalues of structures with random properties[J].Computer Methods in Applied Mechanics and Engineering, 2001,191(8/10): 799-816.
[5] WAN H P, MAO Z, TODD M D, et al. Analytical uncertainty quantification for modal frequencies with structural parameter uncertainty using a Gaussian process metamodel[J].Engineering Structures, 2014,75: 577-589.
[6] 陈塑寰, 张宗芬. 结构固有频率的统计特性[J]. 振动工程学报, 1991,4(1): 90-95.(CHEN Shuhuan, ZHANG Zongfen. Statistics of structural natural frequeneies[J].Journal of Vibration Engineering, 1991,4(1): 90-95.(in Chinese))
[7] 刘春华, 秦权. 桥梁结构固有频率的统计特征[J]. 中国公路学报, 1997,10(4): 50-55.(LIU Chunhua, QIN Quan. Statistics of natural frequencies for bridge structures[J].China Journal of Highway and Transport, 1997,10(4): 50-55.(in Chinese))
[8] ADHIKARI S, FRISWELL M I. Random matrix eigenvalue problems in structural dynamics[J].International Journal for Numerical Methods in Engineering, 2007,69(3): 562-591.
[9] QIU Z P, WANG X J, FRISWELL M I. Eigenvalue bounds of structures with uncertain-but-bounded parameters[J].Journal of Sound and Vibration, 2005,282(1/2): 297-312.
[10] MODARES M, MULLEN R, MUHANNA R. Natural frequencies of a structure with bounded uncertainty[J].Journal of Engineering Mechanics, 2006,132(12): 1363-1371.
[11] MOENS D, VANDEPITTE D. Interval sensitivity theory and its application to frequency response envelope analysis of uncertain structures[J].Computer Methods in Applied Mechanics and Engineering, 2007,196(21/24): 2486-2496.
[12] WANG C, GAO W, SONG C M, et al. Stochastic interval analysis of natural frequency and mode shape of structures with uncertainties[J].Journal of Sound and Vibration, 2014,333(9): 2483-2503.
[13] GAUTSCHI W.Orthogonal Polynomials:Computation and Approximation[M]. Oxford: Oxford University Press, 2004.
[14] WAN H P, REN W X, TODD M D. An efficient metamodeling approach for uncertainty quantification of complex systems with arbitrary parameter probability distributions[J].International Journal for Numerical Methods in Engineering, 2017,109(5): 739-760.
[15] WAN H P, REN W X. Parameter selection in finite-element-model updating by global sensitivity analysis using Gaussian process metamodel[J].Journal of Structural Engineering, 2015,141(6): 04014164.