杨 于1,2， 梁英
在工程结构可靠性的研究中，根据功能函数判断和确定工程的可靠度和失效概率[1-6]．功能函数是工程随机载荷的函数，计算功能函数需要确定随机变量的统计分布[7]．工程随机载荷对应统计分布的尾部信息，在工程结构可靠度计算中起着关键作用[8-9]．目前，常用于描述工程随机载荷的统计分布统称为指数分布，正态分布常用于描述永久载荷[3]，极值Ⅰ型分布常用于描述极大风速[10]．然而这些指数型分布，仅通过观测和试验资料的期望和方差确定工程随机载荷的统计分布，忽略了峰态、非对称、尾部等信息，且不能准确描述载荷概率密度的尖峰和尾部分布的特征[7]．虽然常规指数型统计分布可用于计算工程结构可靠度，但会导致可靠度的计算结果不同程度的偏低或者偏高，不能较全面和真实地反映服役结构的可靠性和剩余寿命等信息，甚至会得出与实际情况相悖的结论[7]．因此，需要新的统计分布描述工程随机载荷的统计特征．
Lévy稳定分布[11]是一类常用于描述非Gauss(高斯)随机变量的统计分布，已用于Brown(布朗)运动、金融领域、反常扩散、信号处理、股票市场模拟、楼面活荷载、水位波动等领域[4,12-17]．该分布可以用于描述工程随机载荷的非指数型统计分布．描述该分布需要4个参数，分别是稳定指数α、倾斜指数β、尺度参数γ和位置参数δ [18]．该分布的概率密度函数具有明显的尖峰、非对称和拖尾特征[18]．Cauchy(柯西)分布(α=1)和Gauss分布(α=2)是Lévy稳定分布的两种特例．Lévy稳定分布的特征函数具有解析表达式，但其概率密度函数和累积分布函数没有具体的解析表达式，利用现有的MATLAB工具箱[19]可以准确数值计算该分布的统计量．采用Lévy稳定分布描述工程随机载荷的统计分布，面临的问题是如何从众多统计分布中选择工程随机载荷的最优统计分布．
香农熵[20]常用于定量分析随机系统的不确定性．一般情况下，任给的随机系统，其随机变量对应统计分布的熵可以度量该随机系统的复杂程度．熵越大，表明该系统越混乱，反之则越有序．目前，累积熵[21]是一种可以用于选择随机载荷统计分布的最优统计分布．其对应的相对距离函数的值越小，表明工程随机载荷的候选统计分布越接近实际分布．但是该方法不能直接利用统计分布的尾部信息，不能体现Lévy稳定分布用于描述工程随机载荷的优势．因此，需要提出一种直接结合工程随机载荷统计分布的尾部信息，选择工程随机载荷的最优统计分布．
本文将基于现有的工作[4,21-22]，提出了一种选择工程随机载荷最优统计分布的剩余累积熵法．该方法可以直接刻画随机载荷的尾部特征，并结合永济第二节制闸工程实例，全面考察上下游水位载荷的统计特征，并与累积熵法进行了比较．
目前常用的两种参数化方法描述Lévy稳定分布，分别是由Samorodnitsky、Taqqu[22]和Nolan[23]提出的．对其X～S(α,γ,β,δ)的具体表达式分别如下：
(1)
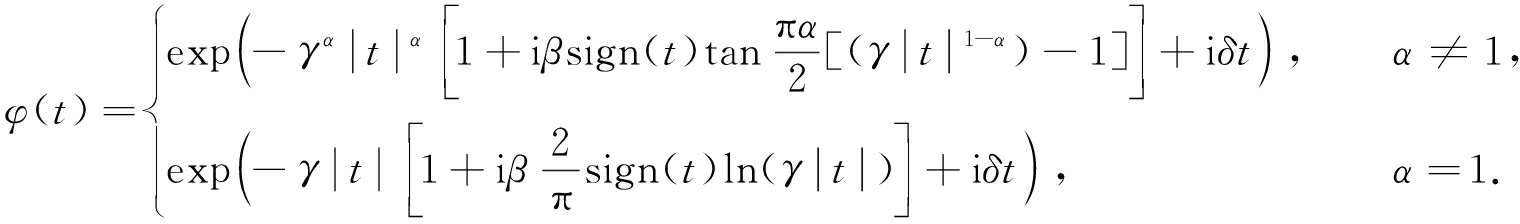
(2)
式(2)克服了α=1处不连续的缺点，其中参数的取值分别为0<α≤2,-1≤β≤1,γ>0,δ∈R [18]．
目前直接积分法是常用于数值计算Lévy稳定分布累积分布函数的方法．直接积分法由Zolotarev[24]提出，在描述该方法时需要定义如下变量：
(3)
(4)
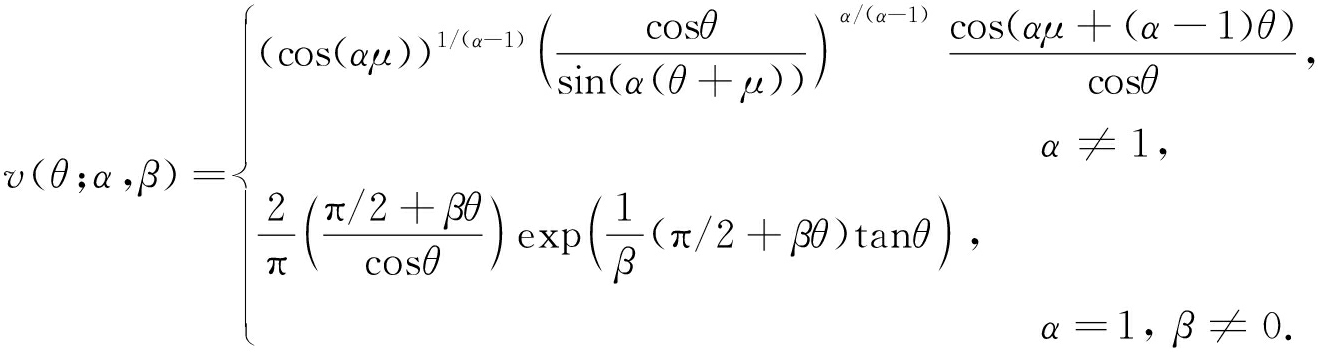
(5)
令X～S(α,β;0)，X的表达式如下：
(a) 当α≠1且x>ζ时，
(6)
其中
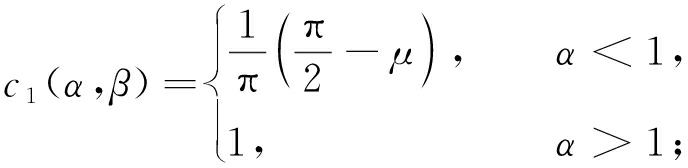
(b) 当α≠1且x=ζ时，
(7)
(c) 当α≠1且x<ζ时，
F(x;α,β)=1-F(-x;α,-β)；
(8)
(d) 当α=1且β=0时，
(9)
(e) 当α=1且β≠0时，
(10)
通过一些性质可以计算出一般形式下Lévy稳定分布的累积分布函数[21]．
离散随机变量xi的香农熵为
(11)
其中，f(xi)为xi出现的频率或者概率，是根据实验数据的直方图得到的，n为系统状态的数量，即样本大小的长度，b为对数的基底[25]．
累积熵根据式(11)推导得到，已用于选择随机变量的最优统计分布[21]：
(12)
其中，p(xi)为xi的累积概率，n为系统状态的数量，即样本大小的长度，b为对数的基底以及
通过验证可知累积熵是非负的和可扩展的．累积熵和香农熵之间最明显的差异在于前者与随机系统的累积分布函数相关，而后者取决于实验数据直方图的间隔长度即概率密度函数．与香农熵相比，累积熵的计算结果更准确[21]．
累积剩余熵的核心思想是将累积剩余概率替代累积熵中的累积概率，用以直接描述随机变量统计分布的尾部信息．累积剩余熵的定义为
(13)
式中，p(xi)为xi的累积概率，n为系统状态的数量，即样本大小的长度，b为对数的基底以及
在文献[21]中，将候选分布对应的累积熵与随机变量的实际分布对应的标准累积熵之间的相对距离定义为ε：
ε=Es-Er，
(14)
其中，Es为候选分布的累积熵，Er为实际分布的标准累积熵[21]．
结合累积剩余熵以及累积熵的相对距离可以定义累积剩余熵的相对距离为
ε=Et-Er，
(15)
其中，Et为候选分布的累积剩余熵，Er为实际分布的标准累积剩余熵．
根据式(14)和(15)可以估计候选分布对应的相对距离，由此得到距离集合，距离集合中最小值对应的分布模型即是候选分布中最优的统计分布[21]．
本节以永济第二节制闸为例，采用1995年—2001年上游和下游水位载荷的实测数据[3](由数据可知，上游水位的变化范围是50～300 cm，下游水位的变化范围是150～400 cm)．上下游水位统计分布的规律直接影响水闸可靠度的计算[4]．根据上述方法，确定水位的最优统计分布．具体来讲：首先分别采用Lévy稳定分布、极值Ⅰ型分布以及正态分布作为候选分布拟合水位的累积分布和尾部分布；然后采用累积熵和累积剩余熵分别计算相对距离；最后比较各候选分布对应的相对距离，确定上下水位的最优统计分布．
上游水位对应的拟合结果详见文献[4]．文献[4]的结果表明，上游水位服从Lévy稳定分布．图1给出了正态分布，极值Ⅰ型分布和Lévy稳定分布拟合下游水位的累积分布函数曲线．由图1可见，与极值Ⅰ型分布相比，正态分布和Lévy稳定分布更接近下游水位的实际分布，并且Lévy稳定分布稳定指数的值为1.95，表明下游水位与正态分布较接近．
为进一步考察下游水位统计分布的尾部特征，图2给出了正态分布，极值Ⅰ型分布和Lévy稳定分布拟合下游水位尾部分布函数曲线．由图2可见，Lévy稳定分布可以准确地刻画尾部分布的特征．
根据累积分布和尾部分布的计算结果，结合式(12)～(15)，分别计算各个候选分布对应累积熵和累积剩余熵的相对距离ε，见表1、2(表1中，ε1表示上游水位不同统计分布对应累积熵和标准累积熵的相对距离，ε2表示下游水位不同统计分布对应累积熵和标准累积熵的相对距离；表2中，ε3表示上游水位不同统计分布对应累积剩余熵和系统标准累积剩余熵的相对距离，ε4表示下游水位不同统计分布对应累积剩余熵和标准累积剩余熵的相对距离)．由表1、表2可知，在4种情况下，Lévy稳定分布对应相对距离的值均最小，也表明Lévy稳定分布是候选分布中最接近随机变量的实际分布，更进一步验证了Lévy稳定分布可有效描述上下游水位的统计分布．需要指出的是，在计算上游水位对应的累积剩余熵时，剔除了水位小于100 cm的数值，主要原因是小的水位数值对应的累积剩余概率较大，则对累积剩余熵的干扰比较大．
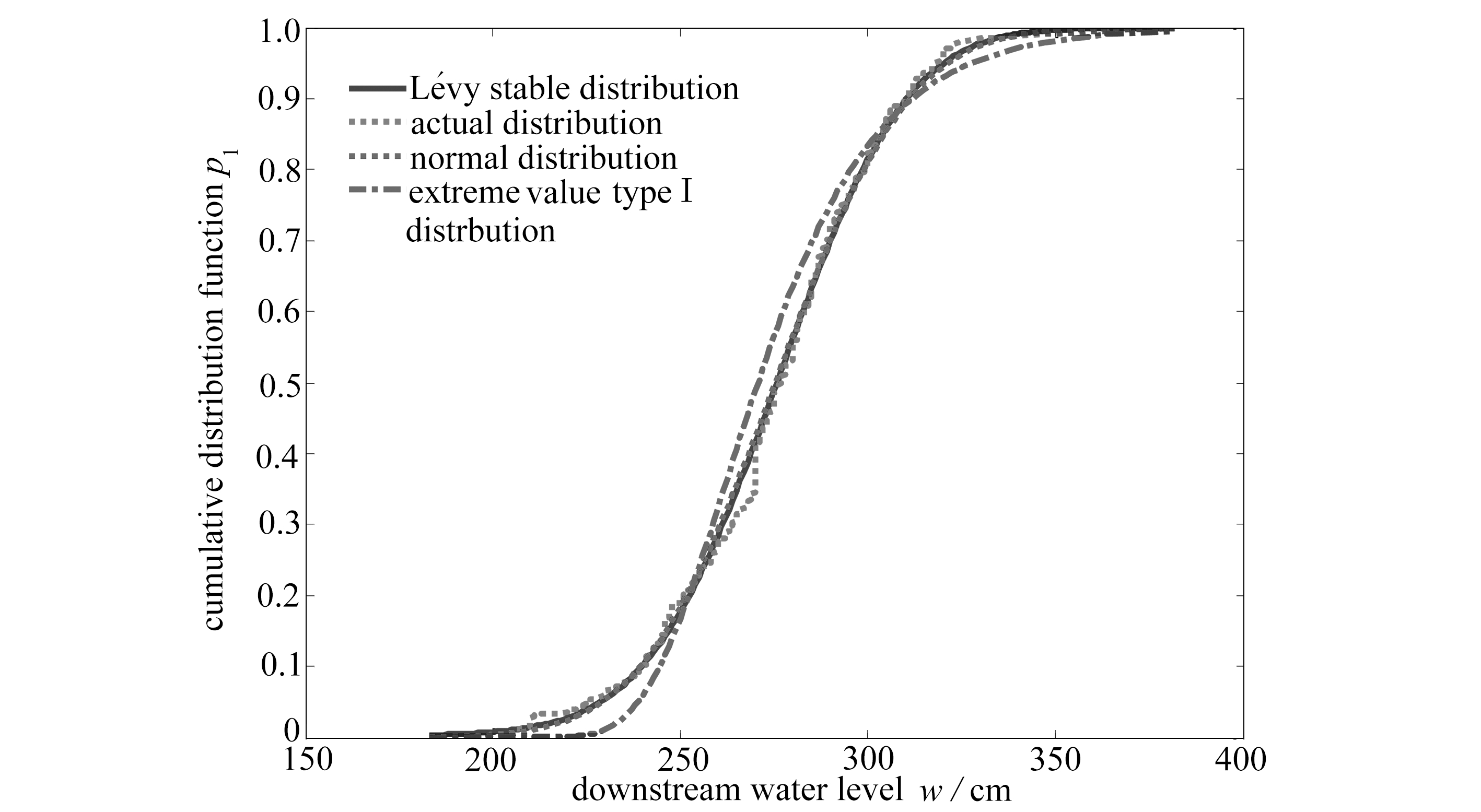
图1 不同统计分布拟合下游水位累积分布函数的曲线
Fig. 1 Plots of the cumulative distribution function for the downstream water level fitted with 3 different statistical distributions
图2 不同统计分布拟合下游水位尾部分布函数的曲线
Fig. 2 Plots of the tail distribution function for the downstream water level fitted with 3 different statistical distributions
表1 上下游水位不同统计分布对应累积熵和标准累积熵的相对距离
Table 1 The relative distance between the cumulative entropy and the standard cumulative entropy of differentstatistical distributions for upstream and downstream water levels
distance functionε1ε2extreme value type I distribution0.014 10.013 3normal distribution0.028 80.005 8Lévy stable distribution0.002 60.002 8
表2 上下游水位不同统计分布对应累积剩余熵和标准累积剩余熵的相对距离
Table 2 The relative distance between the cumulative residual entropy and the standard cumulative residualentropy of different statistical distributions for upstream and downstream water levels
distance functionε3ε4extreme value type I distribution0.021 40.017 1normal distribution0.011 50.009 8Lévy stable distribution0.006 00.006 4
本文基于Lévy稳定分布，给出了一种选择工程随机载荷最优统计分布的累积剩余熵，并将其用于选择永济第二节制闸上下游水位载荷的统计分布．通过计算累积剩余熵的相对距离，确定了上下游水位的最优统计分布，并与累积熵法进行了比较，为准确计算水闸的可靠度提供了保障．所得结论如下：
1) 上下游水位的最优统计分布均是Lévy稳定分布．与正态分布、极值Ⅰ型分布相比，Lévy稳定分布具有更高的拟合精度，可以刻画上下游水位的拖尾特征．
2) 累积剩余熵的相对距离表明Lévy稳定分布与实际分布之间的误差最小，Lévy稳定分布可以有效描述水位的统计分布．
3) 与累积熵法相比，累积剩余熵也是一种有效选择工程随机载荷最优统计分布的方法．
[1] 赵国藩. 结构可靠度理论[M]. 北京: 中国建筑工业出版社, 2000.(ZHAO Guofan.Structural Reliability Theory[M]. Beijing: China Building Industry Press, 2000.(in Chinese))
[2] 李全旺, 李春前, 孙健康. 基于结构可靠性理论的既有桥梁承载能力评估[J]. 工程力学, 2010,27(S2): 142-151.(LI Quanwang, LI Chunqian, SUN Jiankang. Reliability-based capacity assessment of existing bridges[J].Engineering Mechanics, 2010,27(S2): 142-151 (in Chinese))
[3] 邹春霞. 基于最大熵原理的水工建筑物可靠性分析[D]. 硕士学位论文. 呼和浩特: 内蒙古农业大学, 2004.(ZOU Chunxia. Reliability analysis of hydraulic construction based on the principle of maximum entropy[D]. Master Thesis. Hohhot: Inner Mongolia Agricultural University, 2004.(in Chinese))
[4] LIANG Y, CHEN W. Reliability analysis for sluice gate anti-sliding stability using Lévy stable distributions[J].Signal Processing, 2015,107: 425-432.
[5] PROPPE C. Estimation of failure probabilities by local approximation of the limit state function[J].Structural Safety, 2008,30(4): 277-290.
[6] SU Y H, LI X, XIE Z Y. Probabilistic evaluation for the implicit limit-state function of stability of a highway tunnel in China[J].Tunnelling and Underground Space Technology, 2011,26(2): 422-434.
[7] 梁英杰. 分数阶统计力学的研究及其在工程可靠性和反常扩散中的应用[D]. 博士学位论文. 南京: 河海大学, 2016.(LIANG Yingjie. A study on fractional statistical mechanics and its applications in engineering reliability and anomalous diffusion[D]. PhD Thesis. Nanjing: Hohai University. 2016.(in Chinese))
[8] BLUDSZUWEIT H, DOMINGUEZ-NAVARRO J A, LLOMBART A. Statistical analysis of wind power forecast error[J].IEEE Transactions on Power Systems, 2008,23(3): 983-991.
[9] MAHANI A, KAVIAN Y S, NADERI M, et al. Heavy-tail and voice over internet protocol traffic: queueing analysis for performance evaluation[J].Iet Communications, 2011,5(18): 2736-2743.
[10] KWON K, FRANGOPOL D M. Bridge fatigue reliability assessment using probability density functions of equivalent stress range based on field monitoring data[J].International Journal of Fatigue, 2010,32(8): 1221-1232.
[11] WERON R J.Computationally Intensive Value at Risk Calculations[M]//GENTLE J E, H
RDLE W, MORI Y, ed.Handbook of Computational Statistics. Berlin: Springer, 2004.
[12] DAVID A. Lévy processes-from probability to finance and quantum groups[J].Notices of the AMS, 2004,51(11): 1336-1347.
[13] MARIANI M C, BIANCHINI A, BANDINI P. Normalized truncated Levy walk applied to flexible pavement performance[J].Transportation Research Part C, 2012,24: 1-8.
[14] GONZALEZ D S, KURUOGLU E E, RULZ D P. Modelling with mixture of symmetric stable distributions using Gibbs sampling[J].Signal Processing, 2010,90(3): 774-783.
[15] 徐绪松, 马莉莉, 陈彦斌. Lévy分布在中国股票市场中的实证检验[J]. 科技进步与决策, 2005,22(8): 103-105.(XU Xusong, MA Lili, CHEN Yanbin. The empirical tests of Lévy distribution on China’s stock market[J].Science &Technology Progress and Policy, 2005,22(8): 103-105.(in Chinese))
[16] 梁英杰, 陈文. Lévy稳定分布对住宅楼面活荷载的统计分析[J]. 工程力学, 2014,31(6): 166-172.(LIANG Yingjie, CHEN Wen. Statistical anaiysis of live load on residence floor using Lévy stable distributions[J].Engineering Mechanics, 2014,31(6): 166-172.(in Chinese))
[17] 陈文, 孙洪广, 李西成. 力学与工程问题的分数阶导数建模[M]. 北京: 科学出版社, 2010.(CHEN Wen, SUN Hongguang, LI Xicheng.Fractional Derivative Modeling in Mechanical and Engineering Problems[M]. Beijing: Science Press, 2010.(in Chinese))
[18] NOLAN J P.Stable Distribution:Models for Heavy-Tailed Data[M]. Boston: Birkhauser, 2010.
[19] LIANG Y, CHEN W. A survey on computing Lévy stable distributions and a new MATLAB toolbox[J].Signal Processing, 2013,93(1): 242-251.
[20] MURALI R. More on a new concept of entropy and information[J].Journal of Theoretical Probability, 2005,18(14): 967-981.
[21] LIANG Y, CHEN W. A cumulative entropy method for distribution recognition of model error[J].Physica A:Statistical Mechanics and Its Applications, 2015,419: 729-735.
[22] SAMORODNITSKY G, TAQQU M S.Stable Non-Gaussian Random Processes:Stochastic Models with Infinite Variance[M]. Boca Raton: CRC Press, 1994.
[23] NOLAN J P. Parameterizations and modes of stable distributions[J].Statistics &Probability Letters, 1998,38(2): 187-195.
[24] ZOLOTAREV V M.One-Dimensional Stable Distributions[M]. Providence: American Mathematical Society, 1986.
[25] DIONISIO A, MENEZES R, MENDES D A. An econophysics approach to analyse uncertainty in financial markets: an application to the Portuguese stock market[J].The European Physical Journal B:Condensed Matter and Complex Systems, 2006,50(1/2): 161-164.
作者简介： 杨于(1992—)，女，硕士生(E-mail: 18705162653@163.com)；梁英杰(1988—)，男，讲师，博士(E-mail: liangyj@hhu.edu.cn)；
男，教授，博士，博士生导师(通讯作者. E-mail: chenwen@hhu.edu.cn).