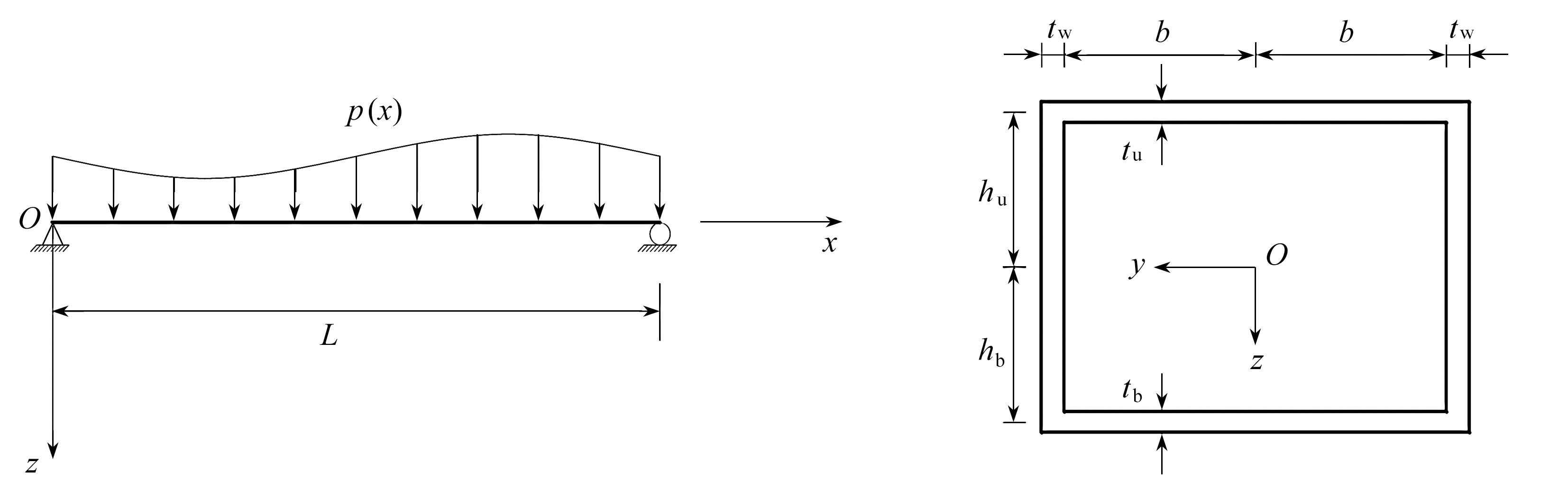
(a) 坐标系及荷载(b) 横截面
(a) Coordinates and loads(b) The cross section
图1 典型无翼板箱梁截面
Fig. 1 The cross section of a typical box girder without flanges
由于箱形梁截面具有良好的结构性能,已广泛应用于现代桥梁工程之中,研究其弯曲力学性能的文献已有很多[1-3],且其剪力滞效应已受到很大的重视[4-9].所谓剪力滞效应[10]是指箱形梁发生对称挠曲变形时,因受到顶、底、翼板平面内剪切变形的影响,使其弯曲正应力沿横向呈现不均匀分布的现象.
近年来,针对剪力滞问题,国内外学者进行了大量的分析研究,研究方法主要有能量变分法、有限元法、比拟杆法、有限条法以及有限段法[1,3,11].由于能量变分法的力学推理比较明晰并可以得到闭合解[12],而被广泛应用.采用能量变分法进行箱形梁剪力滞问题的分析时,多数研究者是先假定描述剪力滞变形状态的翘曲位移函数,然后利用最小势能原理建立控制微分方程并求解.Reissner等早期采用二次抛物线函数 [5-6]作为翘曲位移函数,通过能量变分法分析了无翼板矩形箱梁的剪力滞效应,其他的研究者还选取了三次 [9,13-14]、四次 [15]、五次和六次抛物线[16]、余弦函数[2]、悬链线[15]等形式作为翘曲位移函数,其中选取三次抛物线是比较多的.带翼板的箱形梁在确定其剪力滞翘曲位移函数时,一方面由于箱形梁截面顶、底、翼板的宽度是不相同的,为了提高分析精度,需要分别对顶、底、翼板的剪力滞程度进行考虑;另一方面由于剪力滞效应的影响,使得截面的形心轴偏离了中性轴,分析中截面中性轴仍通过形心轴的假设导致包含了附加轴力的影响,那么带翼板箱梁翘曲正应力的轴向平衡条件无法自动满足.国内学者经过分析与研究,对上述的问题给出了解决的办法.甘亚南等[15]把剪力滞翘曲位移函数采用不同形式的计算结果与有限元的计算结果进行了对比,提出剪力滞翘曲位移函数的基本形式选用二次抛物线或悬链线的建议;张元海等[9]通过对薄壁箱梁弯曲理论的分析研究,推导出了剪力滞翘曲位移函数为二次抛物线的形式;倪元增等[2]和韦成龙等[17]为使轴向平衡条件得到满足,通过研究提出了对剪力滞翘曲位移函数增加常数项的理论.当箱形梁翼板的长度与顶板宽度的一半相等时,有限元的计算结果表明[8,14,18],翼板实际纵向应力比顶板的纵向应力要小,而翼板端部的应力明显小于顶板中部的纵向应力,这是由于箱梁翼板与顶板边界约束的不同造成的.
综上所述,箱梁剪力滞翘曲位移函数的选取目前来说尚未形成完整以及系统的理论分析,并且对剪力滞翘曲位移函数形式的选取仍是不统一的.为此,本文在已有的相关文献的基础上并结合能量变分法求解剪力滞的基本假设,通过基于抽象的翘曲位移函数建立剪力滞控制微分方程,从其形式出发构造了剪力滞翘曲位移函数,并对翼板引入了边界约束影响的修正系数,然后采用能量变分法分析其剪力滞问题.
如图1所示,薄壁箱梁在竖向分布荷载p(x)作用下发生竖向挠曲变形,坐标原点O位于截面形心处,由于受剪力滞效应的影响,其横截面顶、底板的变形不再符合平截面变形的假设,即横截面顶、底板会产生翘曲位移.此时,横截面顶、底板上任意一点的纵向位移u(x,y)由相应的初等梁的弯曲纵向位移和剪力滞引起的附加纵向翘曲位移两部分组成,可表示为
u(x,y)=hi[w′(x)+f(x,y)],
(1)
式中,w(x)为箱梁的竖向挠度,hi为箱梁截面顶、底板中面的z坐标,f(x,y)为剪切变形引起的附加转角函数.

(a) 坐标系及荷载(b) 横截面
(a) Coordinates and loads(b) The cross section
图1 典型无翼板箱梁截面
Fig. 1 The cross section of a typical box girder without flanges
图1中,b为箱梁顶板(底板)的半宽,hu,hb分别为顶、底板中面至箱梁截面水平形心轴(y轴)的距离,tu,tb,tw分别为箱梁顶、底板及腹板的厚度,L为跨度.
采用抽象函数式(1),利用能量变分法推导,由文献[12]可得控制微分方程及边界条件分别为
(2)
f(x,y)y=b=f(x,y)y=-b=0,
(3)
其中
式中,E为弹性模量,G为剪切模量,I为截面抗弯惯性矩,Is为顶、底板抗弯惯性矩之和,Q(x)为截面剪力.
由于![]() 的结果是关于x的函数,所以整理式(2)可得
的结果是关于x的函数,所以整理式(2)可得
(4)
式中,Φ(x)只是关于x的一个函数.
分析式(4)可知,由于该式的右端项只是关于x的函数,则左端的两项Efxx(x,y),Gfyy(x,y)关于y的项一定是被消掉了,而Efxx(x,y)项只是f(x,y)对x求了二阶导数,并没有对y进行求导,Gfyy(x,y)只是f(x,y)对y求了二阶导数,并没有对x进行求导.因此,需要构造的含y的项需要满足其二阶导数等于它本身,则f(x,y)一定含有ey项,同时,由于需要满足
f(x,y) y=b=f(x,y)
y=b=f(x,y) y=-b,
y=-b,
即f(x,y)为偶函数,所以f(x,y)的形式中含有coshy=(ey+e-y)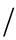 2项,即f(x,y)的形式可表示为
2项,即f(x,y)的形式可表示为
f(x,y)=φ(x)coshy,
(5)
式中,φ(x)只是关于x的一个函数.
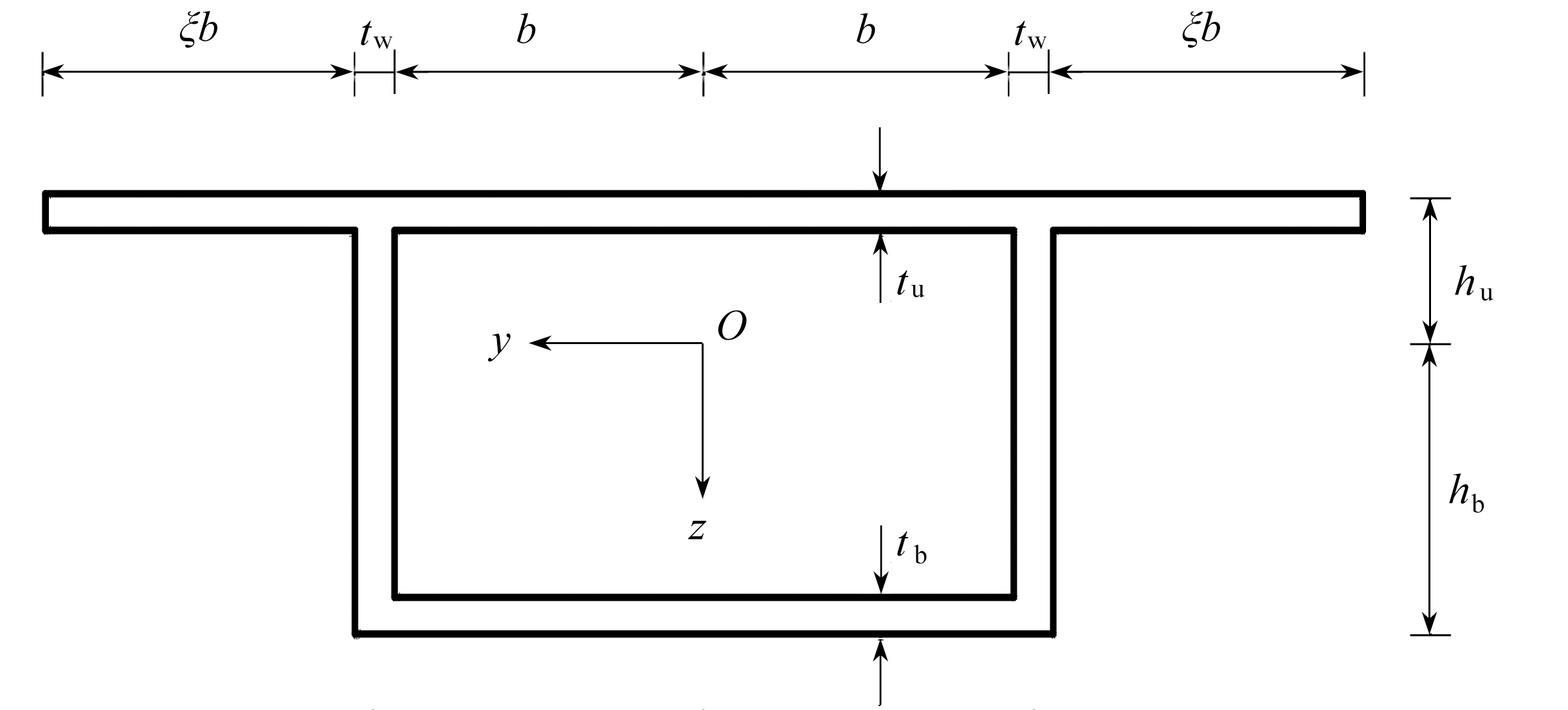
图2 箱形梁横截面图
Fig. 2 The cross section diagram of box girder
根据文献[12]中式(26)的形式,在沿桥纵向剪力Q(x)的分布作用下,考虑到g(y) y=b=g(y)
y=b=g(y) y=-b=0,g(y)
y=-b=0,g(y) y=0=1.因此,可以构造出如下的剪力滞翘曲位移函数,即
y=0=1.因此,可以构造出如下的剪力滞翘曲位移函数,即
(6)
综上分析,同时考虑翼板边界约束的影响,可将如图2所示带翼板的箱形梁剪力滞翘曲位移函数选取如下:
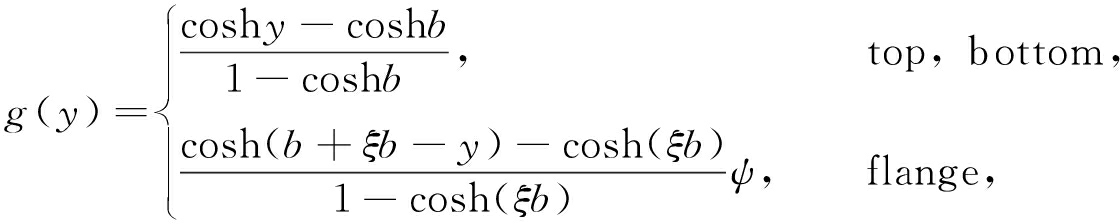
(7)
式中,ψ为考虑翼板边界约束影响的修正系数, 将在后面确定其具体数值,ξb为箱梁的翼板长度.
翘曲位移函数的选取是运用能量变分法求解剪力滞问题的核心,本文将采用式(7)所构造出的翘曲位移函数,利用能量变分法推导剪力滞控制微分方程及有关公式.首先,引入如下两个广义位移的概念,即梁的竖向挠度w(x)和纵向位移u(x,y),并表达为
w=w(x),
(8)
(9)
式中,U(x)为顶、底、翼板剪切转角的最大差值.
将式(7)代入式(9)可得纵向位移为
![]()
(10)
(11)
(12)
式中,uut(x,y)为顶板纵向位移,uuc(x,y)为翼板纵向位移,ub(x,y)为底板纵向位移.
箱梁截面顶、底、翼板纵向位移的横向分布如图3所示,图中uu(x,y)为顶、翼板纵向位移.
其次,基于最小势能原理对总势能变分建立控制微分方程.
梁受弯曲时的外力势能为
(13)
梁应变能的各项为如下:
腹板
(14)
顶、底、翼板
(15)
(16)
其中
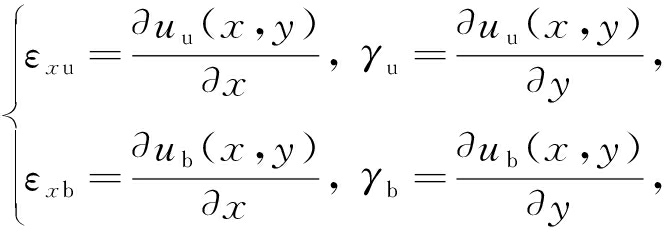
(17)
式中,M(x)为箱梁横截面的弯矩,Iw为腹板的抗弯惯性矩,εxu为顶、翼板的正应变,εxb为底板的正应变,γu为顶、翼板的剪应变,γb为底板的剪应变.
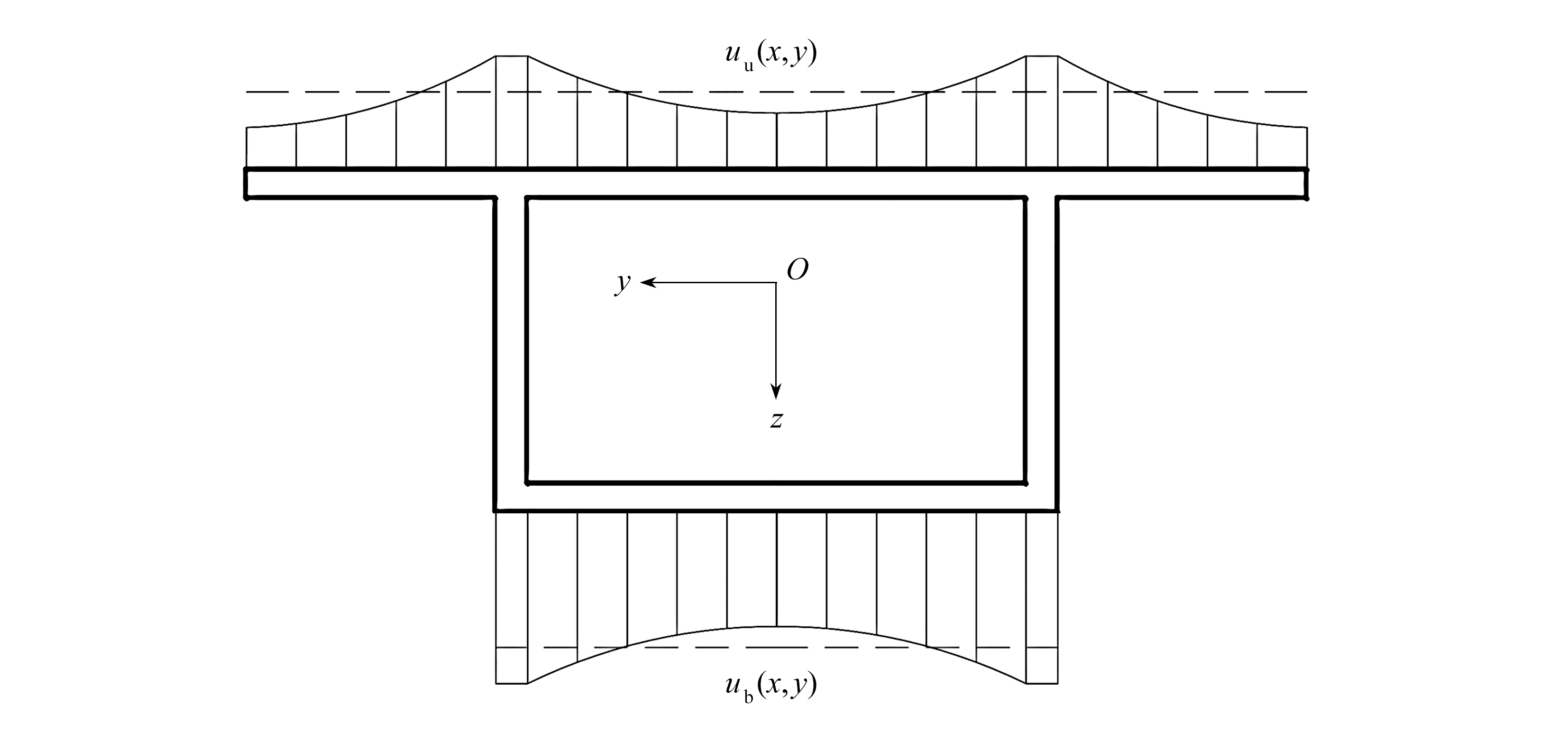
图3 顶、底、翼板纵向位移的横向分布
Fig. 3 Transverse distribution of the top, bottom and flange longitudinal displacements
将式(10)~(12)代入式(17)中,然后将得到的式子代入式(15)、(16)得
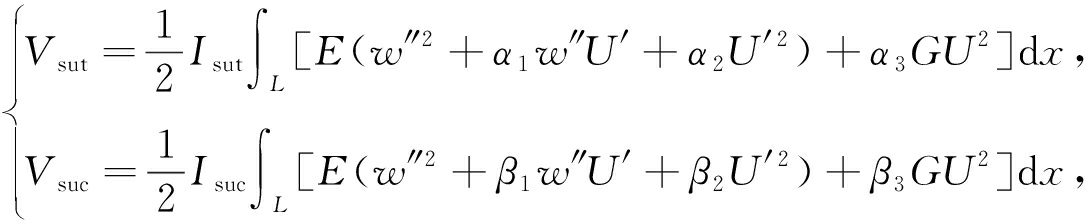
(18)
(19)
其中
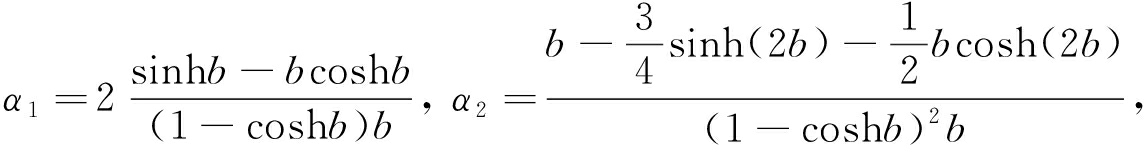
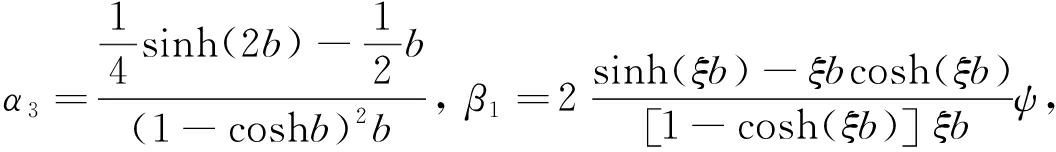
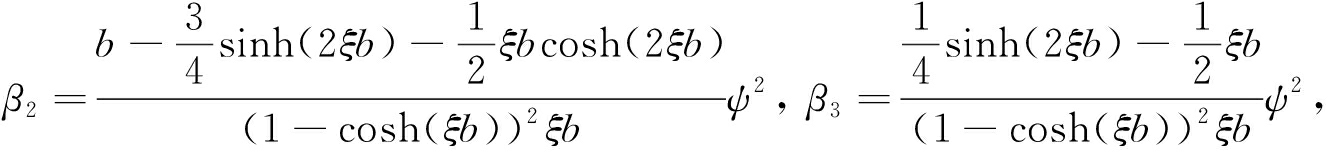
式中,Vsut为顶板的应变能,Vsuc为翼板的应变能,Isut为顶板的抗弯惯性矩,Isuc为翼板的抗弯惯性矩,Isb为底板的抗弯惯性矩.
体系的总势能为
Π=W+Vw+Vsu+Vsb.
(20)
将式(13)、(14)、(18)、(19)代入式(20)(其中Vsu=Vsut+Vsuc)得体系总势能为
(21)
其中
Is=Isut+Isuc+Isb,I=Iw+Is,
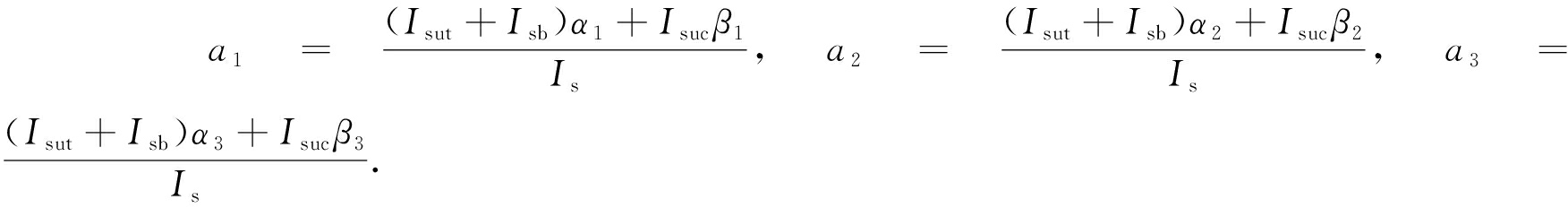
由最小势能原理得δΠ=0,则
(22)
由式(22)可得如下微分方程及对应的边界条件:

(23)
整理式(23),得到如下控制微分方程:
(24)
(25)
其中
式中,n,k为修正的Reissner参数.
式(24)解的一般形式为
(26)
式(26)中U*为仅与剪力Q(x)分布有关的特解,系数c1,c2由边界条件确定.
边界条件:
固定端
U=0, δU=0;
非固定端
![]() =0.
=0.
最后,考虑剪力滞影响的顶、底、翼板弯曲正应力为
(27)
式中,hi=-hu或hi=hb.
如图4所示,等截面简支箱梁(带翼板)在集中荷载P(对称作用于箱梁的腹板上)的作用下,剪力和弯矩均为分段函数,如下:
式中![]()

图4 简支箱梁受集中荷载作用
Fig. 4 A simply supported box girder subjected to a concentrated load
当0≤x≤a时,
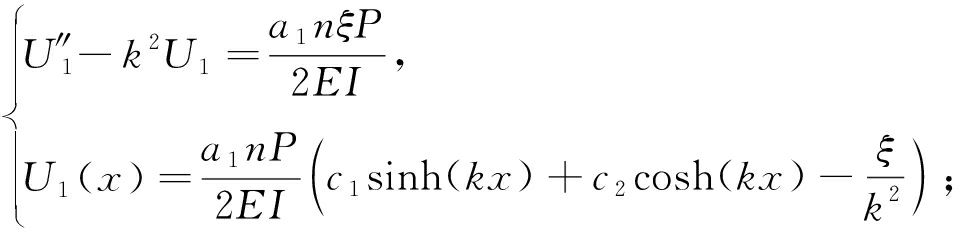
(28)
当a<x≤L时,

(29)
边界条件:![]()
在x=a点的变形连续条件U1=U2,以及变分要求在x=a点:
根据上面4个边界条件,可以求得系数c1,c2,c3及c4,从而可得
(30)
(31)
将式(30)代入式(27)得AC段顶、底、翼板的弯曲正应力:
(32)
将式(31)代入式(27)得CB段顶、底、翼板的弯曲正应力:
(sinh(ka)cosh(kx)-sinh(ka)coth(kL)sinh(kx)).
(33)
当集中力作用在跨中时,ξ=η=1/2,则顶、底、翼板的弯曲正应力为
σx=∓![]()
(34)
如图5所示,等截面简支箱梁(带翼板)在均布荷载q的作用下,剪力和弯矩分别为
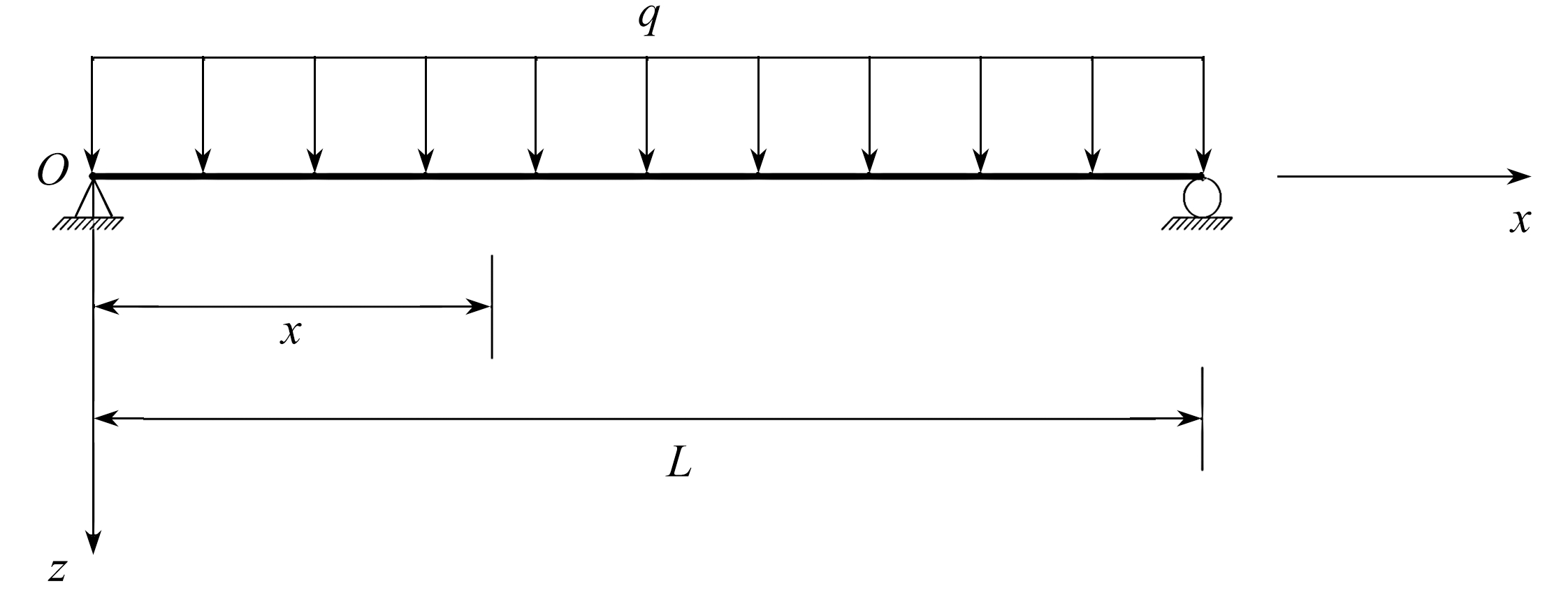
图5 简支箱梁承受均布荷载
Fig. 5 A simply supported box girder subjected to uniform load
剪力滞差值函数的微分方程为
(35)
其解为
(36)
则
(37)
由边界条件:![]() 得
得
将式(37)代入式(27),得顶、底、翼板的弯曲正应力:
σx=∓![]()
(38)
为确定ψ的值以及从数值上验证本文思想及推导结果的正确性,对带有翼板的简支箱梁分别作用集中荷载和均布荷载的情况进行算例分析.
选取计算跨径L=40 m的简支箱梁,截面尺寸及应力计算点位置如图6所示,在跨中截面梁顶腹板位置作用对称集中荷载,总值为P=2 000 kN.材料的弹性模量为E=30 GPa,Poisson(泊松)比为0.2.
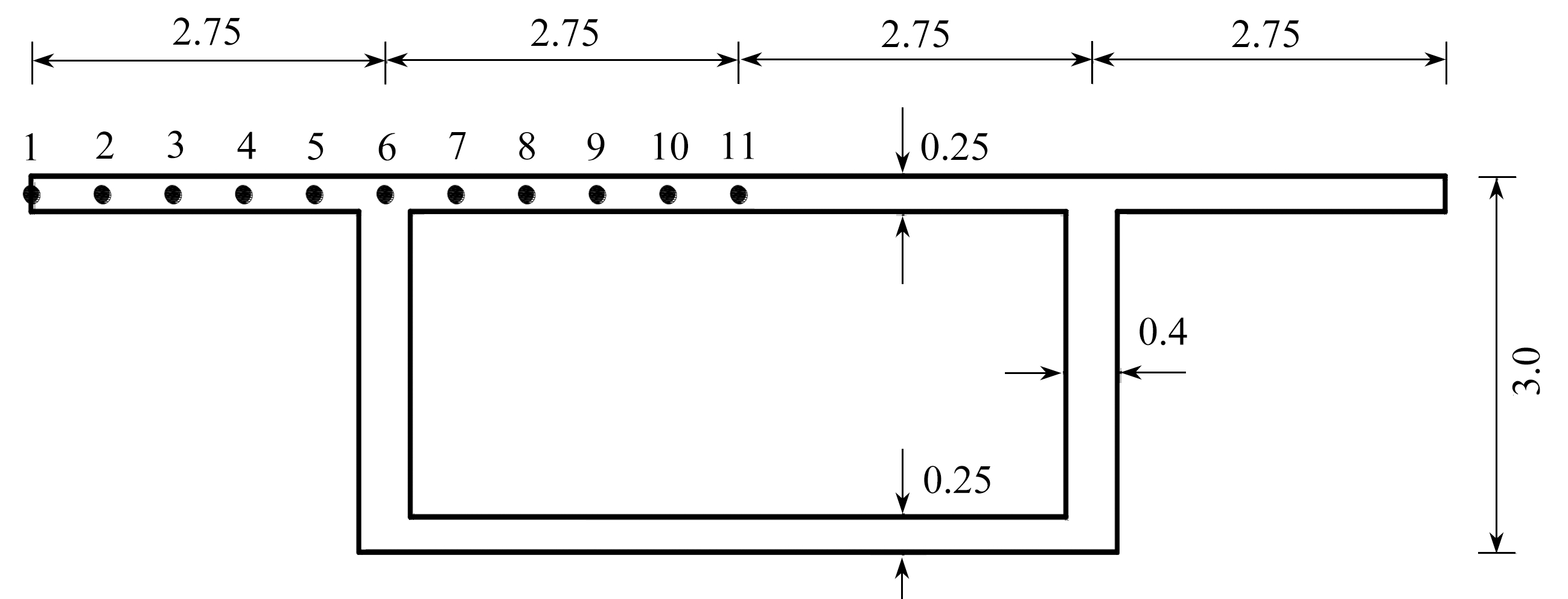
图6 截面尺寸(单位: m)
Fig. 6 The cross section sizes(unit: m)
为了确定ψ的值,采用文献[5]的思路,ψ从1.0开始,以0.1为步长,取到1.8.经过计算,当ψ为1.2时,本文计算的结果与ANSYS结果及按二次函数、三次函数计算所得结果总体吻合良好,如表1所示.
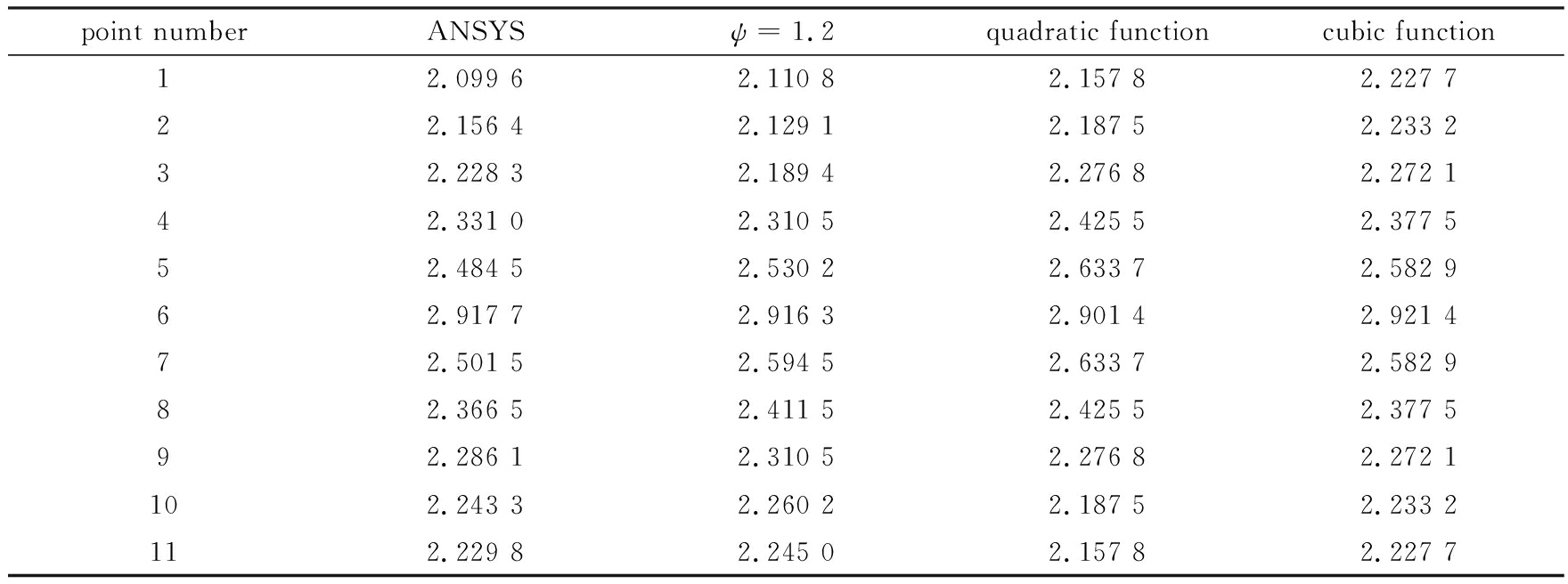
表1 跨中截面计算点应力比较(单位: MPa)
Table1 Comparison of calculation point stresses of the span center cross section(unit: MPa)
point numberANSYS ψ=1.2quadratic functioncubic function12.099 62.110 82.157 82.227 722.156 42.129 12.187 52.233 232.228 32.189 42.276 82.272 142.331 02.310 52.425 52.377 552.484 52.530 22.633 72.582 962.917 72.916 32.901 42.921 472.501 52.594 52.633 72.582 982.366 52.411 52.425 52.377 592.286 12.310 52.276 82.272 1102.243 32.260 22.187 52.233 2112.229 82.245 02.157 82.227 7
从表1可以看出,本文的应力结果反映出了翼板应力小于顶板应力的现象.按本文方法计算所得的应力值与ANSYS值相比,在顶板中心处的误差为0.68%,在顶板与腹板交接处的误差为0.05%.
1) 将5.1小节中的集中荷载改为满跨的均布荷载,荷载集度为q=2 000 N/m(该荷载对称作用于箱梁的腹板上),其余的参数均不变.
按本文方法计算时,ψ仍取为1.2.跨中截面各计算点按本文方法求得的应力值与ANSYS值及翘曲位移函数按二次函数、三次函数求得的应力值列于表2.
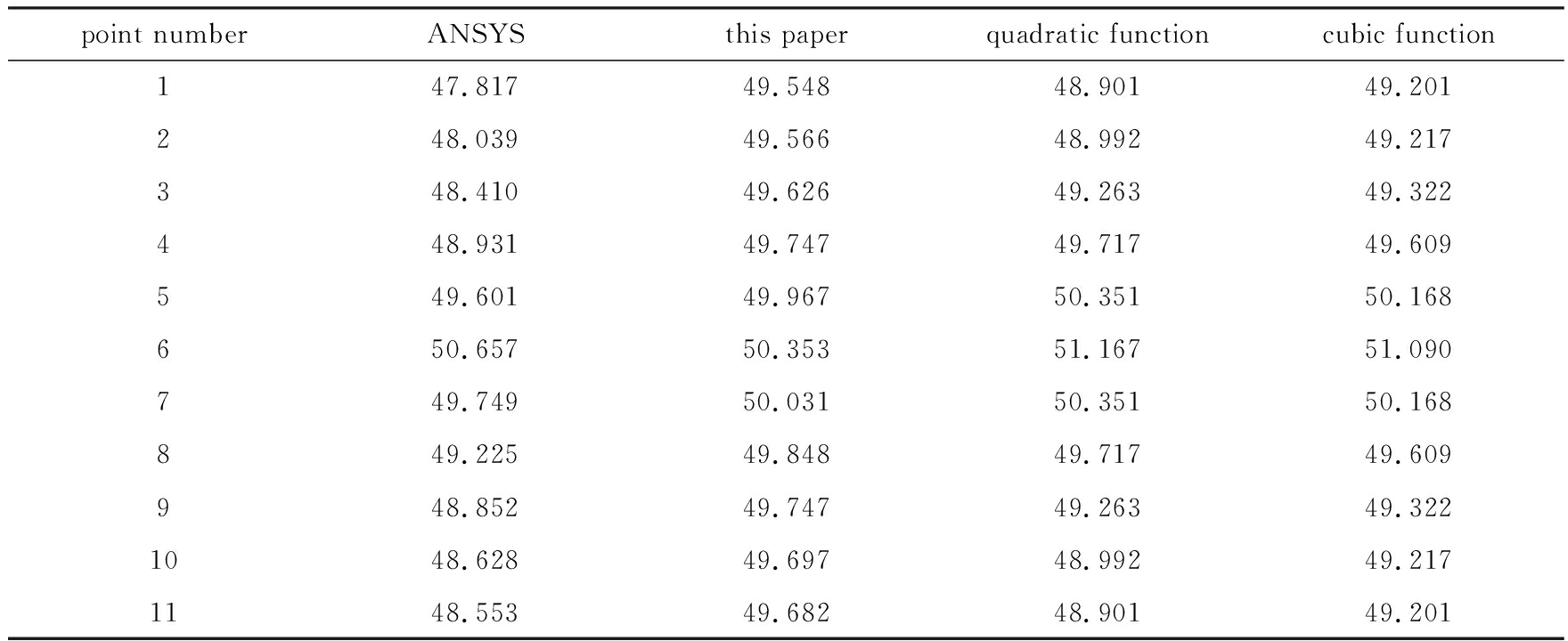
表2 跨中截面计算点应力比较(单位: kPa)
Table 2 Comparison of calculation point stresses of the span center cross section(unit: kPa)
point numberANSYS this paperquadratic functioncubic function147.81749.54848.90149.201248.03949.56648.99249.217348.41049.62649.26349.322448.93149.74749.71749.609549.60149.96750.35150.168650.65750.35351.16751.090749.74950.03150.35150.168849.22549.84849.71749.609948.85249.74749.26349.3221048.62849.69748.99249.2171148.55349.68248.90149.201
由表2可以看出按本文方法求得的应力值与ANSYS值吻合良好,并且计算结果可以反映出翼板应力小于顶板应力的分布规律.按本文方法计算的应力值与ANSYS值相比,在顶板中心处的误差为2.33%,在顶板与腹板交接处的误差为0.60%.
2) 有一跨度L=800 mm的简支箱梁模型,截面尺寸及应力计算点位置如图7所示,集中荷载对称作用在跨中截面梁顶腹板位置,总值为P=272.2 N.材料的弹性模量为E=3 000 MPa,Poisson比为0.385.
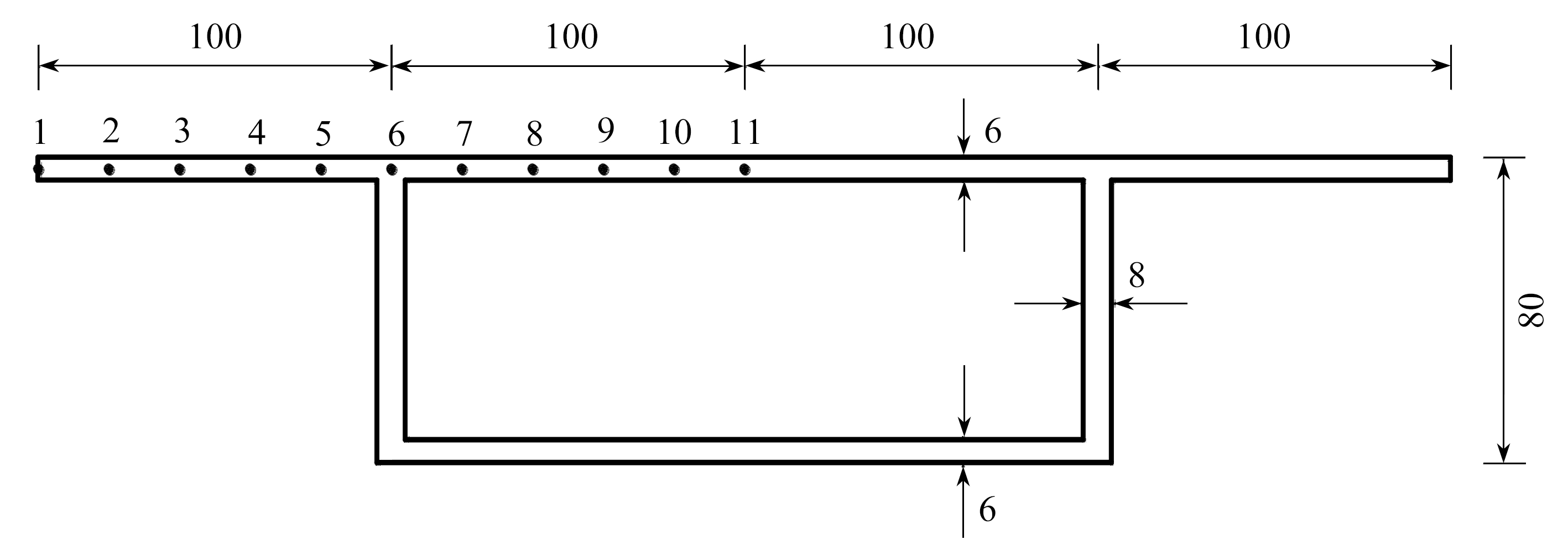
图7 截面尺寸(单位: mm)
Fig. 7 The cross section sizes(unit: mm)
按本文方法计算该简支箱梁模型的顶、底、翼板应力时,ψ仍取为1.2.为了验证本文方法的可靠性,跨中截面各计算点按本文方法求得的应力值与ANSYS值及翘曲位移函数按二次函数、三次函数求得的应力值绘制出应力分布曲线,如图8所示.
对图8的应力分布曲线进行对比分析可得,按本文方法求得的跨中截面顶、翼板应力的计算值与ANSYS结果总体上吻合良好.已有的文献中基本上未考虑翼板边界约束影响的修正系数,不能正确反映翼板应力的实际分布;而本文考虑了翼板边界约束影响的修正系数,因此,本文方法的结果很好地反映了翼板的真实应力分布状态.按本文方法计算的应力值与ANSYS值相比,在顶板中心处的误差为4.97%,在顶板与腹板交接处的误差为0.20%.
对常规截面形式的箱梁而言,按本文的方法分析及求解其剪力滞效应时,经过大量的算例可得翼板边界约束影响的修正系数可采用1.2.
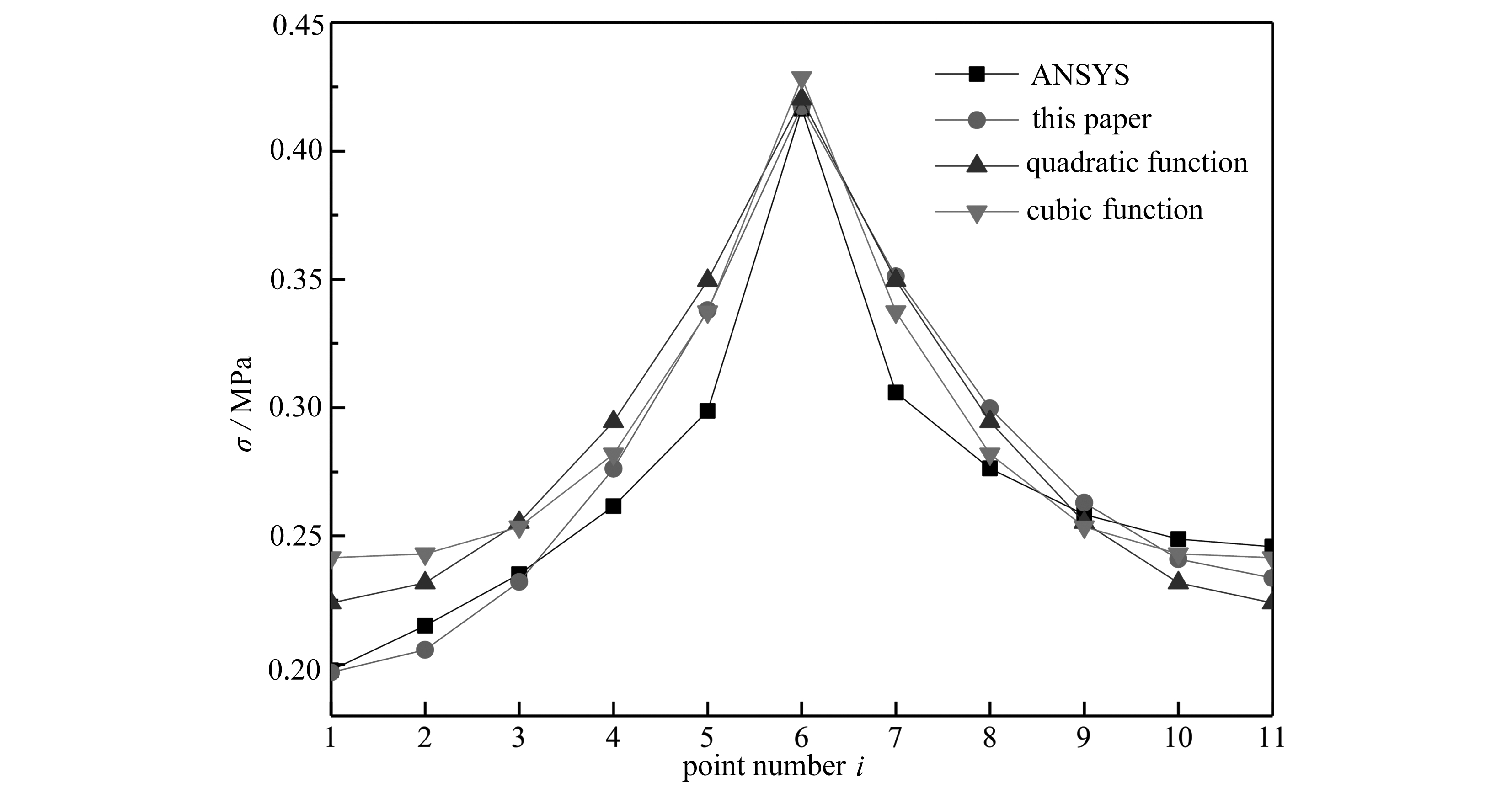
图8 箱梁跨中截面计算点应力分布曲线
Fig. 8 Stress distribution curves for calculation points of the span center cross section of the box girder
1) 在求解箱形梁剪力滞问题时,以往文献直接假定剪力滞翘曲位移函数的形式;而本文从剪力滞控制微分方程的形式出发,通过对微分方程形式的分析,构造出了剪力滞翘曲位移函数及基本形式,然后利用能量变分法推导出了相应的公式.
2) 以带翼板的箱梁分别作用集中荷载与均布荷载为数值算例,按本文方法计算得到的剪力滞结果与有限元结果及其他位移函数计算结果进行对比分析,发现按本文方法计算的结果与有限元结果吻合良好,并且本文结果能够反映出翼板应力小于顶板应力的分布规律,从而验证了本文方法的合理性.
3) 本文算例表明,采用不同的位移函数进行剪力滞分析时,得到的结果虽然分布趋势接近,但数值上仍有较大差别,所以说剪力滞问题的分析受翘曲位移函数形式的较大影响,因此,如何选取翘曲位移函数是分析剪力滞问题的核心.
4) 由本文的算例可知,按本文方法计算的应力值与ANSYS值相比,在顶板中心处和顶板与腹板交接处的误差均未超过5%,在顶板与腹板交接处的误差较小.
[1] 郭金琼, 房贞政, 郑振. 箱形梁设计理论[M]. 北京: 人民交通出版社, 2008.(GUO Jinqiong, FANG Zhenzheng, ZHENG Zhen.Design Theory of Box Girder[M]. Beijing: China Communications Press, 2008.(in Chinese))
[2] 倪元增, 钱寅泉. 弹性薄壁梁桥分析[M]. 北京: 人民交通出版社, 2000.(NI Yuanzeng, QIAN Yinquan.Elastic Analysis of Thin-Walled Beam Bridges[M]. Beijing: China Communications Press, 2000.(in Chinese))
[3] 张士铎, 邓小华, 王文州. 箱形薄壁梁剪力滞效应[M]. 北京: 人民交通出版社, 1998.(ZHANG Shiduo, DENG Xiaohua, WANG Wenzhou.Shear Lag Effect in Box Girders[M]. Beijing: China Communications Press, 1998.(in Chinese))
[4] 李丽园, 周茂定, 张元海. 薄壁箱梁的弯曲纵向位移函数与剪力流[J]. 中南大学学报(自然科学版), 2015,46(10): 3928-3935.(LI Liyuan, ZHOU Maoding, ZHANG Yuanhai. Longitudinal displacement function and shear flow of thin-walled box girders in bending[J].Journal of Central South University(Science and Technology), 2015,46(10): 3928-3935.(in Chinese))
[5] 张元海, 胡玉茹, 林丽霞. 基于修正翘曲位移模式的薄壁箱梁剪力滞效应分析[J]. 土木工程学报, 2015,48(6): 44-50.(ZHANG Yuanhai, HU Yuru, LIN Lixia. Analysis on shear lag effect of thin-walled box girder based on a modified warping displacement mode[J].China Civil Engineering Journal, 2015,48(6): 44-50.(in Chinese))
[6] REISSNER E. On the problem of stress distribution in wide-flanged box-beam[J].Journal of the Aeronautical Sciences, 1938,5(8): 295-299.
[7] 蔺鹏臻, 周世军. 基于剪切变形规律的箱梁剪力滞效应研究[J]. 铁道学报, 2011,33(4): 100-104.(LIN Pengzhen, ZHOU Shijun. Analysis on shear-lag effect of box girders based on flange-slab shear deformation law[J].Journal of the China Railway Society, 2011,33(4): 100-104.(in Chinese))
[8] 郭金琼, 房贞政, 罗孝登. 箱形梁桥剪滞效应分析[J]. 土木工程学报, 1983,16(1): 1-3.(GUO Jinqiong, FANG Zhenzheng, LUO Xiaodeng. Analysis of shear lag effect in box girder bridges[J].China Civil Engineering Journal, 1983,16(1): 1-3.(in Chinese))
[9] 张元海, 白昕, 林丽霞. 箱形梁剪力滞效应的改进分析方法研究[J]. 土木工程学报, 2012,45(11): 153-158.(ZHANG Yuanhai, BAI Xin, LIN Lixia. An improved approach for analyzing shear lag effect of box girders[J].China Civil Engineering Journal, 2012,45(11): 153-158.(in Chinese))
[10] LIN Z B, ZHAO J. Revisit of AASHTO effective flange-width provisions for box girders[J].Journal of Bridge Engineering, 2011,16(6): 881-889.
[11] 罗旗帜. 薄壁箱形梁剪力滞计算的梁段有限元法[J]. 湖南大学学报, 1991,18(2): 33-38.(LUO Qizhi. Calculation of the shear lag in thin walled box girders by the finite segment method[J].Journal of Hunan University, 1991,18(2): 33-38.(in Chinese))
[12] CHEN J, SHEN S L, YIN Z Y, et al. Closed-form solution for shear lag with derived flange deformation function[J].Journal of Constructional Steel Research, 2014,102: 104-110.
[13] LUO Q Z, WU Y M, LI Q S, et al. A finite segment model for shear lag analysis[J].Engineering Structures, 2004,26(14): 2113-2124.
[14] ZHOU S J. Finite beam element considering shear-lag effect in box girder[J].Journal of Engineering Mechanics, 2010,136(9): 1115-1122.
[15] 甘亚南, 周广春. 薄壁箱梁纵向剪滞翘曲函数精度选择的研究[J]. 工程力学, 2008,25(6): 100-106.(GAN Yanan, ZHOU Guangchun. An approach for precision selection of longitudinal shear lag warping displacement function of thin-walled box girders[J].Engineering Mechanics, 2008,25(6): 100-106.(in Chinese))
[16] 陈常松, 邓安. 高次位移函数时箱梁剪滞效应变分法解[J]. 重庆交通大学学报(自然科学版), 2009,28(1): 5-7.(CHEN Changsong, DENG An. Variational solution of shear lag effect of box girder in high order displacement function[J].Journal of Chongqing Jiaotong University(Natural Science), 2009,28(1): 5-7.(in Chinese))
[17] 韦成龙, 曾庆元, 刘小燕. 薄壁箱梁剪力滞分析的多参数翘曲位移函数及其有限元法[J]. 铁道学报, 2000,22(5): 60-64.(WEI Chenglong, ZENG Qingyuan, LIU Xiaoyan. Warping displacement function and finite element method for calculation of shear lag effect in box girder[J].Journal of the China Railway Society, 2000,22(5): 60-64.(in Chinese))
[18] 徐飞鸿, 蔡汶珊. 薄壁箱梁剪力滞效应数值计算[J]. 长沙理工大学学报(自然科学版), 2009,6(4): 16-20.(XU Feihong, CAI Wenshan. Numerical calculation on shear lag effect of thin-walled box girder[J].Journal of Changsha University of Science and Technology(Natural Science), 2009,6(4): 16-20.(in Chinese))