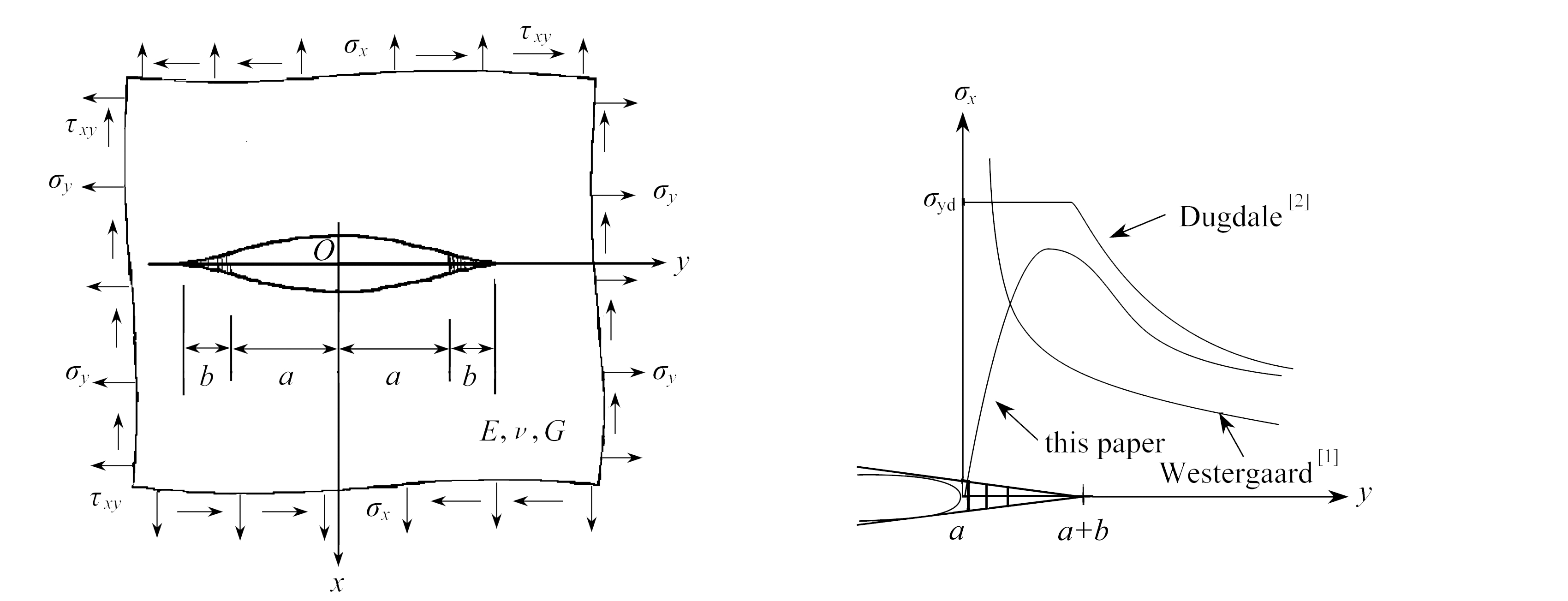
图1 基本问题 图2 内聚区应力分布
Fig. 1 The considered problem Fig. 2 Stress distribution near the crack tip by past studies
对于如图1所示的中心裂纹板弹性平面问题,其解析函数可分为Westergaard[1]的奇异解和以Dugdale模型[2]为代表的内聚区有限应力集中解两大类,如图2所示,其中a为裂纹半长,b为内聚区长度.Barenblatt[3]第一次在主裂纹尖端引入了一原子内聚区,并将其定义为有相互作用力而结合在一起的两平面分离的数学物理模型,即σ=σ(δ),其中σ为内聚力(或称为分子结合力),δ为内聚裂纹宽度(内聚区张开位移),但并不能直接应用于材料破坏强度的评定.Dugdale解中内聚区的内聚应力是恒定的,与张开位移无关,所以只适用于理想刚塑性的情形.理论上Dugdale模型的解可以对荷载的积分求得,但由于积分上的困难,目前用这种方法得到的解析解仅限于内聚区内聚力为恒定[4-5]、内聚力为线性分布[6-7]或线性软化关系[8]等几种简单的情形.
20世纪60年代开始的混凝土、岩石断裂损伤研究与应用促进了对Dugdale模型的再认识和进一步发展.Hillerborg提出了虚裂纹模型(fictitious crack model,简称FCM)[9],其特征是内聚区内的内聚力随张开位移的增大而减小,并把这一区域称为断裂过程区.Bazant等提出了钝裂纹带模型(blunt crack band model, 简称BCM)[10].Elices等[11]于2002年对内聚区模型的研究状况进行了较为全面的综述,强调这一模型的核心是材料软化功能的确定;这一模型可应用于混凝土、PMMA和钢等材料的断裂损伤分析,只是其材料的软化特性不同.由于断裂过程区复杂的拉应变软化特性,这些模型都没有给出相应的解析方法.
目前一般仍采用试件破坏试验与数值分析相结合的方法确定断裂能和拉应变软化曲线等断裂参数,如文献[12-19].
另一方面,基于内聚裂纹模型的概念,对裂纹长度进行加权积分可以在裂纹尖端构成一有限应力集中与张开位移相并存过程区的全场解析函数[6,19].这一方法已经应用于单材料裂纹[6,20-32]和双材料界面裂纹的各种受力问题[33-40].本文对这一系列研究进行综述,并回答作为解析函数如何回避裂纹尖端应力奇异性的问题.

图1 基本问题 图2 内聚区应力分布
Fig. 1 The considered problem Fig. 2 Stress distribution near the crack tip by past studies
以一中心裂纹长度为2a的无限大板为例,Westergaard解的应力分量主项用无理函数表示为![]() 其中复数z=x+iy.此函数在z=±ia两个点奇异,导致了无限大应力的产生.
其中复数z=x+iy.此函数在z=±ia两个点奇异,导致了无限大应力的产生.
由
(1)
定义
(2)
可以将上述应力函数的无理函数型式转换为指数函数的型式:
(3)
笔者在过去的系列研究中提出了以奇异解作为基本函数,对裂纹长a进行积分,在裂纹尖端构造有限连续应力集中解的方法,其中一种是对无理函数中的参数a进行直接加权积分的方法;另一种是对指数部h(z,a)进行间接加权积分的方法.
本文以2次式的权函数为例,采用
(4)
构造应力函数,其中,变量t代替了裂纹长度a,ρ(t)为面积为1的权函数.
对于指数部h(z,a)项进行加权积分,即定义
H(z,t1,t2)=![]() ρ2(t,t1,t2)h(z,t)dt.
ρ2(t,t1,t2)h(z,t)dt.
(5)
结果为
H(z,a,a+b)=f(z,z1,z2)-f(z,-z2,-z1),
(6)
其中,z1=ia,z2=i(a+b)分别为裂纹尖端和过程区尖端的坐标.
f(z,z1,z2)=g1(z,z1,z2)-g1(z,z2,z1)+g2(z,z1,z2),
9(z2-z1)(z-z2)(z-z1),
式中,随着z增大,当6a<|z|时,其计算结果精度变差.可以作如下变换提高计算精度:
(7)
其中,ξ=z-(ζ1+ζ2)/2,β=(ζ1-ζ2)/2.得到的H(z)的实部和虚部曲面分别如图3(a)和3(b)所示.在图3中,裂纹长度2a=2,过渡区长度(对奇异点加权积分区间)b=0.4,作图范围为4×4(x,y=±2).

(a) 实部 (b) 虚部
(a) The real part(b) The imaginary part
图3 函数H(z)
Fig. 3 FunctionH(z)
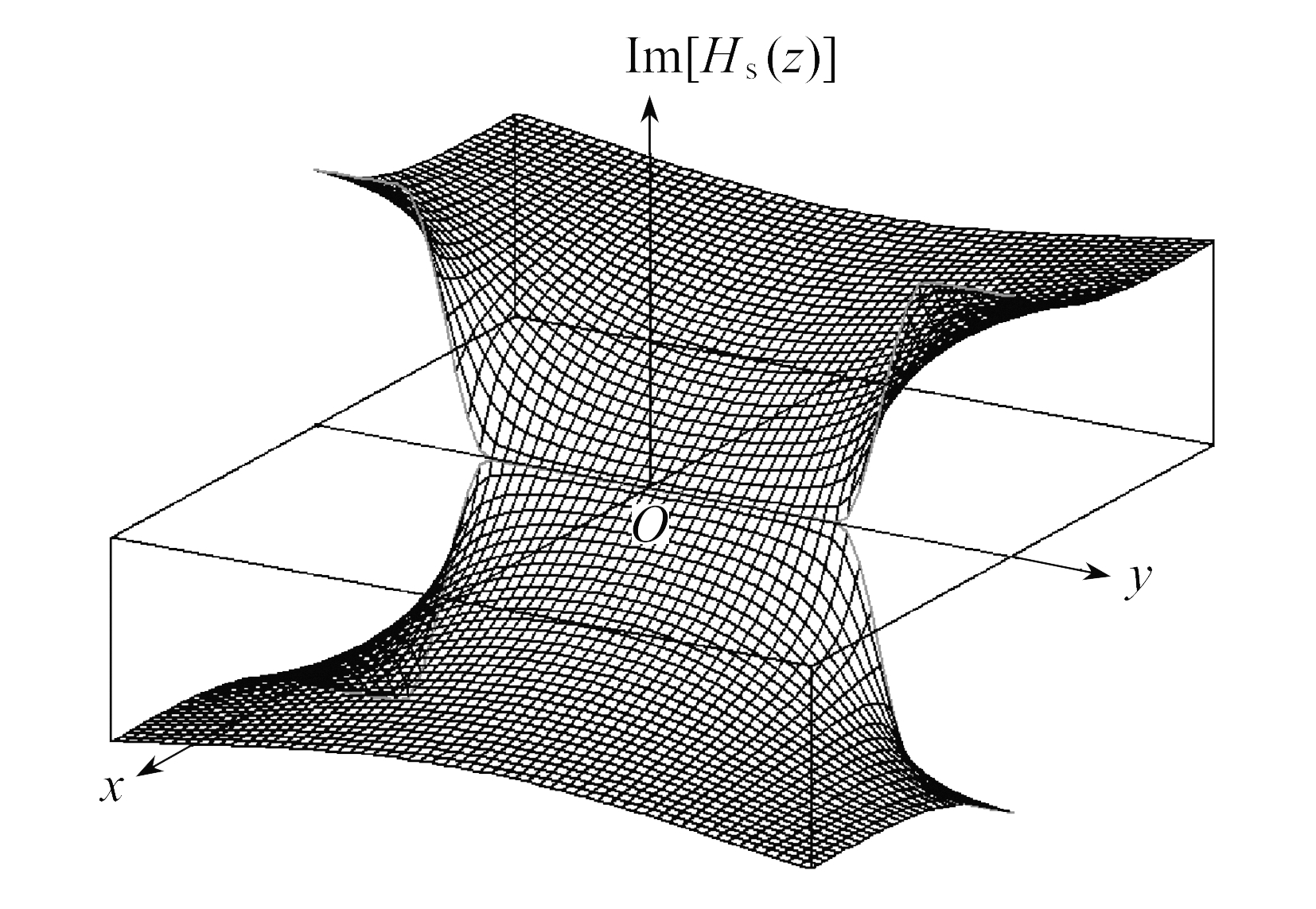
图4Hs(z)的虚部曲面
Fig. 4 The imaginary curve of functionHs(z)
从图3(a)中可以看出,实部曲面上,对数函数的无穷大值支点由于加权积分转换为光滑连续曲面,这是由于在y轴上对距离为2a平行移动的对数曲面实部的差进行积分的结果;随着远离原点,其值趋近于零而不会发散.虚部曲面上(图3(b)),台阶间呈现为光滑有限斜率的坡形过渡.可以这样解释:对数的奇点为±2π周期的螺旋式循环,本文定义的h(z,a)中,冠以了1/2的系数,故在奇异点y=±a呈互减形式,经过加权积分,沿|y|<a线上,仍然构成了±π/2的开口;当|y|>a+b时其值为零即连续;而在a<|y|<a+b形成了光滑连续有限斜率的张开位移.利用这一特性在真实裂纹尖端和连续部分间构成了一有限内聚力集中与光滑有限斜率张开位移相并存的过程区.
如果取
Hs(z,a,a+b)=
H(z,a,a+b)+iπ/2,
(8)
即可构成在y轴上|y|<a连续的双边对称切口(有限连续)无限大板问题的基本解析函数,如图4所示.
下面就函数H(z,a,b)的奇异点进行讨论.由于对数函数h(z,a)为多值函数,故会形成多叶曲面.移动分支奇异点的加权积分实现了曲面的平滑,即在y轴上的区间a<|y|<a+b将双重曲面连接在一起.为了形象地表示这种情况,取式(6)中的函数f((z,ia,i(a+b)),即极点y=a和y=a+b被平滑的函数予以展示,如图5所示.
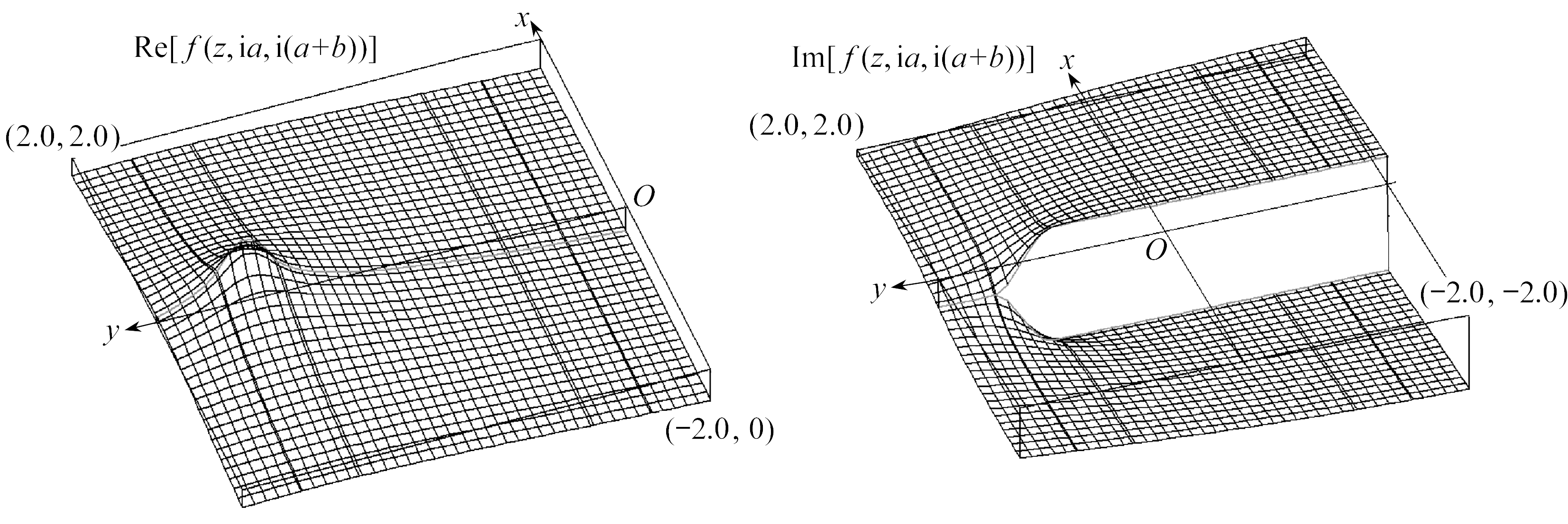
(a) 实部 (b) 虚部
(a) The real part(b) The imaginary part
图5 函数f(z,ia,i(a+b))
Fig. 5 Functionf(z,ia,i(a+b))
图5显示出H(z)是由其曲面在y轴上平行移动并取差值构成的.对数函数的极点被平滑了,并随着z增大函数收敛.函数分支平行于x轴,曲面在区间a<|y|<a+b从0<x区域一侧进入x<0区域一侧的连续曲面,如图6所示.
一般让y轴上产生分支,即在y轴上形成裂纹而不会有曲面的相互侵入.因为此域对数函数的虚部以螺旋式增加,其Riemann(黎曼)曲面的函数值也会随之增加.y轴上区间a<|y|<a+b函数各项的值正负交替形成连接曲面,而在积分区间的两端构成无穷远处的支点.也就是说,多连通曲面是具有发散极点的曲面,本文只是将曲面限定在一定的域内,没有利用不良曲面部分.
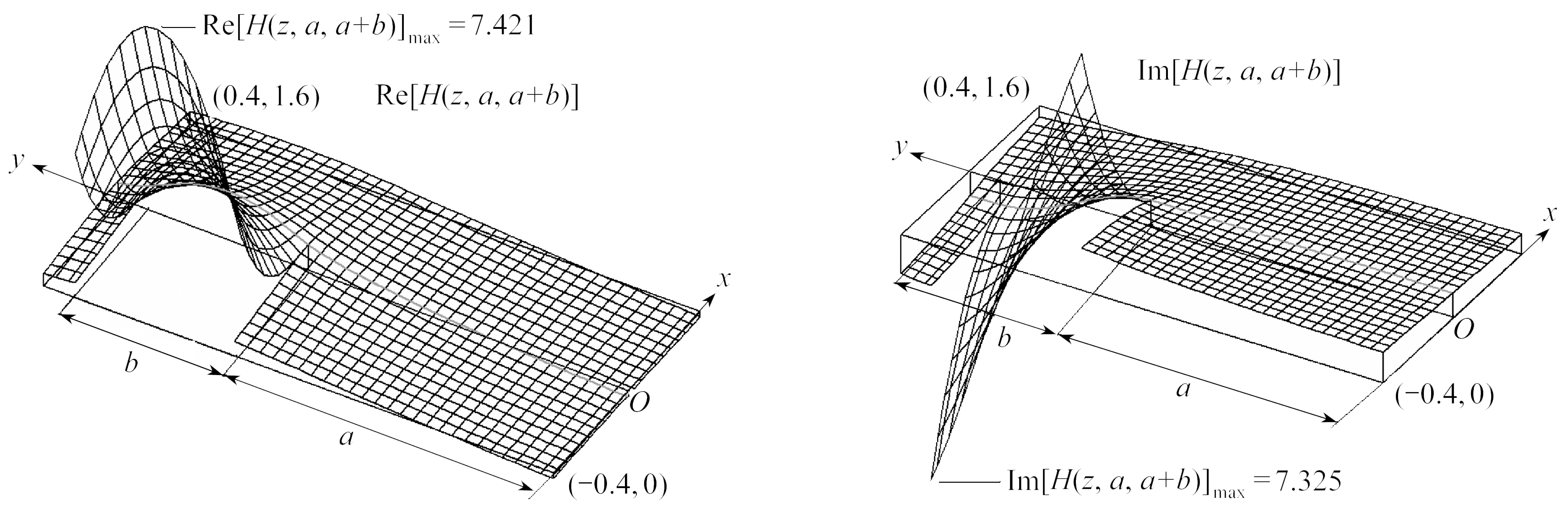
(a) 实部 (b) 虚部
(a) The real part(b) The imaginary part
图6 沿y轴的函数H(z)
Fig. 6 FunctionH(z) along they-axis
对象为一无限大板,平面内受力,沿y轴有一中心裂纹或有限连续(对称边裂纹),取应力函数的一般形式为
(9)
基于式(3),用H(z,a,a+b)替代h(z,a),并简略用H(z)表示.
下面分别给出中心裂纹在张开、滑开、zOy面弯曲、zOx面弯曲作用下的应力函数.
1) 张开型(图7(a))
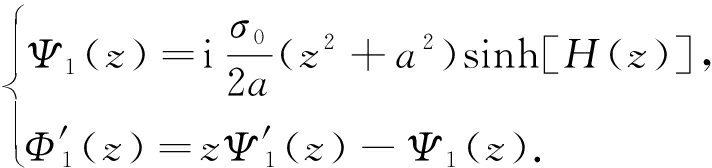
(10)
2) 滑开型(图7(b))[33]

(11)
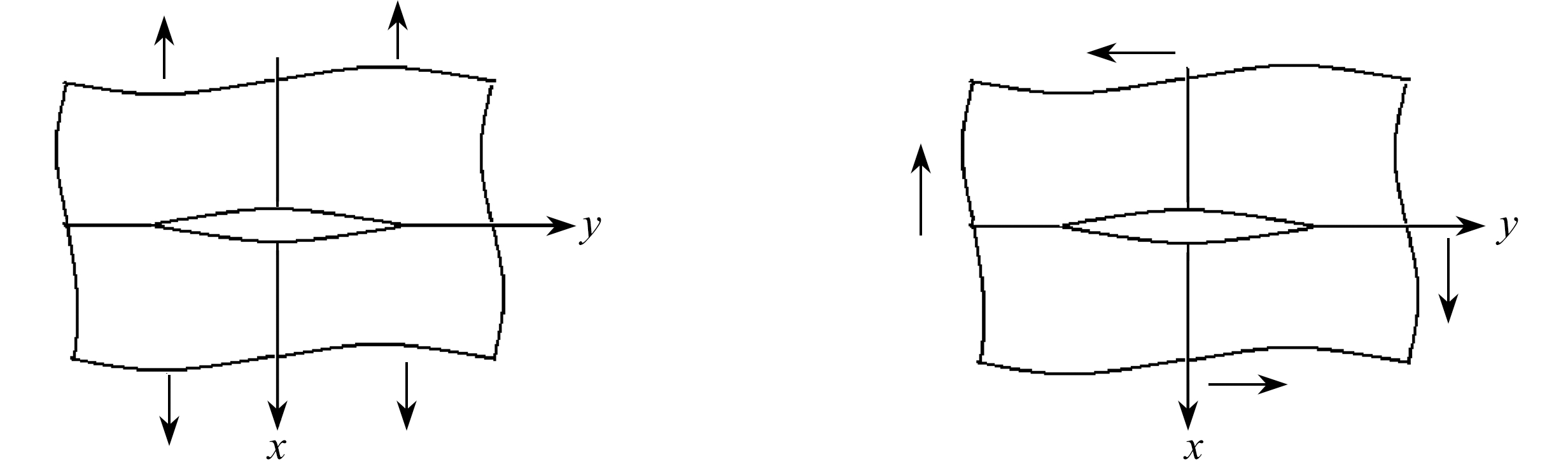
(a) 拉伸 (b)剪切
(a) Tension(b) Shear

(c)zOy面弯曲(d)zOx面弯曲
(c) Bending in thezOy surface(d) Bending in thezOx surface
图7 各种受力形式的中心裂纹板
Fig. 7 A central crack under different loads
3)zOy面弯曲(图7(c))
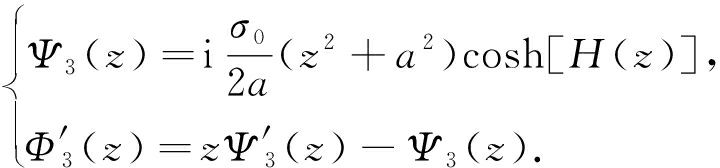
(12)
4)zOx面弯曲(图7(d))
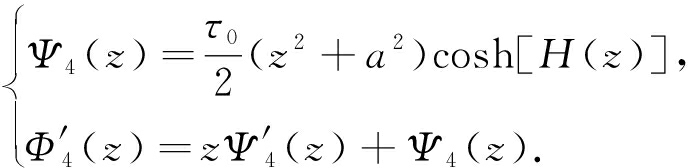
(13)
中间连续对称边裂纹(有限连续)问题的解由2.1小节中心裂纹解的虚数部分构成.解析函数的实数部分与虚数部分为相互共轭的正交函数,应力分布存在非对称关系而可以互换,其解可由函数Hs(z)构成如下:
1)zOy面弯曲(图8(a))
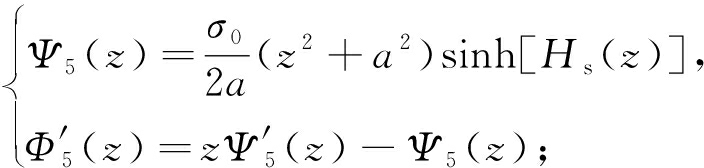
(14)
2)zOx面弯曲(图8(b))
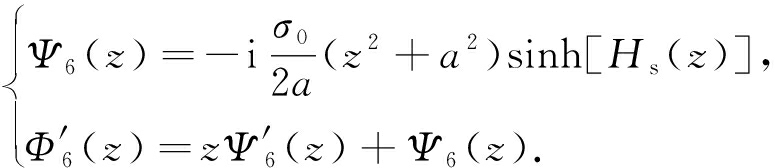
(15)
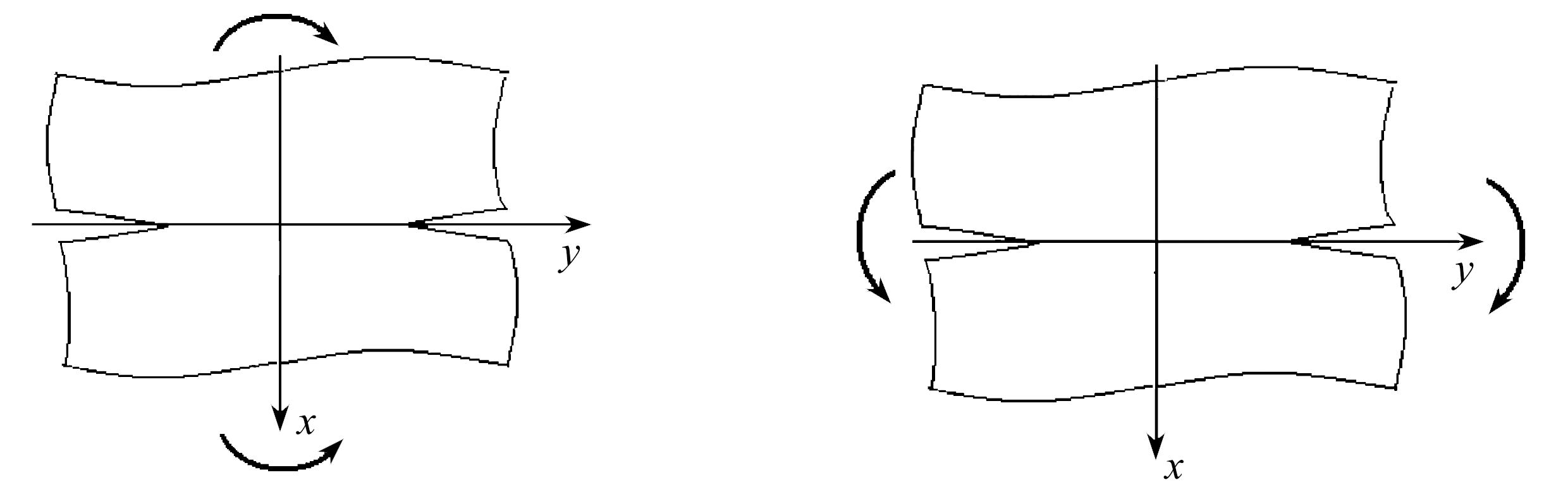
(a)zOy面弯曲(b)zOx面弯曲
(a)Bending in thezOy surface(b) Bending in thezOx surface
图8 各种受力形式的有限连续板
Fig. 8 Edge-cracks under different loads
对函数
(16)
进行直接积分
(17)
即有
(18)
其中
f21(z,a,b1)=b1[(z+ia+ib1)5/2+(z+ia)5/2]+
(i4/7)[(z+ia+ib1)7/2-(z+ia)7/2],
f22(z,a,b2)=b2[(z-ia-ib2)5/2+(z-ia)5/2]-
(i4/7)[(z-ia-ib2)7/2-(z-ia)7/2].
式(16)的无理函数构成双重曲面,由加权积分平滑的双重曲面,当z→∞时发散,但同种曲面只在区间b平行移动取其差值形成了复杂的4重曲面,曲面偏移且值翻番.与前述的H(z)函数相同,只是利用了过渡区间有限梯度光滑连接其他曲面而不相互侵入的特性,实现了值的有限连续.
构造应力函数如下:
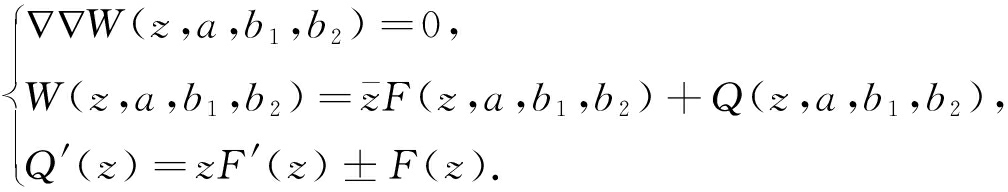
(19)
这样,其实部和虚部都可以构成为裂纹尖端有限应力集中和尖劈型张开位移相并存过程区的应力函数.权函数也可以取为4次式或6次式.
如图9所示的双材料y轴上界面裂纹,其界面双弹性常数α为
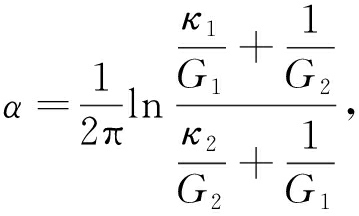
(20)
其中,E,G,ν为材料弹性常数,下标代表介质1或2;对平面应力问题,κ=(3-ν)/ (1+ν),对平面应变问题,κ=3-4ν.为避免繁杂,仍使用H和Hs分别表示中心裂纹和有限连续.
(21)
下面分别给出界面中心裂纹在拉伸、剪切、zOy面弯曲和zOx面弯曲下的基本解.
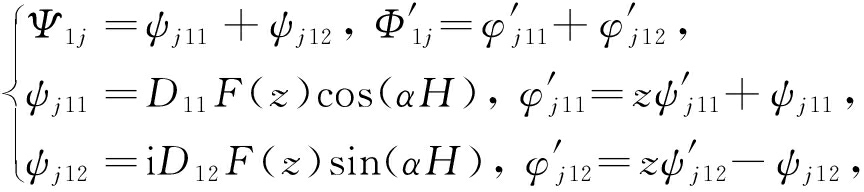
(22)
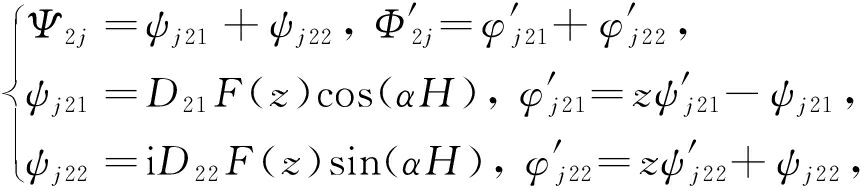
(23)

(24)

(25)

图9 界面中心裂纹
Fig. 9 A central crack at the interface
采用间接积分法[37-38,40]:
F(z)=znsinh[kH(z)]=zncosh[kH(z)],n=0,1,2,3…;k=1,3,5,….
(26)
参照式(17)进行积分,就可以得到裂纹尖端有限应力集中和尖劈型张开位移相并存过程区的应力函数,同时消除了裂纹尖端应力的奇异性和剧烈震荡现象[41-43],也无需引入非常小的接触区[44].
以上给出了4种受力下问题的解,其中D皆为任意常数,由界面上连续部分的位移连续条件确定.各函数项中的下标j=1代表x<0一侧,j=2代表x>0一侧.函数F(z)如式(26)的形式所示,k=1为一般形式;随着k值增大,过程区间的张开位移和内聚力将会出现周期性正负变动(原因为在y轴上,Re[H(z)]=k(±π/2)).但是,如果取足够多的函数进行叠加,就可以得到光滑连续的内聚力分布.式(26)所示,对无理函数直接积分得到的解可以满足界面裂纹的边界条件.如前所述,实函数和虚函数分别对应中心裂纹和有限连续,成对出现.
算例中,取E2/E1=10,ν1=0.1,ν2=0.3,物理裂纹长2a=2 cm,过程区长b=0.3 cm,由
F(z)=(z2+a2)sinh[H(z)]
和式(21)得到的位移和应力分布如图10所示.由于在函数F(z)只取了一项,所以在过程区及附近产生了不自然的波动.如果在式(26)中取多项k=1,3,5,…,并用最小二乘法或选点法进行平滑,就可以得到在过程区连续光滑的应力分布和尖劈状的张开位移,由于篇幅受限,本文予以省略,详见文献[36].
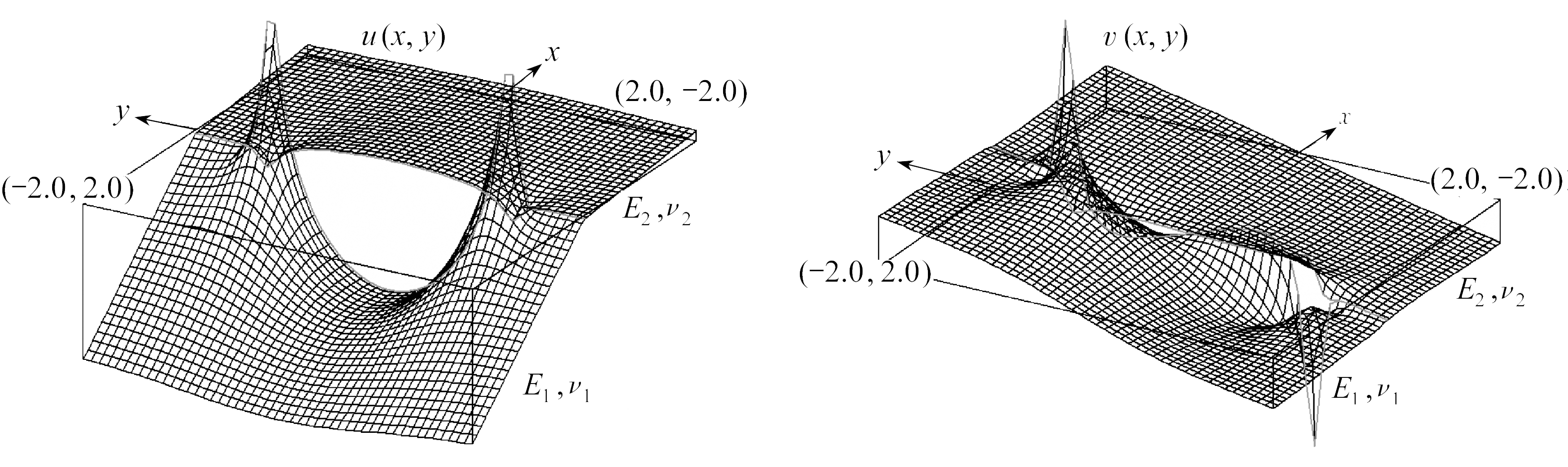
(a) 位移u(x,y)(b) 位移v(x,y)
(a) Displacementu(x,y)(b) Displacementv(x,y)
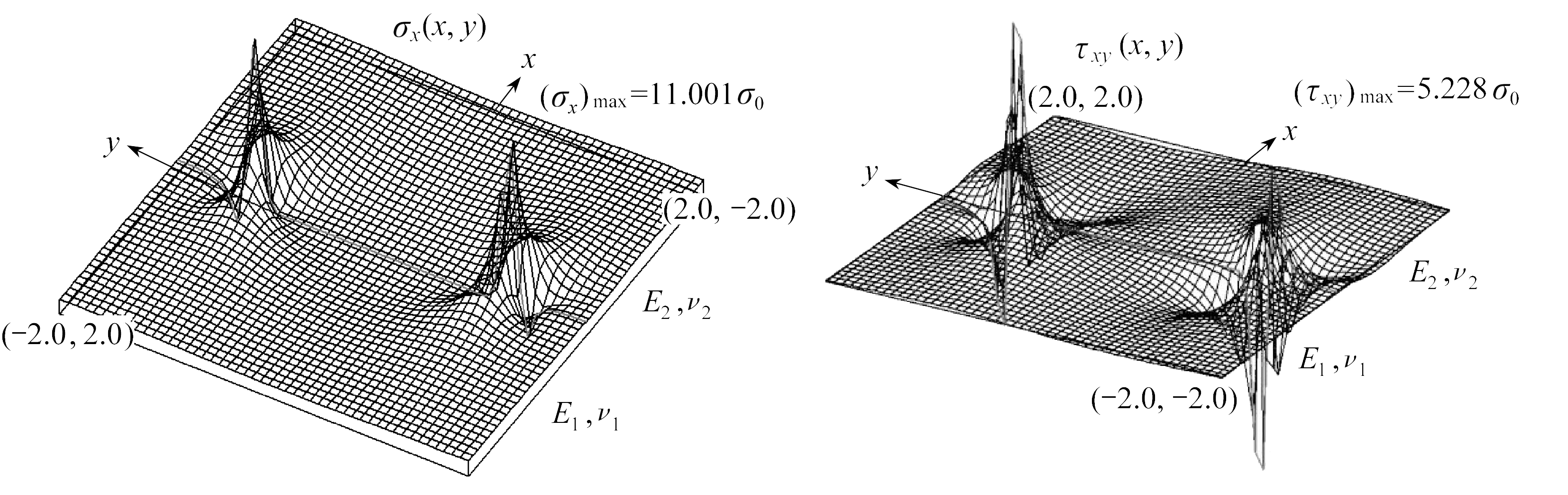
(c) 应力σx(d) 应力τxy
(c) Stressσx(d) Stressτxy
图10 算例: 张开位移与应力分布
Fig. 10 A numerical example: COD and stress distribution
对利用复变函数对数分支性质构成裂纹尖端区域有限内聚力分布的应力函数(重调和函数)的系列研究进行了综述. 这一方法不仅适用于单材料裂纹问题,同样也适用于双材料界面裂纹问题;还可以应用于直线上有多个裂纹的板的弯曲 [28]、在同一弧线上有多个裂纹的板[37-38] 等问题,两端的过程区长度可以对称或不对称.当然,这些分析都是从宏观的角度来处理裂纹尖端部分.得到如下结论:
1) 应力函数的构成方法分为直接积分法和间接积分法.直接积分法简单易行,适用于单材料裂纹问题的求解;而间接积分法结合最小二乘法或选点法可以得到满足精度要求的双材料界面裂纹问题的解.
2) 给出了中心裂纹和对称边裂纹在面内拉伸、剪切和弯曲等6种受力状态下的基本解.
3) 阐述了作为解析函数何以回避裂纹尖端应力奇异性的理由:奇异解采用的是复变函数的代数分支;而有限应力集中解由复变函数的对数分支与有理函数的积构成,这样就可以将奇异点从裂纹尖端移至无穷远处.
4) Dugdale模型解是由对荷载进行积分求得的,构成复杂,目前为止只有内聚力为恒定或线性分布两种特定的解析解;而本文的加权积分方法求解简单,可以给出一般解析解,特别适于表征混凝土、岩石等拉应变软化材料的损伤断裂特性.
5) 但是,本方法的解依赖于假定的权函数.一种可行的解决方法是:叠加有限个一般解析解,用选点法或最小二乘法满足内聚区的张开位移条件,从而得到满足内聚区变形特征的全场解析特解[32],而内聚区的变形特征是可以在实验室测得的量[45].
[1] WESTERGAARD H M. Bearing pressures and cracks[J].Journal of Applied Mechanics, 1939,6: 49-53.
[2] DUGDALE D S. Yielding of steel sheets containing slits[J].Journal of the Mechanics &Physics of Solids, 1960,8(2): 100-104.
[3] BARENBLATT G I. The formation of equilibrium cracks during brittle fracture, general ideas and hypotheses, axially-symmetric cracks[J].Journal of Applied Mathematics &Mechanics, 1959,23(3): 434-444.
[4] FERDJANI H, ABDELMOULA R. Propagation of a Dugdale crack at the edge of a half plate[J].Continuum Mechanics &Thermodynamics, 2018,30(8): 1-11.
[5] TONG D, WU X R. Analysis of crack opening stresses for center- and edge-crack tension specimens[J].Chinese Journal of Aeronautics, 2014,27(2): 291-298.
[6] 段树金, 儿岛弘行, 中川建治. 亀裂先端部分で有限な应力集中を与える应力関数[J]. 土木学会論文集, 1986,374: 399-407.(DUAN S J, KOJIAMA H, NAKAGAWA K. Stress functions with finite magnitude of stress concentration at crack tip[J].Proc JSCE, 1986,374: 399-407.(in Japanese))
[7] 王承强, 郑长良. 裂纹扩展过程中线性内聚力模型计算的半解析有限元法[J]. 计算力学学报, 2006,23(2): 146-151.(WANG Chengqiang, ZHENG Changliang. Semi-analytical finite element method for linear cohesive force model in crack propagation[J].Chinese Journal of Computational Mechanics, 2006,23(2): 146-151.(in Chinese))
[8] WU X, ANTHONY M W. Multiple solutions in cohesive zone models of fracture[J].Engineering Fracture Mechanics, 2017,177: 104-122.
[9] HILLERBORG A. Analysis of fracture by means of the fictitious crack model, particularly for fiber reinforced concrete[J].Endocrine Related Cancer, 1980,2(4): 177-184.
[10] BAZANT Z P, OHB H. Crack band theory for fracture of concrete[J].Matériaux et Construction, 1983,16(3): 155-177.
[11] ELICES M, GUINCA G V, G MEZ I, et al. The cohesive zone model: advantages, limitations and challenges[J].Engineering Fracture Mechanics, 2002,69(2): 137-163.
MEZ I, et al. The cohesive zone model: advantages, limitations and challenges[J].Engineering Fracture Mechanics, 2002,69(2): 137-163.
[12] REDDY K C, SUBRAMANIAMK V L. Analysis for multi-linear stress-crack opening cohesiverelationship: application to macro-synthetic fiber reinforcedconcrete[J].Engineering Fracture Mechanics, 2017,169: 128-145.
[13] ISSA S, ELIASSON S, LUNDBERG A, et al. Cohesive zone modeling of crack propagation influenced by martensiticphase transformation[J].Materials Science &Engineering A, 2018,712: 564-573.
[14] DO B C, LIU W, YANG Q D, et al. Improved cohesive stress integration schemes for cohesive zoneelements[J].Engineering Fracture Mechanics, 2013,107(7): 14-28.
[15] TRYDING J, RISTINMAA M. Normalization of cohesive laws for quasi-brittle materials[J].Engineering Fracture Mechanics, 2017,178: 333-345.
[16] OTTOSEN N S, RISTINMAA M. Thermodynamically based fictitious crack/interface model for generalnormal and shear loading[J].International Journal of Solids and Structures, 2013,50(22/23): 3555-3561.
[17] 管俊峰, 卿龙邦, 赵顺波. 混凝土三点弯曲梁裂缝断裂全过程数值模拟研究[J]. 计算力学学报, 2013,30(1): 143-148.(GUAN Junfeng, QING Longbang, ZHAO Shunbo. Research on numerical simulation on the whole cracking processes of three-point bending notch concrete beams[J].Chinese Journal of Computational Mechanics, 2013,30(1): 143-148.(in Chinese))
[18] 张鹏, 胡小飞, 姚伟岸. 内聚力模型裂纹问题分析的解析奇异单元[J]. 固体力学学报, 2017,38(2): 157-164.(ZHANG Peng, HU Xiaofei, YAO Weian. An analytical singular element to study the cohesive zone model for cracks[J].Chinese Journal of Solid Mechanics, 2017,38(2): 157-164.( in Chinese))
[19] 黄才政, 郑丹. 无限大平板黏聚裂纹模型的数值解[J]. 水利学报, 2014,45(S1): 137-142.(HUANG Caizheng, ZHENG Dan. Numerical solution of the cohesive crack model in finite plate[J].Journal of Hydraulic Engineering, 2014,45(S1): 137-142.(in Chinese))
[20] DUAN S J, NAKAGAWA K. Stress functions with finite stress concentration at the crack tips for a central cracked panel[J].Engineering Fracture Mechanics, 1988,29(5): 517-526.
[21] DUAN S J, FUJII K, NAKAGAWA K. Finite stress concentrations andJ-integrals from normal loads on a penny-shaped crack[J].Engineering Fracture Mechanics, 1989,32(2): 167-176.
[22] DUAN S J, NAKAGAWA K, SAKAIDA T. A mathematical model to approach the fracture process of overconsolidatedclay[J].Engineering Fracture Mechanics, 1991,38(6): 361-369.
[23] FUJII K, DUAN S J, NAKAGAWA K. A mathematical model for fracture process of four point bending concrete beam[J].Engineering Fracture Mechanics, 1991,40(1): 37-41.
[24] 段树金, 中川建治. せん断を受ける円盤状亀裂の周边で有限な应力集中を与える弹性解について[J]. 土質工学論文報告集, 1988,28(1): 153-160.(DUAN S J, NAKAGAWA K. Finite stress concentrations around a penny-shaped crack in three-dimensional body under shear loading[J].Proc JSSC, 1988,28(1): 153-160.(in Japanese))
[25] 段树金, 中川建治. 含有直线状裂纹正交异性板的平面问题的应力函数[J]. 应用数学和力学, 1988,9(6): 491-498.(DUAN Shujin, NAKAGAWA K. Stress functions for central straight cracked anisotropic plates[J].Applied Mathematics and Mechanics, 1988,9(6): 491-498.(in Chinese))
[26] 胡启平. Ⅲ型静态与运动Griffith裂纹的有限应力集中解[J]. 工程力学, 1995,12(S1): 474-478.(HU Qiping. Finite stress concentration solutions of mode-Ⅲ static and moving Griffith cracks[J].Engineering Mechanics, 1995,12(S1): 474-478.(in Chinese))
[27] ZHU M, CHANG W V. An unsymmetrical fracture process zone model and its application to the problem of radical crack with an inclusion in longitudinal shear deformation[C]//Fracture Mechanics of Concrete Structures,Proceedings FRAMCOS-3. Freiburg, Germany, 1997.
[28] 段树金, 前田春和, 藤井康寿, 等. 沿直线有多条裂纹的薄板弯曲问题[J]. 工程力学, 1999,16(3): 21-29.(DUAN Shujin, MAEDA H, FUJII K, et al. On the bending of an elastic plate containing multi-cracks[J].Engineering Mechanics, 1999,16(3): 21-29.(in Chinese))
[29] 栖原秀郎, 中川建治. 亀裂先端で有限な応力集中を構成する応力関数に関する研究[J]. 土木学会論文集, 1994,501: 65-74.(SUHARA H, NAKAGAWA K. Studies on the stress function with finite stress concentration at crack tip[J].Proc JSCE, 1994,501: 65-74.(in Japanese))
[30] 中川建治, 国富康志, 藤井康寿. クラック先端で有限で滑らかな応力集中を与える応力関数の構成法[J]. 名城大学理工学部研究報告, 2002,42: 62-69.(NAKAGAWA K, KUNITOMI Y, FUJII K. Introductions of stress functions with finite magnitude of stress concentrations at the crack tips in a infinite plate[J].Research Reports of the Faculty of Science and Technology Meijou Univ, 2002,42: 62-69.(in Japanese))
[31] 段树金, 张彦龙, 安蕊梅. 基于裂纹尖端二阶弹性解的断裂过程区尺度[J]. 应用数学和力学, 2013,34(6): 598-605.(DUAN Shujin, ZHANG Yanlong, AN Ruimei. Fracture process zone size based on the secondary elastic crack tip stress solution[J].Applied Mathematics and Mechanics, 2013,34(6): 598-605.(in Chinese))
[32] AN Ruimei, DUAN Shujin, GUO Quanmin. A new method to determine tensile strain softening curve of quasi-brittle materials[C]//Sustainable Solutions in Structural Engineering and Construction,Proc of ASEA-SEC-2. Bangkok, Thailand, 2014: 177-182.
[33] DUAN S J, YAZAKI H, NAKAGAWA K. A crack at the interface of an elastic half plane and a rigid body[J].Engineering Fracture Mechanics, 1989,32(4): 573-580.
[34] FUJII K, KATO Y, DUAN S J, et al. Stress analysis around a partially bonded rigid cylinder in an elastic medium with process zones[J].Engineering Fracture Mechanics, 1993,45(1): 31-38.
[35] FUJII K, NAKAGAWA K, DUAN S, et al. Stress function with finite magnitude of stress concentration around an interface crack[J].Engineering Fracture Mechanics, 1994,47(6): 881-891.
[36] 藤井康寿, 中川建治. 面内引張りを受ける境界面き裂問題の応力関数[J]. 土木学会論文集, 1994,502: 23-32.(FUJII K, NAKAGAWA K. Stress function around an interface crack under uniform tension at infinity[J].Proc of JSCE, 1994,502: 23-32.(in Japanese))
[37] MURASE Y, DUAN S J, NAKAGAWA K. Stress analysis around a circular interface crack between dissimilar media loaded by uniform tension at infinity[J].Engineering Fracture Mechanics, 1994,48(3): 325-337.
[38] MURASE Y, NAKAGAWA K, DUAN S. Introduction of stress functions around a circular interface crack between dissimilar materials[J].Engineering Fracture Mechanics, 1996,53(4): 661-673.
[39] 国富康志, 藤井康寿, 中川建治. 面内力問題における等方性き裂と異材界面き裂に対して適用可能な応力関数[J]. 材料, 2005,54(9): 946-951.(KUNITOMI Y, FUJII K, NAKAGAWA K. Some applicable stress functions for an isotropic crack and an interface crack in in-plane problems[J].J Soc Mat Japan, 2005,54(9): 946-951.(in Japanese))
[40] 中川建治, 藤井康寿. 異材界面き裂問題の解析法に関する基礎的な研究[J]. 名城大学理工学部研究報告, 2008,48: 32-35.(NAKAGAWA K, FUJII K. A Study of analytical method of solution of interface crack problems in an infinite plate[J].Research Reports of the Faculty of Science and Technology Meijou University, 2008,48: 32-35.(in Japanese))
[41] ERDOGAN F. Stress distribution in a nonhomogeneous elastic plane with cracks[J].Trans ASME Series E,Journal of Applied Mechanics, 1963,30(2): 232-236.
[42] ENGLAND A H. A crack between dissimilar media[J].ASME Journal of Applied Mechanics, 1965,32(2): 400-402.
[43] MONFARED M M, AYATOLLAHI M, BAGHERI R. In-plane stress analysis of dissimilar materials with multiple interface cracks[J].Applied Mathematical Modelling, 2016,40: 8464-8474.
[44] COMNINOU M. The interface crack[J].Transaction of the ASME Journal of Applied Mechanics, 1977,44(4): 631-636.
[45] 安蕊梅, 段树金. 低体积含量的钢纤维混凝土三折线拉应变软化曲线的确定[J]. 石家庄铁道大学学报(自然科学版), 2017,30(1): 14-18.(AN Ruimei, DUAN Shujin. Determination of trilinear tension softening curve of reinforced concrete with steel fiber in low volume-ratio[J].Journal of Shijiazhuang Tiedao University(Natural Science Edition), 2017,30(1): 14-18.(in Chinese))