电磁轨道炮的概念提出已有100多年的历史.在20世纪70年代,电磁驱动技术有了突破性的进展.电磁轨道炮与传统火炮或导弹比较具有非常大的速度和成本优势,电磁炮的出口速度比传统炮大得多,这种炮弹可以在武器拦截、二次发射等方面取得极大优势[1].同时,电磁炮依靠电能发射,具有发射成本低、隐蔽以及发射控制简单等优点[2].美国在电磁炮的理论和应用研究方面都处于领先地位,并已经宣布将电磁炮列装部队[3].法、 德、 俄也在电磁轨道发射技术、 电磁装甲技术领域开展了多年研究,已经成为继美国之后在电磁发射领域重要的研究力量[4-6].
电磁发射技术已经取得了显著的研究成果,但是在走向实用之前,仍有许多难题亟待解决[7].电磁轨道炮的使用遇到一个严重的问题:炮弹内壁受到高温高压的等离子电弧作用后,会产生烧蚀和变形,影响发射,且降低炮膛寿命[8].一方面,人们对优化电磁轨道炮结构及部件的设计进行了探索,并取得了一些研究成果[9-12];另一方面,满足复杂发射要求的复合型轨道的应用研究也取得了积极进展.铜基复合材料是目前被广泛关注的轨道炮轨道材料,高导电铜基复合材料是一类具有优良综合性能的新型功能材料,既具有优良的导电性,又具有高的强度和优越的高温性能[13],可以克服重复发射问题,已被应用在实际电磁轨道炮的设计中.
近年来,国内外学者关注于电磁轨道炮发射过程中各组件的静动态应力和变形问题:田振国等给出了轨道的受力模型并得到了电枢与轨道接触面附近的局部应力场及轨道的动态响应[14-15];雷彬等研究了典型轨道损伤形式[16];石江波等分析了电磁轨道炮发射时后坐运动的特征[17];张豪等分析了电磁炮轨道表面电流与轨道形状的关系[18];魏存磊等采用有限元法对瞬态冲击载荷下复合材料身管损伤进行数值模拟,讨论了影响复合材料身管损伤的因素[19];乔志明等用数值模拟的方式计算了在不同接触电阻值和速度条件下接触界面的温度分布情况,得到了接触界面不同部位温度随时间的变化规律[20].
本文主要研究电磁轨道炮发射过程中复合型轨道的受力状态,建立了电磁发射器发射状态下铜基复合轨道的力学模型,将一侧轨道简化为一个电枢作用下的双层地基梁的接触问题模型[21-22];然后将轨道进行分层,对轨道的复合层采用复变函数的方法,利用弹性平面基本方程求出复合层轨道的应力分布,以及轨道复合层对轨道基层的作用力;最后将基层轨道上的压应力进行多项式拟合,将其作为轨道复合层的荷载,利用弹性平面基本方程求出轨道复合层的应力分布.
电磁轨道发射系统的炮管部分主要由轨道、绝缘材料、支撑材料及包层组成,如图1所示的轨道炮横截面简图.建立如图2所示的空间坐标系,电流由轨道1的铜基层流入穿过钢复合层流经电枢再穿过轨道2的钢复合层流入铜基层,最后从轨道2的铜基层流出形成一个闭合的电流回路,整个回路电流关于xOy平面对称,线电流位于xOz平面上,原点O在轨道的起始部位.复合轨道2电流源点为(x,0,h2+(b+h1)/2),其中b为轨道间距,h1为铜基层的厚度,h2为钢复合层的厚度,在两轨道间的A(xA,yA,zA)点产生的磁感应强度为[14]
(1)
其中,μ0为真空磁导率;![]() 为轨道2产生的磁感应强度分量;i,j,k分别为x,y,z坐标系的单位向量;R2为由轨道2的电流源点至A点的距离矢量.同理可得到轨道1的电流源点在空间任意点的磁场强度.
为轨道2产生的磁感应强度分量;i,j,k分别为x,y,z坐标系的单位向量;R2为由轨道2的电流源点至A点的距离矢量.同理可得到轨道1的电流源点在空间任意点的磁场强度.
两个轨道在A点z方向上产生的磁感应强度为[23]
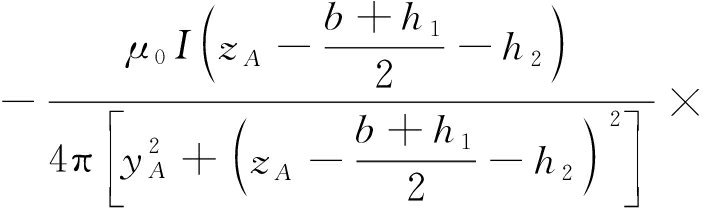
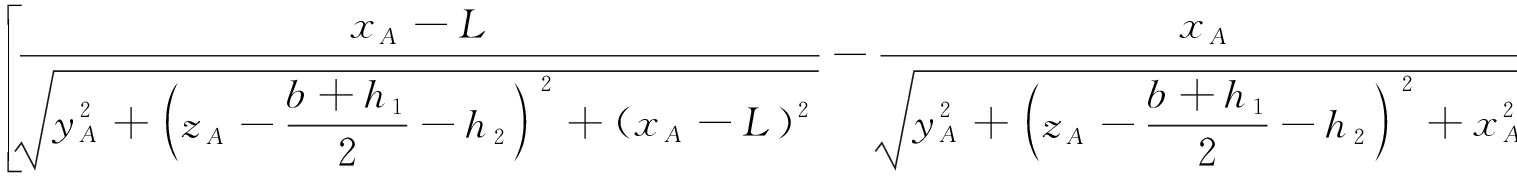
(2)
其中,I为轨道内电流强度,L为电枢沿轨道滑过的距离.
根据Ampere(安培)力计算公式dF=Idl×B,在复合轨道1的单位面积上所受的力的大小为[14]
(3)
式中,h=h1+h2为复合轨道的总厚度,d为轨道的高度.
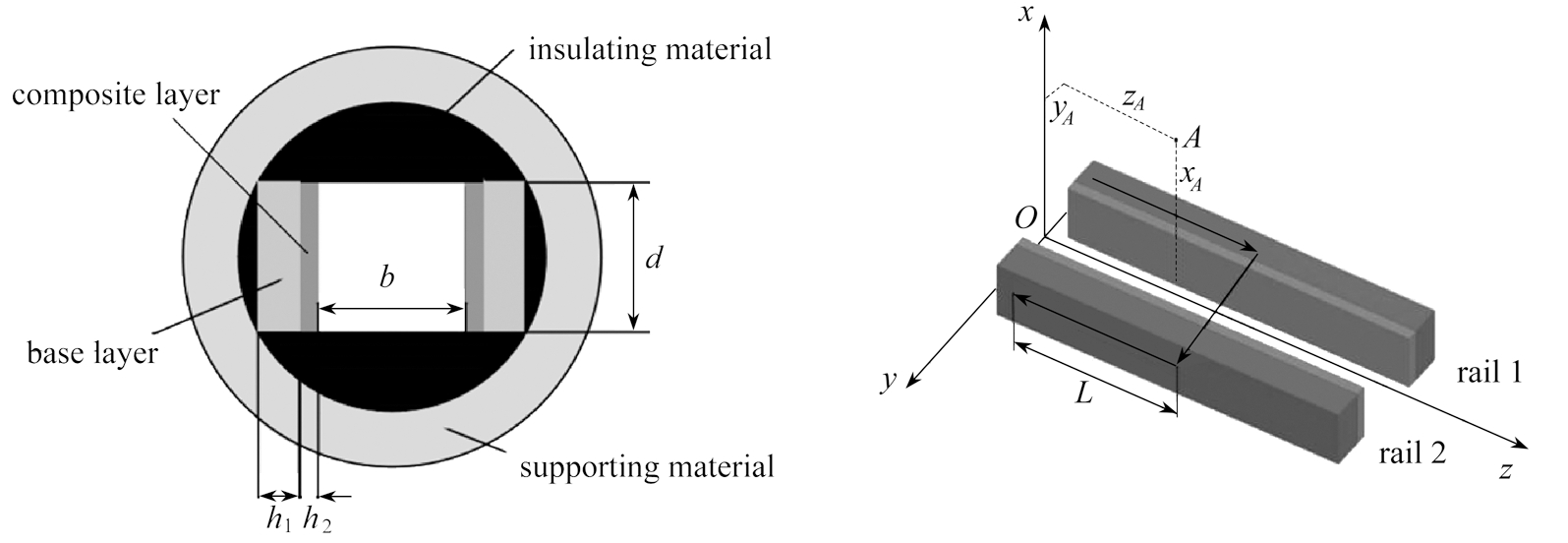
图1 电磁炮截面简图 图2 轨道间电流及磁场坐标
Fig. 1 Schematic of the EM railgun’s section Fig. 2 The current and coordinate system for the magnetic field between rails
在电磁轨道发射过程中电枢中有强电流通过,由于Joule热效应,固体电枢受热膨胀,而轨道对电枢的膨胀有约束作用,因此电枢对轨道侧面产生压力,可将其简化为集中力P.轨道受力模型简图如图3所示.
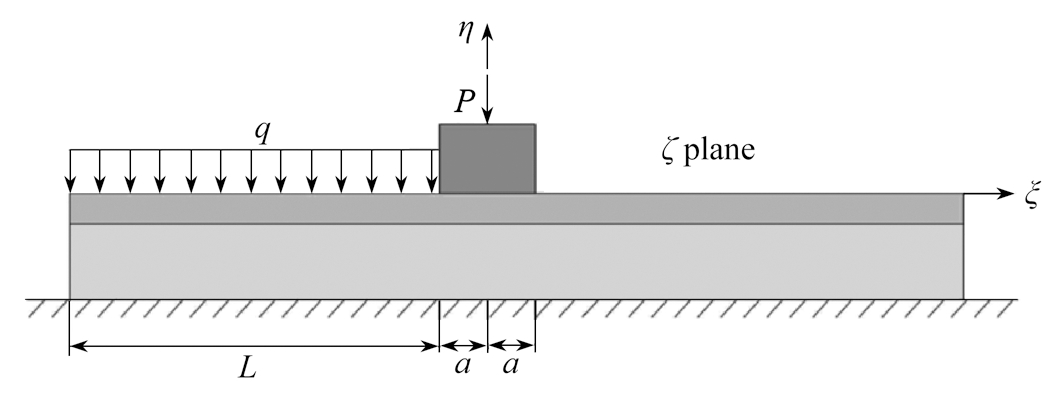
图3 轨道计算简图
Fig. 3 The calculation diagram of the rail
电枢作用在轨道上的合力为[15]
(4)
其中,d为轨道高度,αT为电枢材料的线膨胀系数,Q为电枢的热源功率,2a为电枢沿轨道方向的长度,λa为电枢材料的热传导系数,αa为电枢材料的表面换热系数,Ea为电枢材料的弹性模量.
对于图3所示的复合型轨道计算简图,在计算钢复合层的应力时,由于只计算电枢与轨道接触的应力状态,且只有电枢经过的轨道段有载荷的作用.因此采用复变函数的方法,将轨道近似看作是放在地基上的半无限长弹性梁.
以图3所示的分布载荷的中点为坐标原点,建立坐标系ξ1O1η1,其中ξ1=ξ+l,η1=η,所在复平面称作ζ1平面,在复平面ζ1的实轴O1ξ1上-l≤t1≤l(L=2l)段受有轨道间斥力q,在其他部分不受力,t1定义为实轴ξ1上的点.考虑混合边界条件下半平面的基本方程[24]:
(5)
(6)
(7)
式中,σξ1,ση1为ξ1,η1方向的正应力,τξ1η1为切应力,![]() 为ξ1,η1方向位移的一阶导数,Φ(ζ1)为在下半平面(η1<0) 全纯的函数,
为ξ1,η1方向位移的一阶导数,Φ(ζ1)为在下半平面(η1<0) 全纯的函数,![]() 是Φ(ζ1)的共轭函数,Gs为轨道复合层材料的剪切模量,κs=(λs+3Gs)/(λs+Gs),λs=Esνs/[(1+νs)(1-2νs)]为Lamé(拉梅)常数,
是Φ(ζ1)的共轭函数,Gs为轨道复合层材料的剪切模量,κs=(λs+3Gs)/(λs+Gs),λs=Esνs/[(1+νs)(1-2νs)]为Lamé(拉梅)常数,![]() 是虚数单位,Es为轨道复合层材料的弹性模量,νs为轨道复合层材料的Poisson(泊松)比.
是虚数单位,Es为轨道复合层材料的弹性模量,νs为轨道复合层材料的Poisson(泊松)比.
边界条件
(8)
根据式(6),可以将边界条件表示为
Φ+(t1)-Φ-(t1)=q, -l≤t1≤l.
(9)
由Cauchy(柯西)积分,边值问题(9)的解为
(10)
其中,![]() 分别为复平面内一点ζ1(ξ1,η1)到实轴ξ1上点(-l,0),(l,0)的距离;
分别为复平面内一点ζ1(ξ1,η1)到实轴ξ1上点(-l,0),(l,0)的距离;![]() 分别为点ζ1(ξ1,η1)与实轴ξ1上点(-l,0),(l,0)的连线与实轴的夹角.将式(10)代入到式(5)、(6)中并分离实部和虚部便可得到轨道间斥力作用下轨道上各点的应力分量,其中η1方向正应力为
分别为点ζ1(ξ1,η1)与实轴ξ1上点(-l,0),(l,0)的连线与实轴的夹角.将式(10)代入到式(5)、(6)中并分离实部和虚部便可得到轨道间斥力作用下轨道上各点的应力分量,其中η1方向正应力为
(11)
如图3所示,电枢与轨道接触的“刚印”问题也属于半平面问题,假设电枢与轨道接触面平直,电枢与轨道接触部分有位移g(t),t定义为实轴ξ上的点,电枢与轨道间摩擦因数为k.
在电枢运动到某一位置时有如下边界条件:
ση=τξη=0,t<-a ort>a,
(12)
u″+iv′=g′(t),τξη=-σηk, -a≤t≤a.
(13)
由式(6)可得
Φ+(t)+κsΦ-(t)=2Gsg′(t), -a≤t≤a.
(14)
应力与位移混合形式边界条件问题的解为[25]
(15)
其中,多项式
β=lnκs/(2π),
c0,c1,…,cn-1为待定常数.由式(7)可知c1=c2=…=cn-1=0,考虑到是刚印问题:
因此有
(16)
与处理Φ(ζ1)的方法相同,将式(16)代入式(5)、(6)中并分离实部和虚部得到电枢作用下轨道上各个点的应力分量,其η方向上的应力分量为
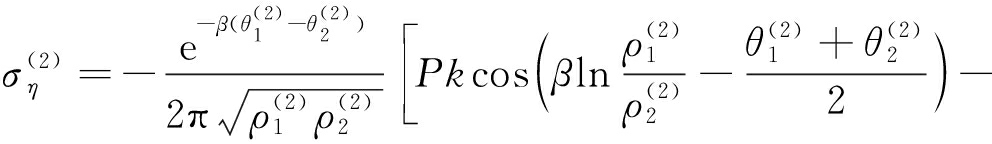
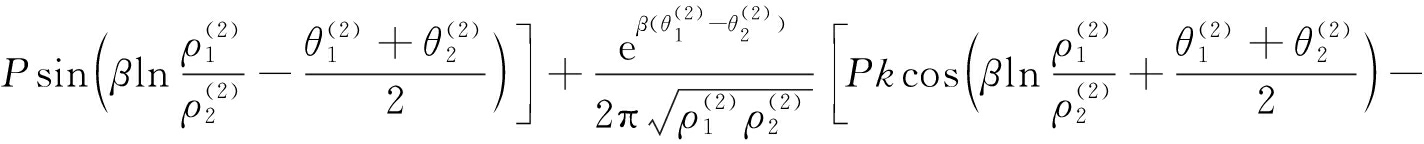
(17)
其中,![]() 分别为复平面内一点ζ(ξ,η)到实轴ξ上点(-a,0),(a,0)的距离;
分别为复平面内一点ζ(ξ,η)到实轴ξ上点(-a,0),(a,0)的距离;![]() 分别为点ζ(ξ,η)与实轴ξ上点(-a,0),(a,0)的连线与实轴的夹角.
分别为点ζ(ξ,η)与实轴ξ上点(-a,0),(a,0)的连线与实轴的夹角.
将式(11)与(17)统一到图3所示的ζ平面内,并将q和P的值代入其中即可得到复合层轨道上各个点在η方向上的应力分量ση.其余各应力分量σξ,τξη也可以用相同的方法得到.
复合轨道的铜基层所承受的载荷来自于钢复合层,因此,将应用上面方法所得到的复合层间的法向正应力作为主动载荷作用在基层上,从而得到基层内部各点处的应力分布.运用MATLAB软件对铜层表面η方向的应力分量ση进行数值分析,并对得到的数据进行多项式拟合,可得到铜层表面的近似作用力方程式为
f(ξ)=p1ξ4+p2ξ3+p3ξ2+p4ξ+p5,
(18)
式中,p1,p2,p3,p4,p5为系数,把f(ξ)作为铜层表面的作用力,并建立坐标系ξ′O′η′,其中ξ′=ξ,η′=η+h2,所在复平面称作ζ′平面.
考虑在基层与复合层的交界面上的b′c′间作用有式(18)所示的载荷,根据Cauchy积分应力边界条件问题的解为[24]
(19)
将式(19)代入到式(5)、(6)中并分离实部和虚部即可得到铜层各点的应力分量,其中![]() 为幅角.则有η′方向的应力为
为幅角.则有η′方向的应力为
(p1r4cos(4θ)+p2r3cos(3θ)+p3r2cos(2θ)+p4rcosθ+p5)+
sin(α1+α2)(p1r4sin(4θ)+p2r3sin(3θ)+p3r2sin(2θ)+p4rsinθ)]-
2p3rcosθ+p4)-(4p1r3sin(3θ)+3p2r2sin(2θ)+2p3rsinθ)-
(20)
其中,r1,r2分别为复平面内一点ζ′(ξ′,η′)到实轴ξ′上点(b′,0),(c′,0)的距离;α1,α2分别为点ζ′(ξ′,η′)与实轴ξ′上点(b′,0),(c′,0)的连线与实轴的夹角.
至此,由式(18)和(20)可得铜基层轨道的η′方向正应力,其他应力分量也可通过相似方法求得.
如图1所示,复合型轨道的复合层、基层材料分别是钢和铜,铜层厚度为h1=15 mm,钢层厚度为h2=5 mm,轨道总长度为2 m,轨道间距b=20 mm,轨道高d=20 mm,电枢沿轨道方向长度2a=20 mm,电枢的高度和宽度都是20 mm,轨道与电枢间的摩擦因数k=0.01.铜的材料参数为:弹性模量Ec=100 GPa,Poisson比νc=0.31.钢复合层材料参数为:弹性模量Es=200 GPa,Poisson比νs=0.27,质量密度ρs=7 800 kg/m2.电枢是由铝材料制成,材料参数为:电导率σa=3.6×107 (Ω·m)-1,质量密度ρa=2 700 kg/m3,热传导系数λT=237 W/(m·℃),线胀系数αT=2.35×10-5 ℃-1,表面放热系数αa=500 W/(m2·℃).真空磁导率μ0=1.256×10-6 H/m,系统放电电压U0=8 000 V,系统外接电阻R0=0.1 Ω.
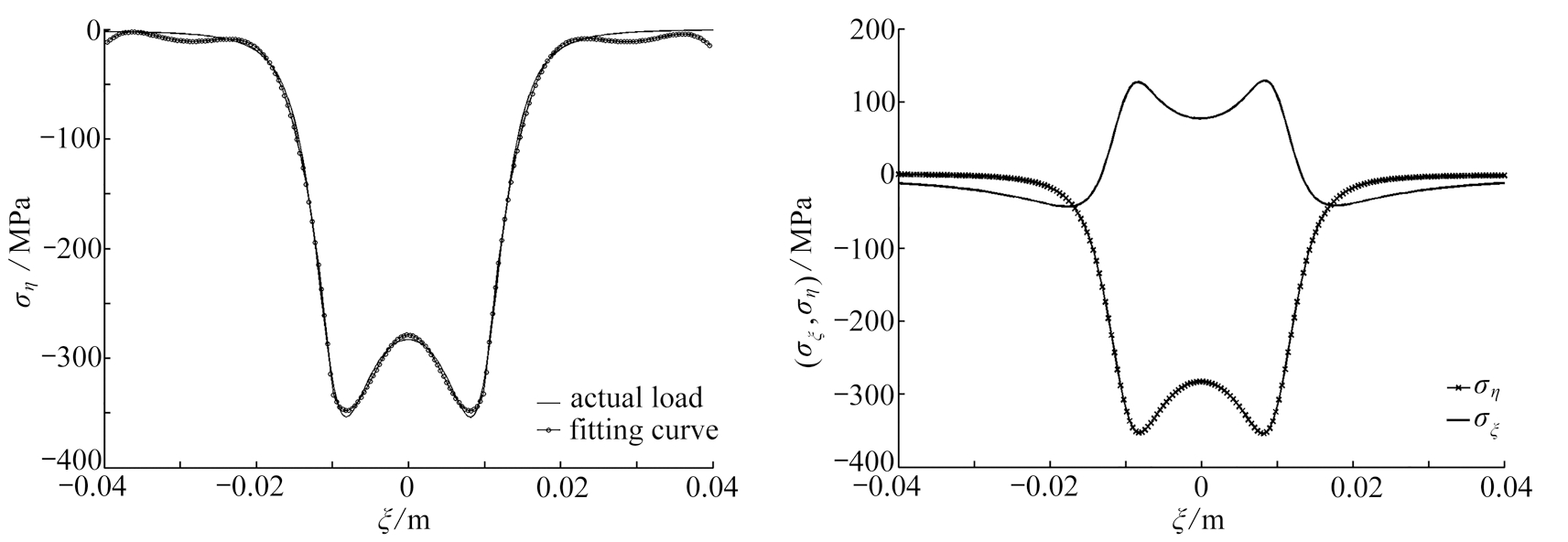
图4 应力曲线拟合前后对比 图5η=-5 mm处,沿ξ方向σξ,ση的分布曲线
Fig. 4 Comparison of the stresses before and after curve fitting Fig. 5 Theσξ,σηdistribution curves along the
ξ direction,η=-5 mm
由式(11)、(17)可得图4所示的η=-5 mm处复合轨道交接面上的正应力ση沿ξ方向的变化,由图可以看出轨道在ξ∈(-0.04,0.04)的应力值较大且变化显著,其余部分的应力几乎趋近于零.所以这里只考虑这一段轨道复合层对基层的作用,用MATLAB软件对这部分应力曲线进行多项式拟合后,即可得式(18)的作用于轨道基层的多项式载荷.由图4铜基层表面沿ξ方向应力曲线ση拟合前后对比图可以看出,拟合前后应力存在一定的误差,拟合后的应力值稍大.
图5为外加系统放电电压为U=8 000 V时,在复合轨道的基层与复合层的交界面上,即η=-5 mm处铜层表面上的应力σξ,ση沿ξ方向的变化.由图可知,电枢下方η方向为压应力,且绝对值较大,ξ方向大多为拉应力,但值相对较小,应力在电枢的两端点处出现峰值,同时电枢位置处的应力值比其他位置的应力值要大得多.
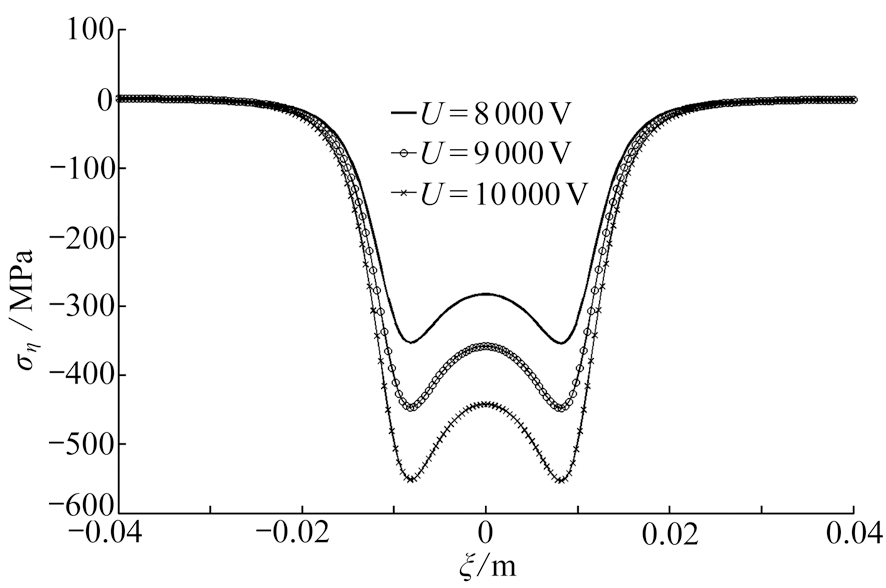
图6 在η=-5 mm处,沿ξ方向ση在不同加载电压作用下的分布曲线
Fig. 6 Theση distribution curves along theξ direction atη=-5 mm with different loading voltages
图6中的各曲线表示的是轨道在不同的加载电压下应力ση沿ξ方向的变化曲线,从图中可以看出,随着加载电压的增大应力绝对值随之增大,且均表现为电枢下方应力绝对值远大于轨道的其他部分.由此可以看出,电枢对轨道的作用大于轨道间斥力的作用.另外从图中可见,电枢两侧端点处轨道的应力绝对值较大.
图7、图8中的各曲线为通入电压U=8 000 V,应力σξ,ση在轨道复合层与基层厚度比h2/h1不同时,基层表面的应力沿ξ方向的变化,在轨道整体厚度不变的情况下,当厚度比为1∶3时基层表面受到的应力值要比厚度比为2∶3和1∶1时大.可见,随着轨道基层厚度的减小其表面的应力值随着减小.一方面,是由于铜基层厚度的减小增加了系统的整体电阻[15],从而电流值减小,而电枢对轨道的作用力与热源功率密度成正比,即与电流密度的平方成正比[15],因此,电枢对轨道的作用力减小;另一方面,是距离轨道表面越远电枢对其影响越小,且复合层对基层起到了一定的保护作用.
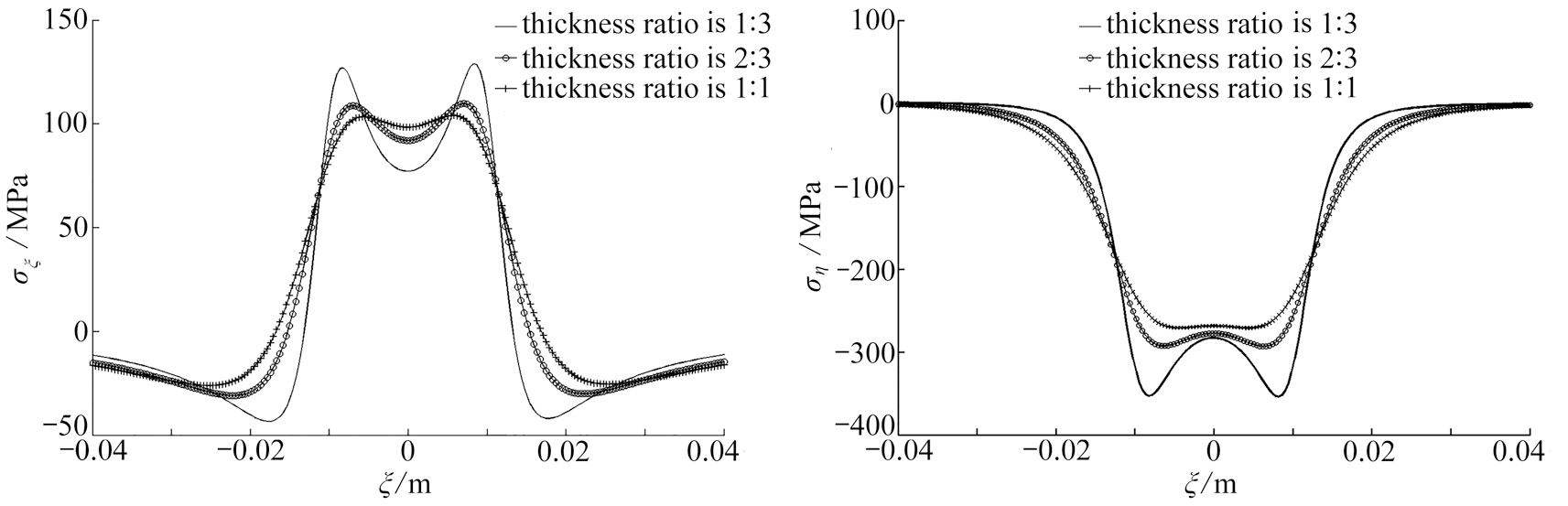
图7 基层表面的应力σξ变化曲线 图8 基层表面的应力ση变化曲线
Fig. 7 Theσξ change curves on the base layer surfaceFig. 8 Theση change curves on the base layer surface
图9中的应力曲线表示的是基层与复合层在离交界面的距离均为1 mm处,应力σξ沿ξ方向的变化曲线.可见,钢复合层上的应力的绝对值要略大于铜基层上的应力值,且变化也相对剧烈.
图10中各曲线表示的是在不同的电压下铜-钢交界面上切应力τξη沿ξ方向的变化曲线.从图中可以看出它的变化规律和正应力σξ,ση变化规律相似,都是随着加载电压的增大而增大,但切应力的绝对值要小得多.切应力的大小和分布是决定复合轨道在发射过程中复合层与基层不发生相对滑动破坏的重要参考指标.
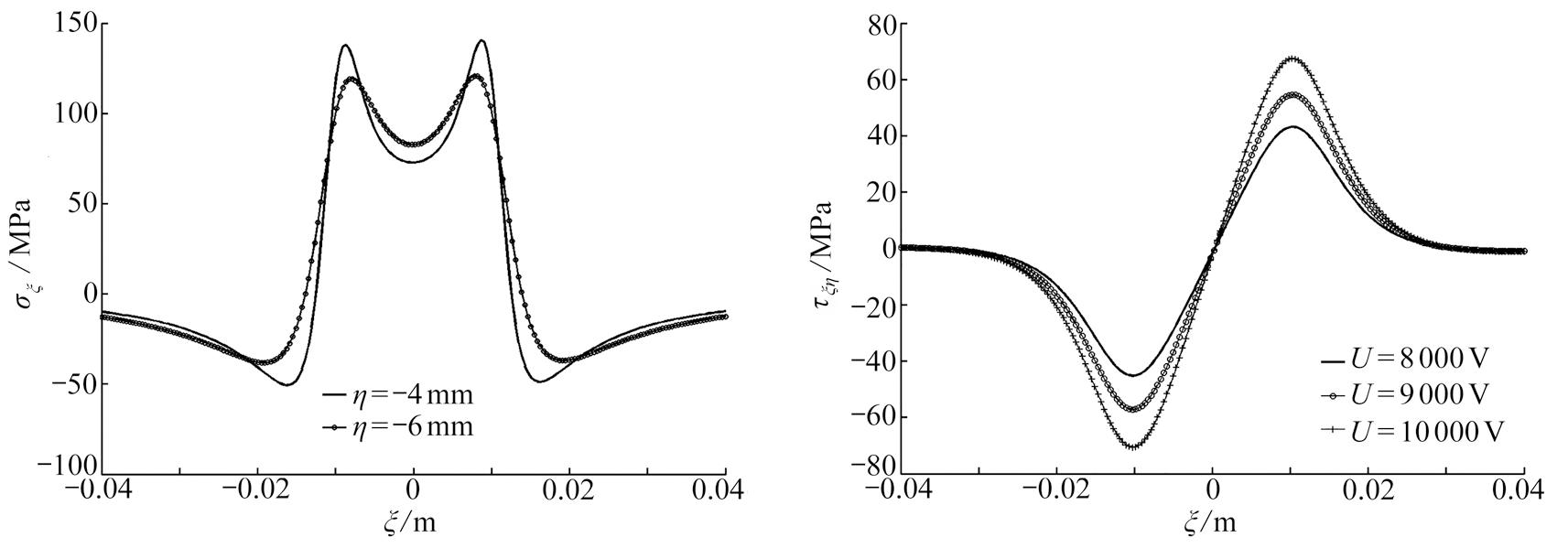
图9 轨道内、外层在离复合界面等距处σξ的变化曲线图10 铜-钢接触面上的切应力τξη沿ξ方向的变化曲线
Fig. 9 Theσξ change curves at the same distance from Fig. 10 Theτξη change curves along theξ direction on
both contact surfaces the copper-steel contact surface
应用COMSOL软件模拟了复合型轨道的发射过程.图11为通入电压U=8 000 V,轨道厚度比为1∶4,在t=1 ms时刻轨道和电枢内电流密度分布云图.从图中可以看出,轨道铜基层内的电流密度要比表面复合层内的电流密度大得多,而在电枢与轨道接触位置的两端处电流密度最大,这是由电流沿最短路径通过的性质所决定的.图12为轨道和电枢的正应力ση的分布云图.从图中可见,在电枢与轨道接触局部的应力要比其他位置正应力大.这与理论计算结果的分布规律是一致的.
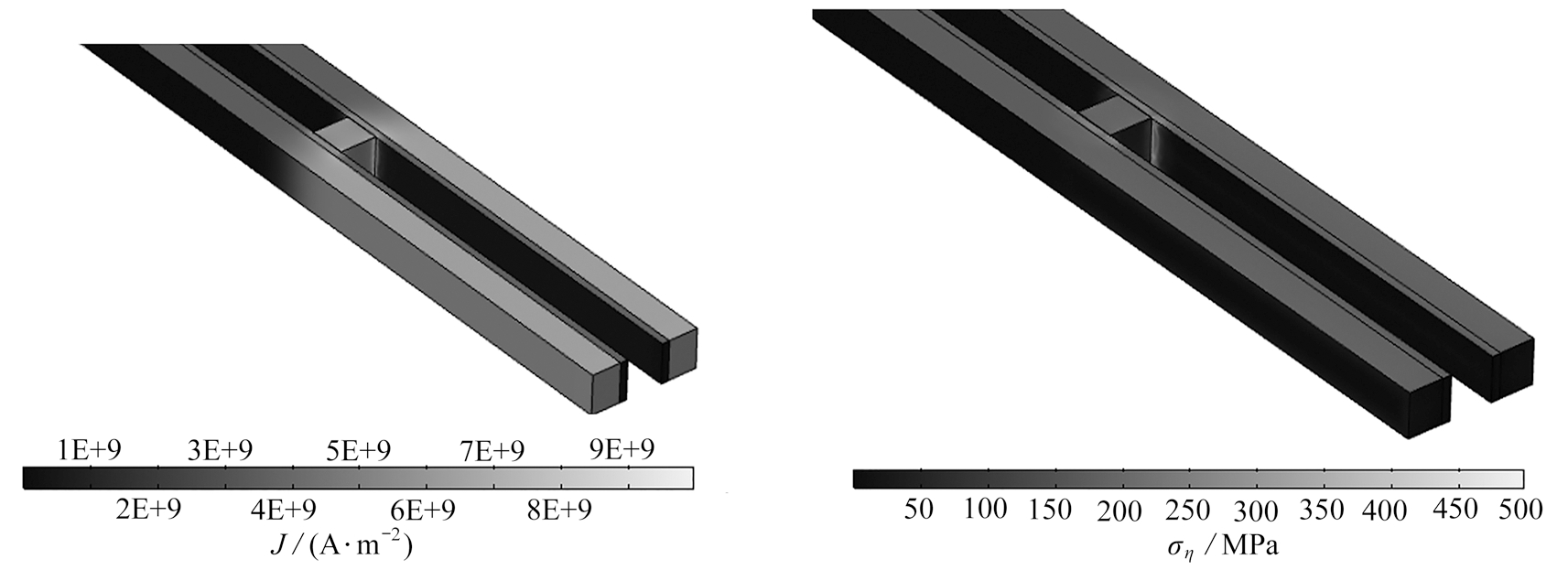
图11 发射过程中电流密度分布云图 图12 发射过程中应力ση的分布云图
Fig. 11 The nephogram of current density Fig. 12 The nephogram of stressση distribution
distribution during launching during launching

图13 交界面上正应力ση的理论与数值计算结果图14 交界面上切应力τξη的模拟计算结果
Fig. 13 The theoretical and numerical results of normal Fig. 14 The theoretical and numerical results of shear
stressση on the interface stressτξη on the interface

图15 交界面上切应力的分布云图
Fig. 15 The nephogram of shear stress distribution on the interface, numerical simulation results
图13、图14分别为轨道基层与轨道复合层交界面上的正应力ση和切应力τξη沿ξ轴分布情况的理论和数值模拟结果.从图13中可见,理论计算结果与数值模拟结果的分布规律是一致的,但理论计算结果更为规则,且应力值的绝对值偏大.这是由于在理论计算时没有考虑电枢的弹性变形所导致的.此外,由图中对比发现,理论计算结果规则、对称,而数值模拟结果则不具有对称性.这是因为理论计算时假定电枢均匀膨胀,则其对轨道的作用也具有对称性,而数值模拟更接近实际情况,即靠近发射端,电流密度大,温升高,则电枢膨胀量就大,其引起轨道的正应力的绝对值也比另外一侧要大.图14中的理论计算结果为厚度比为1∶4时交界面上的切应力分布.与数值计算结果比较可见,切应力的理论结果也比数值模拟的结果偏大.交界面上的切应力的绝对值随着轨道厚度比h2/h1的增大而减小,且在电枢作用的左侧为负值(靠近发射端),在电枢作用的右侧为正值.图15为交界面上切应力分布云图,从图中可见,在电枢作用的角点位置上切应力的绝对值较大.在图中左侧(靠近发射端)切应力达到最大,临近中线位置切应力绝对值变小,在距离电枢作用位置稍远处,切应力的绝对值接近于零.
1) 对于复合型电磁发射轨道在发射状态下的应力问题,将轨道简化为多层弹性地基,引入平面弹性问题的基本方程,可以得到轨道基层在轨道间斥力和电枢压力作用下的应力分布;然后将轨道层间作用力进行多项式拟合, 并将其作为轨道基层的载荷的表达式, 进而得到轨道基层的应力场.这种方式可以有效降低求解难度, 在保证足够精度的基础上得到问题的理论解.
2) 电磁发射轨道的应力主要是由轨道间斥力和电枢作用引起的.由理论和数值的计算结果可以看出,电枢作用位置处轨道内的应力值较轨道其他位置要大得多,且在电枢作用的两个端点位置处应力的绝对值达到最大.这意味着电枢对轨道的影响远大于轨道间斥力的影响,电枢温升所引起的电枢对轨道的压力对轨道应力的贡献是最主要因素.
3) 复合型轨道复合层与基层厚度比对轨道应力有直接影响,厚度比越大,应力值越小,轨道越安全.但是,厚度比的增大会影响轨道的发射速度,因为要提高发射弹丸的速度必须通入大电流,当复合层材料厚度占比过大时,系统电阻增加、基层通过电流的有效截面积减小,轨道间磁场强度减小.所以,复合型轨道复合层与基层所占比例的选择要综合考虑.
[1] 张世英, 裴桂艳, 张俊. 美国海军电磁轨道炮研发计划评析[J]. 现代舰船, 2011,49(9): 46-49.(ZHANG Shiying, PEI Guiyan, ZHANG Jun. The US Navy electromagnetic railgun R&D plan evaluation[J].Modern Ships, 2011,49(9): 46-49.(in Chinese))
[2] 范长增, 王文魁. 发展中的电磁轨道炮[J]. 燕山大学学报, 2007,31(5): 377-386.(FAN Changzeng, WANG Wenkui. Review on the electromagnetic railgun[J].Journal of Yanshan University, 2007,31(5): 377-386.(in Chinese))
[3] FAIR H D. Electromagnetic launch science and technology in the United States enters a new era[J].IEEE Transactions on Magnetic, 2005,41(1): 158-164.
[4] 范光程, 江明阳, 隆小飞, 等. 驱动线圈连接方式对多极矩电磁发射效率的影响研究[J]. 兵工学报, 2017,38(4): 643-650.(FAN Guangcheng, JIANG Mingyang, LONG Xiaofei, et al. Effects of driving coil connection modes on emission efficiency of MFEL[J].Acta Armamentarii, 2017,38(4): 643-650.(in Chinese))
[5] 苏子舟, 张涛, 张博. 欧洲电磁发射技术发展概述[J]. 飞航导弹, 2016,46(1): 80-85.(SU Zizhou, ZHANG Tao, ZHANG Bo. An overview of the development of electromagnetic launch technology in Europe[J].Aerodynamic Missile Journal, 2016,46(1): 80-85 (in Chinese))
[6] SU Z Z, ZHANG T, GUO W, et al. Investigation of armature capture effect on synchronous induction coilgun[J].IEEE Transactions on Plasma Science, 2015,43(5): 1215-1219.
[7] 杨世荣, 王莹, 徐海荣, 等. 电磁发射器的原理与应用[J]. 物理, 2003,32(4): 253-256.(YANG Shirong, WANG Ying, XU Hairong, et al. Principle and applications of electromagnetic launchers[J].Physics, 2003,32(4): 253-256.(in Chinese))
[8] MCNAB I R, BEACH F C. Naval railguns[J].IEEE Transactics on Magnetics, 2007,43(1): 463-468.
[9] 汪治全, 王豫, 严仲明, 等. 基于均匀设计的单级多极矩电磁推进器结构参数优化[J]. 兵工学报, 2016,37(4): 744-750.(WANG Zhiquan, WANG Yu, YAN Zhongming, et al. Research on structural parameters of sigle-stage multipole field launcher based on uniform design approach[J].Acta Armamentarii, 2016,37(4): 744-750.(in Chinese))
[10] 袁晓明, 吴鹏, 陈晓阳, 等. 增强型电磁轨道炮电磁结构耦合有限元分析及结构优化设计[J]. 机械设计, 2016,33(2): 18-23.(YUAN Xiaoming, WU Peng, CHEN Xiaoyang, et al. Electromagnetic structural coupling finite element analysis and structural optimal design of augmented electromagnetic railgun[J].Journal of Machine Design, 2016,33(2): 18-23.(in Chinese))
[11] 李峰, 李豪杰, 殷强. 电枢运动状态下轨道炮膛内磁场仿真分析[J]. 兵器装备工程学报, 2016,37(10): 61-71.(LI Feng, LI Haojie, YIN Qiang. Simulation analysis of railgun in-born magnetic field in armature movement state[J].Journal of Ordnance Equipment Engineering, 2016,37(10): 61-71.(in Chinese))
[12] 李小将, 王志恒, 武昊然. 电磁炮轨道几何尺寸特性分析及优化设计[J]. 火炮发射与控制学报, 2015,36(2): 54-58.(LI Xiaojiang, WANG Zhiheng, WU Haoran. Characteristics analysis and optimization design of rail geometry size of electromagnetic railgun[J].Journal of Gun Launch &Control, 2015,36(2): 54-58.(in Chinese))
[13] 王微, 战再吉, 唐琪, 等. Ti2AlN-La2O3/Cu复合材料的界面反应与性能[J]. 稀有金属材料与工程, 2015,44(5): 1177-1180.(WANG Wei, ZHAN Zaiji, TANG Qi, et al. Interfacial reaction and properties of Ti2AlN-La2O3/Cu composite[J].Rare Metal Materials and Engineering, 2015,44(5): 1177-1180.(in Chinese))
[14] 田振国, 白象忠, 杨阳. 电磁轨道发射状态下导轨侧面的局部接触应力分析[J]. 固体力学学报, 2011,32(1): 74-81.(TIAN Zhenguo, BAI Xiangzhong, YANG Yang. The analysis of local contact stress on the side of rail when electromagnetic rail is at a launching state[J].Chinese Journal of Solid Mechanics, 2011,32(1): 74-81.( in Chinese))
[15] 田振国, 孟晓永, 安雪云, 等. 电磁轨道发射状态下的复合导轨动态响应[J]. 兵工学报, 2017,38(4): 651-657.(TIAN Zhenguo, MENG Xiaoyong, AN Xueyun, et al. Dynamic response of composite rail during launch process of electromagnetic rail[J].Acta Armamentarii, 2017,38(4): 651-657.(in Chinese))
[16] 雷彬, 朱仁贵, 张倩, 等. 电磁轨道发射器刨削产生特征与研究现状[J]. 兵器材料科学与工程, 2011,34(3): 76-80.(LEI Bin, ZHU Rengui, ZHANG Qian, et al. Production features and research status of gouging in electromagnetic railgun[J].Ordnance Material Science and Engineering, 2011,34(3): 76-80.(in Chinese))
[17] 石江波, 栗保明. 电磁轨道炮后坐过程研究[J]. 兵工学报, 2015,36(2): 227-233.(SHI Jiangbo, LI Baoming. Research on recoil process of electromagnetic railgun[J].Acta Armamentarii, 2015,36(2): 227-233.(in Chinese))
[18] 张豪, 谢龙, 高俊杰, 等. 电磁轨道炮轨道形状对电流分布的影响[J]. 火炮发射与控制学报, 2016,37(4): 48-53.(ZHANG Hao, XIE Long, GAO Junjie, et al. The influence of rail shape on the current distribution in electromagnetic railgun[J].Journal of Gun Launch &Control, 2016,37(4): 48-53.(in Chinese))
[19] 魏存磊, 徐亚栋, 马燕颖. 瞬态冲击载荷下复合材料身管损伤研究[J]. 兵器装备工程学报, 2016,37(7): 131-136.(WEI Cunlei, XU Yadong, MA Yanying. Study on damage of composite material barrel under transient impact load[J].Journal of Ordnance Equipment Engineering, 2016,37(7): 131-136.(in Chinese))
[20] 乔志明, 雷彬, 吕庆敖, 等. 轨道炮枢/轨接触界面温度仿真分析[J]. 装甲兵工程学院学报, 2016,30(4): 62-67.(QIAO Zhiming, LEI Bin, LÜ Qing’ao, et al. Simulation and analysis of the temperature distribution near the armature-rail interface in a railgun system[J].Journal of Academy of Armored Force Engineering, 2016,30(4): 62-67.(in Chinese))
[21] 谈至明, 郭晶晶, 陈景亮. 双向弹簧夹层假定的弹性地基上双层板的解[J]. 应用数学和力学, 2016,37(4): 382-390.(TAN Zhiming, GUO Jingjing, CHEN Jingliang. Solutions of double-layer plate with two-way spring interlayers on elastic foundations[J].Applied Mathematics and Mechanics, 2016,37(4): 382-390.(in Chinese))
[22] 马小丹, 李星. 一维六方准晶的两类周期接触问题[J]. 应用数学和力学, 2016,37(7): 699-709.(MA Xiaodan, LI Xing. 2 kinds of periodic contact problems of 1D hexagonal quasicrystals[J].Applied Mathematics and Mechanics, 2016,37(7): 699-709.(in Chinese))
[23] 田振国, 杨阳, 白象忠. 电磁轨道发射过程中电枢与轨道的力学特性[J]. 机械强度, 2012,34(2): 234-238.(TIAN Zhenguo, YANG Yang, BAI Xiangzhong. Rail-armature mechanics behavior during launch process of electromagnetic rail[J].Journal of Mechanical Strength, 2012,34(2): 234-238.(in Chinese))
[24] МУСХЕЛИШВИЛИ Н И. 数学弹性力学的几个基本问题[M]. 赵惠元, 译. 北京: 科学出版社, 1959.(МУСХЕЛИШВИЛИ Н И.Some Basic Problem of the Mathematical Theory or Elasticity[M]. ZHAO Huiyuan, transl. Beijing: Science Press, 1959.(Chinese version))
[25] ПРУСОВИ И А. Некотоые Задачи Термоупругосгн[M]. Мииск: Мзд-во ВГУ, 1972.(ПРУСОВИ И А.Some Problem of Thermal Elasticity[M]. Minsk: Press of National University of White Russia, 1972.(in Russian))