图1 集中力作用下压电/压磁板状复合材料界面裂纹的理论模型
Fig. 1 The theoretical model for interfacial fracture in a piezoelectric and spiezomagnetic composite plate under a concentrated force
多铁性复合材料因具有优越的力电耦合性能而在实际工程中得到广泛应用[1]，但由于材料本身大多为陶瓷材料，其固有的脆性使得材料在严苛的工况下容易萌生裂纹并扩展，从而导致多铁性元器件的失效．因此，分析研究多铁性复合材料的各项物理和几何参数对材料断裂行为的影响，对于该类复合材料的设计优化和性能改善具有重要的工程意义．近年来，不少学者在相关方面的研究取得较大进展，但在研究过程中仍会假设一些较为理想的条件．例如，在建立断裂力学分析模型时会把模型上的加载方式假设为裂纹面上的等效载荷或是模型外表面上的均布载荷．Rekik等研究了裂纹面等效载荷条件下具有功能梯度的磁电弹复合材料中混合型裂纹耦合效应的问题[2]；Liu等研究了多铁性复合材料层间裂纹的平面模型[3]；Zhao等提出了外表面作用有均布载荷时双介电材料界面裂纹的非线性双梁模型[4]；Hu等讨论了将Dugdale裂纹沿着两种不同磁电弹材料的界面移动的情形[5]．然而在实际工程应用中，多铁性器件的工作环境并不理想，往往会存在着某一集中力作用的情况．近来也有许多专家学者进行了相关研究，例如Feng等对磁电弹材料上某点冲击载荷进行了动态断裂力学分析[6]；Herrmann等建立了压电/压磁复合材料界面裂纹上作用有某一集中载荷时的接触区模型[7]；Govorukha等研究了压电相层间条状裂纹面上作用有集中载荷的问题[8]．值得注意的是，以上问题大多仍为理想模型[9-14]，因为在实际应用中外力往往存在于材料的外表面而非裂纹面上．因此，研究多铁性复合材料在外表面集中力作用下的断裂问题更加具有现实意义．针对此类问题，笔者建立了更加符合实际工作情况的断裂力学分析模型，利用Fourier积分变换和Green函数推导出该模型的Cauchy奇异积分方程组，并利用配点法对奇异积分方程组进行数值求解，分析讨论各物理和几何参数对裂纹尖端应力强度因子的影响规律，对多铁性复合材料的结构设计和性能改善提供理论参考．
图1所示为某一压电/压磁板状复合材料的截面图，其内层为压磁层并固定接地，外层为压电层，层间存在一条直线型裂纹，材料外表面任一点处作用有集中力τ0．如图1建立直角坐标系，x轴位于材料底部，正方向水平向右，y轴沿着材料厚度方向，垂直于x轴向上为正，z轴方向根据右手定则确定．由图可知，压磁层和压电层的厚度分别为h1及h2-h1；裂纹两尖端所对应的横坐标分别用a和b表示，则裂纹长度可表示为b-a；集中力作用位置用t表示，方向垂直于xOy平面向内．
图1 集中力作用下压电/压磁板状复合材料界面裂纹的理论模型
Fig. 1 The theoretical model for interfacial fracture in a piezoelectric and spiezomagnetic composite plate under a concentrated force
假设图1中各材料沿z轴方向极化，根据压电理论可知，该板状材料为横观各向同性材料，其横截面为各向同性平面．为方便起见，本文中统一用1，2来分别表示压磁层和压电层．在上述轴向剪切条件下，该界面裂纹属于反平面断裂，于是材料的基本方程具有如下表达式：
(1)
其中，广义应力
和Dk分别为剪切应力、磁感应强度和电位移；广义位移
其中w，φ和φ分别为z轴轴向机械位移、磁场强度和电场强度．
根据断裂理论，材料参数矩阵Mi表示为
(2)
其中c44，e15，μ11，h15和ε11分别为剪切模量、压电系数、磁导率、压磁系数和介电系数；δkθ为Kronecker符号，当k=θ时其值为1，否则为0．
对于常见的压电、压磁材料，一般情况下Mi≠0，i=1,2．于是将式(1)代入式(2)可得材料的控制方程为
2wi=0，i=1,2，
(3)
其中2为二维的Laplace算子．
式(3)可通过Fourier积分变换得如下表达式：
(4)
将式(4)代入式(1)可得广义应力场为
(5)
其中
在断裂力学分析中，撕开型裂纹通常模拟为反平面裂纹模型，此时裂纹通常保持闭合，属于电磁可通模型．因此其边界条件可表示如下：
w1(x,0)=0，
(6)
(7)
(8)
φ1(x,h1)=φ2(x,h1),φ1(x,h1)=φ2(x,h1)，
(9)
w1(x,h1)=w2(x,h1),x∉(a,b)，
(10)
(11)
其中δ(x-t)为Dirac delta函数．
本文利用位错模拟法进行断裂力学分析，其位错密度函数可表示为
(12)
显然边界条件(10)自动满足式(12)．考虑到该问题的可解性，该位错密度函数还需满足以下单值条件：
g(t)dt=0．
(13)
在解决连续性位错问题时，可以先假设在界面上存在一个位错点源，然后利用Green函数模拟实际裂纹区间上的位错密度函数．于是可得
w2,x(x,h1)-w1,x(x,h1)=δ(x-s)．
(14)
对式(14)分别利用Fourier正、余弦积分变换可以得到
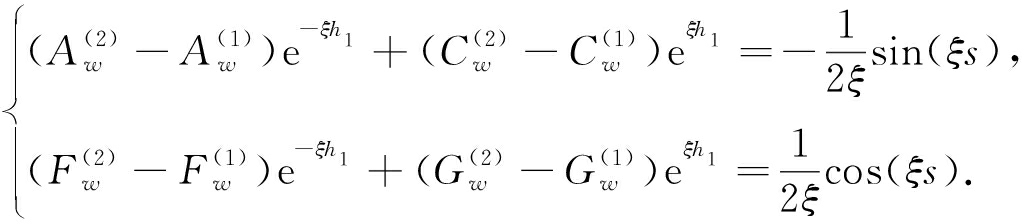
(15)
因为由方程的奇部和偶部分别组成的两组代数方程组具有相同的系数矩阵Ω，因此可得到以下两个方程组的表达式：
ΩP=T1，ΩQ=T2，
(16)
其中Ω为12阶矩阵，
求解两个代数方程组可以分别解得系数矩阵P和Q为
(17)
其中Λ1为Ω-1的第一列向量，Λ2为Ω-1的第二列向量，Ω-1为矩阵Ω的逆矩阵．
将式(17)代入式(11)可得位错点源下的切应力表达式为
(18)
其中
通过计算可知limξ→∞K(ξ)=q，其中q为常数，代入式(18)，利用公式
可得
(19)
其中R(s,x)=
[K(ξ)-q]sin[ξ(s-x)]dξ．
根据断裂力学理论，式(19)中等式右边第一项为裂纹面上位错点源在界面上引起的轴向应力的解，第二项为层合板外表面上集中力在界面上引起的轴向剪应力的解，因此式(19)可以看作裂纹面上位错点源和层合板外表面上集中力在界面处引起的轴向剪应力的合力．于是根据边界条件(11)可知，裂纹面上连续分布的位错共同作用所引起的应力可表示为
(20)
利用式(20)可得标准化的Cauchy奇异积分方程组的表达式，令
于是可得
(21)
其中
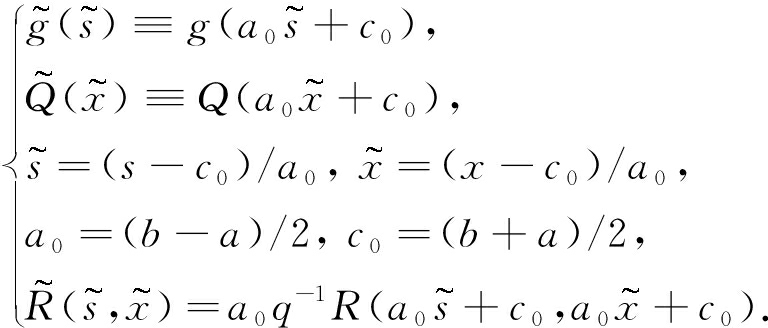
(22)
根据Cauchy奇异积分方程理论，式(21)中
具有平方根型的奇异性，可表达如下：
(23)
式中
为无量纲待定函数．
利用式(23)可通过配点法将式(21)和(13)转化为如下代数方程组：
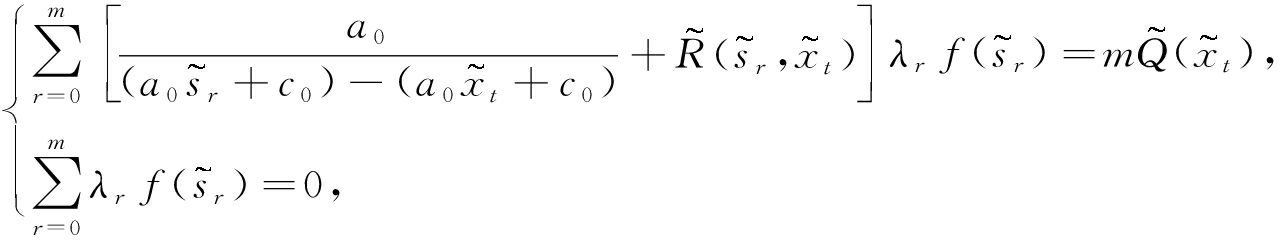
(24)
其中m为求积节点数，其值将依据数值计算收敛速度的大小来确定
根据Ⅲ型裂纹的应力强度因子的定义可得
(25)
其中
为裂纹尖端的奇异应力，具有如下表达式：
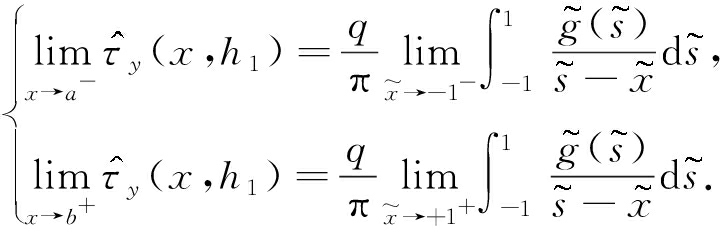
(26)
将式(23)代入式(26)可得
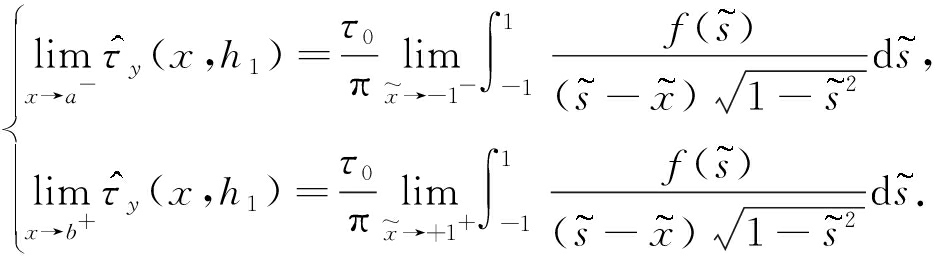
(27)
因为
(28a)
(28b)
在式(28a)和(28b)中，等式右边第一项满足Hölder连续性条件，第二项由于其非奇异性可以忽略不计，进而式(27)可表示为
(29)
因为
(30)
于是可得应力强度因子的最终表达式为
(31)
通过对式(24)进行求解，得到f(1)和f(-1)，进而利用式(31)可计算出裂纹两尖端的应力强度因子的数值解[15]．
本文选用压磁层和压电层材料分别为CoFe2O4和BaTiO3．CoFe2O4的材料参数为
BaTiO3材料参数为
在数值计算时，首先需要确定数值结果的收敛性．为此需要将无量纲核函数
和
中积分区间[0,+∞)分割为有限域[0,ξx]，其中上限ξx的取值取决于核函数和的收敛速度，并且通过计算容易知道其收敛速度并不相同．图2讨论了不同参数条件对两核函数收敛速度的影响
通过计算发现影响核函数收敛速度的因素主要有：压电层厚度h2-h1、裂纹长度b-a和集中力作用位置t，其中集中力作用位置只影响核函数的收敛速度．由计算观察可得，通过增大厚度、减小裂纹长度以及使集中力作用位置向裂纹尖端靠近的方式均可以加快核函数的收敛速度，因此在本计算中设定ξ=400即可满足要求．在计算中设定无量纲核函数的相对收敛精度为1.0×10-6，在该条件下，求积节点数m取值应不小于20．
(a)h1=24 mm,t=20 mm,a=15 mm,b=25 mm(b)h1=16 mm,t=20 mm,a=15 mm,b=25 mm
(c)h1=24 mm,t=45 mm,a=15 mm,b=25 mm(d)h1=24 mm,t=20 mm,a=10 mm,b=30 mm
图2 无量纲核函数的收敛行为
Fig. 2 The convergence behavior of the dimensionless kernel functions
为了验证公式推导及计算的正确性，利用MATHEMATICA软件将多铁性层合板与集中力下层合柱在相同条件下得到的断裂规律进行比对验证[15]．容易知道，当圆柱体的半径取得足够大时，其弧形的界面裂纹可以近似地看作一条直线型裂纹．因此集中力作用于层合柱外表面的断裂模型可以模拟成层合板问题的模型，在此条件下得到在相同参数条件下层合柱和层合板的应力强度因子规律曲线对比图，如图3所示[16]，其中
r0=980 mm,r1=1 000 mm,r2=1 010 mm,α=π/125,γ=π/250,
h1=20 mm,h2=30 mm,a=4π mm,b=8π mm,τ0=1 MPa．
在图3中，α和γ分别表示层合柱模型在极坐标下裂纹两尖端的位置．提请注意的是，在层合柱中，集中力τ0以逆时针方向运动；而在层合板中，集中力τ0沿x轴正方向运动，在模拟过程中二者的运动方向恰好是相反的．由图可知，在相同条件下，当层合柱半径足够大时得到的应力强度因子的规律曲线与层合板在相同条件下得到的规律曲线是吻合的，因此证明了数值计算的正确性．
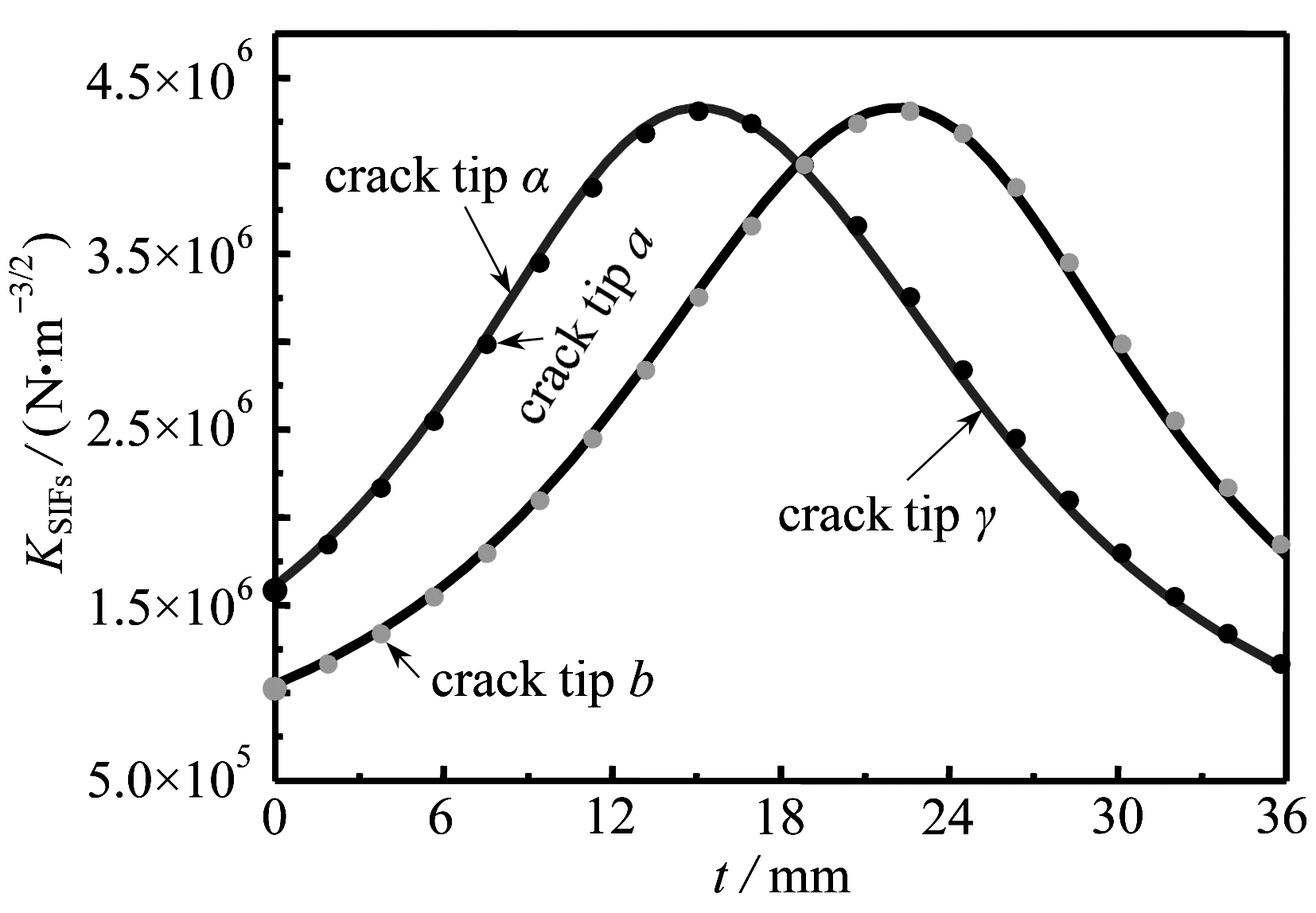
图3 数值验证
Fig. 3 Numerical verification
在压电层厚度不同的条件下，改变集中力作用位置t，得到其对SIF值大小以及SIF峰值点位置的规律曲线，如图4所示(h2=30 mm,a=15 mm,b=25 mm)．
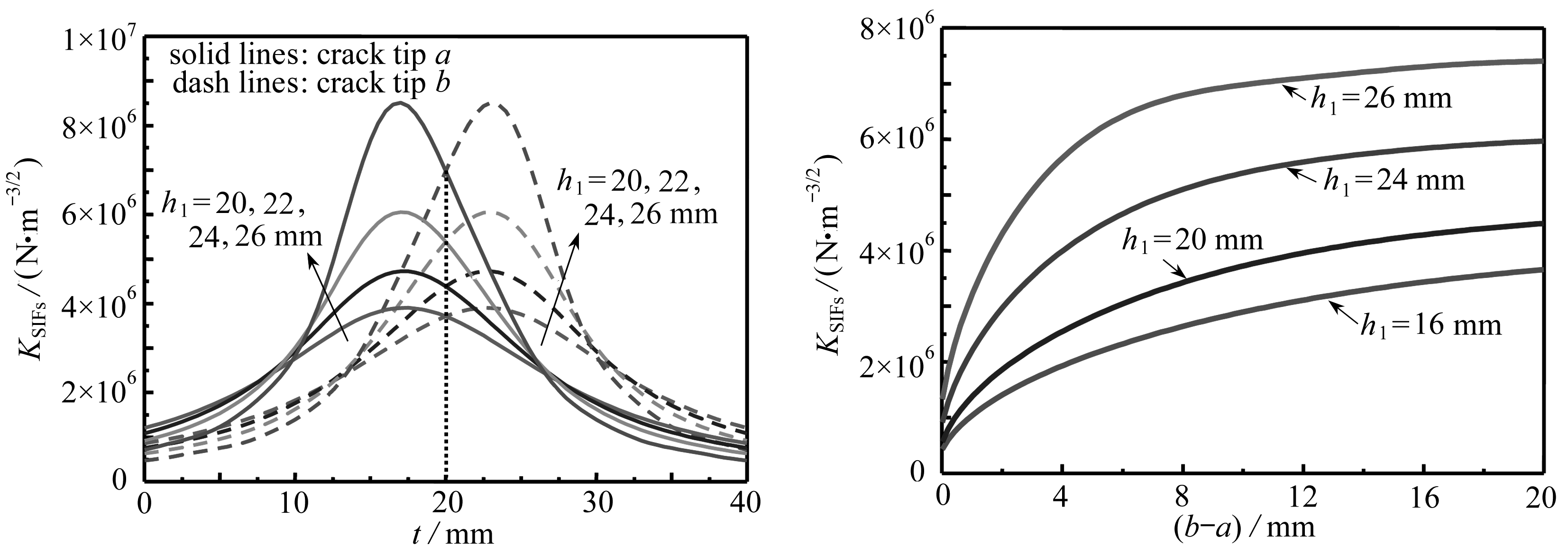
图4 压电层厚度对SIF的影响 图5 裂纹长度对SIF的影响
Fig. 4 Effects of the PE layer on SIF curves Fig. 5 Effects of the crack length on SIF curves
由图4可知： (a) 当h1取值逐渐变大，即压电层逐渐变薄时，SIF峰值点逐渐靠近裂纹尖端点，并且峰值逐渐增大，但SIF值并不是在裂纹尖端处达到最大，即其峰值点与裂纹尖端点位置并不重合．造成这一非理想结果的原因在于该层合板断裂力学模型的非对称性．(b)h1逐渐变大，意味着裂纹逐渐靠近层合板的自由表面，此时SIF显著增长．因此可通过增大压电层厚度来减小SIF． (c) 从集中力对裂纹尖端的影响来看，当集中力作用位置距离裂纹尖端一定范围以内时才具有较为明显的影响，因此该曲线在区间[10 mm, 30 mm]上具有较明显的变化．
由图4中可以看出，裂纹两尖端的SIF曲线关于横坐标x=(a+b)/2对称，因此在下图中仅以裂纹尖端a作图．如图5所示，h1取数个不同参数，在改变裂纹长度b-a的条件下，讨论SIF值的变化规律(h2=30 mm,t=20 mm,(a+b)/2=20 mm)．
通过图5能够得到如下结论： (a) 随着裂纹长度的增加，SIF值也逐渐增大，但逐渐趋于平缓．(b) 压电层越薄，裂纹长度对SIF值得影响越明显．(c) 由于此时集中力作用于裂纹长度对应横坐标中点处，该模型可以看作对称模型，因此裂纹两尖端得到的SIF曲线完全一致．
本文对集中力作用下的压电/压磁板状复合材料进行断裂力学分析，利用Fourier积分变换求得控制方程组的无穷积分解；通过Dirac delta函数表达出边界条件；然后引入位错密度函数并利用Green函数描述位错点源下的剪应力；进而推导出Cauchy奇异积分方程；最后利用配点法求解奇异积分方程，得到了裂纹尖端应力强度因子的数值解．在分析应力强度因子的数值结果中，得到了以下结论： 压电层厚度、裂纹长度以及集中力作用的位置是影响材料中裂纹尖端的应力强度因子大小的主要因素．其中压电层越薄，应力强度因子的数值越大；裂纹越长，其尖端的应力强度因子也越缓慢增大；集中力作用位置的改变使得SIF值在一段区间内呈显著变化．由于整个模型不具有对称性，因此应力强度因子并不是在裂纹尖端这一理想位置达到峰值．因此，若要改善材料性能以提高其使用寿命，可以通过选用合理厚度的压电层材料、改变外加力的作用位置等方式来减小此类裂纹对器件的影响，但并不能完全消除．然而，Ⅲ型裂纹问题在实际应用中属于较为理想的工况，并且材料外表面存在的受力情况也可能更为复杂，其呈现的规律也会更加丰富，因此相关问题仍需进一步研究．
[1] SPALDIN N A , FIEBIG M. The renaissance of magnetoelectric multiferroics[J].Science, 2005,309(5733): 391-392.
[2] REKIK M, EL-BORGI S, OUNAIES Z. An axisymmetric problem of an embeddedmixed-mode crack in a functionally gradedmagnetoelectroelastic infinite medium[J].Applied Mathematical Modelling, 2014,38(4): 1193-1210.
[3] LIU S L, LI Y D, XIONG T. In-plane fracture analysis on the magneto-electro-elastic interfacial region in a multiferroic composite effects of volume fraction[J].European Journal of Mechanics, 2017,63: 110-121.
[4] ZHAO M H, LIU H T, FAN C Y, et al. A nonlinear bilayer beam model for an interfacial crack in dielectric bimaterials under mechanical/electrical loading[J].International Journal of Fracture, 2014,188(1): 47-58.
[5] HU K Q, CHEN Z T, FU J W. Moving Dugdale crack along the interface of two dissimilar magnetoelectroelastic materials[J].Acta Mechanica,2015,226(6): 2065-2076.
[6] FENG W J, LIU J X. Dynamic analysis of a magneto-electro-elastic material with a semi-infinite mode-III crack under point impact loads[J].Structural Engineering &Mechanics, 2007,27(5): 609-623.
[7] HERRMANN K P, LOBODA V V, KHODANEN T V. An interface crack with contact zones in a piezoelectric/piezomagnetic biomaterial[J].Archive of Applied Mechanics, 2010,80(6): 651-670.
[8] GOVORUKHA V, KAMLAH M, SHEVELEVA A. Influence of concentrated loading on opening of an interface crack between piezoelectric materials in a compressive field[J].Acta Mechanica, 2015,226(7): 1-13.
[9] BAGHERI R, AYATOLLAHI M, MOUSAVI S M. Stress analysis of a functionally graded magneto-electro-elastic strip with multiple moving cracks[J].Mathematics &Mechanics of Solids, 2017,22(3): 304-323.
[10] GUOYK, LI Y D, PAN J W. Effects of complex modulus and residual stress on the vibration induced resonant fracture behavior of a multiferroic cylindrical structure[J].Engineering Fracture Mechanics, 2017,171: 98-109.
[11] ZHOU K, LI Y D, LIU S L. Effects of the volume fraction of piezoelectric particulates in the magneto-electro-elastic interfacial region on the fracture behavior of a laminate multiferroic plate[J].Acta Mechanica, 2016,228(4): 1-20.
[12] HU K Q, CHEN Z T. Strip yield zone of a penny-shaped crack in a magnetoelectroelastic material under axisymmetric loadings[J].Acta Mechanica, 2016,227(8): 2343-2360.
[13] GRYNEVYCH A A, LOBODA V V. An electroded electrically and magnetically charged interface crack in a piezoelectric/piezomagnetic biomaterial[J].Acta Mechanica, 2016,227(10): 1-19.
[14] VIUN O, LAPUSTA Y, LOBODA V. Pre-fracture zones modelling for a limited permeable crack in an interlayer between magneto-electro-elastic materials[J].Applied Mathematical Modelling, 2015,39(21): 6669-6684.
[15] ZHANG J, JIN Y, LI Y D. Concentrated force-induced fracture of a multiferroic composite cylinder[J].Acta Mechanica, 2017,229(5): 1215-1228.
[16] THEOCARIS P S, IOAKIMIDS N I. Numerical integration methods for the solution of singular integral equations[J].Quarterly of Applied Mathematics, 1977,35:173-183.