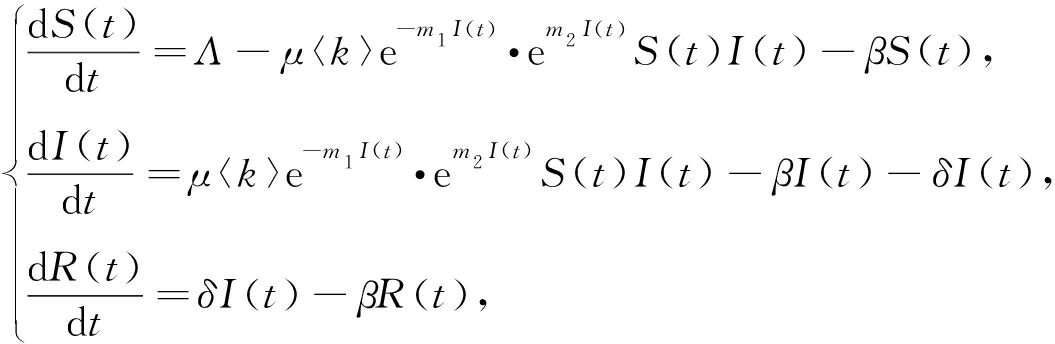
QQ、微博和微信等社交服务网络的迅猛发展,在为人们的工作和日常生活带来了极大便利的同时,也加快了谣言、不良广告等恶意消息的传播,扩大了谣言的影响范围,给社会稳定和国家安全带来了极大的危害.如2011年由日本核泄漏引发的“碘可以防核辐射”谣言导致全国的食盐脱销;2013年关于“成都将发生9.2级地震”的谣言在网络上迅速传播开,大量的群众因此产生了恐慌,扰乱了正常的社会秩序.如何揭示谣言的传播特点和规律,探寻有效的谣言抑制策略,降低谣言对社会带来的危害,具有重要的理论意义和实用价值.
谣言的散布与传染病在人群中传播和扩散有许多相似之处.因此,借鉴传染病建模思想,通过建立数学模型来讨论谣言传播机理是一个行之有效的方法,已有许多研究成果相继出版[1-9].尽管上述研究对谣言传播理论的发展起到了极大的推动作用,然而这些模型并未考虑媒体宣传报道对谣言传播的影响.众所周知,媒体宣传报道不仅能改变人们的行为,而且还能改变其认知和判断[10-11].因此,研究媒体宣传报道对谣言传播和控制的影响有着重要的现实意义.2014年,霍良安等[12]基于系统动力学思想,提出了一类不实信息的动态传播模型.数值仿真显示,在突发事件的初期,媒体及时的正面报道非常关键,能减少由于不实信息传播带来的负面影响.2015年,赵洪涌等[13]建立了一类具有媒体报道函数的谣言传播模型,讨论了平衡态的稳定性和周期震荡性.其成果表明,媒体对社交网络谣言的深度报道可以极大地减小谣言传播者的规模,并扩大网络稳定运行的范围.陈华[14]提出了一类具有媒体播报效应的谣言传播模型,分析了媒体报道频率对谣言传播和控制的影响情况.梁新媛等[15]结合社交网络中媒体澄清谣言对谣言传播的影响,建立了媒体介入下的谣言传播模型,给出了谣言传播的局域控制策略.Huo等[16]研究了具有两种不同形式媒体报道的谣言传播模型,利用Lyapunov函数方法分析了边界平衡点和正平衡点的全局稳定性.但以上成果仅仅讨论了媒体的正面报道对谣言传播和扩散的影响,很少有研究涉及媒体的正面和负面报道对谣言传播的共同影响.
本文的目的是建立具有媒体正面报道和负面报道的谣言传播模型,在理论上分析平衡点的存在性和全局稳定性,在应用上给出网络谣言控制的策略建议.
本文在经典SIR模型的基础上,考虑媒体对信息的正面报道和负面报道影响谣言传播率的情况,将社交网络上的人群分成3类:谣言易感者S;谣言传播者I,此类人会传播谣言;谣言免疫者R,并且不再传播谣言.首先对上述SIR模型作出以下假设:
1) 将进入社交网络的人群视为易感人群.
2) 谣言传播率受媒体对信息正面报道程度和负面报道程度的影响.
3) 随着时间的变化、社会认知的影响等会有一定概率β的谣言易感者、谣言传播者以及谣言免疫者离开系统.
4) 由于自身意识等变化,会有一定概率δ的谣言传播者变成谣言免疫者.
下面对谣言传播的规则进行阐述:
ⅰ) 单位时间有Λ人进入系统.处在状态S的人群,将会在接触到谣言传播者之后,以一定的概率变成谣言传播者,此概率可以用谣言基本传播率μ,e-m1I(t)以及em2I(t)描述.e-m1I(t)表示由于媒体报道正面信息使谣言基本传播率减少,其中,m1描述了正面信息的报道对谣言基本传播率的影响程度.em2I(t)表示由于媒体报道负面信息使谣言基本传播率增加,其中,m2描述了媒体的负面报道对谣言基本传播率的影响程度.此外,考虑到在社交网络中每个节点拥有的实际节点数对谣言基本传播率的影响,本文引入网络平均度〈k〉来刻画.同时,根据假设3),可以得出单位时间谣言易感者S的数量变化表达式:
Λ-μ〈k〉e-m1I(t)·em2I(t)S(t)I(t)-βS(t).
ⅱ) 根据假设3)和假设4),可以求得单位时间内处在I状态的人群的数量变化表达式:
μ〈k〉e-m1I(t)·em2I(t)S(t)I(t)-βI(t)-δI(t).
ⅲ) 同样,单位时间处在状态R的人群的数量表达式为:δI(t)-βR(t).
综上,建立如下SIR模型的平均场方程:
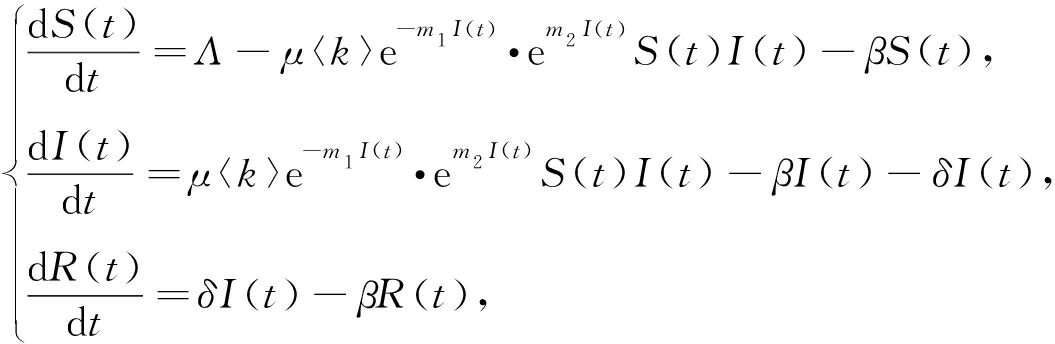
(1)
其中,〈k〉代表网络平均度.
通过简单计算可得,系统(1)有唯一边界平衡点为E0=(Λ/β,0,0).根据下一代矩阵计算方法,可得基本再生数
由μ〈k〉e(m2-m1)I(t)S(t)I(t)-βI(t)-δI(t)=0,求解得
根据δI(t)-βR(t)=0,求解得
由Λ-μ〈k〉S(t)I(t)e(m2-m1)I(t)-βS(t)=0,可知I*满足下面一元二次方程:
(2)
显然,
且
Case 1 m2-m1<0
易知,F′(I(t))<0.即F(I(t))关于I(t)单调递减.
又当R0>1时,F(0)>0,故方程 (2)有唯一正根I*.
Case 2 m2-m1>0
ⅰ) 若![]()
则
又当R0>1时,F(0)>0,故方程(2)有唯一正根I*.
ⅱ) 若m2-m1>μ〈k〉/β,则由F′(I(t))=0可求出正解
所以,当0<I<I0时,F′(I(t))>0,又R0>1时F(0)>0,所以F(I(t))>0且为增函数;当I>I0时,F′(I(t))<0,即F(I(t))是减函数,且当I(t)→+∞时,F(I(t))→-∞.故当R0>1时,方程(2)有唯一正根I*.
综上分析,有下面的结论成立:
定理1 当R0>1时, 系统(1)存在唯一正平衡点E1=(S*,I*,R*).
定理2 集合Γ=(S(t),I(t),R(t))|S(t),I(t),R(t)≥0,S(t)+I(t)+R(t)≤Λ/β是系统(1)的正不变集,也是其吸引集.
证明 记N(t)=S(t)+I(t)+R(t),将其对时间t求导得
因此N(t)=e-βt(N(0)-Λ/β)+Λ/β.故对任意N(0)∈Γ,有
0≤S(t)+I(t)+R(t)≤Λ/β.
从而Γ是系统(1)的正不变集.
下面,将分两种情形证明Γ是系统(1)的吸引集.
1) 若N(0)∈Γ,由Γ是系统(1)的正不变集知0≤N(t)≤Λ/β.
2) 若N(0)∉Γ,由前面分析可知,当t→+∞时,有0≤N(t)≤Λ/β.
因此,Γ是系统(1)的吸引集.
综上所述,Γ 既是系统(1)的正不变集又是全局吸引集.
定理3 在m2<m1的条件下,当R0<1时,系统(1)的边界平衡点E0全局渐近稳定.而当R0>1时,系统(1)的边界平衡点不稳定.
证明 构造Lyapunov函数
其中
ε为任意小的正数.当R0<1时,可知θ>0.因此V(t)是正定函数.
函数V(t)沿着系统(1)关于时间t求导得
βI(t)-δI(t))+θ(δI(t)-βR(t))=
当m2<m1时,
所以
显然, dV(t)/dt=0当且仅当S=Λ/β,I=0,R=0.根据Lasalle不变原理知,边界平衡点E0全局吸引.由V(t)为正定无穷大函数,故E0是全局渐近稳定的.
下证当R0>1时,边界平衡点E0不稳定.
系统(1)在边界平衡点处的Jacobi矩阵为

其对应的特征根为
显然,当R0>1时,特征根λ3>0,故边界平衡点E0不稳定.
定理4 当R0>1时,系统(1)的正平衡点E1=(S*,I*,R*)全局渐近稳定.
证明 由定理1知,当R0>1时,正平衡点E1=(S*,I*,R*)存在且唯一.
下证E1=(S*,I*,R*)的稳定性.
令N(t)=S(t)+I(t)+R(t),系统(1)可化为下面的等价系统:
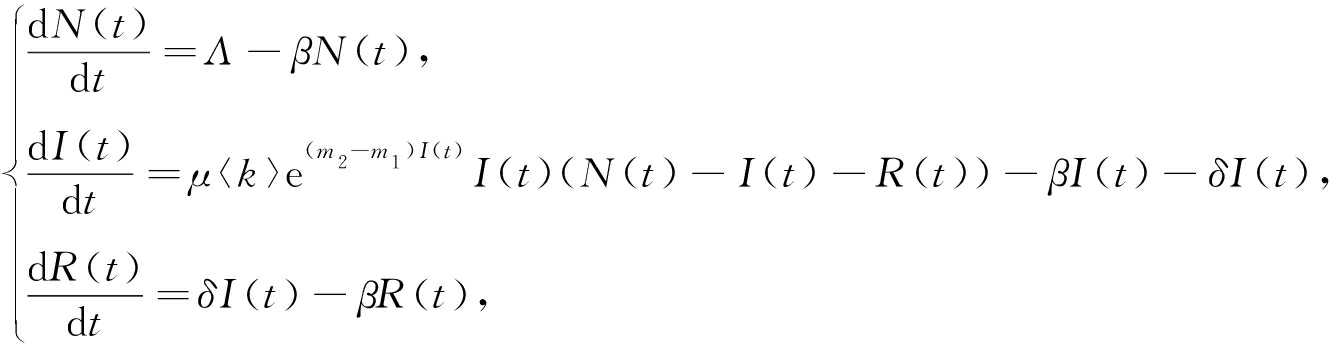
(3)
正平衡点可变为![]() 其中N*=S*+I*+R*.
其中N*=S*+I*+R*.
构造如下形式的Lyapunov函数:
其中
函数V(t)沿着系统(1)对时间t求导得
k1(μ〈k〉I(t)e(m2-m1)I(t)(N(t)-I(t)-R(t))-βI(t)-δI(t)-
μ〈k〉I*e(m2-m1)I(t)(N(t)-I(t)-R(t))+βI*+δI*)+
k2(R(t)-R*)(δI(t)-βR(t))=
-β(N(t)-N*)2-μ〈k〉k1e(m2-m1)I*(I(t)-I*)2-k2β(R(t)-R*)2+
k1μ〈k〉(N(t)-I(t)-R(t))(I(t)-I*)(e(m2-m1)I(t)-e(m2-m1)I*)+
μ〈k〉k1e(m2-m1)I*(N(t)-N*)(I(t)-I*)+
(k2δ-μ〈k〉k1e(m2-m1)I*)(R(t)-R*)(I(t)-I*)≤
当且仅当N=N*,I=I*时等号成立.此时R=R*.根据Lasalle不变原理和函数V(t)的正定性可知,![]() 全局渐近稳定.从而系统(1)的正平衡点E1=(S*,I*,R*)全局渐近稳定.
全局渐近稳定.从而系统(1)的正平衡点E1=(S*,I*,R*)全局渐近稳定.
例1(系统(1)边界平衡点的全局渐近稳定性) 在系统(1)中,取参数值Λ=0.6,μ=0.1,β=0.3,δ=0.5,m1=0.2,m2=0.1,〈k〉=2.经计算,边界平衡点E0=(3,0,0),基本再生数R0=0.5<1,满足定理3的条件,于是,系统(1)是全局渐进稳定的.使用MATLAB软件进行仿真,分别做出如下图像(图1).在这种情况下,无论3类人的初值是多少,谣言传播者将不存在.也就是说,谣言最终将会消失,并不会对社会产生影响.
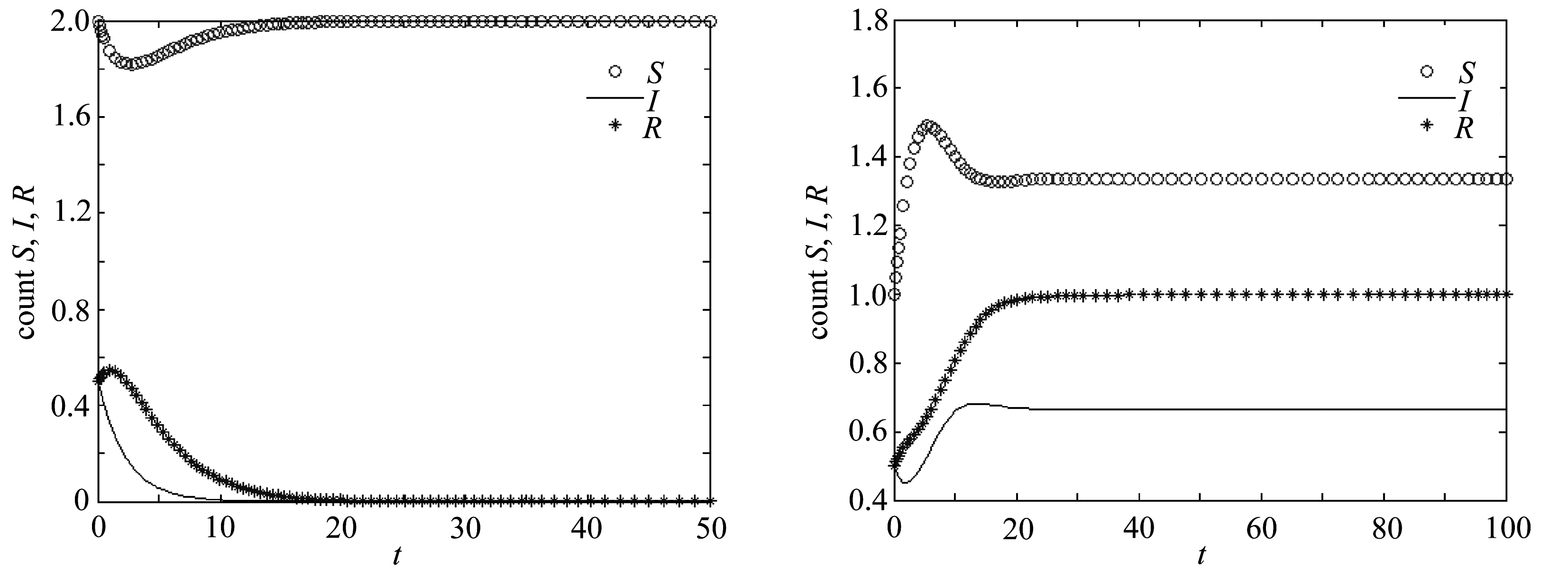
图1 边界平衡点的全局稳定性图2 正平衡点的全局渐近稳定性
Fig. 1 Global stability of boundary equilibrium Fig. 2 Global stability of positive equilibrium
例2(系统(1)正平衡点的全局渐近稳定性) 在系统(1)中,取参数值Λ=0.6,μ=0.2,β=0.2,δ=0.3,m1=0.2,m2=0.1,〈k〉=2.此时,正平衡点E1=(2.546,0.182,0.273),基本再生数R0=2.4>1,并且满足定理4的条件,于是,系统(1)是全局渐进稳定的.使用MATLAB软件进行仿真,分别做出如下图像(图2).在这种情况下,无论3类人的初值是多少,谣言传播者将仍然存在.也就是说,谣言最终将仍然存在,并会对社会产生消极影响.
例3(谣言传播的控制策略1) 在系统(1)中,考虑一个谣言传播者在一个周期内可以传播的人数与谣言传播率有关.取定参数值Λ=0.6,β=0.3,δ=0.5,m1=0.2,m2=0.1,〈k〉=2.而描述谣言基本传播率的参数μ在区间[0,0.5]之间连续变化.使用MATLAB软件做出基本再生数R0随μ的变化曲线图,如图3所示.从图3中可以看出,随着μ的增加,基本再生数R0也会随之增加.当谣言基本传播率μ取较小值时,基本再生数R0<1.即在社交网络中,谣言基本传播率较小,会使一个谣言传播者在单位周期内传播的人数小于1,此时,边界平衡点存在而正平衡点不存在,谣言将会消失.所以,有关部门应该积极采取措施,减少谣言基本传播率,使得基本再生数R0<1,最终将会使谣言消失,减少对社会的消极影响.
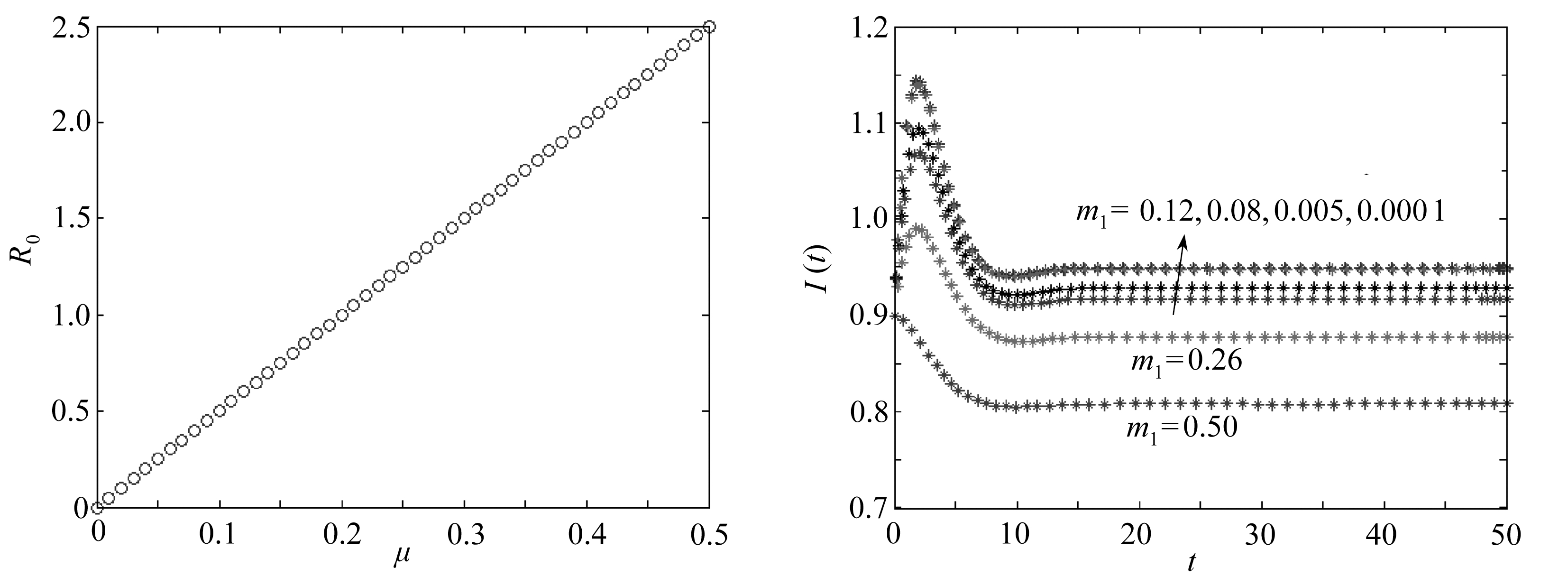
图3R0随μ的变化曲线 图4 不同m1取值下谣言传播者数量
Fig. 3 TheR0 curve withμ 随时间的变化曲线
Fig. 4 The curve of the rumor communicator number changing with time under differentm1 values
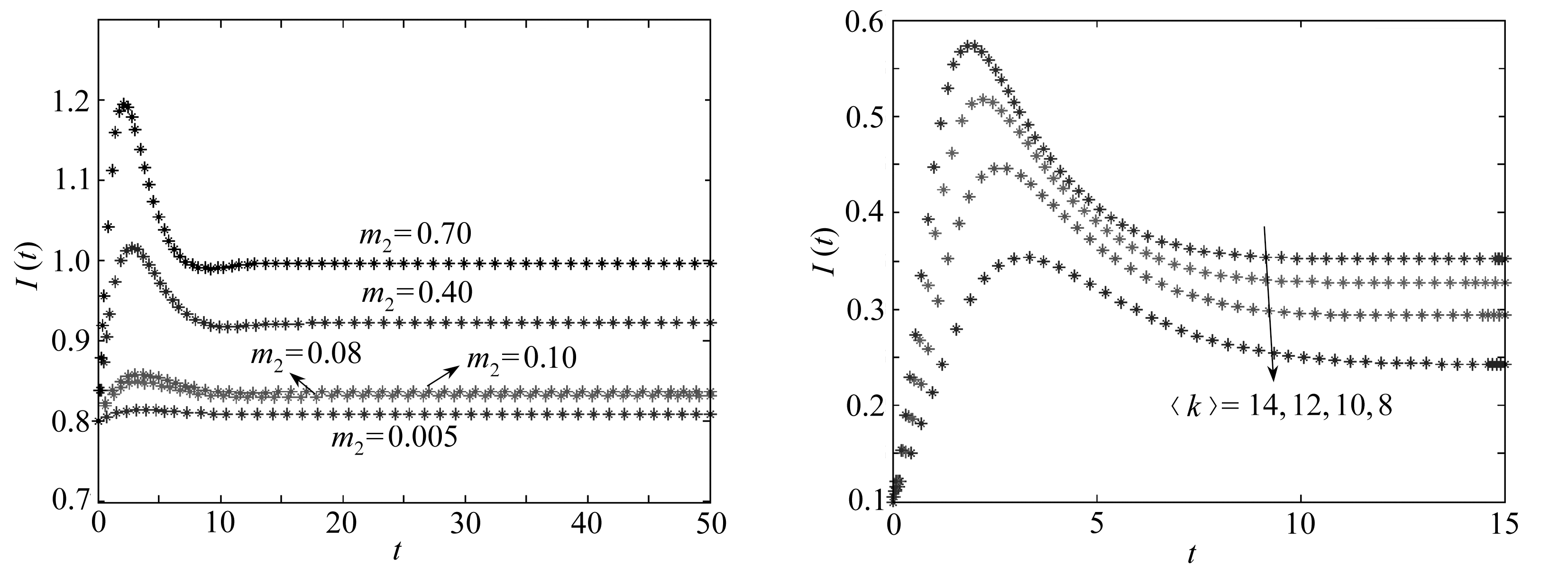
图5 不同m2取值下谣言传播者数量 图6 不同网络平均度下谣言传播者数量
随时间的变化曲线 随时间的变化曲线
Fig. 5 The curve of the rumour communicator number
Fig. 6 The curve of the rumour communicator number changing with time under differentm2 values changing with time under different 〈k〉 values
例4(谣言传播的控制策略2) 考虑谣言传播者数量受媒体报道正面信息和报道负面信息的影响.在系统(1)中取定参数值:Λ=0.6,β=0.2,δ=0.3,μ=0.2,〈k〉=3.下面分析媒体正面报道和媒体负面报道对谣言传播者数量的影响.先取定描述媒体负面报道参数m2=0.3,媒体正面报道参数m1分别取值0.000 1,0.005,0.08,0.12,0.26,0.50.在这6种情况下,正平衡点存在并且全局渐近稳定,不存在边界平衡点.使用MATLAB软件做出上述6种取值情况下谣言传播者数量随时间的变化曲线,如图4所示.在图4中,随着媒体正面报道强度的增加,谣言传播者密度衰减速度越快.也就是说,谣言的传播将会得到缓解.取定描述媒体报道正面信息的参数m1=0.2,媒体负面报道的参数m2分别取值0.005,0.08,0.10,040,0.70.在这5种取值下,正平衡点存在并且全局渐近稳定,边界平衡点不存在.使用MATLAB软件绘制出上述5种取值下,谣言传播者数量随时间的变化曲线,如图5所示.根据图5可以看出,随着媒体负面报道强度的减小,谣言传播者数量也将逐渐减少.此时,谣言的传播也将会得到缓解.所以,有关部门应该积极采取措施,增加媒体对信息正面的报道,减少媒体对信息负面的报道,最终使谣言得到控制,降低谣言带来的危害.
例5(网络平均度对谣言传播的影响) 在系统(1)中取参数值Λ=0.3,μ=0.1,β=0.4,δ=0.2,m2=0.3,m1=0.4,取网络平均度〈k〉=8,〈k〉=10,〈k〉=12,〈k〉=14.在MATLAB中绘制出谣言传播者数量随时间的变化情况图,如图6所示.由于网络平均度描述了每个节点与其他相邻节点链接数目,通过研究不同网络平均度的谣言传播情况,可以探究出网络平均度对谣言传播的影响.从图6中可以看出,网络平均度不同,谣言传播者到达的峰值不同,达到峰值的时间也不同,网络平均度越大,谣言传播者达到的峰值越大,达到峰值越快,并且达到的稳定值越大.所以,有关部门应该采取一定的措施,减少谣言传播者与外界的联系.
媒体报道对信息传播有显著的影响.本文考虑媒体正面报道和负面报道共存的情况,构建了一类新的谣言传播模型.利用稳定性相关理论,讨论了两类平衡点的存在性和全局渐近稳定性,并通过数值仿真,分析了媒体报道和网络的平均度对谣言传播到达峰值和传播规模的影响.在谣言未大范围扩散之前,加大媒体正面报道并减少负面报道力度,谣言将不会爆发,最终将消失.在谣言爆发时加大媒体正面报道虽不能消除谣言但能缩减谣言传播的最终规模.此外,网络平均度越大,谣言传播者达到的峰值越大.因此,政府等相关管理部门应加强对新闻媒体报道的监督和管控,减少谣言传播给社会带来的危害.
致谢 本文作者衷心感谢江苏大学科研立项资助项目(16A310)对本文的资助.
[1] DALEY D, KENDALL D. Epidemics and rumors[J].Nature, 1964,204(4963): 1118.
[2] MAKI D, THOMPSON M.Mathematical Models and Applications[M]. Prentice-Hall, 1973.
[3] ZANETTE D. Critical behavior of propagation on small-world networks[J].Physical Review E, 2001,64(1): 050901.
[4] DIFONZO N, BORDIA P. Rumor, gossip and urban legends[J].Diogenes, 2007,54(1): 19-35.
[5] NEKOVEE M, MORENO Y, BIANCONI G, et al. Theory of rumour spreading in complex social networks[J].Physica A:Statistical Mechanics and Its Applications, 2008,374(1): 457-470.
[6] ZHAO L, WANG Q, CHENG J, et al. Rumor spreading model with consideration of forgetting mechanism: a case of online blogging LiveJournal[J].Physica A:Statistical Mechanics and Its Applications, 2011,390(13): 2619-2625.
[7] HUO L, JIANG J, GONG S, et al. Dynamical behavior of a rumor transmission model with Holling-type Ⅱ functional response in emergency event[J].Physica A:Statistical Mechanics and Its Applications, 2016,450: 228-240.
[8] ZHAO H, ZHU L. Dynamic analysis of a reaction-diffusion rumor propagation model[J].International Journal of Bifurcation and Chaos, 2016,6(26): 1650101-1650111.
[9] QIU X, ZHAO L, WANG J, et al. Effects of time-dependent diffusion behaviors on the rumor spreading in social networks[J].Physica A:Statistical Mechanics and Its Applications, 2016,80(24): 2054-2063.
[10] 刘玉英, 肖燕妮. 一类受媒体影响的传染病模型的研究[J]. 应用数学和力学, 2013,34(4): 399-407.(LIU Yuying, XIAO Yanni. An epidemic model with saturated media /psychological impact[J].Applied Mathematics and Mechanics, 2013,34(4): 399-407.(in Chinese))
[11] 廖书, 杨炜民. 考虑媒体报道效应的双时滞传染病模型[J]. 应用数学和力学, 2017,38(12): 1412-1424.(LIAO Shu,YANG Weiming. An epidemic model with dual delays in view of media coverage[J].Applied Mathematics and Mechanics, 2017,38(12): 1412-1424.(in Chinese))
[12] 霍良安, 黄培清. 科普教育及媒体报道对于不实信息传播的影响[J]. 系统工程理论与实践, 2014,34(2): 365-375.(HUO Liang’an, HUANG Peiqing. Study of the impact of science popularization and media coverage on the transmission of the unconfirmed information[J].System Engineering-Theory and Practice, 2014,34(2): 365-375.(in Chinese))
[13] 赵洪涌, 朱霖河. 社交网络中谣言传播动力学研究[J]. 南京航空航天大学学报, 2015,47(3): 332-342.(ZHAO Hongyong, ZHU Linhe. Research on rumor spreading dynamics in social networks[J].Journal of Nanjing University of Aeronautics and Astronautic, 2015,47(3): 332-342.(in Chinese))
[14] 陈华. 一类具有媒体播报效应的谣言传播模型的定性分析[J]. 西安科技大学学报, 2016,36(2): 255-264.(CHEN Hua. Qualitative analysis of a rumor transmission model with media coverage[J].Journal of Xi’an Science and Technology, 2016,36(2): 255-264.(in Chinese))
[15] 梁新媛, 万佑红. 媒体介入下的谣言传播模型及其控制策略[J]. 南京邮电大学学报(自然科学版), 2017,37(1): 120-126.(LIANG Xinyuan, WAN Youhong. Rumor spreading model and control strategy considering media intervention[J].Journal of Nanjing University of Posts and Telecommunications(Natural Science), 2017,37(1): 120-126.(in Chinese))
[16] HUO L, WANG L, SONG G. Global stability of a two-mediums rumor spreading model with media coverage[J].Physica A:Statistical Mechanics and Its Applications, 2017,482: 757-771.