ojasiewicz不等式，当增广Lagrange(拉格朗日)函数的罚参数充分大时，证明了GADMM所产生的迭代序列收敛到增广Lagrange函数的稳定点．最后，给出了该算法的收敛速度分析．摘要： 考虑利用广义交替方向法(GADMM)求解线性约束两个函数和的最小值问题，其中一个函数为凸函数，另一个函数可以表示为两个凸函数的差．对GADMM的每一个子问题，采用两个凸函数之差算法中的线性化技术来处理．通过假定相应函数满足Kurdyka-ojasiewicz不等式，当增广Lagrange(拉格朗日)函数的罚参数充分大时，证明了GADMM所产生的迭代序列收敛到增广Lagrange函数的稳定点．最后，给出了该算法的收敛速度分析．
关 键 词： 广义交替方向法; Kurdyka-ojasiewicz不等式; 非凸优化; 收敛性
交替方向法(ADMM)[1]是求解如下线性约束两块可分优化问题的经典方法:
(1)
其中d:Rm→R∪+∞是正常下半连续函数，g:Rn→R是光滑函数，A∈Rr×m，B∈Rr×n，c∈Rr．通常d表示正则项，g表示数据拟合项．问题(1)的ADMM迭代格式为
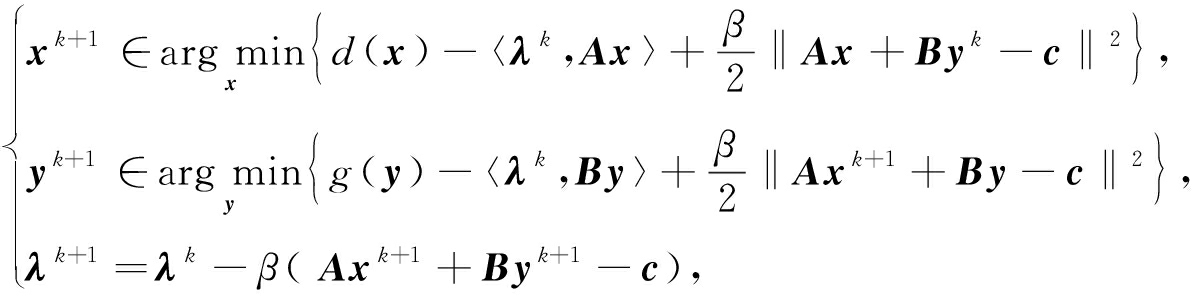
(2)
其中λ是线性约束的Lagrange乘子，β>0是罚参数．由于式(2)中x，y的子问题往往没有显示解，文献[2]通过线性化技术把子问题转化为求d和g的邻近映射，从而可以精确地求解．当d和g都是凸函数时，ADMM(2)的收敛性已经有了很多结果[3-5]．然而，在一些实际问题中，非凸正则函数d能够更好地近似原问题，因此，非凸ADMM的收敛性分析引起了极大的关注[6-9]．文献[10]指出，ADMM(2)实际上是将著名的Douglas-Rachford分裂方法(DRSM)[11]应用到问题(1)的对偶; 在文献[12]中，DRSM进一步解释为邻近点算法(PPA)[13]的应用．鉴于此，文献[12]运用PPA加速形式来加速原始的ADMM(2)，得到了广义交替方向法，其迭代格式为
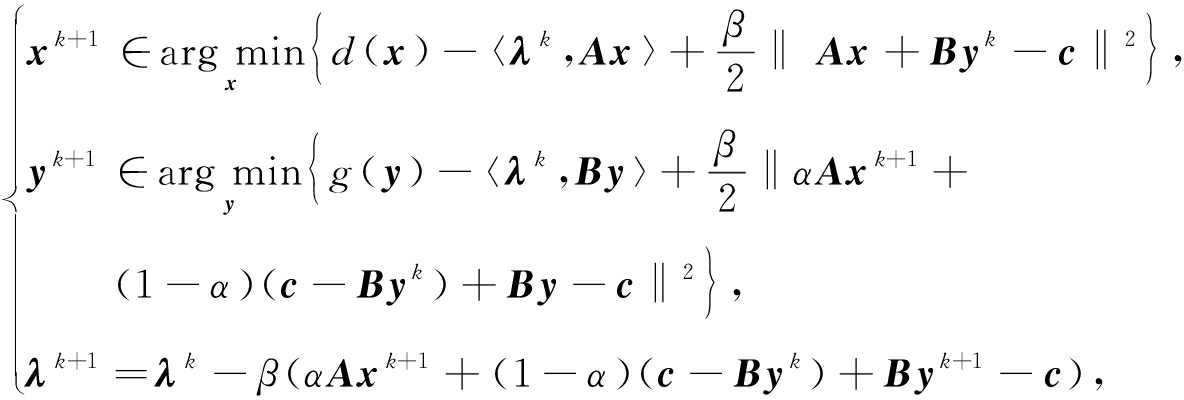
(3)
其中参数α∈(0,2)．容易得知，当α=1时，GADMM(3)退化为经典ADMM(2)．
由于某些非凸罚函数可以表示为两个凸函数的差[14-16]，在本文中，考虑如下形式的非凸优化问题:
(4)
其中f:Rm→R∪+∞是正常下半连续凸函数，h:Rm→R∪+∞是正常下半连续凸函数，g:Rn→R是光滑函数，
g是Lipschitz连续且Lipschitz常数Lg>0，A∈Rr×m，B∈Rr×n，c∈Rr，线性方程Ax+By=c有解．
在最近的研究中，文献[17]利用ADMM(2)并结合Bregman距离求解问题(4)．文献[17]指出在第k+1次迭代中，用〈hk，x〉替换h(x)，其中hk∈∂h(xk)是h在xk的次微分．在本文中，考虑运用GADMM(3)求解问题(4)．问题(4)的GADMM迭代格式为
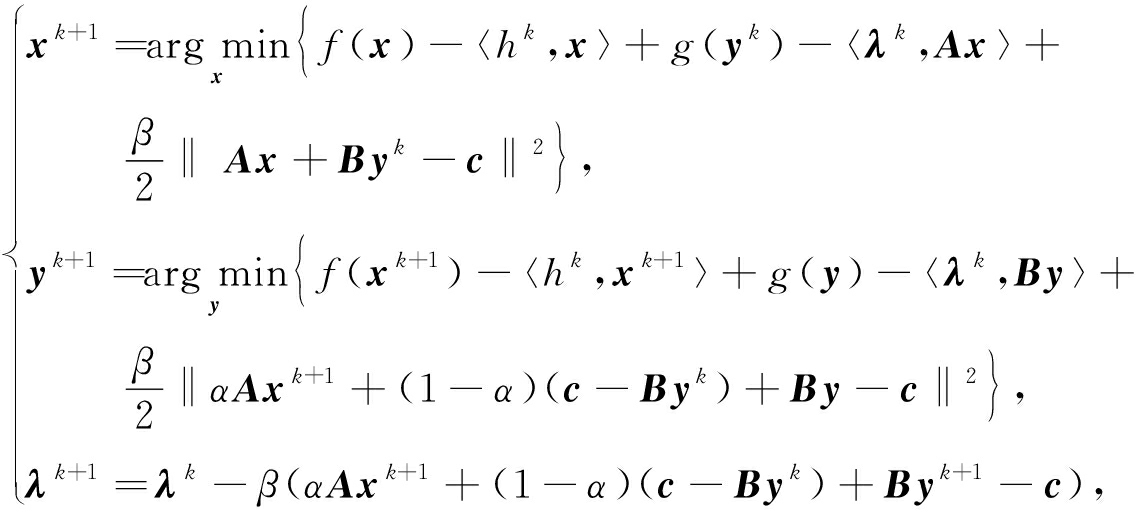
(5)
其中λ是线性约束的Lagrange乘子，β>0是罚参数，参数α∈(0,2)．这里运用了文献[17]中的线性化技术处理h(x)．
因此，本文旨在研究算法(5)的收敛性．通过假定相应函数满足Kurdyka-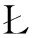
ojasiewicz不等式，当问题(4)的增广Lagrange函数的罚参数充分大时，证明了GADMM(5)产生的迭代序列收敛到增广Lagrange函数的稳定点．在一些更多的假设下，分析了GADMM(5)算法的收敛速度．本文第1节主要介绍了所需的一些基本知识．第2节是文章的主要结果，分析了GADMM(5)算法的收敛性以及证明了该算法的收敛速度．最后，在第3节给出了一些总结．
在本节中，将给出一些在论文中需要用到的基本知识．
设集值映射F:Rn
Rm，它的图像定义为
GraphF
(x，y)∈Rn×Rm:y∈F(x)．
对任意的集合S⊆Rn及任意的点x∈Rn，记d(x,S)为x到S的距离，定义为
d(x,S)
特别地，若S=∅，对任意的x，令d(x,S)+∞．
设函数f:Rn→R∪+∞，其有效域和上图分别定义为
domfx∈Rn:f(x)<+∞, epif(x,α)∈Rn×R:f(x)≤α．
如果domf≠∅，则称函数f是正常的; 如果epif是闭的，则称函数f是下半连续的．
定义1 设函数f:Rn→R∪+∞是一个正常下半连续函数．
函数f在x∈domf处的Fréchet次微分，记作
定义为所有满足下述关系的x*的集合
若x∉domf，令
∅;
函数f在x∈domf处的极限次微分，记作∂f(x)，定义为
∂f(x)x*∈Rn:
次微分的定义可以在文献[18]中找到．当f为凸函数时，其定义与凸分析[19]中的一致，即
∂f(x)v:f(y)≥f(x)+〈v,y-x〉,∀y∈Rn．
注1 从上述定义，可以得到
∂f(x),∀x∈Rn，其中
为闭凸集，而∂f(x)仅为闭集．
设
且收敛到(x，x*)．由∂f(x)的定义，当k→+∞时，若f(xk)收敛到f(x)，则(x，x*)∈Graph ∂f．
x∈Rn为函数f稳定点的必要条件是
0∈∂f(x)．
(6)
如果f:Rn→R∪+∞是正常下半连续函数，g:Rn→R是连续可微函数，那么对∀x∈domf，都有∂(f+g)(x)=∂f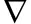(x)+
g(x)．
满足式(6)的点x称为稳定点，函数f的所有稳定点集合记为critf．
引理1 设H(x，y,z)f(x)+g(y)+h(z)，其中f:Rn→R∪+∞,g:Rm→R∪+∞,h:Rp→R∪+∞均为正常下半连续函数．对任意(x，y,z)∈domHdomf×domg×domh，有
∂H(x，y,z)=∂xH(x，y,z)×∂yH(x，y,z)×∂zH(x，y,z)．
定义2(Kurdyka-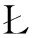ojasiewicz不等式)[20] 设函数f:Rn→R∪+∞是正常下半连续函数．令-∞<η1<η2≤+∞，记
[η1<f<η2]x∈Rn:η1<f(x)<η2．
称函数f在x*∈dom ∂f具有KL性质，若存在η∈(0，+∞]，x*的邻域U及连续凹函数φ: [0,η)→R+，使得
φ(0)=0;
φ在(0，η)上连续可微且在0处连续;
φ′(s)>0,∀s∈(0，η);
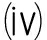对∀x∈U∩ [f(x*)<f<f(x*)+η]，Kurdyka-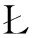ojasiewicz不等式都成立:
φ′(f(x)-f(x*))d(0，∂f(x))≥1．
定义3(Kurdyka-ojasiewicz函数)[20] 记Φη是满足定义2中、和的函数集合．若函数f在dom ∂f中的每一点都满足KL性质，则函数f称为KL函数．
注2[20] 函数f:Rn→R∪+∞是正常下半连续函数，设
是函数f的非稳定点，则存在c>0，使得
正常下半连续函数f在非稳定点，
∉
都满足Kurdyka-ojasiewicz性质．
引理2(KL性质)[21] 设Ω为紧集，函数f:Rn→R∪+∞是正常下半连续函数．假设函数f在Ω上为常数且在Ω的每一点都满足KL性质，则存在
>0，η>0，φ∈Φη，使得对任意
及任意x属于下述交集
有
定义4[22] 设函数g:Rn→R是光滑函数，称其梯度Lipschitz连续，即存在Lipschitz常数Lg>0，如果对任意x,y∈Rn，有
‖g(x)-g(y)‖≤Lg‖x-y‖．
(7)
定义5 称(x*，y*，λ*)是问题(4)增广Lagrange函数Lβ(·)(12)的稳定点，如果下述条件成立：
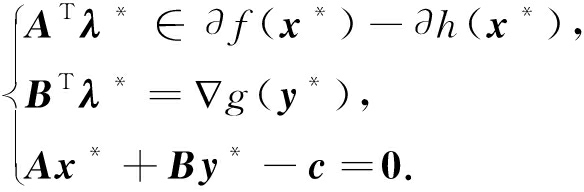
由算法(5)的最优性条件，经过变形得到
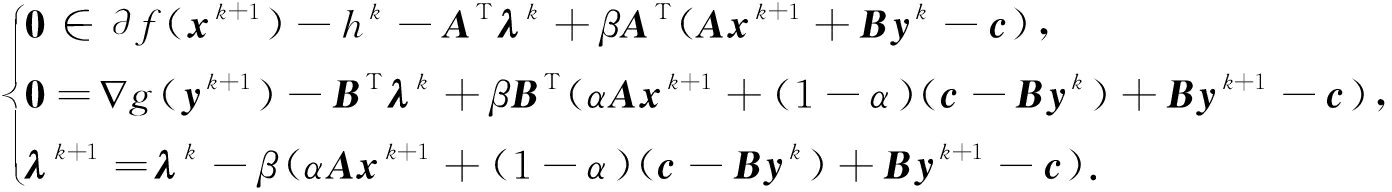
(8)
将式(8)的最后一个等式经过变形得到
(9)
和
(10)
假设1 设f:Rm→R∪+∞是正常下半连续凸函数，h:Rm→R∪+∞是正常下半连续凸函数，g:Rn→R是光滑函数，g是Lipschitz连续且Lipschitz常数Lg>0．假设以下条件都是满足的:
infx∈Rm f(x)>-∞, infy∈Rn g(y)>-∞;
ATA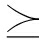
μI对任意μ>0;
对任意矩阵A∈Rr×m，有Im(A)Ax|x∈Rm，且
Im(A)∪cIm(B)．
(11)
记θ是(BBT)1/2最小正奇异值．
为了后面证明更方便，记ωk(xk,yk,λk)k∈N和vk(xk,yk)k∈N．问题(4)的增广Lagrange函数定义为
Lβ(x，y,λ)f(x)-h(x)+g(y)-
(12)
其中，λ是线性约束的Lagrange乘子，β>0是罚参数．问题(4)的线性化增广Lagrange函数定义为
其中hk∈∂h(xk)．为了方便证明，记
f(x)-〈hk，x〉+g(y)-〈λ，Ax+By-c〉+
从下面的引理开始收敛性分析．
引理3 若假设1中的成立，则
‖λk+1-λk‖2≤η‖yk+1-yk‖2，
(13)
其中η
证明 由式(8)的第二个等式得
g(yk+1)-BTλk+βBT(αAxk+1+(1-α)(c-Byk)+Byk+1-c)=0，
(14)
而
λk+1=λk-β(αAxk+1+(1-α)(c-Byk)+Byk+1-c),
故有
g(yk+1)-BTλk+1=0．
(15)
用k替换上式中的k+1可得
g(yk)-BTλk=0．
(16)
在假设1的条件下，λk+1-λk∈Im(BT)．然后得出
g(yk+1)-
从而可以得到
(17)
证毕．
引理4 设ωkk∈N是由GADMM(5)产生的一个序列，假设该序列是有界的，则有
Lβ(ωk+1)≤Lβ(ωk)-δ‖vk+1-vk‖2．
(18)
证明 首先，由定义得
f(xk)-f(xk+1)+〈hk,xk+1-xk〉+〈λk，Axk+1-Axk〉+
f(xk)-f(xk+1)+〈hk,xk+1-xk〉+〈λk，Axk+1-Axk〉+
(19)
由式(8)的第一个等式得
hk+ATλk-βAT(Axk+1+Byk-c)∈∂f(xk+1)，
(20)
因为f是凸函数，由式(20)可得
f(xk)≥f(xk+1)+〈hk+ATλk-βAT(Axk+1+Byk-c)，xk-xk+1〉．
由假设1的可得
‖Axk+1-Axk‖2≥μ‖xk+1-xk‖2．
则将上述3个不等式代入式(19)得到
(21)
同样地,
f(xk+1)-〈hk,xk+1〉+g(yk)-〈λk，Axk+1+Byk-c〉+
g(yk)-g(yk+1)+〈λk，B(yk+1-yk)〉-αβ〈Axk+1+Byk-c，B(yk+1-yk)〉-
由g的凸性以及式(15)，可得
g(yk)-g(yk+1)≥〈g(yk+1)，yk-yk+1〉=〈BTλk+1,yk-yk+1〉．
(22)
因此，结合式(10)和(22)可以得出
(23)
第二个不等式由假设1的可得．接下来，估计剩下的部分：
因为
f(xk+1)-〈hk,xk+1〉+g(yk)-〈λk，Axk+1+Byk-c〉+
(24)
且
f(xk+1)-〈hk,xk+1〉+g(yk+1)-〈λk，Axk+1+Byk+1-c〉+
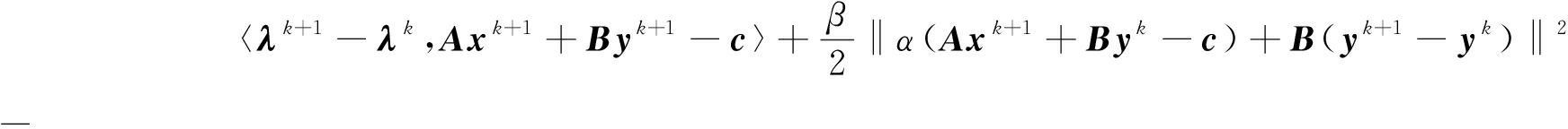
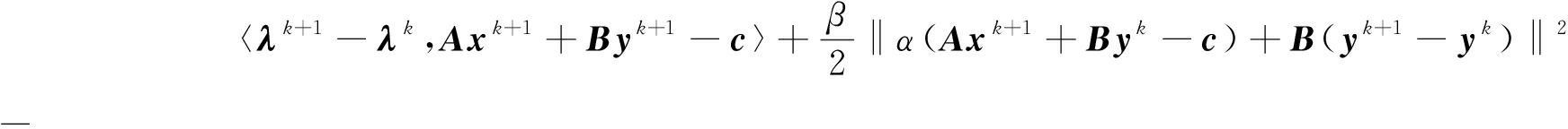
αβ〈Axk+1+Byk-c,B(yk+1-yk)〉-
(25)
将式(24)和(25)相加，得到
〈λk+1-λk，Axk+1+Byk+1-c〉-(1-α)β〈Axk+1+Byk-c，B(yk+1-yk)〉 =
(1-α)β
=
(26)
其中第二个等式从式(9)、(10)可以得到，最后一个不等式由假设1的可得．由引理4可知
‖λk+1-λk‖2≤η‖yk+1-yk‖2．
因此，可得
(27)
注意到
Lβ(xk,yk,λk)-Lβ(xk+1,yk+1,λk+1)=
(28)
且
(29)
由于h是凸函数，hk∈∂h(xk)，故
h(xk+1)-h(xk)≥〈hk,xk+1-xk〉．
(30)
结合式(28)、(29)和(30)可得
观察到
Lβ(ωk)-Lβ(ωk+1)=
Lβ(xk,yk,λk)-Lβ(xk+1,yk+1,λk+1)≥
(31)
因此，将式(21)、(23)和(27)代入式(31)，可得
令
δminδ1,δ2,
其中
δ1
δ2
故得到式(18)成立．证毕．
引理5 设ωkk∈N是由GADMM(5)产生的一个序列，假设该序列是有界的，则有下式成立：
(32)
证明 因为ωkk∈N是有界的，故存在子列ωkjj∈N使得ωkj→ω*．首先，由函数g的连续性和函数f的闭性可知，Lβ(·)是下半连续的，即
因此，Lβ(ωkj)j∈N是有下界的．又由式可得Lβ(ωk)k∈N是非增的，因此Lβ(ωkj)j∈N是收敛的．进而可知Lβ(ωk)k∈N是收敛的且Lβ(ωk)≥Lβ(ω*)．由式(18)变形得到
δ‖vk+1-vk‖2≤Lβ(ωk)-Lβ(ωk+1)．
将上述不等式从k0,1,…,m求和得
令m→+∞，可得
由于δ>0，则有
因此，得到
(33)
此外，从式(18)和(33)可得
因此
证毕．
□
引理6 设ωkk∈N是由GADMM(5)产生的一个序列，假设该序列是有界的，则存在ζ>0使得
d(0,∂Lβ(ωk+1))≤ζ‖yk+1-yk‖．
(34)
证明 根据增广Lagrange函数Lβ(·)的定义和注1的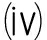，有
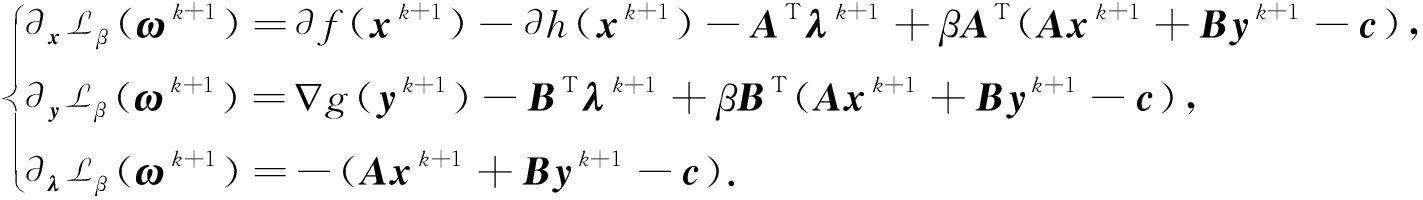
(35)
将式(15)和式(20)代入式(35)，得到
(36)
因此，若记
则从引理1可得
进而，存在ζ1,ζ2>0使得
(37)
可以从式(13)得出
记ζ
有
设ωkk∈N是从ω0开始由GADMM(5)产生的一个序列，其极限点集合记为S(ω0)，即S(ω0)ω* :ωkk∈N的一个收敛到ω*的子列ωkjj∈N．接下来，总结了极限点集合的几个性质．
引理7 设ωkk∈N是由GADMM(5)产生的一个序列，假设该序列是有界的．S(ω0)表示它的极限点集合，则有
S(ω0)是一个非空紧集，当k →+∞时，d(ωk,S(ω0))→0;
S(ω0)⊂crit Lβ;
Lβ(·)在S(ω0)中是有限常数，等价于
证明 逐项证明这些结果．
由极限点定义可得．
取(x*,y*,λ*)∈S(ω0)，存在子列(xkj,ykj,λkj)j∈N收敛到(x*,y*,λ*)．根据增广Lagrange函数Lβ(·)(12)的定义，式(5)的子问题等价于xk+1∈arg minx Lβ(x,yk,λk),则xk+1是Lβ(x,yk,λk)的全局最小值，有
Lβ(xk+1,yk,λk)≤Lβ(x*,yk,λk)．
利用上述不等式和Lβ(·)关于y和λ的连续性得
(38)
此外，式(32)推出了‖ωk+1-ωk‖→0，得到子列(xkj+1,ykj+1,λkj+1)j∈N也收敛到(x*,y*,λ*)．由Lβ(·)的下半连续性得
(39)
然后通过结合式(38)和(39)得到
则可得
(40)
在式(35)中沿着子列(xkj+1,ykj+1,λkj+1)j∈N传递极限，运用式(40)和g的连续性，可以得出
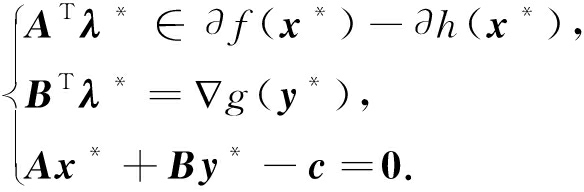
因此，(x*,y*,λ*)∈crit Lβ．
对任意(x*,y*,λ*)∈S(ω0)， 存在一个子列(xkj,ykj,λkj)j∈N 收敛到(x*,y*,λ*)．因为Lβ(ωk)是非增的，结合式(38)和(39)可得
因此，Lβ(·)在S(ω0)中为常数．进而有
证毕．
□
定理1 设ωkk∈N是由GADMM(5)产生的一个序列，假设该序列是有界的．假设Lβ(·)是一个KL函数，则ωkk∈N是有限长的，即
因此ωkk∈N收敛到Lβ(·)的稳定点．
证明 我们知道对所有的ω*∈S(ω0)，Lβ(ωk)→Lβ(ω*)．考虑下面两种情况:
1) 若存在整数k0使得Lβ(ωk0)= Lβ(ω*)成立，改变式(18)的形式，对任意k>k0，有
δ‖vk+1-vk‖2≤Lβ(ωk)-Lβ(ωk+1)≤Lβ(ωk0)-Lβ(ω*)=0,
对任意k>k0推出vk+1=vk．结合式(11)对任意k>k0+1，由此可知ωk+1=ωk且推论成立．
2) 现在假设对任意k有Lβ(ωk)>Lβ(ω*)，存在
使得对任意
有
δ‖vk+1-vk‖2≤ζ·‖vk-vk-1‖·Δk,k+1,
(41)
其中Δp,qφ(Lβ(ωp)-Lβ(ω*))-φ(Lβ(ωq)-Lβ(ω*))．注意到d(ωk,S(ω0))→0和Lβ(ωk)→Lβ(ω*)，则对任意
,κ>0存在
使得对所有
有
d(ωk,S(ω0))<, Lβ(ω*)<Lβ(ωk)<Lβ(ω*)+κ．
因为S(ω0)是非空紧集且Lβ(·)在S(ω0)中为常数，由引理4和ΩS(ω0)知，对所有有
φ′(Lβ(ωk)-Lβ(ω*))d(0,∂Lβ(ωk))≥1．
由Lβ(ωk)-Lβ(ωk+1)=(Lβ(ωk)-Lβ(ω*))-(Lβ(ωk+1)-Lβ(ω*))以及φ的凹性可得
φ(Lβ(ωk)-Lβ(ω*))-φ(Lβ(ωk+1)-Lβ(ω*))≥
φ′(Lβ(ωk)-Lβ(ω*))(Lβ(ωk)-Lβ(ωk+1))．
利用不等式d(0,∂Lβ(ωk))≤ζ‖yk-yk-1‖≤ζ‖vk-vk-1‖和φ′(Lβ(ωk)-Lβ(ω*))>0，得到
Lβ(ωk)-Lβ(ωk+1)≤
ζ·‖vk-vk-1‖·[φ(Lβ(ωk)-Lβ(ω*))-φ(Lβ(ωk+1)-Lβ(ω*))]．
(42)
结合引理4和式(42)，由式(41)推出
由于对所有α,β>0有
则可得
将不等式(41)从k
求和，可得
因为φ(Lβ(ωm+1)-Lβ(ω*))>0，经过变形，令m→+∞得到
(43)
从而有
因此，得到
结合式(13)，有
此外，可得
‖ωk+1-ωk‖=
(‖xk+1-xk‖2+‖yk+1-yk‖2+‖λk+1-λk‖2)1/2≤
‖xk+1-xk‖+‖yk+1-yk‖+‖λk+1-λk‖．
因此
证毕．
□
定理2 设ωkk∈N是由GADMM(5)产生的一个序列且收敛到ω*(x*，y*，λ*)．假设Lβ(·)在(x*,y*,λ*)满足KL性质且φ(s)cs1-ι，ι∈[0,1)，c>0．则以下结论成立:
若ι=0，则序列ωkk∈N在有限次迭代后收敛;
若ι∈(0,1/2]，则存在c>0和τ∈[0,1)，使得
‖(xk,yk,λk)-(x*,y*,λ*)‖≤cτk;
若ι∈(1/2,1)，则存在c>0，使得
‖(xk,yk,λk)-(x*,y*,λ*)‖≤ck(ι-1)/(2ι-1)．
证明 在ι=0的情况下，有φ(s)=cs和φ′(s)=c．若ωkk∈N在有限次迭代后不收敛，则对任意足够大的k，在(x*,y*,λ*)处由KL性质有c·d(0,∂Lβ(ωk))≥1， 这与式(34)矛盾．假设ι>0，记作
Δk
由三角不等式Δk≥‖vk-v*‖，可以估计出Δk．进而从式(43)得到
因为Lβ在(x*,y*,λ*)满足KL性质，所以
由于φ(s)=cs1-ι，上述不等式等价于
(44)
由式(34)推出
(45)
结合式(44)和(45)，则存在γ>0使得
于是有
Attouch和Bolte在文献[23]中研究了满足这种不等式的序列，即
若ι∈(0,1/2]，则存在c1>0和τ∈[0,1)，使得
‖vk-v*‖≤c1τk；
(46)
若ι∈(1/2,1)，则存在c2>0，使得
‖vk-v*‖≤c2k(ι-1)/(2ι-1)．
(47)
则可以推出
若ι∈(0,1/2]，则存在c1>0和τ∈[0,1)，使得
‖xk-x*‖≤c1τk, ‖yk-y*‖≤c1τk；
(48)
若ι∈(1/2,1)，则存在c2>0，使得
‖xk-x*‖≤c2k(ι-1)/(2ι-1), ‖yk-y*‖≤c2k(ι-1)/(2ι-1)．
(49)
在假设1的条件下，λk-λ*∈Im(BT)，所以
g(yk)-
(50)
上面的最后一个不等式是由g的Lipschitz连续性得出．
将式(48)代入式(50)，有
若ι∈(0,1/2]，则存在c3c1Lg/θ和τ∈[0,1)，使得
‖λk-λ*‖≤c3τk；
(51)
若ι∈(1/2,1)，则存在c4c2Lg/θ，使得
‖λk-λ*‖≤c4k(ι-1)/(2ι-1)．
(52)
结合式(51)和(52)，从式(46)和(47)可得所证不等式成立．证毕．
□
本文主要分析了GADMM求解线性约束两个可分函数和的最小值问题．对广义交替方向法的每一个子问题，采用凸函数差分算法中的线性化技术来类似地处理．假设增广Lagrange函数满足 Kurdyka-ojasiewicz不等式，当增广Lagrange函数的罚参数大于阈值时，证明了由GADMM产生的迭代序列收敛到增广Lagrange函数的稳定点．在更多的假设条件下，证明了算法的收敛速度．在将来的研究中，可以考虑利用GADMM并结合Bregman距离求解线性约束两个可分函数和的最小值问题．
致谢 本文作者衷心感谢西华师范大学国家一般培育项目(18B031)和西华师范大学博士科研启动项目(17E084)对本文的资助．
[1] GLOWINSKI R, MARROCCO A. Sur l’approximation par éléments finis d’ordre un et la résolution par pénalisation-dualité d’une classe de problèmes de Dirichlet non linéaires[J].Journal of Equine Veterinary Science, 1975,2: 41-76.
[2] YANG J F, YUAN X M. Linearized augmented Lagrangian and alternating direction methods for nuclear norm minimization[J].Mathematics of Computation, 2013,82(281): 301-329.
[3] HE B S, YUAN X M. On non-ergodic convergence rate of douglas-rachford alternating direction method of multipliers[J].Numerische Mathematik, 2015,130(3): 567-577.
[4] HE B S, YUAN X M. On theo(1/n) convergence rate of the Douglas-Rachford alternating direction method[J].Society for Industrial and Applied Mathematics, 2012,50(2): 700-709.
[5] HONG M Y, LUO Z Q. On the linear convergence of the alternating direction method of multipliers[J].Mathematical Programming, 2017,162(2): 165-199.
[6] GUO K, HAN D R, WU T T. Convergence of alternating direction method for minimizing sum of two nonconvex functions with linear constraints[J].International Journal of Computer Mathematic, 2017,94(8): 1653-1669.
[7] GUO K, HAN D R, WANG Z W, et al. Convergence of ADMM for multi-block nonconvex separable optimization models[J].Frontiers of Mathematics in China, 2017,12(5): 1139-1162.
[8] LI G Y, PONG T K. Global convergence of splitting methods for nonconvex composite optimization[J].SIAM Journal on Optimization, 2015,25(4): 2434-2460.
[9] YU W, YIN W T, ZENG J S. Global convergence of ADMM in nonconvex nonsmooth optimization[J/OL].Journal of Scientific Computing, 2015. [2017-12-27]. https: // doi.org/ 10.1007/s10915-018-0757-z.
[10] GABAY D. Applications of the method of multipliers tovariational inequalities[C]//In Augmented Lagrangian Methods:Applications to the Numerical Solution of Boundary-Value Problems. Amsterdam, Holland, 1983.
[11] LIONS P L, MERCIER B. Splitting algorithms for the sum of two nonlinear operators[J].Siam Journal on Numerical Analysis, 1979,16(6): 964-979.
[12] ECKSTEIN J, BERTSEKAS D. On the Douglas-Rachford splitting method and proximal point algorithm for maximal monotone operators[J].Mathematical Programming, 1992,55(1): 293-318.
[13] MARTIENT B. Regularisation d’inéquations variations par approximations succesives[J].Rev Française Informat Recherche Opérationnelle, 1970,4(4): 154-159.
[14] YIN P A, XIN J. Iterativel1-minimization for non-convex compressed sensing[J].Journal of Computational Mathematics, 2017,35(4): 439-451.
[15] LOU Y F, YIN P H, XIN J. Point source super-resolution via non-convexl1 based methods[J].Journal of Scientific Computing, 2016,68(3): 1082-1100.
[16] YIN P H, LOU Y F, HE Q, et al. Minimization of 1-2 for compressed sensing[J].SIAM Journal on Scientific Computing, 2015,37(1): A536-A563.
[17] SUN T, YIN P H, CHENG L Z, et al. Alternating direction method of multipliers with difference of convex functions[J].Advances in Computational Mathematics, 2017,44(3): 1-22.
[18] ROCKAFELLAR R T, WETS R J.Variational Analysis[M]. Berlin: Springer-verlag, 1998.
[19] ROCKAFELLAR R T.Convex Analysis[M]. Princeton: Princeton University Press, 1970.
[20] ATTOUCH H, BOLTE J, REDONT P, et al. Proximal alternating minimization and projection methods for nonconvex problems: an approach based on the Kurdyka-
ojasiewicz inequality[J].Mathematics of Operations Research, 2010,35(2): 438-457.
[21] BOLTE J, SABACH S, TEBOULLE M. Proximal alternatinglinearized minimization for nonconvex and nonsmooth problems[J].Mathematical Programming, 2014,146(1): 459-494.
[22] NESTEROV Y.Introductory Lectures on Convex Optimization:A Basic Course[M]. Boston: Kluwer Academic Publishers, 2004.
[23] ATTOUCH H, BOLTE J. On the convergence of the proximal algorithm for nonsmooth functions involving analytic features[J].Mathematical Programming, 2009,116(1): 5-16.
Abstract: The generalized alternating direction method of multipliers (GADMM) for the minimization problems of the sum of 2 functions with linear constraints was considered, where one function was convex and the other can be expressed as the difference of 2 convex functions. For each subproblem in the GADMM, the linearization technique in the convex function difference algorithm was employed. Under the assumptions that the associated functions satisfy the Kurdyka-ojasiewicz inequality, the sequence generated with the GADMM converges to a critical point of the augmented Lagrangian function, while the penalty parameter in the augmented Lagrangian function is sufficiently large. At last, the convergence rate of the algorithm was established.
Key words: generalized alternating direction method of multipliers; Kurdyka-ojasiewicz inequality; nonconvex optimization; convergence