我国自改革开放以来，经济快速发展的同时也导致化石能源大量的消耗，并引出了一系列的资源环境问题，大力发展清洁能源已刻不容缓．天然气作为优质清洁能源，近年来消费需求量不断增加[1]．研究天然气生产企业适应产业升级和市场选择的竞争机制，提出中国天然气市场供给侧改革的有效措施，具有重要的现实意义．由于自然垄断、规模和范围经济等显著特点，中国天然气供给市场将长期处于“中石油”“中石化”和“中海油”三寡头垄断局面[2]．对于三寡头垄断市场结构，学者们做了大量的研究：吉伟卓等[3]运用非线性需求成本函数研究了电力市场三寡头博弈模型，分析了最佳的产量生产决策；Elabbasy等[4]构建了三寡头在具有不同理性基础上的离散模型，并分析了系统存在平衡点的相关稳定性条件；Chen和Ma等[5]研究了中国移动通信市场伯川德三寡头博弈模型，得出寡头之间的价格调整在一定条件下会导致整个市场进入无序竞争状态的结论；Ma和Ji[6]刻画了电力市场不同过网费情形的三寡头竞争行为，并研究得出过网费过高将增加企业转移成本并减少消费者剩余的结论；Agiza等[7]通过构建有限理性Bowley模型，分析了系统的时滞反应情形，探究了平衡点的存在与稳定性问题；谢英超等[8]利用Lyapunov-LaSalle不变集原理，研究了一类具有非线性发生率的时滞SIRS传染病模型,通过分析动力学行为及线性化近似系统特征方程，证明了无病平衡点的局部稳定性；孙继涛等[9]通过引进随机Liapunov-Krasovskii泛函, 使用自由权矩阵技术，研究了具有时变滞后与时变结构不确定的跳跃系统的随机稳定性与H∞扰动衰减；高琴[10]通过建立非线性模型，针对集装箱码头公司之间的竞争与合作，研究系统的稳定性；Son等[11]研究了延迟系统的动态模型，并分析了局部稳定性；徐伟等[12]研究了保险市场中三寡头垄断的动态博弈模型，并分析了参数变化对系统稳定性的影响；杨俊等[13]研究了天然气市场不同预期规则下的三寡头博弈模型，分析了天然气市场三寡头在不同预期情形下决策过程的动力学特性．随着知识竞争日趋激烈,技术、管理、制度等知识创新竞争已经成为寡头垄断市场各企业竞争的核心竞争力[14]，中国天然气市场也不会例外．
综上所述，可以看出：1) 现有文献对中国天然气三寡头垄断市场的研究较少，文献[13]研究了天然气三寡头在不同利润预期情形下的决策过程动力学特性，但没有涉及生产动能转换的创新投入转化问题； 2) 一些文献对其他产业寡头博弈模型研究相对较多，但主要关注于价格、成本调整策略本身，对于影响价格、成本关键因素的技术进步问题鲜有涉及； 3) 一些文献虽然研究了寡头垄断市场整个系统的平衡点存在性及其各自的稳定情况，但对影响系统平衡稳定因素探讨还不够深入．本文在综合借鉴上述文献系统论、寡头博弈、平衡点稳定性分析等研究方法基础上，以天然气产业创新投入决策博弈视角，将创新投入产出周期、价格调整幅度与速度等作为变量，建立基于创新驱动的天然气市场三寡头动态微分博弈定价模型，刻画了中国天然气三寡头垄断市场企业间采取创新协同与价格竞争相结合的决策行为，分析了系统均衡和寡头创新投入最优策略，以期为中国天然气产业健康发展和天然气生产企业科学决策提供一些有效的参考依据．
为简化分析过程,下文用A、B、C表示天然气市场三寡头，A为天然气主导企业, B和C为采取有限理性决策的企业．一方面，他们充分运用各自拥有的知识、技术、制度(以下简称知识创新)来独立地开展本职业务;另一方面，他们各自独立决策对知识创新的投入来降低成本，而对知识创新的成果由于信息透明导致成果共享．这里，用m表示业务分工努力，用n表示创新努力并假定其全部转化为价值链上的新知识．(mA,nA)，(mB,nB)，(mC,nC)分别表示A、B、C的两种努力向量．A、B、C的两种努力成本可用下面的凸函数表示[15]:
其中，σi(i=1,2,3,4,5,6)为不同努力成本影响系数．可用式(1)表示天然气三寡头垄断市场企业价值链协同创新过程：
(1)
其中，K(t)表示t时刻整个市场价的总体知识水平,其初始值为K(0)=K0;nA，nB，nC为A、B、C创造出的新知识,α，β，γ分别表示A、B、C各自对天然气行业的知识创新投入产出贡献系数，φ表示整个行业知识创新水平随时间推移的衰减系数．
由于mA，mB，mC代表A、B、C各自行业分工上的努力,根据委托-代理理论关于收益是努力的线性函数的假设,A、B、C所在市场的收益函数可用式(2)表示:
Q(mA(t),mB(t),mC(t),K(t))=εmA(t)+ηmB(t)+ωmC(t)+δK(t),
(2)
其中,ε，η，ω均为常数,分别代表A、B、C在行业知识分工努力的收益影响因子；δ为知识价值转化因子,δK(t)反映了A、B、C对整个行业知识创新贡献．
假设A、B、C合作产生的收益只在三个寡头A、B、C之间分配,θ1，θ2，θ3分别为常数代表A、B、C获得收益的份额，满足条件θ1，θ2，θ3∈[0,1]且θ1+θ2+θ3=1．假定A、B、C各自独立地开展知识创新，由于知识创新的溢出效应和行业信息的透明，寡头企业各自进行理性同时博弈．如用μ表示折现率,则A、B、C的目标函数可分别设定为
(3)
(4)
(5)
为了求解该微分博弈的反馈Nash平衡,引入动态规划的方法[16]以及Stackelberg微分博弈模型的求解方法[17]．通过动态规划求解,可以推导该寡头垄断市场协同创新的反馈Nash平衡．先确定一组连续、可微 、有界的值函数[18]VA(K)，VB(K)，VC(K), 并构建Hamilton-Jacobi-Bellman(HJB)方程式如下[19]:
(6)
(7)
(8)
方程右端通过HJB方程最大化有
(9)
(10)
(11)
把式(9)～(11)分别代入到上文构建的HJB方程式(6)～(8)右端，则有
(12)
(13)
(14)
根据式(12)～(14)可以判断, 上述方程关于K的线性最优值函数必然是上文构建的HJB方程的解．设
VA(K)=a1K+a2,VB(K)=b1K+b2，VC(K)=c1K+c2,
a1,a2,b1,b2,c1,c2为常量，将其代入到式(12)～(14)，则有
μ(a1K+a2)=(θ1δ-a1φ)K+
(15)
μ(b1K+b2)=(θ2δ-b1φ)K+
(16)
μ(c1K+c2)=(θ3δ-c1φ)K+
(17)
由式(15)～(17)可以得到最优值函数系数:
将系数a1，a2，b1，b2，c1，c2代入式(9)～(11)中，可以推导出市场三寡头创新的反馈Nash平衡：
(18)
(19)
(20)
将式(18)～(20)代入式(1)，可得
(21)
如果pi(t),i=1,2,3分别表示A、B、C天然气生产厂商对其各自天然气产品的定价；qi,i=1,2,3为各天然气生产厂商其天然气产品的市场需求量，那么A、B、C各天然气生产厂商相应的需求函数分别为
(22)
其中,a,bi,gi,hi>0(i=1,2,3),a为整个天然气市场的最大需求量，bi为各天然气生产厂商的需求弹性，gi,hi为其中两个天然气生产商产品的替代率．由于天然气上游产业具有技术含量高、投资密度大、风险成本高、沉入成本多、链路一体化等特性[20]，根据剑桥能源研究所Marie N Fagan(玛丽·菲根)2006年发表论文指出，采掘成本受到技术改进而降低成本和油气耗竭导致增加成本的双向竞争影响[21]．为了刻画天然气生产采掘和运输供给这一上游特征，本文假定有足够的创新投入产出来降低可变成本，因此，设cfi为各天然气生产商其产品单位成本中在当期创新难以改变的部分(简称当期固定成本)，ci>0,i=1,2,3分别为第i个天然气生产商其产品单位成本中可以通过当期创新改变的部分(简称当期可变成本)．那么可以假定A、B、C天然气生产商的单位成本函数为式(23)的形式：
(23)
因此，天然气市场商的利润函数可表示为
πi(p1,p2,p3)=piqi-ciqi．
(24)
将式(22)代入式(24)，得
(25a)
(25b)
(25c)
根据式(25)，三寡头A、B、C的边际利润可用式(26)表示：
(26)
这里假定天然气生产商A采取自适应决策，根据∂π1(p1,p2,p3)/∂p1=0计算出的价格
与实施知识创新τ时刻之前的价格p1(t-τ)之差实施价格博弈[22]：当差大于零时，则实施提高价格策略；差小于零时，则实施降价策略．如果用ai(pi),i=1,2,3表示第i个天然气生产商的产品价格调整程度，那么天然气生产商A的价格调整的动态过程为
(27)
假设天然气生产商B、C采取有限理性决策，由于市场信息存在时滞或不完全，他们通过对边际利润的分析判断实施价格调整，以实现利润最大化．若边际利润大于零，则实施提高价格策略；若边际利润小于零，则实施降价策略．所以天然气生产商B、C的价格调整动态过程为
(28)
假设ai(pi),i=1,2,3是线性的，即
ai(pi)=υipi,i=1,2,3，
(29)
其中，υi是一个正数，表示第i个公司的价格调整速度．因此，综合式(27)～(29)，可以得出天然气生产商A、B、C价格决策的最终博弈模型为
(30a)
(30b)
(30c)
对模型(30)求解，可以得到以下8个平衡点(考虑到经济学实际意义只取非负解)：
E1(0,0,0),
E2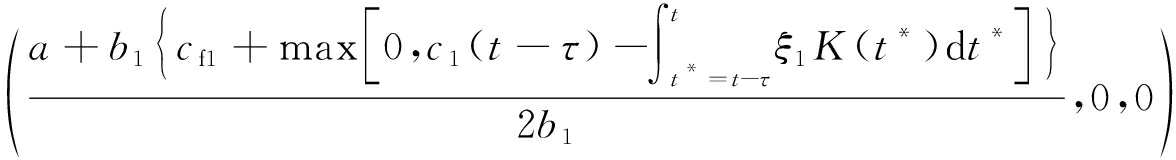
,
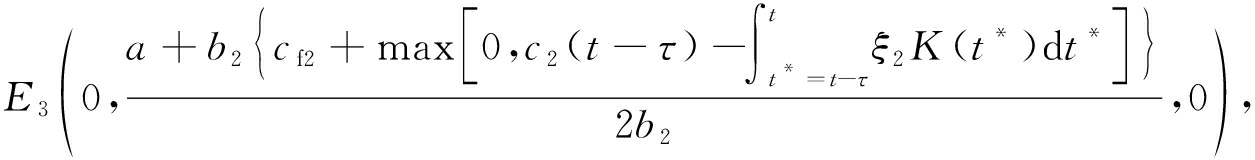
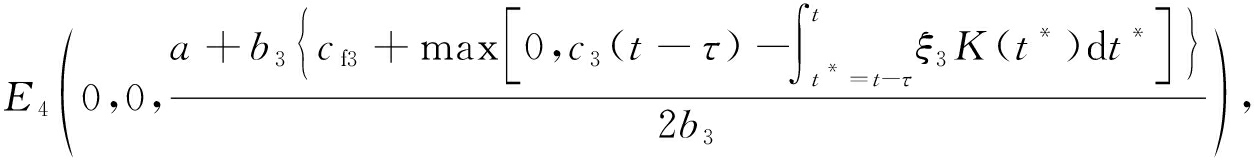
其中
s1=4ab2b3+2ab3g1+2ab2h1+ag1g2-ag2h3+ah1h3,
s3=4ab1b3+2ab1g2+2ab3h2+ag2g3-ag3h1+ah1h2,
s5=4ab1b2+2ab2g3+2ab1h3+ag1g3-ag1h2+ah2h3,
s7=8b1b2b3-g1g2g3-h1h2h3,
s8=2b1g2h3+2b2g3h1+2b3g1h2．
通过求解可得，E1,E2,E3,E4,E5,E6,E7为边界平衡点，有且仅有一个Nash平衡点E8．对于平衡状态E1(0,0,0)，意味着天然气生产厂商A、B、C的产品定价为零，显然生产不可持续．对于平衡状态E2,E3,E4，表示有两个天然气生产厂商的产品定价为零，只有一个天然气生产商受另外两个厂商零定价的冲击而亏损并最终因实行零定价的厂商倒闭而独占市场．对于平衡状态E5,E6,E7，则表示有两个天然气生产商可以分享市场， 有一个天然气生产商因实行零定价而退出市场．对于平衡状态
是指A、 B、 C通过寡头垄断竞争达到的稳定状态， 三寡头各占一定的市场份额而不被淘汰， 只有这个状态是博弈三方参与者能够接受的结果．
为研究Nash平衡点E8的稳定性，做变换
则系统(30)变换为
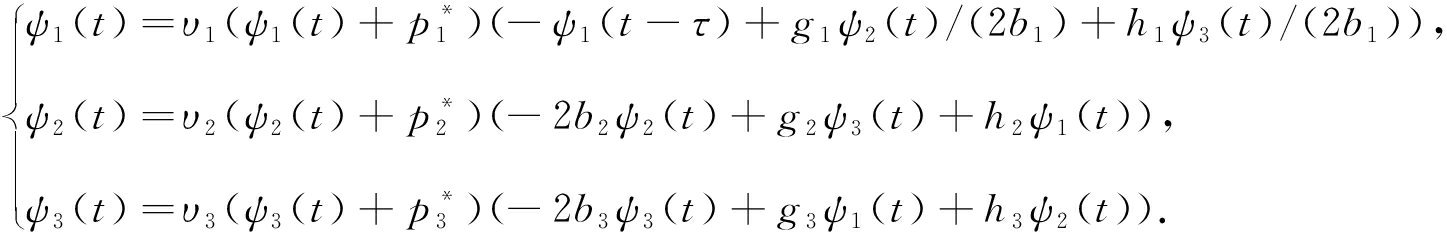
(31)
所以，就转换为研究(0,0,0)点的稳定性了．而系统(31)在ψ=0处的线性部分为
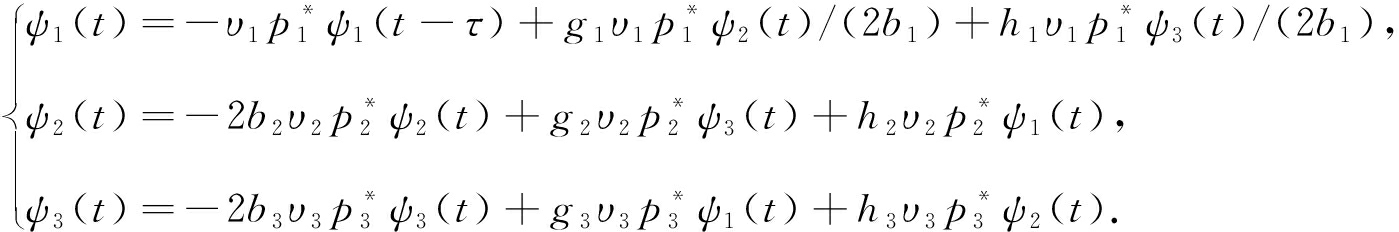
(32)
系统(32)的特征方程为
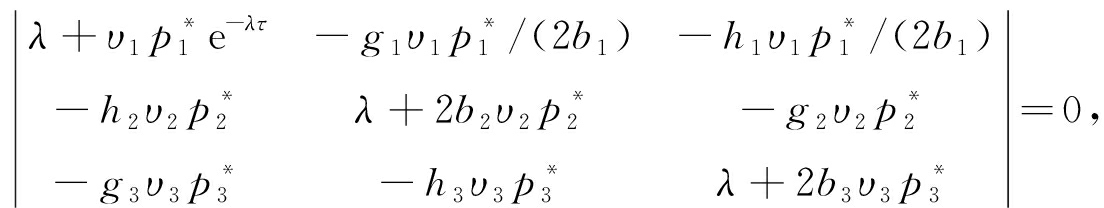
(33)
即
λ3+R1λ2+R2λ+R3+(R4λ2+R5λ+R6)e-λτ=0，
(34)
其中
如果λ=iω(ω>0)是方程(34)的一个根，则
-ω3i-R1ω2+R2ωi+R3+(-R4ω2+R5ωi+R6)(cos(ωτ)-isin(ωτ))=0．
对实部和虚部进行分离，则有
(35)
把方程(35)中两式平方后相加，有
(36)
令
则
s3+Es2+Fs+G=0．
(37)
记
f(s)=s3+Es2+Fs+G，
则
如果Δ=4(E2-3F)≤0，那么f(s)在s∈[0,+∞)上是单调递增的．当G≥0且Δ≤0时，方程(37)没有正根．当G<0时，方程(37)至少有一个正根．当G≥0且Δ>0时，方程df(s)/ds=0的根为
因此当且仅当s1>0且f(s1)≤0时，方程(37)有正根．假设方程(37)有3个正根
则有
将ωk(k=1,2,3)代入方程(35)，可得
k=1,2,3;j=0,1,2,…．
所以±iωk是特征方程(34)的纯虚根，并记
当τ0=0时，特征方程(34)变为
λ3+(R1+R4)λ2+(R2+R5)λ+R3+R6=0．
(38)
根据Routh-Hurwitz判据，如果
(R1+R4)(R2+R5)-(R3+R6)>0, →R1+R4>0，R3+R6>0．
(39)
显然方程(38)的根都存在负实部．如果式(39)成立，那么可以得到以下结论：1) 若G≥0且Δ≤0，则τ≥0，E8渐近稳定； 2) 若G<0或G≥0,Δ>0,s1>0,f(s1)≤0，对于τ∈[0,τ)，E8也渐近稳定； 3) 如结论2)中的条件成立，但
那么当
时，系统(30)在平衡点E8处出现Hopf分岔．将式(21)和(30)联立进行计算机符号求解可以看出，如果结论2)中的条件成立，且当不变时，α，β，γ在一定取值范围内，α，β，γ随着的数值增大，系统(30)的平衡点E8是渐近稳定的；随着α，β，γ的数值减小，平衡点E8呈现周期解，且周期运动幅度不断增大．
在现实中表现为，在天然气三寡头垄断竞争市场，各天然气生产商为了获得更多的利润，可以通过创新来降低成本，提高利润率．一方面，在一定时间范围内，天然气市场知识创新周期短有利于市场的平衡；创新周期在某一取值点会出现市场平衡的临界点；随着创新周期的延长最终会打破市场平衡．另一方面，由于现实条件制约和技术水平限制，创新周期往往变动幅度不大，在创新周期一定的情况下，天然气生产商可以通过选择知识创新投入产出强度来改变自身的竞争策略，若寡头各方都降低知识创新的投入产出强度，将导致天然气行业创新水平整体降低，使天然气市场趋于不稳定，博弈各方都会受损；各寡头确定的知识创新投入产出强度组合，在某一取值点会出现市场平衡的临界点；而寡头各方加大知识创新投入产出强度，有利于市场的平衡，但超过一定取值范围，会增加当期成本．因此，保持适度的知识创新投入产出强度，有利于天然气市场的平衡和各自利润的最大化．
这里以边界平衡点
为例做稳定性分析．根据3.1小节求解结果可知
按照3.1小节的方法在式(31)和(32)基础上可推导系统特征方程为
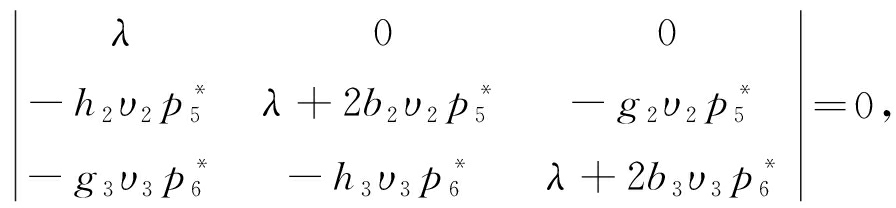
(40)
即
λ3+R1λ2+R2λ+R3+(R4λ2+R5λ+R6)e-λτ=0，
(41)
其中
R3=0,R4=0,R5=0,R6=0．
当τ0=0时，特征方程(41)变为
λ3+R1λ2+R2λ=0．
(42)
根据式(39)Routh-Hurwitz判据，这里因R3+R6=0，使得系统(30)的边界平衡点不具备稳定条件．同理也可以分析得出E1,E2,E3,E4,E5,E6其余6个边界平衡点也不满足稳定条件．这表明，天然气三寡头垄断市场，两个天然气生产商可以分享市场而另外一个天然气生产商的价格为零而被淘汰的状态是不稳定的，而三个生产商都面临难以继续生产甚至倒闭危险的状态也是不稳定的．这在理论上也进一步表明，在天然气三寡头垄断市场，各生产商在创新投入、定价决策博弈上充分考虑市场均衡和多方共赢,尽可能接近Nash平衡点才是理性选择．
设天然气生产商A、B、C三寡头在知识创新博弈时的有关参数如下：
α=0.635，β=0.517，γ=0.514，μ=0.045，δ=2.0，φ=0.012，K0=2，
σ1=0.15，σ2=0.3，σ3=0.25，σ4=0.35，σ5=0.26，σ6=0.22，
θ1=0.40，θ2=0.35，θ3=0.25，a=5，b1=2.6，b2=2.4，b3=2.0，
g1=0.3，g2=0.4，g3=0.5，h1=0.4，h2=0.5，h3=0.6．
A、B、C天然气生产商各自的当期可变本分别为c1=1.6，c2=1.8，c3=1.9，当期固定成本分别为cf1=0.6，cf2=0.7，cf3=0.8．
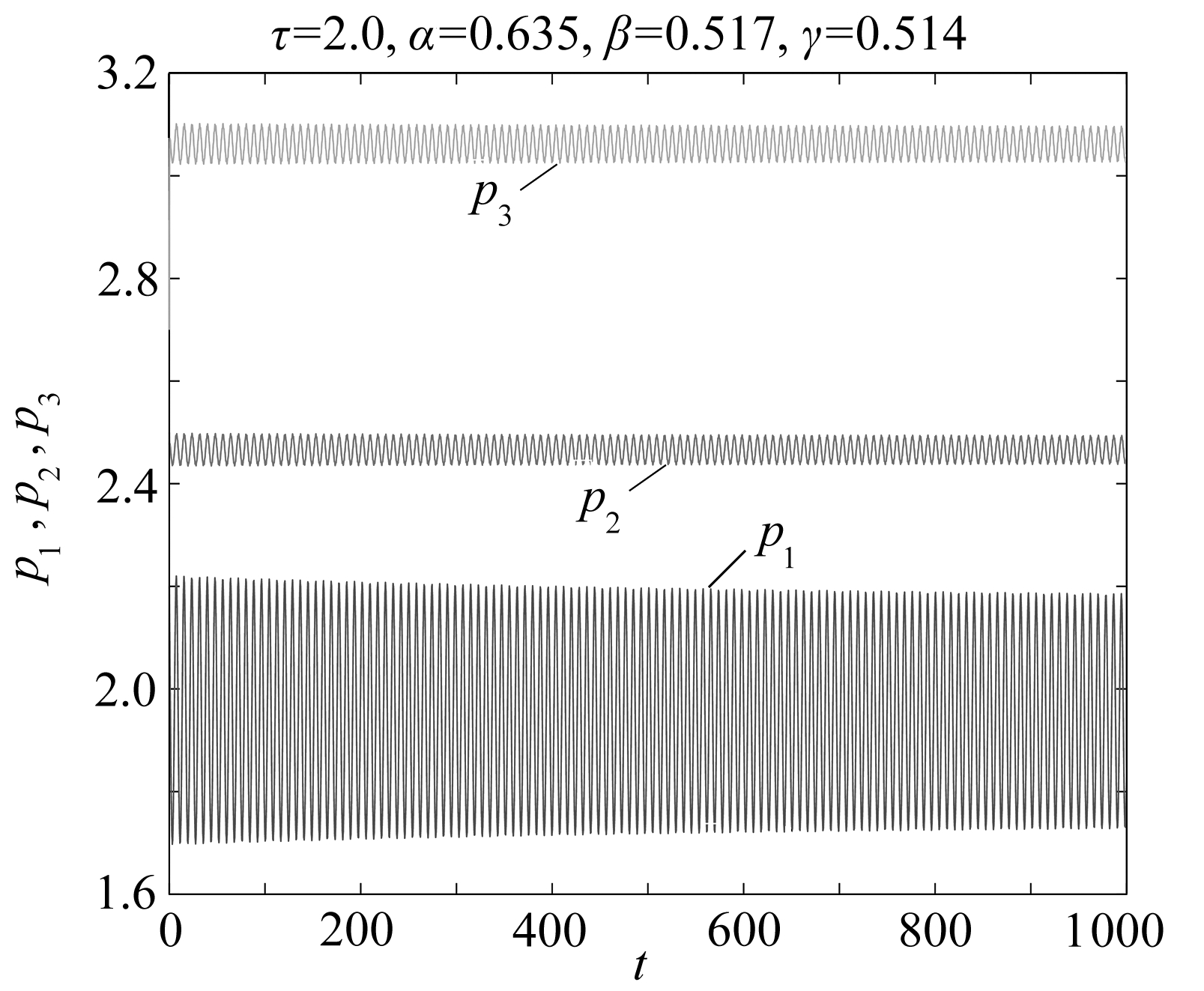
图1 系统发生Hopf分岔
Fig. 1 The Hopf bifurcation in the system
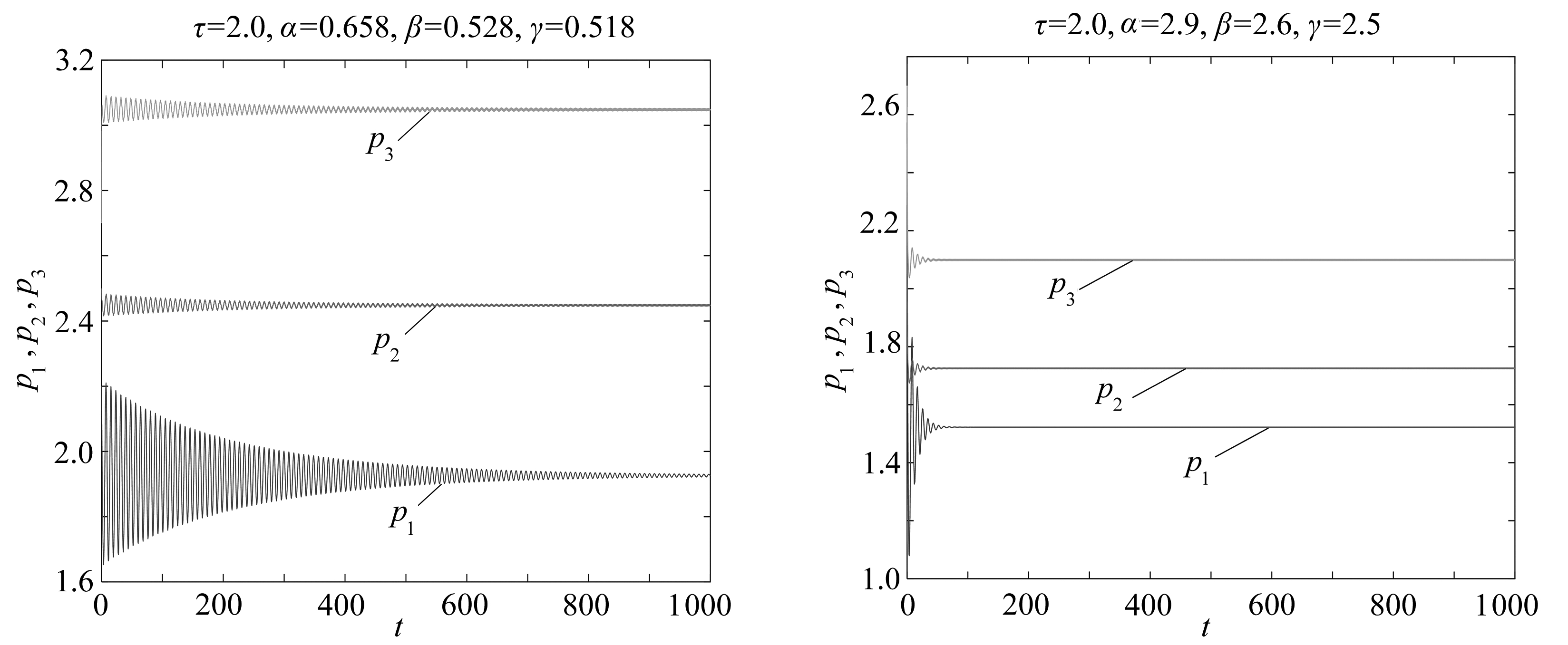
图2 系统稳定到平衡状态 图3 系统稳定到平衡状态
Fig. 2 The system stabilizes at equilibrium Fig. 3 The system stabilizes at equilibrium
3个天然气生产商A、 B、 C自身产品价格的初值分别为p1(0)=2.2，p2(0)=2.5，p3(0)=2.7，价格调整速度为υ1=υ2=υ3=0.4．此时，可以计算出延迟参数的临界值τ0=2.0，系统的平衡解为E8(1.951 5,2.465 5,3.059 9)．利用MATLAB2015软件对系统(30)进行数值模拟，其他参数不变，若取α=0.635,β=0.517,γ=0.514时系统发生Hopf分岔，出现周期解，模拟结果如图1所示；增大α,β,γ取值，如取α=0.658,β=0.528,γ=0.518时系统渐进到平衡状态，模拟结果如图2所示；进一步增大α,β,γ取值，如取α=2.9,β=2.6,γ=2.5时模拟结果如图3所示，系统处于平衡状态．
若减小α,β,γ取值，如取α=0.620,β=0.508,γ=0.505时系统发生周期解，模拟结果如图4所示．进一步减小α,β,γ取值，如取α=0.220,β=0.125,γ=0.110时系统周期运动幅度急剧增大，模拟结果如图5所示．在图5所示系统基础上，α,β,γ中其中两个取值不变，其余一个增大取值，如取α=1.00,β=0.125,γ=0.110时，系统又可以达到平衡状态，模拟结果如图6所示，即领导者创新可以使系统达到平衡状态．
图4 系统发生周期解
Fig. 4 The periodic solution in the system
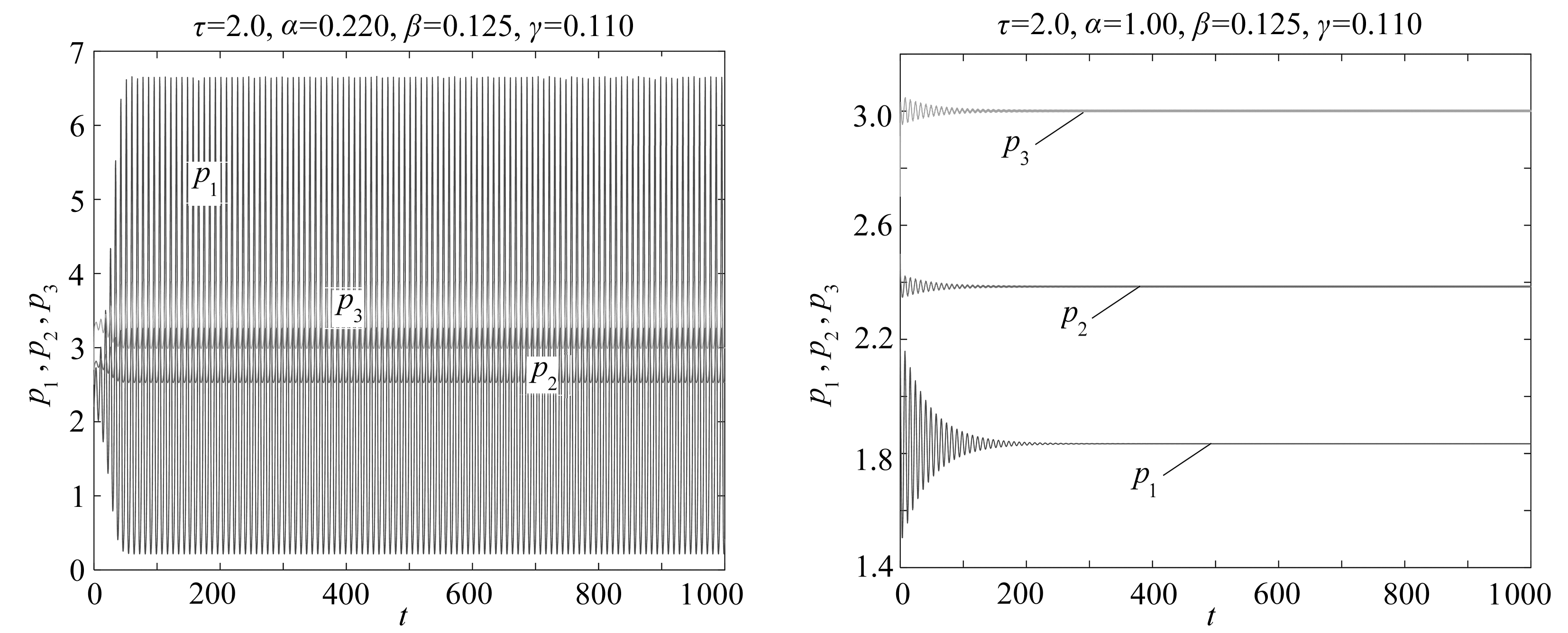
图5 系统周期运动幅度增大 图6 领导者加大创新投入使系统平衡
Fig. 5 The range of periodic motion of Fig. 6 Stepping up of innovation by the market leader
the system expands makes the system reach equilibrium
假设天然气生产商A、B、C加快自身的价格调整速度，并保持其他参数的值不变，如依次取υ1=0.46,υ2=0.46,υ3=0.46，模拟结果如图7所示，系统出现周期解．在图7所示系统基础上增大α,β,γ值，如取α=3.0,β=2.8,γ=2.6时模拟结果如图8所示，系统又可以达到平衡状态．在图2所示系统基础上，其他参数不变，增大延迟参数τ的取值，如取τ=3.0时模拟结果如图9所示，系统将出现周期解，表明降价反应滞后于创新周期系统将会出现周期解．
从数值模拟结果可以看出，在天然气三寡头垄断竞争市场，过低的创新投入产出强度会破坏整个市场平衡，因此，生产商A、B、C应适当加大α,β,γ值，这有利于降低自身企业成本，并维护市场平衡；当其他生产商创新投入产出强度不足时，行业领导者可以通过自适应决策加大创新投入产出强度，从而维护整个市场的平衡．通过创新降低成本后，对于各寡头实施降价策略提供了可能，但过快的降价速度也会破环整个市场的平衡，这需要A、B、C寡头各方理性选择适当的降价速度υ1,υ2,υ3取值；如因过快的降价速度打破市场平衡时，除了调低降价速度外，在一定范围内也可通过创新即适当加大α,β,γ值，使市场恢复平衡状态．同时还发现，各天然气生产商应努力减小创新周期τ值，以利于市场平衡，避免导致市场混乱，以利于天然气产业的健康发展．
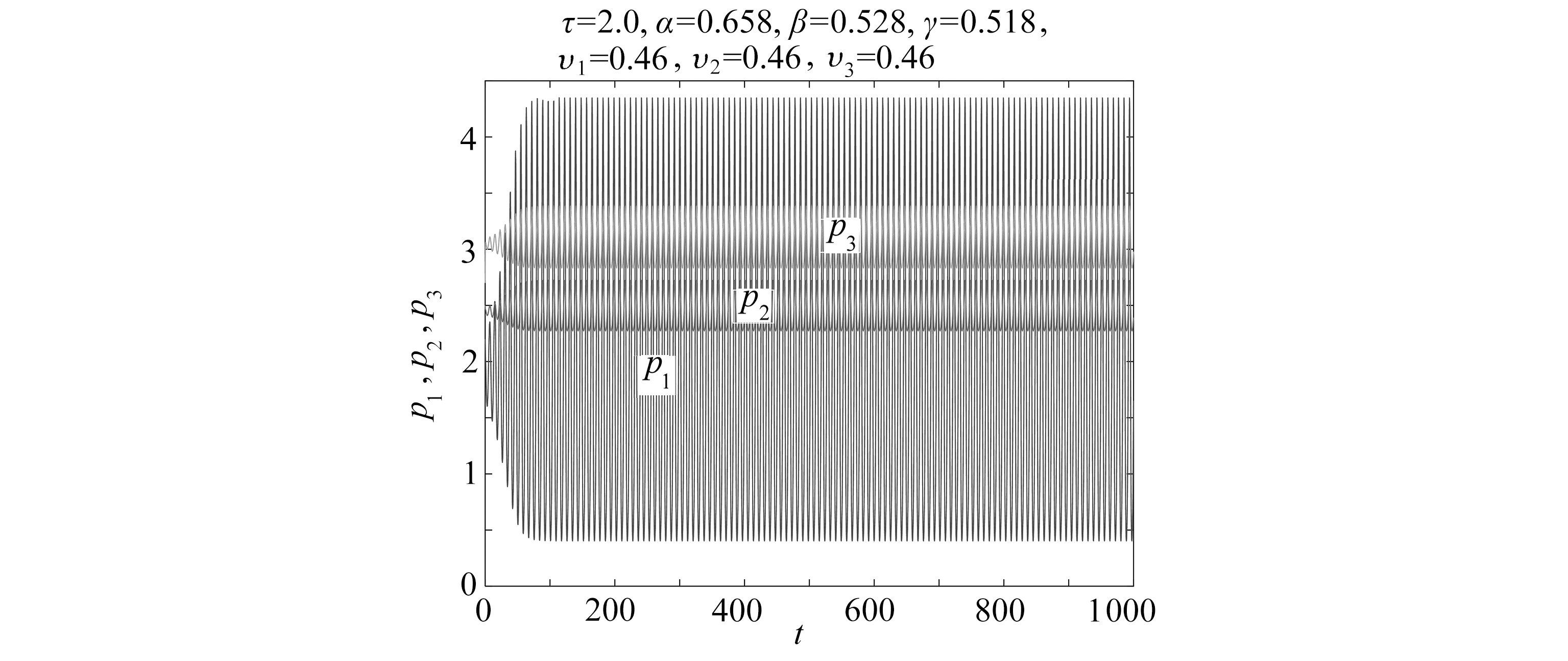
图7 提高降价速度后系统发生周期解
Fig. 7 The periodic solution in the system after an increase of the price reduction rate
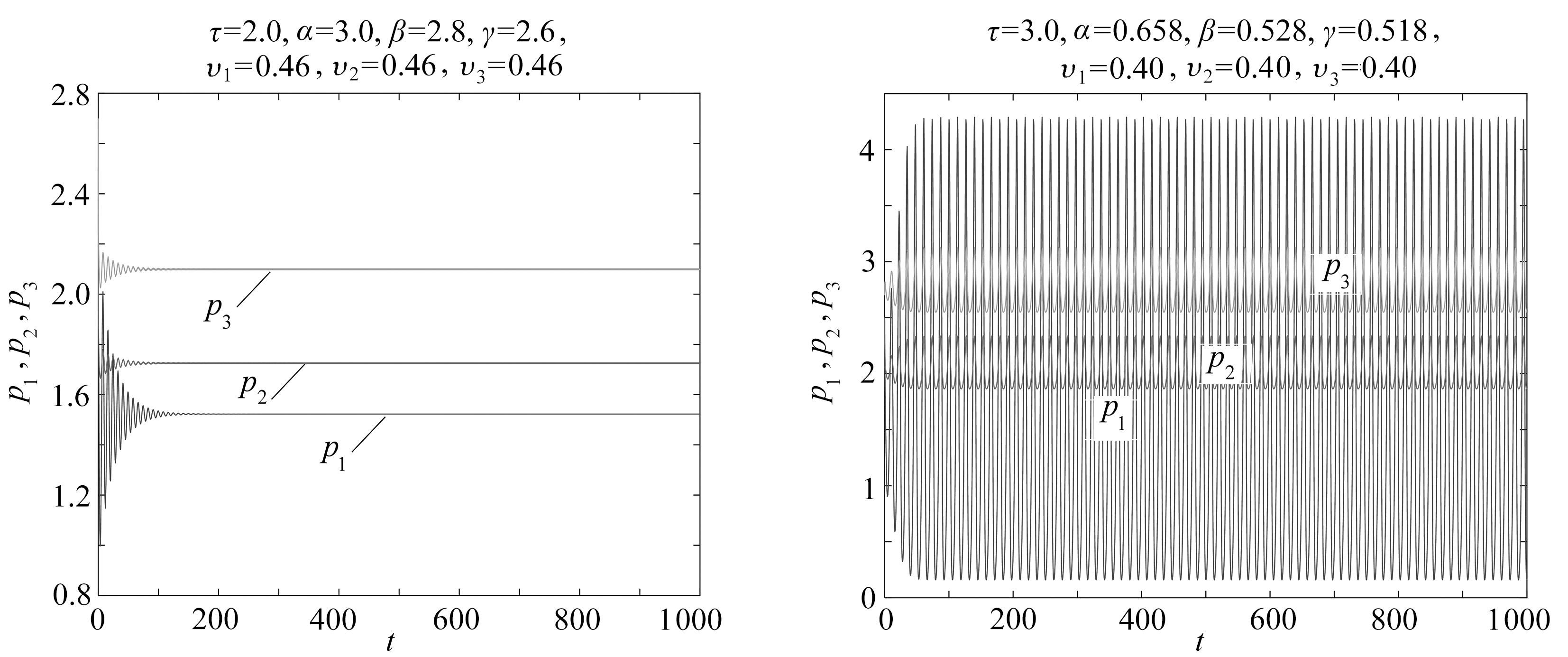
图8 提高降价速度基础上加大 图9 降价反应滞后于创新周期
α,β,γ值系统恢复平衡 系统将会出现周期解
Fig. 8 The system restores in equilibrium at Fig. 9 The periodic solution appears in the system
increases of the price reduction rate when the price reduction response lags
and theα,β,γ values behind the innovation period
本文针对天然气行业上游生产商三寡头垄断市场，基于知识创新所产生的成本降低和降价决策反应时滞，建立定价决策动态微分博弈模型．通过理论分析和数值模拟，得出如下结论：
1) 知识创新周期越短越有利于维护市场平衡，而过长的创新周期会破环整个市场的平衡；
2) 在知识创新周期不变时，企业适当提高知识创新投入产出强度，有利于降低成本，提高自身利润率，并维护市场保持平衡状态；
3) 在一定条件下，各寡头实施创新驱动和及时、适速降价策略,系统会出现Hopf分岔并有唯一的Nash平衡点,可以实现博弈三方利润最大化，这也是天然气生产商三寡头垄断市场，各生产商应当追寻的最佳策略．
[1] 尹春华, 顾培亮. 基于灰色序列生成中缓冲算子的能源预测[J]. 系统工程学报, 2003,18(2): 189-192.(YIN Chunhua, GU Peiliang. Energy forecast based on gray series spanning buffering operator[J].Journal of Systems Engineering, 2003,18(2): 189-192.(in Chinese))
[2] 杨世旭, 段万春, 孙永河, 等. 基于混合策略的电信企业竞合博弈分析[J]. 经济问题探索, 2014(8): 179-183.(YANG Shixu, DUAN Wanchun, SUN Yonghe, et al. An analysis of the competition and merger game of telecommunications enterprises based on a mixed strategy[J].Inquiry Into Economic Issues, 2014(8): 179-183.(in Chinese))
[3] 吉伟卓, 马军海. 发电市场不同决策规则三寡头博弈模型研究[J]. 系统工程学报, 2008,23(3): 257-263.(JI Weizhuo, MA Junhai. Study of game model based on different decision rules in electric power triopoly market[J].Journal of Systems Engineering, 2008,23(3): 257-263.(in Chinese))
[4] ELABBASY E M, AGIZA H N, ELSADANY A A. Analysis of nonlinear triopoly game with heterogeneous players[J].Computers &Mathematics With Applications, 2009,57(3): 488-499.
[5] CHEN F, MA J H, CHEN X Q. The study of dynamic process of the triopoly games in Chinese3G telecommunication market[J].Chaos,Solitons &Fractals, 2009,42(3): 1542-1551.
[6] MA J H, JI W Z. Complexity of repeated game model in electric power triopoly[J].Chaos,Solitons &Fractals, 2009,40(4): 1735-1740.
[7] AGIZA H N, HEGAZI A S, ELSADANY A A. The dynamics of Bowley’s model with bounded rationality[J].Chaos,Solitons &Fractals, 2001,12(9): 1705-1717.
[8] 谢英超, 程燕, 贺天宇. 一类具有非线性发生率的时滞传染病模型的全局稳定性[J]. 应用数学和力学, 2015,36(10): 1107-1116.(XIE Yingchao, CHENG Yan, HE Tianyu. Global stability of a class of delayed epidemic models with nonlinear incidence rates[J].Applied Mathematics and Mechanics, 2015,36(10): 1107-1116.(in Chinese))
[9] 孙继涛, 王庆国, 高含俏. 具有时变滞后的随机系统的时滞依赖鲁棒稳定性与H∞分析[J]. 应用数学和力学, 2010,31(2): 236-244.(SUN Jitao, WANG Qingguo, GAO Hanqiao. Delay-dependent robust stability andH∞ analysis of stochastic systems with time-varying delay[J].Applied Mathematics and Mechanics, 2010,31(2): 236-244.(in Chinese))
[10] 高琴. 港口产业集群的复杂性研究[D]. 博士学位论文. 天津: 天津大学, 2009.(GAO Qin. The research of the complexity of port industrial clusters[D]. PhD Thesis. Tianjin: Tianjin University, 2009.(in Chinese))
[11] SON W S, PARK Y J. Delayed feedback on the dynamical model of a financial system[J].Chaos,Solitons &Fractals, 2011,44(4): 208-217.
[12] 徐伟, 马军海. 保险市场中三寡头垄断的动态博弈模型研究[J]. 复杂系统与复杂性科学, 2013,10(2): 52-58.(XU Wei, MA Junhai. Study on the dynamical model of a triopoly game in insurance market[J].Complex Systems and Complexity Science, 2013,10(2): 52-58.(in Chinese))
[13] 杨俊, 张亚军, 张小漫. 天然气市场不同预期规则下的三寡头博弈模型研究[J]. 华东经济管理, 2016,30(8): 7-15.(YANG Jun, ZHANG Yajun, ZHANG Xiaoman. A study of three oligopolistic firms game model based on different expectation rules in natural gas supply market[J].East China Economic Management, 2016,30(8): 7-15.(in Chinese))
[14] RAYPORT J F, SVIOKLA J J. Exploiting the virtual value chain[J].Harvard Business Review, 1995,73(6): 75-85.
[15] 赵小惠, 陈菊红, 孙林岩, 等. 制造商-供应商协同产品创新合作机制研究[J]. 工业工程, 2005,8(6): 60-63.(ZHAO Xiaohui, CHEN Juhong, SUN Linyan, et al. Cooperation mechanisms of collaboration product innovation for manufacturer-supplier[J].Industrial Engineering Journal, 2005,8(6): 60-63.(in Chinese))
[16] DOCKNER E, JORGENSEN S, LONG N V, et al.Differential Games in Economics and Management Science[M]. Oxford: Cambridge University Press, 2000.
[17] BAGCHI A.Stackelberg Differential Games in Economic Models[M]. Berlin: Springer Verlag, 1984.
[18] 张庶萍, 张世英. 基于微分对策的供应链合作广告决策研究[J]. 控制与決策, 2006,21(2): 153-157.(ZHANG Shuping, ZHANG Shiying. Dynamic cooperative advertising strategies based on differential games in a supply chain[J].Control and Decision, 2006,21(2): 153-157.(in Chinese))
[19] 胡震云, 陈晨, 张玮. 基于微分博弈的绿色信贷与水污染控制反馈策略研究[J]. 审计与经济研究, 2013,28(6): 100-109.(HU Zhenyun, CHEN Chen, ZHANG Wei. Study on the feedback strategy of water pollution control differential game from the view of green credit[J].Journal of Audit &Economics, 2013,28(6): 100-109.(in Chinese))
[20] 郝晓晨. 天然气产业链架构的和谐性分析与优化[J]. 天然气工业, 2006,26(12): 162-164.(HAO Xiaochen. Analysis and optimization on the integrity and harmony of natural gas industry chain[J].Natural Gas Industry, 2006,26(12): 162-164.(in Chinese))
[21] 白兰君. 在对比研究中深入探寻油气采掘成本规律[J]. 天然气经济, 2006(6): 4-7.(BAI Lanjun. A profound probe into rules of oil and gas producing costs by comparative study[J].Natural Gas Technology and Economy, 2006(6): 4-7.(in Chinese))
[22] 潘玉荣, 贾朝勇. 不同理性双寡头博弈模型的复杂性分析[J]. 复杂系统与复杂性科学, 2007,4(2): 71-76.(PAN Yurong, JIA Chaoyong. Complex dynamics analysis for a duopoly game with heterogeneous players[J].Complex Systems and Complexity Science, 2007,4(2): 71-76.(in Chinese))