引 言
定向器是火箭武器系统的重要组成部分,是火箭弹与火箭发射系统直接联系的构件.传统纯钢制定向器重量大,且特别容易生锈和受到环境的腐蚀,需要很高要求的日常保养程序;玻璃钢定向器不仅满足发射时的刚强度要求,而且质量轻、耐腐蚀性能好[1].为了适应现代战争突发性、速决性、机动性和灵活性等要求,必须将武器轻量化作为一个重要研究方向,采用非金属复合材料是实现轻量化的重要途径之一,玻璃钢逐步取代传统金属成为定向器用材料的首要选择[2-3],这样就可以满足火箭炮轻量化需要,并且使武器系统安全性得到很大的提高,玻璃钢定向器被广泛应用于储运发射箱技术[4-5].
目前,国内外对玻璃钢材料的性能进行了很多研究,针对玻璃钢的耐老化性能,建立了很多性能试验,很多科研机构将其作为一项重大课题.如朱子华[6]运用标记法测试拉伸均匀度,加热前在测试区域做好标记,如圆形或方形,在加热取向大分子充分回弹后观察标记的改变,如不均匀圆形会变为椭圆,方形会变为菱形.吕锡慈等[7]运用会聚偏振光方法,测试双轴定向有机玻璃的双折射值,但这种方法比较复杂,且无法实现不同方向和层面拉伸度的测量.
但是目前相关的研究仍处于探索和积累阶段,研究方向的资料十分稀缺,很不全面.因此,本文构建玻璃钢定向管的力学模型,再结合实验数据,建立玻璃钢定向器蠕变模型,在结构模型中进行计算分析,所得的计算参数为建立非金属定向管长贮性能分析的计算模型提供材料参数.
1 玻璃钢定向器力学模型
定向器用玻璃钢材料是具有各向异性的纤维增强复合材料,玻璃钢定向器的基本结构则可以看成是层合圆柱壳[4],如图1所示.
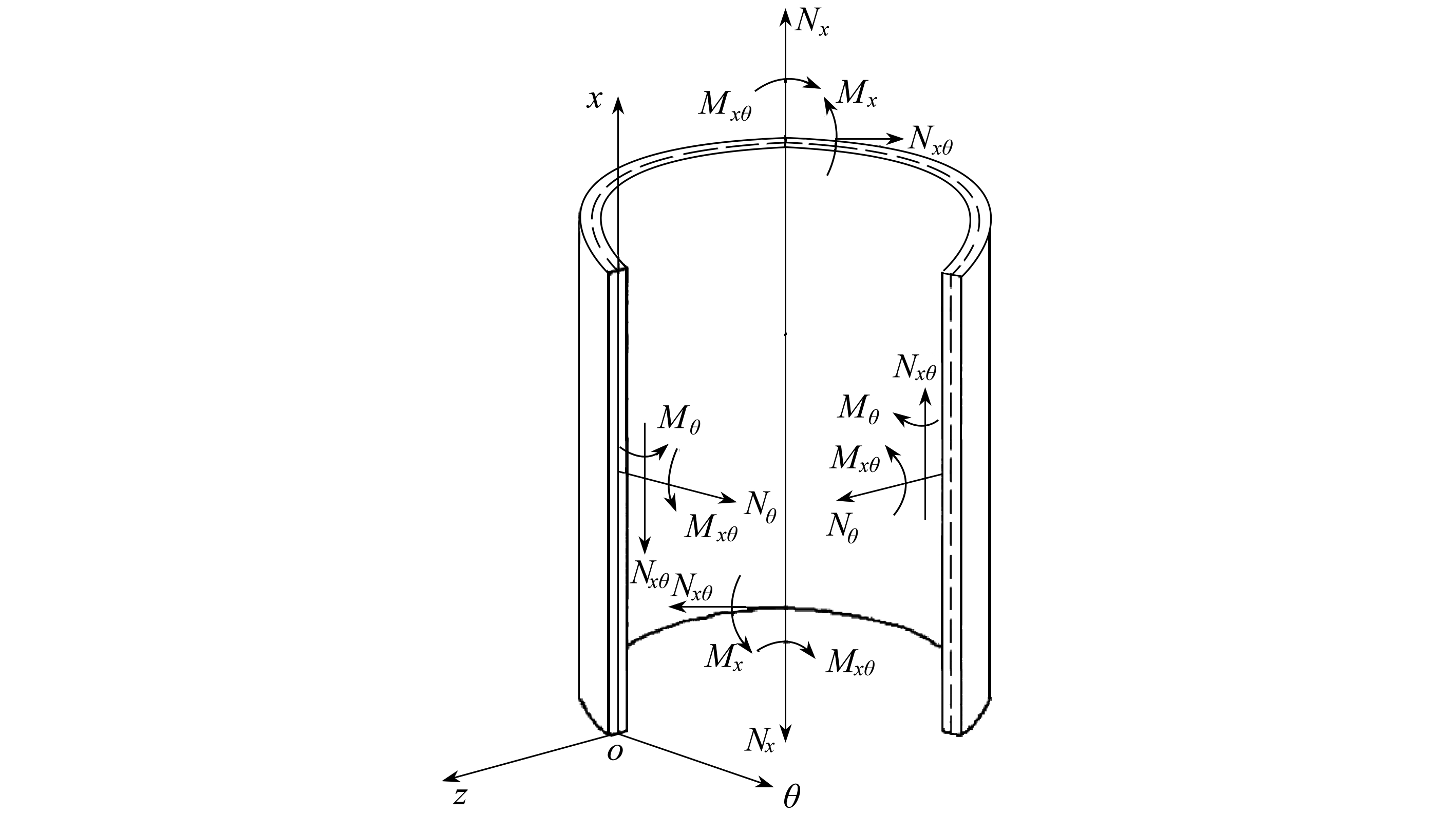
图1 定向器基本结构坐标关系图
Fig. 1 Coordinate diagram of the basic structure of the GFRP launching tube
设基本结构是半径为R的曲面,各作用力都是直接作用在曲面上,若沿着x,θ,z方向的位移分量分别是u0,v0,w0,则圆柱壳体的中曲面应变![]() 以及曲面上的曲率改变量kx,kθ,kxθ可以通过下式计算得出:
以及曲面上的曲率改变量kx,kθ,kxθ可以通过下式计算得出:
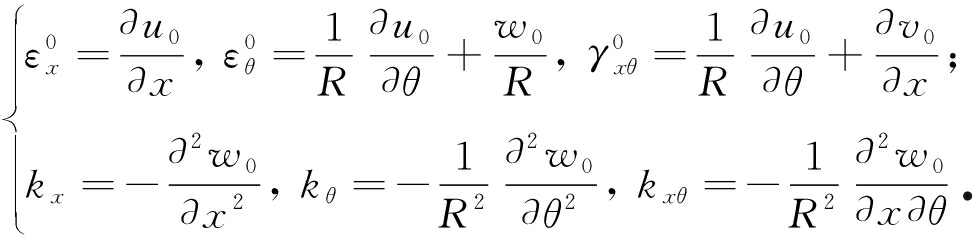
(1)
设Aij为拉伸强度,Bij为耦合刚度,Cij为弯曲强度,则圆柱壳的应力-应变方程为

(2)
令a=A-1,b=A-1B,c=bT,d=BA-1B-C,则上式可以转换为
(3)
其中M和N表示单一方向上的力矩和应力的简单表达式,与式(2)中的M和N写法不同,含义相同.
玻璃钢定向器所用的材料为层合结构,所以其简化圆柱壳也要按层合的关系进行计算,对于第n层,可以用Hooke(胡克)定律来描述其应力-应变关系:
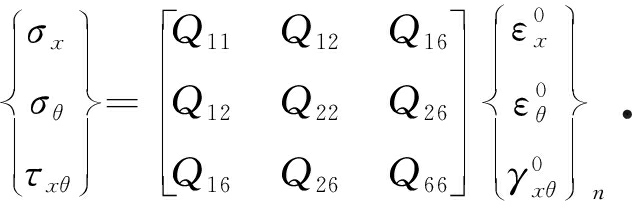
(4)
相对于中曲面,第n层的应变可以用下式表示:
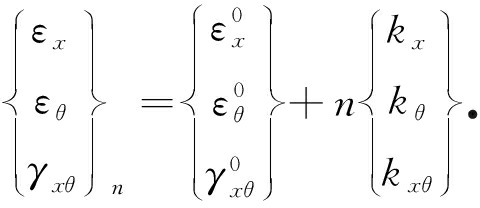
(5)
在图1所示的曲线坐标中,其应力函数Ys满足以下关系:
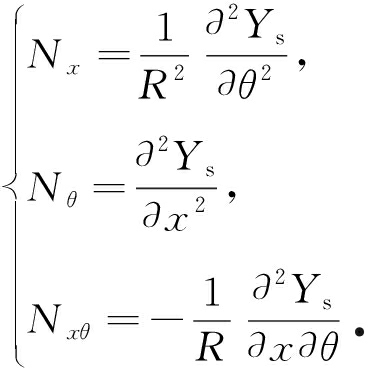
(6)
将式(1)、(3)、(6)代入式(5),则第n层的应变也可以用下式表示:

(7)
将上式代入式(4),计算得玻璃钢定向器简化圆柱壳的应力表达式:
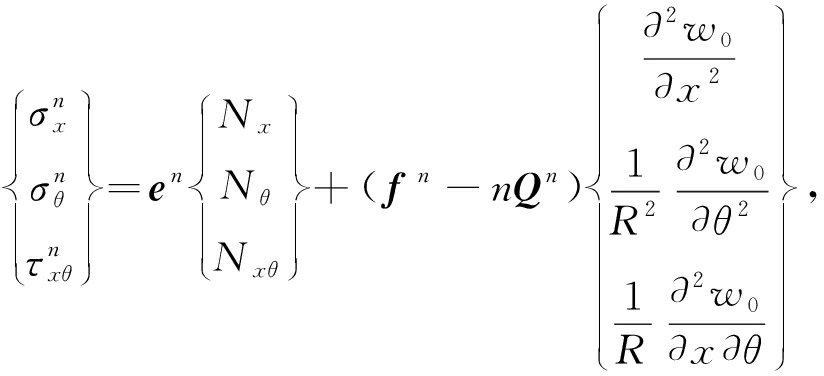
(8)
式中,Q为单层刚度矩阵;en, fn为所求应力处的材料参数,并且en=Qnan, fn=Qncn[8].
2 玻璃钢定向管实验方案
玻璃钢单向板基本力学性能试验的目的为通过试验和测量,获得定向管玻璃钢材料的基本热力学性能,含加速老化后的基本力学性能.
2.1 实验项目
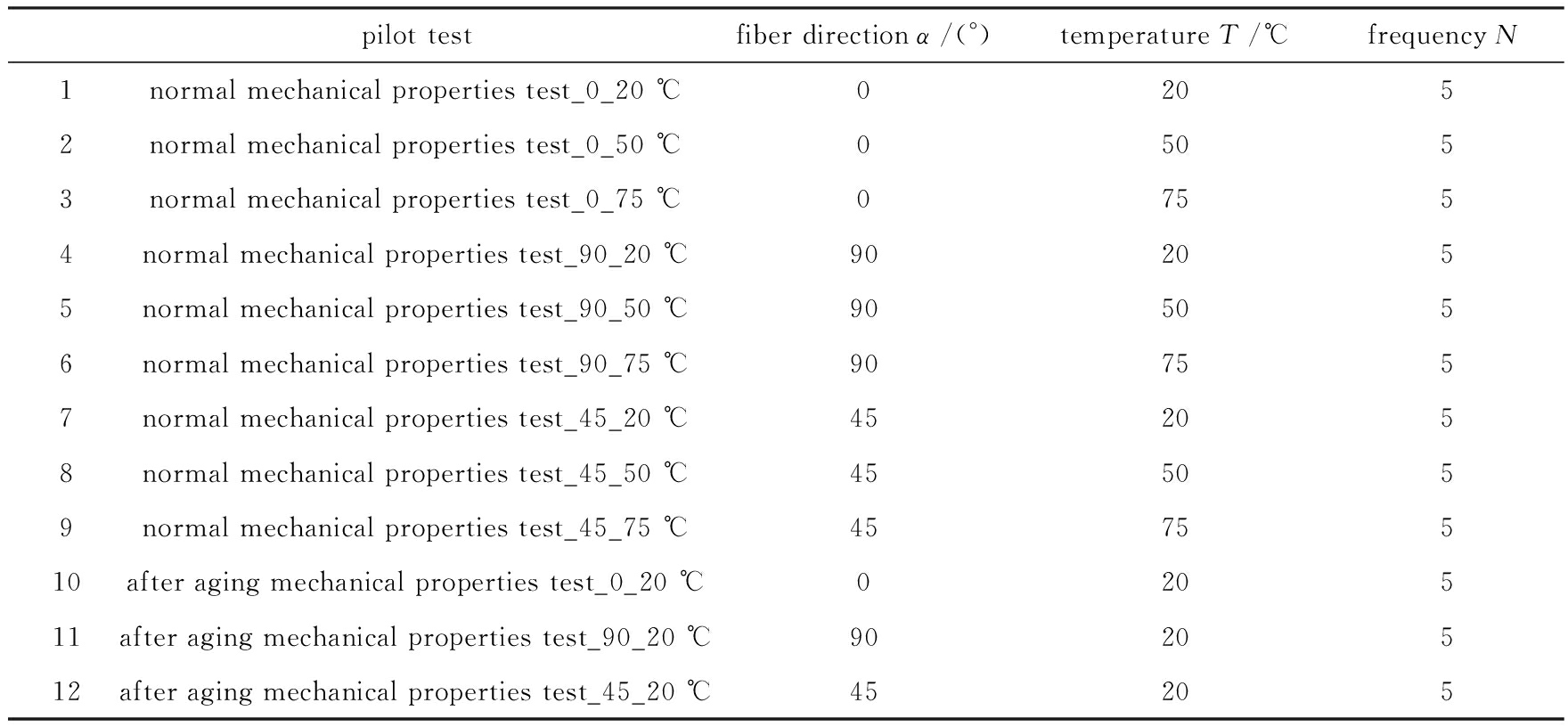
在一定温度范围内,玻璃钢材料的基本力学性能随温度变化较小.因此这里不参照蠕变试验温度选择测试温度,而是依据标准大气环境、高温贮存指标温度和极限贮存温度选定正常试件的基本力学性能试验温度为20 ℃,50 ℃和75 ℃.由于加速老化试验中选择的考察温度为20 ℃,因此对老化后试件只进行20 ℃温度条件下的基本力学性能试验.具体试验项目如表1所示.
表1 玻璃钢单向板基本力学性能试验
Table 1 Basic thermomechanical performance tests of the one-way GFRP slabs
玻璃钢单向板基本力学性能试验和热空气加速老化试验的试件依据《GB/T3354-2014定向纤维增强塑料拉伸性能试验方法》制备,其外形如图2所示,其中定义横向(即水平方向)为玻璃钢单向板中纤维方向的基准方向.其中加强片采用铝合金板或纤维增强塑料板,为保证加强片在试验过程中不脱落,胶黏剂固化温度不高于试件层板成型温度,对胶接表面处理时,不允许损伤试件纤维.
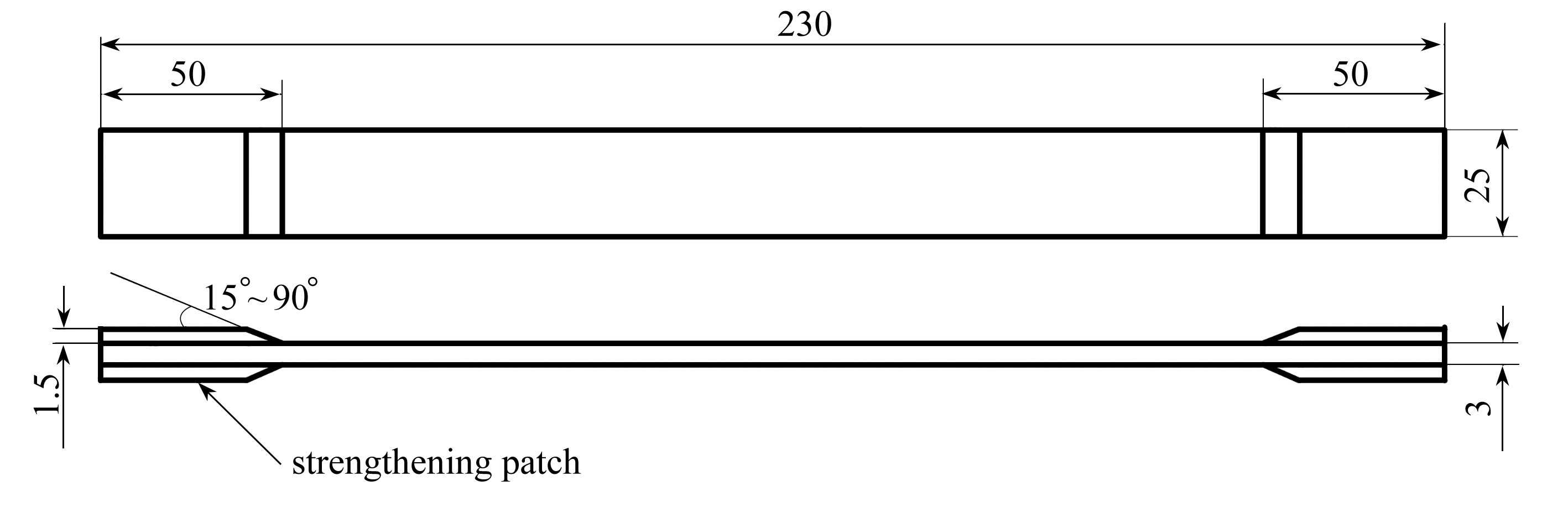
图2 玻璃钢单向板试件外形示意(单位: mm)
Fig. 2 Geometry of the one-way GFRP slab specimen(unit: mm)
玻璃钢单向板试件的具体数量和技术状态如表2所示.
表2 玻璃钢单向板试件数量与技术状态
Table 2 The quantity and technical status of the one-way GFRP slabs

2.2 实验结果
实验获得结果如表3~5所示.从表中可以看出:
在0°拉伸状态下,玻璃钢单向板常温拉伸模量约为52.9 GPa,拉伸强度约为1.17 GPa;在50 ℃条件下,拉伸模量减小,但变化量较小;在75 ℃条件下,拉伸模量的减小幅值不大,但拉伸强度显著减小,约为814 MPa.经过一段时间老化后,玻璃钢单向板拉伸模量有所减小,拉伸强度有所增加,但是增加量并不大.
在45°拉伸状态下,表现为玻璃钢承受纵横剪切的能力,常温状态下剪切模量约为3.55 GPa,剪切强度约为29.6 MPa;随着温度的增加,剪切模量减小;经过一段时间老化后,剪切模量有所增加,剪切可能与非金属粘接材料的老化性能变化有关.
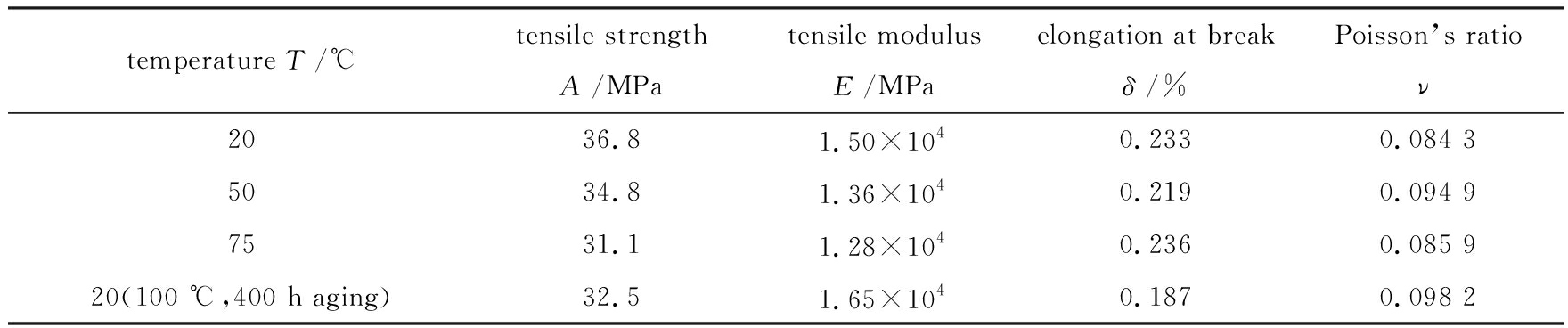
在90°拉伸状态下,玻璃钢单向板常温拉伸模量约为15 GPa,拉伸强度约为36.8 MPa;随着温度的增加,拉伸模量和拉伸强度均减小,但变化幅度不大;经过一段时间老化后,拉伸模量增加,但拉伸强度减小.
表3 玻璃钢力学性能试验结果(0°)
Table 3 Test results of GFRP mechanical behavior (0°)
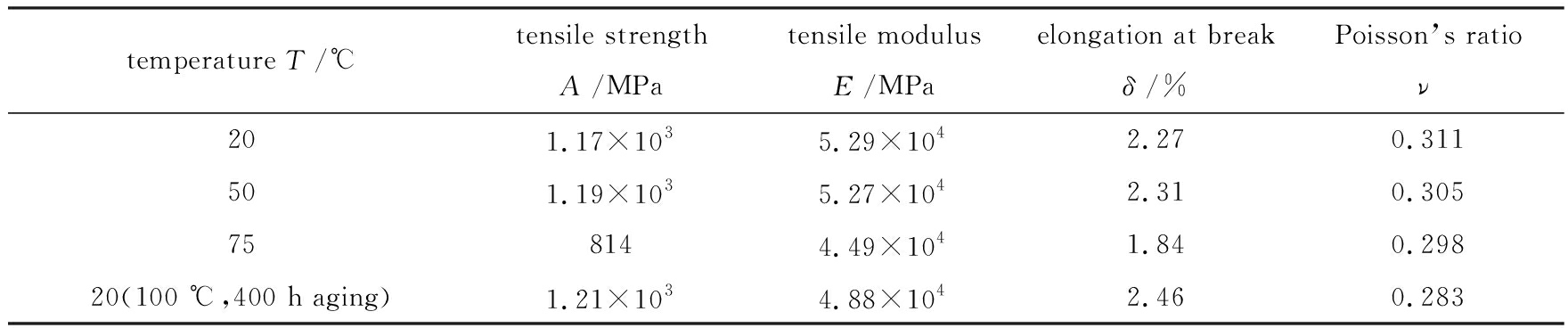
注 此表格为5组实验组的平均值,以下表格中的数据也是如此.
Note This table is the average of 5 experimental groups, as are the data in the following tables.
表4 玻璃钢力学性能试验结果(45°)
Table 4 Test results of GFRP mechanical behavior (45°)
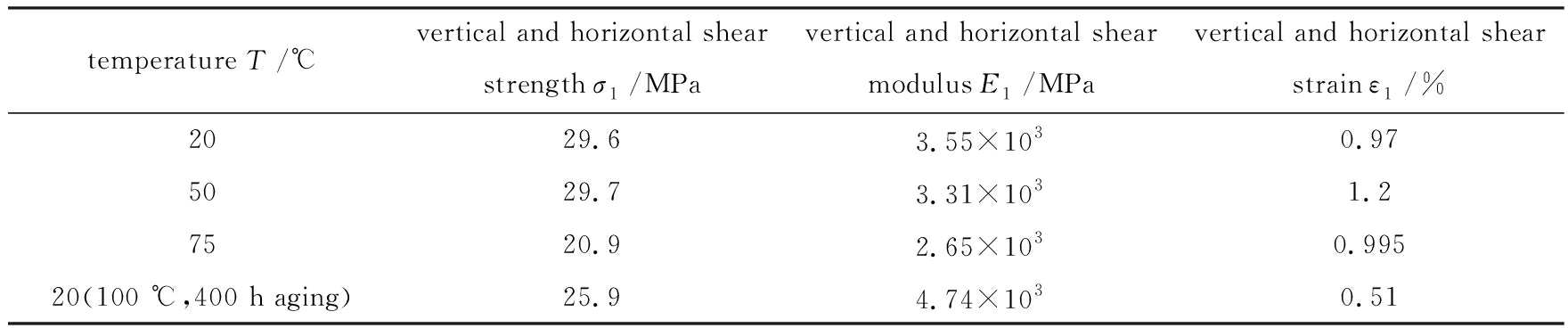
表5 玻璃钢力学性能试验结果(90°)
Table 5 Test results of GFRP mechanical behavior (90°)
3 玻璃钢定向管等效模型
为进行玻璃钢定向管的蠕变分析[9],需要将单向板材料力学性能施加到实际45°交叉铺层形式的定向管结构中,并建立合理的材料等效模型进行计算.结合玻璃钢定向管铺层形式,建立两种形式的材料模型.一种为复合材料铺层模型,即依据玻璃钢定向管铺层方式和厚度建立分层模型,各层模型参数由单向板测定数据给出;另一种为各向异性模型,即在铺层模型基础上,通过计算获得各向异性材料参数,并施加到结构模型中进行计算分析.
3.1 复合材料铺层模型及校验
复合材料铺层模型的各层材料参数由单向板测定数据给出,并建立与单向板试验相同的模型进行校验分析.铺层材料的建模方式如图3所示.
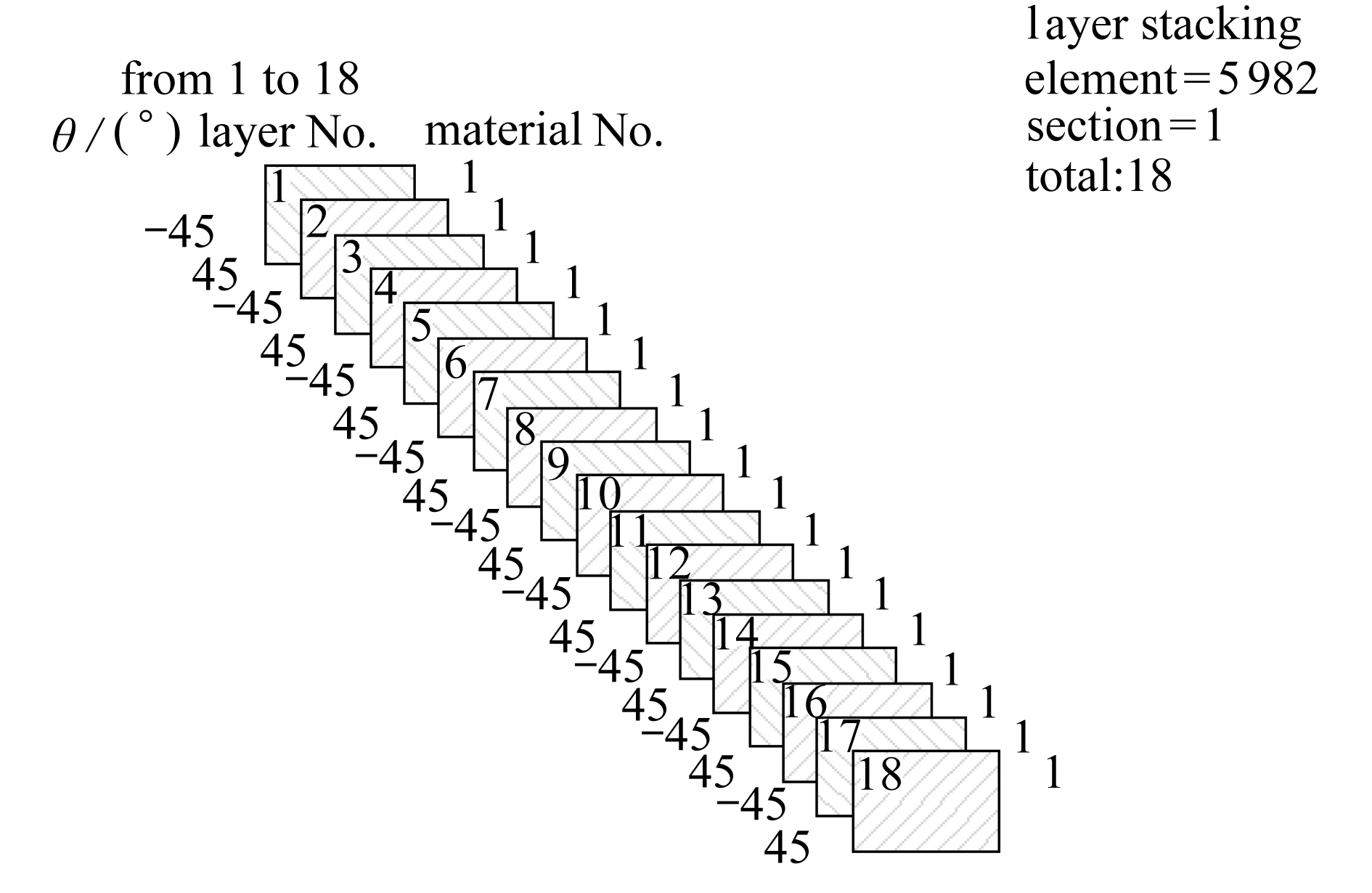
图3 复合材料铺层模型建模方式
Fig. 3 The composite laminate modeling method
参考单向板试验状态,建立0°和90°复合材料铺层模型如图4所示.其中的作用载荷参考其拉伸的极限载荷给定,即0°铺层模型采用1 170 MPa拉伸载荷,90°铺层模型采用36.8 MPa拉伸载荷.
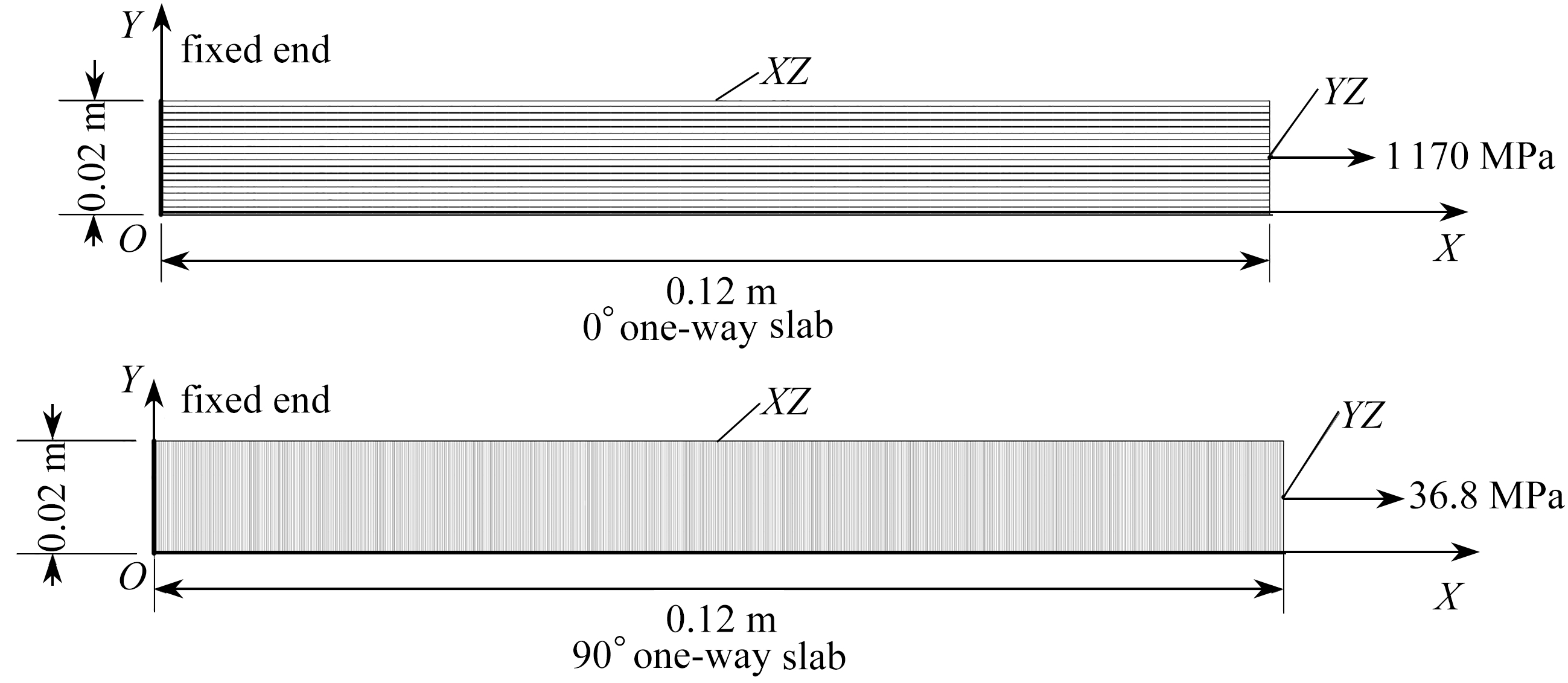
图4 单向板试验的复合材料铺层模型
Fig. 4 The composite laminate model for the one-way slab tests
通过计算分析,获得单向板复合材料铺层模型的结果与实验结果对比如表6所示.从表中可以看出,在玻璃纤维承拉的0°铺层状态下,计算结果与仿真结果的误差小于3%;在主要由粘接材料承拉的90°铺层状态下,计算结果与仿真结果的误差小于6%.更多计算结果云图如图5、图 6所示.
从表中的对比分析可以看出,采用复合材料铺层模型能够有效模拟复合材料结构的力学性能,因此针对玻璃钢定向管结构,主要采用复合材料铺层模型对各向异性材料模型进行校验分析.
由图5可知,0°单向板拉伸X向变形最大量为0.000 294 m,而90°单向板拉伸X向变形最大量为0.002 652 m.
表6 单向板铺层材料模型结果对比(20 ℃条件)
Table 6 Comparison of the results of the one-way slab laminate material model (at 20 ℃)

注 Poisson比通过纵向应变和横向应变比值给定.
Note Poisson’s ratio is given by the ratio of the longitudinal strain to lateral strain.
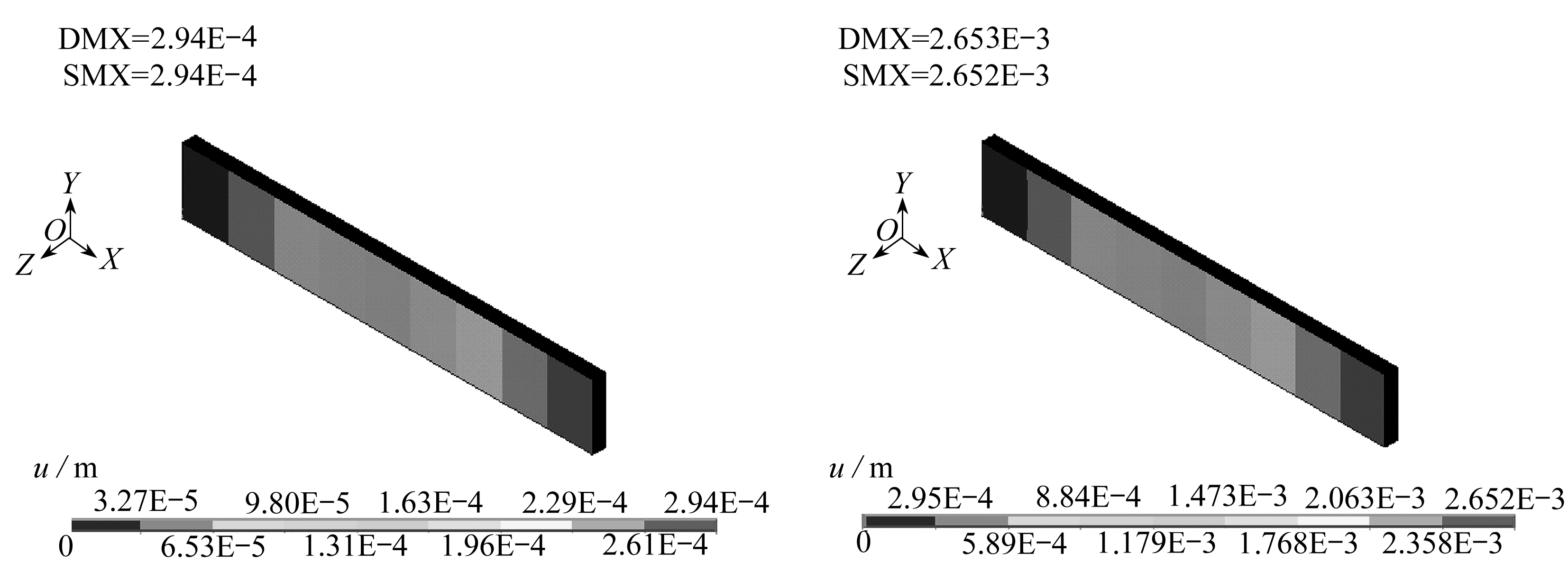
图5 0°单向板拉伸X向变形云图 图6 90°单向板拉伸X向变形云图
Fig. 5 The 0° unidirectional plate’s stretching Fig. 6 The 90° unidirectional plate’s stretching X-direction deformation contour X-direction deformation contour
3.2 各向异性模型
定向管玻璃钢材料的各向异性模型依据定向管玻璃钢的铺层形式计算获得(利用MSC.PATRAN计算获得).通过计算分析,获得定向管玻璃钢材料的各向异性参数如表7~10所示.
表7 玻璃钢定向管的各向异性材料参数(20 ℃)
Table 7 Anisotropic material parameters of the GFRP launching tube (20 ℃)

表8 玻璃钢定向管的各向异性材料参数(50 ℃)
Table 8 Anisotropic material parameters of the GFRP launching tube (50 ℃)
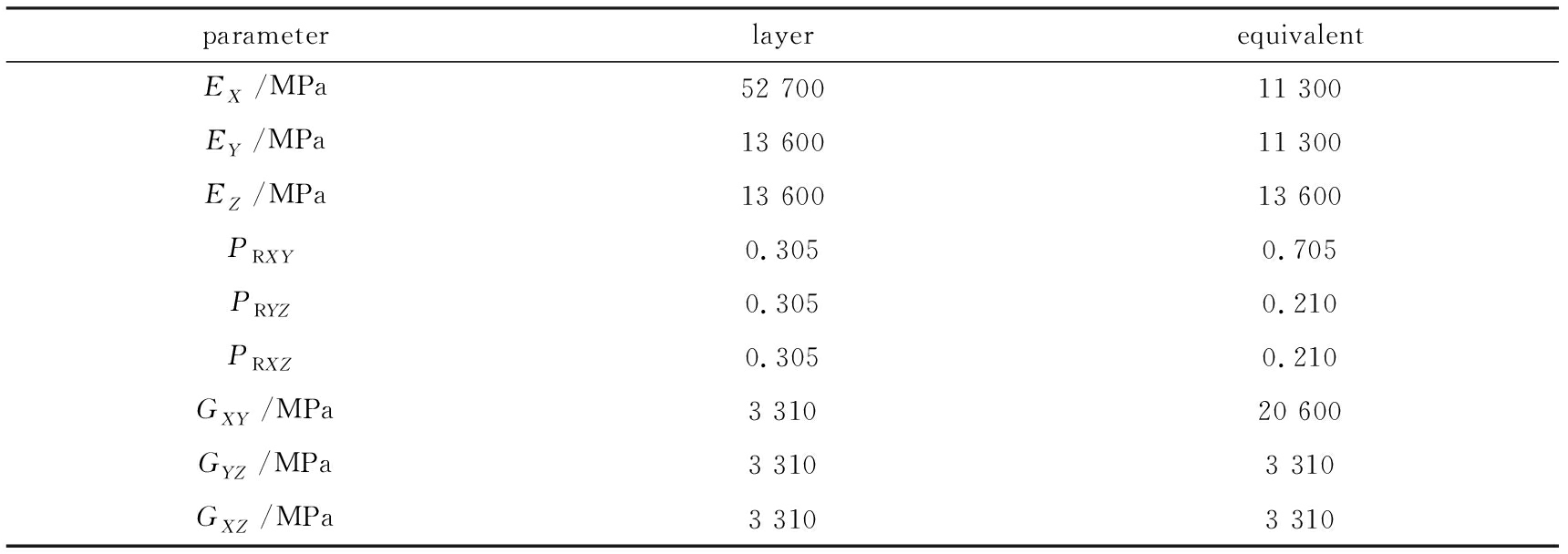
表9 玻璃钢定向管的各向异性材料参数(75 ℃)
Table 9 Anisotropic material parameters of the GFRP launching tube (75 ℃)
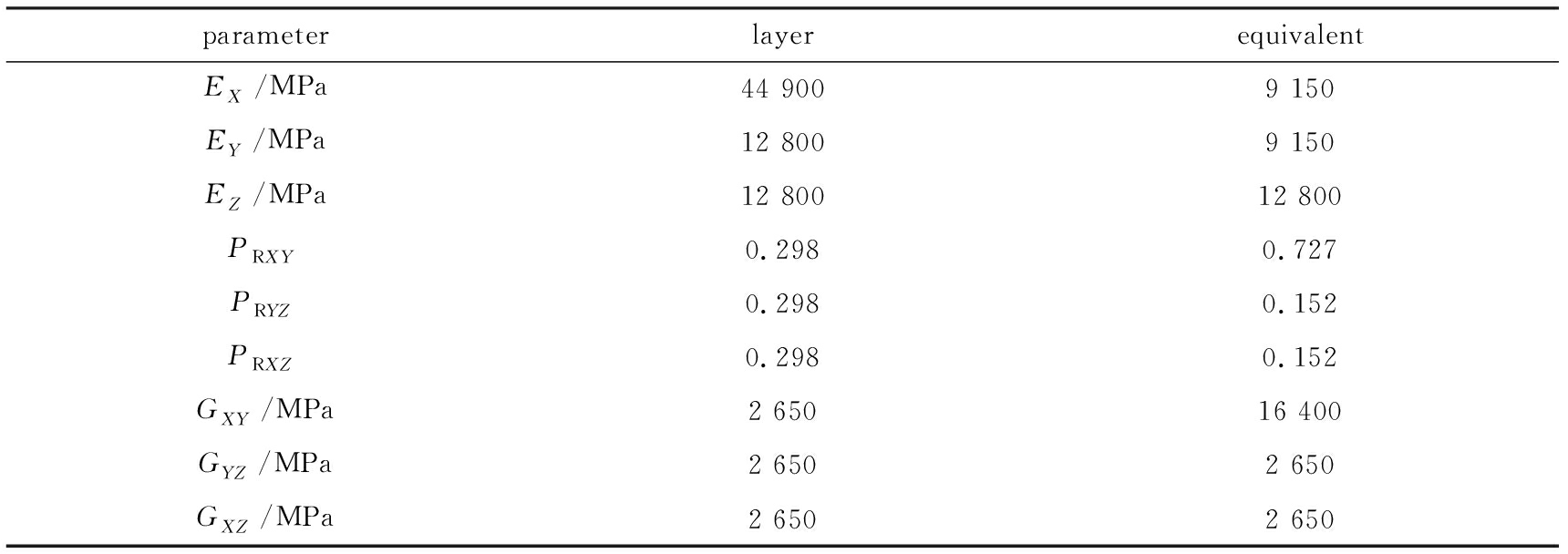
表10 玻璃钢定向管的各向异性材料参数(20 ℃, 老化后)
Table 10 Anisotropic material parameters of the GFRP launching tube (after 20 ℃, aging)
3.3 各向异性模型校验
为校验各向异性材料模型的有效性,以20 ℃条件为例,分别采用复合材料铺层模型和各向异性材料模型对玻璃钢定向管承压3 MPa和承拉0.3 MPa的状态进行对比分析.通过有限元计算[10],获得典型结果对比如表11所示,典型结果云图如图7~10所示.从表中和图中可以看出,不论是内表面承压状态还是端面承拉状态,等效材料模型与复合铺层模型的误差均小于10%,表明这里采用的各向异性材料模型能够较好地等效非金属材料特性,可用于后继的蠕变分析.
表11 仿真分析数据对照表
Table 11 Comparison of the simulation data

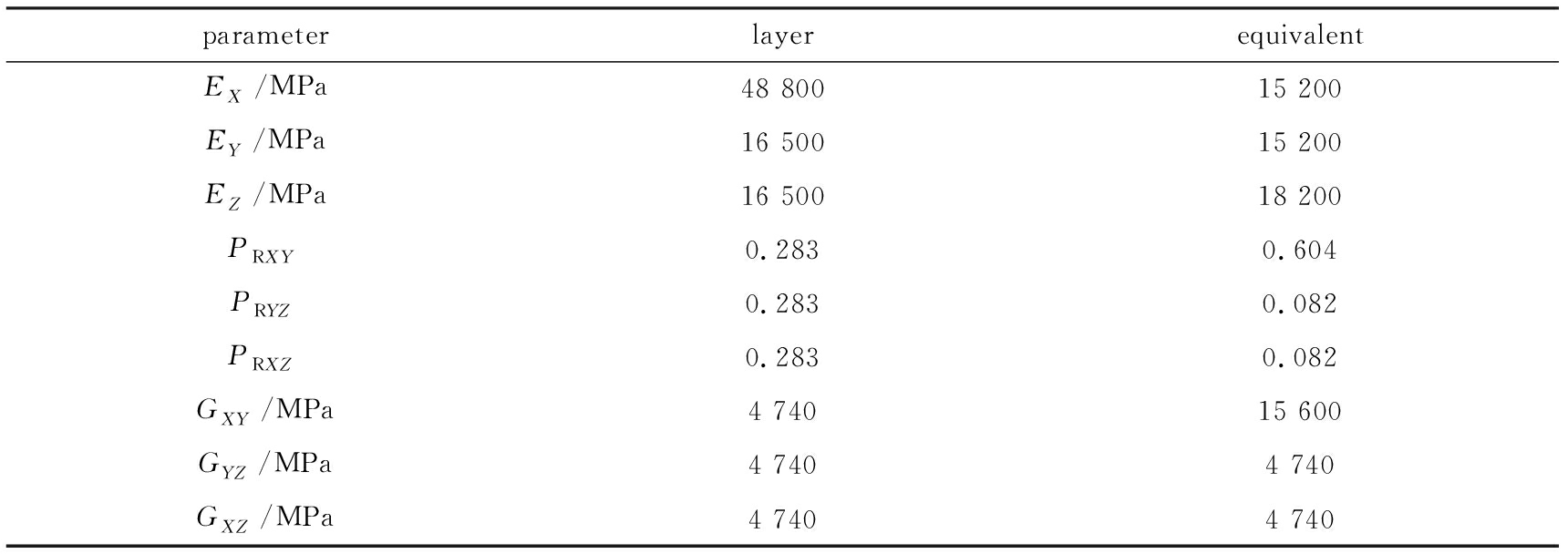
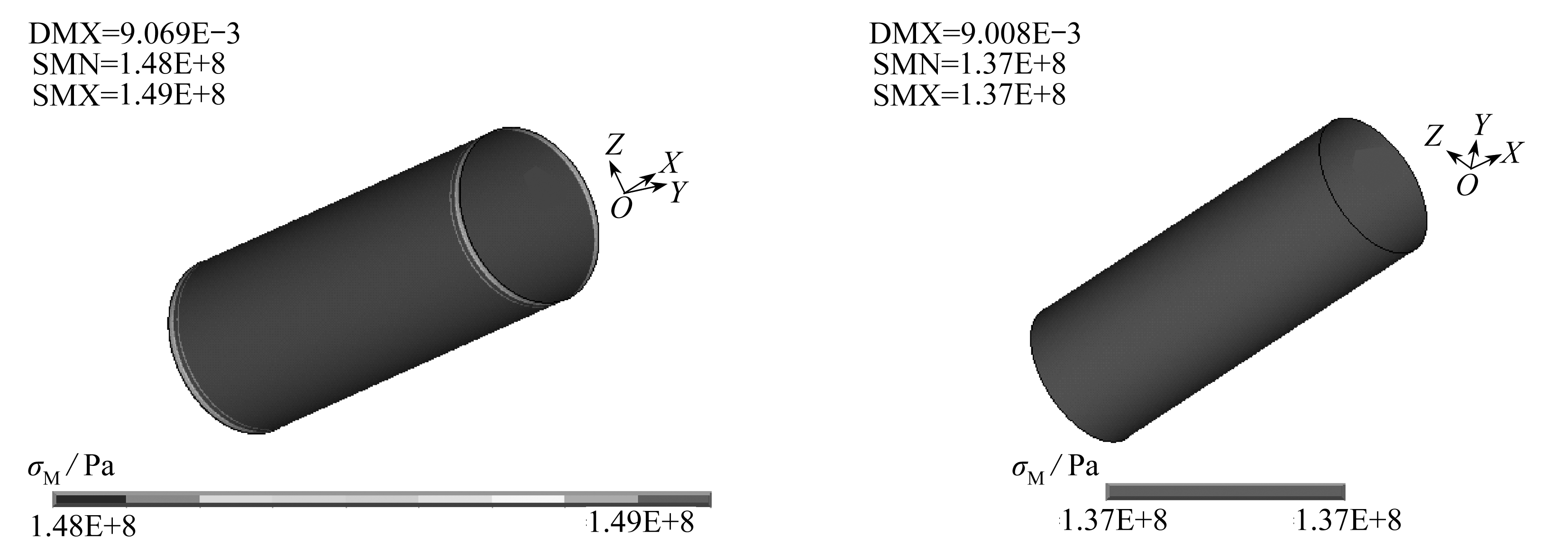
图7表示玻璃钢定向管内表面承压3 MPa时总位移云图,复合铺层模型中的最大位移量为0.009 069 m,而等效材料模型中的最大位移量为0.009 008 m,两个模型的位移量基本相差不大.
图8表示玻璃钢定向管内表面承压3 MPa时的von Mises应力云图,复合铺层模型中最大应力为1.49×108 Pa,而等效材料模型中的最大应力为1.37×108 Pa,两个模型的应力在误差允许范围内合理.

(a) 复合铺层模型 (b) 等效材料模型
(a) The composite laminate model (b) The equivalent material model
图7 内表面承压3 MPa时的总位移云图
Fig. 7 The total displacement contours(the inner surface is under a pressure of 3 MPa)
(a) 复合铺层模型 (b) 等效材料模型
(a) The composite laminate model (b) The equivalent material model
图8 内表面承压3 MPa时的von Mises应力云图
Fig. 8 The von Mises stress contours(the inner surface is under a pressure of 3 MPa)
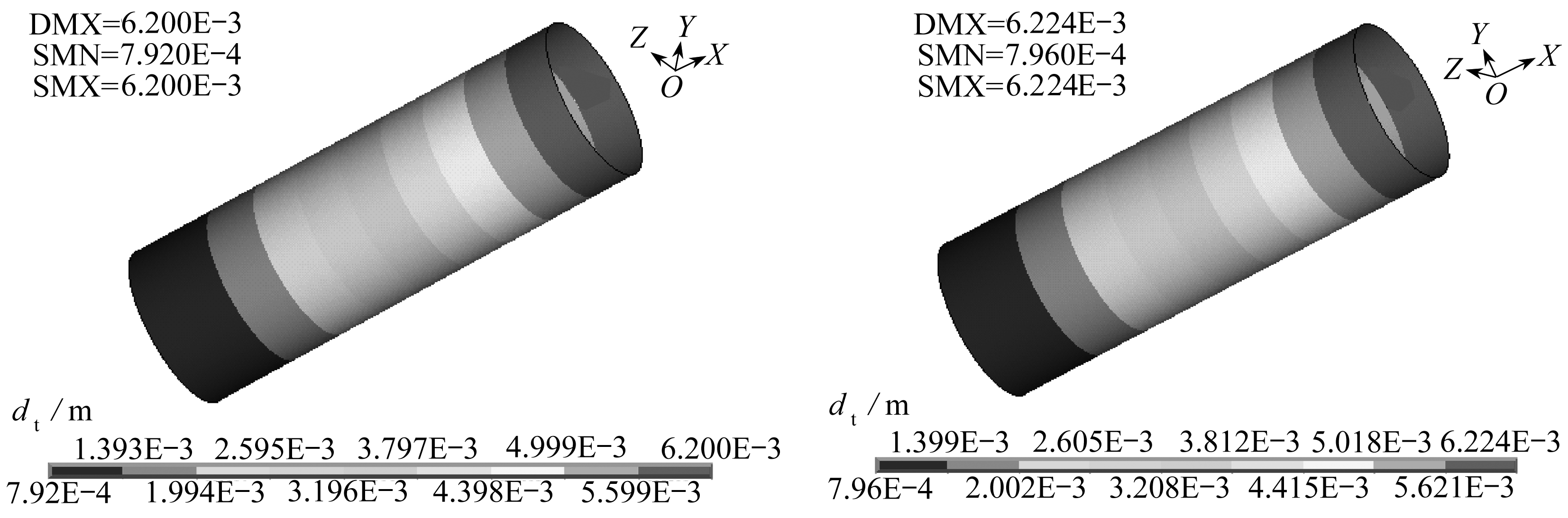
图9表示玻璃钢定向管端面承拉0.3 MPa时总位移云图,复合铺层模型中最大位移量为0.006 2 m,而等效材料模型中的最大位移量为0.006 224 m,两个模型的位移量基本相差不大.
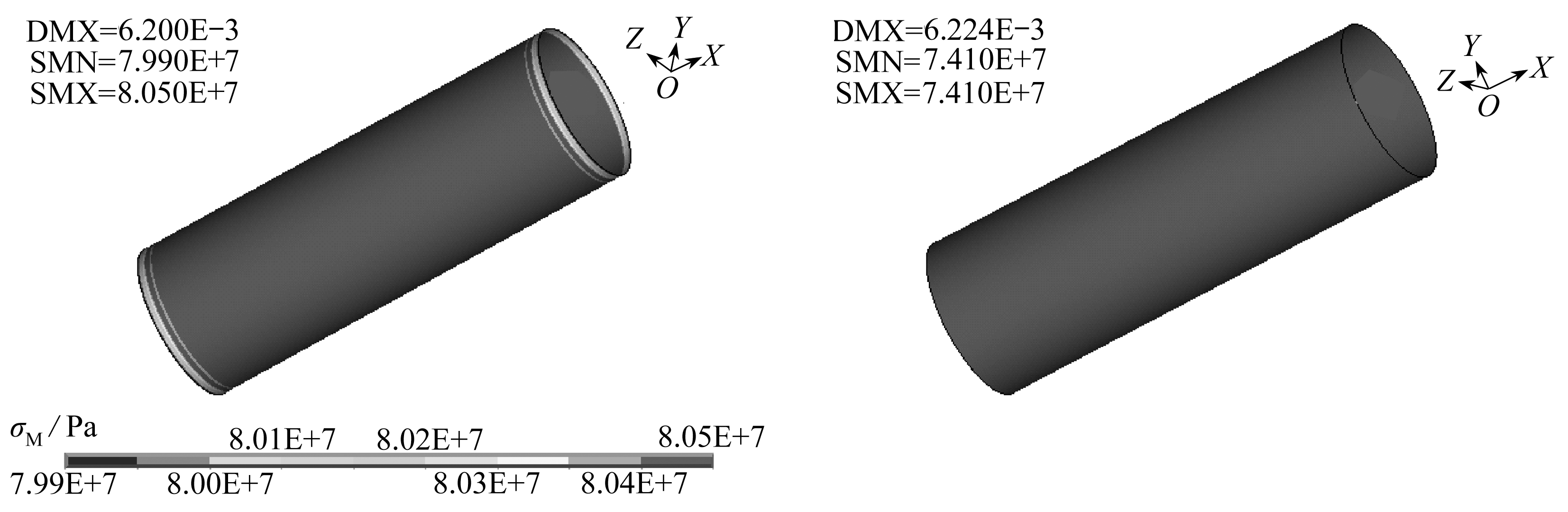
图10表示玻璃钢定向管端面承拉0.3 MPa时的von Mises应力云图,复合铺层模型中最大应力为8.05×107 Pa,而等效材料模型中的最大应力为7.41×107 Pa,两个模型的应力在误差允许范围内合理.
(a) 复合铺层模型 (b) 等效材料模型
(a) The composite laminate model (b) The equivalent material model
图9 端面承拉0.3 MPa时的总位移云图
Fig. 9 The total displacement contours(the end face is under a tension of 0.3 MPa)
(a) 复合铺层模型 (b) 等效材料模型
(a) The composite laminate model (b) The equivalent material model
图10 端面承拉0.3 MPa时的von Mises应力云图
Fig. 10 The von Mises stress contours(the end face is under a tension of 0.3 MPa)
4 结 论
通过建立玻璃钢定向管的力学模型,进行了玻璃钢单向板基本力学性能的试验和测量,获得定向管玻璃钢材料的基本力学性能,含加速老化后的基本力学性能,为建立非金属定向管长贮性能分析的计算模型提供材料参数.
经仿真建模与数值计算,可得出采用复合材料铺层模型能够有效模拟复合材料结构的力学性能,因此针对玻璃钢定向管结构,主要采用复合材料铺层模型对各向异性材料模型进行校验分析.
采用的各向异性材料模型能够较好地等效非金属材料特性,可用于后继的蠕变分析.并且,所得试验数据也为建立非金属定向管长贮性能分析的计算模型提供材料参数.
参考文献(References):
[1] 王禹阶. 有机无机玻璃技术问答[M]. 北京: 化学工业出版社, 2001.(WANG Yujie. Organic and Inorganic Glass Technical Quiz[M]. Beijing: Chemical Industry Press, 2001.(in Chinese))
[2] 胡波, 李壮. 国外弹道导弹突防的关键技术与发展[J]. 战术导弹技术, 2010(2): 124-128.(HU Bo, LI Zhuang. The breakthrough of foreign ballistic missiles: key techniques and development[J]. Tactical Missile Technology, 2010(2): 124-128.(in Chinese))
[3] 李强, 崔岩. 切比雪夫多项式在单台经纬仪记忆跟踪中的应用[J]. 激光与光电子学进展, 2013, 50(4): 169-173.(LI Qiang, CUI Yan. Application of Chebyshev polynomial in memory tracking of single theodolite[J]. Advances in Laser and Optoelectronics, 2013, 50(4): 169-173.(in Chinese))
[4] 胡建国, 仲健林, 马大为. 某运发箱定向器多目标优化设计研究[J]. 兵器材料科学与工程, 2014, 37(3): 1046-1051.(HU Jianguo, ZHONG Jianlin, MA Dawei. Multi-objective optimization for orientator of airdropping launch canister[J]. Ordnance Material Science and Engineering, 2014, 37(3): 1046-1051.(in Chinese))
[5] 张中利, 党玉功, 乐贵高. 玻璃钢定向器热弹性能数值仿真与分析[J]. 系统仿真学报, 2010, 22(4): 877-880.(ZHANG Zhongli, DANG Yugong, LE Guigao. Numerical simulation and analysis of thermal and elastic performance for glass-steel launch tube[J]. Journal of System Simulation, 2010, 22(4): 877-880.(in Chinese))
[6] 朱子华. 双轴拉伸定向有机玻璃的定向度均匀性的研究[J]. 材料工程, 1993(3): 42-44.(ZHU Zihua. Study on the phenomenon and pattern of orientation of diaxial strenthching orientiated organic glass[J]. Journal of Materials Engineering, 1993(3): 42-44.(in Chinese))
[7] 吕锡慈, 罗和璋. 用会聚偏振光测定双轴热拉伸有机玻璃板的双折射值的研究[J]. 高分子通讯, 1980(1): 45-50.(LÜ Xici, LUO Hezhang. Study on birefringence of biaxially hot-stretched acrylics by using convergent polarized light[J]. Acta Polymerica Sinica , 1980 (1): 45-50.(in Chinese))
[8] 苏腾腾, 于存贵, 宋涛. 玻璃钢定向器老化性能及蠕变行为研究[J]. 四川兵工学报, 2015, 36(10): 139-141.(SU Tengteng, YU Cungui, SONG Tao. Research on aging properties and creep behavior about glass-steel launching tube[J]. Journal of Sichuan Ordnance, 2015, 36(10): 139-141.(in Chinese))
[9] 王坷, 张福祥. 玻璃钢制火箭炮定向器的强度研究[J]. 弹道学报, 2003, 15(2): 39-43.(WANG Ke, ZHANG Fuxiang. The strength research of the rocket launcher GFRP tube[J]. Journal of Ballistics, 2003, 15(2): 39-43.(in Chinese))
[10] 沈叔曾. 玻璃钢的蠕变性能[J]. 上海力学, 1982(2): 71-78.(SHEN Shuzeng. The creep behaviour of glass reinforced plastics[J]. Shanghai Mechanics, 1982(2): 71-78.(in Chinese))
引用本文/Cite this paper:
何泽鹏, 毕世华, 马越, 罗碧霞. 玻璃钢定向管热力学性能研究与模拟[J]. 应用数学和力学, 2018, 39(6): 645-656.
HE Zepeng, BI Shihua, MA Yue, LUO Bixia. Research and simulation of mechanical properties of GFRP launching tubes[J]. Applied Mathematics and Mechanics, 2018, 39(6): 645-656.