引 言
航空发动机机匣内侧与叶片之间常用蜂窝结构,紧贴叶片外环的外围,具有足够的强度和韧性、良好的密封性,并且耐腐蚀、抗氧化.在航空发动机的首次运转过程中,其叶片叶尖将蜂窝结构切割成希望的形状,并由此形成一种几乎呈气密性的密封[1].当发动机转子发生超转时,叶片与机匣内侧的蜂窝之间不可避免地发生碰摩,由于零件受到高速冲击载荷作用,在分析这类问题中,仿真分析时材料必须考虑应变率效应.高速冲击状态下的材料模型与准静态是完全不同的,如何选择材料动态力学模型进行拟合与标定,也是仿真建模中最重要和最困难的工作之一[2-6].
在工业界,LS-DYNA、ABAQUS等显式动力学商业软件被广泛应用于高速撞击过程的数值仿真分析.这类软件中通常包含了各类考虑高应变率效应的材料模型,如J-C模型、Cowper-Symonds模型,以表格形式定义的应变率相关弹塑性模型等.而蜂窝结构作为各向异性材料,LS-DYNA中有MAT_HONEYCOMB和MAT_MODIFIED_HONEYCOMB两种专门针对蜂窝和泡沫等多孔材料的模型,分别描述材料各主应力和剪切应力的非线性弹塑性本构模型.然而,这两种模型都涉及较多的模型参数,在航空发动机设计和实际应用中受到较大限制.本文通过合理的参数标定及对蜂窝进行各向同性简化假设,综合考虑不同应变率下的屈服特性、温度及绝热温升导致的热软化影响等,应用模型参数较少的J-C模型进行蜂窝结构的仿真分析,有效地降低了模型参数的标定成本.
1 本 构 模 型
1.1 蜂窝等效模型
在早期的蜂窝结构分析模型中,为了简化分析,蜂窝芯层的面内刚度和弯曲刚度通常被忽略.事实上,虽然蜂窝芯层很软,但由于其相对背板而言具有较大的厚度,因此忽略其面内刚度和弯曲刚度必然会导致不可忽视的误差.蜂窝等效理论是对蜂窝进行等效的一种有效方法.假定芯层能抵抗横向剪切变形并且具有一定的面内刚度,背板服从Kirchhoff 假设,忽略其抵抗横向剪应力的能力,则蜂窝芯层可以等效为一均质的厚度不变的正交异性层.正六边形蜂窝夹芯等效弹性参数为[7]
(1)
(2)
(3)
(4)
(5)
(6)
其中t为正六边形蜂窝胞元界面厚度,l为正六边形蜂窝胞元界面长度,ES,GS,μ为夹芯层材料参数.蜂窝等效理论由于在有限元计算软件中有相应的等效单元,建模简便,有较好的精度,得到广泛的应用.
1.2 J-C模型
J-C模型是一个经验型的黏塑性本构模型,该模型可以较好地描述材料的加工硬化效应、应变率效应和温度软化效应.由于其形式简单、使用方便而在工程中得到了广泛的应用.其表达式如下[8]:
(7)
式中A为参考应变率和参考温度下的初始屈服应力;B和n为材料应变硬化模量和硬化指数;C为材料应变率强化参数;m为材料热软化指数;![]() 为无量纲应变率,
为无量纲应变率,![]() 为参考应变率;T*=(T-Tr)/(Tm-Tr)为同系温度,Tr为参考温度,Tm为材料的熔点温度.
为参考应变率;T*=(T-Tr)/(Tm-Tr)为同系温度,Tr为参考温度,Tm为材料的熔点温度.
2 两种材料模型的应用
2.1 冲击试验
试验所用蜂窝结构的背板部分基体材料为GH3536,蜂窝部分基体为铬和钼固溶强化的一种含铁量较高的高温合金,蜂窝尺寸126 mm×17 mm×6.7 mm,背板尺寸140 mm×20 mm×2 mm.利用空气炮装置发射高速弹体撞击蜂窝靶板,试验设备为内径12.7 mm高速气炮冲击系统、多通道动态数据采集处理系统、多通道应变自动采集处理系统、高速摄像机等.蜂窝结构靶板试验件通过夹具安装在试验台架上,本试验根据蜂窝在发动机中实际工作状态,进行了三种速度(50,150,250 m/s),三种冲击角度(0°,45°,75°),两种温度(25,600 ℃)下的冲击试验.
室温下不同角度、不同速度下蜂窝结构的冲击试验结果见表1,由于本试验采用同等质量的弹体,为了使试验结果更直观地描述,图1给出了冲击能量(E=0.5mv2)与凹坑深度的关系:在一定冲击能量范围内(E<20 J),随着冲击能量的提高,蜂窝结构的凹坑深度呈线性增加,并且随着冲击角度的增大,凹坑深度的增加越缓慢.为进一步研究该蜂窝结构对温度的敏感性,进行了600 ℃下(典型发动机工作时蜂窝温度)相同速度不同角度下的冲击试验,详见表2.通过表1和表2试验结果对比分析可知该蜂窝结构对温度较为敏感.
表1 室温(25 ℃)下蜂窝冲击试验结果
Table 1 Experimental results of honeycomb impact at room temperature (25 ℃)

表2 600 ℃下蜂窝冲击试验结果
Table 2 Experimental results of honeycomb impact at 600 ℃

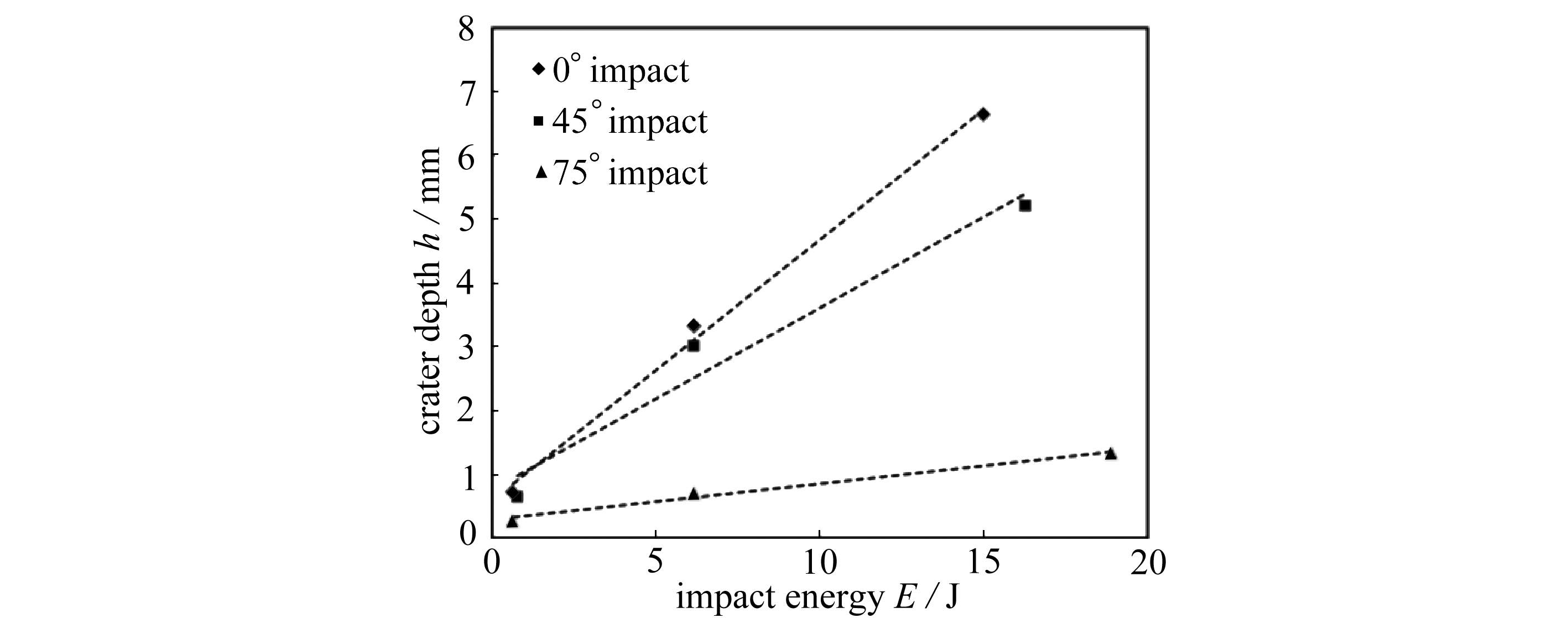
图1 凹坑深度-冲击能量曲线
Fig. 1 The relation between the crater depth and the impact energy
为了进一步研究该蜂窝结构在冲击载荷下的变形过程和破坏模式,将0°冲击后蜂窝结构的变形部分适当切割(图2), 观察变形截面可以发现, 该蜂窝结构受到面外冲击压缩过程可分为3个阶段: ① 初期孔壁弯曲,表现出短暂的线弹性变形; ② 紧接着多由塑性变形和塑性屈曲所代替,当达到某一临界应力时,孔穴开始失稳并逐渐坍塌, 同时存在局部的撕裂破坏; ③ 当进一步坍塌至蜂窝处于高应变时,孔穴充分坍塌以致相对孔壁发生接触,断裂的片段堆积在一起,进一步的变形即压缩到孔壁材料本身.蜂窝材料相对密度的加大,增加了孔壁的相对厚度.故而,孔壁的弯曲抗力和孔穴的坍塌抗力均提高,造成较高的模量.这样的机理使得蜂窝结构在受到面外冲击后,可以将变形和破坏控制在较小范围内.
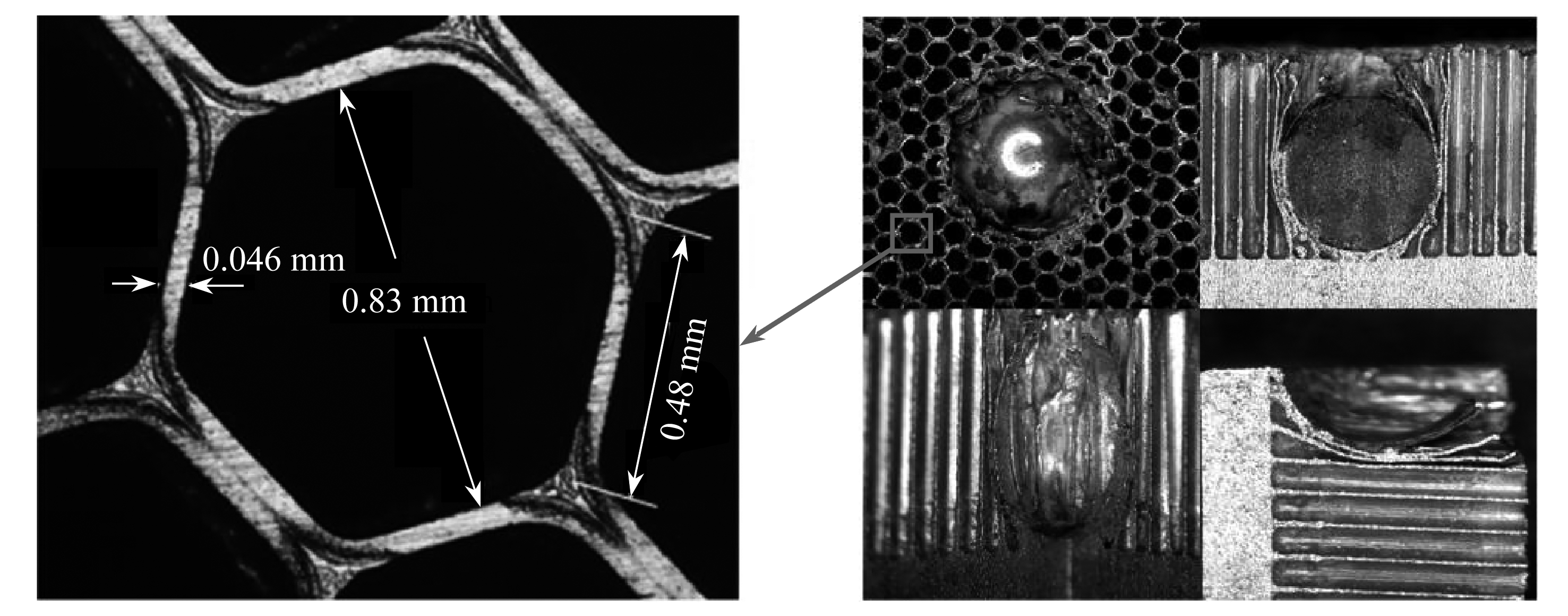
图2 冲击后的蜂窝损伤
Fig. 2 Damage of the honeycomb after impact
2.2 仿真结果对比
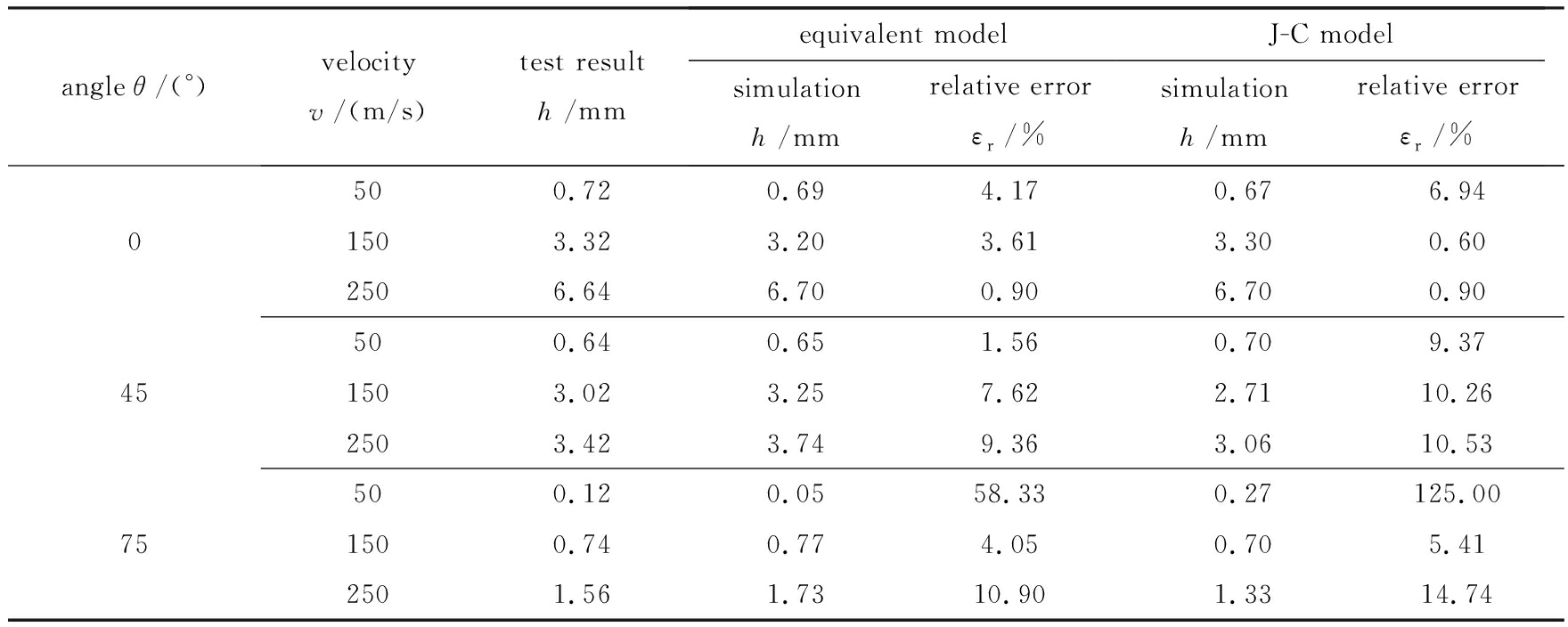
根据弹道冲击试验,将模型分为弹丸、蜂窝靶板两个部分,如图3所示.弹丸采用刚体单元,蜂窝结构采用实体单元.按照蜂窝等效理论,将窝芯层等效为一块同尺寸的正交各向异性材料均匀体,蜂窝芯层材料参数见表3.将蜂窝简化为各向同性材料均匀体,直接参照材料的J-C模型参数,结果如表4所示.
采用J-C材料模型参数开展的钢珠冲击蜂窝靶板动力学仿真分析见图4,表5给出了两种本构模型与试验结果对比分析.从对比中发现:除75°浅坑情况外,其余试验深度和模拟深度的相对误差在15%以内,从而证明模拟结果具有一定的可靠性.蜂窝夹层结构破坏机理可简化为主要承受z向压缩失效和横向剪切失效[9],对于0°冲击主要为蜂窝结构的z向压缩失效.而45°和75°冲击主要为蜂窝结构的z向压缩失效和剪切失效的复合失效模式,钢珠和蜂窝平面内接触时会产生横向摩擦载荷,随着冲击角度的增大,横向摩擦载荷与z向压缩载荷的比例将会增大,同时横向摩擦载荷与动摩擦因数以及静摩擦因数直接相关.而本文未考虑静摩擦因数和动摩擦因数随着冲击速度和角度的变化,均取0.15,因此45°和75°冲击情况下的试验和模拟结果比0°冲击下有较大误差.综合上述,采用J-C材料模型和蜂窝等效模型的有限元仿真结果十分接近,都可以较好地满足工程应用.相对而言,蜂窝等效模型在工程使用方面,存在参数复杂问题,而J-C材料模型使用简单,工程应用较为方便.

图3 有限元模拟冲击过程与试验结果对比
Fig. 3 Comparison between finite element simulation of the impact process and experimental results
表3 蜂窝等效材料参数
Table 3 Equivalent material parameters of the honeycomb

表4 蜂窝J-C模型参数
Table 4 J-C model parameters of the honeycomb
表5 2种模型仿真深度和试验对比
Table 5 Comparison between the 2 models simulation results and the test results
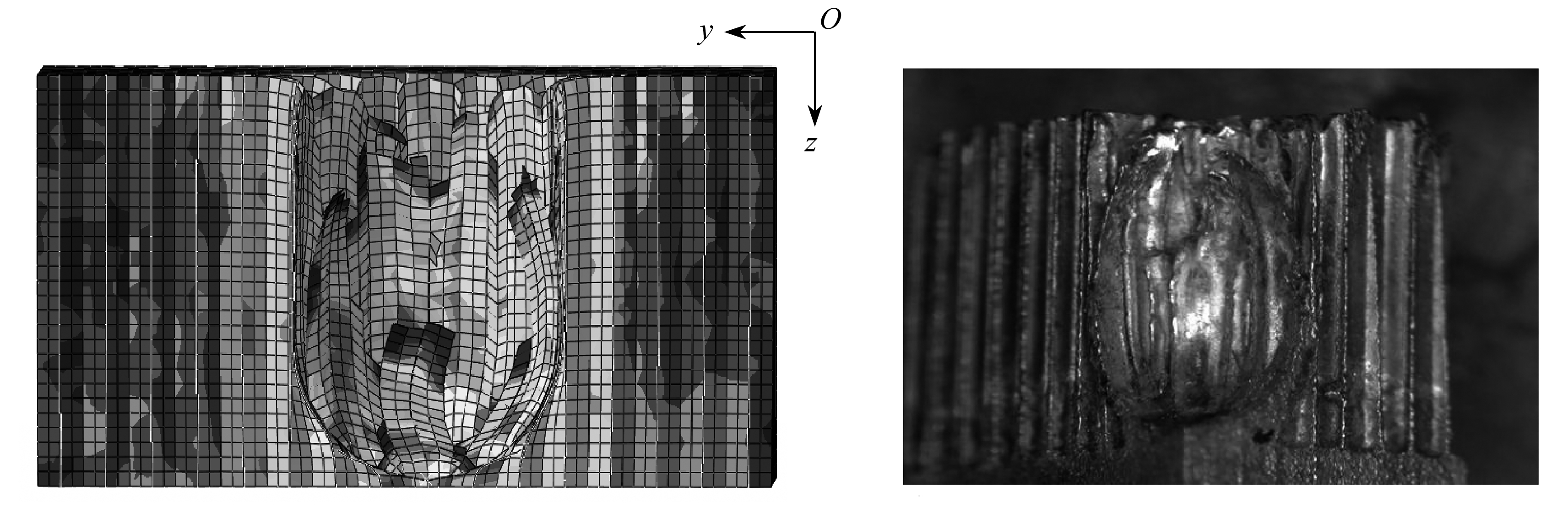
(a) 0°冲击
(a) The 0° impact

(b) 45°冲击
(b) The 45° impact
图4 不同角度冲击靶板仿真(J-C模型)
Fig. 4 Simulation of the honeycomb impact test at different angles(J-C model)
3 结 论
1) 在一定冲击能量范围内(E<20 J),随着冲击能量的提高,蜂窝结构的凹坑深度呈线性增加,并且随着冲击角度的增大,凹坑深度的增加越缓慢,同时该蜂窝结构对温度较为敏感.
2) 通过合理的参数标定及各向同性简化假设,J-C模型可提供满意的仿真结果,其中蜂窝损伤预测与试验结果符合较好.
致谢 本文作者衷心感谢中国航空研究院的航空科学基金(KYHJ150182)对本文的资助.
参考文献(References):
[1] 刘艳辉, 杜鹏. 金属蜂窝夹层板的研究进展[J]. 机械制造与自动化, 2013, 41(1): 9-15.(LIU Yanhui, DU Peng. Research process of metal honeycomb sandwich boards[J]. Machine Building & Automation, 2013, 41(1): 9-15.(in Chinese))
[2] 柳爱群, 黄西成. 高应变率变形的Johnson-Cook动态本构模型参数识别方法[J]. 应用数学和力学, 2014, 35(2): 219-225.(LIU Aiqun, HUANG Xicheng. Identification of high-strain-rate material parameters in dynamic Johnson-Cook constitutive model[J]. Applied Mathematics and Mechanics, 2014, 35(2): 219-225.(in Chinese))
[3] 肖云凯, 方秦, 吴昊, 等. Johnson-Cook本构模型参数敏感度分析[J]. 应用数学和力学, 2015, 36(S): 21-28.(XIAO Yunkai, FANG Qin, WU Hao, et al. Analysis of parameter sensitivity for the Johnson-Cook constitutive model[J]. Applied Mathematics and Mechanics, 2015, 36(S): 21-28.(in Chinese))
[4] GAMBIRASIO L, RIZZI E. An enhanced Johnson-Cook strength model for splitting strain rate and temperature effects on lower yield stress and plastic flow[J]. Computational Materials Science, 2016, 113: 231-265.
[5] 宣海军, 陆晓, 洪伟荣, 等. 航空发动机机匣包容性研究综述[J]. 航空动力学报, 2010, 25(8): 1860-1870.(XUAN Haijun, LU Xiao, HONG Weirong, et al. Review of aero-engine case containment research[J]. Journal of Aerospace Power, 2010, 25(8): 1860-1870.(in Chinese))
[6] 温登哲, 陈予恕. 航空发动机机匣动力学研究进展与展望[J]. 动力学与控制学报, 2013, 11(1): 12-19.(WEN Dengzhe, CHEN Yushu. Review and prospect on the research of aero-engine casing dynamics[J]. Journal of Dynamics and Control, 2013, 11(1): 12-19.(in Chinese))
[7] 李贤冰, 温激鸿, 郁殿龙, 等. 蜂窝夹层板力学等效方法对比研究[J]. 玻璃钢/复合材料, 2012(S1): 11-15.(LI Xianbing, WEN Jihong, YU Dianlong, et al. The comparative study of equivalent mechanical methods on honeycomb sandwich plate[J]. Fiber Reinforced Plastics/Composites, 2012(S1): 11-15.(in Chinese))
[8] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[C]//Proceedings of the 7th International Symposium on Ballistics. Hague, Netherlands, 1983, 21: 541-547.
[9] 法洋洋, 陈秀华. 蜂窝夹层结构拉脱破坏的有限元分析[J]. 机械工程材料, 2012, 36(10): 86-91.(FA Yangyang, CHEN Xiuhua. Finite element analysis of honeycomb sandwich in pull-off damage[J]. Materials for Mechanical Engineering, 2012, 36(10): 86-91.(in Chinese))
引用本文/Cite this paper:
孟卫华, 王建军, 米栋, 汪文君, 郭伟国. 航空发动机用蜂窝材料应变率相关本构模型及应用研究[J]. 应用数学和力学, 2018, 39(6): 665-671.
MENG Weihua, WANG Jianjun, MI Dong, WANG Wenjun, GUO Weiguo. Application of strain-rate-dependent material models to aero-engine honeycomb casing analysis[J]. Applied Mathematics and Mechanics, 2018, 39(6): 665-671.