引 言
高超声速飞行器在出入大气层时会承受剧烈的气动热载荷作用,内部相互约束的结构在热变形的影响下产生应力使变形加剧造成结构整体翘曲,阻碍飞行器飞行[1].夹芯结构作为金属热防护系统(MTPS)最外层部件,承受了巨大的气动力、热载荷而变形,夹芯结构厚度方向强烈的温度变化加剧了结构的变形[2].分析夹芯结构在力热载荷作用下的变形已有了很多研究工作,但基本都是基于有限元数值方法或等效夹层梁、板模型的方法进行分析[3-11].
对于具有周期子结构的格栅夹芯梁,由于夹芯内部空间的存在,夹芯内腹板自身变形影响结构的整体变形,使其具有明显的非局部特性[12].利用等效的夹层梁、板模型计算时得到的结果在某些时候会出现较大的误差.利用有限元或结构矩阵的方法,已经有大量的工作研究了格栅夹芯梁结构在温度和机械力载荷作用下的变形问题.尽管有限元方法可以得到问题较为精确的结果,但也存在一些无法避免的问题.对于大型的格栅夹芯梁结构,单元个数的限制要求单元不能太小,许多时候依然需要利用板、壳单元来进行分析,使面板与腹板连接处的计算精确度降低;若要将结构对于某些不同载荷条件进行优化,需要大量的计算且不易找到各变量与总体变形的直接关系.
针对格栅夹芯结构内部子结构具有周期性的特点,若选取胞元分析其受力与变形间的关系,并通过等效的方式将胞元等效为连续介质的一部分,就能将问题纳入到连续介质的范畴内,通过理论建模得到问题的通解.不但简化了分析过程,各变量对结果的影响也可以直观地表现出来,便于对结构进行优化设计[12-14].本文通过合理的胞元选取、精确的胞元变形分析,得到了胞元的整体变形能;利用能量等效方法确定了与格栅夹芯结构等价的微极介质的本构关系;最后利用几何关系与平衡条件建立了微极梁受热变形的控制方程组,给出了微极梁位移随温度载荷变化的表达式.通过与夹层梁、ANSYS有限元软件计算的非均匀温度影响下悬臂格栅夹层梁受热弯曲变形的数值结果对比表明:将不连续的格栅夹芯结构等效为连续介质构成的模型时,由于约束的增加、自由度的减少,需要更多的应力、应变参量来描述其非局部的特性,同时也验证了本文模型的有效性.
1 模 型 建 立
1.1 微极等效模型
考虑如图1所示的金属格栅夹芯梁受温度载荷影响下的变形,取典型胞元进行结构分析(图1中,坐标系原点在腹梁中点,x方向沿梁轴线方向,y方向沿梁厚度方向).上、下梁的厚度为t;温度分别为θ1x和θ2x(θ1,θ2为常系数,可由加热程度决定);腹梁的厚度为t1,高度为h;其内温度为(θ1+θ2)x/2-(θ1-θ2)xy/h;上、下梁长度为L;夹芯结构的宽度为b.
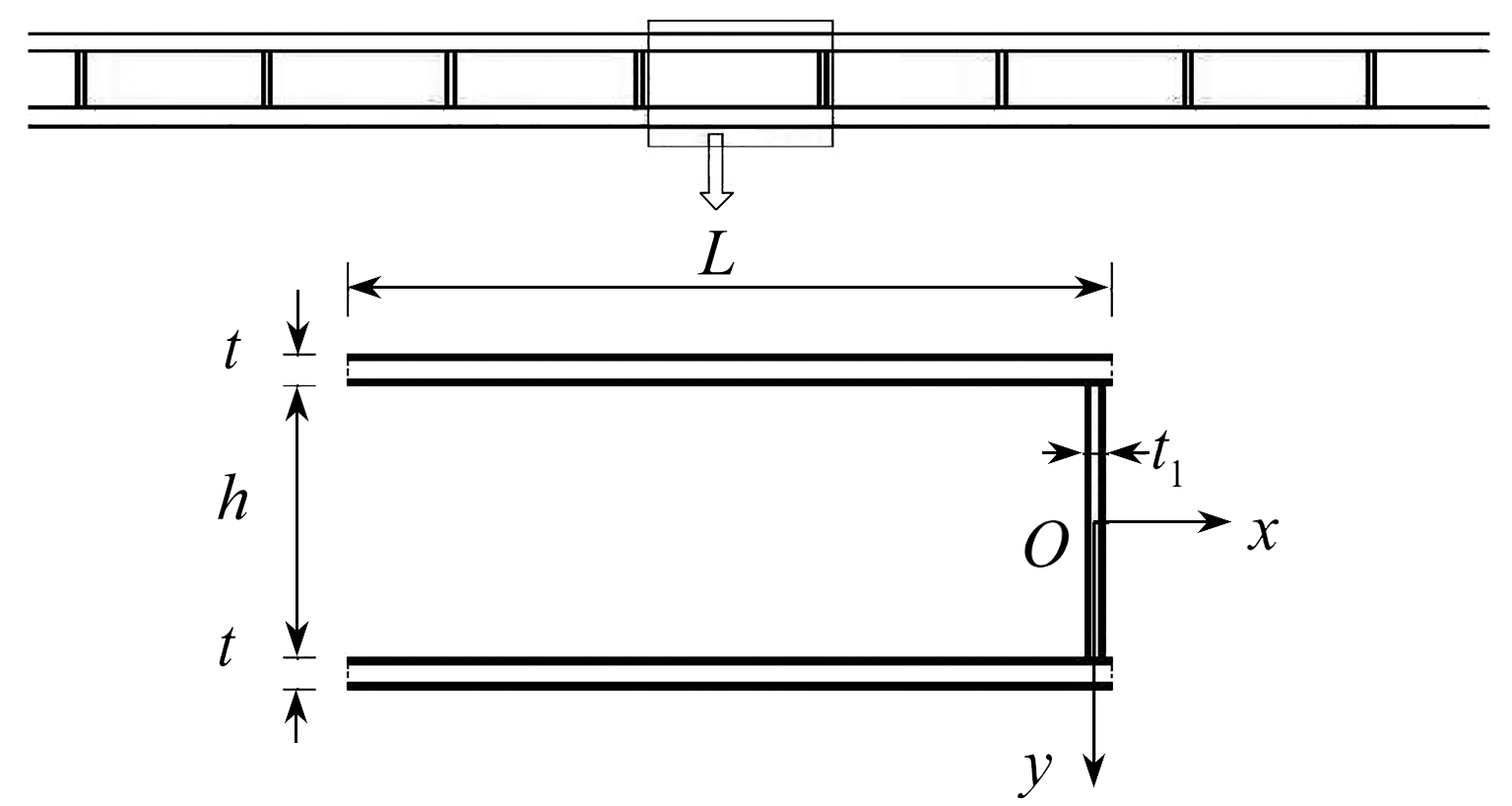
图1 格栅夹芯梁结构及胞元
Fig. 1 A grid sandwich beam structure and a cell
不考虑格栅夹芯梁厚度变化,假设x坐标为xi的第i根腹梁与坐标为xi+1的第i+1根腹梁间胞元两边横向、纵向位移及转角满足关系[12]:
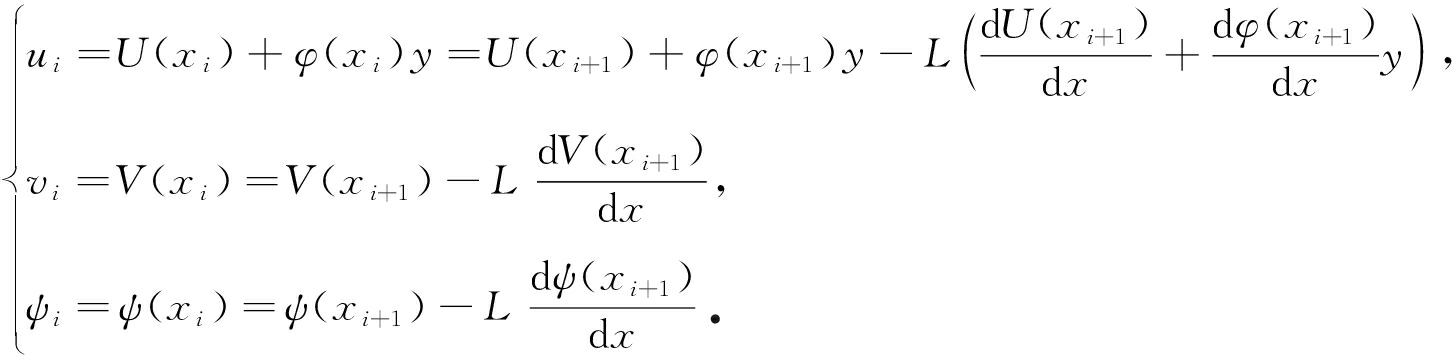
(1)
利用结构矩阵法,在上、下梁材料和尺寸相同的情况下,胞元能量可表示为(上、下梁弹性模量、热膨胀系数、截面面积和惯性矩分别为E,α,A=bt和I=bt3/12,腹梁的弹性模量和惯性矩分别为E1和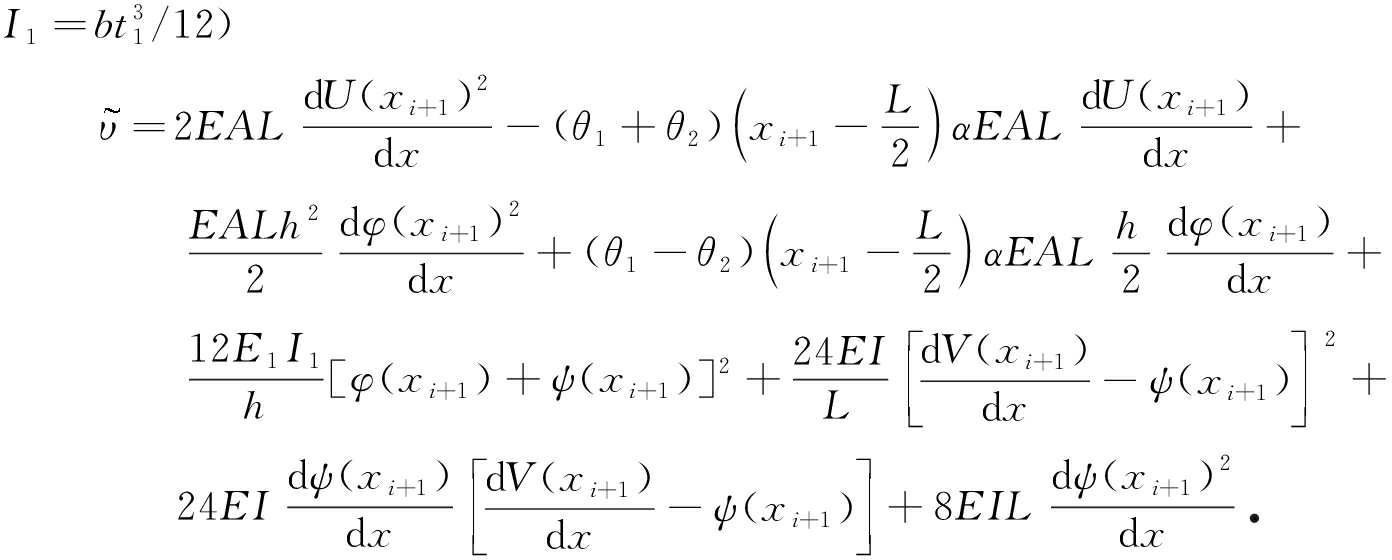
(2)
在平面微极热弹性理论的框架下,假设平面微极弹性介质本构关系如下:

(3)
其中
由胞元能量等效得到
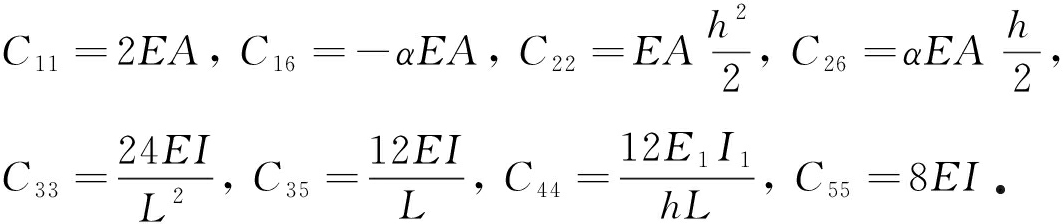
将平面热弹性微极平衡方程沿梁厚度方向积分,乘以y后再沿梁厚度方向积分得到[14]
N,x+τyx,y=0, M,x=0, τxy,x=0, ω,x+τxy-τyx=0.
(4)
利用方程(3)、(4)得到微极梁热变形控制方程:

(5)
取固支端在x=0处的格栅夹芯悬臂梁,取总长度为x=l=nL(n为胞元个数),固支端边界条件:
U(0)=0, φ(0)=0, ψ(0)=0, V(0)=0, V,x(0)=0.
(6)
自由端x=l处边界条件:
N(l)=0, τxy(l)=0, M(l)+ω(l)=0.
(7)
最后得到等效悬臂微极梁的热变形为
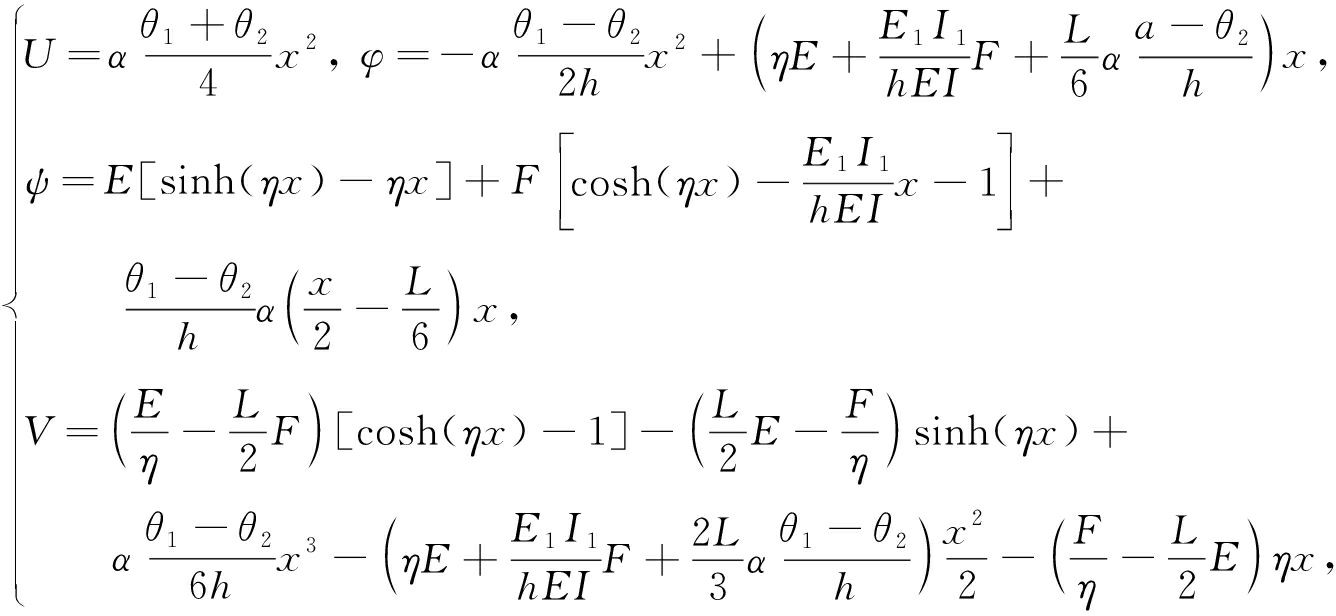
(8)
其中
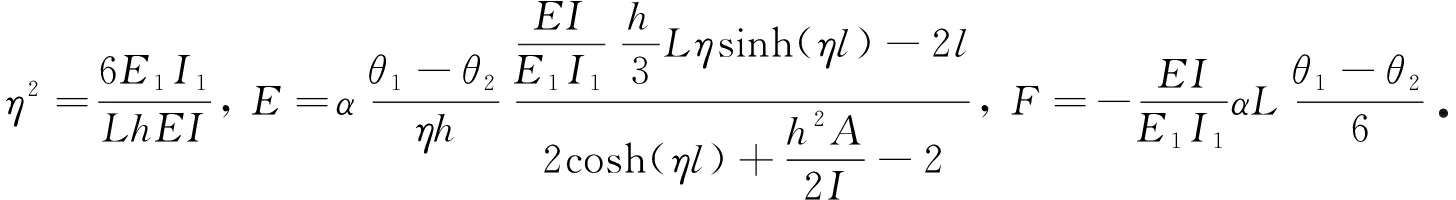
1.2 夹层梁模型
参考文献[10]中的模型,假设上、下梁及中间夹芯横向位移u+,u-和uc,纵向位移w+,w-和wc如下:
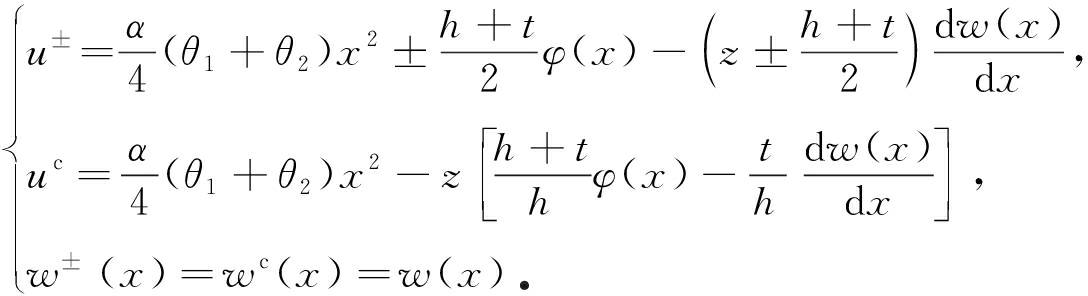
(9)
上、下梁内力及其对夹芯梁中间层的弯矩为
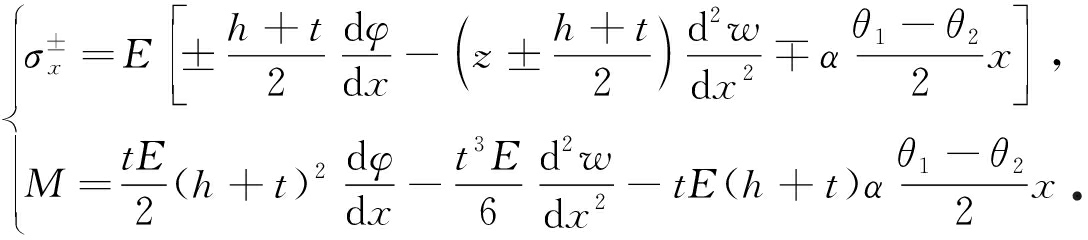
(10)
由夹芯位移得到其剪应变(不考虑温度引起的剪应变):
(11)
假设夹芯中仅有剪力(夹芯剪切模量为Gc):
(12)
由表层梁平衡方程
积分得到上、下梁内剪力:
(13)
将总剪应力Q=Q++Q-+Qc代入平衡方程得到
(14)
在无初始面内载荷和弯曲载荷的情况下得到
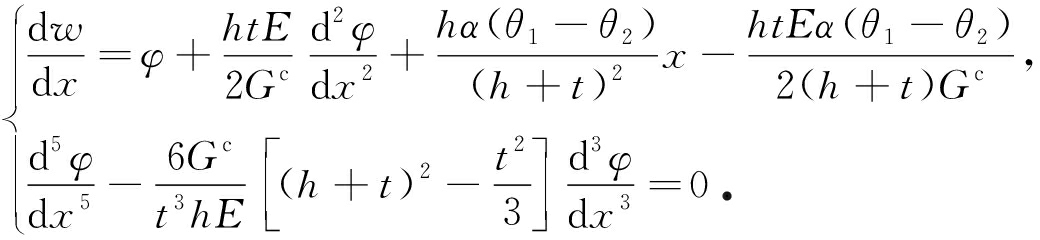
(15)
考虑固支端边界条件:
φ(0)=0, w(0)=0, w,x(0)=0,
(16)
自由端边界条件:
Q(l)=0, M(l)=0.
(17)
得到夹层梁热变形为

(18)
其中
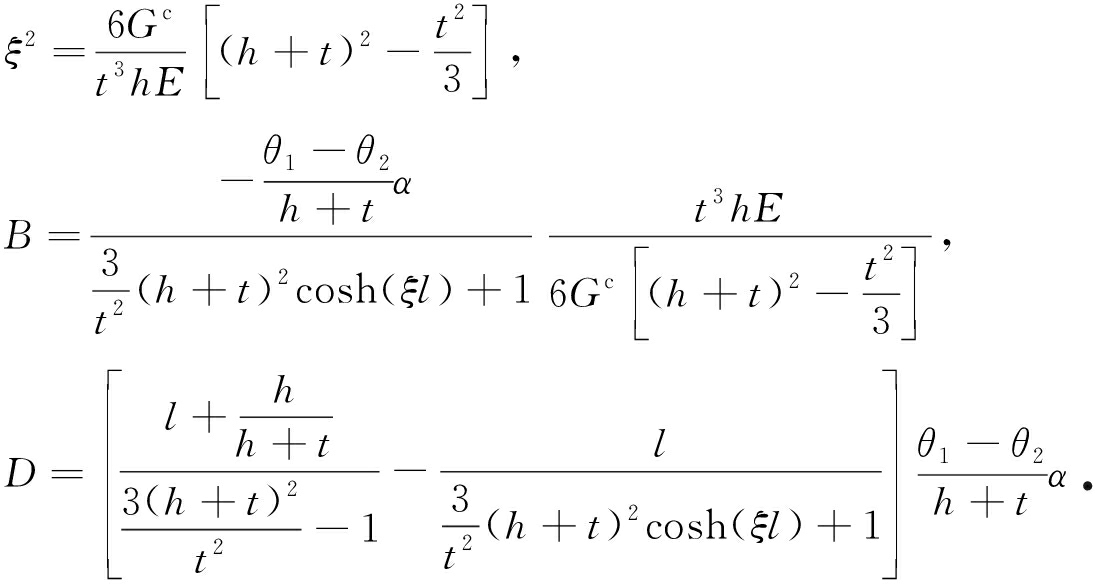
2 数值结果比较
以固支端在x=0处,总长度为l=nL的悬臂格栅夹层梁结构作为算例,利用本文等效微极梁方法和夹层梁模型计算上、下梁温度不同且温度沿梁厚度方向有梯度的悬臂格栅夹层梁受热后的弯曲变形,并与有限元方法(FEM)计算得到的结果进行比较.应用ANSYS有限元软件计算时,采用Solid45三维体单元.上、下梁和中间腹梁材料相同,均为铝合金材料,弹性模量为E=E1=75 GPa、Poisson(泊松)比为ν=ν1=0.3、热膨胀系数为α=α1=1.8×10-5 ℃-1.夹层结构的形状可由几何参数L=1 cm,t=t1=0.04 cm,b=0.04 cm和h=0.96 cm得到.上梁内的温度60x ℃,下梁内的温度30x℃.
分别取胞元数n=10,20,30,应用本文两种等效模型与有限元模型计算得到的悬臂夹芯结构受热后挠度曲线结果如图2所示(横坐标为悬臂梁沿长度方向任意点距固支端的长度与胞元长度比值x/L).随着格栅夹芯梁长度的变化,上、下梁的温度逐渐升高,温差逐渐加剧,结构整体的弯曲变形也越来越剧烈.以胞元数n=20时作为参考,从有限元软件的结果可以看到:相比于结构的整体挠度,上、下梁的挠度相差非常小,几乎可以忽略不计;对比n=10和n=30的情况,夹芯结构整体长度的变化对结构各点的挠度会产生影响,即结构具有非局部的特性.利用微极模型计算得到的结果比有限元结果小,而利用夹层梁模型计算得到的结果比有限元结果大.这可能是由于微极模型中忽略了夹芯腹梁的伸长,导致结构整体刚度增大;而夹层梁模型中仅考虑了夹芯的剪切模量,未考虑夹芯腹梁的弯曲,导致整体刚度较小.且从结果中可以明显看出连续夹层梁模型并没有明显的非局部特性,而利用微极梁模型对结构进行等效更为合适.
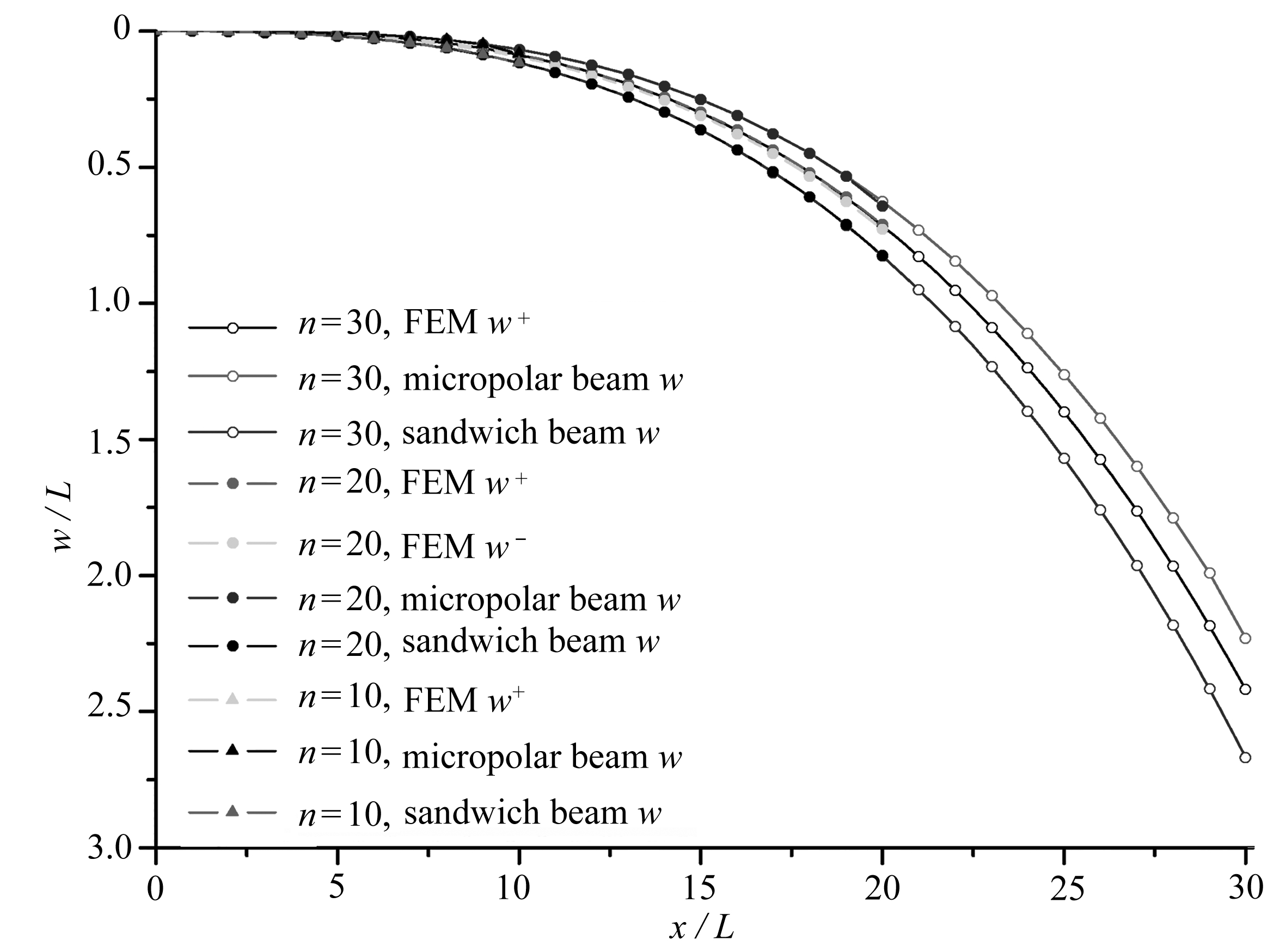
图2 悬臂格栅夹芯梁挠度曲线
Fig. 2 The deflection curves of the cantilever grid sandwich beam
表1 自由端挠度随胞元长度变化
Table 1 The deflection at the free end varying with the length of the cell

表1给出了胞元数n=20的格栅夹芯梁在非均匀温度下自由边界处的挠度值随胞元长度的变化情况.从表中可以看出,利用通常的弹性介质构成的夹层梁模型计算得到的结果并不随胞元长度的变化而变化,即其对结构的敏感性较差,并不能将结构整体的非局部特性表现出来.由有限元软件和微极梁模型计算得到的结构都对胞元形状有一定的敏感性,且微极梁模型的变化较有限元软件的变化还大.这主要是因为微极梁模型中假设的上、下梁挠度相同,忽略的夹芯中腹梁的变形,使其非局部的效应对胞元形状更加敏感所致.
3 结 论
本文针对格栅夹芯结构具有周期性子结构的特点,选取合理的胞元进行受力变形分析,得到了胞元的整体变形能;利用胞元能量等效的方法确定了与格栅夹芯结构等价的微极介质的本构关系;进而利用几何关系与平衡条件建立了微极梁受热变形的控制方程组,给出了微极梁位移随温度载荷变化的表达式.通过与夹层梁、ANSYS有限元软件计算的非均匀温度影响下悬臂格栅夹层梁受热弯曲变形的数值结果对比,表明本文微极梁模型在一定条件下计算得到的结果与有限元软件计算得到的结果较为接近;相比于夹层梁,微极梁模型可将格栅夹芯结构整体非局部效应表现出来.通过将夹芯中腹梁的转动和上、下梁内力矩与微极介质中微转动和偶应力相联系,将不连续的格栅夹芯结构等效为连续介质.相比于弹性介质,微极介质中的微转动可以增加连续介质内各点的运动维度,并与局部位移或转动相联系,从而将结构整体的非局部性表现出来.
致谢 本文作者衷心感谢天津市轻工与食品工程机械装备集成设计与在线监控重点实验室(热力耦合作用下弹塑性材料空穴萌生及增长对材料性能的影响(2016LIMFE04))对本文的资助.
参考文献(References):
[1] 范绪箕. 高速飞行器热结构分析与应用[M]. 北京: 国防工业出版社, 2009.(FAN Zhuqi. Thermal Structures Analysis and Applications of Highspeed Vehicles[M]. Beijing: National Defend Industry Press, 2009.(in Chinese))
[2] KO W L. Heat shielding characteristics and thermostructural performance of a superalloy honeycomb sandwich thermal protection system (TPS): NASA/TP-2004-212024[R]. 2004.
[3] 马玉娥. 可重复使用运载器热防护系统热/力耦合数值计算研究[D]. 博士学位论文. 西安: 西北工业大学, 2005.(MA Yu’e. Study of thermo-mechanical coupled computation for thermal protection system of reusable launch vehicle[D]. PhD Thesis. Xi’an: Northwestern Polytechnical University, 2005.(in Chinese))
[4] 唐羽烨, 薛明德. 蜂窝夹芯板的热学与力学特性分析[J]. 复合材料学报, 2005, 22(2): 130-136.(TANG Yuye, XUE Mingde. Thermo-mechanical characteristics analysis of sandwich panel with honeycomb core[J]. Acta Materice Compositae Sinica, 2005, 22(2): 130-136.(in Chinese))
[5] 刘振祺, 梁伟, 杨嘉陵, 等. MTPS蜂窝夹芯结构传热性能及热应力分析[J]. 航空学报, 2009, 30(1): 86-91.(LIU Zhenqi, LIANG Wei, YANG Jialing, et al. Analysis of thermal and mechanical properties of honeycomb structure of MTPS[J]. Acta Aeronautic et Astronautica Sinica, 2009, 30(1): 86-91.(in Chinese))
[6] 李红. 高超声速飞行器金属蜂窝夹芯结构的热机耦合行为分析[D]. 硕士学位论文. 哈尔滨: 哈尔滨工程大学, 2011.(LI Hong. Research on thermo-mechanical-coupled properties of metallic honeycomb structure of high-speed vehicle[D]. Master Thesis. Harbin: Harbin Engineering University, 2011.(in Chinese))
[7] 张锐, 尚新春. 格栅夹层梁的热弯曲变形[J]. 复合材料学报, 2014, 31(6): 1558-1565.(ZHANG Rui, SHANG Xinchun. Thermal bending deformation of grid sandwich beam[J]. Acta Materiae Compositae Sinica, 2014, 31(6): 1558-1565.(in Chinese))
[8] 张锐, 尚新春. 考虑腹板弯曲的一维格栅夹层结构热变形[J]. 北京理工大学学报, 2015, 35(4): 331-335.(ZHANG Rui, SHANG Xinchun. Thermal deformation of the sandwich structure with 1-D grid considering the bending of the webs[J]. Transactions of Beijing Institute of Technology, 2015, 35(4): 331-335.(in Chinese))
[9] NOORA K, MALIK M. An assessment of five modeling approaches for thermo-mechanical stress analysis of laminated composite panels[J]. Computational Mechanics, 2000, 25(1): 43-58.
[10] 中国科学院, 北京力学研究所, 固体力学研究室板壳组. 夹层板壳的弯曲、稳定和振动[M]. 北京: 科学出版社, 1977.(Plate and Shell Group, Laboratory of Solid Mechanics, Institute of Mechanics, Chinese Academy of Sciences. Bending, Stability and Vibration of Sandwich Plates and Shells[M]. Beijing: Science Press, 1977.(in Chinese))
[11] SAVOIA M, REDDY J N. Three-dimensional thermal analysis of laminated composite plates[J]. International Journal of Solids and Structures, 1995, 32(5): 593-608.
[12] NOOR A K, NEMETH M P. Micropolar beam models for lattice grids with rigid joints[J]. Computer Methods in Applied Mechanics and Engineering, 1980, 21(2): 249-263.
[13] IE![]() AN D. Thermal effects in chiral elastic rods[J]. International Journal of Thermal Sciences, 2010, 49(9): 1593-1599.
AN D. Thermal effects in chiral elastic rods[J]. International Journal of Thermal Sciences, 2010, 49(9): 1593-1599.
[14] 张锐, 尚新春. 格栅夹层梁热弯曲的等效微极热弹性分析[J]. 应用数学和力学, 2015, 36(9): 936-944.(ZHANG Rui, SHANG Xinchun. Equivalent micropolar thermoelastic analysis of thermal bending for grid sandwich beams[J]. Applied Mathematics and Mechanics, 2015, 36(9): 936-944.(in Chinese))
[15] 易斯男, 程耿东, 徐亮. 一维周期性梁结构等效性能计算方法讨论[J]. 计算力学学报, 2016, 33(5): 704-710.(YI Sinan, CHENG Gengdong, XU Liang. Discussion of effective properties prediction methods for 1D periodic beam structure[J]. Chinese Journal of Computational Mechanics,2016, 33(5): 704-710.(in Chinese))
[16] GESUALDO A, IANNUZZO A, PENTA F, et al. Homogenization of a Vierendeel girder with elastic joints into an equivalent polar beam[J]. Journal of Mechanics of Materials & Structures, 2017, 12(4): 485-504.
[17] PENTA F, ESPOSITO L, PUCILLO G P, et al. On the homogenization of periodic beam-like structures[J]. Procedia Structural Integrity, 2018, 8: 399-409.
引用本文/Cite this paper:
张锐, 冯亚, 杨硕. 非均匀温度影响下格栅夹芯结构微极梁等效方法[J]. 应用数学和力学, 2018, 39(6): 672-680.
ZHANG Rui, FENG Ya, YANG Shuo. An equivalent micropolar beam method for grid sandwich structures under inhomogeneous temperature conditions[J]. Applied Mathematics and Mechanics, 2018, 39(6): 672-680.