符 号 注 释
λ,GLamé常数, Paui位移分量, mσij应力分量, Paρ质量密度, kg/m3εij应变分量T热力学温度, KT0参考温度, KK热传导系数, W/(m·℃)τ热松弛时间, sp超孔隙水压力, Pan0孔隙率αs土颗粒的线性热膨胀系数, ℃-1ρs土颗粒的密度, kg/m3αw孔隙水的线性热膨胀系数, ℃-1ρw孔隙水的密度, kg/m3cs土颗粒的比热容, J/(kg·℃)g重力加速度, m/s2cw孔隙水的比热容, J/(kg·℃)kd渗透系数, m/sH波高, mv土体深度, mθ=T-T0, β1=(3λ+2G)αs, m=n0ρwcw+(1-n0)ρscs
引 言
地基的稳定性问题对很多工程施工都有很大的影响,尤其是在公路和铁路的施工中.针对这类问题,饱和多孔地基中水的渗流作用、热传导和热扩散的现象都是不可忽视的.因此,针对饱和多孔地基的热-水-力多场耦合问题的研究具有非常重要的意义和作用.
经典热弹性理论有两个与现实不相符的物理现象: 1) 热传导方程中不含有弹性项; 2) 热在介质中以无限大的速度传播.Biot[1]提出的热弹性理论仅消除了经典热弹性理论中的第一个悖论,而并没有解决热在介质中以无限大的速度传播这个问题.为了消除这一悖论,Lord和Shulman[2]修正了Maxwell-Cattaneo理论[3-4],并引入了一个热松弛时间,从而得到了L-S广义热弹性理论[4];Green和Lindsay[5]在热传导方程中考虑了温度变化率,并引入了两个热松弛时间,得到了G-L广义热弹性理论;Green和Naghdi[6-8]提出了在熵平衡方程和能量平衡方程之上建立的一种无能量耗散的G-N广义热弹性理论(模型Ⅰ、Ⅱ、Ⅲ).这几种理论都能很好地描述热在介质中以有限的速度传播,且在很多工程领域都有很好的应用,例如在土木、水利工程、能源工程、核废料回收和垃圾填埋等领域,国内外学者针对此类问题进行了一定研究[9-12].
近十几年来,国内外学者也对多孔材料的热-水-力耦合问题进行了一系列的研究.Booker和Savvidou[13]提出一种方法解决周边不透水土壤的超固结问题.Biot[14]也建立了一种数学方法来研究多孔介质的热弹问题.白冰[15]研究了在双层多孔介质上施加随指数函数衰减的热荷载作用时的热弹性动态响应问题.Bai[16]解决了一个一维饱和多孔材料受到循环热荷载作用的热固结问题.基于热力学的不可逆性,Bai和Li[17]研究了一个饱和多孔长圆柱受到热荷载和静水压力作用的热流固耦合问题.Lu等[18]基于广义热弹性理论,研究了一个多孔弹性介质受到冲击荷载和温度荷载作用的热流固耦合问题.Liu等[19-20]提出了一种新的方法,研究了一维多孔弹性圆柱和空腔球壳受到热冲击和机械冲击时的热流固耦合问题.Kumar等[21]研究了Lamb波在含液体的固体和成层半无限大体中传播的问题.Kumar和Devi[22]研究了一个边界处可渗透的多孔弹性介质受到热源作用的热弹动态响应问题.热-水-力耦合问题在隧道、核废料的处理、垃圾填埋、人工地层冻结等陆地上的工程中也有很好的应用.高娟等[23]引入热-水-力耦合模型,采用冻结法研究了地铁联络通道施工中的问题.Armand等[24]通过热-水-力耦合实验解决了高放射性核废料的降解和处理问题.郑荣跃等[25]研究了考虑扩散效应的隧洞热弹性耦合动力响应问题.热-水-力耦合问题不仅解决了上述陆地上的施工问题,也在沿海内陆水系、海床等施工中得到了很好的应用.Zhou等[26]主要研究了在受到海水波浪作用时,海底的土体以及管道的耦合动态响应.王立忠等[27]基于平面应变条件下的Biot方程,研究了线性波浪荷载作用下海床的动力响应问题.Nguyen-Tuan等[28]引入热-水-力耦合模型,利用数值计算的方法研究了圬工坝的动态响应问题,这种方法大大降低了施工成本.这些问题将对今后的施工有指导性的意义.
目前,上述问题引起了广大学者的研究兴趣,他们大多采用数值计算或者有限元模拟的方法.在数值计算中,大多数学者采用Fourier(傅里叶)变换及其反数值变换的方法或者Laplace(拉普拉斯)变换及其反数值变换的方法.这两种方法是先将方程通过Fourier变换变到频域中或者通过Laplace变化到拉氏域中,再通过数值反变换将其变换到时域中,这两种方法需要两次变换,相对麻烦,而且数值反变换存在一定的局限性.然而正则模态法利用本文中式(16),将方程分成两部分,能达到快速解耦的目的.
本文基于L-S广义热弹性理论同时结合Darcy定律,采用正则模态法研究了饱和多孔地基的热-水-力多场耦合问题.根据Biot[29]的固结理论,假设该饱和多孔地基为均质各向同性半无限大体,分析了不同渗透系数和频率对热-水-力耦合地基动力响应的影响,最终得到了无量纲的竖向位移、超孔隙水压力、竖向应力和温度的分布规律.本文的结果可广泛应用于岩土工程领域,特别在高速铁路、高速公路、能源基础等领域,具有指导性的意义.
1 基 本 方 程
考虑饱和多孔土体为流固耦合的两相介质,根据Biot[29]的固结理论,假设该饱和多孔地基为均质各向同性半无限大体.当土体的流相和固相处于热平衡时,土体的变形为小变形.不计体力时,考虑温度效应的多孔地基的运动方程为
(1)
考虑广义热松弛时间的能量方程为
(2)
结合Darcy定律,流体的平衡方程为
(3)
根据L-S广义热弹性理论[4],不考虑体力和内热源时,多孔弹性地基的本构方程为
σij=2Gεij+(λe-β1θ-p)δij;
(4)
饱和多孔地基的几何方程为
(5)
饱和多孔地基的体积应变可写成如下形式:
(6)
为简便起见,引入如下无量纲量:
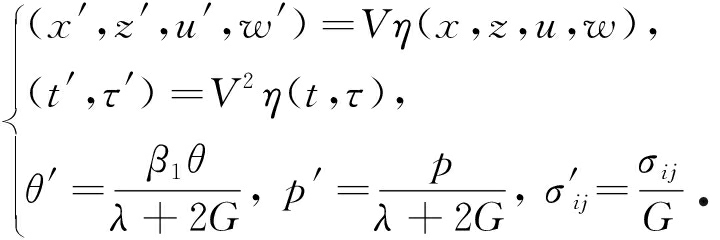
(7)
控制方程(1)~(5)经过简化后,利用上述定义的无量纲式(6)进行无量纲化,可得到如下形式(为方便起见,省掉各个变量上方的符号):
(8)
(9)
(10)
(11)
(12)
(13)
(14)
![]()
 2p-
2p- 2θ=0,
2θ=0,
(15)
其中,![]() 是二维Laplace算子,
是二维Laplace算子,
求解方程,就可以求得地基在受到椭圆余弦波作用时竖向位移、超孔隙水压力、竖向应力和温度的变化规律.这些量的求解要借助于问题的边界条件:
1) 地基上表面不考虑热荷载作用,因此有θ(x,0,t)=0;
2) 地基边界处应力自由,因此有σxz(x,0,t)=0, σzz(x,0,t)=0;
3) 地基上表面受到椭圆余弦波作用,因此有p(x,0,t)=pbψ(x,t),其中
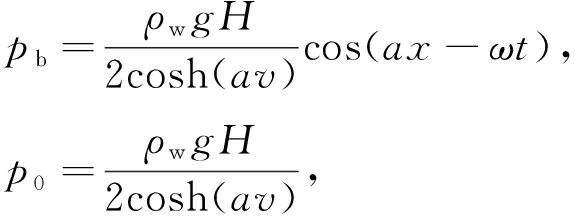
为了方便计算,此处取一个远大于波长的值,即波无法传到的深度,仍可将其视为半无限大.
对于方程的求解,采用下面的正则模态法.
2 正则模态分析
根据正则模态分析,所考虑物理量的解可被分解为下面的形式:
[u,w,e,σij,p](x,z,t)=
[u*(z),w*(z),e*![]()
(16)
其中ω是频率,i是虚数单位,a是x方向的波数.利用方程(16),由方程(10)、(11)和(15)可以得到关于θ*(z),p*(z)和e*(z)的方程.消去θ*(z)和p*(z),可以得到e*(z)满足的四阶偏微分方程:
(D4-AD2+B)e*(z)=0,
(17)
其中
D=d/dz,
A=2a2+b1, B=a4+b1a2+b2,
b1=ω+τω2+ω2+φ1ω+φ3ω2+φ0ω+φ0τω2,
b2=ω3+τω4+φ1ω2+φ1τω3+φ3ω3+φ3τω4-φ0φ2ω2-φ0φ2τω3.
方程(17)可被分解为
(18)
其中,![]() 是特征方程的根,方程(17)的解为
是特征方程的根,方程(17)的解为
(19)
当z→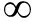 时,方程(18)的有界解可以表示成下面的形式:
时,方程(18)的有界解可以表示成下面的形式:
(20)
其中,Ri(a,ω)是关于a和ω的参数.因此得到e*(z)的解:
(21)
与求解e*(z)的过程类似,可以得到
θ*![]()
(22)
式中,![]() 也是关于a和ω的参数.可得到以下关系:
也是关于a和ω的参数.可得到以下关系:
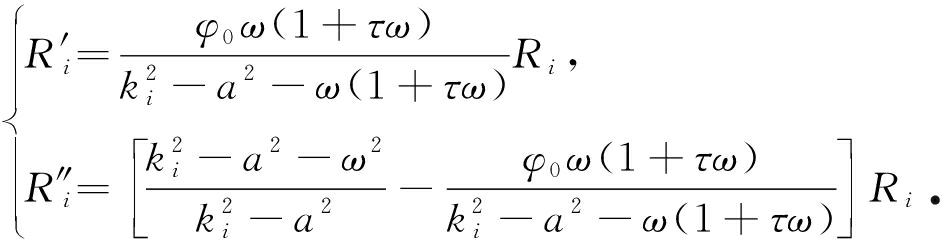
(23)
方程(22)可写成如下形式:
θ*![]()
(24)
p*![]()
(25)
为了得到位移u,w的表达式,根据式(16),由方程(6)、(8)、(9)、(24)和(25)可得到
w*![]()
(26)
u*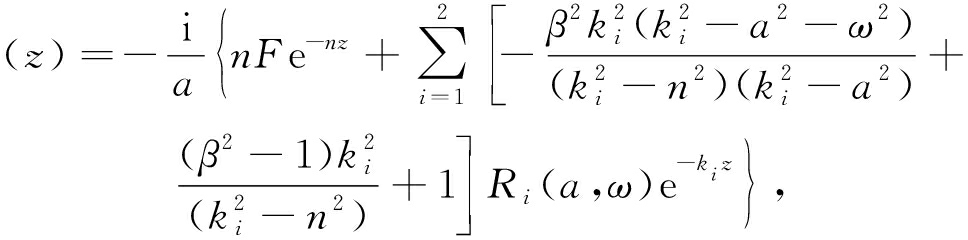
(27)
其中,n2=a2+β2ω2, F=F(a,ω)是关于a和ω的参数.
利用式(16),将方程(21)、(24)~(27)代入方程(13)、(14)中,得到

(28)
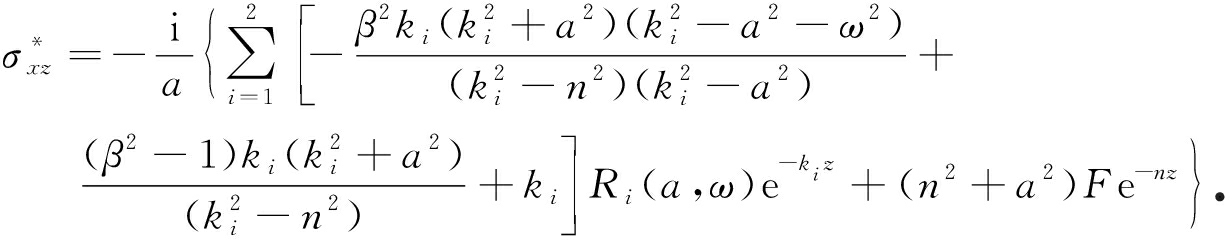
(29)
将所考虑物理量的表达式代入上述边界条件,可得到如下方程:
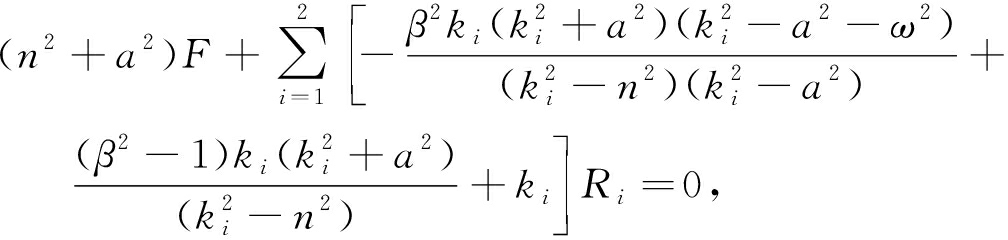
(30)

(31)
(32)
(33)
其中
ψ(x,t)=ψ*(a,ω)exp(ωt+iax).
求解方程(30)~(33),可以得到参数Ri(i=1,2)和F的表达式.上述方程组的求解可以借助于MAPLE软件包.由于求解得到待定参数的表达式过于繁复,在此省略未列出.
3 算例及结果讨论
选择均质各向同性饱和多孔土体进行数值计算,其材料常数以及椭圆余弦波的参数如下所示[16,26]:
E=6.0×105Pa, μ=0.3, G=E/[2(1+μ)],
λ=Eμ/[(1+μ)(1-2μ)],
αs=1.5×10-5 ℃-1, αw=2.0×10-4 ℃-1,
cs=800 J/(kg·℃), cw=4 000 J/(kg·℃),
ρs=2.6×103kg/m3, ρw=1.0×103kg/m3, n0=0.4, K=0.5 W/(m·℃),
kd=1.0×10-8 m/s, τ=0.02 s, T0=293 K, a=1.2, H=2 m, v=70 m.
由于ω=ω0+iζ,式中i是虚数单位,则eωt=eω0t(cos(ζt)+isin(ζt)),当所考虑时间很小时,可取ω=ω0.

图1 ω=0.75时竖向位移分布 图2 ω=0.75时超孔隙水压力分布
Fig. 1 The distribution of vertical displacement Fig. 2 The distribution of excess pore water for ω=0.75 pressure for ω=0.75
本文主要通过正则模态法来探讨渗透系数变化和频率的变化对饱和多孔地基的影响.以下8幅图分为两组,第一组为图1~4,分别研究了不同渗透系数时无量纲竖向位移w′=w/p0、 无量纲超孔隙水压力p′=p/p0、无量纲竖向应力σ′=σ/p0和无量纲温度θ′=θ/p0的变化规律.第二组为图5~8,分别研究了无量纲竖向位移w″=w/p0、无量纲超孔隙水压力p″=p/p0、无量纲竖向应力σ″=σ/p0和无量纲温度θ″=θ/p0随椭圆余弦波频率的变化规律(为了方便起见,图中和下文均省略表达式中的上标).计算时取x=1.0和时间t=1.0.
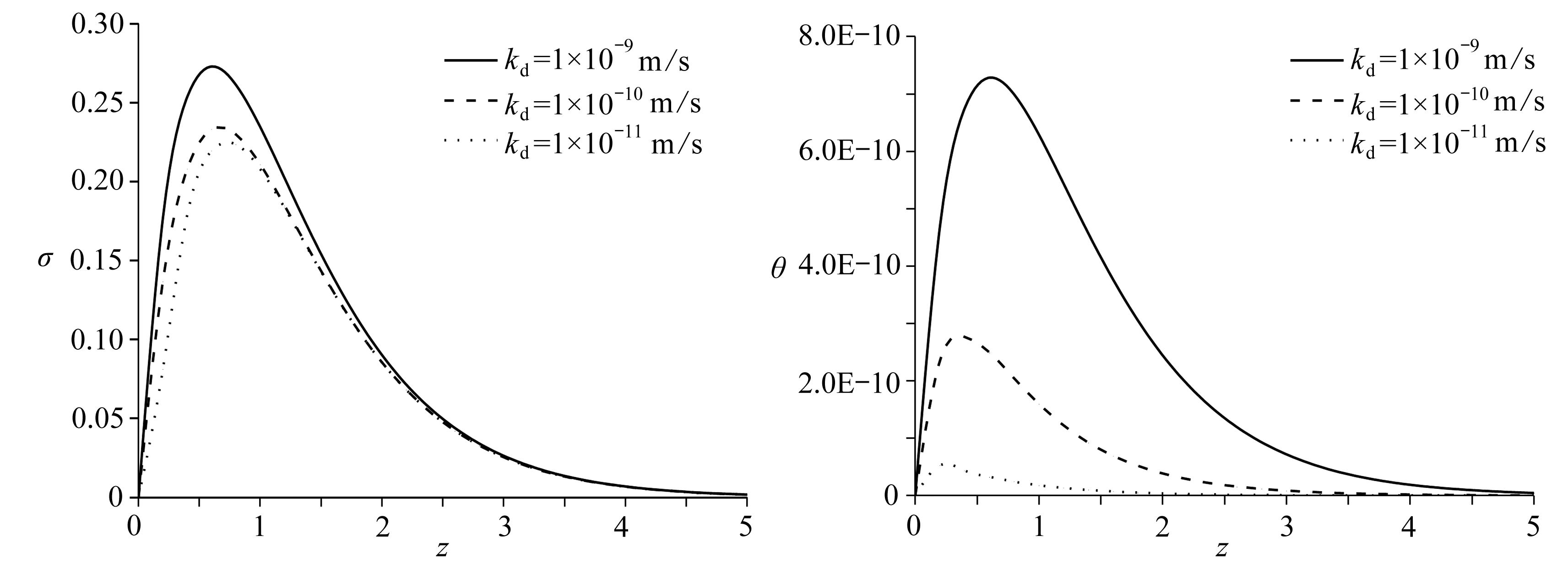
图3 ω=0.75时竖向应力分布 图4 ω=0.75时温度分布
Fig. 3 The distribution of vertical stress for ω=0.75 Fig. 4 The distribution of temperature for ω=0.75
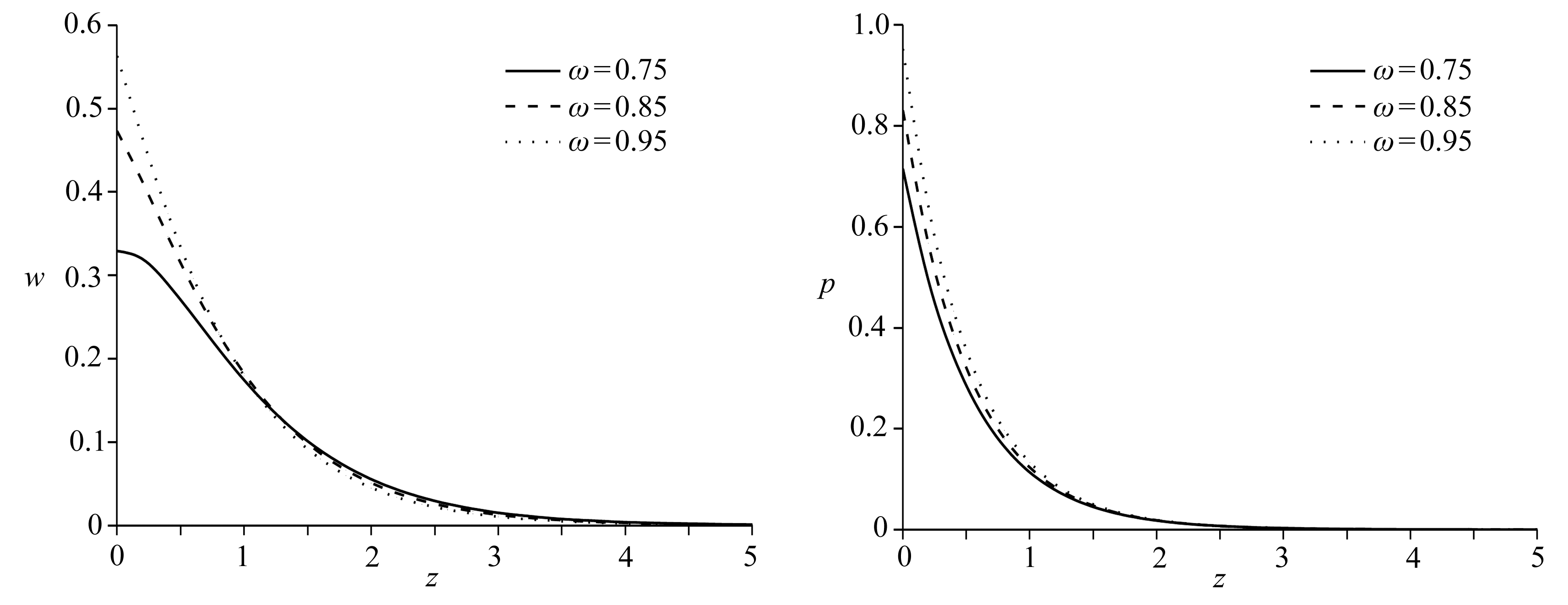
图5 kd=10-9 m/s时竖向位移分布 图6 kd=10-9 m/s时超孔隙水压力分布
Fig. 5 The distribution of vertical displacement Fig. 6 The distribution of excess pore water pressure for kd=10-9 m/s for kd=10-9 m/s
图1~4分别描述了不同的渗透系数变化对无量纲的竖向位移、超孔隙水压力、竖向应力和温度的变化规律.图1说明随着渗透系数的变小,无量纲竖向位移逐渐增大.图2是无量纲超孔隙水压力的变化,随着渗透系数的减小,无量纲超孔隙水压力逐渐减小,同时衰减速度增加,这是由于当渗透系数减小,相当于地基中的孔隙变少,超孔隙水压力也随之减小;当渗透系数达到足够小时就可以认为是一个密实的半无限土体,这时饱和多孔地基就可以近似衰减成一个密实的半无限大弹性地基,而这时超孔隙水压力即为0.图3描述了无量纲竖向应力随渗透系数的变化规律.随着地基深度的增大,无量纲竖向应力先增大后减小,在深度为0.5~1 m的区间内达到峰值.随着渗透系数的减小,无量纲竖向位移的峰值在不断减小.图2、3所反映的渗透系数变化对无量纲的超孔隙水压力和应力场的影响的变化规律和趋势与文献[26]完全一致,从而不仅能看出该结果是正确的,更能反映正则模态法在此类问题中可以很好地应用.图4反应了渗透系数变化对无量纲温度的影响,随着渗透系数减小,无量纲温度减小的速度非常明显,这是因为水的导热系数远大于土体的导热系数,当渗透系数减小,说明地基中的孔隙水含量减少,从而对温度的影响越来越不明显.同时可以看出,在不同的理论模型条件下,无量纲温度值都很小,为10-10数量级,这是由于渗透系数变化对温度的影响很小.
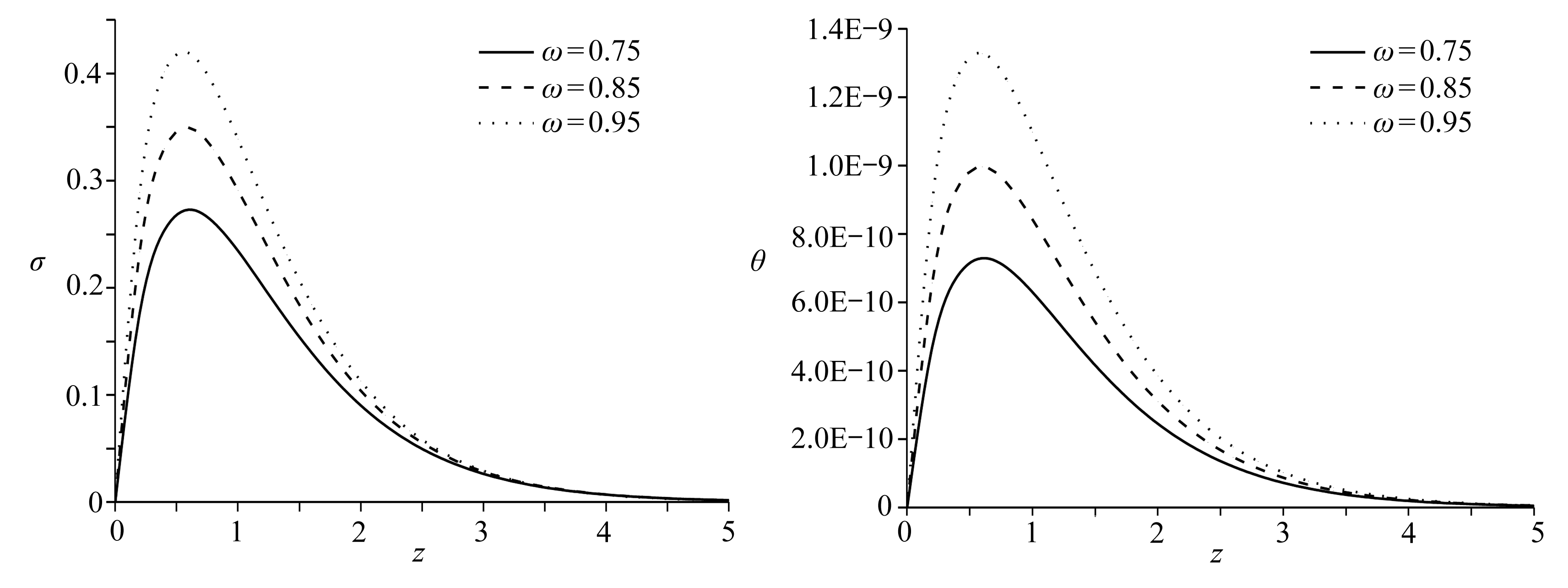
图7 kd=10-9 m/s时竖向应力分布 图8 kd=10-9 m/s时温度分布
Fig. 7 The distribution of vertical stress Fig. 8 The distribution of temperature for kd=10-9 m/s for kd=10-9 m/s
图5~8描述了频率变化对无量纲竖向位移、超孔隙水压力、竖向应力和温度的影响.图5反映了无量纲竖向位移受频率变化的响应,3条曲线相交于1<z<1.5区间内,在交点前随着频率增加,无量纲竖向位移也随之增大;交点后则反之.图6表示随着频率增大,无量纲超孔隙水压力逐渐增大.图7描述了无量纲竖向应力随频率变化的分布规律,随着频率增加,无量纲竖向应力明显增大,这是由于随着频率增加,地基排出孔隙水的时间变短,孔隙水也承担了一定压力.图8反应了频率变化对无量纲温度的影响,随着频率增大,无量纲温度也明显增大.这同样也是由于频率增大,地基中的孔隙水不容易排出,而水的导热系数远大于土的导热系数所造成的.与此同时可以看出,在不同的理论模型条件下,无量纲温度值都很小,为10-9数量级,这是由于频率变化对温度的影响很小.
4 结 论
基于广义热弹性理论,结合Darcy定律,对Biot波动方程进行了修正,研究了一个受到椭圆余弦波作用的均质各向同性半无限大饱和多孔地基的热-水-力多场耦合动态响应问题.分析了渗透系数和频率对热-水-力耦合地基动力响应的影响.主要结论有:
1) 正则模态法能够很好地解决半无限大多孔饱和地基的热-水-力耦合问题,最终得到了各物理量的变化规律图.
2) 渗透系数的变化对地基中各物理量都有非常明显的影响,尤其是渗透系数对无量纲超孔隙水压力的影响,当渗透系数足够小的时候,饱和多孔弹性体就可以近似退化为密实的弹性体,而实际施工中的土体没有绝对密实的,所以饱和多孔弹性体的热-水-力耦合问题在施工中显得尤为重要.
3) 椭圆余弦波的频率变化对地基中除温度场外的各物理量有很大的影响,从而说明单纯在地基表面施加荷载,对温度场的影响并不明显.
4) 结果可广泛应用于岩土工程领域,特别在高速铁路、高速公路、能源基础等领域,具有指导性的意义.
参考文献(References):
[1] BIOT M A. Thermoelasticity and irreversible thermodynamics[J]. Journal of Applied Physics, 1956, 27: 240-253.
[2] LORD H W, SHULMAN Y. A generalized dynamical theory of thermoelasticity[J]. Journal of the Mechanics and Physics of Solids, 1967, 15(5): 299-309.
[3] JOSEPH D D, PREZIOSI L. Heat waves[J]. Reviews of Modern Physics, 1989, 61(1): 41-73.
[4] JOSEPH D D, PREZIOSI L. Addendum to the paper “heat waves”[J]. Reviews of Modern Physics, 1990, 62: 375-391.
[5] GREEN A E, LINDSAY K A. Thermoelasticity[J]. Journal of Elasticity, 1972, 2(1): 1-7.
[6] GREEN A E, NAGHDI P M. A re-examination of the basic postulates of thermomechanics[J]. Proceedings of the Royal Society A, 1991, 432(1885): 171-194.
[7] GREEN A E, NAGHDI P M. On undamped heat waves in an elastic solid[J]. Journal of Thermal Stresses, 1992, 15(2): 253-264.
[8] GREEN A E, NAGHDI P M. Thermoelasticity without energy dissipation[J]. Journal of Elasticity, 1993, 31(3): 189-208.
[9] 王颖泽, 王谦, 刘栋, 等. 弹性半空间热冲击问题的广义热弹性解[J]. 应用数学和力学, 2014, 35(6): 640-651.(WANG Yingze, WANG Qian, LIU Dong, et al. Generalized thermoelastic solutions to the problems of thermal shock on elastic half space[J]. Applied Mathematics and Mechanics, 2014, 35(6): 640-651.(in Chinese))
[10] 王颖泽, 王谦, 刘栋, 等. 有限厚度圆柱壳热冲击问题的广义热弹性解[J]. 应用数学和力学, 2016, 37(6): 644-654.(WANG Yingze, WANG Qian, LIU Dong, et al. Generalized solution to the thermoelastic problem of finite-thickness hollow cylinders subjected to thermal shock[J]. Applied Mathematics and Mechanics, 2016, 37(6): 644-654.(in Chinese))
[11] XIONG Chunbao, GUO Ying, DIAO Yu. Normal mode analysis to a poroelastic half-space problem under generalized thermoelasticity[J]. Latin American Journal of Solids and Structures, 2017, 14: 930-949.
[12] HETNARSKI R B, IGNACZAK J. Generalized thermoelasticity[J]. Journal of Thermal Stresses, 1999, 22(4/5): 451-476.
[13] BOOKER J R, SAVVIDOU C. Consolidation around a spherical heat source[J]. International Journal of Solids and Structures, 1984, 20(11/12): 1079-1090.
[14] BIOT M A. Variational Lagrangian-thermodynamics of non-isothermal finite strain mechanics of porous solids and thermomolecular diffusion[J]. International Journal of Solids and Structures, 1977, 13(6): 579-597.
[15] 白冰. 变温度荷载作用下半无限成层饱和介质的热固结分析[J]. 应用数学和力学, 2006, 27(11): 1341-1348.(BAI Bing. Thermal consolidation of layered porous half-space to variable thermal loading[J]. Applied Mathematics and Mechanics, 2006, 27(11): 1341-1348.(in Chinese))
[16] BAI Bing. Fluctuation responses of saturated porous media subjected to cyclic thermal loading[J]. Computers and Geotechnics, 2006, 33(8): 396-403.
[17] BAI Bing, LI Tao. Solutions for cylindrical cavity in saturated thermoporoelastic medium[J]. Acta Mechanica Solida Sinica, 2009, 22(1): 85-94.
[18] LU Zheng, YAO Hailin, LIU Ganbin. Thermomechanical response of a poroelastic half-space soil medium subjected to time harmonic loads[J]. Computers and Geotechnics, 2010, 37(3): 343-350.
[19] LIU Ganbin, XIE Kanghe, ZHENG Rongyue. Model of nonlinear coupled thermo-hydro-elastodynamics response for a saturated poroelastic medium[J]. Science in China, Series E: Technological Sciences, 2009, 52(8): 2373-2383.
[20] LIU Ganbin, XIE Kanghe, ZHENG Rongyue. Thermo-elastodynamic response of a spherical cavity in saturated poroelastic medium[J]. Applied Mathematical Modelling, 2010, 34(8): 2203-2222.
[21] KUMAR R, KAUR M, RAJVANSHI S C. Propagation of waves in micropolar generalized thermoelastic materials with two temperatures bordered with layers or half-spaces of inviscid liquid[J]. Latin American Journal of Solids and Structures, 2014, 11(7): 1091-1113.
[22] KUMAR R, DEVI S. Thermomechanical intereactions in porous generalized thermoelastic material permeated with heat sources[J]. Multidiscipline Modeling in Materials and Structures, 2008, 4(3): 237-254.
[23] 高娟, 冯梅梅, 高乾. 地铁联络通道冻结施工的热-流-固(THM)耦合分析[J]. 冰川冻土, 2013, 35(4): 904-912.(GAO Juan, FENG Meimei, GAO Qian. THM coupling analysis of connected aisle in metro construction by artificial freezing method[J]. Journal of Glaciology and Geocryology, 2013, 35(4): 904-912.(in Chinese))
[24] ARMAND G, BUMBIELER F, CONIL N, et al. Main outcomes from in situ thermo-hydro-mechanical experiments programme to demonstrate feasibility of radioactive high-level waste disposal in the Callovo-Oxfordian claystone[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2017, 9: 415-427.
[25] 郑荣跃, 刘干斌, 唐国金. 考虑扩散效应圆形隧洞热弹性耦合动力响应研究[J]. 国防科技大学学报, 2008, 30(3): 27-31.(ZHENG Rongyue, LIU Ganbin, TANG Guojin. Thermodynamic response of a cylindrical tunnel in the theory of generalized thermoelastic diffusion[J]. Journal of National University of Defense Technology, 2008, 30(3): 27-31.(in Chinese))
[26] ZHOU Xianglian, ZHANG Jun, GUO Junjie, et al. Cnoidal wave induced seabed response around a buried pipeline[J]. Ocean Engineering, 2015, 101: 118-130.
[27] 王立忠, 潘冬子, 凌道盛. 海床波浪响应的积分变换解及其分析应用[J]. 岩石工程学报, 2006, 28(7): 847-852.(WANG Lizhong, PAN Dongzi, LING Daosheng. Analysis on integral transform of the wave-induced response in seabed and its application[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(7): 847-852.(in Chinese))
[28] NGUYEN-TUAN L, KÖNKE C, BETTZIECHE V, et al. Numerical modeling and validation for 3D coupled-nonlinear thermo-hydro-mechanical problems in masonry dams[J]. Computers & Structures, 2017, 178: 143-154.
[29] BIOT M A. General theory of three-dimensional consolidation[J]. Journal of Applied Physics, 1941, 12: 155-164.
引用本文/Cite this paper:
熊春宝, 郭颖, 刁钰. 考虑热-水-力耦合效应的饱和多孔地基动力响应分析[J]. 应用数学和力学, 2018, 39(6): 689-699.
XIONG Chunbao, GUO Ying, DIAO Yu. Dynamic responses of saturated porous foundations under coupled thermo-hydro-mechanical effects[J]. Applied Mathematics and Mechanics, 2018, 39(6): 689-699.