引 言
薄结构由于具有某些方面的特点,已被广泛应用于各类实际问题中,如涂层问题、各种层合结构问题以及电子器件的散热问题等.利用通常的体单元(如8节点线性元)分析薄结构问题时,由于单元最大几何尺度受薄层厚度控制,需要使用更多的单元数才能确保数值解的计算精度,但由此也将导致计算工作量剧增[1-2].实际计算时,需要采用薄单元(其一个方向的尺寸远小于其他两个方向的尺寸)进行网格剖分,这种单元属于典型的各向异性单元.相应的高阶单元在计算精度、划分数量、抗畸变程度等方面具有非常明显的优势,使得它们在实际计算中被广泛使用.但与低阶元相比,高阶单元需要更多的计算机存储空间,离散化线性系统具有更高的计算复杂性.另一方面,这类薄单元对应的线性代数系统的系数矩阵是严重病态的,采用通常的求解方法其效率将大大降低.
代数多重网格(algebraic multigrid, AMG)法是求解有限元离散化线性代数系统最为有效的计算方法之一,目前已有非常多的研究工作,如文献[3-10].对高阶元离散系统AMG法(包括多水平方法及其预条件技术)的研究,也取得了一些很好的成果,如文献[11-15].但这些方法主要是针对各向同性网格下的高阶有限元离散代数系统而设计的.对各向异性网格情形,文献[16-17]研究了几种有代表性的复杂各向异性网格对AMG法效率的影响,并设计了基于“距离矩阵”的DAMG法;文献[18]为几类薄结构问题设计和分析了相应的预处理方法;文献[19]提出了一种点结块粗化算法的AMG法,再结合AMGe插值算子来提高AMG法效率.这些方法主要是针对薄结构线性元方程而设计的,对高阶元情形,还未见相关研究工作.
本文针对三维薄结构稳态热传导问题,为其分层二次元离散系统设计了基于DAMG法的多水平方法.基于局部块Gauss-Seidel的光滑子,对薄结构各向异性单元具有更好的磨光效果,相应的两水平方法具有更好的计算效率.由于采用了分层基,在设计两水平方法时,不需建立判定变量指标与所属几何节点类型对应关系的代数判据[14],也不需生成网格转换矩阵,粗水平(线性元)矩阵也可由最细网格矩阵直接获取,从而大大节省了计算CPU时间,提高了运算效率.数值实验结果验证了该方法的有效性和鲁棒性.
1 模型问题及分层有限元离散
考虑如下三维稳态热传导问题:
(1)
T=TΓ, on Γ1,
(2)
(3)
(4)
其中,T=T(x,y,z)为温度函数,ki=ki(x,y,z)(i=1,2,3)为导热系数,Qv=Qv(x,y,z)为单位体积中的内热源生热量,n1,n2和n3为边界单位外法向分量,TΓ为边界Γ1上的已知温度,qΓ为Γ2上的热流密度,hΓ和Ta分别是Γ3上的对流换热系数和周围环境温度,Γ=∂Ω为求解域Ω的边界,满足Γ=Γ1+Γ2+Γ3,且Γ1∩Γ2∩Γ3=∅.
上述问题对应的变分问题可描述为,求T∈H1(Ω)且T|Γ1=TΓ,使得对任意的![]() 且w|Γ1=0},下式总成立:
且w|Γ1=0},下式总成立:
a(T,W)=F(W),
(5)
其中
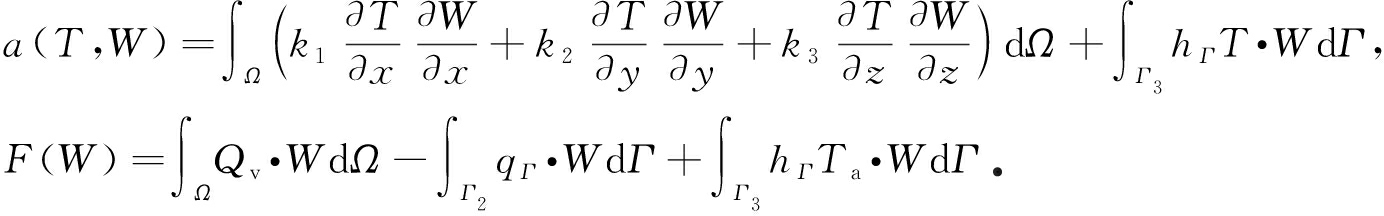
对区域Ω进行六面体网格剖分,为了更加方便地构造求解高阶有限元方程的两水平方法或多水平方法,常采用分层单元(hierachical element)[20]对变分问题(5)进行离散.
考虑整体坐标系Oxyz下的20节点六面体二次单元,其在局部坐标系oξηζ(如图1所示)下分层单元的插值函数为:
顶点(vertex)基函数
(6)
其中,(ξi,ηi,ζi)为i点的坐标,Ni为8节点线性等参单元对应的节点插值函数.
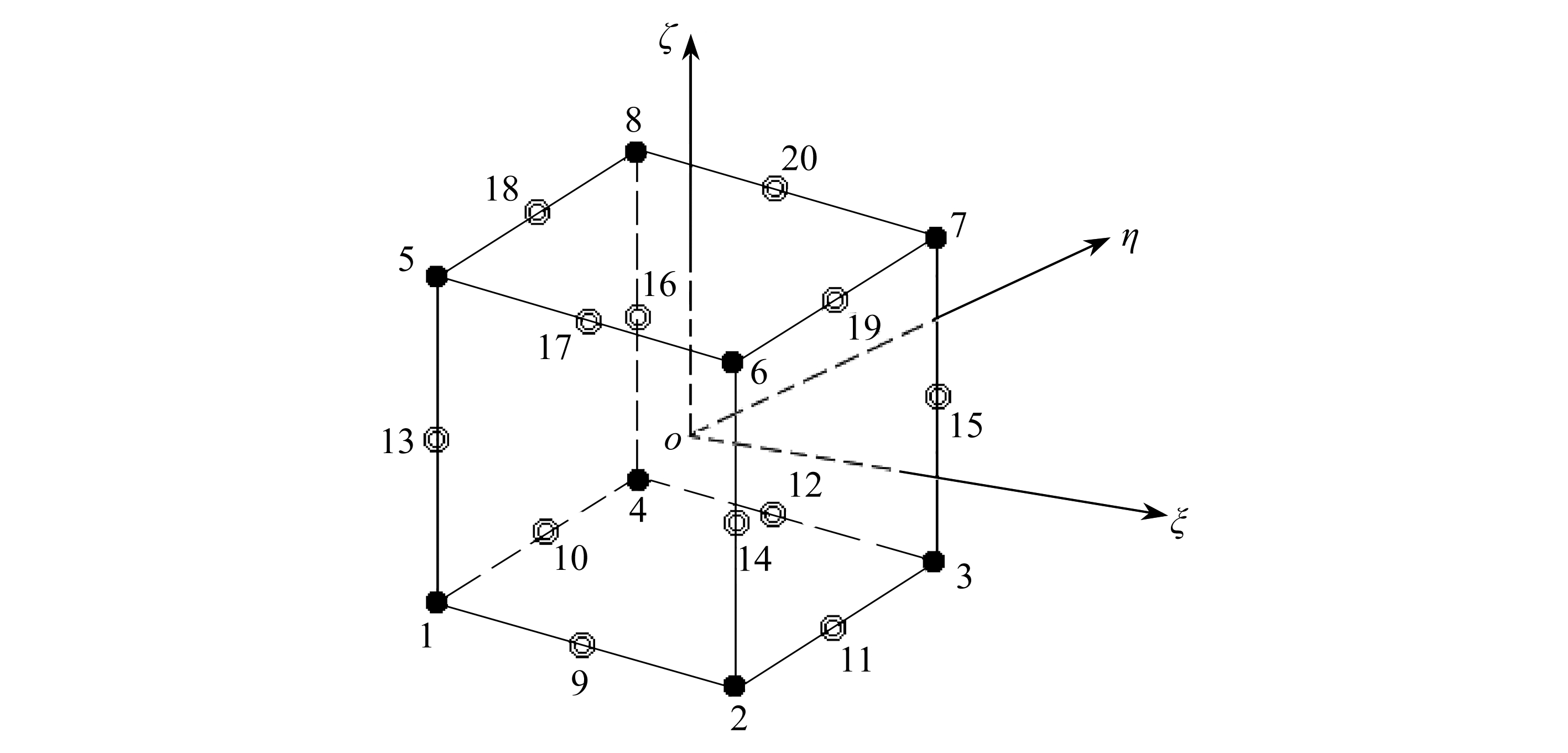
图1 局部坐标系下的20节点标准二次单元
Fig. 1 The 20-node reference element in the local coordinate system
边中点(midside)基函数
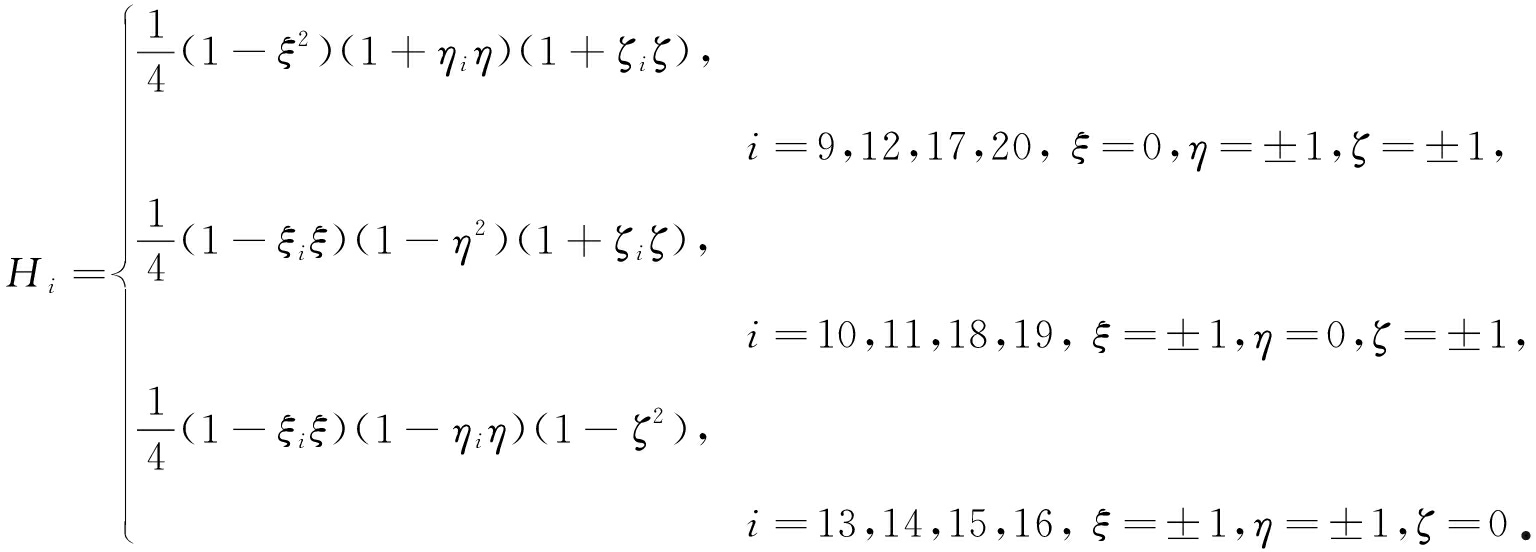
按照通常有限元法,由生成的单元特性矩阵和单元右端列阵,按单元进行组集得到整体矩阵和整体右端列阵,再处理已知温度,可得如下具有分层形式的二次元方程:
Kq=p,
(7)
或
(8)
其中,q=[T1,T2,…,Tn]T为所有节点温度列阵,Ti为节点i处的温度值,qv为二次元单元顶点对应的温度列阵,qm为二次元单元所有边中点对应的温度列阵.
下面以常系数热传导细长梁(详见第2节算例1)为例,计算了相应的分层二次元矩阵K及标准节点基下二次元矩阵![]() 的条件数(分别记为κ(K)和
的条件数(分别记为κ(K)和![]() 列出了共轭梯度(CG)法的迭代次数(iter_CG),总结如表1所示,其中迭代控制精度为‖r(k)‖/‖r(0)‖≤10-6,这里r(k)=P-Kq(k)或
列出了共轭梯度(CG)法的迭代次数(iter_CG),总结如表1所示,其中迭代控制精度为‖r(k)‖/‖r(0)‖≤10-6,这里r(k)=P-Kq(k)或![]() 为第k步迭代解残量,解向量
为第k步迭代解残量,解向量![]() 与q(k)中的各分量满足
与q(k)中的各分量满足

(9)
其中,n为总节点数,np为剖分节点(顶点)数,i1和i2分别表示与边中点i相邻的顶点编号.
表1 分层二次元矩阵K和节点基下二次元矩阵![]() 的条件数以及CG法的迭代次数
的条件数以及CG法的迭代次数
Table 1 Condition numbers of 2 matrices K and ![]() and the iteration counts of the CG method
and the iteration counts of the CG method
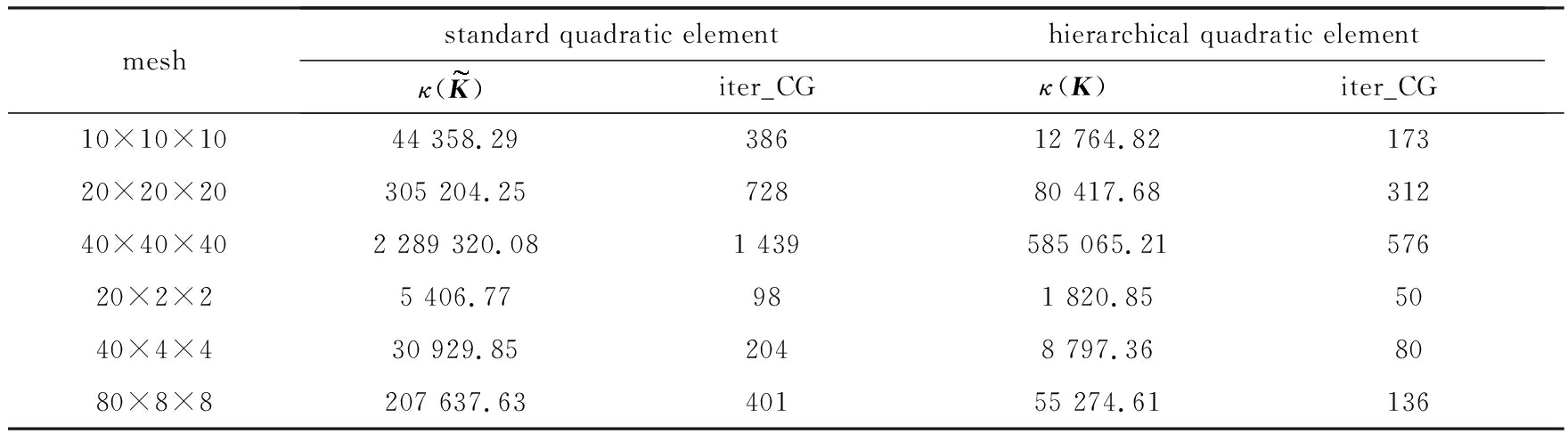
由此可见,分层基下离散系统的条件数得到大大改善,但当问题规模增加,尤其是采用各向异性网格时,CG法的求解效率将变差.采用分层有限元法的最大优点之一是,在处理高阶问题时,可以利用低阶的计算结果,大大减少前处理量和计算量,且自适应过程相对容易实现.在构造求解高阶有限元方程的两水平方法或多水平方法时,由于采用了分层基,相应网格转换算子(限制算子和插值算子)的构造将变得非常简单,程序实现中不需建立判定变量指标与所属几何节点类型对应关系的代数判据,可大大提高求解效率.
2 分层二次元方程的多水平方法
构造代数多水平方法的基本做法是,首先,将分层二次元方程的求解化归为线性元方程的求解,从而建立相应的两水平迭代方法.然后,通过调用适合于薄单元(各向异性网格)的DAMG法求解相应线性元方程,建立代数多水平方法.
2.1 两水平方法
利用分层二次元方程的分块形式(8),可以建立求解热传导问题的两水平迭代算法.两水平方法的本质是将二次有限元计算化归于线性元的计算, 从而减少运算规模、 提高计算效率.由于采用了分层基, 在设计两水平方法时, 限制算子![]() 和插值算子
和插值算子![]() 的构造将变得非常简单.即
的构造将变得非常简单.即
(10)
其中,I为单位矩阵,0为零矩阵,上标“c”表示粗水平(线性元),上标“f”表示细水平(二次元).对任意细水平向量q=[qv qm]T和粗水平向量qv,有
(11)
这样,求解分层二次元方程(7)的两水平迭代算法可描述如下.
算法1 两水平迭代算法
步0) 令k=0,给定控制精度εtol,对任意迭代初值q(0),计算r(0)=P-Kq(0).
步1) 前光滑:
步2) 计算残量:
步3) 利用直接法或迭代法精确求解粗水平(线性元)方程:
(12)
步4) 更新解:
步5) 后光滑:
q(k+1)=q2+ST(P-Kq2), j=1,2,…,m2.
步6) 计算r(k+1)=P-Kq(k+1),若
则结束;否则,令k=k+1,q(k)=q(k-1),转步1).
算法1中,S为光滑子,常取为point-wise Gauss-Seidel迭代,m1和m2分别为前、后光滑次数,常取m1=m2=m,相应的两水平方法记为HTL(p_GS(m)).
注1 影响上述两水平迭代算法效率的主要因素是光滑子S的选取.通常的光滑子p_GS(m)对各向同性网格问题具有很好的磨光效果,仅需迭代几次就能消除误差的高频部分,但对各向异性网格问题其磨光效果将变差,需要选取特殊的光滑子,如线迭代、面迭代及块迭代等.前两种程序上不好实现,特别是对非结构网格情形.本文考虑块迭代(简记为LBGS),即对每一个节点,在其支集(patches)上整体求解子问题,以更有效地消除由于网格的各向异性而产生的误差高频部分,具体算法见算法2.
算法2 一次LBGS迭代
对于j=1,2,…,n,有
步1) 获取落在supp φj内部的节点数Nj及其下标值,并保存其局部、整体间的对应关系.
步2) 形成Nj×Nj子问题:
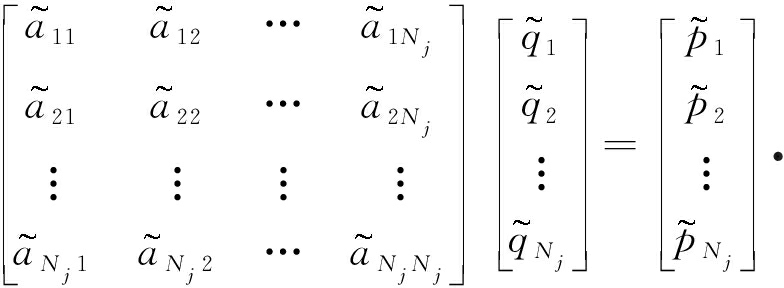
步3) 求解上述方程组,得解向量
步4) 更新解向量
q=(q1,q2,…,qn)T.
由文献[21]知,有两种特殊的块磨光算子,即LBGS_v或LBGS_m迭代,可简单描述为
① LBGS_v smoother:仅对所有顶点,在其patches上做一次LBGS迭代;
② LBGS_m smoother:仅对所有边中点,在其patches 上做一次LBGS迭代.
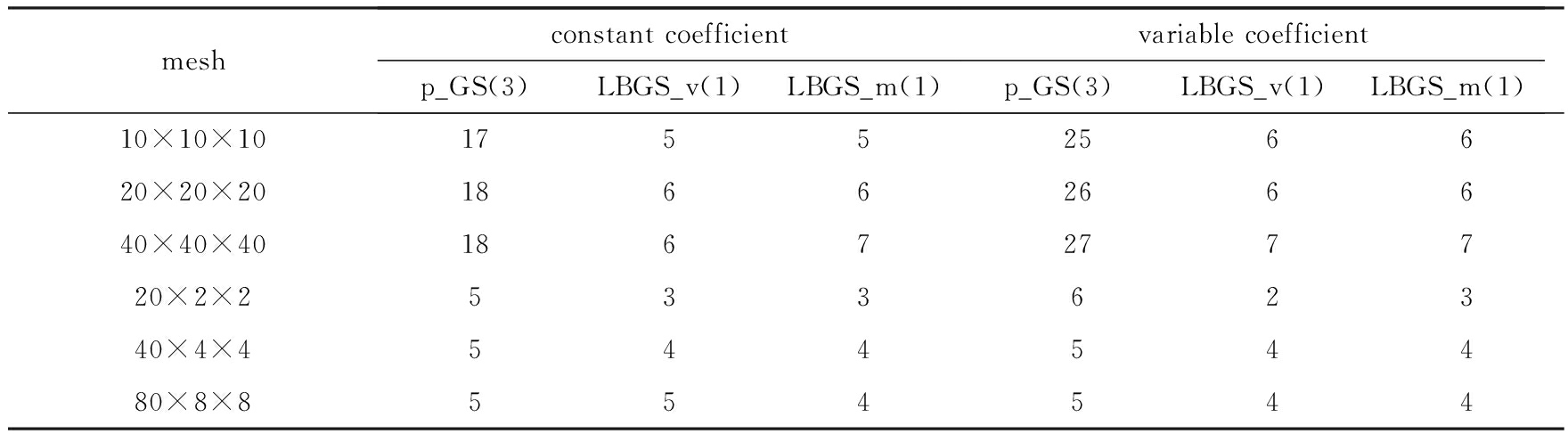
基于上述光滑子的两水平方法分别简记为HTL(LBGS_v(1))和HTL(LBGS_m(1)).下面,将这些方法应用于薄结构稳态热传导问题分层二次元方程的求解,其中εtol=10-6,相应的结果总结如下.
算例1 热传导细长梁[22] 考虑如图2所示的长为0.1 m、宽和高均为0.01 m的细长梁.取左侧面的形心为坐标原点建立坐标系,左侧面(x=0 m)施加已知温度TΓ=0 ℃,上表面与周围环境发生对流,设对流系数hΓ=1 500 W/(m2·℃),环境温度Ta=400 ℃,右侧面(x=0.1 m)上的热流密度qΓ=2 000 W/m2,其余面均为绝缘面.
对细长梁采用六面体一致网格进行剖分,即分别沿x,y和z方向进行等距剖分,设每个方向的剖分步长分别为hx, hy和hz,整个区域含有nx×ny×nz个单元.实际应用时,常采用两种类型的单元: 一种是各向同性网格, 如图3(a)所示, 其特点是单元在3个方向的尺寸相差不大; 另一种是各向异性网格, 如图3(b)所示, 其特点是单元在3个方向的尺寸相差很大, 如大的长宽比.为了验证3种方法的有效性和鲁棒性,针对下述两种情形,相应迭代次数如表2所示.
 常系数:
常系数:
k1=15.0 W/(m2·℃), k2=10.0 W/(m2·℃), k3=5.0 W/(m2·℃), Qv=0 W/m2;
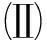 变系数:
变系数:
k1=25x2-10y-33z+4, k2=20x-50y2+12z+3, k3=10x+48y+5z2+2,
Qv=1/((x+0.001)(y+0.01)(z+0.01)).

图2 三维热传导梁几何结构示意图
Fig. 2 The geometry structure of the conduction beam considered

(a) 各向同性网格(20×2×2) (b) 各向异性网格(10×10×10)
(a) The isotropic hexahedral mesh with 20×2×2 elements (b) The anisotropic hexahedral mesh with 10×10×10 elements
图3 热传导梁两种网格剖分
Fig. 3 Two types of meshes used for the conduction beam
表2 基于不同光滑子S的HTL方法求解热传导细长梁分层二次元方程的迭代次数
Table 2 Iteration counts of the HTL methods for the hierarchical quadratic discretizations of the conduction beam
算例2 扇形薄结构 考虑如图4所示的扇形薄结构,内径r1=4 m,外径r2=12 m,厚度l=0.8 m,左侧面(r1=4 m)施加已知温度TΓ=1 000 ℃,右侧面(r2=12 m)施加已知温度TΓ=100 ℃,其余面均为绝缘面,导热系数k1=k2=k3=3 W/(m2·℃),Qv=0 W/m2.采用六面体网格剖分下的分层二次元进行求解,在不同网格剖分下,3种方法的迭代次数如表3所示.

图4 扇形薄结构几何结构示意图及网格剖分(8×8×8)
Fig. 4 The geometry structure of the thin-walled sector and one sample mesh (8×8×8)
表3 基于不同光滑子S的HTL方法求解扇形薄结构分层二次元方程的迭代次数
Table 3 Iteration counts of the HTL methods for the hierarchical quadratic discretizations of the thin-walled sector

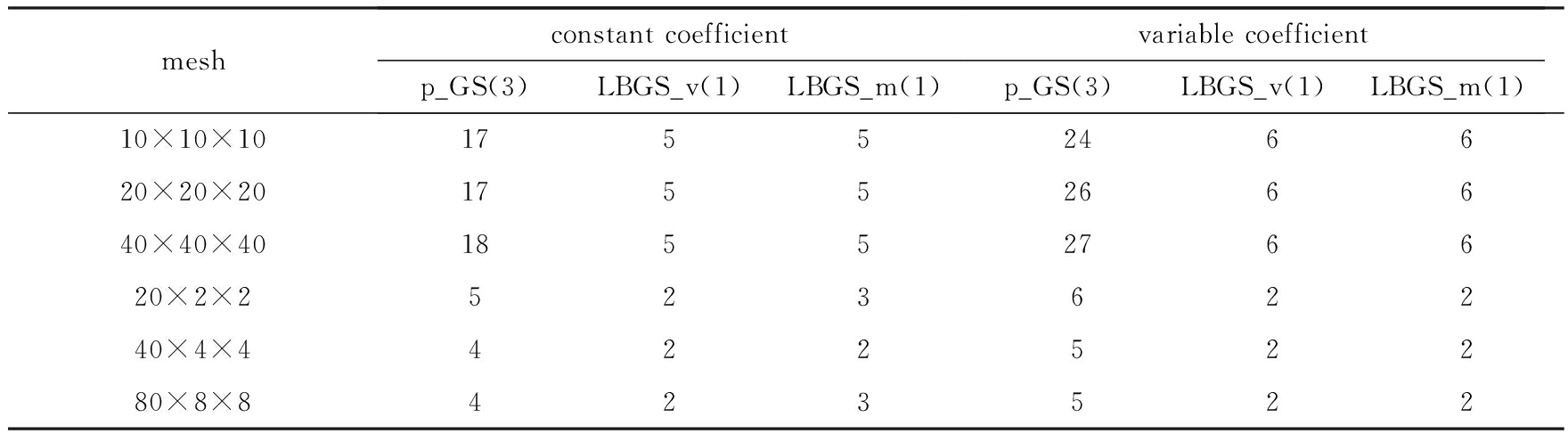
算例3 散热片问题 散热片几何结构示意图如图5(a)所示,其中,基础表面的尺寸为10 m×10 m×0.5 m,每个肋片的尺寸为0.1 m×10 m×5 m,肋片数目为11,在基础表面的下底面施加已知温度TΓ=100 ℃,其余表面的外法向流量均为qΓ=0.1 W/m2,导热系数为k1=k2=k3=20 W/(m2·℃).采用六面体单元进行网格剖分(如图5(b)),在不同单元数下,3种方法的迭代次数如表4所示.
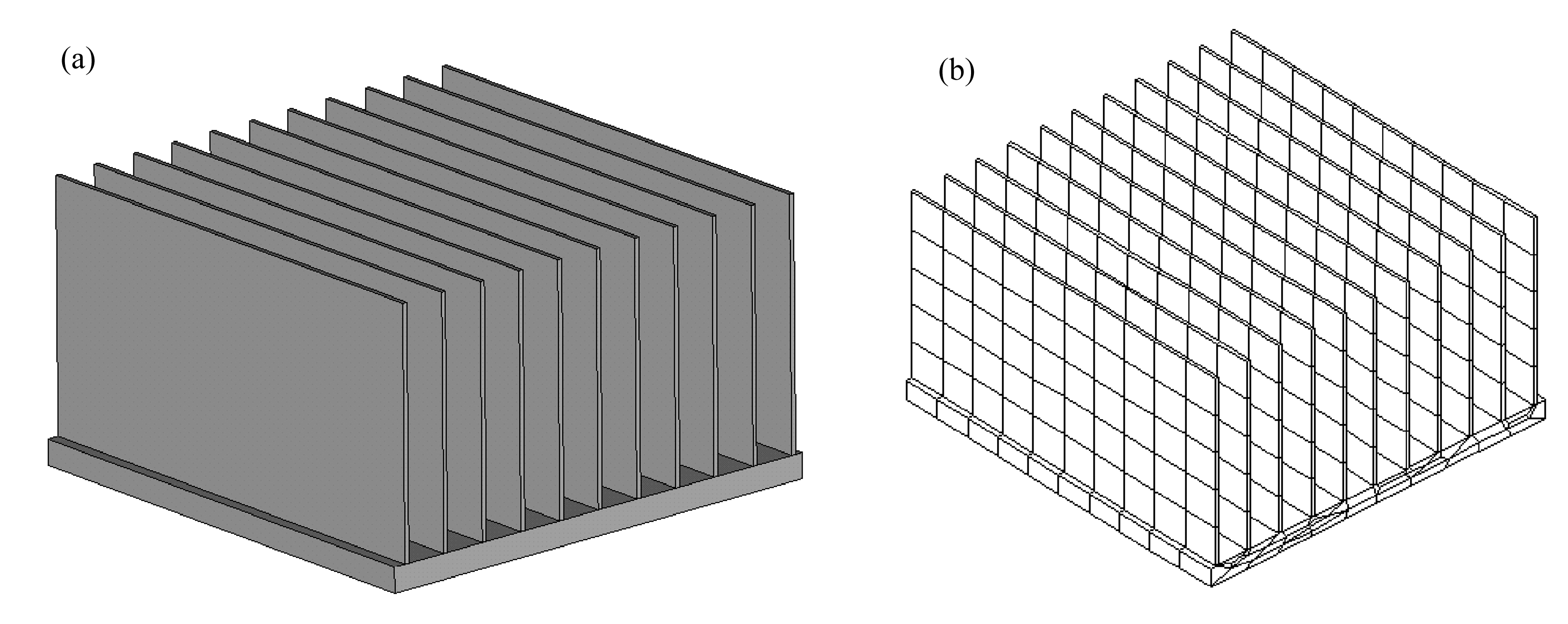
图5 散热片几何结构示意图及其网格剖分(990个单元)
Fig. 5 The geometry structure of the radiator and one sample mesh with 990 elements
表4 基于不同光滑子S的HTL方法求解散热片问题分层二次元方程的迭代次数
Table 4 Iteration counts of the HTL methods for the hierarchical quadratic discretizations of the radiator

算例4 LED单芯片 上述3个算例涉及的均为一种介质材料,本算例讨论LED单芯片问题的热传导有限元分析.考虑如图6所示的单芯片几何模型,它从上往下依次由芯片、黏结材料、基板、热沉基板以及翅片组成,对应的几何尺寸和热导率如表5所示.芯片的热源密度为Qv=2×108 W/m2,翅片的各裸露表面为对流面,换热系数hΓ=10 W/(m2·℃),环境温度Ta=27 ℃,其余裸露面为绝缘面.在网格剖分时,既有各向同性单元,也有横向各向异性单元,还有竖向各向异性单元,对这种复杂情形,通常的迭代方法求解效率是很差的.3种方法求解不同单元数下的分层二次元方程的迭代次数如表6所示.
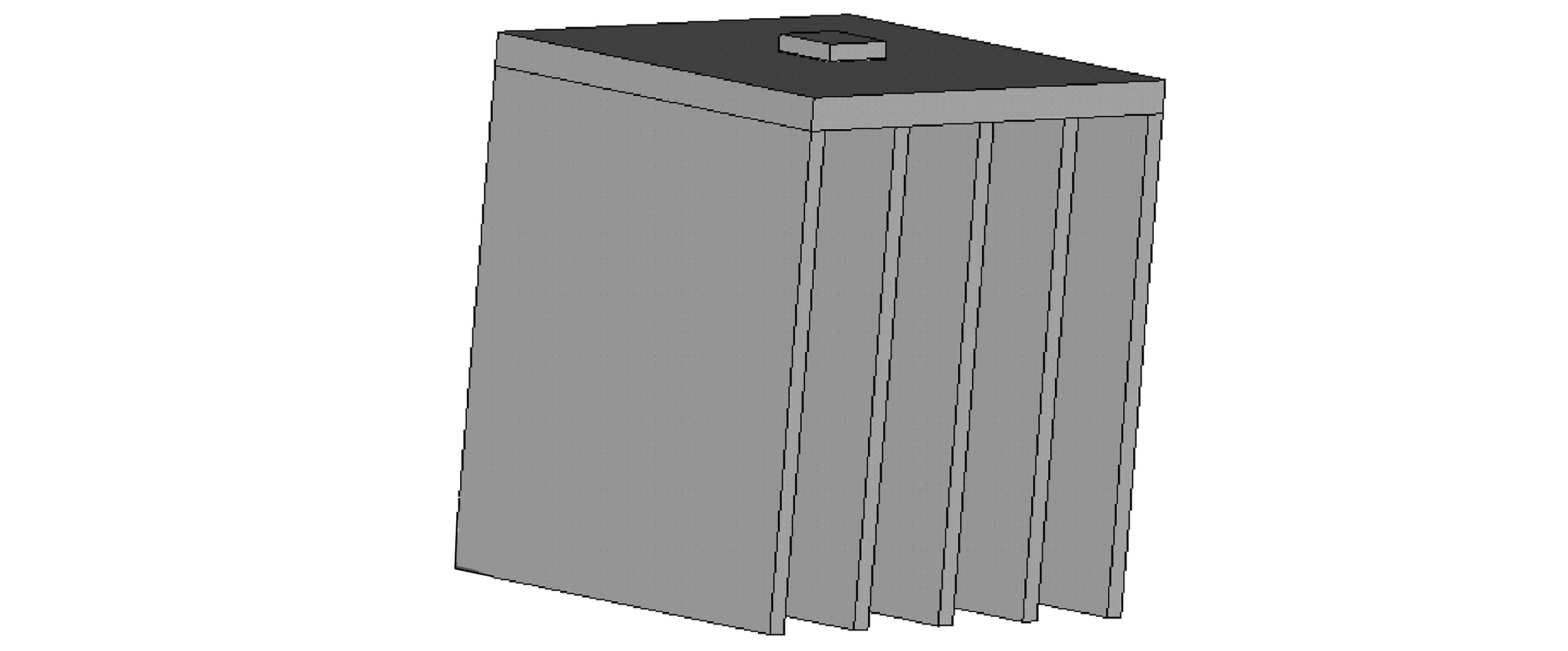
图6 LED单芯片几何结构示意图
Fig. 6 The geometry structure of the LED single chip
表5 LED单芯片模型的相关参数
Table 5 The sizes and the thermal conductivity of each component of the LED single chip

表6 基于不同光滑子S的HTL方法求解LED单芯片问题分层二次元方程的迭代次数
Table 6 Iteration counts of the HTL methods for the hierarchical quadratic discretizations of the LED single chip

由上述数值结果可见:
1) 对各向同性网格问题,p_GS法具有很好的磨光效果,相应的两水平迭代法求解分层二次有限元方程具有很好的计算效率和鲁棒性.例如,对热传导细长梁问题,不管是常系数还是变系数,HTL(p_GS(3))的迭代次数基本不随问题规模的增加而增加.
2) 对各向异性网格(薄单元)问题,p_GS法的磨光效果将变差,两种特殊块磨光算子(LBGS_v或LBGS_m)具有更好的磨光效果,相应两水平迭代法的收敛性基本不依赖于问题规模.比较而言,基于LBGS_v的两水平迭代法的迭代次数更少,对薄结构热传导问题,在设计块磨光算子时,仅需对所有的顶点在其patches上进行块Gauss-Seidel迭代,以提高运算效率.
2.2 多水平方法
两水平迭代算法1是通过调用直接法或迭代法精确求解粗水平(线性元)方程(12)的,当问题规模很大时,这肯定不可取.为了提高整体分析效率,需要为粗水平(线性元)方程提供高效的求解器.对薄结构热传导问题,由于结构的特殊性,在进行网格剖分时,常常需要采用大量的薄单元(各向异性单元),这将大大影响其有限元离散代数系统的求解效率.由文献[16-17]可知,基于“距离矩阵”的DAMG法对求解各向异性网格下的线性元方程具有很好的效率.本节将这种方法应用于粗水平(线性元)方程(12),以建立相应的多水平方法.
在AMG法中,一个最为重要的环节是粗网格节点的选取.下面,仅对两层网格DAMG法中网格粗化方法给出简单描述,具体如下.
首先,利用剖分节点的坐标信息,生成与矩阵Kvv=(kij)vv相对应的距离矩阵D=(dij),即
(13)
其中,Ni![]() {j|(kij)vv≠0},(x(i),y(i),z(i))为节点i的几何坐标,i=1,2,…,n;利用距离矩阵D生成强连通“关系”矩阵S=(sij),即对∀i∈Nh,sij满足
{j|(kij)vv≠0},(x(i),y(i),z(i))为节点i的几何坐标,i=1,2,…,n;利用距离矩阵D生成强连通“关系”矩阵S=(sij),即对∀i∈Nh,sij满足
(14)
其中,![]() ∀j∈Ni}称为点i的强连通集,其中,c为一大于1的常数,一般情形下,其值的变化范围为1.5~2.5,这里,
∀j∈Ni}称为点i的强连通集,其中,c为一大于1的常数,一般情形下,其值的变化范围为1.5~2.5,这里,![]() 以及Nh={1,2,…,n}.
以及Nh={1,2,…,n}.
然后,利用上述距离矩阵及强连通“关系”矩阵,将所有剖分节点分离为各向异性部分和各向同性部分,对各向异性点在强连通方向上进行粗化,对各向同性点暂不粗化,直至粗网格点分布比较均匀时,再将所有的节点按找极大不相关子集(简记为MIS)的方法进行粗化.
最后, 生成由粗网格到细网格的插值算子, 再利用Galerkin方法构造限制算子和粗网格矩阵.
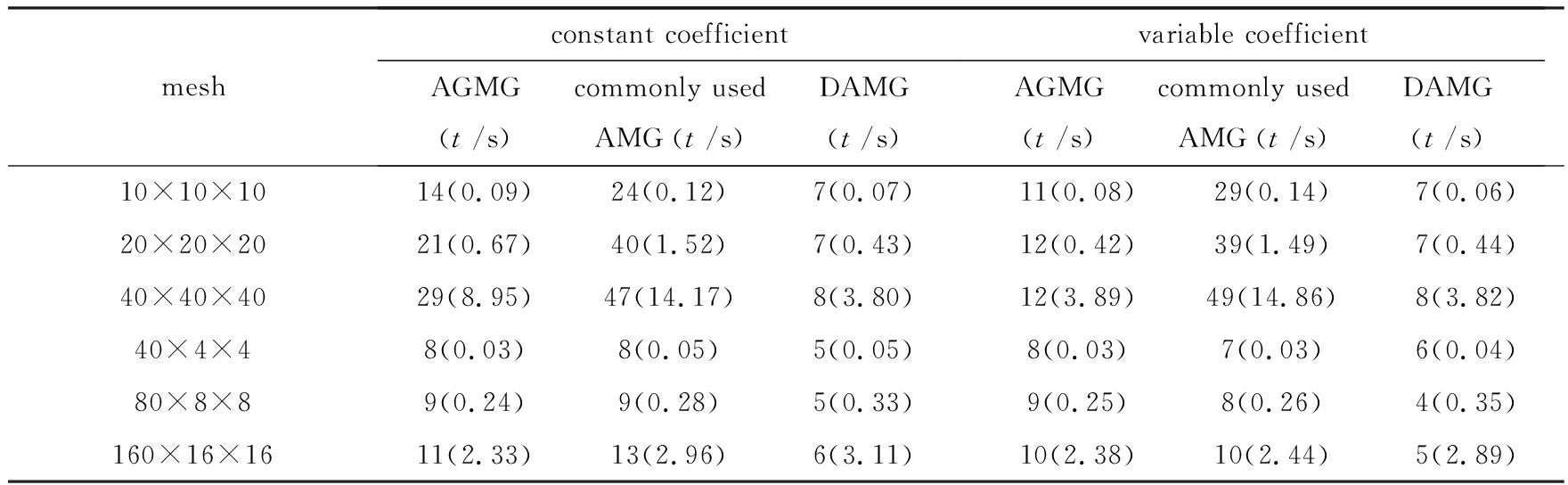
下面,将DAMG法应用于三维热传导细长梁8节点线性元方程(12)的求解,并与两种求解椭圆型问题的AMG法(常用AMG法和AGMG法[10])进行了比较,结果如表7所示.由此可见,基于“距离矩阵”的DAMG法对求解各向异性网格线性元方程具有更好的计算效率和鲁棒性.例如,对40×40×40网格剖分情形,对常系数问题,AGMG法的迭代次数为29,计算CPU时间为8.95 s,常用AMG法的迭代次数为47,计算CPU时间为14.17 s,DAMD法的迭代次数为8,计算CPU时间为3.80 s;对变系数问题,3种方法的迭代次数分别为12,49和8,计算CPU时间分别为3.89,14.86,3.82 s.本文所有数值实验均在Intel(R) Core(TM) i5-3470 CPU微型机(内存为4.00 GB,CPU为3.20 GHz)的Windows 7 环境下进行.
表7 几种AMG法求解热传导细长梁8节点线性元方程的迭代次数和计算CPU时间
Table 7 The iteration counts and CPU time of several AMG methods for the linear
discretizations of the conduction beam

(a) 基于MIS粗化方法
(a) The coarse grid selection process based on the MIS method

(b) 基于“距离矩阵”粗化方法[19]
(b) The coarse grid selection process based on the distance matrix[19]
图7 两种粗化方法所得结果之比较,其中黑方块表示粗网格点,其余均为细网格点
Fig. 7 Comparison of the results obtained by 2 coarse grid selection processes, where the coarse nodes are denoted by black square and the rest are fine nodes
注2 基于“距离矩阵”的粗化算法对各向异性网格能得到更好的粗网格,如对二维情形,两种粗化算法得到的结果如图7所示.显然,由该粗化算法得到的粗网格各节点分布更为合理.反复利用该算法,即可将各向异性网格粗化为一各向同性网格,再对此粗网格按MIS粗化方法进行粗化,可得到一系列各向同性网格,可利用直接法或迭代法快速求解最粗网格层方程.同时,形如Gauss-Seidel迭代等磨光子对各向同性网格问题磨光效果好.上述两个因素综合作用,使得相应的DAMG法具有更好的计算效率.
在两水平方法中,粗水平方程是不需要精确求解的,一般仅需调用一次DAMG法即可,从而大大提高内迭代的计算效率.求解分层二次元方程(7)的多水平迭代算法可简单描述如下.
算法3 多水平迭代算法
将算法1中的步3)修改为:
步3) 调用一次DAMG法近似求解粗水平方程:![]()
简记该多水平方法为HML(S),通过结合不同的光滑子,可以得到3种多水平方法,即HML(p_GS(3))、HML(LBGS_v(1))和HML(LBGS_m(1)).将这3种方法分别应用于薄结构热传导问题分层二次元方程的求解,结果如下.
表8 基于不同光滑子的HML(S)方法求解分层二次元方程的迭代次数
Table 8 The iteration counts of the HML(S) methods with different smoothers
for the hierarchical quadratic discretizations
(a) 热传导细长梁
(a) The case of the slender conduction beam
(b) 扇形薄结构
(b) The case of the thin-walled sector

(c) 散热片问题
(c) The case of the radiator

(d) LED单芯片
(d) The case of the LED single chip

由上述结果可知,基于DAMG法的多水平方法对求解薄结构热传导问题是有效的.DAMG法可大大提高内迭代的计算效率,从而提高薄结构热传导问题有限元分析的整体效率.
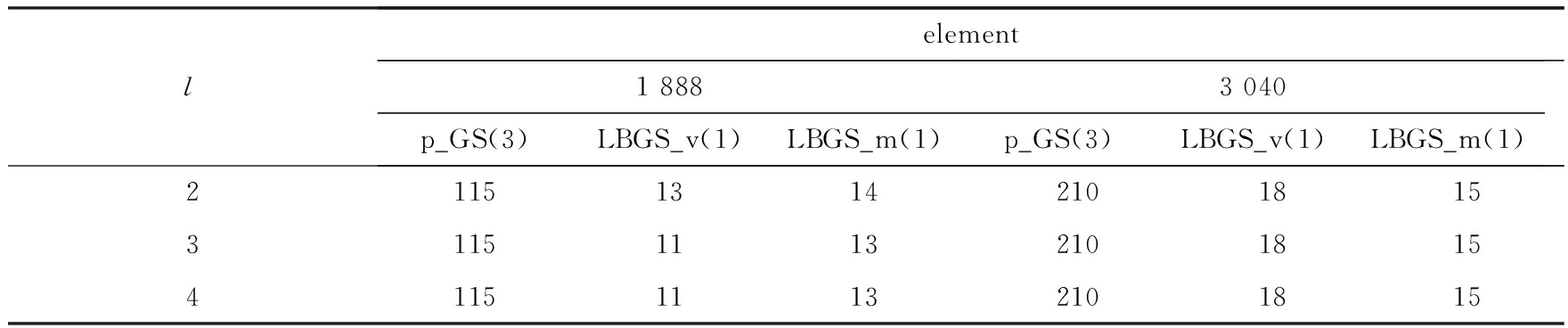
对LED单芯片问题,计算中所使用的单元,有各向同性的,有x方向的薄单元,也有y方向或z方向的薄单元,调用一次DAMG法近似求解粗水平方程虽能确保多水平方法收敛,但外迭代次数将增加,从而影响整体收敛速度.为此,需要调用l(l>1)次DAMG法近似求解粗水平方程,相应的计算结果如表9所示.由此可见,对较复杂情形,一般也仅需调用2至3次DAMG法近似求解粗水平方程,就可获得与两水平方法一样的迭代次数.
表9 调用l(l>1)次DAMG法求解粗水平方程时HML(S)方法的迭代次数
Table 9 The iteration counts of the HML(S) methods by calling l times of
DAMG to solve the coarse level discretizations
3 结 语
高阶有限元法是求解三维薄结构热传导问题的有效数值方法之一,但要提高其分析整体效率必须为相应的离散系统设计快速求解算法.本文的目的就是为薄结构热传导问题分层二次元方程设计相应的两水平方法和多水平方法.对各向同性网格问题,通常的点Gauss-Seidel具有很好的磨光效果;但对薄结构各向异性单元,需要选取基于局部块Gauss-Seidel的光滑子,相应的两水平方法具有更好的计算效率和鲁棒性.基于“距离矩阵”的DAMG法能加速各向异性网格下粗水平(线性元)方程的求解,从而能有效提高薄结构热传导问题有限元分析的整体效率.另外,还需要对更一般的问题,如LED多芯片组的散热问题、一般的非结构网格问题,进行更广泛的数值测试,以验证新方法的有效性和鲁棒性.本文方法也可推广应用于一般的热传导问题以及三维薄体结构固体力学计算,这些将是今后进一步研究的问题.
参考文献(References):
[1] BOUZAKIS K D, VIDAKIS N. Prediction of the fatigue behavior of physically vapor deposited coating in the ball-on-rod rolling contact fatigue test, using an elastic-plastic finite elements method simulation[J]. Wear, 1997, 206(1/2): 197-203.
[2] ![]() L A,
L A,  LIWA A, KWA
LIWA A, KWA NY W. Employment of the finite element method for determining stresses in coatings obtained on high-speed steel with the PVD process[J]. Journal of Materials Processing Technology, 2005, 164/165: 1192-1196.
NY W. Employment of the finite element method for determining stresses in coatings obtained on high-speed steel with the PVD process[J]. Journal of Materials Processing Technology, 2005, 164/165: 1192-1196.
[3] BRANDT A, MCCORMICK S, RUGE J. Algebraic multigrid (AMG) for sparse matrix equations[C]//Sparsity and Its Applications. Loughborough, 1983: 257-284.
[4] BREZINA M, CLEARY A J, FALGOUT R D, et al. Algebraic multigrid based on element interpolation (AMGe)[J]. SIAM Journal on Scientific Computing, 2000, 22(5): 1570-1592.
[5] CLEARY A J, FALGOUT R D, HENSON V E, et al. Robustness and scalability of algebraic multigrid[J]. SIAM Journal on Scientific Computing, 2000, 21(5): 1886-1908.
[6] GRIEBEL M, OELTZ D, SCHWEITZER M A. An algebraic multigrid method for linear elasticity[J]. SIAM Journal on Scientific Computing, 2003, 25(2): 385-407.
[7] BAKER A H, KOLEV T V, YANG U M. Improving algebraic multigrid interpolation operators for linear elasticity problems[J]. Numerical Linear Algebra With Applications, 2010, 17(2/3): 495-517.
[8] SHU Shi, XU Jinchao, YANG Ying, et al. An algebraic multigrid method for finite element systems on criss-cross grids[J]. Advances in Computational Mathematics, 2006, 25(1/3): 287-304.
[9] VAN K P, MANDEL J, BREZINA M. Algebraic multigrid by smoothed aggregation for second and fourth order elliptic problems[J]. Computing, 1996, 56(3): 179-196.
K P, MANDEL J, BREZINA M. Algebraic multigrid by smoothed aggregation for second and fourth order elliptic problems[J]. Computing, 1996, 56(3): 179-196.
[10] NOTAY Y. An aggregation-based algebraic multigrid method[J]. Electronic Transactions on Numerical Analysis, 2010, 37: 123-146.
[11] RUGE J, MCCORMICK S, MANTEUFFEL T, et al. AMG for higher-order discretizations of second-order elliptic problems[C]//Abstracts of the Eleventh Copper Mountain Conference on Multigrid Methods. 2003.
[12] HEYS J J, MANTEUFFEL T A, MCCORMICK S F, et al. Algebraic multigrid for higher-order finite elements[J]. Journal of Computational Physics, 2005, 204: 520-532.
[13] EL MALIKI A, GUÉNETTE R, FORTIN M. An efficient hierarchical preconditioner for quadratic discretizations of finite element problems[J]. Numerical Linear Algebra With Applications, 2011, 18: 789-803.
[14] SHU S, SUN D, XU J. An algebraic multigrids for higher order finite element discretizations[J]. Computing, 2006, 77(4): 347-377.
[15] XIAO Yingxiong, SHU Shi. A robust preconditioner for higher order finite element discretizations in linear elasticity[J]. Numerical Linear Algebra With Applications, 2011, 18: 827-842.
[16] 谭敏, 肖映雄, 舒适. 一种各向异性四边形网格下的代数多重网格法[J]. 湘潭大学自然科学学报, 2005, 27(1): 78-84.(TAN Min, XIAO Yingxiong, SHU Shi. An algebraic multigrid method on anisotropic quadrilateral grid[J]. Natural Science Journal of Xiangtan University, 2005, 27(1): 78-84.(in Chinese))
[17] XIAO Yingxiong, SHU Shi, ZHANG Ping, et al. An algebraic multigrid method for isotropic linear elasticity on anisotropic meshes[J]. International Journal for Numerical Methods in Biomedical Engineering, 2010, 26: 534-553.
[18] GRAHAM E, FORSYTH P A. Preconditioning methods for very ill-conditioned three-dimensional linear elasticity problems[J]. International Journal for Numerical Methods in Engineering, 1999, 44(1): 77-99.
[19] SUMANT P S, CANGELLARIS A C, ALURU N R. A node-based agglomeration AMG solver for linear elasticity in thin bodies[J]. Communications in Numerical Methods in Engineering, 2009, 25: 219-236.
[20] YSERENTANT H. On the multi-level spliting of finite element spaces[J]. Numerische Mathematik, 1986, 49(4): 379-412.
[21] XIAO Yingxiong, ZHOU Zhiyang, SHU Shi. An efficient AMG method for quadratic discretizations of linear elasticity problems on some typical anisotropic meshes in three dimensions[J]. Numerical Linear Algebra With Applications, 2015, 22(3): 465-482.
[22] WU S C, LIU G R, ZHANG H O, et al. A node-based smoothed point interpolation method (NS-PIM) for three-dimensional heat transfer problems[J]. International Journal of Thermal Sciences, 2009, 48(7): 1367-1376.
引用本文/Cite this paper:
张申, 肖映雄, 郭瑞奇. 三维薄结构热传导问题分层二次元方程的多水平方法[J]. 应用数学和力学, 2018, 39(6): 700-713.
ZHANG Shen, XIAO Yingxiong, GUO Ruiqi. A multi-level method for hierarchical quadratic discretizations of thin-walled structures in 3D heat conduction[J]. Applied Mathematics and Mechanics, 2018, 39(6): 700-713.