引 言
大型轻质网状结构被广泛应用于结构工程中.董石麟和夏亨熹[1-2]曾提出拟板法分析此类结构.其优点是降低计算量,并可采用连续介质力学方法进行结构整体性能的分析.在实际工程中,材料的布局方式表现为结构形式.若不考虑尺度效应[3-4],从材料的角度看,此类结构中部件(桁架)可看作是具有周期性杆件胞元的轻质复合材料[5].均匀化方法[6]是分析这类问题的有效方法.故而,上述的拟板法也可看作是一种均匀化分析方法.
非均质材料在近年备受结构与材料界研究者的关注[7-14].在20世纪,Gibson、Ashby[7]就对非均质材料/结构进行了系统性的研究,并提出相关的均匀化策略.结构的尺度也不再局限于宏观结构[8-11].比如Tollenaere和Caillerie[8]利用均匀化方法给出晶格结构材料的等效连续体模型.不过,因宏观桁架类网格结构已经广泛应用,结构的尺寸不断增大,其非线性变形增强以及多场耦合问题等均需深入研究解决.Hutchinson和Fleck[12]研究了周期桁架结构的整体力学行为.周加喜和邓子辰[13]讨论了类桁架夹层板的等效弹性性能.张洪武等[14]给出一种求解周期性点阵桁架结构的等效材料性能的多尺度求解方法.梁军、杜善义等[15]讨论采用边界力法解决含周期性胞元的复合材料的等效弹性性能问题.
上述分析工作主要集中在采用均匀化方法寻求材料弹性性能的数值解.其原因在于胞元形式的多样性与复杂性[15]造成解析解的获取极为困难、甚至不可行.基于此,史姣、蔡坤等[16-18]结合结构力学和均匀化思想,给出了含周期性胞元的桁架类结构的等效弹性参数的解析解.这对此类结构的设计极为有利.但上述工作[16-18]没有涉及材料/结构的热-力耦合问题[19].本文将分析含周期性正交铰接杆件胞元的二维网格结构的热弹性性能解析解,并利用数值算例进行了验证.
1 二维网格结构及其单胞模型
图1(a)所示为二维周期性网格结构,其单胞如图1(b)所示,其结构说明如下:水平方向(x向)为1号等直杆件;竖直方向(y向)为2号等直杆件;斜向对角杆件为3号等直杆件.各杆件几何与物理参数见表1.

(a) 平面网格结构
(a) The 2D lattice structure

(b) 网格结构的纯杆单胞 (c) 单胞的拟膜
(b) A link-hinged unit cell (c) Pseudo-membrane simulation of a unit cell
图1 平面网格结构及其矩形胞元(无热膨胀)
Fig. 1 The plane lattice structure with rectangular unit cells(without thermal expansion)
表1 杆件几何及物理参数
Table 1 Geometrical and physical parameters of links

图1胞元中各杆件之间铰接, 但两根斜杆之间无直接约束.1、2号杆正交,即满足![]() 其中θ∈(0°, 90°),ki=Ei·Ai(i=1,2,3).同时,记t为网格结构连续体化后拟膜(PM)(图1(c))的厚度, ΔT为增温值.
其中θ∈(0°, 90°),ki=Ei·Ai(i=1,2,3).同时,记t为网格结构连续体化后拟膜(PM)(图1(c))的厚度, ΔT为增温值.
2 等效热弹性参数分析
2.1 基本假设
 结构处于小变形状态.
结构处于小变形状态.
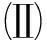 各杆件抗拉刚度(ki(i=1,2,3))在增温前后保持不变.
各杆件抗拉刚度(ki(i=1,2,3))在增温前后保持不变.
2.2 单胞拟膜的等效热膨胀系数
易知,图1(b)网格结构胞元中各杆件在组装前(不相互铰接条件下),增温ΔT后的杆长如下:

(1)
同时,记组装后各杆件的杆长如下:
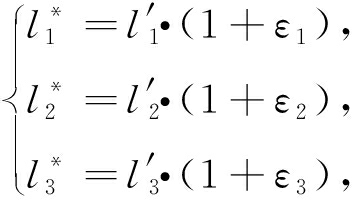
(2)
其中ε1,ε2和ε3分别为1、2和3号杆件的轴向(综合)应变.因微结构(胞元)对称、温度荷载对称,故三根杆件长度满足下式:
(3)
由式(2)和(3)可得
(4)
由假设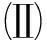 知,组装后各杆件内力分别为
知,组装后各杆件内力分别为
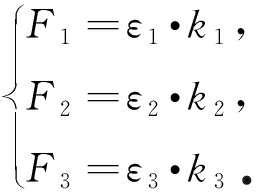
(5)
选取任意一个节点,由节点受力平衡条件可知
(6)
(7)
将式(5)代入式(6)可得
(8)
即
(9)
故有
(10)
同理,将式(5)代入式(7)可得
(11)
由假设 (即小变形假设)及将式(10)和(11)代入式(4)可得(见附录)
(即小变形假设)及将式(10)和(11)代入式(4)可得(见附录)
(12)
其中
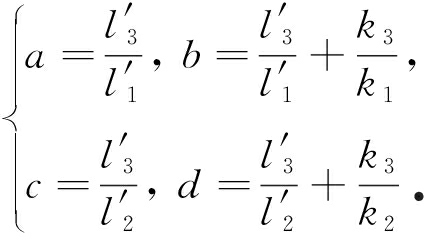
(13)
由式(2)及式(10)~(12)可得,温度荷载作用下的胞元内各杆件的长度如下:
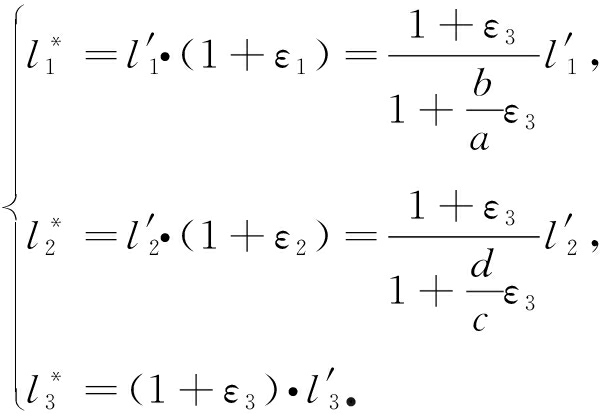
(14)
记
(15)
亦即,θ*为热膨胀后胞元内斜杆与水平杆的夹角,其与温度变化相关.
胞元拟膜后的等效热膨胀系数αx,αy满足下式:
(16)
同时,由式(14)和(16)可知拟膜的等效热膨胀系数为
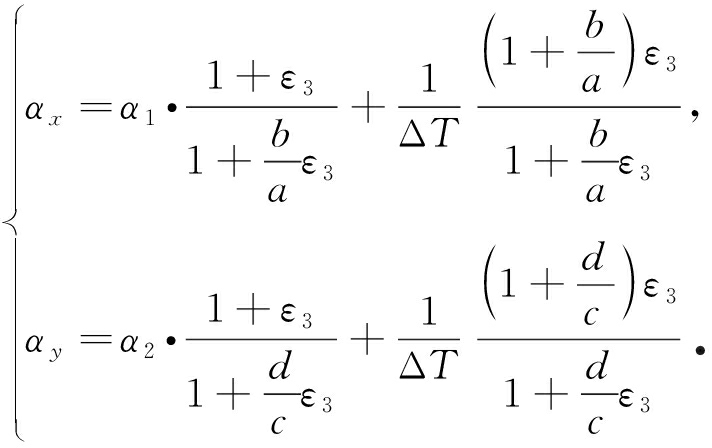
(17)
2.3 单胞拟膜的等效弹性参数
由以前工作[16-18]知,含周期性纯杆胞元的网格结构的拟膜的等效弹性参数如下:
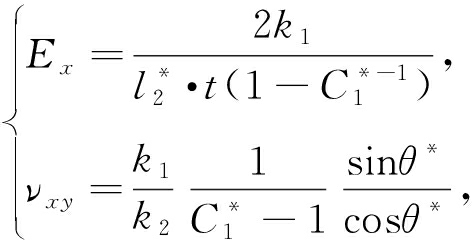
(18)
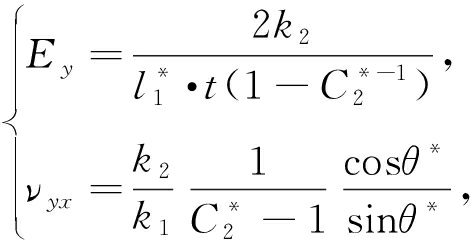
(19)
(20)
其中
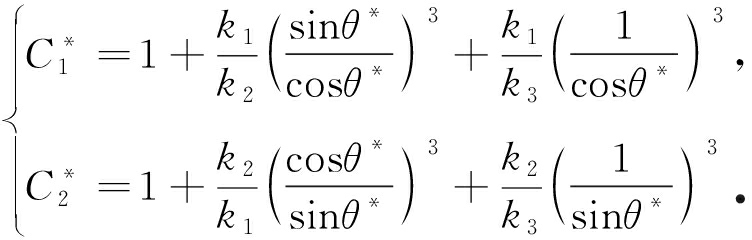
(21)
因θ*与温度变化相关,故上述弹性参数也随温度变化而变化.
3 算 例
3.1 算例1
图2所示悬臂梁,(拟膜)厚度为t=0.01 m,分布压力p=10 kN/m.网格胞元内各杆件几何及物理参数如表 2所示.采用ANSYS软件获得结构变形.结构变形中暂不考虑屈曲.梁左端仅在中性轴处完全固定,其余部分仅受法向位移约束.
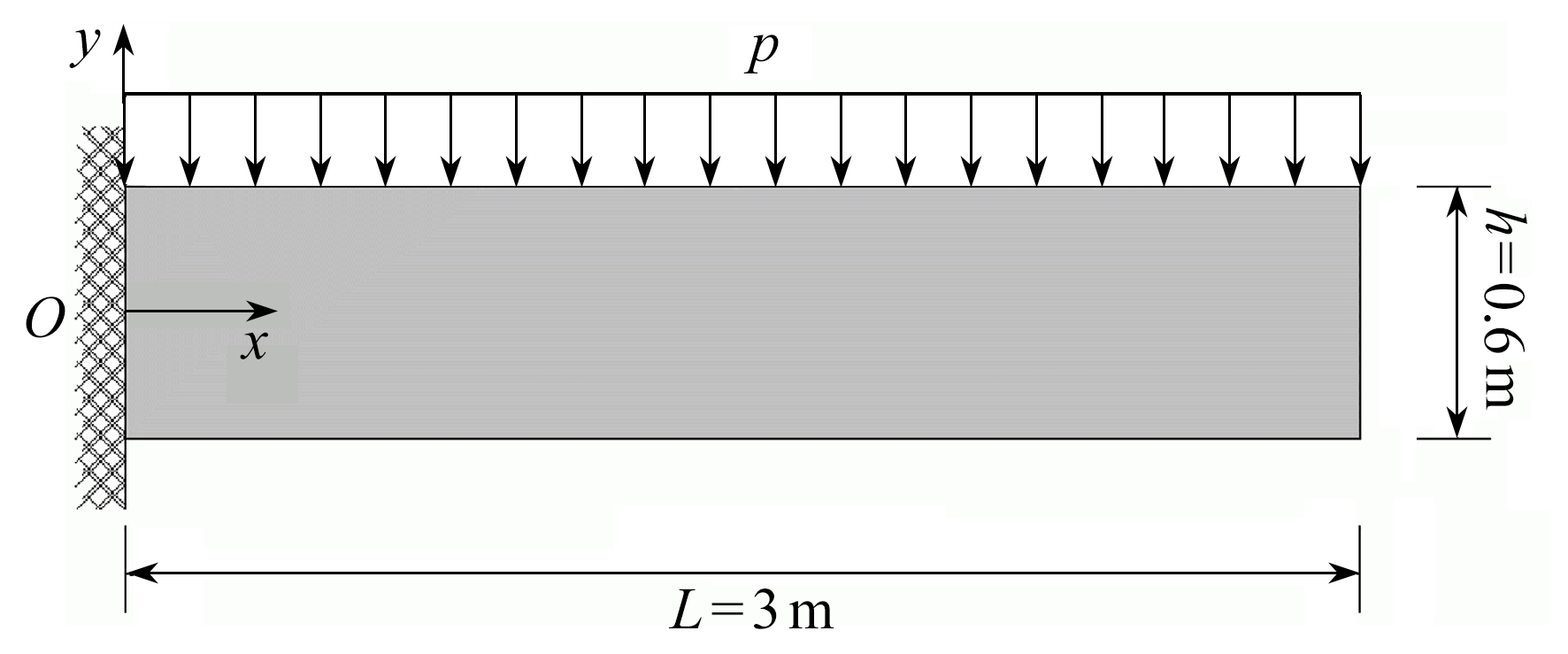
图2 悬臂梁模型
Fig. 2 The cantilever beam model
受均布压力作用连续体悬臂梁中性层挠度的近似理论解由下式控制:
(22)
其中Uy=0为中性层挠度,p为作用于梁上的均布压力,L为梁跨度,Ex为连续体梁中材料沿轴向的弹性模量,Iz为梁中性轴惯性矩,Gxy为梁在xOy面内的剪切模量,A为梁横截面面积,截面系数κ=1.2.
3.1.1 网格梁模型及参数
为了验证拟膜法给出的等效热弹性参数的正确性,表2给出了网格悬臂梁中杆件的几何与物理参数.其中,s为胞元尺寸单位.考虑到便于计算和分析,本文选取模量为规整的100 GPa(铝合金模量).此外,结构的工作环境温度变化幅度往往在100 ℃以内,为了放大热膨胀效应,将实际材料的热膨胀系数放大4~10倍用于算例分析.同时,为了验证网格无关性,本文考虑了3种不同尺寸下构造出具有相同热弹性的网格结构,即
① s=0.05 m时,对应于15×4(x向15×y向4,后同)网格结构悬臂梁(见图3(a));
② s=0.025 m时,对应于30×8网格结构悬臂梁(见图3(b));
③ s=0.012 5 m时,对应于60×16网格结构悬臂梁(见图3(c)).
表2 网格悬臂梁中杆件几何及物理参数
Table 2 Geometrical and physical parameters of links in the lattice cantilever beam


(a) 含15×4个胞元的网格结构
(a) The lattice beam with 15×4 unit cells
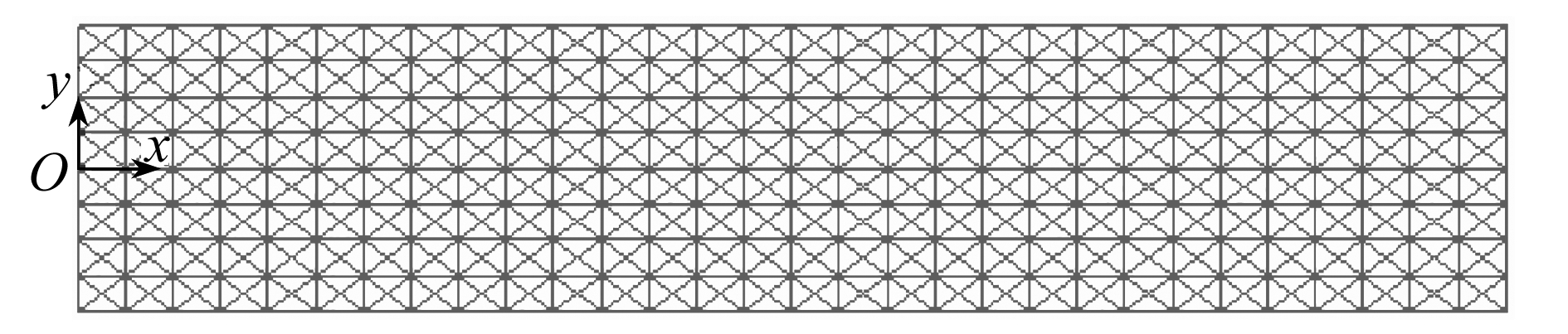
(b) 含30×8个胞元的网格结构
(b) The lattice beam with 30×8 unit cells
(c) 含60×16个胞元的网格结构
(c) The lattice beam with 60×16 unit cells
图3 具有相同拟膜热弹性性能的3种网格结构
Fig. 3 Three lattice structures with the same thermo-elastic PM
3.1.2 拟膜梁的物理参数
现考虑结构不增温和增温、降温条件下的变形问题.设结构均匀增温ΔT=0 ℃,ΔT=-20 ℃或ΔT=+50 ℃.由式(17)~(20)知,胞元拟膜的弹性参数如表3所示.
表3 拟膜材料物理参数
Table 3 Physical parameters of the pseudo-membrane cell in fig. 3

3.2 数值结果
3.2.1 ΔT=0 ℃(无增温)时的解答
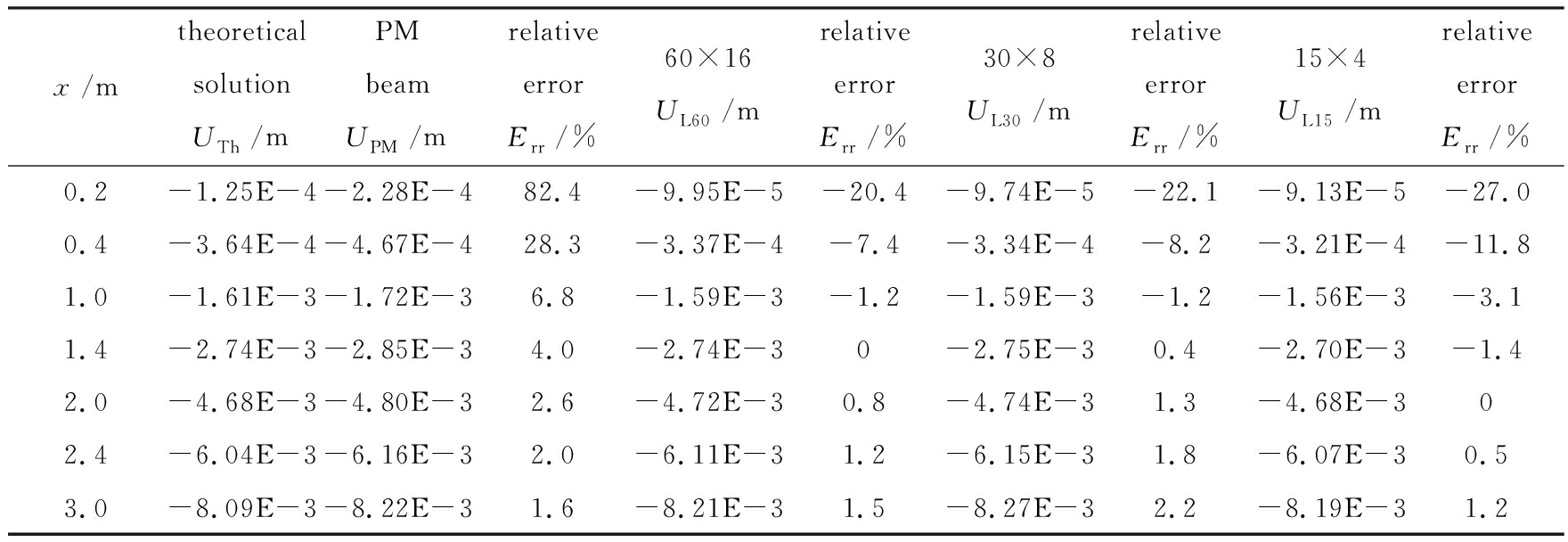
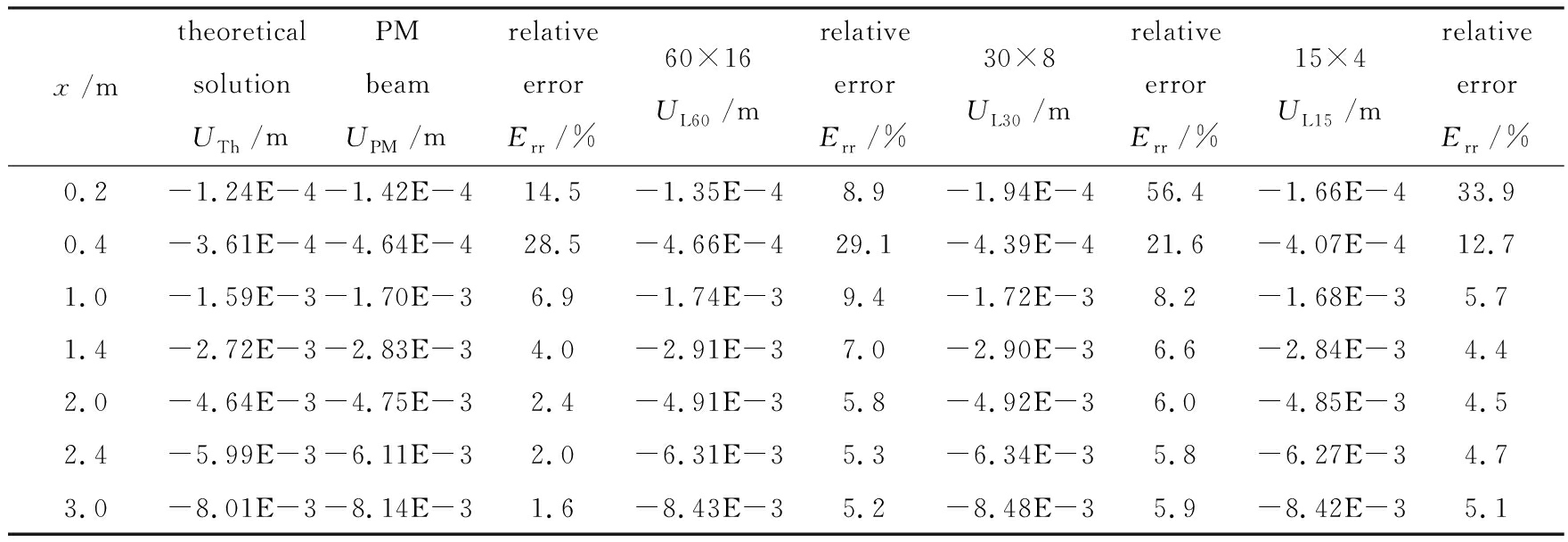
图4给出梁在无温度变化条件下中性层的变形解答.表明拟膜梁与网格结构梁的解答相对误差很小(网格越密,误差越小)(见表4).而由式(22)给出的理论解在不同位置处均低于其余解答(见表4),表明理论解对应的梁比实际结构刚度偏大.其部分原因是当前梁的高跨比较大(1∶5).梁的根部(x=0处)相对误差较大(但绝对误差较小)可用Sait-Venant(圣维南)原理解释.
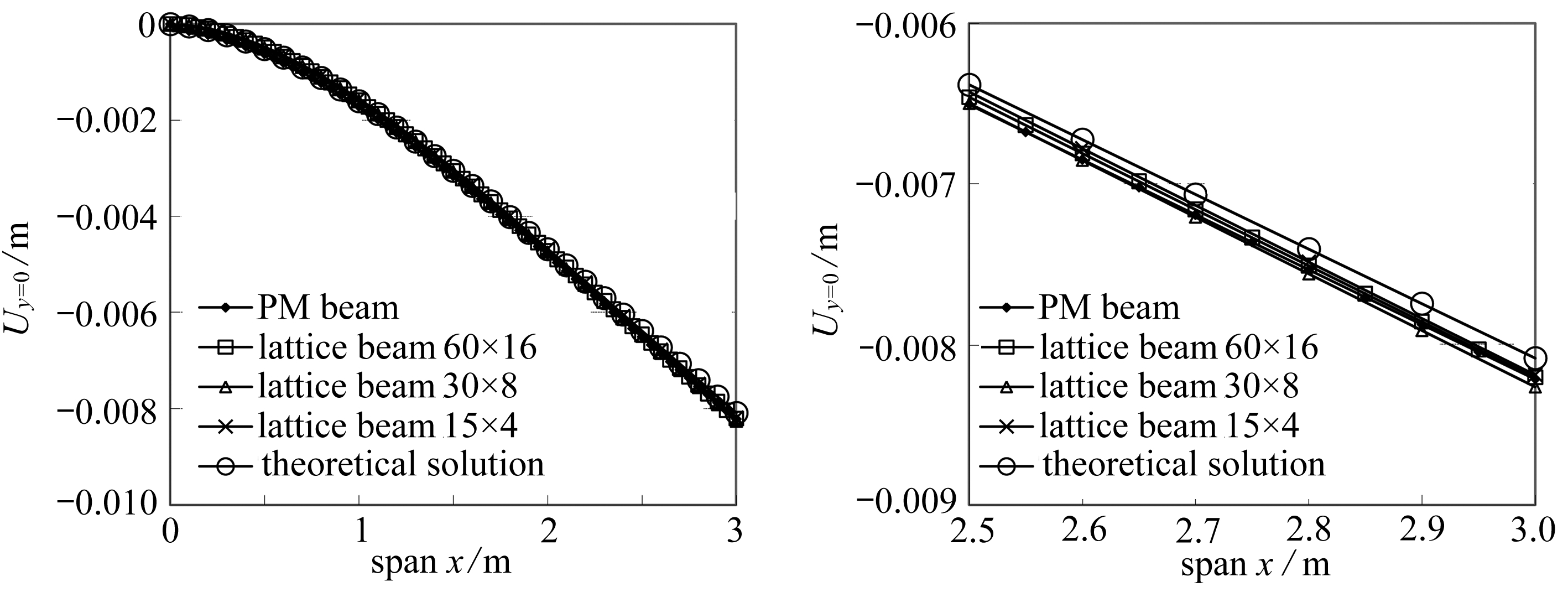
(a) 0≤x≤3 (b) 2.5≤x≤3
图4 梁中性层y-向位移曲线
Fig. 4 The y-displacement curves of neutral layers of the beams
表4 ΔT=0℃时梁中性层中节点的y-向位移解
Table 4 The y-displacements of nodes on neutral layers of the beams for ΔT=0℃
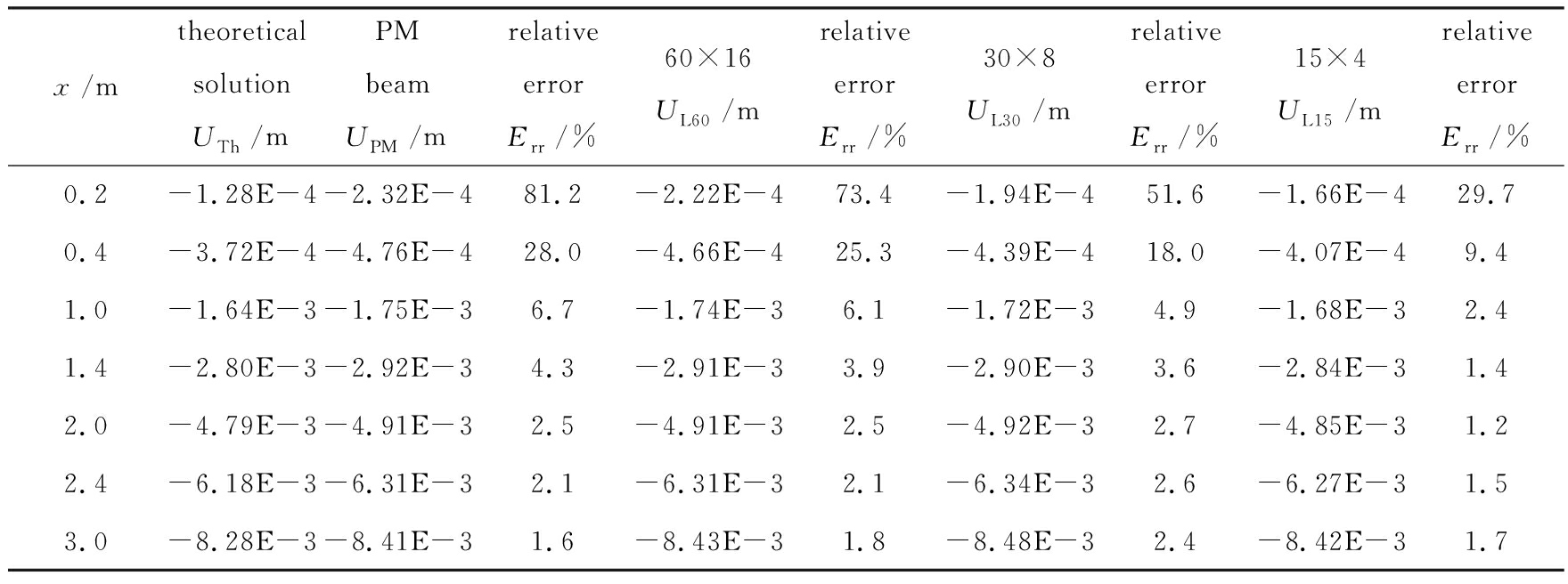
对于线性问题,结构受力与热荷载同时作用下的变形解答可以由两部分独立解答累加.为考虑温度荷载对结构变形的影响,设定结构分别处于降温或增温状态.由上述解答给出数值解答与理论解作比较.相对误差的定义为:相对误差=(当前解-理论解)/理论解.上述3种悬臂梁的高度和跨度均相同.如果这3种梁的计算结果与理论解的相对误差绝对值不超过5%,即证明网格无关性.这对于设计相同形状和相同热-力性能的网格结构非常重要.
3.2.2 ΔT=-20 ℃(降温)时的解答
图5给出了降温(ΔT=-20 ℃)条件下结构上、中和下表面y-向位移解.表明拟膜梁的位移较网格结构的位移略低.在梁的中性层处,拟膜梁的数值解与理论解(采用式(22)及表3第二行参数获得)更为接近,见表5.从图6也可发现,拟膜梁与网格梁的位移场差异极小.
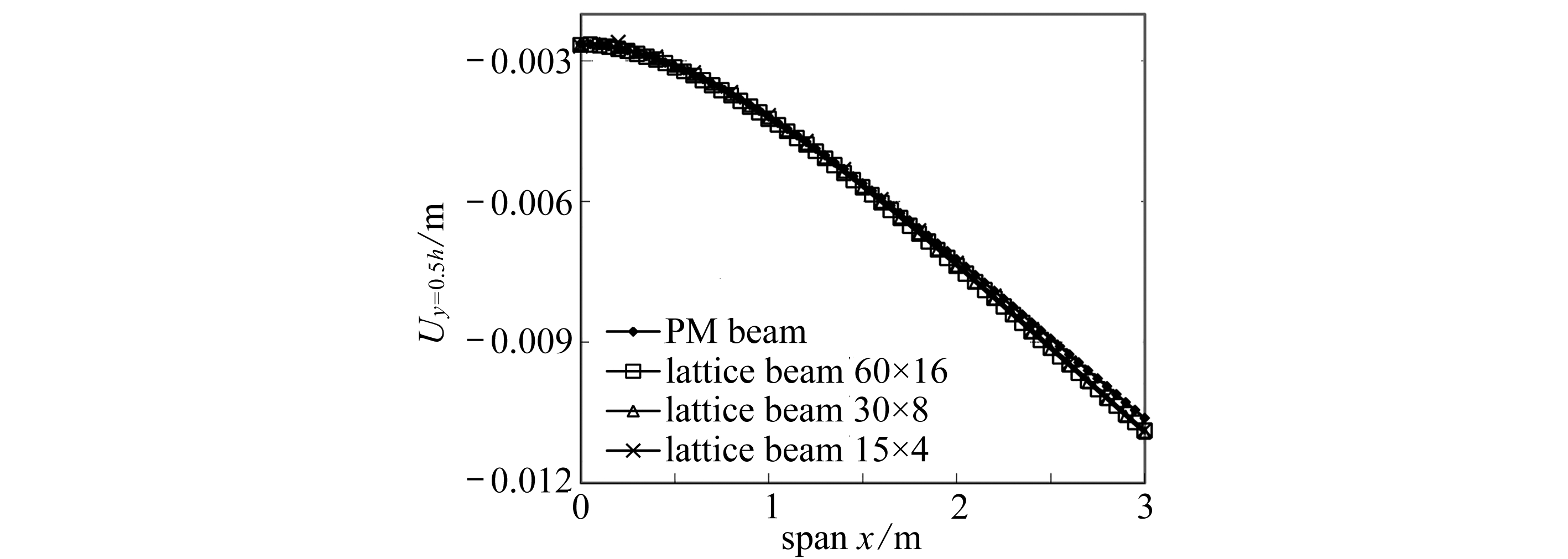
(a) 梁上表面挠度
(a) The upper-surface displacements of the beams
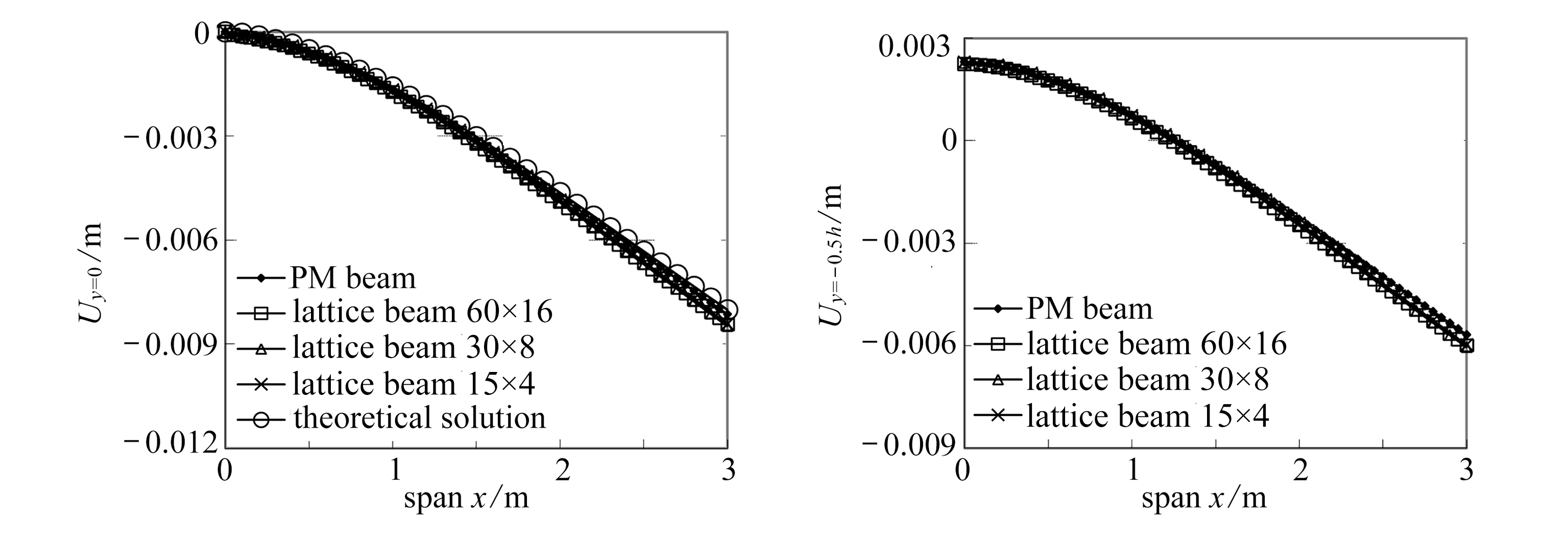
(b) 梁中性层挠度 (c) 梁下表面挠度
(b) The neutral-layer displacements of the beams(c) The lower-surface displacements of the beams
图5 ΔT=-20℃时梁顶层、中性层和底层y-向位移曲线
Fig. 5 The y-displacement curves of top, neutral and bottom layers of the beams for ΔT=-20℃
表5 ΔT=-20℃时梁中性层中节点的y-向位移解
Table 5 The y-displacements of nodes on neutral layers of the beams for ΔT=-20℃
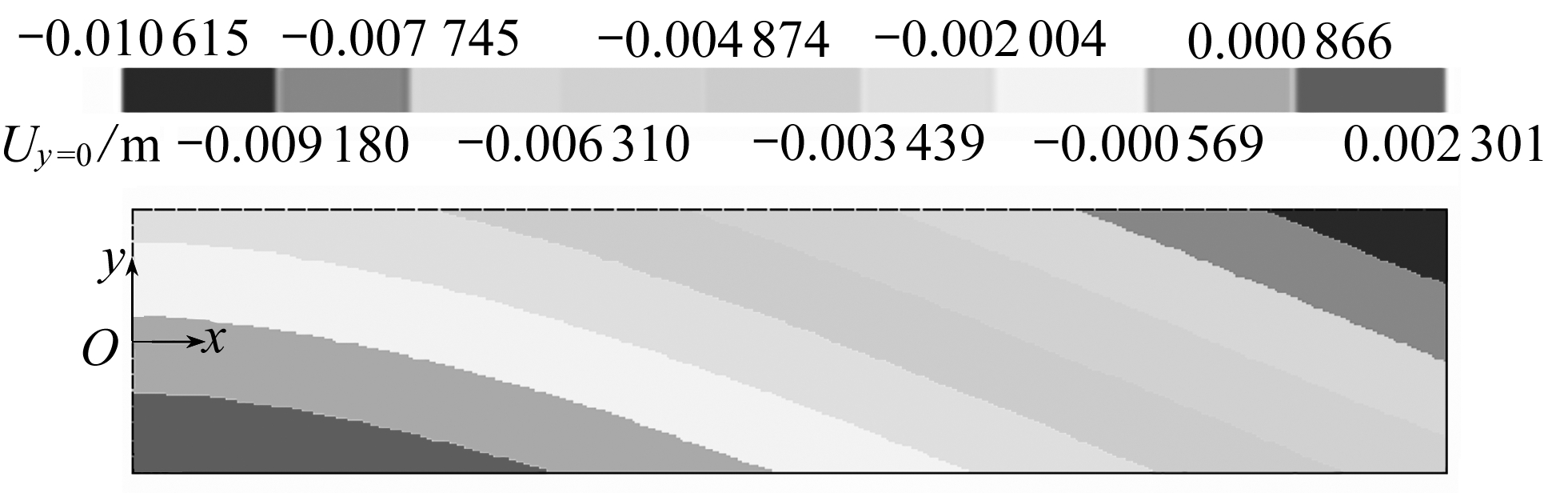
(a) 拟膜梁
(a) The PM beam

(b) 网格梁
(b) The lattice beam with 60×16 unit cells
图6 ΔT=-20℃时悬臂梁y-向位移云图
Fig. 6 The y-displacement distributions of neutral layers of the beams for ΔT=-20℃
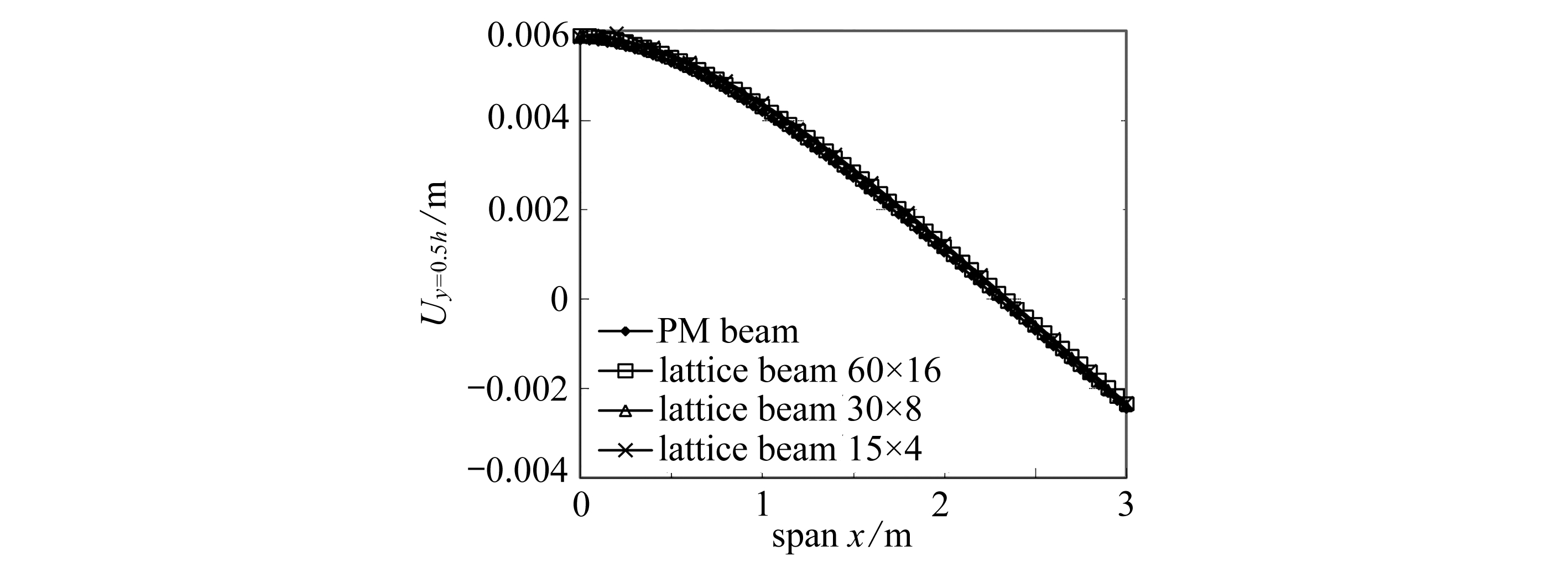
(a) 梁上表面挠度
(a) The upper-surface displacements of the beams
(b) 梁中性层挠度 (c) 梁下表面挠度
(b) The neutral-layer displacements of the beams(c) The lower-surface displacements of the beams
图7 ΔT=+50℃时梁顶层、中性层和底层y-向位移曲线
Fig. 7 The y-displacement curves of top, neutral and bottom layers of the beams for ΔT=+50℃
3.2.3 ΔT=+50 ℃(升温)时的解答
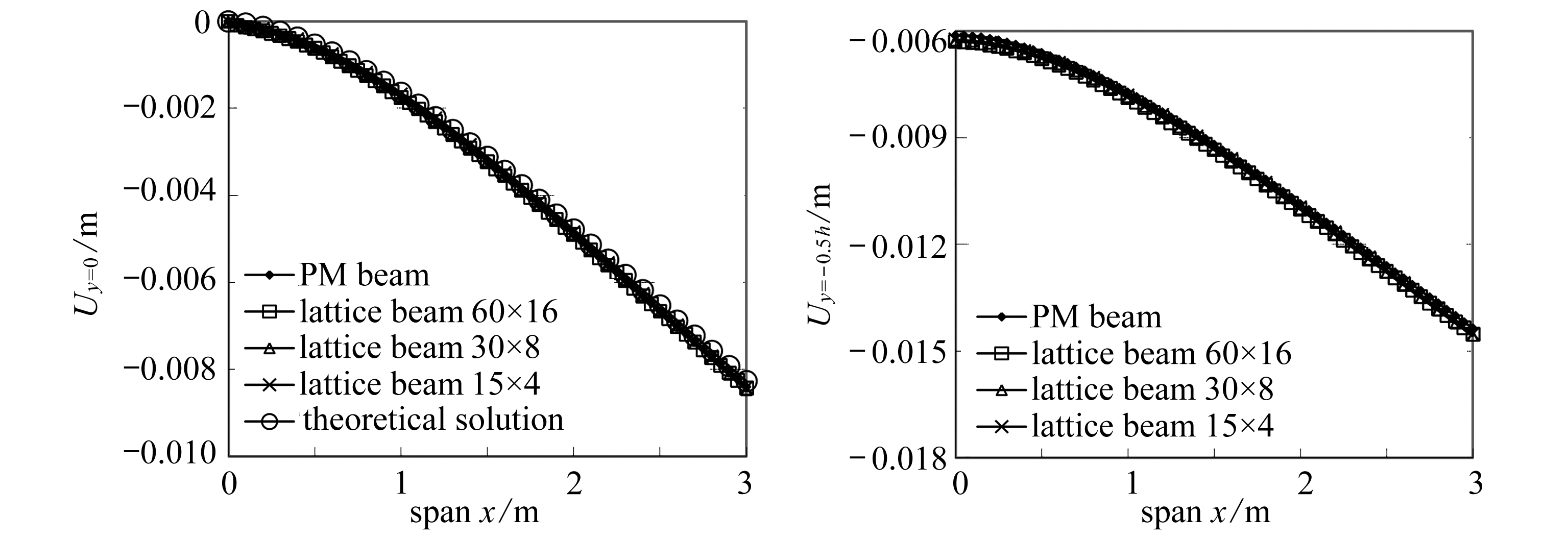
图7(a)和(c)给出了梁(拟膜梁以及不同网格结构梁)上下表面的挠度.结果显示拟连续体结构边界的变形与网格结构边界变形吻合极好.图7(b)给出了梁的中性层挠度的数值解与式(22)的理论解比较.发现拟连续体(拟膜)结构与原网格结构的中性层挠度解答极为吻合,而它们与理论解的差异较大(见表6).比如,离端部约束1 m处的拟膜梁数值解与理论解的误差约为6%,在自由端相对误差约为1.6%.
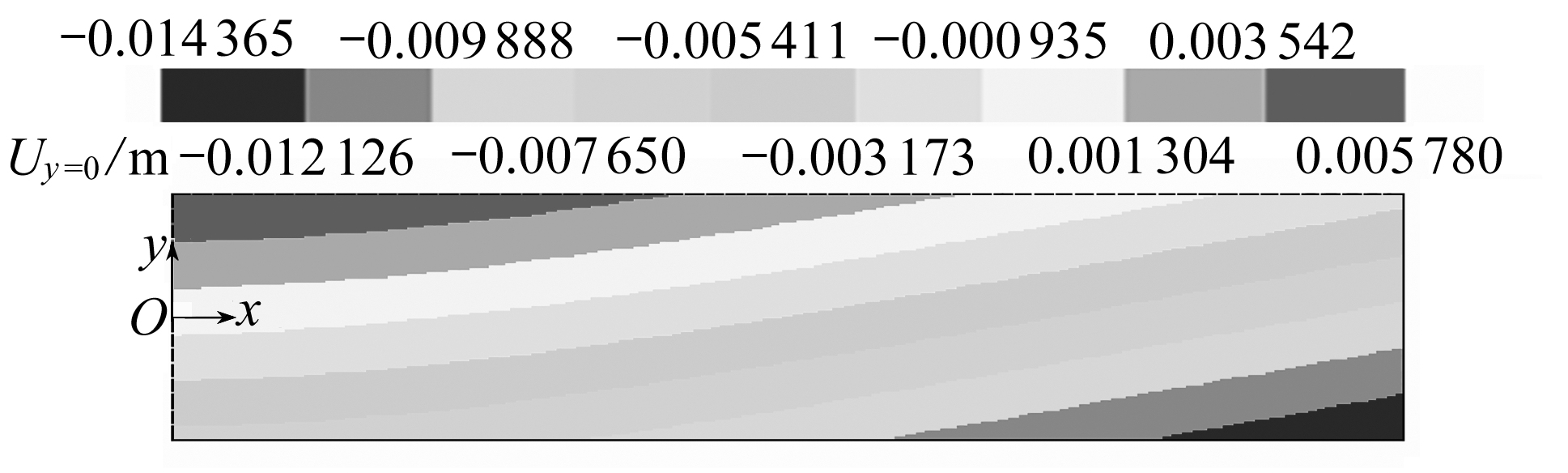
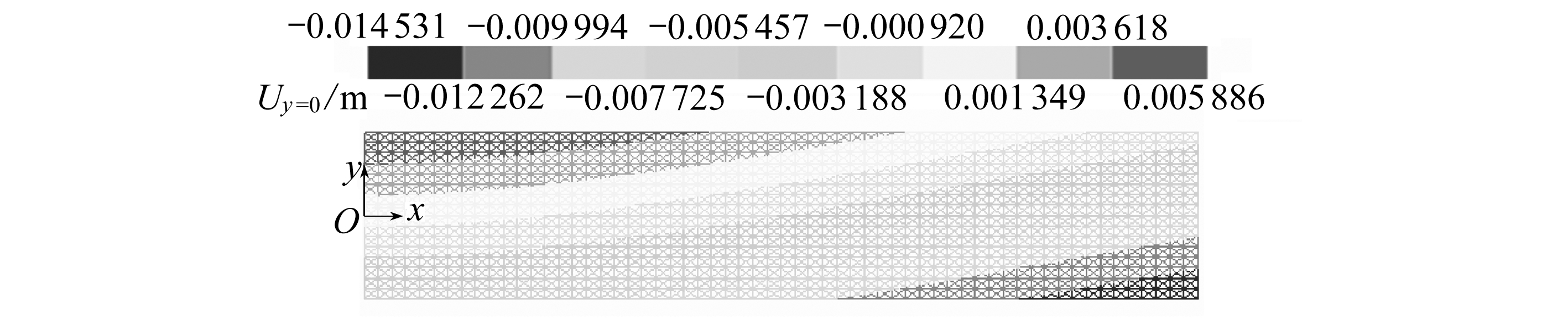
图8给出了拟膜梁与60×16网格结构梁的节点y-向位移云图.表明两者位移场不仅在边界吻合极好,在其他区域相对误差也低于5%.
表6 ΔT=+50 ℃时梁中性层中节点的y-向位移解
Table 6 The y-displacements of nodes on neutral layers of the beam for ΔT=+50 ℃
(a) 拟膜梁
(a) The PM beam
(b) 网格梁
(b) The lattice beam with 60×16 unit cells
图8 ΔT=+50℃时悬臂梁y-向位移云图
Fig. 8 The y-displacement distributions of neutral layers of the beams for ΔT=+50℃
比较表5、表6与表4中理论解及拟膜梁数值解发现,对应节点处的绝对误差基本一致.这表明结构均匀温度变化下,理论解与拟膜梁数值解的绝对误差并非由热膨胀造成.这也表明结构的热弹性参数(表 3)结果正确.
4 结 论
上述数值分析表明,二维网格结构胞元的拟膜热膨胀系数解答正确,进而可知拟膜的弹性参数的温度相关性正确.由数值解还可看出,结构在不同温度下变形差异显著.对于实际网格结构,在室外温度变化条件下,有必要考虑结构的热荷载才能更准确的预测结构变形.
本文仅给出了考虑均匀热荷载作用下结构受力变形问题.原因之一在于结构往往处于几乎均匀的温度条件下.其二,瞬态热问题涉及拟膜的热传导系数[20],笔者将在未来的工作中予以考虑.
附 录
将文中式(10)和(11)代入式(4)可得
(A1)
即
(A2)
或者
(A3)
记
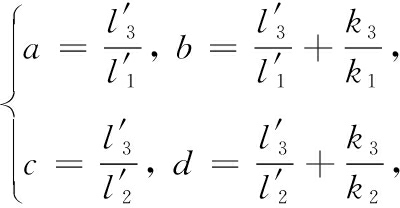
(A4)
则式(A3)可转化为
(a2+c2-a2c2)+2[ab+cd-(a2cd+abc2)]ε3+
(A5)
当线应变小于等于5%(小变形)时,可得线性近似解,即
(A6)
当线应变小于等于10%(中等程度变形)时,可得二次近似解,即
(A7)
其中

(A8)
本文选用线性近似解.
致谢 本文作者衷心感谢西北农林科技大学“博士启动金”(2452016176)对本文的资助.
参考文献(References):
[1] 董石麟, 夏亨熹. 正交正放类网架结构的拟板(夹层板)分析法(上)[J]. 建筑结构学报, 1982, 3(2): 14-25.(DONG Shilin, XIA Hengxi. Analysis of orthogonal and ortho-laid space truss as equivalent (sandwich) plate (part I)[J]. Journal of Building Structures, 1982, 3(2): 14-25.(in Chinese))
[2] 董石麟, 夏亨熹. 正交正放类网架结构的拟板(夹层板)分析法(下)[J]. 建筑结构学报, 1982, 3(3): 14-22.(DONG Shilin, XIA Hengxi. Analysis of orthogonal and ortho-laid space truss as equivalent (sandwich) plate (part II)[J]. Journal of Building Structures, 1982, 3(3): 14-22.(in Chinese))
[3] 阎军, 程耿东, 刘书田, 等. 周期性点阵类桁架材料等效弹性性能预测及尺度效应[J]. 固体力学学报, 2005, 26(4): 421-428.(YAN Jun, CHENG Gengdong, LIU Shutian, et al. Prediction of equivalent elastic properties of truss materials with periodic microstructure and the scale effects[J]. Acta Mechanica Solida Sinica, 2005, 26(4): 421-428.(in Chinese))
[4] 张卫红, 骆金威, 戴高明, 等. 周期性多孔材料等效剪切模量与尺寸效应研究[J]. 力学学报, 2011, 43(1): 144-153.(ZHANG Weihong, LUO Jinwei, DAI Gaoming, et al. Numerical predictions of effective shear modulus and size effect for periodic cellular materials[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(1): 144-153.(in Chinese))
[5] 胡更开, 郑泉水, 黄筑平. 复合材料有效弹性性质分析方法[J]. 力学进展, 2001, 31(3): 361-393.(HU Gengkai, ZHENG Quanshui, HUANG Zhuping. Micromechanics methods for effective elastic properties of composite materials[J]. Advances in Mechanics, 2001, 31(3): 361-393.(in Chinese))
[6] HASSANI B, HINTON E. A review of homogenization and topology optimization I: homogenization theory for media with periodic structure[J]. Computers and Structures, 1998, 69(6): 707-717.
[7] GIBSON L J, ASHBY M F. Cellular Solids: Structure and Properties[M]. Cambridge University Press, 1997.
[8] TOLLENAERE H, CAILLERIE D. Continuous modeling of lattice structures by homogenization[J]. Advances in Engineering Software, 1998, 29(7/9): 699-705.
[9] OSTOJA-STARZEWSKI M. Lattice models in micromechanics[J]. Applied Mechanics Reviews, 2002, 55(1): 35-60.
[10] WADLEY H N G, FLECK N A, EVANS A G. Fabrication and structural performance of periodic cellular metal sandwich structures[J]. Composites Science and Technology, 2003, 63(16): 2331-2343.
[11] ABOUDI J, GILAT R. Micromechanical analysis of lattice blocks[J]. International Journal of Solids and Structures, 2005, 42(15): 4372-4392.
[12] HUTCHINSON R G, FLECK N A. The structural performance of the periodic truss[J]. Journal of Mechanics and Physics of Solids, 2006, 54(4): 756-782.
[13] 周加喜, 邓子辰. 类桁架夹层板的等效弹性常数研究[J]. 固体力学学报, 2008, 29(2): 187-192.(ZHOU Jiaxi, DENG Zichen. On the effective elastic constants of truss-core panel[J]. Chinese Journal of Solid Mechanics, 2008, 29(2): 187-192.(in Chinese))
[14] 张洪武, 吴敬凯, 付振东. 周期性点阵桁架材料力学性能分析的一种新的多尺度计算方法[J]. 固体力学学报, 2011, 32(2): 109-118.(ZHANG Hongwu, WU Jingkai, FU Zhendong. A new multiscale computational method for mechanical analysis of periodic truss materials[J]. Chinese Journal of Solid Mechanics, 2011, 32(2): 109-118.(in Chinese))
[15] 梁军, 黄富华, 杜善义. 周期性单胞复合材料有效弹性性能的边界力方法[J]. 复合材料学报, 2010, 27(2): 108-112.(LIANG Jun, HUANG Fuhua, DU Shanyi. Boundary force method to predict the effective elastic properties of periodical unit cell composite material[J]. Acta Materiae Compositae Sinica, 2010, 27(2): 108-112.(in Chinese))
[16] 史姣, 蔡坤, 王正中. 拟膜分析法及应用[J]. 应用基础与工程科学学报, 2008, 16(5): 749-756.(SHI Jiao, CAI Kun, WANG Zhengzhong. Pseudo-membrane method and its application[J]. Journal of Basic Science and Engineering, 2008, 16(5): 749-756.(in Chinese))
[17] 蔡坤, 陈飙松, 张洪武. 二维连续体结构的拓扑和材料一体化设计[J]. 应用基础与工程科学学报, 2008, 16(1): 92-102.(CAI Kun, CHEN Biaosong, ZHANG Hongwu. Integrative design of topology and material of two-dimensional continuum structures[J]. Journal of Basic Science and Engineering, 2008, 16(1): 92-102.(in Chinese))
[18] 蔡坤, 史姣. 含周期性索-杆胞元的二维网格结构拟膜分析[J]. 工程力学, 2011, 28(10): 27-33.(CAI Kun, SHI Jiao. Pseudo-membrane method for two-dimensional lattice structure with periodic cable-link cells[J]. Engineering Mechanics, 2011, 28(10): 27-33.(in Chinese))
[19] 吴世平, 唐绍锋, 梁军, 等. 周期性复合材料热力耦合性能的多尺度方法[J]. 哈尔滨工业大学学报, 2006, 38(12): 2049-2053.(WU Shiping, TANG Shaofeng, LIANG Jun, et al. Multi-scale method for thermo-elasticity properties of composite materials with small periodic configuration[J]. Journal of Harbin Institute of Technology, 2006, 38(12): 2049-2053.(in Chinese))
[20] 张卫红, 汪雷, 孙士平. 基于导热性能的复合材料微结构拓扑优化设计[J]. 航空学报, 2006, 27(6): 1229-1233.(ZHANG Weihong, WANG Lei, SUN Shiping. Topology optimization for microstructures of composite materials based on thermal conductivity[J]. Acta Meronautica et Astronautica Sinica, 2006, 27(6): 1229-1233.(in Chinese))
引用本文/Cite this paper:
张朝晖, 李宝辉, 史姣. 二维周期性单胞网格结构的等效热弹性分析[J]. 应用数学和力学, 2018, 39(6): 714-727.
ZHANG Zhaohui, LI Baohui, SHI Jiao. Equivalent thermo-elasticity analysis of 2D lattice structures with periodic unit cells[J]. Applied Mathematics and Mechanics, 2018, 39(6): 714-727.