引 言
在工程研究中经常会遇到层合材料瞬态传热的问题[1-3].这些材料每层的热物理参数一致,但是每层之间又各不相同.层合材料因其本身的非线性,在求解瞬态传热的温度场时常采用数值方法[4-6].主要的研究可归结如下:
2010年盛宏玉、李和平等运用状态空间理论,建立了时域空间内的差分方程,分析了层合材料传热问题[7].2011年蓝林华、富明慧等将层合材料的传热问题转化为在时间域内的常微分方程问题,给出了一种有效的解法[8].2011年李金娥等对某一双层结构进行研究,建立了Fourier(傅里叶)和非Fourier层合材料传热差分方程,研究了其温度场和热应力情况[9].2012年富明慧等利用半解析精细积分法求解了层合圆柱体的三维温度场[10].2012年Liu等利用Laplace(拉普拉斯)变换的方法研究了三层结构传热的问题[11].2014年Movahedian等利用指数函数法研究了层合材料的传热问题[12].2016年Mohajer等利用数值方法研究了层合材料传热的非Fourier问题[13].
从文献分析可以看出,针对层合材料,求解一般运用有限元和有限差分等数值方法.本文针对层合材料,基于微分思想,结合分离变量法求解了其瞬态传热问题的半解析解.并且利用此方法对某三层结构的传热问题进行了算例分析,将结果和有限元法求得的结果进行了对比验证,讨论了几个参数对温度场的影响.
1 模 型 建 立
问题的几何模型如图1所示,在层合材料表面进行q(t)的热流量加热的同时进行流体冷却.流体的温度为Tf,流体和层合材料表面的对流换热系数为h0,在层合材料另一端的温度为fn(t)=T0.层合材料第n层密度为ρn,第n层的比热容为cn,第n层热传导系数为kn,Tn为层合材料第n层的瞬时温度函数.t为时间变量,x为厚度方向位置变量,同时考虑材料内部产热与换热问题,产热量为Qn,第n层的换热系数为hn,第n层的基础换热温度为Textn,Tina为材料的初始温度.

图1 几何模型
Fig. 1 The geometrical model
控制方程为[14]
(1)
相应的边界条件为,当x=0时
(2)
当x=ln时
Tn(ln,t)=fn(t)=T0.
(3)
相应的初始条件为
Tn(x,0)=Tina.
(4)
2 求 解 思 路
对于多层材料传热问题,如果满足第1节描述的边界条件和初始条件,求解的温度场情况应该如图2(a)所示.材料表面因受到恒定热流量加热和流体冷却,温度逐渐上升.各层交界处的温度也逐渐上升,交界处的温度变化应如图2(b)所示.第1层和第2层温度随时间变化的函数记为f1,2(t),由微分思想可知如果Δt足够小,可近似为f1,2(t)=v1,2t(其中v1,2为第1、2层交界温度随时间变化曲线的近似直线段的斜率).此时对于第一层在[0,Δt]时间内,两个边界条件已知,初始条件已知,因此可以利用分离变量法求解第一层的温度场解析式,其中v1,2未知.同理,[0,Δt]时间内,设第n-1层和第n层温度随时间变化的函数为fn-1,n(t)=vn-1,nt(其中vn-1,n为第n-1层和第n层交界温度随时间变化曲线的近似直线段的斜率),可求解第n层的温度场解析解,其中vn-1,n未知.然后根据热传导时两层交界处必须满足温度相等和能量平衡,可列出n-1个方程的方程组,求解此方程组可求得vn-1,n,进一步可求解各层在[0,Δt]时间内的解析解.在求解出[0,Δt]时间内的温度场解析解后,以Δt时刻为初始条件,进一步求解第二个[0,Δt]时间内的解析解.以此循环,可求得整个时间域的半解析解.

(a) 温度场示意图 (b) 交界处温度变化
(a) Schematic diagram of the temperature field (b) Temperature variation at the interface
图2 方法原理示意图
Fig. 2 Schematic diagram of the method
3 公 式 推 导
为表述简单,本文只推导在第1个[0,Δt]时间内的解析解,第i个时间段的推导过程和第1个时间段的过程一致.
3.1 第一层解析解
对于第1层,在[0,Δt]时间内,相应的控制方程和边界条件可表示如下:
(5)
当x=0时
(6)
当x=l1时
T1(l1,t)=f1,2(t)=v1,2t,
(7)
相应的初始条件为
T1(x,0)=Tina.
(8)
因为此偏微分方程为非齐次,在求解时需要先对边界条件进行齐次化.在此令
T1(x,t)=v1(x,t)+w1(x,t),
(9)
(10)
将式(9)代入式(5)可得
(11)
其中
(12)
构造的函数w1(x,t)满足
(13)
w1(l1,t)=f1,2(t).
(14)
结合式(6)、(7)、(13)、(14)可知
(15)
v1(0,t)=0.
(16)
由式(8)、(9)可知
v1(x,0)=Tina-w1(x,0).
(17)
在将边界条件齐次化之后需对其分离变量,式(11)的特征方程为
(18)
根据分离变量法的思想,式(18)的试探解为
v1(x,t)=Y1(x)G1(t).
(19)
将原问题转化为本征函数和本征值的问题,如果本征函数满足正交特性即可将其解耦,将式(19)代入式(18)中可得到
(20)
(21)
将式(19)代入式(15)、(16)可得
(22)
Y1(l1)=0.
(23)
结合式(20)、(22)、(23)可得本征函数为
(24)
其中本征值λm为式(25)的正根:
(25)
本征函数Ym(x)满足式(26),所以其满足正交特性:
(26)
式中
此时令
(27)
将式(27)代入式(11)并将其两端在[0,l1]内积分可得
(28)
其中
(29)
式(28)的解为[15]
(30)
其中
(31)
(32)
至此
(33)
3.2 第n(n≥2)层解析解
与3.1小节同样的过程,可求得第n层解析解,可表示为
(34)
其中

(35)
(36)
![]() 为式(36)的正根.
为式(36)的正根.
(37)
(38)
(39)
(40)
(41)
δn,m=![]() Yn,mYn,kdx=
Yn,mYn,kdx=
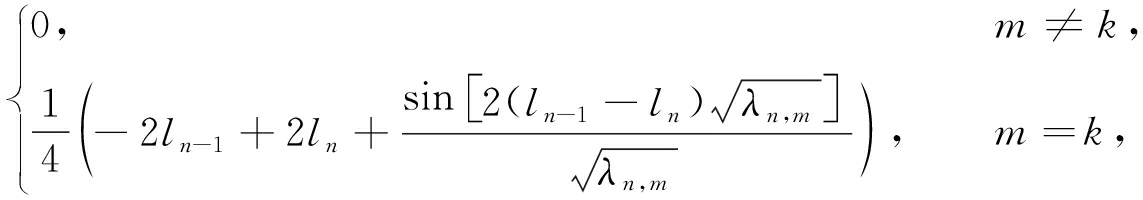
(42)
(43)
3.3 确定vn-1,n的值
在求得各层在第1个[0,Δt]时间内的解析解后,根据各层交界处的温度相等、能量平衡,可得
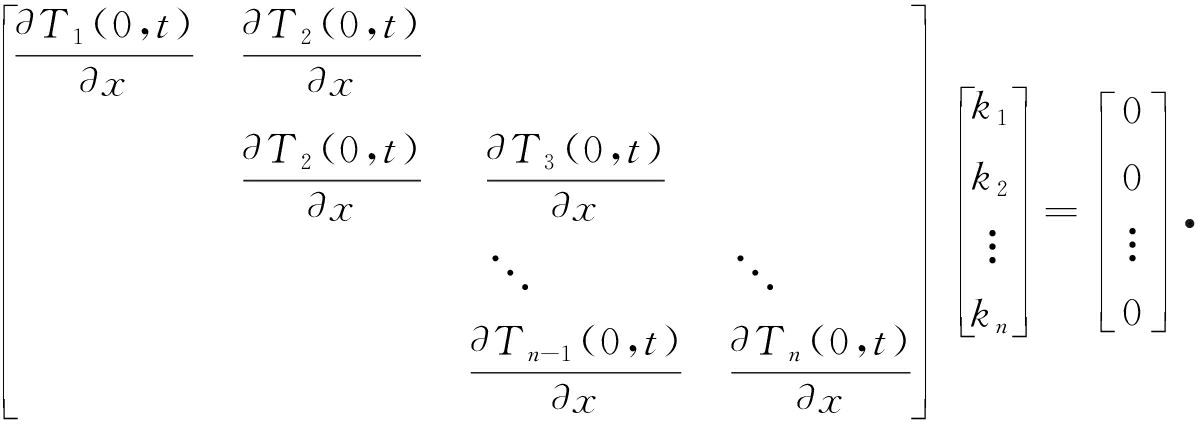
(44)
取微小时间段Δt,将t=Δt代入式(44)可得
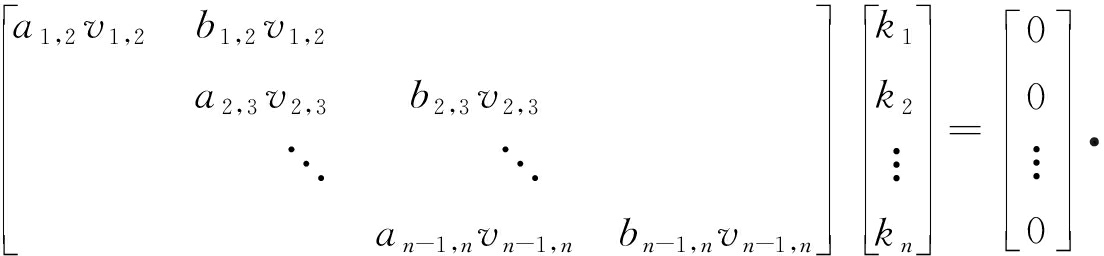
(45)
此时式(45)中an-1,n和bn-1,n均为常数.求解式(45)即可得到vn-1,n的值.
在求得第1个[0,Δt]时间内的温度场之后可以第1段Δt时刻作为初始条件,继续求解第2个[0,Δt]时间内的温度场,直至求解出整个时间域内的温度场.
4 算 例 分 析
在此以某三层结构为例验证方法的正确性,为使结果具有可比性,各参数取值按文献[14]中[14,16]的取值.该文献用有限元法和有限差分法研究了某三层结构传热问题.具体参数经过换算后如表1所示.
图3表示了不同时刻温度沿着x方向的分布曲线(各参数取值为:h0=10 W/(m2·℃);Tf=20 ℃;h2=2×105 W/(m2·℃)).从图中可以看出在t=15 s时,利用本文计算的结果和利用有限元方法计算的结果完全一致.在利用有限元法和本文方法求解过程中发现:有限元法经过多年的发展,根据有限元基本理论产生了很多商业软件,这些软件的计算精度和效率都很高.但是有限元的算法在计算过程中将整个区域进行分解,将实际问题进行简化,得到的是数值解.本文的方法完全按照解析解的思路推导,物理意义更加明确,程序编写也较简单,相对于封装于商业软件的有限元法更容易对其修改而适应其他不同情况.
从图中还可以看出随着加热时间增加,层合材料内部温度逐渐增加,因材料各层参数不一致,所以三层材料温度分布趋势亦有区别,计算结果符合实际物理现象.
表1 层合材料参数
Table 1 Parameters of the layered structure

图4表示了层合材料表面温度随时间变化的情况.曲线A和B分别为本文方法计算的结果和有限元方法计算的结果,二者完全一致.比较曲线A(各参数取值为:h0=10 W/(m2·℃);Tf=20 ℃;h2=105 W/(m2·℃))和曲线C(各参数取值为:h0=10 W/(m2·℃);Tf=20 ℃;h2=2×105 W/(m2·℃))发现h2越大温度上升越慢,因为h2为第二层内部换热系数.算例中,基础温度Text2为37 ℃不变.在材料表面加热后,第二层材料温度T2升高相对于基础温度会有一个差值T2-Text2,此时内部换热系数越大则h2(T2-Text2)越大,内部损失热量越多,温度上升越缓慢.
图3 温度沿x方向分布 图4 结构表面温度随时间变化情况
Fig. 3 The temperature distribution along x-axis Fig. 4 The temperature variation at the structural surface
比较曲线A和D(各参数取值为: h0=60 W/(m2·℃); Tf=20 ℃;h2=105 W/(m2·℃))发现结构表面的对流换热系数越大温度上升越缓慢.比较曲线D和E(各参数取值为: h0=60 W/(m2·℃);Tf=0 ℃;h2=105 W/(m2·℃))发现冷却流体温度越低,温度上升越缓慢.这些计算结果和实际的物理现象均符合.可以推断计算结果是合理的.
5 结 论
针对层合材料瞬态传热问题,本文做了如下的研究:
1) 基于微分思想,将层合材料交界处的温度变化曲线在微小时间段内近似为直线后利用分离变量法对各微小时间段的温度场进行了求解,进而求得了整个时间域内的温度场.
2) 用本文的方法对某三层材料传热问题进行了分析,计算结果符合实际物理现象并且和有限元方法计算结果一致,进而验证了该方法的正确性.
该方法基于分离变量法推导,物理意义较有限元法更明确,容易稍做修改后解决其他不同情况的问题.
参考文献(References):
[1] WANG B L, CUI Y J. Transient inter laminar thermal stress in multi-layered thermoelectric materials[J]. Applied Thermal Engineering, 2017(2): 55-67.
[2] KUMAR D, KUMAR P, RAI K N. A study on DPL model of heat transfer in bi-layer tissues during MFH treatment[J]. Computers in Biology & Medicine, 2016, 75(2): 160-172.
[3] MATSUMOTO N, OKUNO T, OBARA H, et al. Multi-layer heat conduction analysis using SPH method[J]. Transactions of the Japan Society of Mechanical Engineers, 2016, 82(3): 77-82.
[4] LU S, LIU J, LIN G, et al. Modified scaled boundary finite element analysis of 3D steady-state heat conduction in anisotropic layered media[J]. International Journal of Heat & Mass Transfer, 2017, 108(1): 2462-2471.
[5] 刘芳, 施卫平. 用格子Boltzmann方法模拟非线性热传导方程[J]. 应用数学和力学, 2015, 36(11): 1158-1166.(LIU Fang, SHI Weiping. Simulation of the nonlinear heat conduction equation with the lattice Boltzmann method[J]. Applied Mathematics and Mechanics, 2015, 36(11): 1158-1166.(in Chinese))
[6] 詹涌强, 张传林. 解抛物型方程的一族高精度隐式差分格式[J]. 应用数学和力学, 2014, 35(7): 790-797.(ZHAN Yongqiang , ZHANG Chuanlin. A family of high accuracy implicit difference schemes for solving parabolic equations[J]. Applied Mathematics and Mechanics, 2014, 35(7): 790-797.(in Chinese))
[7] 盛宏玉, 李和平, 叶建乔, 等. 介质热传导瞬态分析的一种新半数值解法[J]. 合肥工业大学学报(自然科学版), 2010, 33(5): 709-712.(SHENG Hongyu, LI Heping, YE Jianqiao, et al. A new semi-numerical approach for the transient heat conduction analysis of laminated medium[J]. Journal of Hefei University of Technology(Natural Science), 2010, 33(5): 709-712.(in Chinese))
[8] 蓝林华, 富明慧, 刘祚秋. 结构瞬态热传导方程的一种精细解法[J]. 中山大学学报(自然科学版), 2011, 50(5): 1-6.(LAN Linhua, FU Minghui, LIU Zuoqiu. A precise solution of transient heat conduction equation for laminate structure[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2011, 50(5): 1-6.(in Chinese))
[9] 李金娥, 王保林, 常冬梅. 材料的非傅里叶热传导及热应力[J]. 固体力学学报, 2011, 32(S1): 248-253.(LI Jin’e, WANG Baolin, CHANG Dongmei. Non-Fourier heat conduction and thermal stress of non-Fourier heat conduction an thermal stress of layered materials[J]. Chinese Journal of Solid Mechanics, 2011, 32(S1): 248-253.(in Chinese))
[10] 富明慧, 陈焯智. 层合圆柱三维温度场分析的半解析-精细积分法[J]. 应用力学学报, 2012, 29(1): 15-20.(FU Minghui, CHEN Chuozhi. The semi-analytical precise integration method for the analysis of three dimensional temperature field of laminated cylinders[J]. Chinese Journal of Applied Mechanics, 2012, 29(1): 15-20.(in Chinese))
[11] LIU K C, WANG Y N, CHEN Y S. Investigation on the bio-heat transfer with the dual-phase-lag effect[J]. International Journal of Thermal Sciences, 2012, 58: 29-35.
[12] MOVAHEDIAN B, BOROOMAND B. The solution of direct and inverse transient heat conduction problems with layered materials using exponential basis functions[J]. International Journal of Thermal Sciences, 2014, 77: 186-198.
[13] MOHAJER M, AYANI M B, TABRIZI H B. Numerical study of non-Fourier heat conduction in a biolayer spherical living tissue during hyperthermia[J]. Journal of Thermal Biology, 2016, 62: 181-185.
[14] XU F, LU T J, SEFFEN K A. Bio-thermomechanics of skin tissues[J]. Journal of the Mechanics & Physics of Solids, 2008, 56(5): 1852-1884.
[15] LIN S M, LI C Y. Analytical solutions of non-Fourier bio-heat conductions for skin subjected to pulsed laser heating[J]. International Journal of Thermal Sciences, 2016, 110: 146-158.
[16] LIU K C, CHEN H T, CHENG P J. Inverse investigation of non-Fourier heat conduction in tissue[J]. Journal of Thermal Biology, 2016, 21(2): 68-73.
引用本文/Cite this paper:
李细霞, 戴海燕, 李长玉. 基于微分思想的层合材料传热问题新解法[J]. 应用数学和力学, 2018, 39(6): 728-736.
LI Xixia, DAI Haiyan, LI Changyu. A new method for solving heat transfer problems of laminate materials based on the differential theory[J]. Applied Mathematics and Mechanics, 2018, 39(6): 728-736.