钟万勰1,2, 吴 锋1, 孙 雁2, 姚 征3
(1. 大连理工大学 工程力学系, 辽宁 大连 116023; 2. 上海交通大学 船舶海洋与建筑工程学院, 上海 200240; 3. 大连海事大学 交通运输工程学院, 辽宁 大连 116026)
(我刊编委钟万勰来稿)
水波的应用分析,通常是在Euler表示下进行的,见著作[1]以及许多其他著作.美国工程院院士梅强中的著作《水波动力学》[1]是他给中国提供的一个比较全方位的水波动力学著作,还有周培源先生写的序言.其中第七、八两章,讲非线性水波,是很认真的.当然,其思路也是基于流体力学传统的Euler表示法.但自从Russell在1834年观察到孤立波以来,当时的理论在Euler表示之下,却总也不能得到解释,成为一个严峻的问题.其间出现了现在还广泛使用的SVE方程也不能解释孤立波的存在.一直到1895年出现了KdV方程,方才可以解释孤立波的存在.在著作[1]的第七章,也给出了KdV方程.然而KdV方程给出的孤立波理论, 只能用于单方向的传播, 其相反方向传播的孤立波还是表达不了, 这说明违反了对称性原理, 因此不够理想.
然而,将位移法分析引入,并用于浅水波的分析,完全可以成功,详见文献[2-7].
著作[1]名《水波动力学》,我们首先看到动力学,然后冠之以水波的范围.既然是动力学,则辛对称性质就与之密切关联.大数学家Weyl[8]在1939 提出辛对称时写道:“The name ‘complex group’ formerly advocated by me in allusion to line complexes, … has become more and more embarrassing through collision with the word ‘complex’ in the connotation of complex number. I therefore propose to replace it by the Greek adjective ‘symplectic’.” 这里为了避免“complex”容易产生的混淆,特地引入了希腊形容词“symplectic”.表明“symplectic group”,辛群之意.辛对称性是动力学解的本质.然而《水波动力学》对辛对称群却完全没有考虑.这是一个欠缺,所以本文的标题是《保辛水波动力学》,以突出动力学的本来性质.
《水波动力学》是很认真的水波著作,继承了传统的以速度为基本未知数的Euler描述体系在水波方面的发展.然而这是不充分的,尤其是进入到非线性波的分析方面.本文一改传统思路,采用以位移为基本未知数,就是以动力学的辛对称群为基础的动力学体系来讲述问题随后的发展.既然采用了不同的体系、不同的基础、不同的未知函数,还能够继续下去,当然也会有不完全相同的结果.而且因为考虑了辛对称群的基础,以及冯康院士等[9]提出差分离散要保辛,本文还能够将以往课题的困难,予以解决推进;尤其有数值解法,可在计算机上执行求解,以适应时代科技的需要,比以往体系好多了.
首先要看辛对称群的出现,这是在动力学范畴内的表达.而在结构力学方面,则《计算结构力学与最优控制》出现了其模拟关系,而这是先从离散的角度讲述的.《力、功、能量与辛数学》则从结构力学的角度,将离散的传递辛矩阵,讲清楚了.只有传递辛矩阵才能构成传递辛矩阵群,而不是一个解向量.抽象一点讲,传递辛矩阵是一个算子.
Russell在1834年观察到有浅水孤立波,随后有许多研究.线性理论对此无能为力,只能采用非线性的理论.著作[10]第三章讲述了浅水之中的长波,推导了经常使用的传统SVE理论方程却不能得到浅水孤立波的解.一直到1895年发表的KdV理论的解方才能得到一个方向正向传播的浅水孤立波解.然而反方向传递的浅水孤立波却不能得到,这表明对称性已经被破坏.从其推导过程以及波速的结果看,并不理想,也详见著作[1].
笔者采用位移法,采纳了浅水波理论的基本假定[3-4]后,将垂直方向的动力因素加入[2-3, 11],就可将双方向传播的浅水孤立波予以分析求解,不但给出了正确的波速,而且也求解了孤立波交会的情况等许多问题[5, 7].这表明对称性得到了保持.因为采用了基本的最小作用量变分原理进行分析推导,故动力学的基本性质得以保持.
但这些是在浅水波的基本假定(u(x,z,t)=u(x,t),即刚性平移)之下得到的.在此基本假定下,根据不可压缩条件就得到了水面,而随之就得到势能.采用了不可压缩条件,非线性也随之而来.具体的推导过程在著作[3]中5.9小节已经给出.因此孤立波必然伴随着非线性.然而由于当时著作[3]并未注重流体力学方面的进展,只是展示了辛数学方法的广泛适应性就结束了.现在重新审视水波动力学方面的问题,从动力学的角度看,以往未能加以重视的辛对称群,以及数值分析要保辛等方面,就成为新的因素,很可能可以走出一条自己的辛路子来.
将孤立波通过动力学最小作用量变分原理加以分析,辛对称群、保辛等一整套内容,就成为应有之义,显示出其重要性了.首先,浅水波的积分不只是出现孤立波,选用不同的积分常数,还有椭圆余弦波.这些在文献[7]等之中已经讲过了,但还不够完整.椭圆余弦波是非线性周期性的,而且在波幅η0很小时会与Stokes的线性理论波相衔接;而在波峰相距L很大时,又会与孤立波相衔接.所以说,椭圆余弦波是一种两端会与不同的波浪理论想衔接中间状态的浅水周期波.笔者关注椭圆余弦波,正是因为它的中间态势.
浅水波的椭圆余弦波虽然要求波幅远小于水深η0≪h,然而毕竟是考虑了非线性因素的.当波幅η0非常小时,它就会逼近线性分析解.
本文采用位移描述水波的运动,在水平方向和竖直方向的坐标分别记为(x,z),时间记为t,水平方向和竖直方向的位移分别记为u(x,z,t)和w(x,z,t).水假设无黏,密度记为ρ,水的压强记为p(x,z,t).重力加速度记为g.
水深设为常数,记为h,水底为z=-h.静止水面记为z=0,变形后的水面记为z=w(x,0,t)=η(x,t).波幅记为η0,即为水面波η(x)的最大值.另外将波高记为A,表示水波波峰与波谷之间的相对高度,即为η(x)的最大值和最小值之差.波长记为L.
以变量u(x,z,t)为例,为表示方便,u(x,z,t)对某个自变量求偏导时,以下标表示.如u(x,z,t)对x和z的偏导分别记为ux和uz,但u(x,z,t)对时间t的偏导记为![]() 其余变量的偏导采用相同标记方法.
其余变量的偏导采用相同标记方法.
浅水问题采用刚性平移假定,即u(x,z,t)=u(x,t),该假定只能在浅水时适用.采用位移法,考虑水的不可压缩性,在不考虑任何假定的情况下,位于(x,z)的质点在水平方向和竖直方向分别产生位移u(x,z,t)和w(x,z,t),移动后的位置为(x+u,z+w).根据Jacobi矩阵,显然有不可压缩条件为
(1+wz)(1+ux)-uzwx=1,
(1)
其中u(x,z,t),w(x,z,t)分别为水平方向和竖直方向的位移(见著作[7]中式(2.1.3)).但因为刚性平移假定uz=0,式(1)的约束成为(1+wz)(1+ux)=1,乘出来有ux+wz(1+ux)=0,从而wz=-ux/(1+ux).设水底为z=-h,在水底有w=0的边界条件,积分一次就得到了w(x,z,t)的表达式.而波面就是η0=w(x,0,t).从而Lagrange函数的重力势能就得到了.以上考虑的是浅水孤立波的一端.还要从线性理论的另一端进行考虑.当然线性理论就不采用刚性平移u(x,z,t)=u(x,t)的假定了.
在传统流体力学Euler表示求解时,只出现速度未知数.求解速度势一直是主流的方法.在Euler表示下求解,在平稳流(steady state flow)问题方面是有很大优点的.然而水波问题,显然是非平稳流.而与速度势对偶,改换到以位移为基本未知数后,基本未知数是位移u,w,体系变化了,就可以用动力学最小作用量变分原理来推导基本方程.
利用最小作用量变分原理分析水波问题,首先分析动能.二维水波问题的动能可写为
(2)
其中ρ为水密度.势能为重力势能,可表示为
(3)
再考虑不可压缩条件,还有不可压缩条件的修正项:
(4)
其中p是压强,也是Lagrange参数,压强p与约束条件为对偶变量,不得不考虑.根据最小作用量原理,推得水波动力学方程可以写为
(5)
其中
p=-ρg(z+w)+β.
(6)
即将压强p分解为重力压强-ρg(z+w)和波动产生的动压强β(x,z,t)之和.动压强β(x,z,t)是内力,在势能表达式之中是不出现的.
考虑无旋水波问题,需给出位移形式的无旋条件.方程组(5)中有两个方程,有u,w和β共3个变量,因此可以将β消去.首先利用不可压缩条件(1),可将方程(5)写为
(7)
将上述方程组中第一、二两式分别对z和x求偏导之后再相减,并考虑到初始水波是无旋的特点,可得
(8)
此式即为位移形式的无旋条件,早在著作[12]的式(12.1. 4)中就已经给出.
将β消去后,根据不可压缩条件(1)和无旋条件(8)就可以分析水波的运动.
式(1)和(5)是水波的控制方程.式(1)是不可压缩条件, 而式(5)是水波的动力学微分方程, 除此之外分析水波问题还需边界条件.在水底z=-h处, 竖向位移为零,即w(x,-h,t)=0.水面z=0处要求压强p(x,0,t)=0,根据式(6)可得
β(x,0,t)=ρgw(x,0,t),
(9)
再将上式对x求偏导, 可得βx(x,0,t)=ρgwx(x,0,t), 结合式(7)可得到以纯位移表示的边界条件:
(10)
从分析的角度分析水波问题,最方便的就是线性理论的波.线性理论中,认为位移非常小,在约束方程之中可只保留速度的一次线性项,从而约束方程成为
ux+wz=0,
(11)
这样就有流函数ψ(x,z,t),可自动满足线性不可压缩条件(11):
u=-∂ψ/∂z,w=∂ψ/∂x.
(12)
对于无旋条件(10),考虑线性情况时,忽略高阶项,可得
(13)
这与Euler表示的水动力学相一致,然而其是在位移法基础下推导的.另一方面从水动力学讲,因为一般不考虑黏滞性,所以也不会产生旋涡,无旋条件是必然的.故有速度势函数φ(x,z,t):
(14)
以反映流动是无旋的,![]()
综合两方面,有∂φ/∂x=-∂ψ/∂z, ∂φ/∂z=∂ψ/∂x,其中![]() 分别为x,z方向的速度.这样,(φ,ψ)相互间是Cauchy-Riemann方程的一对对偶函数,可以用复变函数来描述.当然全部分别满足Laplace算子方程.只是可惜,它没有考虑非线性项的作用.本文采用位移法,在位移比较大时,就应当将不可压缩条件考虑进去.而将非线性项考虑进去后,方程(13)就不再成立了.
分别为x,z方向的速度.这样,(φ,ψ)相互间是Cauchy-Riemann方程的一对对偶函数,可以用复变函数来描述.当然全部分别满足Laplace算子方程.只是可惜,它没有考虑非线性项的作用.本文采用位移法,在位移比较大时,就应当将不可压缩条件考虑进去.而将非线性项考虑进去后,方程(13)就不再成立了.
按线性理论求解,对于矩形区域,则因无旋条件而有速度势函数φ(x,z,t).该势函数φ(x,z,t)满足Laplace方程.因此区域成为矩形,这样Laplace方程就可用分离变量法求解.当然这只能在波幅η0足够小时才成立,不能用于η0不够小的孤立波的解析.以上讲的只是线性理论.
线性理论时的解给出的是Stokes波,也可以选择流函数ψ(x,z,t)的Laplace方程用分离变量法求解.线性时位移可按流函数表示,即式(12).将式(12)代入无旋方程(13)可得到Laplace方程:
(15)
而在水底,则要求位移满足边界条件w(x,-h,t)=0,根据式(12)可知
(16)
在水面z=0处的边界条件也可将位移用流函数表示,即将式(12)代入边界条件(10),并忽略非线性高阶项,有
(17)
根据Laplace方程(15)和边界条件(16)、(17)即可求解.
水波的周期行波解,对于定性认识水波问题特别重要.如果求解行波,则流函数形式为
ψ(x,z,t)=Ψ(ξ,z),ξ=x-Ct,
(18)
其中C为波速.Ψ(ξ,z)与位移的关系是
于是Laplace方程和边界条件可以写为
(19)
水面z=0和水底z=-h的边界条件分别为
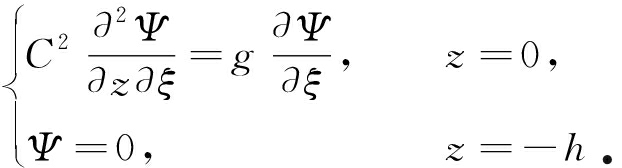
(20)
采用分离变量法求解上式,最终可得
(21)
再根据式(12)、(7)可得线性理论时的位移和压强为
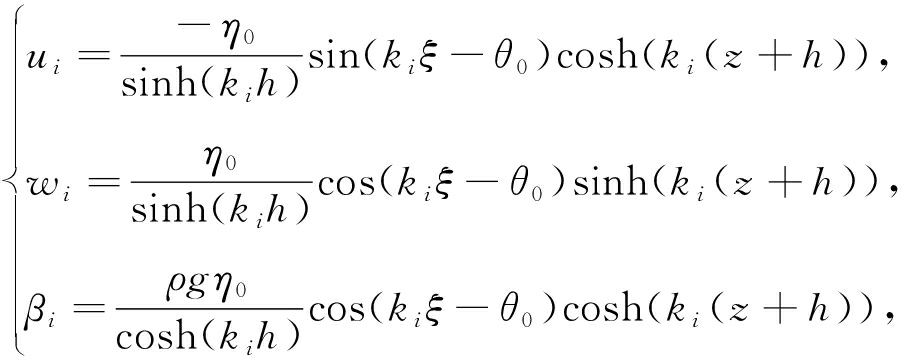
(22)
其中θ0是积分常数,η0是波幅.ki=2iπ/Li(i=1,2,…),Li为波长.这些解对于任何水深皆可运用,但只是线性理论的解.线性理论中,波的行进速度是
(23)
水波理论,只讲线性理论而不考虑非线性因素是不行的.观察到的浅水波,就是非线性的.因此不能停留在Laplace方程的求解,虽然这是非常漂亮的分析理论.非线性水波在表面上也常常表现出行波的形式,但非线性时的波速不同于线性波速,也不再适用线性时的式(22)了,非线性理论将在第4节讨论.
Russell早年观察到的浅水孤立波,这是线性理论所不能解释的.问题在于在水面附近,exp(kz)的因子还未能起重要作用,此时的水表面附近,由于波幅η0已经不是很小,不可压缩条件为非线性的因素将要起重要作用.因此不能再说方程(1)的非线性项可以忽略.再说浅水波,水底的z=-h,只能使kh很小,浅么,所以还是接近于1.浅水波还是要从波幅η0起作用而造成的非线性因素考虑.
按线性理论,水底是没有垂直速度的,解不能简单地采用很深的解,而应当考虑到水底的边界条件.按式(9)的解,当水深h比较小时,在0>z>-h的区域内,水平位移、速度沿深度变化很小.当kz≪1时,基本上是平移,这符合浅水波的基本假定.
线性理论本来是对于深水波讲的.如果kz≪1,则因为有函数cosh(k(z+h))的因子,当然在浅水的区域内,该cosh(k(z+h))基本上就没有什么变化,所以就支持了浅水波的基本假定.两套理论是可以互相衔接的.
然而KdV方程,著作[1]中7.4小节给出的一般形式,却不能达到保辛,而且只能在一个方向传播孤立波,有悖于对称性;而在线性波方面,本来双方向传递是对称的.因为这些全部是在Euler表示下描述的.
有鉴于此,文献[2-5]提出选择Lagrange坐标,以位移为基本未知数,并通过最小作用量变分原理,同样在浅水波基本假定下,推导出的浅水波方程,简单明了,并且双方向传播等对称性条件全部满足,还能达到保辛对称群的要求.在动力学中,对称性是具有根本重要意义的性质,以往的文献对此注意不够.海浪的周期性质是明显的,Stokes线性波就呈现出周期性质.而到浅水阶段,椭圆余弦波虽然非线性,却也是周期的,虽然不是正弦或余弦的形式.再说,从著作[1]的7.3小节开始,就是永形色散长波,色散表明不是余弦波的形式,余弦波是单色的,那是因为非线性之故.
笔者在之前的工作已经比较深入地研究了浅水波的位移描述理论[2-5, 7, 13],这里给予简单介绍.基本的位移浅水波方程可以写为
(24)
水面可以表示为
η=-hux/(1+ux)≈-hux.
(25)
浅水波理论给出的行波解是椭圆余弦波,可表示为
(26)
其中A为波高,指的是行波的波峰与波谷之差,L为波长,ε=A/h,
(27)
依据上式可以计算出m.
(28)
波速为
(29)
当考虑线性浅水理论时,行波退化为余弦形式:
(30)
《椭圆余弦波的位移法分析》[13]一文中分析指出:当A≤0.42h且Ur≤5.34-12.85A/h时(Ur为著名的Ursell参数),非线性比较弱,线性余弦波是椭圆余弦波的很好近似.当非线性较强时,解为椭圆余弦波,其实际包含了多种不同波数的线性余弦波,现在分析椭圆余弦波(26)的Fourier分解.在一个波长ξ∈[-L/2,L/2]内,将式(26)表示为Fourier级数的形式:
(31)
其中an为各阶余弦波的波幅,可表示为
(32)
求解an只能采用数值积分计算,其中涉及到椭圆函数则采用精细积分[3]计算,以保证精度.A=1 m,h=10 m,取L=50, 100, 200, 500 m计算得到的不同an列于下表1.
表1Fourier系数
Table 1 Fourier coefficients

从表1可以看到,当波长L=50 m时,非线性程度较弱,椭圆余弦波主要由第一阶余弦波构成,而第二阶波的波幅a2只有第一阶波波幅a1的3%.当波长L=500 m时,非线性很强,椭圆余弦波形状几乎接近孤立波(见图1).然而即便是在这种非线性很强的情况下,其Fourier分解中,第十阶波的波幅a10也只有第一阶波波幅a1的1%,第十五阶波的波幅a15也只有第一阶波波幅a1的0.04%,两者相差3个数量级,再往后更多的波可以忽略不计.表明采用Fourier分解求解时,不必采用很多项展开,而只要选择例如10~20项进行数值积分就可以了.
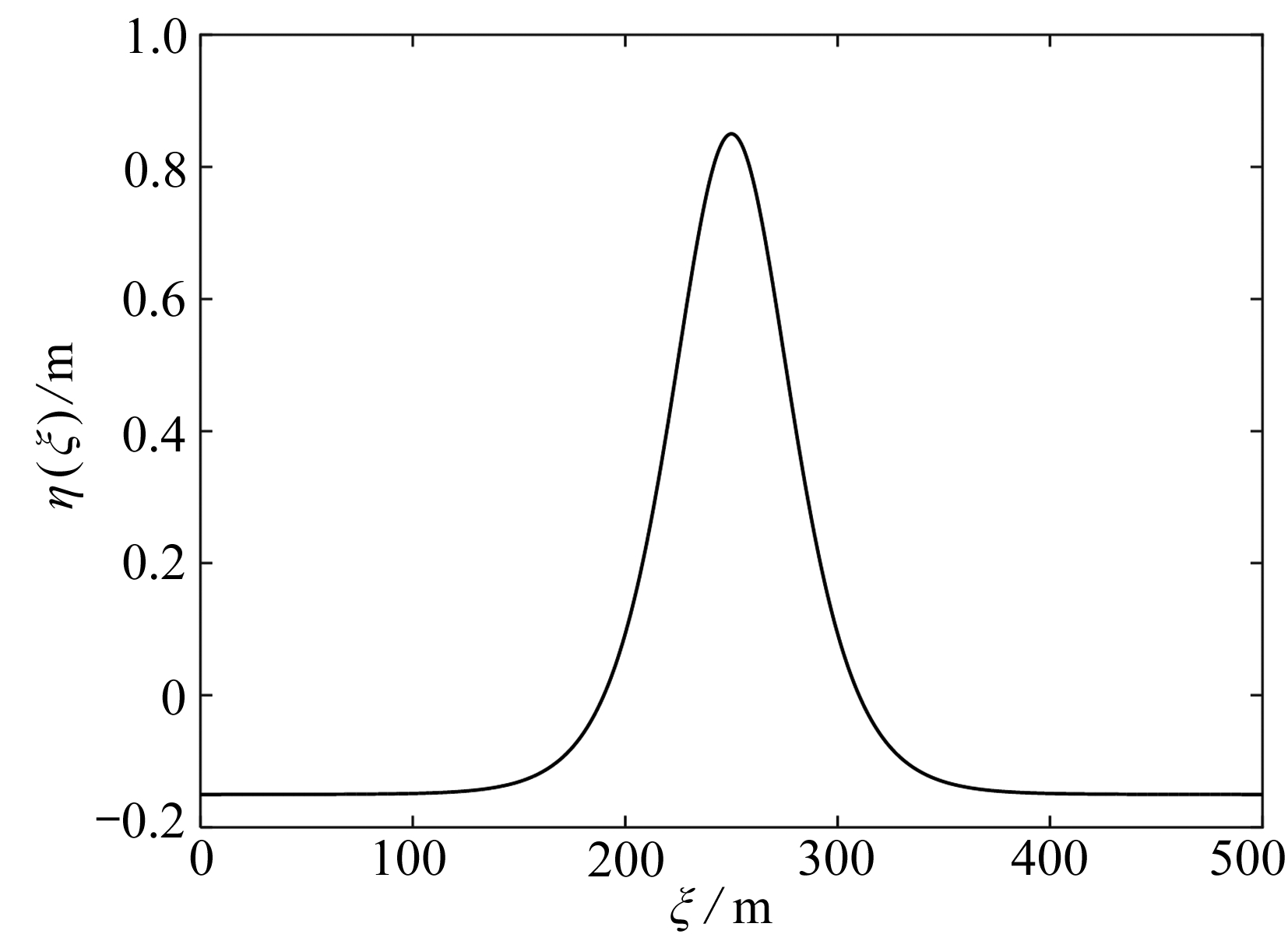
图1 椭圆余弦波(A=1 m,L=500 m)
Fig. 1 The cnoidal wave(A=1 m,L=500 m)
本文将限于在xOz的二维平面讲述.水波动力学问题,应当更进一步考虑三维问题,既然是动力学,同样的方法论也可推广到三维.然而那是以后再解决的课题了.
波浪理论到了非线性阶段,求解就非常困难,即使早已观察到的浅水孤立波,也引起了长时间争论.即使给出了KdV方程,也不甚理想;即动力学的对称性质,还没有顾及.
1968年,苏联学者Zakharov给出非线性三次方Schrödinger方程,以求解深水中的非线性波.当然这个思路也是在Euler表示体系下推导的.本文则是在位移法的基础上进行的;思路不同,已经分道扬镳了.然而,Zakharov的工作代表了以往大量工作基础的一个高峰,其结论有较大的启发性,即使在位移法表示下也可有所借鉴.例如,椭圆余弦波的周期性,那是因为基于其基本假定而得到的,在进入到深水区域时,其分析也还依然在xOz的二维平面雷同的周期区域进行.基于以前长期大量的观察,以及Zakharov的分析工作,位移法体系的分析还依然应当是在雷同的周期区域进行.基于基本假定,浅水椭圆余弦波的x方向的周期用L代表,根据L以及水深就可以确定波幅η0; 然而, 在xOz的二维平面则只能给出L以及水深; 然后, 通过求解非线性动力学方程, 以求解波幅, 波幅是怎么规定的等一些问题, 也要在求出数值解后再考虑其规定.周期L成为了求解时的一个基本参数.本文既要面对非线性方程还要给出恰当有效的数值求解法.
考虑非线性因素,并在确定了求解区域后,如何进行数值求解,是一个大问题.仅仅给出一套非线性方程,而不能数值求解,显然不能满足数值化时代的需求,“世界潮流,浩浩汤汤,顺之者昌,逆之者亡”,则前途堪忧.
用位移法进行数值分析,依然是针对周期波的.周期波表明了许多对称性.这可将数值分析的区域局限于半个周期,有利多了.在线性Stokes波的课题上,给出了波长L与周期的关系L=2π/k,k称为波常数.
而在非线性波的条件下,在一个周期内不是直接的单色波而是波形复杂的一个周期,例如椭圆余弦波,它在一个周期内是多个余弦合成的,给出的只能是一个周期L的波形;而不像线性理论那样,一定是单色的,这些概念必须很清楚.给出周期以后,就可使用Fourier展开,而得到各种颜色单色波的叠加.
式(12)表示的流函数ψ(x,z,t)只考虑了线性部分,而事实上非线性部分是非常重要的.因此不可压缩条件(1)的非线性部分,必须考虑进去.回顾位移法在浅水波基本假定的条件下,满足了不可约束条件,就得到了势能函数,并未采用流函数等手段.所以说,位移法推导中,水的不可压缩性是产生波浪不可缺少的因素.方程(1)可以写成
(33)
所以考虑非线性时的流函数为
(34)
上式也可写为
u=-ψz-uwz,w=ψx+uwx.
(35)
求解行波问题,令ψ(x,z,t)=Ψ(ξ,z),于是有
u=-Ψz-uwz,w=Ψξ+uwξ.
(36)
再将式(36)代入无旋条件(10)可得
(37)
其中
(38)
还有边界条件.在水底要求Ψ(ξ,-h)=0.将式(36)代入水面边界条件(10)可得
(39)
其中
(40)
将非线性项εc突出出来,是二次和以上的项,可以集中注意力对付它.
采用位移法的动力学系统,其动力学方程可以用最小作用量变分原理导出,而不是一定要走Laplace偏微分方程的路,虽然它是很有帮助的.线性理论的解从来是非线性理论的一个近似.既然到了非线性问题,该近似解可用来作为摄动迭代求解的出发点.这样就成为沿0<ξ<L方向的“波数域”Fourier展开了.
当然关于摄动的迭代求解还要在下文明确.摄动出发点还是线性理论未知函数的方程.方程(1)就给出了非线性的不可压缩条件,可以结合线性理论的基本解,再通过变分原理用保辛摄动的方法迭代求解.从水波的形状看,可以在(ξ,z)平面的0<ξ<L,0>z>-h柱形区域内,沿采用Fourier展开的“波数域”求解.
信号处理时,往往愿意在频域求解而不是在原来的时间域求解,现在0<ξ<L的长度域转换到波数域求解,是一样的道理.前面对于椭圆余弦波的Fourier分解,给出了直观的效果.
说到摄动法,当然有一些小量ε.基于该小量,一些摄动法教材马上就是Taylor级数展开.在SVE方程基础上,Boussinesq方法采用的就是Taylor级数展开的概念.但是加法摄动不符合保辛的要求.其实一概用Taylor级数展开,本来也是不必要的.数学方法中,除Taylor展开无穷级数外,还有无穷乘积的展开,它也可用于摄动的.在著作[3]的5.7小节,介绍了边界层的乘法摄动求解,就采用了乘法摄动.而根据辛对称群的要求,群内只有乘积而没有加法.所以现在更应当采用了.因为乘法符合辛对称群的性质.
当前面对非线性保辛摄动问题,难以直接对复杂的非线性问题求得其分析解.只能采用逐步逼近的解法,就要靠乘法摄动.
以上只是概念性的描述.还要有一系列的具体问题的算法予以支持,并且要收敛到真实解.基本方程依然可从非线性不可压缩条件给出.当然希望有精确的非线性变分原理,但就是给了变分原理仍不能数值求解,也是枉然.不如给出一系列的近似系统,其解能够保辛,解的合成是乘法.
具体地,既然非线性项εc是非线性变动函数,一下子不能给出,那么逐步逼近还是可能的.设计一系列的保辛算法予以逼近.
实际上,非线性就体现在εc之中.变分原理可为
(41)
变分原理推导出的就是Poisson方程
ΔΨξ=εc,
(42)
以及边界条件(39).其中εc和ε2为小量的给定函数.这是由不可压缩条件以及边界条件的非线性求得的.如果一下子就能给出这个给定的εc和ε2,那么求解一次就可得到Ψ(ξ,z),但难以做到.非线性方程的求解,迭代法几乎是必然的.迭代要给出具体算法.
线性理论的解可以作为非线性问题迭代的零次近似.此时的求解是认为εc=0的.此时得到了Ψ0(ξ,z),从而也有了零次近似的位移:
ui,0(ξ,z),wi,0(ξ,z),j=0.
进一步j=1次近似时,已经有零次近似的位移,于是将根据零次近似的位移代入εc的公式,得到j=1次近似的给定εc.求解式(42)的Poisson方程,得到Ψ1(ξ,z),从而有了j=1次近似的位移.也就是说,将上一次(第(j-1)次)得到的位移,用于计算下一次(第j次)迭代的εc;如此类推.松弛法(relaxation method)就是这么干的.
那么为什么说这是乘法摄动呢?因为Poisson方程是从变分原理(41)来的.其中εc认为是给定的函数,是不随变分函数Ψ(ξ,z)而变的.位移函数是Ψ(ξ,z)确定的,所以Ψ(ξ,z)具有位移的品质.设采用有限元法离散求解,根据有限元法常规,未知的Ψ成为节点上的向量.Ψ(ξ,z)变分函数将改变为由向量Ψ表示.以前线性分析时,得到一系列的波(i=1,2,…)是互相正交的,也即互相独立的,但非线性时互相独立的性质已经不能达到,它们是互相联系在一起的.只能逐步逼近.
Laplace方程ΔΨ(ξ,z)的算子离散给出的是ΨTDΨ/2,其中D是同维的对称正定矩阵,而给定εc得到的项则是同维的给定εc向量,它所产生的项是![]() 这样,离散后的泛函成为
这样,离散后的泛函成为
(43)
上式表示一个二次泛函,很明显这是一个二次的Hamilton函数.
按文献[5]第四章给出了Poisson括号为基础的Lie(李)代数讲述.用于当前,则Hamilton函数离散后给出的正是Lie代数,有限元法对于非线性Hamilton函数离散给出的正是Lie代数,还给出了具体验证.这里要指出,Lie代数并不排斥加法,所以Taylor级数展开等手段完全可以用于Lie代数体上.而离散后得到的二次Hamilton矩阵,符合文献[5]所述.
而当积分后,相当于对Lie代数体进行了指数运算,则得到的是Lie群.以前Lie代数的加法,成为辛Lie群的乘法,而辛Lie群则没有加法.故说对于辛Lie群的积分只可以用乘法摄动以达到保辛,而不能将加法摄动运用于辛Lie群.这方面一定要弄清楚.
第5节的深水波理论,理论上能包含第3节的线性水波解和第4节的椭圆余弦波.现在利用第4节的椭圆余弦波验证以上理论的正确性.非线性水波计算时,取波长L=30 m,初始迭代时线性水波的波幅取η0=0.1h.计算结果如图2所示.
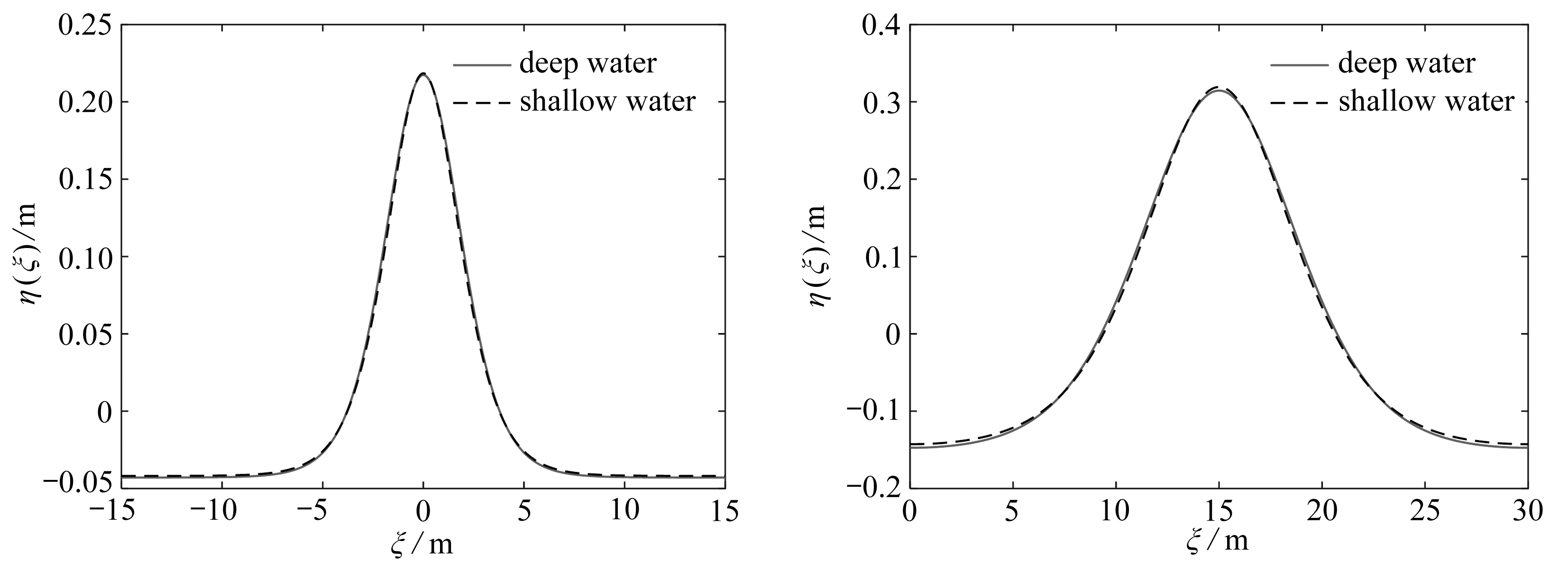
(a) h=1 m (b) h=2 m
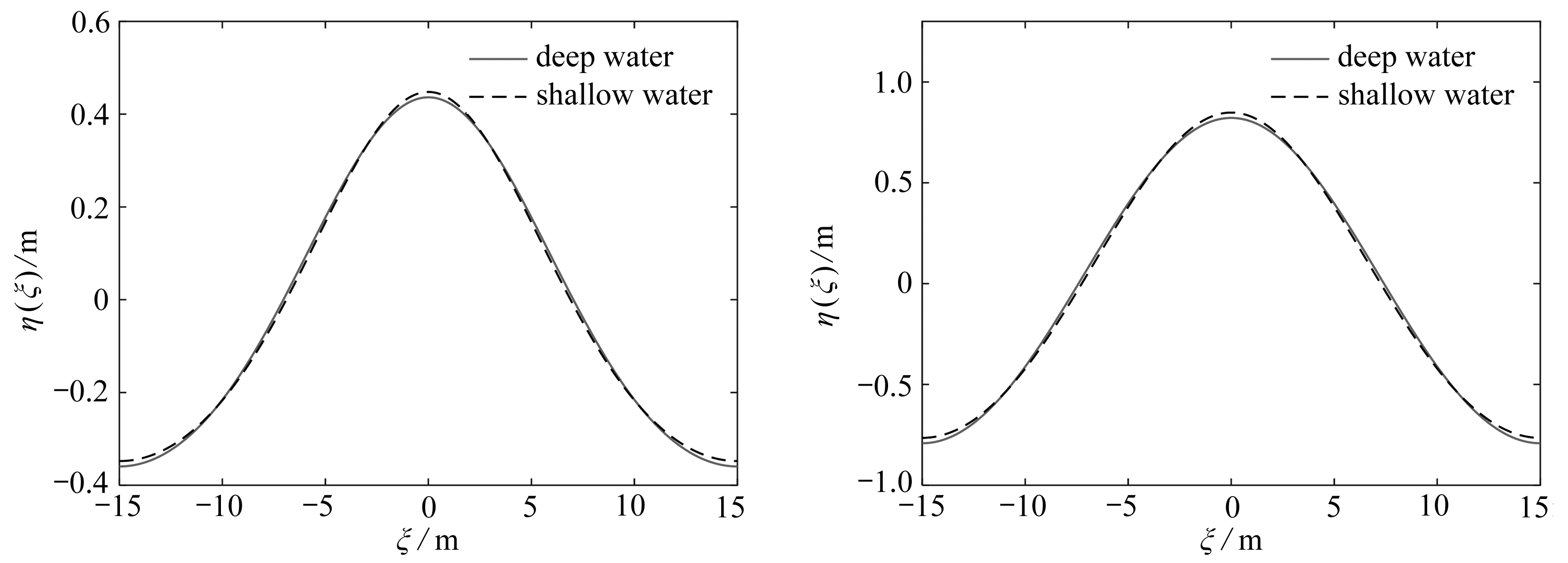
(c) h=4 m (d) h=8 m
图2 深水理论与浅水理论对比(L=30 m, η0=0.1h)
Fig. 2 The deep water theory vs. the shallow water theory(L=30 m, η0=0.1h)
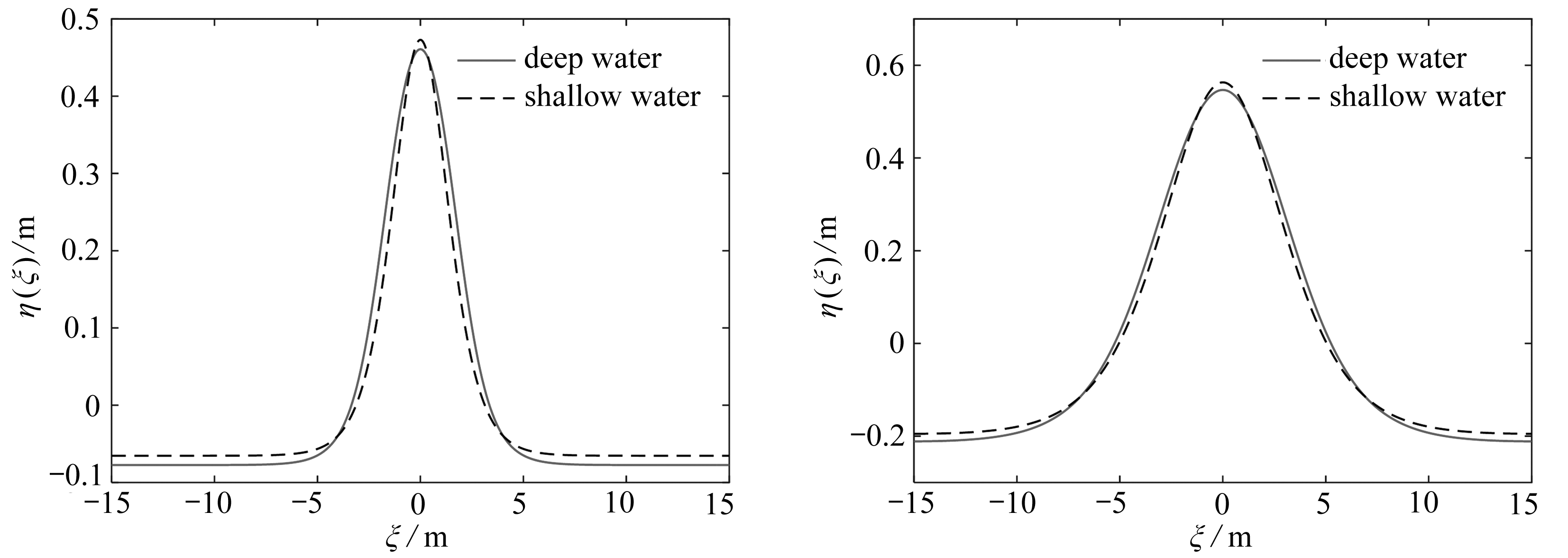
(a) h=1 m (b) h=2 m
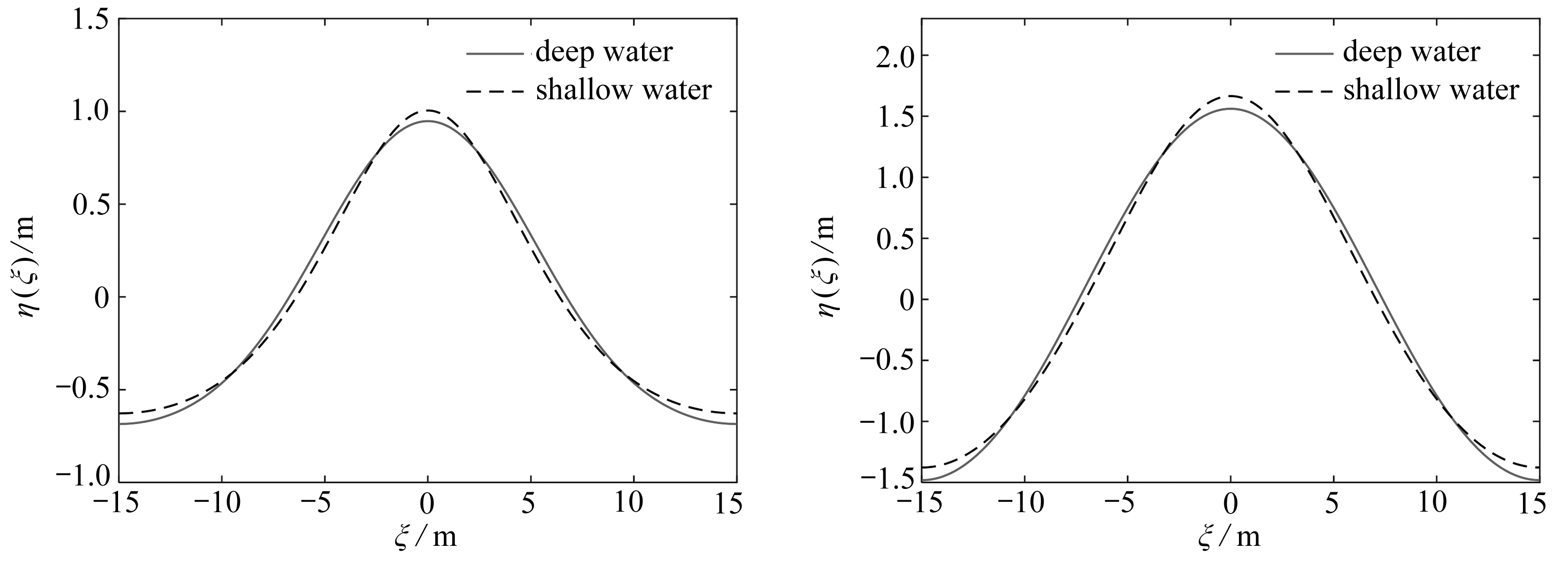
(c) h=4 m (d) h=8 m
图3 深水理论与浅水理论对比(L=30 m, η0=0.2h)
Fig. 3 The deep water theory vs. the shallow water theory(L=30 m, η0=0.2h)
表2图2、3中不同水波的波长、波高、波速和Ur等参数
Table 2 Wave lengths, wave heights, wave speeds andUrfor the waves displayed in figs. 2,3
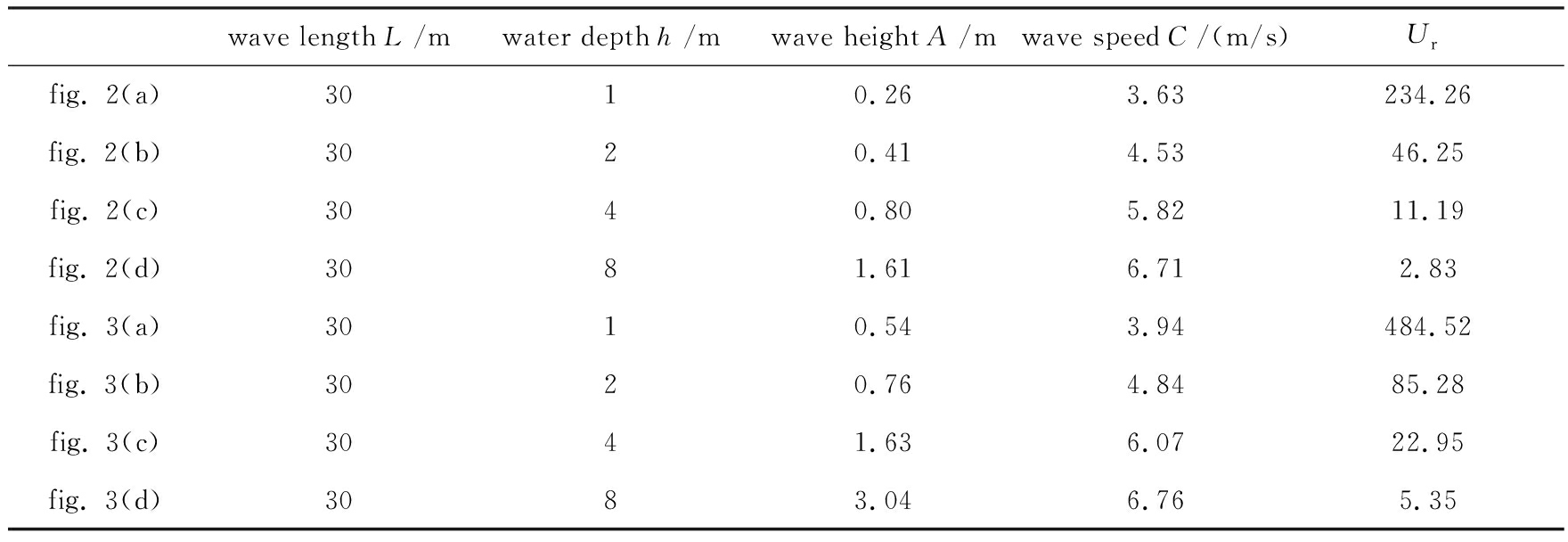
如果初始迭代时线性水波的波幅取η0=0.2h,计算结果如图3所示.表2给出了图2、3中不同水波的波长、波高、波速和Ur等参数对比.
再取波长L=200 m,水深h=10,20,30,40 m,初始迭代时线性水波的波幅取η0=0.1h和η0=0.2h,计算结果分别如图4和5所示.表3给出了图4、5中不同水波的波长、波高、波速和Ur等参数对比.

(a) h=10 m (b) h=20 m
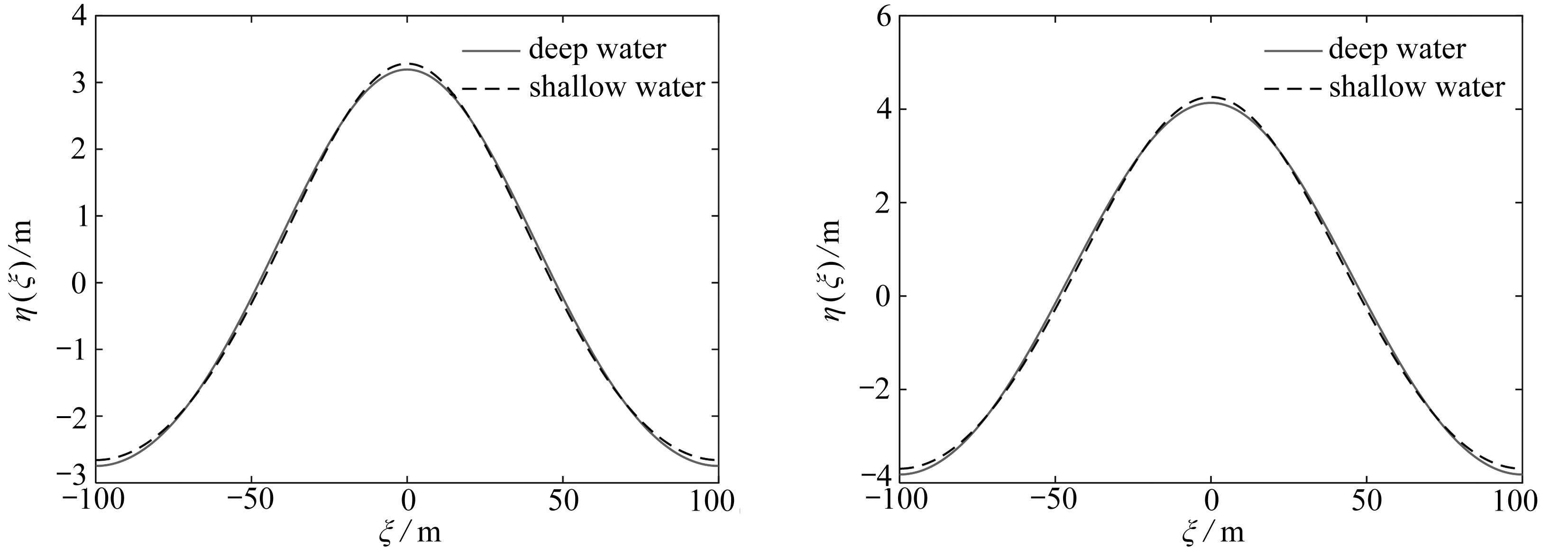
(c) h=30 m (d) h=40 m
图4 深水理论与浅水理论对比(L=200 m, η0=0.1h)
Fig. 4 The deep water theory vs. the shallow water theory(L=200 m, η0=0.1h)
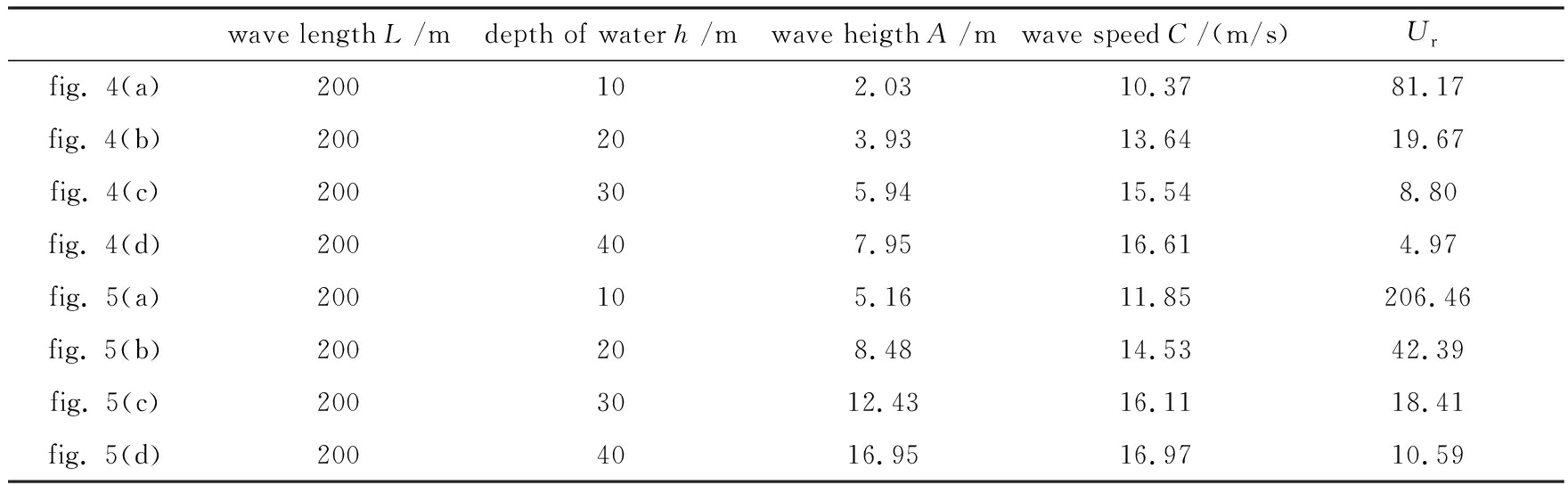
表3图4、5中不同水波的波长、波高、波速和Ur等参数
Table 3 Wave lengths, wave heights, wave speeds andUrfor the waves displayed in figs. 4,5
通过这几个数值结果,可以得到一些概念:
1) 深水理论给出的是具有周期性的行波解.当水深相对于波长较小时,该解与基于浅水假定给出的椭圆余弦波吻合.
2) 在波长不变以及初始迭代的波幅与水深之比不变的条件下,当水深逐渐增加时,深水理论给出的周期行波解趋向于线性水波解,此时Ursell参数Ur逐渐减小,意味着非线性逐渐减小.
3) 在波长相同,水深相同的条件下,随着波幅的增加,Ursell参数Ur增加,意味着水波的非线性变强,此时深水理论的周期行波解与基于浅水假定的椭圆余弦波解差异也随之增加.
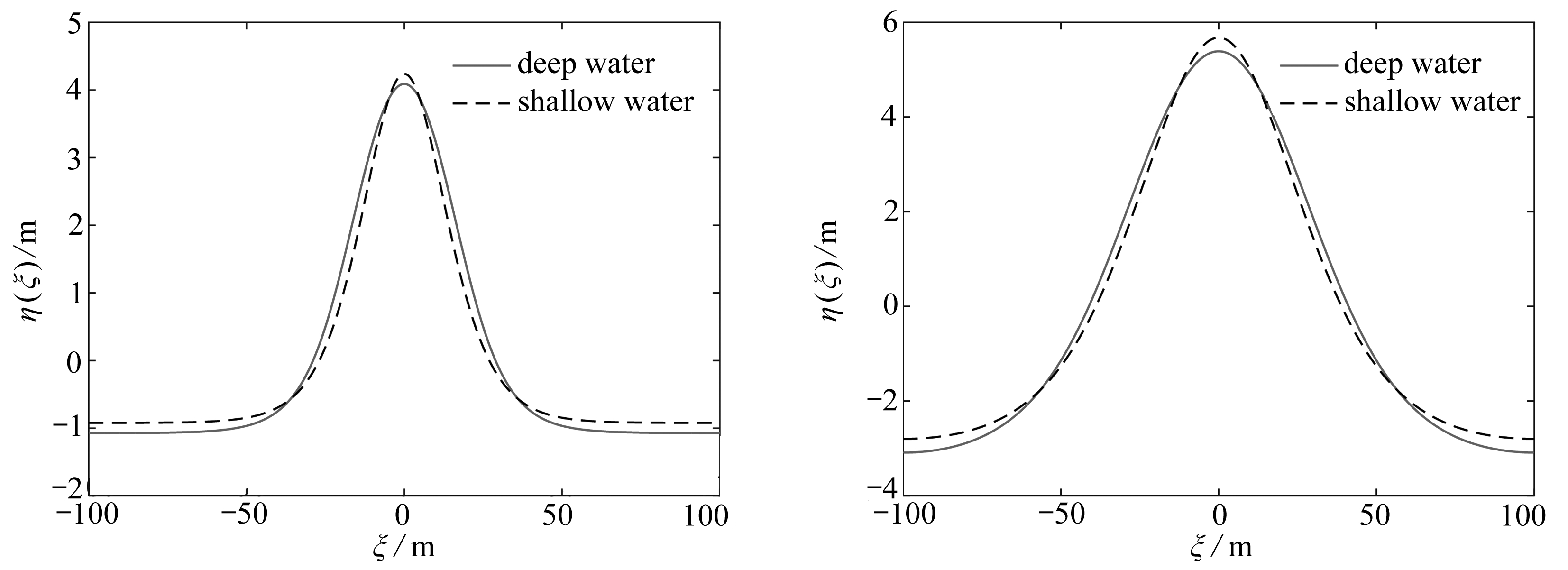
(a) h=10 m (b) h=20 m
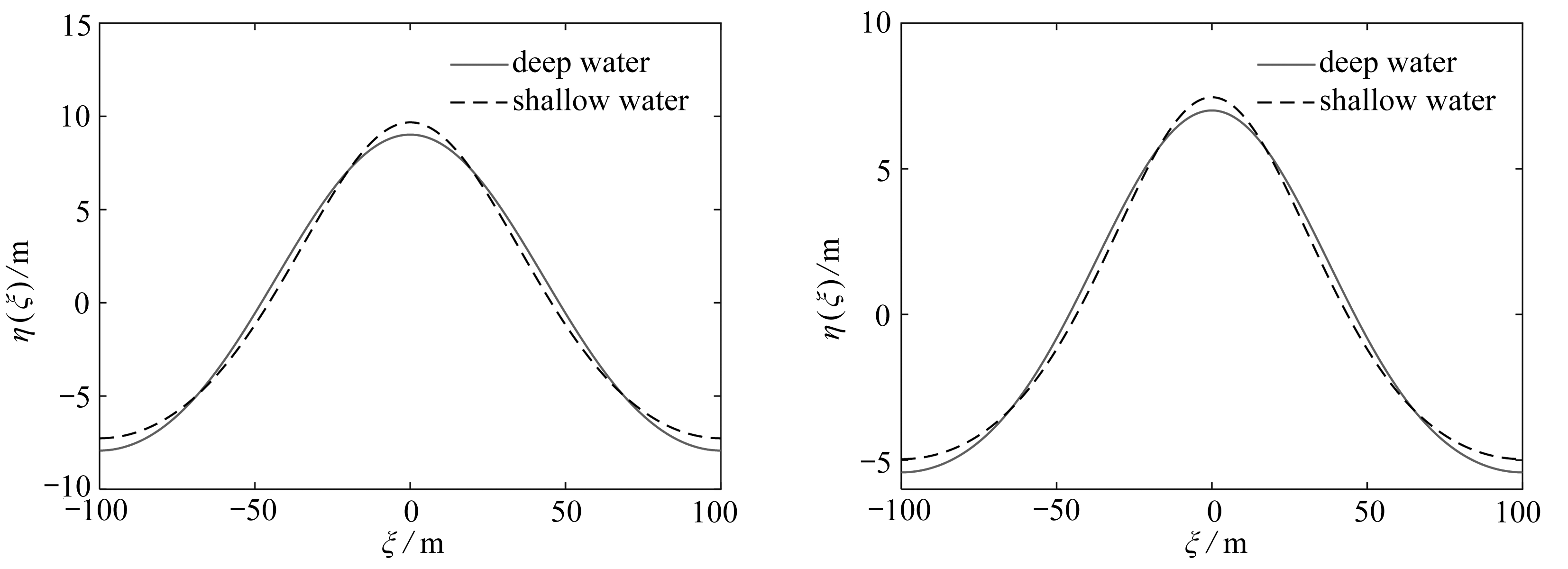
(c) h=30 m (d) h=40 m
图5 深水理论与浅水理论对比(L=200 m, η0=0.2h)
Fig. 5 The deep water theory vs. the shallow water theory(L=200 m, η0=0.2h)
在水底平坦的浅水区域可以观察到椭圆余弦波,而在较深水域,可以观察到一种水面较尖的行波,如图6所示.
这种水面尖锐的行波, 被称为涌波(swell wave), 通常认为是由风作用产生, 沿行进方向传播.涌波一般难以肉眼察觉, 但可以通过照相观察.在澳大利亚曾观察到涌波传播距离超过8 000 km.
文献[14]认为涌波不能由线性的Stokes波描述,因为Stokes波所给出的水面显然是正弦或余弦形式,然而在该文献中并未给出尖锐水面行波的数值解.这里采用位移水波理论,模拟出这种水面尖锐的涌波.首先观察位移线性水波解(22),根据该解,水面可表示为
z=w(x,0,t)=η(ξ,0)=η0cos(kiξ)=η0cos(ki(x-Ct)).
(44)
式(44)所描述的水面看似为余弦形式,但请注意这里采用的位移描述,真实的水面由水面处所有质点的位置包络组成.在水面任意点(x,0)的质点位置可以写为(X(x,0,t),Z(x,0,t)),其中
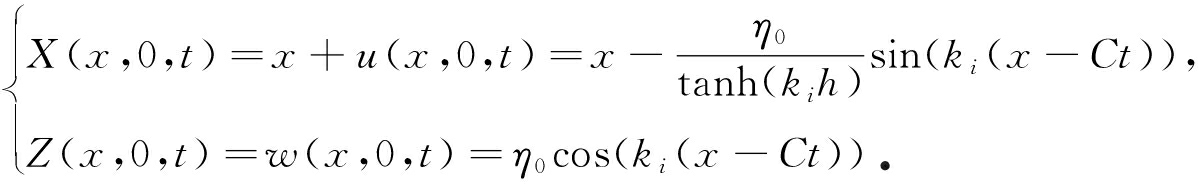
(45)
描述行波水面,可以不考虑时间的影响,因此取t=0,水面实际可以表示为
(46)
上式可以描述尖锐的水面,下面给出数值算例.

图6 自然中观察到的尖锐水面(摘自文献[14])
Fig. 6 Sharp water surface observed in nature(taken form ref. [14])
数值计算可以直接从深水波理论出发,水深取h=50 m,波长取L=50 m,初始迭代时,取线性波的波数i=4,ki=4(2π/L)迭代,初始迭代时线性波的波幅取η0=0.02h,0.03h,0.035h,0.06h,经过一步迭代即收敛,实际上收敛到线性水波解,其水面如图7所示,其中横坐标水面处不同粒子在水平方向的位置X=x+u(x,0,t),纵坐标表示水面处不同粒子在竖向的位置Z=w(x,0,t).
由图7可见, 采用位移描述给出了涌波, 且随着波幅的增加, 水面越来越尖, 而当η0=0.06h时,水面出现了绕圈,成为非物理水波.由数值结果可以分析知,必然存在一个极值波幅,此时涌波的波峰达到最尖,超过此波幅水面则破碎.在极值波幅处,波峰必然是水面的一个奇点,该点处水面不再光滑,其斜率为无穷,据此可找出基于线性位移水波理论的极值波幅为
(47)
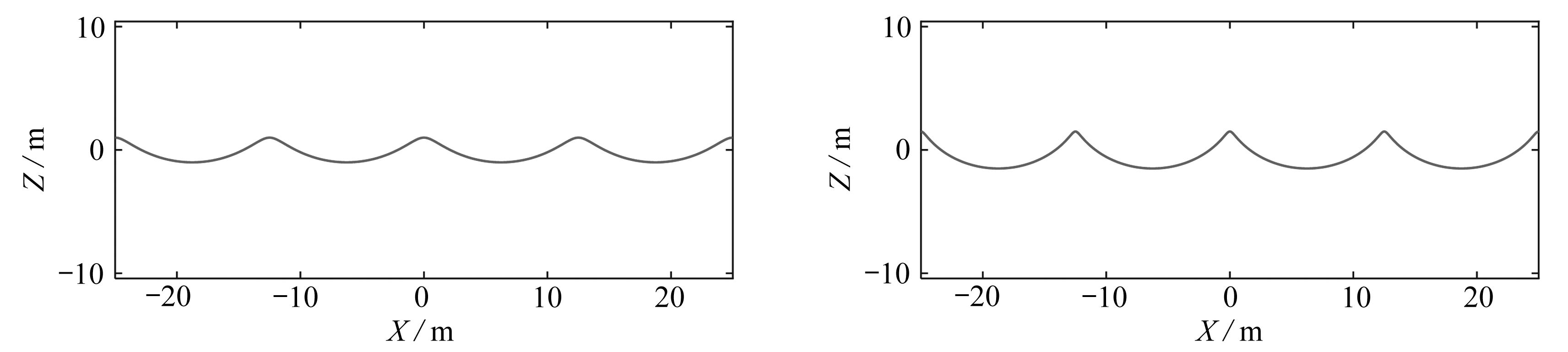
(a) η0=0.02h (b) η0=0.03h
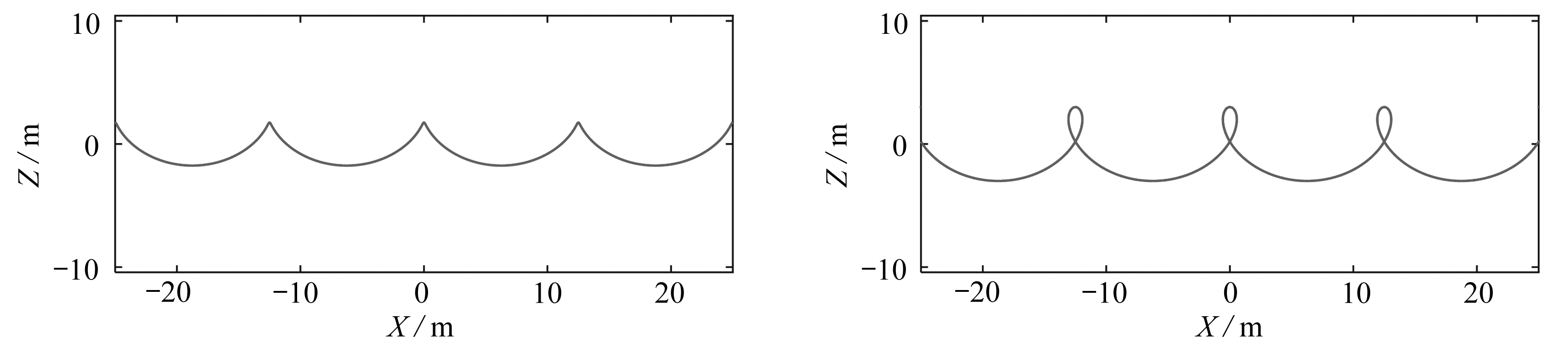
(c) η0=0.035h (d) η0=0.06h
图7 不同波幅对应的水面
Fig. 7 The water surfaces with different wave amplitudes
水波内各质点轨迹的研究对于研究河流泥沙堆积、海水内盐分、营养元素等浓度分布密切相关,然而传统基于Euler描述的水波理论很难给出质点轨迹的精确解.Constantin等[15-16]在《Inventiones Mathematicae》《Bulletin of the American Mathematical Society》等数学公认的顶尖期刊发表文章对水波内质点轨迹进行了论述,然而仅限于定性分析.本文发展的保辛水波理论可以直接给出质点的轨迹.本小节利用保辛水波理论研究不同水深、波长、波幅对于水波内质点轨迹的影响.
首先取h=1 m, 初始迭代时波幅均取η0=0.1h, 波长取L=30 m和50 m分别计算, 结果如图8所示.图中绘制了5个不同深度的粒子轨迹, 其中横坐标表示粒子在水平方向不同时刻的位置X(0,z,t),纵坐标表示粒子在竖向不同时刻的位置Z(0,z,t), 从上到下分别为z=0,-0.3,-0.6,-0.9,-1 m.
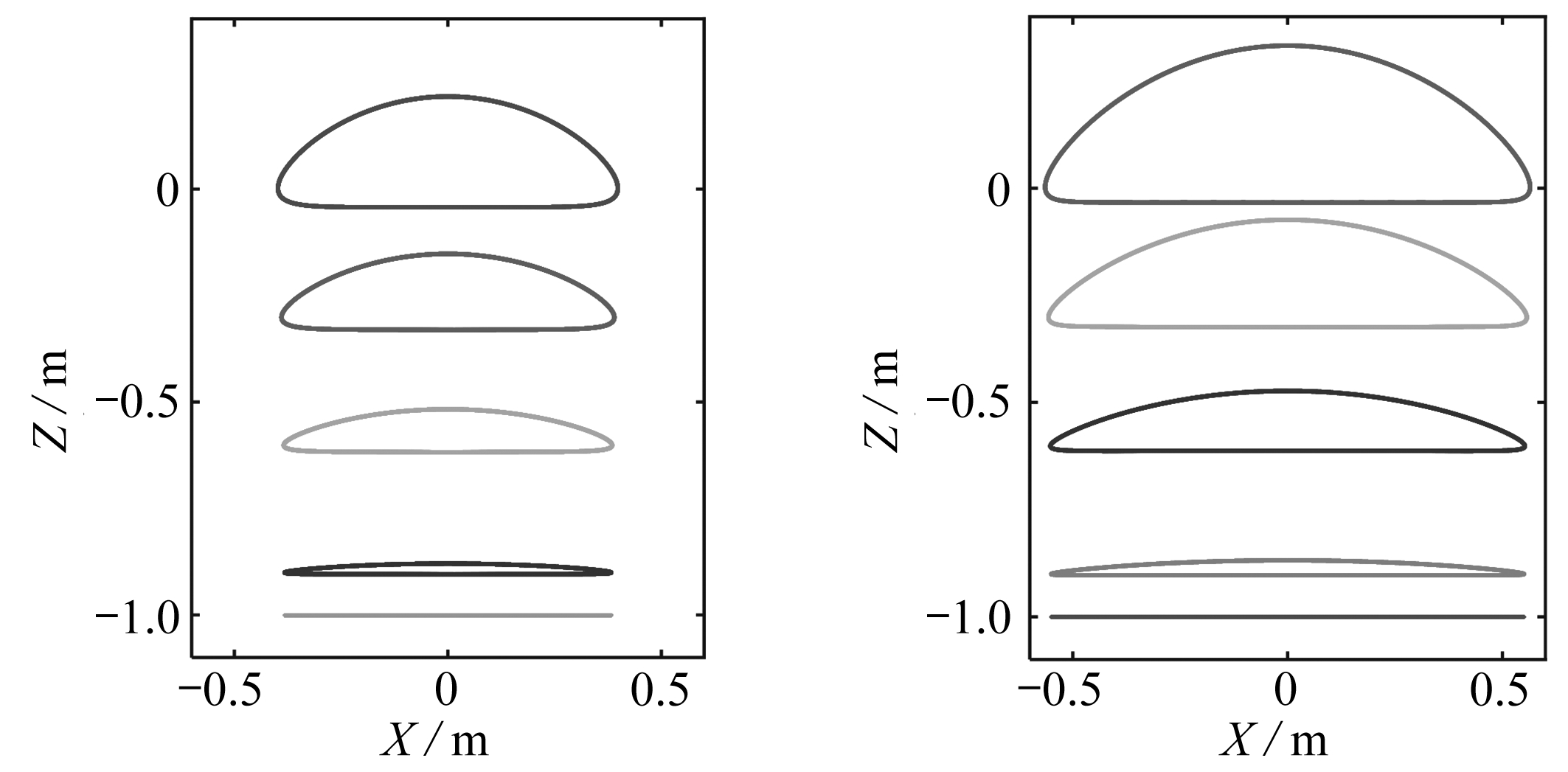
(a) L=30 m (b) L=50 m
图8 在5个不同深度的粒子轨迹
Fig. 8 The trajectories of the particles at 5 different depths
图8(a)所对应的水面即为图2(a).由图2(a)可见,此时的水波十分接近孤立波.比图8(b)中的波长L=50 m,比图8(a)的波长还要大,其水波更加接近孤立波.由图8可见,当波从左向右传来的时候,粒子沿一个拱形轨迹向上和向右运动,直至波幅达到该粒子时,粒子的位置处于最高,之后沿拱形向下和向右传播,波传过去之后,该粒子沿几乎水平的位置回到原点.在整个波传播过程中,粒子在水平方向的运动范围完全超过1 m,比水深还大,而在竖直方向的运动范围远小于水平方向的运动范围,且粒子的位置越深,运动范围也越小.这说明在浅水区域,水波的波长越大,波幅越大,波越陡,水波对于水中泥沙、营养元素等运输作用越强.
大海是深水,但总会逐渐过渡到海滩.有如中国东海,大陆架是一直延伸到冲绳海沟的,有数百公里之遥.大陆架会逐渐过渡到海滩,那就是浅水了.所以单纯计算浅水波,就显得非常局限.所以水深要逐步变深.现在取h=10 m,波长取L=30,50,100,200 m分别计算.相对于h=10 m,波长L=30 m和50 m相当于深水波,而100 m和200 m相当于浅水波,比较相互之间的差异.计算时,初始迭代时波幅均取η0=0.1h,结果如图9所示.图中绘制了6个不同深度的粒子轨迹,其中横坐标表示粒子在水平方向不同时刻的位置X(0,z,t),纵坐标表示粒子在竖向不同时刻的位置Z(0,z,t),从上到下分别有z=0,-2,-4,-6,-8,-10 m.
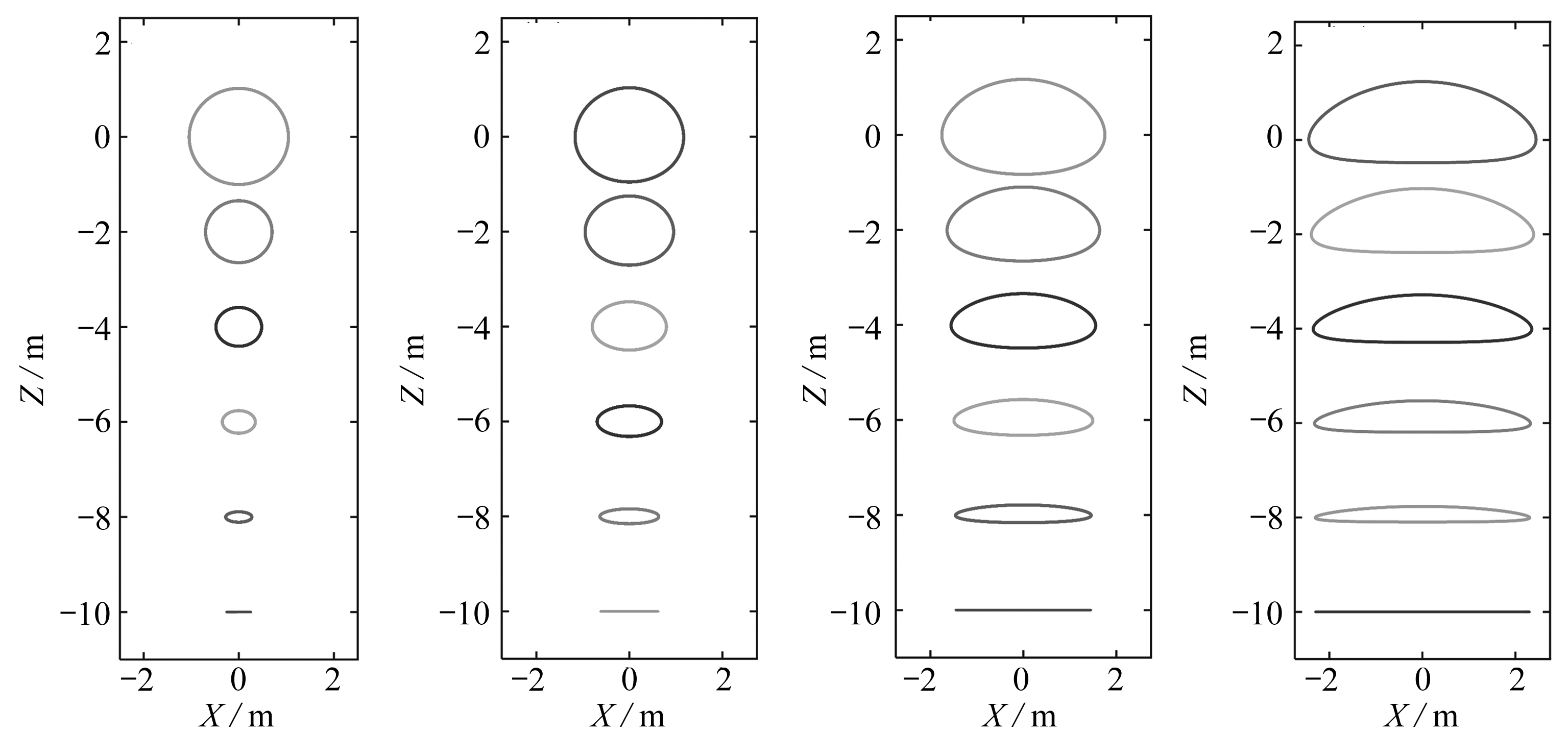
(a) L=30 m (b) L=50 m (c) L=100 m (d) L=200 m
图9 在6个不同深度的粒子轨迹
Fig. 9 The trajectories of the particles at 6 different depths
由图9的4个不同波长的粒子轨迹图可见,当水深相同以及初始迭代波幅相同时,如果波长变短,粒子轨迹趋向于绕圆圈运动;波长越长,粒子的运动轨迹越扁.L=30 m对应于深水波,此时粒子的运动范围由上而下指数衰减,非线性效应减弱.
水波动力学隶属于动力学问题,研究对象为水波,因此也是Hamilton体系,辛对称是其基本属性.研究水波的主流理论是基于Euler描述,以速度或者速度势为基本变量,再采用各种加法摄动做渐近分析,往往忽视了辛这一动力学的基本属性.本文研究水波动力学,特征是采用位移描述水波的运动,并注重水波的动力学属性,基于最小作用量变分原理给出水波方程.
本文通过最小作用量变分原理,首先给出了基于位移的不可压缩条件、水波方程、无旋条件以及边界条件.接着基于位移描述,研究线性水波问题.在线性近似下,引入位移势函数从而得到Laplace方程,由此给出线性水波的周期性行波解.当波长远大于水深时,该线性水波的理论解可以退化为线性浅水余弦波解,这为浅水理论中刚性平移假定的合理性提供了理论依据.
基于位移描述的水波理论,不仅能用于线性水波问题,也可用于非线性水波理论.基于刚性平移假定,本文介绍了浅水波的位移椭圆余弦波解,并分析了椭圆余弦波的Fourier分解.数值算例表明,仅需为数不多的几个不同波数的线性余弦波,就可以组成非线性很强的浅水椭圆余弦波,为研究深水非线性水波理论提供了铺垫.
本文最后研究了深水非线性水波问题.通过引入非线性位移势函数,建立了Possion方程,将非线性水波解用线性水波解展开,并以线性水波解为初始迭代解,通过一系列的保辛迭代,给出非线性周期行波解的保辛摄动算法.通过具体的数值算例分析表明:在浅水情况下,基于深水理论给出的具有周期性的行波解,与基于浅水假定给出的椭圆余弦波吻合.在除水深之外的计算参数不变的条件下,当水深逐渐增加时,深水理论给出的周期行波解趋向于线性水波解.对于浅水来说,波幅增加会导致水波解趋向于孤立波;而对于深水波来说,波幅的增加,会导致水面变得更为尖锐,出现自然界中的涌波.
必须指出的是,本文只是给位移水波理论画了一个粗线条.笔者早在2006年以及之后工作中详细介绍了浅水波位移描述的基本理论[2-6, 11, 13, 17-22];在2015、2017年的工作中,详细介绍了线性水波的流函数及界带有限元,关于位移流函数、浅水椭圆余弦波等详细内容[7, 23].可以参考这些工作.在本文的基础上,还有许多工作有待进一步展开,如水波破碎、水波演化的保辛积分等.笔者相信,位移水波理论将逐渐丰满,为水波动力学问题提供一套“辛”解.
参考文献(References):
[1] 梅强中. 水波动力学[M]. 北京: 科学出版社, 1984.(MEI Qiangzhong.Water Wave Dynamics[M]. Beijing: Science Press, 1984.(in Chinese))
[2] 钟万勰, 姚征. 位移法浅水孤立波[J]. 大连理工大学学报, 2006,46(1): 151-156.(ZHONG Wanxie, YAO Zheng. Shallow water solitary waves based on displacement method[J].Journal of Dalian University of Technology, 2006,46(1): 151-156.(in Chinese))
[3] 钟万勰. 应用力学的辛数学方法[M]. 北京: 高等教育出版社, 2006.(ZHONG Wanxie.Symplectic Solution Methodologyin Applied Mechanics[M]. Beijing: Higher Education Press, 2006.(in Chinese))
[4] 钟万勰, 陈晓辉. 浅水波的位移法求解[J]. 水动力学研究与进展, 2006,21(4): 486-493.(ZHONG Wanxie, CHEN Xiaohui. Solving shallow water waves with the displacement method[J].Journal of Hydrodynamics, 2006,21(4): 486-493.(in Chinese))
[5] 钟万勰, 吴锋. 力-功-能-辛-离散: 祖冲之方法论[M]. 大连: 大连理工大学出版社, 2016.(ZHONG Wanxie, WU Feng.Force-Work-Energy-Symplecticity-Discretization:ZU Chongzhi’s Methodology[M]. Dalian: Dalian University of Technology Press, 2016.(in Chinese))
[6] 吴锋, 钟万勰. 浅水问题的约束Hamilton变分原理及祖冲之类保辛算法[J]. 应用数学和力学, 2016,37(1): 1-13.(WU Feng, ZHONG Wanxie. The constrained Hamilton variational principle for shallow water problems and the Zu-type symplectic algorithm[J].Applied Mathematics and Mechanics, 2016,37(1): 1-13.(in Chinese))
[7] 吴锋. 基于位移的水波数值模拟: 辛方法[M]. 大连: 大连理工大学, 2017.(WU Feng.Numerical Modeling of Water Waves Based on Displacement:Symplectic Method[M]. Dalian: Dalian University of Technology Press, 2017.(in Chinese))
[8] WEYL H.The Classical Groups:Their Invariants and Representations[M]. Princeton, New Jersey: Princeton University Press, 1939.
[9] 冯康, 秦孟兆. 哈密尔顿系统的辛几何算法[M]. 杭州: 浙江科学技术出版社, 2004.(FENG Kang, QIN Mengzhao.Symplectic Geometric Algorithms for Hamiltonian Systems[M]. Hangzhou: Zhejiang Science and Technology Press, 2004.(in Chinese))
[10] 吴云岗, 陶明德. 水波动力学基础[M]. 上海: 复旦大学出版社, 2011.(WU Yungang, TAO Mingde.The Foundation of Hydrodynamic[M]. Shanghai: Fudan University Press, 2011.(in Chinese))
[11] 钟万勰, 吴锋, 孙雁. 浅水机械激波[J]. 应用数学和力学, 2017,38(8): 845-852.(ZHONG Wanxie, WU Feng, SUN Yan. Shallow water mechanical shock wave[J].Applied Mathematics and Mechanics, 2017,38(8): 845-852.(in Chinese))
[12] STOKER J J.Water Waves:the Mathematical Theory With Applications[M]. New York: Interscience Publishers Ltd, 1957.
[13] 吴锋, 孙雁, 姚征, 等. 椭圆余弦波的位移法分析[J]. 计算机辅助工程, 2018,27(2): 1-5.(WU Feng, SUN Yan, YAO Zheng, et al. Analysis on cnoidal wave using the displacement method[J].Computer Aided Engineering, 2018,27(2): 1-5.(in Chinese))
[14] ADRIAN C.Nonlinear Water Waves With Applications to Wave-Current Interactions and Tsunamis[M]. New York: Society for Industrial & Applied Mathematics, 2011.
[15] CONSTANTIN A. The trajectories of particles in Stokes waves[J].Inventiones Mathematicae, 2006,166(3): 523-535.
[16] CONSTANTIN A, ESCHER J. Particle trajectories in solitary water waves[J].Bulletin of the American Mathematical Society, 2007,44(3): 423-431.
[17] 吴锋, 钟万勰. 浅水动边界问题的位移法模拟[J]. 计算机辅助工程, 2016,25(2): 5-13.(WU Feng, ZHONG Wanxie. Simulation on moving boundaries of shallow water using displacement method[J].Computer Aided Engineering, 2016,25(2): 5-13.(in Chinese))
[18] 姚征, 钟万勰. 位移法浅水波方程解及其特性[J]. 计算机辅助工程, 2016,25(2): 21-25.(YAO Zheng, ZHONG Wanxie. Solutions and characteristics of shallow water equation based on displacement method[J].Computer Aided Engineering, 2016,25(2): 21-25.(in Chinese))
[19] 吴锋, 钟万勰. 不平水底浅水波问题的位移法[J]. 水动力学研究与进展, 2016,31(5): 549-555.(WU Feng, ZHONG Wanxie. Displacement method for the shallow water wave problems with uneven bottoms[J].Chinese Journal of Hydrodynamics, 2016,31(5): 549-555.(in Chinese))
[20] WU Feng, ZHONG Wanxie. On displacement shallow water wave equation and symplectic solution[J].Computer Methods in Applied Mechanics and Engineering, 2017,318: 431-455.
[21] WU F, YAO Z, ZHONG W. Fully nonlinear (2+1)-dimensional displacement shallow water wave equation[J].Chinese Physics B, 2017,26(5): 253-258.
[22] WU F, ZHONG W. A shallow water equation based on displacement and pressure and its numerical solution[J].Environmental Fluid Mechanics, 2017,17(5): 1-28.
[23] 吴锋, 钟万勰. 水波的界带有限元[J]. 应用数学和力学, 2015,36(12): 1219-1227.(WU Feng, ZHONG Wanxie. Simulation of water waves based on the inter-belt finite element method[J].Applied Mathematics and Mechanics, 2015,36(12): 1219-1227.(in Chinese))
ZHONG Wanxie1,2, WU Feng1, SUN Yan2, YAO Zheng3
(1.Department of Engineering Mechanics,Dalian University of Technology,Dalian,Liaoning116023,P.R.China; 2.School of Naval Architecture,Ocean&Civil Engineering,Shanghai Jiao Tong University,Shanghai200240,P.R.China;
3.Transportation Engineering College,Dalian Maritime University,Dalian,Liaoning116026,P.R.China)
(Contributed by ZHONG Wanxie, M. AMM Editorial Board)
Abstract:Here, an elementary introduction to the displacement method-based water wave dynamics theory was presented. The periodic travelling wave solutions of the linear water waves and shallow water waves were given. The symplectic perturbation method was proposed to analyze the periodic travelling wave solution for the water system with a general depth. Numerical tests were given to demonstrate the correctness of the proposed method. The present research emphasizes the dynamics property of water waves. By means of the proposed theory, the particle trajectory can be obtained directly, and the periodic travelling wave with sharp surface can be simulated.
Key words:water wave; dynamics; displacement method; symplectic; Hamilton
Foundation item:The National Natural Science Foundation of China(11472076;51609034;51278298)
引用本文/Cite this paper: 钟万勰, 吴锋, 孙雁, 姚征. 保辛水波动力学[J]. 应用数学和力学, 2018,39(8): 855-874.ZHONG Wanxie, WU Feng, SUN Yan, YAO Zheng. Symplectic water wave dynamics[J].Applied Mathematics and Mechanics, 2018,39(8): 855-874.
*收稿日期:2018-02-09;
修订日期:2018-04-11
基金项目:国家自然科学基金(11472076;51609034;51278298);中央高校基本科研业务费(DUT17RC(3)069)
作者简介:
钟万勰(1934—),男,教授,中科院院士(通讯作者. E-mail: zwoffice@dlut.edu.cn);
吴锋(1985—),男,副教授(E-mail: vonwu@dlut.edu.cn);
孙雁(1965—),女,副教授(E-mail: sunyan@sjtu.edu.cn);
姚征(1978—),男,副教授(E-mail: yaozheng@dlmu.edu.cn).
摘要:初步介绍了基于位移表示的水波动力学理论,给出了线性水波、浅水波的位移周期行波解.提出保辛摄动法,计算一般水深周期行波解,并通过数值算例验证了算法的正确性.该研究注重水波的动力学属性,可以直接给出质点粒子的轨迹,模拟出水面尖锐的周期行波解.
关 键 词:水波; 动力学; 位移法; 辛; Hamilton
中图分类号:O352; O353.2
文献标志码:A
DOI:10.21656/1000-0887.390062