李 锐, 田 宇, 郑新然, 王 博
(大连理工大学 工程力学系; 国际计算力学研究中心; 工业装备结构分析国家重点实验室(大连理工大学), 辽宁 大连 116024)
(第五届“钱令希计算力学奖(青年奖)”特邀论文)
弹性地基上的矩形中厚板是土木工程、机械工程、航空航天及海洋工程中的一种常见的结构形式,主要用于刚性路面、桥面板、舰船甲板等承重结构.由于Kirchhoff薄板理论忽略了板在弯曲时的横向剪切变形,其应用于实际工程中较厚的板时往往会产生较大误差.于是学者们相继建立了若干中厚板理论,其中Mindlin中厚板理论是应用最为广泛的理论之一[1],自其建立以来,不断有学者致力于求解相应的弯曲问题.然而,由于中厚板的偏微分控制方程阶次较高,其边值问题的解析求解成为一类难题:除了半逆法容易处理的对边简支情况以外,其余边界条件下矩形中厚板的弯曲问题都不易获得解析解,其中尤以含自由边的板难以求解.上述状况引得学者们采用多种数值方法求解相关问题,例如Rayleigh-Ritz法[2]、有限差分法[3]、有限元法[4]、样条元法[5]、边界元法[6]、微分求积法[7]、微分容积法[8]、离散奇异卷积法[9]、小波配点法[10]、状态空间法[11]等.
各类有效的数值方法无疑可以获得工程上可接受的中厚板问题的解,但这并未动摇解析解的地位.首先,由于能够精确反映各参量之间的关联,解析解在力学研究中具有重要价值.例如,解析解可以作为检验各类近似/数值方法的基准,能为快速参数分析和优化提供有力的工具,也是高效指导复杂实验设计的重要理论基础.此外,有限元等数值方法本身就是一种近似解,其在求解板壳问题时也存在着一些问题,例如边界条件不能总是精确满足、应力等位移的高阶导数结果不够精确等.可以说,解析解的获得不仅对板壳力学求解理论的发展和完善具有重要价值,而且对工程结构分析与设计具有重要的指导意义.
近年来,基于钟万勰院士、姚伟岸教授等开创的辛弹性力学求解体系[12],李锐等提出了一种板壳力学求解新方法:辛-叠加方法(symplectic superposition method),获得了若干矩形薄板、中厚板弯曲、振动和稳定性问题的新解析解[13-21].辛-叠加方法的基本思路是:将待求问题导入Hamilton体系,形成Hamilton对偶方程边值问题;将原问题拆分为若干子问题,对这些子问题,运用辛数学方法构建相应的本征值问题,解析地获得本征解,进而利用辛本征展开等手段,精确表征子问题中板的挠度(弯曲问题)、振型(振动问题)或屈曲模态(稳定性问题)等控制变量;通过叠加子问题的解,获得原问题的解.通过该方法,对于静力问题,将直接得到结构的位移场解析解;对于振动问题,将解析获得结构的固有频率和相应的振型;对于稳定性问题,将解析得到结构的临界屈曲载荷和相应的屈曲模态.辛-叠加方法兼备了辛数学方法无需事先假定解形式的优点以及叠加法程式化的优点,具有统一的数学结构,不受问题具体类型的限制.该方法一方面克服了其他传统方法求解过程中遇到的分离变量、半逆法失效等难题,同时规避了运用传统辛数学方法所出现的本征值方程无法解析求解等问题,在解析求解板壳力学问题中展现出独特的优势.
本文首次应用辛-叠加方法解析求解了基于Mindlin理论的弹性地基上四边自由矩形中厚板的弯曲问题.由于边界约束最弱,因此该类问题实际上是各类边界条件下矩形板问题中最难求解的情况之一.最终的数值算例表明,无论是所关心的位移还是内力解,本文结果均与精细有限元分析结果吻合得很好,从而证明了该方法对于求解中厚板问题的适用性.
在xOy直角坐标系下,弹性地基上中厚板的平衡方程为
(1)
(2)
(3)
其中,q为横向分布外载荷;K为地基刚度;板内单位长度的内力包括弯矩Mx和My,扭矩Mxy,以及剪力Qx和Qy.上述各内力可以由广义位移(挠度W、转角ψx和ψy)表达为
(4)
(5)
(6)
(7)
(8)
其中,板的抗弯刚度D和剪切刚度C与弹性模量E、厚度h以及Poisson比ν存在以下关系:
D=Eh3/[12(1-ν2)],C=5Eh/[12(1+ν)],
剪切修正系数取为5/6.
由式(2)、(3)、(7)和(8),可得
(9)
(10)
令
(11)
(12)
可得
(13)
(14)
将式(13)和(14)代入式(1),可得
(15)
将式(7)代入式(13),可得
(16)
将式(8)代入式(14),可得
(17)
对式(16)两边关于x求导,得
(18)
对式(17)两边关于y求导,得
(19)
利用式(11)和(15),对式(18)和(19)求和,可给出
C( 2W-M)=KW-q.
2W-M)=KW-q.
(20)
对式(16)两边关于y求导,得
(21)
对式(17)两边关于x求导,得
(22)
利用式(12),将式(21)和(22)相减,可给出
(23)
综上,求解弹性地基上中厚板的弯曲问题可归结为求解关于控制函数M,W和Ψ的方程组(15)、(20)和(23):所有关键力学量均可经式(16)、(17)连同式(4)~(8),由上述3个函数表达.
为将所求问题导入Hamilton体系,令
(24)
(25)
(26)
由式(23),注意到2C/[D(1-ν)]=10/h2,可得
(27)
由式(15)和(20),可得
(28)
(29)
式(24)~(29)可以写成如下矩阵形式:
(30)
其中
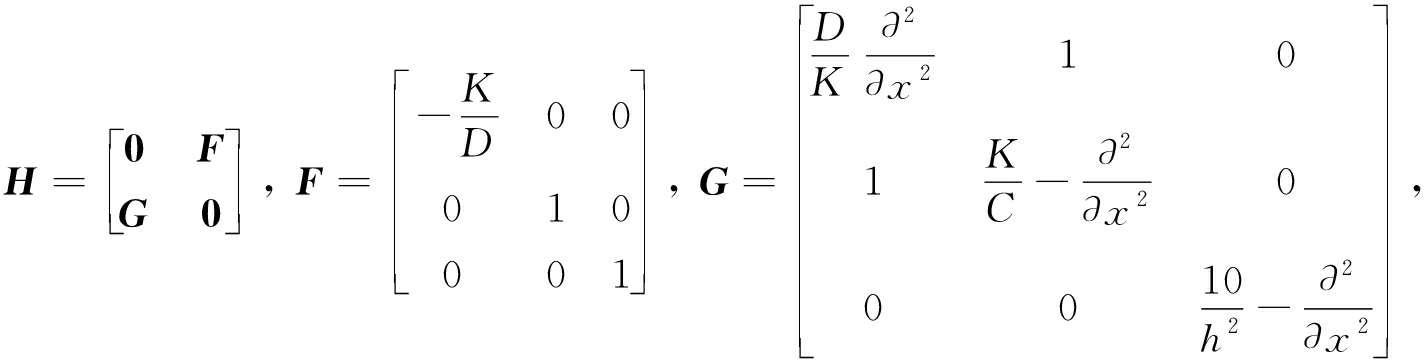
矩阵H满足HT=JHJ,其中![]() 是单位辛矩阵,I3是三阶单位矩阵,因此H是一个Hamilton算子矩阵[12],而式(30)即为弹性地基上中厚板弯曲问题的Hamilton对偶方程.容易看出,该对偶方程形式非常简洁,因此对后续求解非常有利.
是单位辛矩阵,I3是三阶单位矩阵,因此H是一个Hamilton算子矩阵[12],而式(30)即为弹性地基上中厚板弯曲问题的Hamilton对偶方程.容易看出,该对偶方程形式非常简洁,因此对后续求解非常有利.
需要指出,式(30)仅是所求问题控制方程的一种Hamilton体系表达,采用其他推导方法(例如基于Hellinger-Reissner变分原理)也可以导出其他形式的Hamilton对偶方程.当然,此时的状态向量Z所包含的元素也将有所不同.
本节利用辛数学方法求解弹性地基上对边滑支矩形中厚板的弯曲问题,从而为子问题的求解奠定基础.
方程(30)的齐次方程为
(31)
在辛数学求解框架下,分离变量法有效[12],因此令
Z=X(x)Y(y),
(32)
其中
X(x)=[M(x),W(x),Ψ(x),β(x),α(x),θ(x)]T.
将式(32)代入式(31),得
HX(x)=μX(x),
(33)
(34)
其中μ为本征值,X(x)为本征向量.
与式(33)对应的特征方程为

(35)
其中k=-K/D,δ=D/C.展开式(35),得
(36)
方程(36)的根为
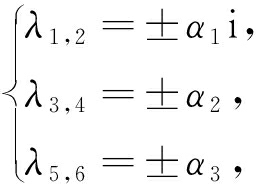
(37)
其中为i为虚数单位,

(38)
因此可以写出方程通解:
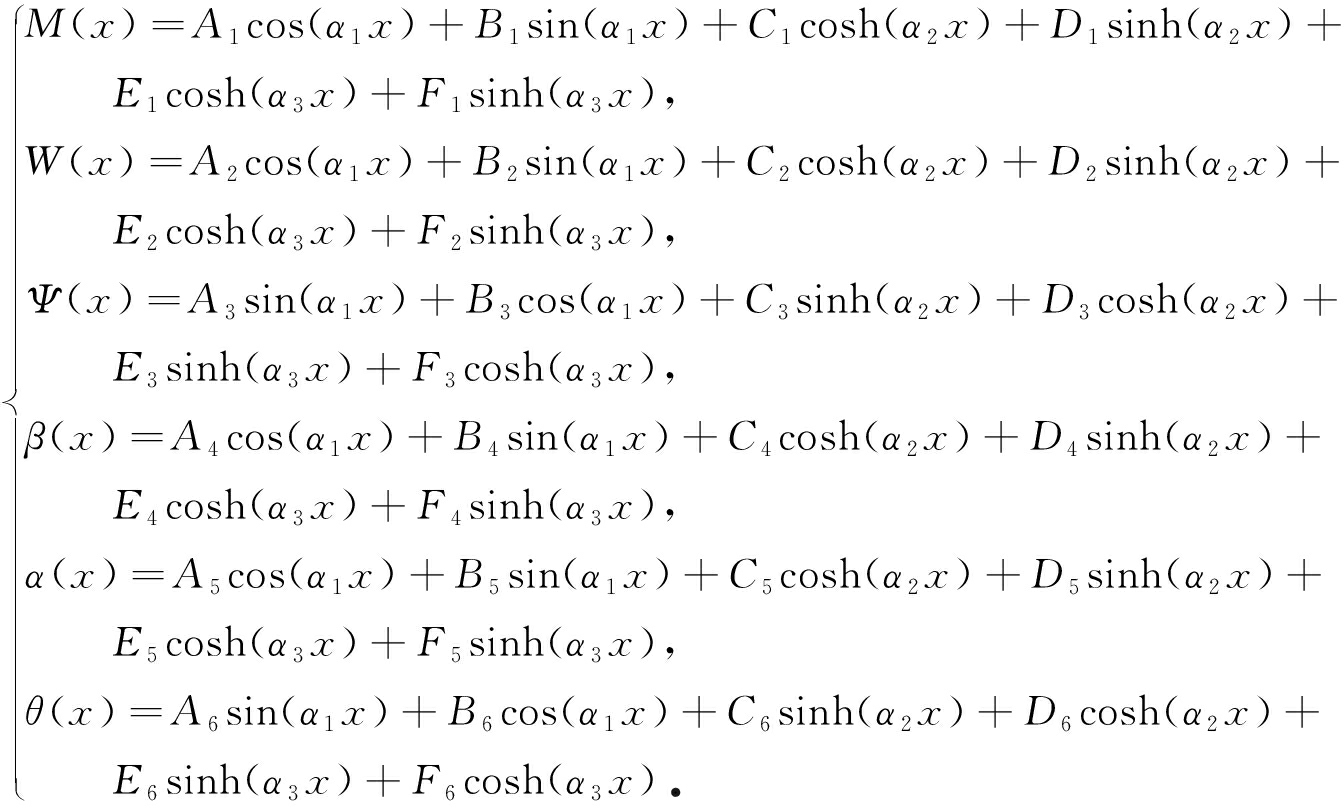
(39)
将其代入式(33),得到各常数之间的关系:

(40)
其中
(41)
对于x=0和x=a边滑支的矩形中厚板,其x方向的边界条件为

(42)
将式(39)和(40)代入式(42),令所得方程组的系数矩阵行列式为0,即得到弹性地基上对边滑支矩形中厚板弯曲问题的本征值超越方程:
sin(α1a)sinh(α2a)sinh(α3a)=0.
(43)
求解得到两组本征值,即
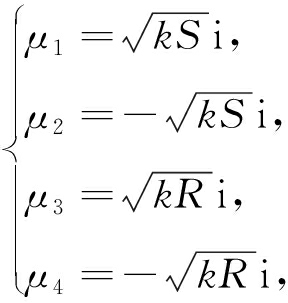
(44)

(45)
其中αm=mπ/a(m=1,2,3,…).
本征值μ1~μ4对应的本征向量分别为

(46)
本征值μm1~μm6对应的本征向量分别为

(47)
本征向量组(46)及(47)满足共轭辛正交关系[12].
非齐次方程(30)的解可写成
Z=X(x)Y(y),
(48)
其中
X(x)=[X1(x),X2(x),X3(x),X4(x),…,Xm1(x),Xm2(x),
Xm3(x),Xm4(x),Xm5(x),Xm6(x),…],
Y(y)=[Y1(y),Y2(y),Y3(y),Y4(y),…,Ym1(y),Ym2(y),
Ym3(y),Ym4(y),Ym5(y),Ym6(y),…]T.
将式(48)代入式(30),得到
X(x)dY(y)/dy=HX(x)Y(y)+f.
(49)
注意到
HX(x)=X(x)M,
(50)
其中M=diag(P0,…,Qm,…),P0=diag(μ1,μ2,μ3,μ4),Qm=diag(μm1,μm2,μm3,μm4,μm5,μm6)(m=1,2,3,…).而f可以按辛本征向量展开为
f=X(x)G,
(51)
其中
G=[g1,g2,g3,g4,…,gm1,gm2,gm3,gm4,gm5,gm6,…]T
为展开系数列阵,各元素可通过对式(51)两边同时左乘X(x)TJdx并关于x从0到a积分,由共轭辛正交关系求出.于是式(49)给出
dY(y)/dy-MY(y)=G.
(52)
对于在(x0,y0)处作用一集中载荷p的板,可得

(53)
其中H(y-y0)为单位阶跃函数,c1~c4以及cm1~cm6为待求常数,由板在y方向的边界条件决定.
如图1(a)所示,弹性地基上四边自由矩形中厚板在(x0,y0)处作用一集中载荷p.该问题可由图1(b)、 (c)、 (d)这3类子问题叠加求解: 子问题1为集中载荷作用下的四边滑支板(图1(b));子问题2为四边滑支板在y=0和y=b边分别承受级数![]() 和
和![]() 表示的转角作用(图1(c)); 子问题3为四边滑支板在x=0和x=a边分别承受级数
表示的转角作用(图1(c)); 子问题3为四边滑支板在x=0和x=a边分别承受级数![]() 和
和![]() 表示的转角作用(图1(d)),其中βm=mπ/b.
表示的转角作用(图1(d)),其中βm=mπ/b.

对于子问题1,y方向的边界条件为
ψy|y=0,b=0,Qy|y=0,b=0,Mxy|y=0,b=0.
(54)
将式(46)、(47)及(53)代入式(48),求出ψy,Qy,Mxy的表达式,然后代入式(54),求出常数c1~c4以及cm1~cm6,最终得到集中载荷作用下弹性地基上四边滑支矩形中厚板弯曲问题的辛解析解:
(55)
其中
对于子问题2,代入相应的边界条件,同理可得问题的解:
(56)
其中
对于子问题3,其解为
(57)
其中
通过以上推导给出了3个子问题的挠度解,其余力学量容易类似求出.
为满足x=0边自由的边界条件,叠加以上3个子问题在x=0边的弯矩,并令其等于零,化简后得到第一组方程:
(58)
[Em-Fmcos(iπ)]+
![]()
(59)
其中i=1,2,3,….
为满足x=a边自由的边界条件,叠加子问题在x=a边的弯矩,并令其等于零,得到第二组方程:
(60)
![]() ϑβi[E0-cos(iπ)F0]+
ϑβi[E0-cos(iπ)F0]+
[Em-Fmcos(iπ)]+
![]()
(61)
其中i=1,2,3,….
为满足y=0边自由的边界条件,叠加子问题在y=0边的弯矩,并令其等于零,得到第三组方程:
(62)
[Gm-Hmcos(iπ)]=0,
(63)
其中i=1,2,3,….
为满足y=b边自由的边界条件,叠加子问题在y=b边的弯矩,并令其等于零,得到第四组方程:
(64)
(65)
其中
i=1,2,3,…,
Sδ=(S-δ)/[b2(1+kS2)],kR=1+kRδ,kS=1+kSδ,
求解式(58)~(65)所示联立方程,解出各常数,将它们代回式(56)和(57),连同式(55)进行求和,即得到弹性地基上四边自由矩形中厚板弯曲解:
(66)
当然,由于计算机求解的限制,对于本是无穷联立方程的式(58)~(65),实际当中必须取有限组进行计算:本文对各组常数均取N+1项求解,即令式(59)、(61)、(63)、(65)对于i=1,2,3,…,N成立,通过求解4N+4组方程,得到Em,Fm,Gm和Hm(m=0,1,2,…,N),进而通过式(66)得到最终解.
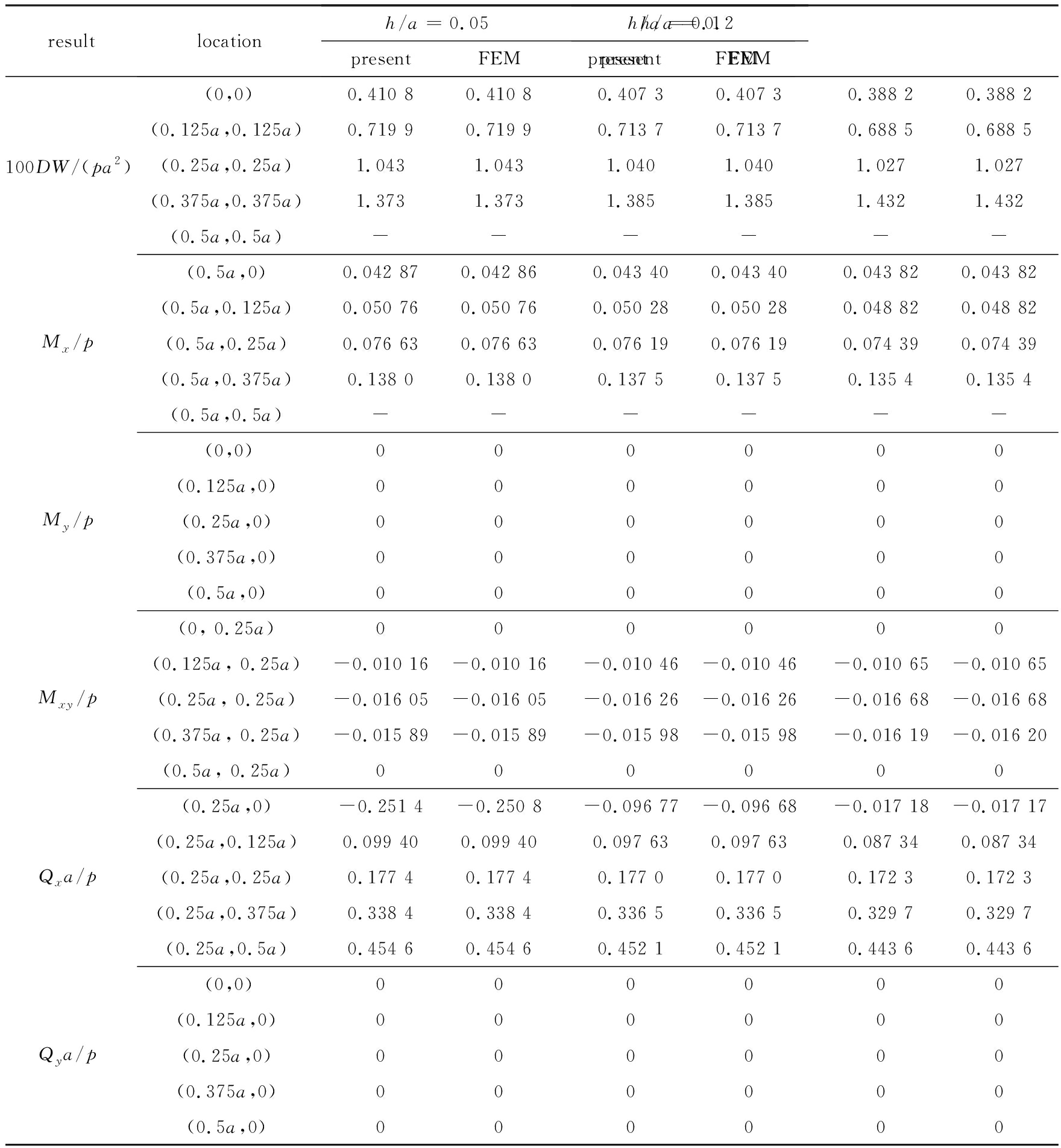
为了验证本文求解的正确性, 表1给出了中心集中载荷p作用下弹性地基上不同宽厚比的四边自由正方形中厚板(ν=0.3,K/D=100)弯曲解.计算中取N=100,以使得所有计算结果均具有四位有效数字的精度.通过与精细有限元分析(采用ABAQUS软件中S8R单元,400×400网格)的收敛结果进行对比可见, 不同厚宽比下板的挠度、 弯矩、 扭矩及剪力解均与有限元结果吻合得很好, 从而证明了本文求解方法的精确性.需要指出, 当前理论下集中载荷作用处的力学量不收敛, 有限元分析也证实了这一点, 因此表1中并未给出(0.5a, 0.5a)处的计算结果.图2给出了h/a=0.05时中心集中载荷作用下弹性地基上四边自由正方形中厚板的挠度图.
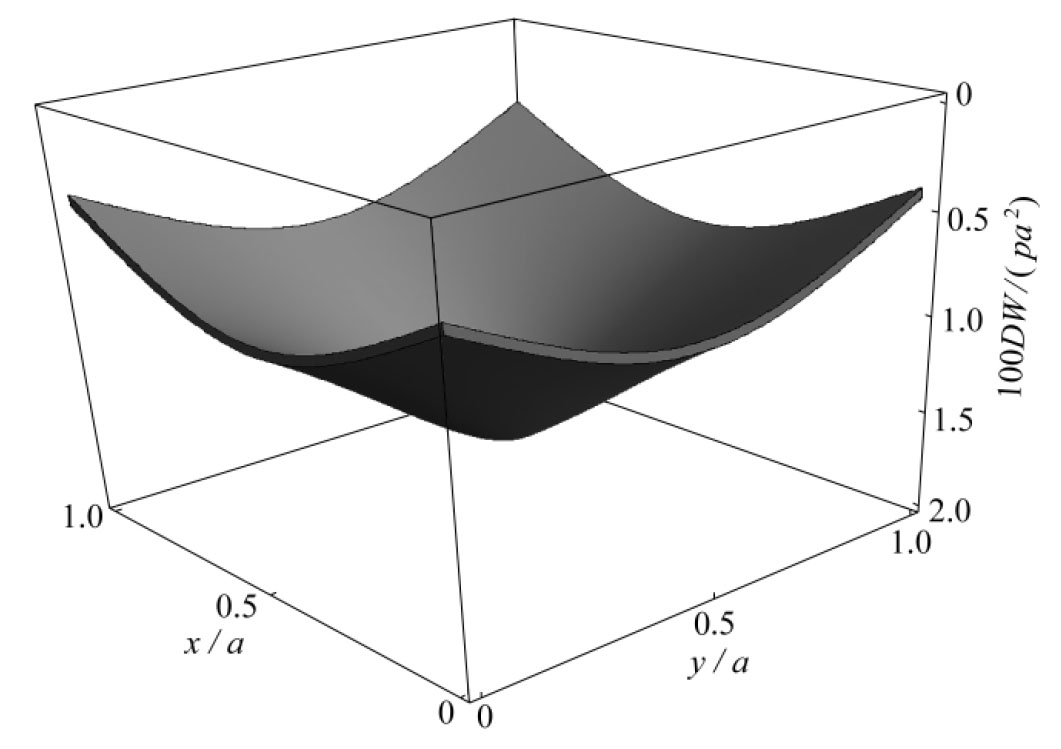
图2 h/a=0.05时中心集中载荷作用下弹性地基上四边自由正方形中厚板的挠度图
Fig. 2 The deflection graph of a rectangular thick plate with all edges free and resting on an elastic foundation, with a concentrated load applied at the center of the plate (h/a=0.05)
表1中心集中载荷p作用下弹性地基上四边自由正方形中厚板的弯曲解
Table 1 Bending solutions of a rectangular thick plate with all edges free and resting on an elastic foundation,with a concentrated loadpapplied at the center of the plate
四边自由板弯曲问题的解析求解通常被认为是各类边界条件下矩形板问题中最难求解的情况之一.本文基于笔者近年来提出的辛-叠加方法,解析求解了弹性地基上自由矩形中厚板的弯曲问题.与经典的Lagrange体系相比,本文的求解框架基于Hamilton体系,通过辛数学方法推导出子问题的解析解,进而通过叠加获得原问题的解.由于求解中无需假定解的形式,而是从基本控制方程出发,逐步严格推导,因此本文解法拓展了可求解问题的范围,可以得到一些经典解析方法难以获得的新结果.数值算例表明,本文获得的解析解与精细有限元分析结果吻合得很好,从而证实了所采用方法的有效性和计算结果的准确性,为检验各类近似/数值方法提供了对比基准.本文仅以自由板为例进行了求解,其他许多类似的板壳力学问题同样可以基于本文方法进行求解.
参考文献(References):
[1] MINDLIN R D. Influence of rotary inertia and shear on flexural motions of isotropic, elastic plates[J].Journal of Applied Mechanics, 1951,18(1): 31-38.
[2] LOK T S, CHENG Q H. Bending and forced vibration response of a clamped orthotropic thick plate and sandwich panel[J].Journal of Sound&Vibration, 2001,245(1): 63-78.
[3] HENWOOD D J, WHITEMAN J R, YETTRAM A L. Finite difference solution of a system of first-order partial differential equations[J].International Journal for Numerical Methods in Engineering, 1981,17(9): 1385-1395.
[4] BUCZKOWSKI R, TORBACKI W. Finite element modelling of thick plates on two-parameter elastic foundation[J].International Journal for Numerical and Analytical Methods in Geomechanics, 2001,25(14): 1409-1427.
[5] SHEN P, HE P. Bending analysis of rectangular moderately thick plates using spline finite element method[J].Computers&Structures, 1995,54(6): 1023-1029.
[6] PEREIRA W L A, KARAM V J, CARRER J A M, et al. A dynamic formulation for the analysis of thick elastic plates by the boundary element method[J].Engineering Analysis With Boundary Elements, 2012,36(7): 1138-1150.
[7] LIEW K M, HAN J B. Bending solution for thick plates with quadrature boundary[J].Journal of Engineering Mechanics, 1998,124(1): 9-17.
[8] LIU F L, LIEW K M. Differential cubature method for static solutions of arbitrarily shaped thick plates[J].International Journal of Solids and Structures, 1998,35(28/29): 3655-3674.
[9] CIVALEK Ö. Three-dimensional vibration, buckling and bending analyses of thick rectangular plates based on discrete singular convolution method[J].International Journal of Mechanical Sciences, 2007,49(6): 752-765.
[10] FERREIRA A J M, CASTRO L M S, BERTOLUZZA S. Analysis of plates on Winkler foundation by wavelet collocation[J].Meccanica, 2011,46(4): 865-873.
[11] LÜ C F, LIM C W, CHEN W Q. Semi-analytical analysis for multi-directional functionally graded plates: 3-D elasticity solutions[J].International Journal for Numerical Methods in Engineering, 2010,79(1): 25-44.
[12] YAO W, ZHONG W, LIM C W.Symplectic Elasticity[M]. Singapore: World Scientific, 2009.
[13] LI R, ZHONG Y, LI M. Analytic bending solutions of free rectangular thin plates resting on elastic foundations by a new symplectic superposition method[J].Proceedings of the Royal Society A:Mathematical Physical&Engineering Sciences, 2013,469(2153): 20681.
[14] LI R, NI X Q, CHEN G G. Symplectic superposition method for benchmark flexure solutions for rectangular thick plates[J].Journal of Engineering Mechanics, 2015,141(2): 04014119.
[15] LI R, WANG B, LI G. Benchmark bending solutions of rectangular thin plates point-supported at two adjacent corners[J].Applied Mathematics Letters, 2015,40: 53-58.
[16] LI R, WANG P, TIAN Y, et al. A unified analytic solution approach to static bending and free vibration problems of rectangular thin plates[J].Scientific Reports, 2015,5: 17054.
[17] WANG B, LI P, LI R. Symplectic superposition method for new analytic buckling solutions of rectangular thin plates[J].International Journal of Mechanical Sciences, 2016,119: 432-441.
[18] LI R, TIANY, ZHENGX, et al. New analytic bending solutions of rectangular thin plates with a corner point-supported and its adjacent corner free[J].European Journal of Mechanics:A/Solids, 2017,66: 103-113.
[19] LI R, WANG P, ZHENG X, et al. New benchmark solutions for free vibration of clamped rectangular thick plates and their variants[J].Applied Mathematics Letters, 2017,78: 88-94.
[20] LI R, WANG P, WANG B, et al. New analytic free vibration solutions of rectangular thick plates with a free corner by the symplectic superposition method[J].Journal of Vibration and Acoustics, 2018,140(3): 031016.
[21] LI R, ZHENG X, WANG H, et al. New analytic buckling solutions of rectangular thin plates with all edges free[J].International Journal of Mechanical Sciences, 2018,144: 67-73.
LI Rui, TIAN Yu, ZHENG Xinran, WANG Bo
(Department of Engineering Mechanics;International Research Center for Computational Mechanics,Dalian University of Technology;State Key Laboratory of Structural Analysis for Industrial Equipment(Dalian University of Technology),Dalian,Liaoning116024,P.R.China)
Abstract:Based on the symplectic superposition method proposed in recent years, the bending problems of free-edge rectangular thick plates resting on elastic foundations were analytically solved. The original problem was split into 3 subproblems corresponding to the bending problems of rectangular thick plates with 2 opposite edges slidingly clamped and resting on elastic foundations, which were solved with the symplectic geometry method. The analytic solution of the original problem was then obtained through superposition. Compared to the conventional analytic approaches such as the semi-inverse method, the symplectic superposition method has the advantages of both rationality of the symplectic method and regularity of the superposition method. The solution procedure starts from the basic equations of elasticity, and a rigorous derivation yields the analytic solutions, thus extending the scope of problems to be solved. The present method can serve as an effective analytic approach to complex boundary value problems of high-order partial differential equations in elasticity, as represented by the rectangular plate problems.
Key words:symplectic superposition method; elastic foundation; moderately thick plate; bending
Foundation item:The National Basic Research Program of China(973 Program)(2014CB049000);The National Natural Science Foundation of China(11302038)*
引用本文/Cite this paper: 李锐, 田宇, 郑新然, 王博. 求解弹性地基上自由矩形中厚板弯曲问题的辛-叠加方法[J]. 应用数学和力学, 2018, 39(8): 875-891.LI Rui, TIAN Yu, ZHENG Xinran, WANG Bo. A symplectic superposition method for bending problems of free-edge rectangular thick plates resting on elastic foundations[J]. Applied Mathematics and Mechanics, 2018, 39(8): 875-891.
文章编号:1000-0887(2018)08-0875-17
ⓒ 应用数学和力学编委会,ISSN 1000-0887
*收稿日期:2018-06-28
基金项目:国家重点基础研究发展计划(973计划)(2014CB049000);中国科协青年人才托举工程项目(2015QNRC001);国家自然科学基金(11302038)
作者简介:
李锐(1985—),男,副教授,博士,博士生导师 (E-mail: ruili@dlut.edu.cn);
田宇(1994—),男,硕士生 (E-mail: 1379342663@qq.com);
郑新然(1994—),男,博士生 (E-mail: zhengxinran@mail.dlut.edu.cn);
王博(1978—),男,教授,博士,博士生导师 (通讯作者. E-mail: wangbo@dlut.edu.cn).
摘要:基于近年来提出的辛-叠加方法,解析求解了弹性地基上自由矩形中厚板的弯曲问题.首先将原问题拆分为3类子问题,在Hamilton体系下,运用辛几何方法推导出子问题对应的弹性地基上对边滑支矩形板弯曲问题的辛解析解;以此为基础,通过叠加法思想,求出弹性地基上四边自由矩形中厚板的弯曲解.与半逆法等传统解析方法相比,辛-叠加方法兼备了辛方法理性和叠加法规律性的优点,在求解过程中不需要预先假定解的形式,而是由弹性力学基本方程出发,经过逐步严格推导获得解析解,因而大大拓展了可求解问题的范围,成为一种求解以矩形板问题为代表的弹性力学高阶偏微分方程复杂边值问题的有效解析方法.
关 键 词:辛-叠加方法; 弹性地基; 中厚板; 弯曲
中图分类号:O302
文献标志码:A
DOI:10.21656/1000-0887.390186

特邀作者简介:王博,1978年出生,大连理工大学教授,博士生导师,973计划青年首席科学家,教育部首批青年长江学者. 现任大连理工大学科学技术研究院院长,工业装备结构分析国家重点实验室副主任,中国力学学会青年工作委员会秘书长,中国科协全国委员会委员.
从事工程力学、计算力学研究,主要方向为:航空航天结构强度与轻量化设计、结构与多学科优化、大型结构力学实验研究等.近年从事的复杂板壳结构力学与优化研究工作尤其被同行关注,并解决了我国航天多个型号结构研制中的实际困难.主持青年973项目、国家自然科学基金、国防973课题、总装预研教育部支撑重点项目等.发表学术期刊论文90余篇,其中SCI论文50余篇,授权国内外发明专利10余项,成果被写入航天行业标准3项.曾获教育部技术发明一等奖(第1完成人)、辽宁省青年科技奖“十大英才”、辽宁省五一奖章等奖励荣誉,2018年获钱令希计算力学奖(青年奖).