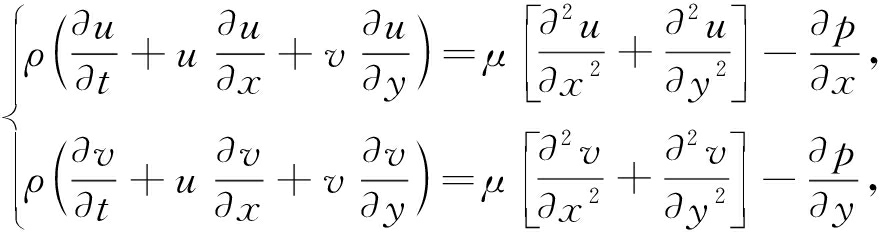
罗 骁1, 张新燕1, 张 珺2, 李立州1, 杨明磊1, 原梅妮1
(1. 中北大学 机电工程学院, 太原 030051; 2. 太原学院 数学系, 太原 030001)
随着现代航空发动机日益向着高负载、高效率和高可靠性发展,发动机中的上下游干涉引起的叶片颤振问题也更加突出.当上下游叶片相对转动时,上游叶片流场的尾流会使下游叶片表面气动力产生周期性振荡[1-2],引起叶片颤振[3-5],甚至导致叶片疲劳破坏[6].随着计算机的发展和计算机性能的提高,数值模拟方法成为研究非定常流下叶片颤振特性的主要方法,但其计算效率较低,工程应用不便[6-7].因此,如何准确快速地预测和分析尾流作用下叶片的颤振,成为发动机设计的重点难点问题.
近年来,气动力降阶模型被广泛用于叶片和机翼颤振的研究[7-15].其中,常用谐波平衡法将发动机中的非定常流场问题转化为振幅定常问题求解[8,12,14-15].Ekici等[4]用谐波平衡方法研究了叶片颤振,认为该方法极大地降低了计算时间,并与势流理论的结果符合较好.He[11]通过一阶谐波法,对叶栅周围流场非定常流分离的情况进行了研究,准确地预测了叶栅的颤振.Ashcroft等[14]用谐波平衡法研究了二维压气机叶栅在亚音速和跨音速条件下的颤振特性,发现谐波平衡法可以准确地预测叶栅的颤振.
为准确快速地预测尾流引起的叶片振动,提出了基于谐波平衡法的尾流激励的叶片振动降阶模型方法.该方法首先通过Fourier变换将上游尾流分解为若干尾流谐波,得到这些尾流谐波引起的叶片气动力谐波的振幅;通过这些气动力谐波振幅建立气动力降阶模型得到尾流引起的叶片气动力;再通过叶片的结构运动方程快速分析这些气动力作用下的叶片振动特性.
本文以二维叶片(见图1)为例,介绍尾流激励的叶片振动降阶模型方法.上游尾流以速度w在流场进口处移动,下游叶片在上游尾流作用下发生强迫振动.描述叶片周围流场的动量方程为
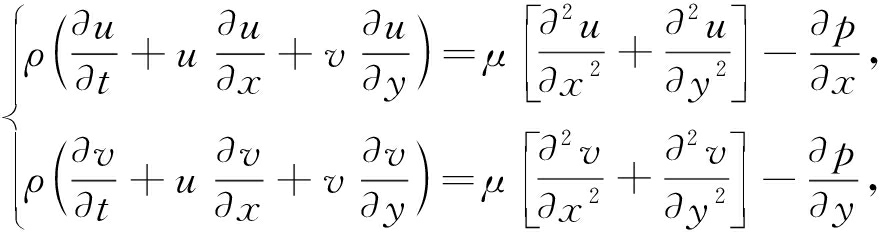
(1)
式中,u为x方向流速,v为y方向流速,p为压力.

图1 尾流激励的叶片气动力系统
Fig. 1 The system of aerodynamic forces on a blade under the wake
根据谐波平衡法线性化理论[1,10,15],在该尾流激励下,叶片周围的非定常流场可以用Fourier级数表示为

(2)
式中,p,u,v分别为流场中的压力、x方向速度和y方向速度分量;p0,u0,v0为流场压力和流速的定常部分;pk,uk,vk为流场压力和流速谐波振荡部分的振幅.
将式(2)代入式(1),按照文献[1]将非定常的N-S方程变换为定常的振幅方程,并根据由尾流引起的进口边界条件

(3)
求解式(2)中叶片周围流场谐波振荡部分的振幅![]() 将这些振幅代入式(2)就可确定尾流激励下叶片周围的流场状态.沿叶片表面压力积分,可得尾流激励下叶片的气动力:
将这些振幅代入式(2)就可确定尾流激励下叶片周围的流场状态.沿叶片表面压力积分,可得尾流激励下叶片的气动力:

(4)
其中
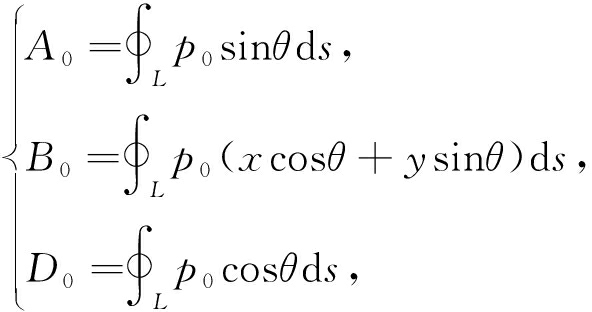
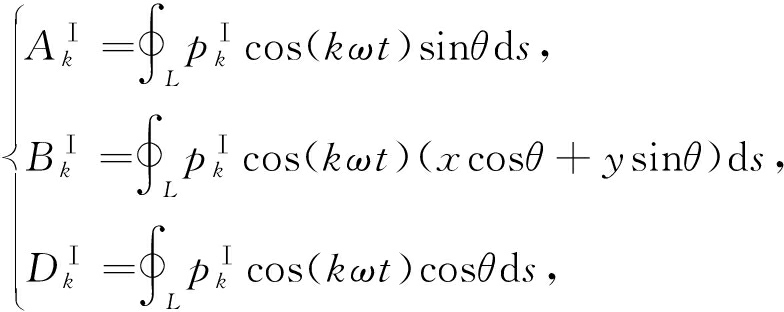

Cl为叶片气动升力,Cm为叶片气动力矩,Cd为叶片气动阻力,A0,B0,D0是叶片气动力的定常值,![]() 是叶片气动力谐波振荡部分的振幅.由于式(4)中气动力谐波振幅的计算过程十分复杂,本文通过将各尾流谐波加载在CFD模型进口进行计算,得到这些气动力谐波的振幅.
是叶片气动力谐波振荡部分的振幅.由于式(4)中气动力谐波振幅的计算过程十分复杂,本文通过将各尾流谐波加载在CFD模型进口进行计算,得到这些气动力谐波的振幅.
由式(4)可知:适当的选择频率阶次N,就可以在满足精度要求的前提下,快速地估计尾流激励下的叶片气动力.在气动力的作用下叶片发生振动,从而影响叶片性能.叶片气动力作用下的叶片结构运动方程为
(5)
其中,M为广义质量矩阵,K为广义刚度矩阵,C为广义阻尼矩阵,![]() 分别为广义位移、广义速度和广义加速度.
分别为广义位移、广义速度和广义加速度.
基于这一想法,本文提出的尾流激励的叶片振动降阶模型的建立步骤如下(见图2):
(a) 通过Fourier变换将尾流分解为不同频率的尾流谐波.
(b) 计算尾流Fourier分解后定常状态下的叶片气动力.
(c) 将各尾流谐波加载在CFD模型进口,获得各尾流谐波引起的叶片气动力谐波,并得到这些气动力谐波的振幅.
(d) 将步骤(c)中的气动力谐波的振幅代入式(4)得到尾流引起的叶片气动力.
(e) 通过式(5)的叶片结构运动方程,分析尾流激励下二维叶片的形心振动特性.
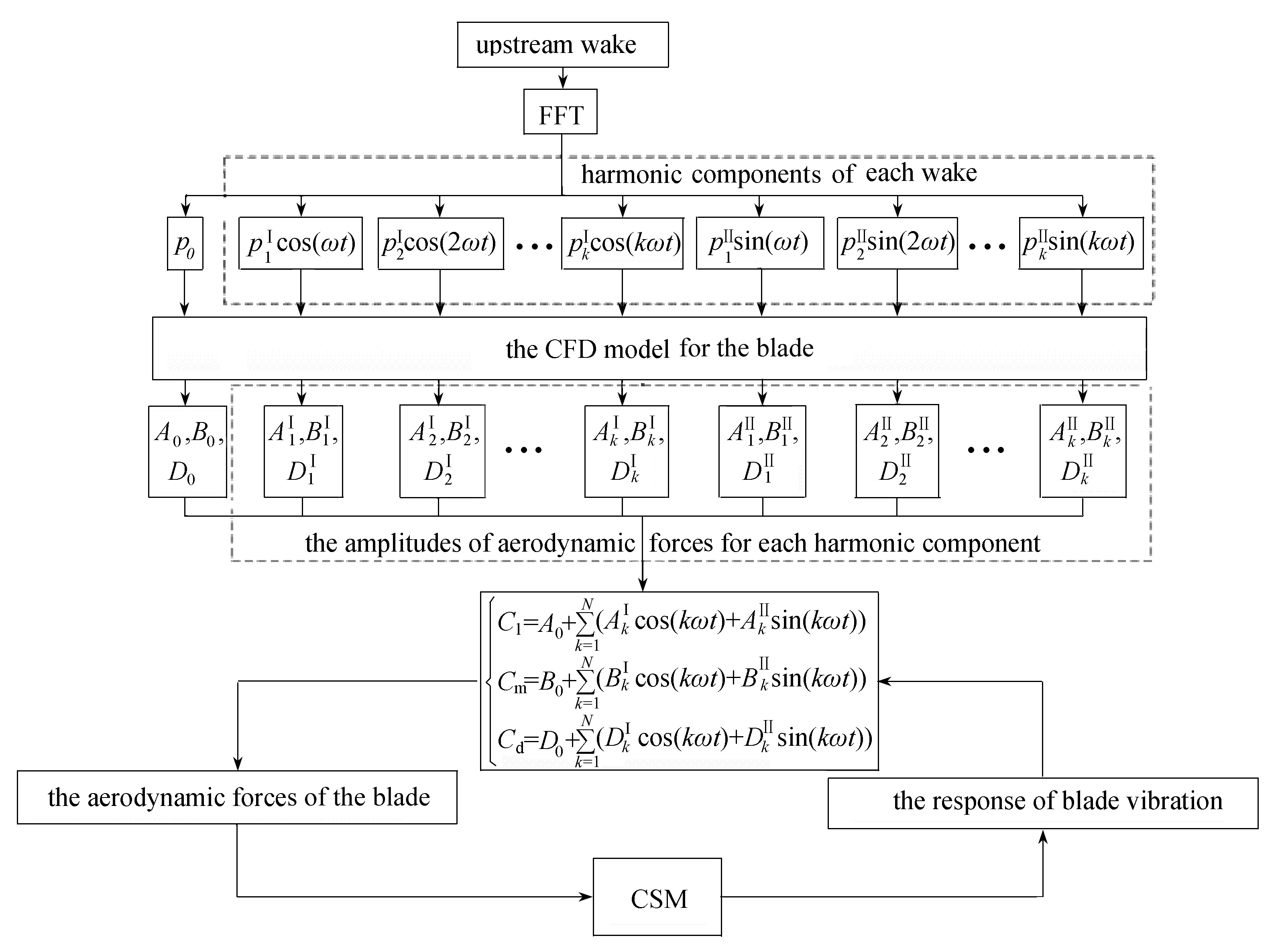
图2 尾流激励下叶片的颤振分析
Fig. 2 The analysis of the blade vibration under the wake
为简化表述,以上游尾流在模型进口的压力波动为例来验证本文的方法,CFD模型见图3.叶片流场采用FLUENT求解,理想气体, Spallart-Allmaras模型,无滑移壁面,稳态进口总压为120 300 Pa,稳态出口压力为101 325 Pa,温度为300 K.上游尾流以10 m/s的速度沿着进口y方向移动.
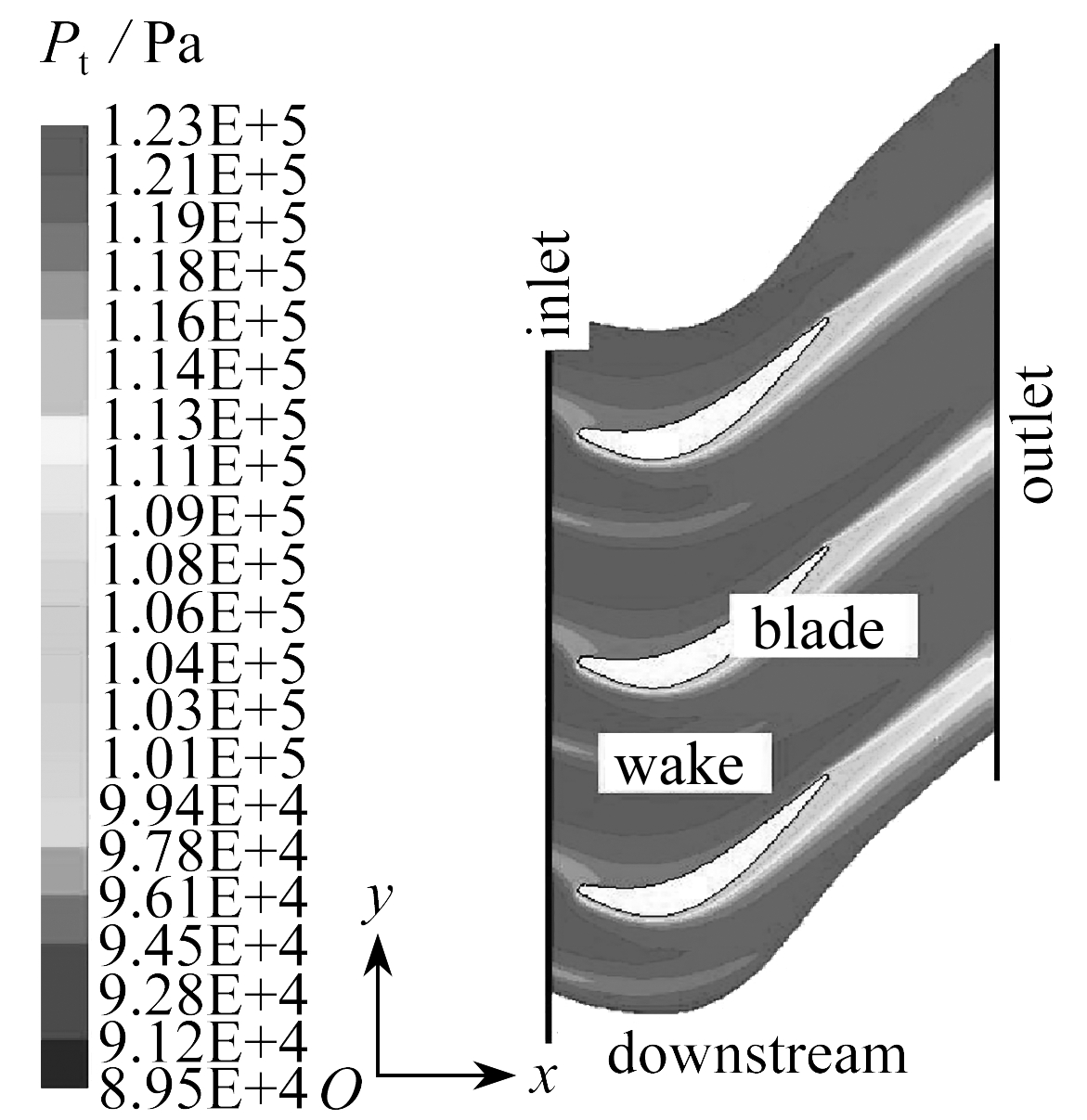
图3 叶片CFD模型
Fig. 3 The flow field model of CFD
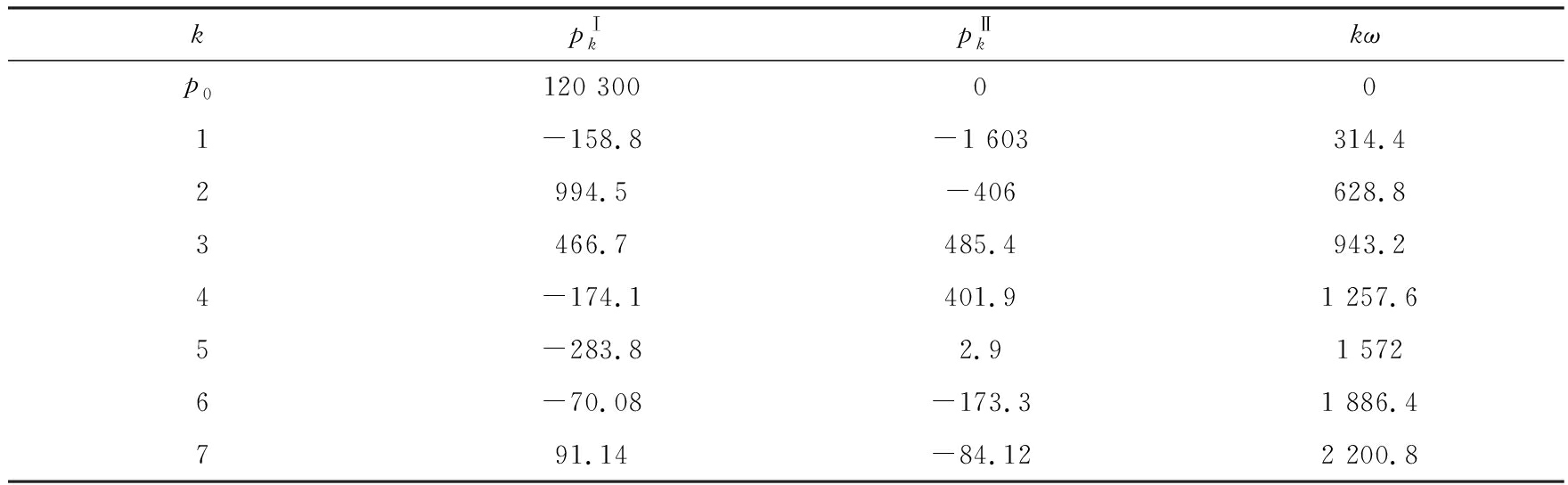
流场进口边界压力随时间的变化见图4中的实线.对该压力波进行Fourier分解, 取前7阶波形, 求得的Fourier级数的系数见表1.用7阶Fourier级数拟合的尾流压力波形见图4中的虚线.

图4 尾流及其Fourier级数拟合
Fig. 4 The wake and the fitting curve of Fourier series
表1尾流Fourier级数展开的系数和频率
Table 1 The coefficients and frequencies of the wake by FFT
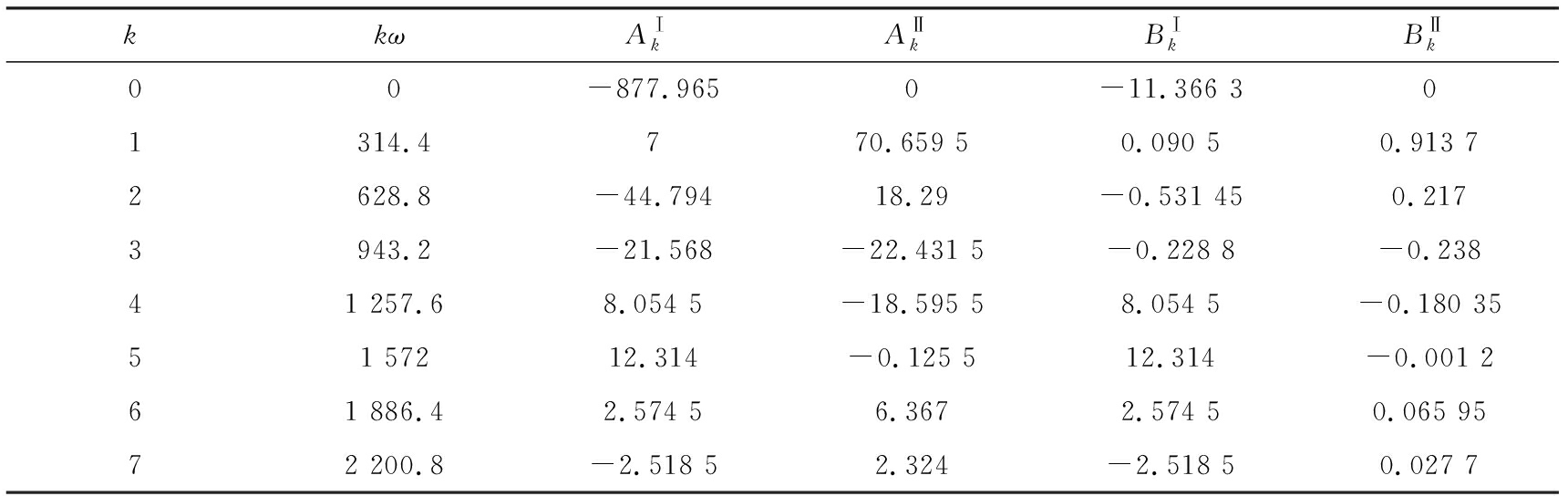
将表1中各尾流谐波分量逐个加载在CFD模型进口,进行短时间的CFD计算,获得各尾流谐波分量引起的叶片升力和力矩谐波,得到气动升力谐波的振幅,结果见表2.将表2的气动力振幅代入式(4),就可以得到尾流引起的叶片升力和力矩响应(见图5).
表2叶片气动力振幅
Table 2 The amplitudes of aerodynamic forces for the blade
在叶片气动力的作用下,叶片随上游尾流发生强迫振动,从而严重影响叶片性能.为快速分析尾流激励下叶片振动特性,本文通过叶片的结构运动方程对尾流引起的叶片振动进行分析.在得到尾流引起的叶片气动力(见图5)后,通过建立的叶片振动降阶模型计算出叶片的角速度、角位移、y方向的位移和速度.结果如图6所示,其中实线为降阶模型的计算结果,虚线为CFD的计算结果.

(a) 叶片升力 (b) 叶片力矩 (a) The lift on the blade (b) The moment on the blade
图5 尾流引起的叶片气动力
Fig. 5 The aerodynamic forces on the blade under the wake
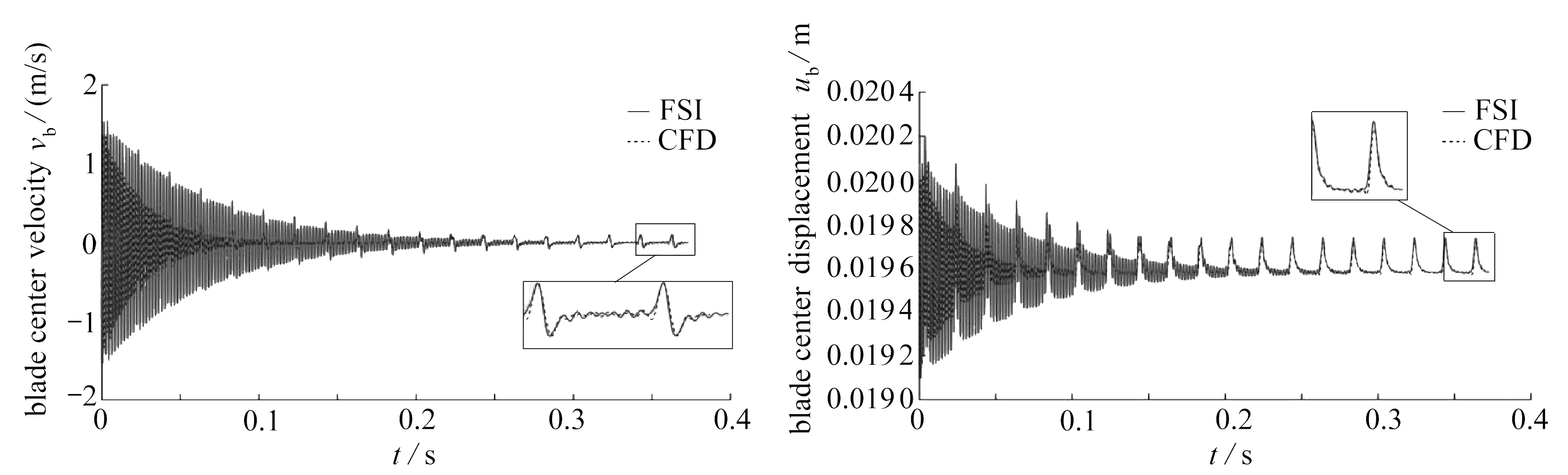
(a) 叶片形心速度 (b) 叶片形心位移 (a) The blade center velocity (b) The blade center displacement
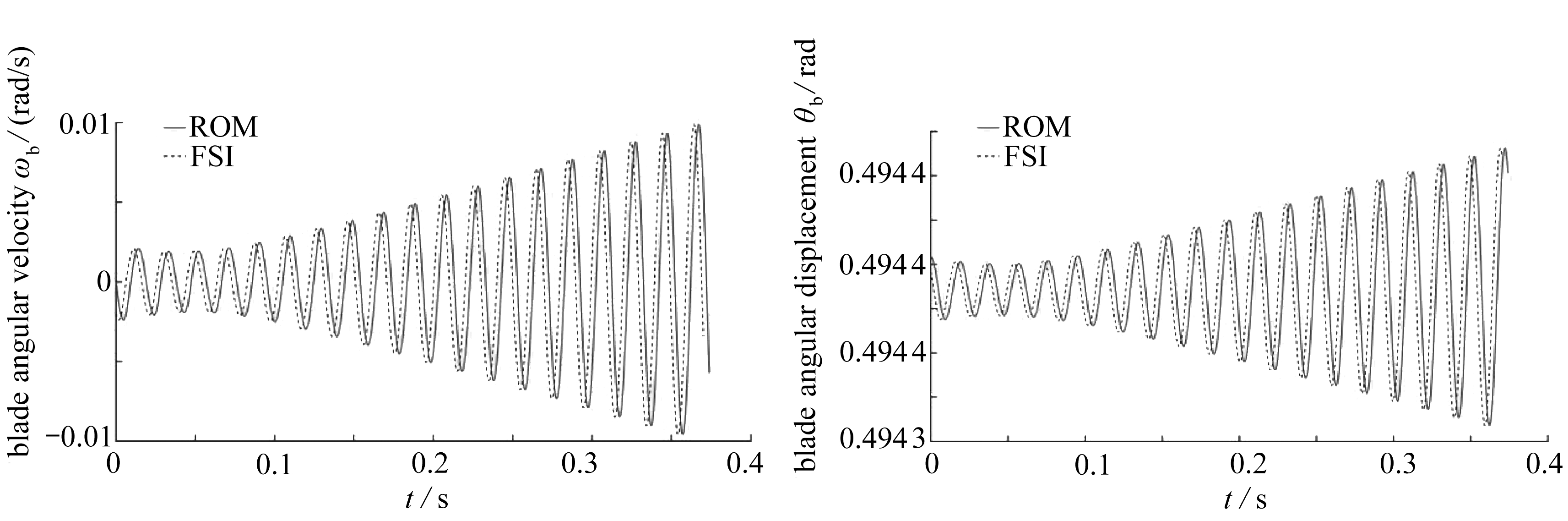
(c) 叶片角速度 (d) 叶片角位移 (c) The blade angular velocity (d) The blade angular displacement
图6 叶片的振动
Fig. 6 The vibration of the blade
从图6可以看出:
1) 冲击段之后,叶片振动降阶方法的计算结果与CFD的计算结果一致.
2) 叶片振动降阶模型很好地描述了叶片振动的周期特性.
为快速地对尾流激励下的叶片颤振特性进行分析,提出了尾流激励的叶片振动降阶模型方法.该方法通过求解尾流Fourier分解后各谐波分量引起的叶片气动力振幅,得到尾流激励下的叶片气动力,建立叶片振动降阶模型分析尾流激励下的叶片振动.算例的结果表明:尾流激励的叶片振动降阶模型可以快速准确地分析尾流激励下的叶片振动特性.
致谢本文作者衷心感谢飞行器结构完整性技术工业和信息化部重点实验室基金对本文的资助.
参考文献(References):
[1] 陈佐一. 流体激振[M]. 北京: 清华大学出版社, 1988: 24-27.(CHEN Zuoyi.Oscillating Fluid Mechanics[M]. Beijing: Tsinghua University Press, 1988: 24-27.(in Chinese))
[2] 王梅, 江和甫, 吕文林. 在尾流激振情况下叶片振动应力预估计技术[J]. 航空动力学报, 2007,22(4): 608-613.(WANG Mei, JIANG Hefu, LÜ Wenlin. Method to predict the blade vibration stress induced by wake flow[J].Journal of Aerospace Power, 2007,22(4): 608-613.(in Chinese))
[3] ZHAO Zhenhua, LÜ Wenliang, CHEN Wei, et al. Vibration numerical analysis of counter-rotating turbine with wake-flow using fluid-structure interaction method[J].Transaction of Nanjing University of Aeronautics&Astronautics, 2011,28(1): 66-72.
[4] EKICI K, KIELB R E, HALL K C. The effect of aerodynamic asymmetries on turbomachinery flutter[J].Journal of Fluids and Structures, 2013,36(1): 1-17.
[5] LAU Y L, LEUNG R C K, SO R M C. Vortex-induced vibration effect on fatigue life estimate of turbine blades[J].Journal of Sound And Vibration, 2007,307(3): 698-719.
[6] 陈刚, 李跃明. 非定常流场降阶模型及其应用研究进展与展望[J]. 力学进展, 2011,41(6): 686-701.(CHEN Gang, LI Yueming. Advances and prospects of the reduced order model for unsteady flow and its application[J].Advances in Mechanics, 2011,41(6): 686-701.(in Chinese))
[7] 张伟伟, 苏丹, 张陈安, 等. 一种基于CFD的叶轮机非定常气动力组合建模方法[J]. 推进技术, 2012,33(1): 37-41.(ZHANG Weiwei, SU Dan, ZHANG Chen’an, et al. A CFD-based compositional methodology of unsteady aerodynamic modeling for turbomachinery[J].Journal of Propulsion Technology, 2012,33(1): 37-41.(in Chinese))
[8] DIMITRIADIS G. Continuation of higher-order harmonic balance solutions for nonlinear aeroelastic systems[J].Journal of Aircraft, 2008,45(2): 523-537.
[9] BOURGUET R, BRAZA M, DERVIEUX A. Reduced-order modeling of transonic flows around an airfoil submitted to small deformations[J].Journal of Computational Physics, 2011,230(1): 159-184.
[10] SILVA W A. Reduced-order models based on linear and nonlinear aerodynamic impulse responses[J].AIAA Journal, 1999,233: 1-11.
[11] HE L. Harmonic solution of unsteady flow around blades with separation[J].AIAA Journal, 2008,46(6): 1299-1307.
[12] SU Dan, ZHANG Weiwei, YE Zhenyin. A reduced order model for uncoupled and coupled cascade flutter analysis[J].Journal of Fluids and Structures, 2016,61: 410-430.
[13] LIOU M S, YAO W G. Flutter analysis for turbomachinery using volterra series[C]//Proceedings of ASME Turbo Expro. Düsseldorf, Germany, 2014.
[14] ASHCROFT G, FREY C, KERSKEN H P. On the development of a harmonic balance method for aeroelastic analysis[C]//The6th European Conference on Computational Fluid Dynamics(ECFD VI). Barcelona, Spain, 2014.
[15] HUANG H, EKICI K. An efficient harmonic balance method for unsteady flows in cascades[J].Aerospace Science and Technology, 2013,29(1): 144-154.
LUO Xiao1, ZHANG Xinyan1, ZHANG Jun2, LI Lizhou1, YANG Minglei1, YUAN Meini1
(1.College of Mechatronics Engineering,North University of China,Taiyuan030051,P.R.China; 2.Department of Mathematics,Taiyuan University,Taiyuan030001,P.R.China)
Abstract:In aero-engines, downstream blades are forced to vibrate by the upstream wake, which often severely affects the flutter and fatigue performance of blades. Hence, an efficient method is needed for the analysis of this complex fluid-structure interaction phenomenon. A reduced-order model (ROM) method for blade vibration was proposed based on the harmonic balance method. The upstream wake was firstly decomposed into a number of harmonic waves by FFT (fast Fourier transform), and the aerodynamic forces on the blade were obtained through calculation of the amplitudes of aerodynamic forces on the blade due to each harmonic wave; then the blade vibration was fast analyzed by means of the structure dynamic equations for the blade coupled with the aerodynamic ROM. The results show that this method can analyze the flutter characteristics of the blade under wake excitation quickly and accurately.
Key words:wake; flutter; aerodynamic force; blade; Fourier series
Foundation item:The National Natural Science Foundation of China(51775518)
引用本文/Cite this paper: 罗骁, 张新燕, 张珺, 李立州, 杨明磊, 原梅妮. 基于谐波平衡法的尾流激励的叶片振动降阶模型方法[J]. 应用数学和力学, 2018,39(8): 892-899.LUO Xiao, ZHANG Xinyan, ZHANG Jun, LI Lizhou, YANG Minglei, YUAN Meini. A reduced-order model method for blade vibration due to upstream wake based on the harmonic balance method[J].Applied Mathematics and Mechanics, 2018,39(8): 892-899.
文章编号:1000-0887(2018)08-0892-08
ⓒ 应用数学和力学编委会,ISSN 1000-0887
*收稿日期:2017-11-23;
修订日期:2018-06-07
基金项目:国家自然科学基金(51775518)
作者简介:
罗骁(1992—),男,硕士生(E-mail: 18011524681@163.com);
李立州(1977—),男,副教授,博士(通讯作者. E-mail: lilizhou@163.com).
摘要:在航空发动机中下游叶片在上游尾流的作用下易发生受迫振动,严重影响叶片的颤振和疲劳性能.对于这种尾流作用下复杂的流固耦合情况需要一种有效的方法来分析.针对这一问题,提出了基于谐波平衡法的尾流激励的叶片振动降阶模型方法.该方法首先将上游尾流Fourier(傅立叶)分解为若干尾流谐波,并计算各尾流谐波下叶片气动力谐波的振幅,得到尾流引起的叶片气动力;再通过叶片的结构运动方程和气动力降阶模型的耦合分析尾流激励下叶片的振动.算例结果表明,该方法可以快速准确地分析尾流激励下叶片的振动特性.
关 键 词:尾流; 振动; 气动力; 叶片; Fourier级数
中图分类号:V231.3
文献标志码:A
DOI:10.21656/1000-0887.380294