 ·u=0,
·u=0,熊 英1,3, 关 晖2, 吴锤结3
(1. 中国人民解放军91550部队, 辽宁 大连 116023; 2. 国防科技大学 气象海洋学院, 南京 211101; 3. 大连理工大学 航空航天学院, 辽宁 大连 116024)
(我刊编委吴锤结来稿)
海洋中存在连续流体分层,潜体在分层流中运动时会受到分层效应的作用,产生不同于均匀流体的流动现象.例如,当潜艇在密度分层海洋中航行时,潜艇的航行扰动会激发内波,推进器的能量会被内波消耗,使潜艇航速突然变慢,像被海水黏住似的,发生所谓的“死水”现象.当水中运动体以较高航速在密度分层流体中作振荡运动航行时,有可能会出现负阻尼的现象,导致其辐射不稳定[1].对于物体在分层流中运动的问题,以往的研究主要集中于运动物体的尾流、体效应激发内波和尾流效应激发内波的问题,对分层流下运动体的受力研究并不多,同时,对于椭球体经历非定常运动的现象研究也很少.Lofquist等[2]的研究认为,在一定的Reynolds数下,垂向分层流中的水平运动体受到的阻力与Reynolds数几乎没有太大关系,而主要是受到内Froude数变化的影响.Greenslade[3]的研究表明,和均匀流体相比,密度分层效应会在横向和垂向对运动体产生更大的剪切作用,增加了物体运动姿态的不确定性和不稳定性;同时,内波、流场、湍尾流之间的相互作用形成了复杂的流场结构,这种复杂的流体结构将反作用于水下运动目标,往往会对水下运动目标的控制和运动轨迹产生无法预计的后果.密度分层加剧了负阻尼现象,在密度分层流体中,即使在较小的航速下,也有可能会出现负阻尼现象[4].总之,当潜艇在密度层化海洋中作这些运动时,会发生诸多与均匀流体中不同的现象,甚至会使潜艇的运动稳定性发生突变,操纵失控等.对于潜艇等水下运动体来说,透彻了解这种源致内波产生机理、流形态、力学作用过程,对于潜艇的外形设计、结构优化、目标识别和反识别具有重要的意义.本文建立了连续密度分层流下的6∶1椭球体自由俯仰振荡衰减模型.数值模拟了不同内Froude数Fri下的椭球体动态绕流流场,对椭球体受到黏性阻力和黏性升力进行了细致分析.
密度分层流体指在重力场的作用下,在某一方向上密度不均匀的流体的总称.对于垂直方向上的上重下轻的流体称作稳定成层,否则就是不稳定成层,本研究的对象是稳定成层流体.在变密度N-S方程的处理上引入了Boussinesq近似[5],Boussinesq近似包括3个方面的内容: 1) 利用体积守恒代替质量守恒; 2) 动量方程中仅考虑与浮力作用相关的密度变化,而对其他作为参考数的密度项则采用常数代替; 3) 状态方程包含密度的变化,仅由热膨胀和盐度变化引起.基于此,在连续性方程中忽略密度的个别变化,将动量方程中作为系数出现的密度取为常数,只在状态方程和静力方程中考虑热膨胀以及盐度对密度的影响.在Boussinesq近似下,对于不可压缩密度分层Newton(牛顿)流体,在Euler(欧拉)观点下,其满足的连续性方程和动量方程(N-S方程)分别是
 ·u=0,
·u=0,
(1)
![]()

![]()

![]()
(2)
其中,u表示三维瞬时速度向量,ρa表示参考密度,pd表示压力的上下波动值,通常称为动压,ρ表示当地密度,ρa表示平均密度,ρs=ρs(z)表示垂向连续密度分层在z处的未扰动状态下的值,k表示z方向单位矢量.Boussinesq近似只在重力项中考虑密度的变化,而控制方程的其他项中不考虑浮力作用,适用于密度变化不大的分层流问题中.为了实现对密度分层流体的模拟,采用多相流建模思想来建立密度分层流模型,将密度最小和密度最大的两种流体看作两种流体相,通过指定分布,组合两种流体相来实现对密度分层流体的模拟.在Boussinesq近似下,密度标量场是温度和盐度的线性函数,引入归一化无量纲密度α,并且,α=(ρ-ρl)/(ρh-ρl).对于密度垂向线性分布流场,ρl表示密度的最小值,ρh表示密度的最大值,那么α∈(0,1).以归一化密度α表示的密度输运方程:
![]()
 ·(αu)=Γα
·(αu)=Γα 2α,
2α,
(3)
这里,Γα表示质量的扩散系数.湍流模型采用k-ωSST模型[6].该模型的核心思想是近壁面利用k-ω湍流模型良好的鲁棒性,以捕捉到黏性底层的流动,而在主流动区域采用k- 湍流模型避免了k-ω模型对入口湍流参数敏感的缺点.k-ωSST将两个模型结合起来,实现了对反压力梯度区更精确的模拟,能够提供较高的精度和可靠性.
湍流模型避免了k-ω模型对入口湍流参数敏感的缺点.k-ωSST将两个模型结合起来,实现了对反压力梯度区更精确的模拟,能够提供较高的精度和可靠性.
研究对象是初始俯仰角45°的回转椭球体,研究其在一定的初始角速度的驱动下,绕质心做俯仰振荡的流体动力学过程.受到流体阻力和黏性剪切的作用,椭球体在黏性分层流体中的自由俯仰振动属于阻尼振动.在一定范围的俯仰角内,可以把椭球体振动过程近似看作线性过程.首先依据刚体转动定律和黏性阻尼理论建立椭球自由振动数学模型.椭球在转动过程中受到恢复力矩和黏性阻尼力矩的作用.椭球在转动过程中产生恢复力矩M1,恢复力矩的方向始终指向平衡位置.在一定角度范围内,恢复力矩M1与系统振动的角位移成正比,方向与椭球运动方向相反,即M1=-bθ,b表示椭球的刚度系数,在弹性限度内近似为常数.根据黏性阻尼理论,阻尼是椭球振动系统中,由于流体阻力、摩擦剪切引起的振动幅度下降的特性.椭球在水中振动过程中受到水介质黏性引起的黏性阻尼力矩的作用.黏性阻尼是指当振动速度不大的时候,由于介质黏性引起的阻力近似地与速度成正比.即,当振动速度不大时,可以认为黏性阻尼力矩与角速度成正比,方向与椭球运动方向相反,M2=-C(ω)dθ/dt.其中,C(ω)表示阻尼系数,一般在小角度范围内可以把C(ω)看做常数,但是,如果作为常数对待,那么,流体和椭球体相互作用的耦合过程将是单向的,这种单向耦合数值计算稳定性不好,极易导致数值震荡,同时,这种单向耦合对时间步长的要求也比较苛刻.本研究在流固耦合的处理上采用双向耦合[7].所以,这里将黏性系数作为角速度ω的函数,将在数值计算过程中借助流体求解器进行计算,并反馈给椭球振动求解器.关于角位移θ的椭球单一自由度的振动方程表示如下:
(4)
其中,J为振动系统的转动惯量,这是一个二阶常系数线性微分方程,通过四阶Runge-Kutta方法进行数值求解.本研究的初始条件:初始角位移为θ|t=0=0°,初始角速度为![]() 定义无阻尼振动固有频率
定义无阻尼振动固有频率![]() 系统阻尼比
系统阻尼比![]() 将方程(4)写成更为方便和清晰的表达式:
将方程(4)写成更为方便和清晰的表达式:
(5)
研究只针对ζ<1的欠阻尼情况,在ζ<1的情况下,微分方程(5)的解为一幅度按照指数衰减的振荡曲线:
其中,A和φ0由初始条件可以确定.可见,ζ<1条件下,对于单自由度阻尼振荡的椭球体,其振荡曲线为指数衰减的振荡曲线.在系统黏性阻尼系数和刚度系数确定的情况下,通过初始条件,可以确定椭球体自由衰减振荡曲线.
椭球阻尼振荡线性微分方程,通过四阶Runge-Kutta方法进行求解.黏性分层流体控制方程的离散采用有限体积方法.时间积分项的离散采用二阶隐式后向Euler格式.非线性对流项的离散基于Rhie-Chow修正方法[8],采用带TVD限制器的线性迎风格式和中心差分格式的混合格式进行离散[9].在扩散项的离散中,采用基于超松弛修正方法[9]的中心差分离散格式.对于梯度项的离散,采用最小二乘法.固壁边界条件采用无滑移边界条件.椭球振动方程通过四阶Runge-Kutta方法进行数值求解.流体控制方程利用压力的隐式算子分割(pressure implicit with splitting of operators,PISO)算法[10]求解.
对于离散后的线性代数方程组,采用PISO算法进行压力和速度的耦合.PISO算法对压力进行了两次修正,对速度进行了一次估值一次修正.对于瞬态问题,与SIMPLE算法相比,PISO算法的优点收敛速度快.将离散后的控制方程(2)写成如下形式:
Amum=H- pd,
pd,
(6)
其中,Am是第m个网格节点上所求速度um的系数.H表示非对角线系数以及除了压力梯度外的源项,并且
un和an分别表示除了第m个网格节点外的其他网格节点的速度和速度系数,um0/Δt表示时间项的差分值,S(ρ)表示密度源项的值.因为压力项还没有进行离散,所以这是一个半离散的方程.把操作项Am移到右侧,由前一时间步的压力和速度场得到速度的第一估值:
![]()
 pd.
pd.
(7)
以上就是PISO算法的第1步.把H/Am记作![]() 即
即![]() 对式(7)两边取散度,并根据连续性方程得关系式:
对式(7)两边取散度,并根据连续性方程得关系式:
 ·um=
·um=
![]()

![]()
则可得到关于压力的Poisson(泊松)方程:

![]()

![]()
(8)
方程(8)两侧对网格体积单元积分,再利用Gauss(高斯)公式,将体积分转化成面积分,用网格单元表面流率φf来表示![]() 即
即![]() 得到
得到
(9)
其中,sf表示网格点m的单位面法向量,其方向指向网格外侧.这样,不但避开了求体速度,而且将压力项的求解阶数从2降到了1,二阶的Poisson方程转化成一阶.这就是PISO 算法的第2步,求解Poisson方程得到压力的第一估值.根据压力的第一估值,由
![]()
 pd
pd
得到速度的第一修正值.用速度的第一修正值修正H,再求解Poisson方程得到压力的第二修正值,这就是PISO算法的第3步,速度的显式修正.
从耦合方法上,流体结构物相互作用分为紧耦合法和松耦合法.紧耦合法将流体和固体方程在同一矩阵中求解.理论上这种耦合十分理想,但在具体实现上,紧耦合方法很难将计算流体力学(CFD)和计算固体力学(CSD)真正结合起来.松耦合法不需要耦合流体方程和固体方程,而是通过流固交界面传递流体域和固体域的数据.相比于紧耦合方法,松耦合方法易于实现,易于将已有的流体模块和固体模块有效连接起来,同时具有计算效率高,易于验证的优越性.本文在流固耦合方法上选择松耦合方法.
从数据传递方式上,流体结构物相互作用分为单向耦合和双向耦合.在数据传递方式上选择双向耦合方式.结构体部分用Lagrange(拉格朗日)网格求解,流体部分用Euler网格求解.首先进行流场初始化,计算流场压力场和黏性力场,求解固体力学方程,求得固体Lagrange网格点的速度,继而计算固体上各个网格点的位移,并将新的位置坐标传递给Euler网格,进行Euler网格更新,计算更新后的流场并将相应的结果反馈给Lagrange网格.
如图1(a),具体的变量通过流固之间的接触表面通过节点到节点的方式传递.通过耦合,压力项和黏性力项被传递到流体域,速度和位移量被传递到固体域.如图1(b),通过Aitken亚松弛适应算法实现双向耦合过程的加速:
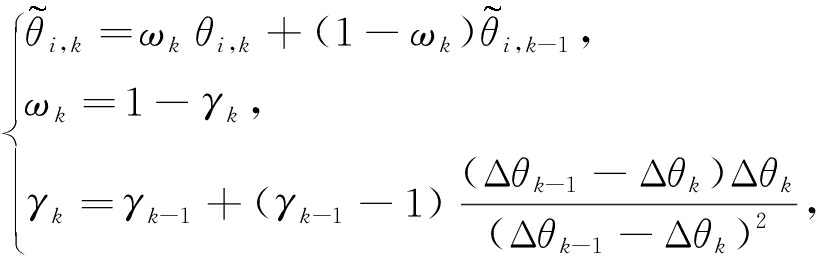
(10)
其中,![]() 这样,通过对压力的迭代和位移的松弛,实现了流体和固体之间的双向耦合.其数据传递过程是:1) 根据上一时间步计算的位移量更新网格; 2) 根据上一时间步计算的速度更新恢复力力矩和黏性阻尼力矩; 3) 用上一时间步计算的位移量场计算离散后的动量方程,对位移量进行迭代,即反复计算振动方程和流动方程;通过Aitken算法对迭代进行加速,直至残差收敛到满意值.相对于单向耦合,这种双向耦合能够很好地抑制数值振荡,并且能降低计算时间步长,通过Aitken加速,提高计算效率.
这样,通过对压力的迭代和位移的松弛,实现了流体和固体之间的双向耦合.其数据传递过程是:1) 根据上一时间步计算的位移量更新网格; 2) 根据上一时间步计算的速度更新恢复力力矩和黏性阻尼力矩; 3) 用上一时间步计算的位移量场计算离散后的动量方程,对位移量进行迭代,即反复计算振动方程和流动方程;通过Aitken算法对迭代进行加速,直至残差收敛到满意值.相对于单向耦合,这种双向耦合能够很好地抑制数值振荡,并且能降低计算时间步长,通过Aitken加速,提高计算效率.
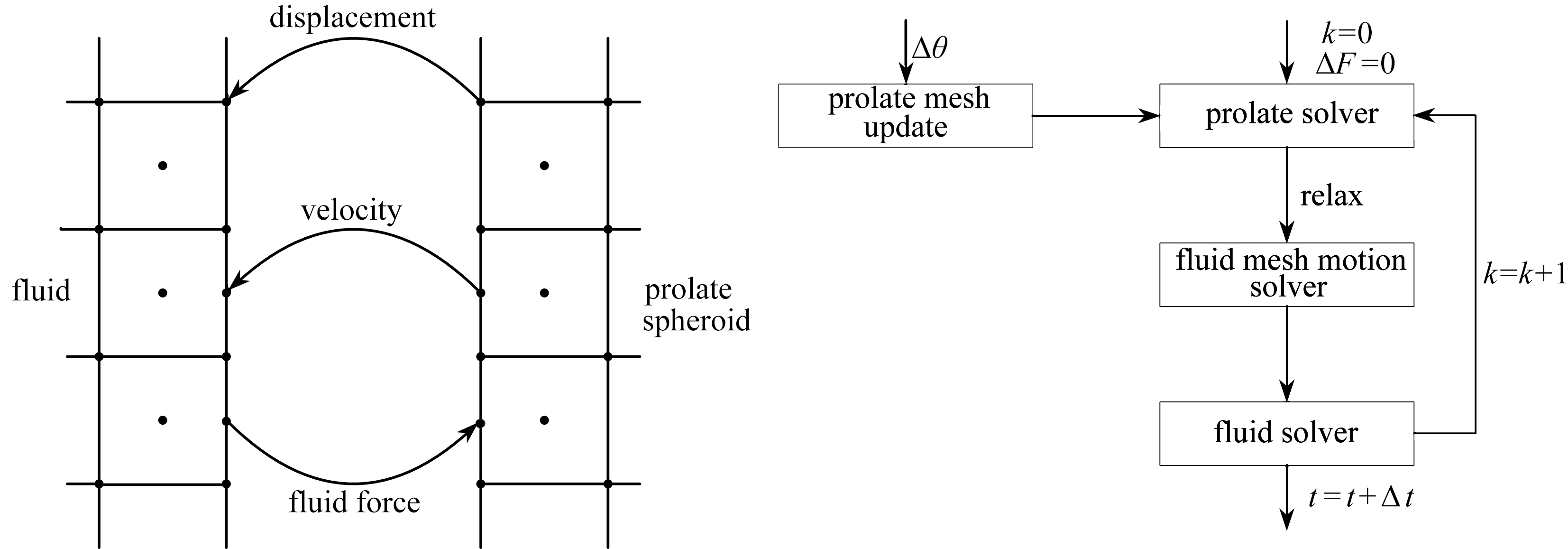
(a) 流固耦合数据交互 (b) 基于Aitken亚松驰适应算法的双向耦合 (a) The fluid-solid interaction data interchange (b) The 2-way coupling based on the Aitken algorithm
图1 流结构双向耦合
Fig. 1 The fluid structure 2-way coupling
垂向密度连续分层流体中受到水平来流作用的小球,密度分层流体的浮力频率N=1.55 s-1,动力黏性系数ν=1×10-6,小球半径r=1.26 cm,采用六面体网格,网格数350万个,采用速度入口.为了验证湍流模型对于计算密度分层流体绕流问题的稳定性, 计算了来流速度u∞=0.2 m/s,内Froude数Fri=10(Fri=u∞/Nr),Reynolds数Re=4 000(Re=2ru∞/ν)下的小球绕流激发内波流场.时间步长Δt=0.005 s,经过20Nt(浮力频率周期Nt=2π/N),大约81 s后,流场基本稳定.经过小球几何中心的水平剖面涡量和垂直剖面涡量如图2所示.在此Fri下,Lee波已经不再出现,小球绕流场在近尾区以湍尾流的形式传播,湍尾流在中尾区大约15倍小球直径的位置发生了塌陷,这种塌陷在远尾区激发了随机内波,随机内波位于大约20倍小球直径距离以外.比较图2(a)和2(b),可以发现,近尾尾涡、中尾塌陷区和远尾随机内波的传播在垂直方向均受到抑制,在水平方向则逐渐向展向拓宽,这是由于密度的垂向分层抑制了流场的垂向传播.可见, 所建立的数值模型无论是在近尾尾涡流场, 还是在远尾随机内波流场, 都能够真实地反映实际流场情况.这说明, 所建立的数值模型能够定性描述密度分层流绕流场.

(a) 水平剖面总涡量 (b) 垂向剖面总涡量 (a) The horizontal plane vorticity magnitude (b) The vertical plane vorticity magnitude
图2 小球黏性绕流涡量值云图
Fig. 2 Sphere viscous stratified flow vorticity magnitude contours
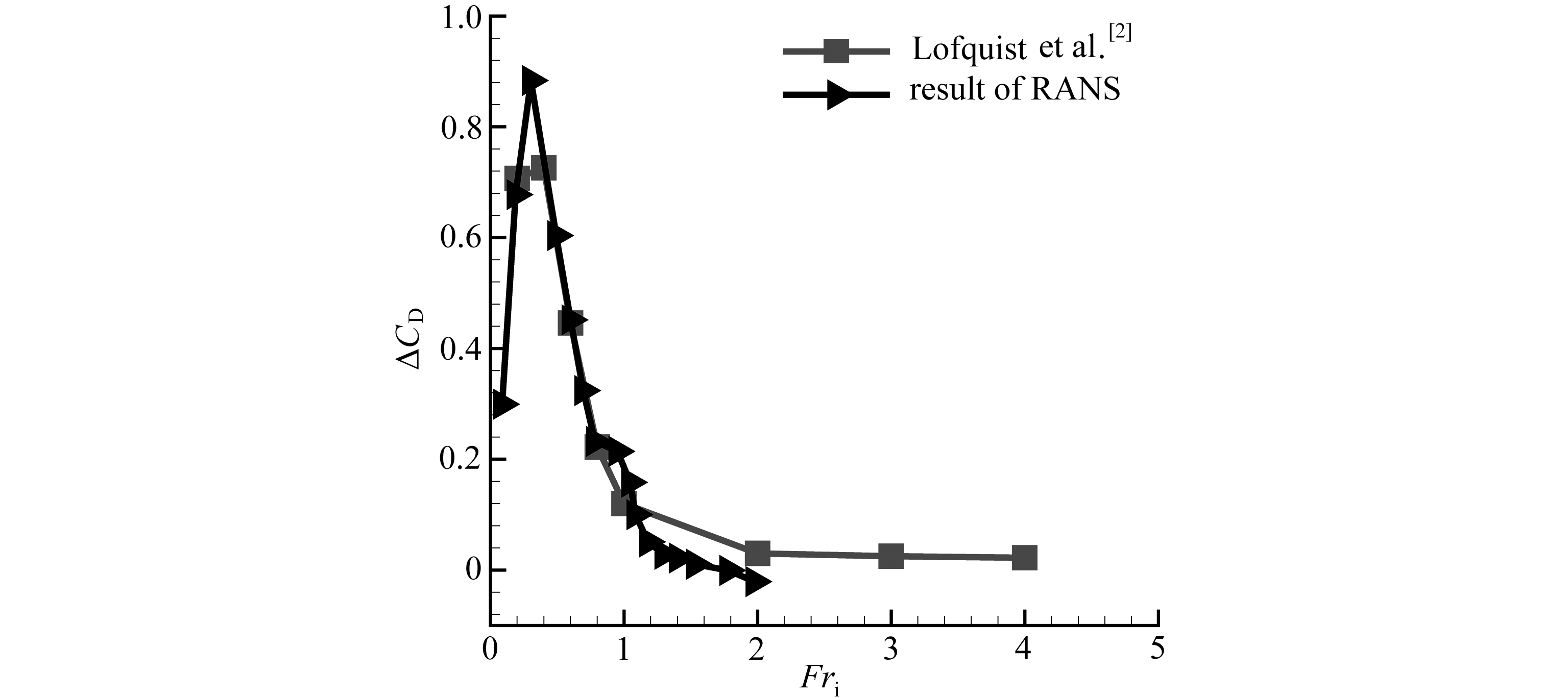
图3 增阻系数ΔCD随着Fri变化关系
Fig. 3 The relationship of increasing drag coefficient ΔCDwith Fri
为了进一步验证数值模型的正确性,考察在不同Fri下的小球绕流增阻系数.小球绕流的阻力系数用下式表示:
(11)
其中,FD表示小球在水平方向受到的阻力,ρ0表示小球中心处的水平线上的未扰动密度,u∞表示来流速度.对于密度均一流体,Fri=∞,阻力系数表示为CD(Re, ∞).为了考察密度分层效应对阻力的影响,增阻系数ΔCD表示为
ΔCD(Re,Fri)=CD(Re,Fri)-CD(Re, ∞).
(12)
对小球在垂向密度线性分布的流体中做水平运动绕流的增阻系数进行数值计算,并与试验结果进行对照.考察不同Fri下小球绕流的增阻系数,并与Lofquist等[2]的试验结果进行比较,验证结果如图3所示.可以看出数值模拟方法计算的结果与Lofquist等的试验结果基本吻合,当Fri=0.35附近,增阻系数出现极大值.随着Fri的逐渐增加,增阻系数由正值逐渐减小,甚至出现负值.这说明,在低Fri下,密度分层效应增加了阻力,而在高Fri下,湍流尾流的垂向扩散受到抑制.小球尾流分离点后移,前后压力差减少,阻力降低.通过对增阻系数的数值计算可以看出,所建立的数值模型能够对密度分层流场进行准确定量描述,进一步验证了所建立数值模型的准确性.
如图4(a)所示,计算域是三维长方体空间,流场长宽高是2 m×1 m×1 m,且x∈(-0.75 m,1.25 m),y∈(-0.5 m,0.5 m),z∈(-0.5 m,0.5 m),椭球体位于流场前端(0,0,0)处,本文中的6∶1椭球体的几何特征是一长轴,两短轴,两短轴长度相等,椭球体的长轴直径L=0.15 m,短轴直径D=0.025 m,长短比6∶1,初始俯仰角45°.

(a) 计算域 (b) 线性密度分层图 (a) The simulation domain (b) The vertical linear stratified contour
图4 三维连续密度分层流场
Fig. 4 The flow field

图5 椭球表面多边形网格
Fig. 5 The polygonal mesh on the prolate spheroid surface
Reynolds数ReD根据椭球体的短轴的长度D来进行定义.椭球体在初始时刻之前没有扰动的情况下,在密度分层流体中处于静态平衡状态,即其密度垂向成线性分布,椭球体将静态悬浮于流体中,如图4(b)所示.密度沿着z轴线性分布,密度的最小值ρl位于y=0.5 m处,并且ρl=988 g/m3,密度的最大值ρh位于y=-0.5 m处,并且ρh=1 012 kg/m3.椭球体在初始时刻受到一个瞬态俯仰力矩的作用开始做俯仰自由振荡,由于流体阻尼的作用,其振荡将随着时间的推进逐渐衰减.采用六面体半结构网格划分方法,网格总数400万个.椭球表面网格5 000个,如图5所示,其表面是以四边形为主的多边形网格.
在动态运动过程中,椭球体的运动幅度不大,网格变形技术就能够满足需要,网格变形采用径向基函数插值方法.其基本思想是运用径向基函数对椭球面网格节点的位移进行插值.然后,利用构造出来的径向基函数插值序列将物面的位移效应光滑地分散到整个三维空间网格节点上.网格变形过程如图6所示,椭球体在5°的小角度俯仰过程中,网格的变化光滑均匀,整体适应性较好.这种动网格方法只是调整原有的网格,而不增加新的节点,提高了计算的效率,非常适用于运动幅度不大的动态模拟.同时,这种方法因为保留原始网格的结构和密度以及正交性等特点,不会在求解过程中引入误差.

(a) 45°俯仰角 (b) 50°俯仰角 (a) The 45°attack angle (b) The 50° attack angle
图6 椭球俯仰运动过程中的网格变形
Fig. 6 The mesh deformation during pitching up
表1三种工况条件的说明
Table 1 Illustration of 3 cases

数值模拟程序基于OpenFOAM模型库进行开发,采用32个节点并行计算方法,时间步长Δt=0.000 05 s,程序走了4.4 s共花费30 d的时间.运动黏性系数ν=1×10-6m2·s-1,考察表1所示的3种工况下的分层流动态绕流场.角位移θ随时间的变化如图7所示,随着时间的推移,角位移呈指数振荡迅速减小并最终达到微幅振荡状态.
如图8给出了工况3下2.5 s的时间内密度变化的等值线和云图.椭球体的振荡搅动了周围的流体,把密度大的流体卷上来,密度小的流体卷下去,并在两端和中间处形成密度涡.虽然这种搅动使得周围流体发生了剧烈的掺混效应,其尾流密度等值线仍然呈现汇聚状态,体效应内波幅度随着搅动增大.虽然随着椭球体振荡幅度的衰减,这种掺混有平缓的趋势,但是仍然不同于椭球体静止状态下的绕流场.

图7 自由衰减振荡角位移随时间变化图
Fig. 7 The angular displacement with time changing during attenuated oscillations

(a) t=0 s (b) t=0.5 s (c) t=1 s

(d) t=1.5 s (e) t=2 s (f) t=2.5 s
图8 归一化密度α的等值线和变化云图
Fig. 8 Density α contours
进一步考察自由振荡的涡量等值面Q,如图9给出了工况3下2.5 s的时间内的涡的演化,椭球体上下两侧对称形成4个密度涡环,随着自由振荡的不断衰减,上面两个涡环较快消失,下面两个涡环消失得较慢.同时,密度的垂向分层限制了涡环的垂向传播,也加速了涡环的消失.这种限制助长了水平运动的发展,远场尾涡流场将以水平波动的形式传播.俯仰振荡将上下搅动周围流体,将上层低密度流体向下搅动,下层高密度流体向上搅动,并在椭球体上下两侧对称形成4个密度涡环.随着自由振荡的不断衰减,上面两个涡环较快消失,下面两个涡环消失得较慢,这种差异产生的涡升力造成了升力系数极值的产生.同时,密度的垂向分层限制了涡环的垂向传播,也加速了涡环的消失.这种限制助长了水平运动的发展,远场尾涡流场将以水平波动的形式传播.
对于椭球体的水下整体受力情况,相比于流体表面压力,在实际的工程应用中,更关注黏性力对椭球体的剪切作用.参考文献[11]中引用的等效直径d,对于6∶1扁球体的等效直径d=1.817D,D表示扁球体的短轴.那么,黏性阻力系数和黏性升力系数的定义如下:
(13)
其中,γx和γz分别表示黏性阻力和黏性升力.
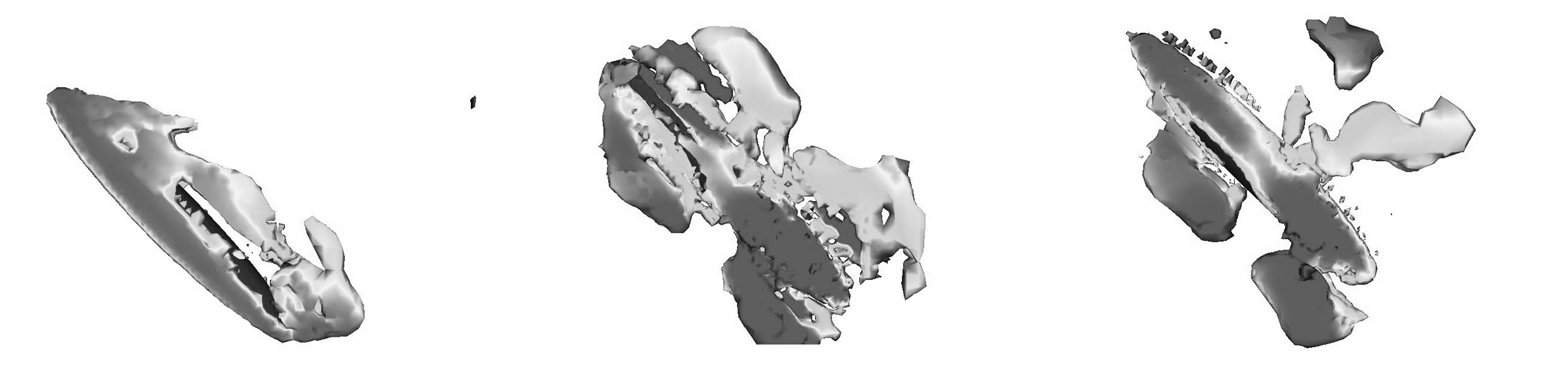
(a) t=0 s (b) t=0.5 s (c) t=1 s

(d) t=1.5 s (e) t=2 s (f) t=2.5 s
图9 涡量等值面,Q=0.5
Fig. 9 The vorticity isosurface, Q=0.5
研究了3种工况下的黏性阻力系数和黏性升力系数的变化特征.如图10(a)所示,3种工况下的黏性阻力系数Cf都在0.8 s附近达到最大值,并在之后缓慢减小,并微幅振荡变化,随着Fri的增加,黏性阻力系数逐渐减小.对于工况1的情况,黏性阻力系数的变化更为剧烈,即使在t=3 s以后椭球体小幅振荡的时候,其变化仍然均匀起伏波动,这是因为小Fri下,其水平运动减弱变像加剧了垂向运动.而对于工况3的情况,其黏性阻尼系数的变化要平缓的多.这说明,水平流速的增加消弱了密度的垂向运动趋势,尾涡流场拖后,剪切作用减小.如图10(b)所示,黏性升力在0.5 s附近就达到最小值,这是因为椭球体振荡在上下形成对称的4个涡环,上面的涡环先于下面的涡环消失,使上下产生剪切力差增加,从而出现极值.值得一提的是升力一直为负值,即便是最后慢慢趋向于0,也仍然为负值.同时还发现,对于工况2和工况3两种情况,双向耦合较好地抑制了数值震荡,而对于工况1的情况,在初期,数值震荡仍然明显.这说明,这种双向耦合模型更适用于较大的Fri和较高的Re下的数值计算.而对于较低的Fri和Re,分子黏性力作用更加明显,其数值震荡在初期没有得到很好抑制.比较3种情况还发现,随着来流速度的增加,阻力系数不增反降.这说明,对于自由俯仰振荡的椭球体,负阻尼现象仍然出现.

(a) 黏性阻力系数变化图
(a) Curves of the viscous force drag coefficient

(b) 黏性升力系数变化图
(b) Curves of the viscous force lift coefficient
图10 受力分析
Fig. 10 Stress analysis
本文研究了海水密度线性分层条件下6∶1椭球体经历俯仰振荡逐渐衰减的动态绕流问题,并对自由衰减振动下的椭球体绕流流场进行分析.对于透彻了解潜艇等水下航行体在密度分层海水中低频振动的流动结构具有重要意义.数值计算结果表明,随着来流速度的增加,阻力系数不增反降.这说明,对于自由俯仰振荡的椭球体,负阻尼现象规律仍然出现.本文将阻尼系数作为流体求解器的动态反馈,基于Aitken亚松弛适应算法实现了流体和椭球体运动之间的双向流固耦合,这种处理方法避免了单向耦合容易导致的数值震荡.因计算区域所限,本文未对远场激发流场进行分析,这也是下一步的研究方向.
参考文献(References):
[1] NEWMAN J N. The damping of an oscillating ellipsoid near a free surface[J].Ship Research, 1961,5(3): 44-58.
[2] LOFQUIST K K, PURTELL L P. Drag on a sphere moving horizontally through a stratified liquid[J].Journal of Fluid Mechanics, 1984,148(1): 271-284.
[3] GREENSLADE M D. Drag on a sphere moving horizontally in a stratified fluid[J].Journal of Fluid Mechanics, 2000,418: 339-350.
[4] STUROVA I V. Radiation instability of a circular cylinder in a uniform flow of a two-layer fluid[J].Journal of Applied Mathematics and Mechanics, 1997,61(6): 957-965.
[5] GUSHCHIN V A, MITKIN V V, ROZHDESTVENSKAYA T I, et al. Numerical and experimental study of the fine structure of a stratified fluid flow over a circular cylinder[J].Journal of Applied Mechanics and Technical Physics, 2007,48(1): 34-43.
[6] MENTER F R, KUNTZ M, LANGTRY R. Ten years of industrial experience with the SST turbulence model[J].Turbulence Heat and Mass Transfer, 2003,4(1): 625-632.
[7] XIONG Ying, GUAN Hui, WU Chuijie. Unsteady analysis of six-DOF motion of a 6∶1 prolate spheroid in viscous fluid[J].Science China(Physics,Mechanics&Astronomy), 2017,60(11): 114711. DOI: 10.1007/s11433-017-9071-y.
[8] RHIE C M, CHOW W L. Numerical study of the turbulent flow past an airfoil with trailing edge separation[J].AIAA Journal, 1983,21(11): 1525-1532.
[9] 熊英, 关晖, 吴锤结. 基于有限体积法的非结构网格大涡模拟离散方法研究[J]. 应用数学和力学, 2016,37(11): 1129-1144.(XIONG Ying, GUAN Hui, WU Chuijie. LES discretization methods for unstructured meshes based on the finite volume method[J].Applied Mathematics and Mechanics, 2016,37(11): 1129-1144.(in Chinese))
[10] SSA R I. Solution of the implicitly discretised fluid flow equations by operator-splitting[J].Journal of Computational Physics, 1986,62(1): 40-65.
[11] JIANG F, GALLARDO J P, ANDERSSON H I. The laminar wake behind a 6∶1 prolate spheroid at 45° incidence angle[J].Physics of Fluids, 2014,26(11): 1044-1050.
XIONG Ying1,3, GUAN Hui2, WU Chuijie3
(1.Unit91550of PLA,Dalian,Liaoning116023,P.R.China; 2.College of Meteorology and Oceanography,National University of Defense Technology,Nanjing211101,P.R.China; 3.School of Aeronautics and Astronautics,Dalian University of Technology,Dalian,Liaoning112024,P.R.China)
(Contributed by WU Chuijie, M. AMM Editorial Board)
Abstract:The numerical calculation model for the continuous stratified flow was established through the study on the decaying process of the free pitching oscillation of the prolate spheroid in viscous stratified flow. The correctness of the numerical model was verified through numerical simulation of the viscous flow field of a sphere and calculation of its increasing drag coefficient. Under the 45° prolate spheroid initial angle the pitching oscillation process was investigated, with the Aitken sub-relaxation self-adaptive algorithm-based 2-way fluid-solid coupling method, and numerical simulation of the flow field around the prolate spheroid in pitching decaying oscillation at different values of Froude numberFriwas performed. The numerical results show that, the pitching up and down agitates the surrounding fluid, and forms 4 symmetric density vortex rings on both sides of the prolate spheroid; the vertical density stratification limits vertical propagation of the vortex rings and accelerates disappearance of the vortex rings, and this limitation contributes to the development of horizontal motion. At higherFriand Reynolds numberRe, the 2-way coupling method suppresses numerical oscillations. The research also finds that, with the increase of the incoming velocity, the drag coefficient decreases, which means that for the prolate spheroid with free pitching oscillation, the phenomenon of negative drag still appears.
Key words:viscous stratified flow; prolate spheroid; free decaying; pitching oscillation
Foundation item:The National Natural Science Foundation of China(11572350;11372068); The National Basic Research Program of China(973 Program)(2014CB-744104)
引用本文/Cite this paper: 熊英, 关晖, 吴锤结. 黏性分层流中椭球体俯仰振荡研究[J]. 应用数学和力学, 2018,39(8): 900-912.XIONG Ying, GUAN Hui, WU Chuijie. Study on prolate spheroid pitching oscillation in viscous stratified flow[J].Applied Mathematics and Mechanics, 2018,39(8): 900-912.
文章编号:1000-0887(2018)08-0900-13
ⓒ 应用数学和力学编委会,ISSN 1000-0887
*收稿日期:2018-01-24;
修订日期:2018-05-25
基金项目:国家自然科学基金(11572350;11372068);国家重点基础研究发展计划(973计划)(2014CB-744104)
作者简介:熊英(1978—),女,博士生(E-mail: yxiong_2011@163.com); 关晖(1970—),女,副教授(E-mail: guanhui70@163.com); 吴锤结(1955—),男,教授(通讯作者. E-mail:cjwudut@dlut.edu.cn).
摘要:以黏性密度分层流下椭球体自由俯仰振荡衰减过程为研究内容,建立了密度连续分层流数值计算模型.通过对经典小球黏性绕流场的数值模拟和增阻系数的计算验证了数值模型的正确性.以初始45°攻角下的椭球体俯仰振荡过程为研究对象,采用基于Aitken亚松弛适应算法的双向流固耦合方法,数值模拟了不同内Froude(弗汝德)数Fri下椭球体俯仰衰减振荡的动态绕流场.数值研究结果表明,俯仰振荡将上下搅动周围流体,在椭球体上下两侧对称形成四个密度涡环,密度的垂向分层限制了涡环的垂向传播,也加速了涡环的消失,这种限制助长了水平运动的发展,远场尾涡流场将以水平波动的形式传播.在较高的内Froude数Fri和Reynolds(雷诺)数Re下,双向耦合抑制了数值震荡.研究还发现,随着来流速度的增加,阻力系数不增反降,这说明,对于自由俯仰振荡的椭球体,负阻尼现象仍然会出现.
关 键 词:黏性分层流; 椭球体; 自由衰减; 振荡
中图分类号:O357.41
文献标志码:A
DOI:10.21656/1000-0887.390041