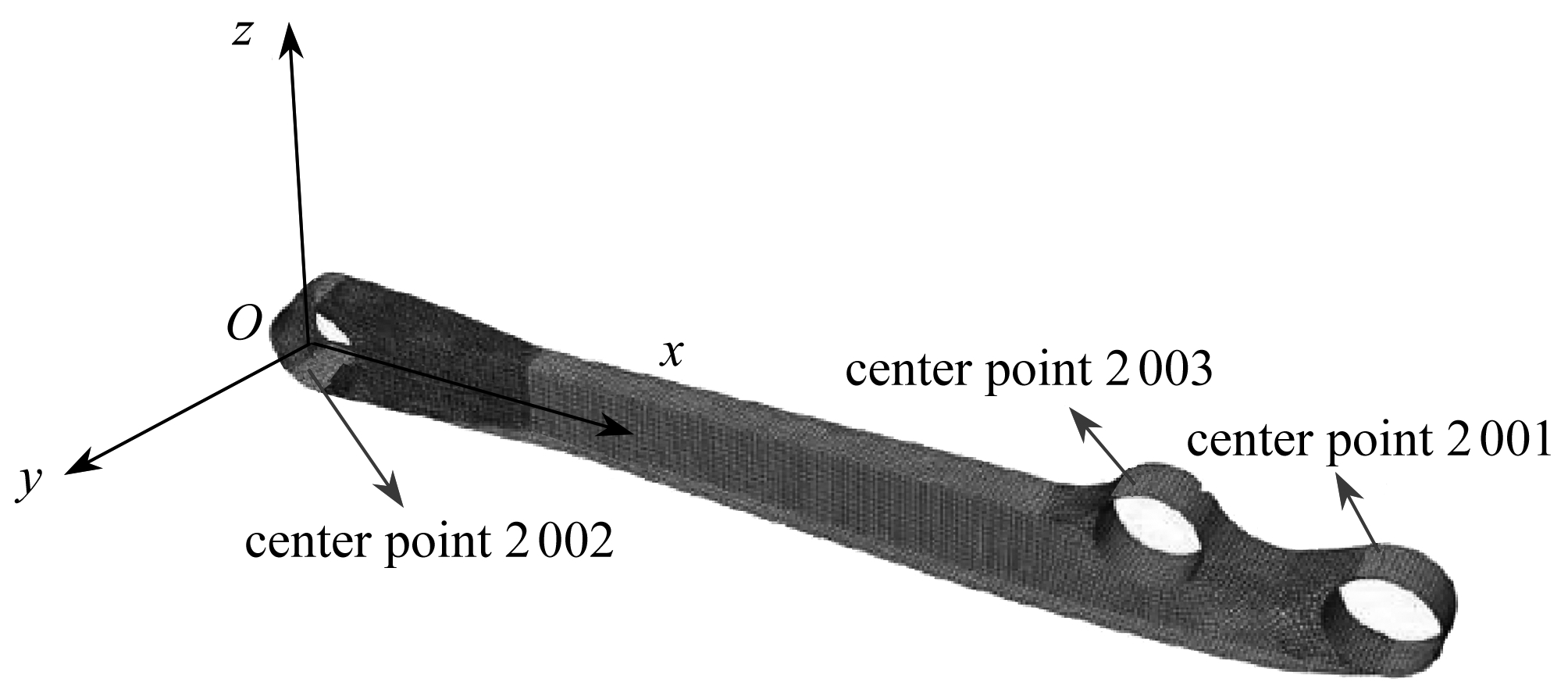
图1 碳纤维复合材料(CFRP)后纵臂三维有限元模型
Fig. 1 The 3D finite element model of the CFRP rear longitudinal arm
朱 迪, 姚 远, 彭雄奇
(上海交通大学 材料科学与工程学院, 上海 200030)
(我刊编委彭雄奇来稿)
新能源汽车因电池自重大,故进行底盘的轻量化设计就显得十分重要和迫切,以期大幅度降低底盘自重、延长电池的续航里程[1].碳纤维增强复合材料以其高的比强度、比刚度、耐疲劳以及耐腐蚀等优异的力学和物理性能,成为汽车底盘零部件轻量化发展方向之一[2].在复合材料零件优化设计中,采用模拟仿真而非试验的方法找出最优解,可以减少试验消耗和预算开支.国内外通常将算法分为确定型优化算法和概率型优化算法,确定型优化算法的理论基础完善,但无法解决复杂性高、数据量大的问题且易陷入局部寻优,实际使用较少.概率型优化算法将随机搜索引入优化算法中,有效改善了确定型优化算法的不足[3-4].在复合材料层合板设计中常见的概率型算法有遗传算法和群智能算法.在遗传算法方面,Dileep等基于圆孔的有效测试数据,将神经遗传算法用于石墨/环氧树脂层压板切口强度的预测,具有一个隐层的NME神经元网络的层压板的强度预测与实测数据吻合得非常好[5].刘振国等提出了一种铺层分级遗传优化的方法,对受力分布极度不均匀的层合板进行优化[6].在群智能算法方面,Rao等提出了应用混合蛙跳算法(SFLA),求解组合优化问题与层压复合材料结构的铺层顺序优化相结合[7],对复合材料板的屈曲和破坏载荷优化问题进行了数值试验,然后对加筋复合材料圆柱壳进行了优化设计.Salamat等研究了4种简支横向荷载作用下反对称角铺设层合板和正交铺设层的优化问题,使用了蜜蜂算法以优化提高层合板的强度[8].但这两种算法的特点决定了对数据量大小要求高.所以本文从碳纤维复合材料的使用入手,对多工况下各角度铺层厚度占比的有效值和最优值进行了计算.引入基于树的深度学习算法,提出了一种优化方案解决传统有限元耗时长的问题,大幅度降低了计算所需时间,为复合材料零部件设计提供了有益的参考.
基于Yao等的研究[9], 利用SOLIDWORKS软件进行复材后纵臂的三维造型.接着将其导入HYPERMESH中进行几何清理、 网格划分, 根据纵臂各部分几何特征分别采用CAE商业软件ABAQUS中的S3和S4R壳单元,以及C3D8R、 C3D6和C3D4实体单元, 纵臂CAE模型见图1.

图1 碳纤维复合材料(CFRP)后纵臂三维有限元模型
Fig. 1 The 3D finite element model of the CFRP rear longitudinal arm
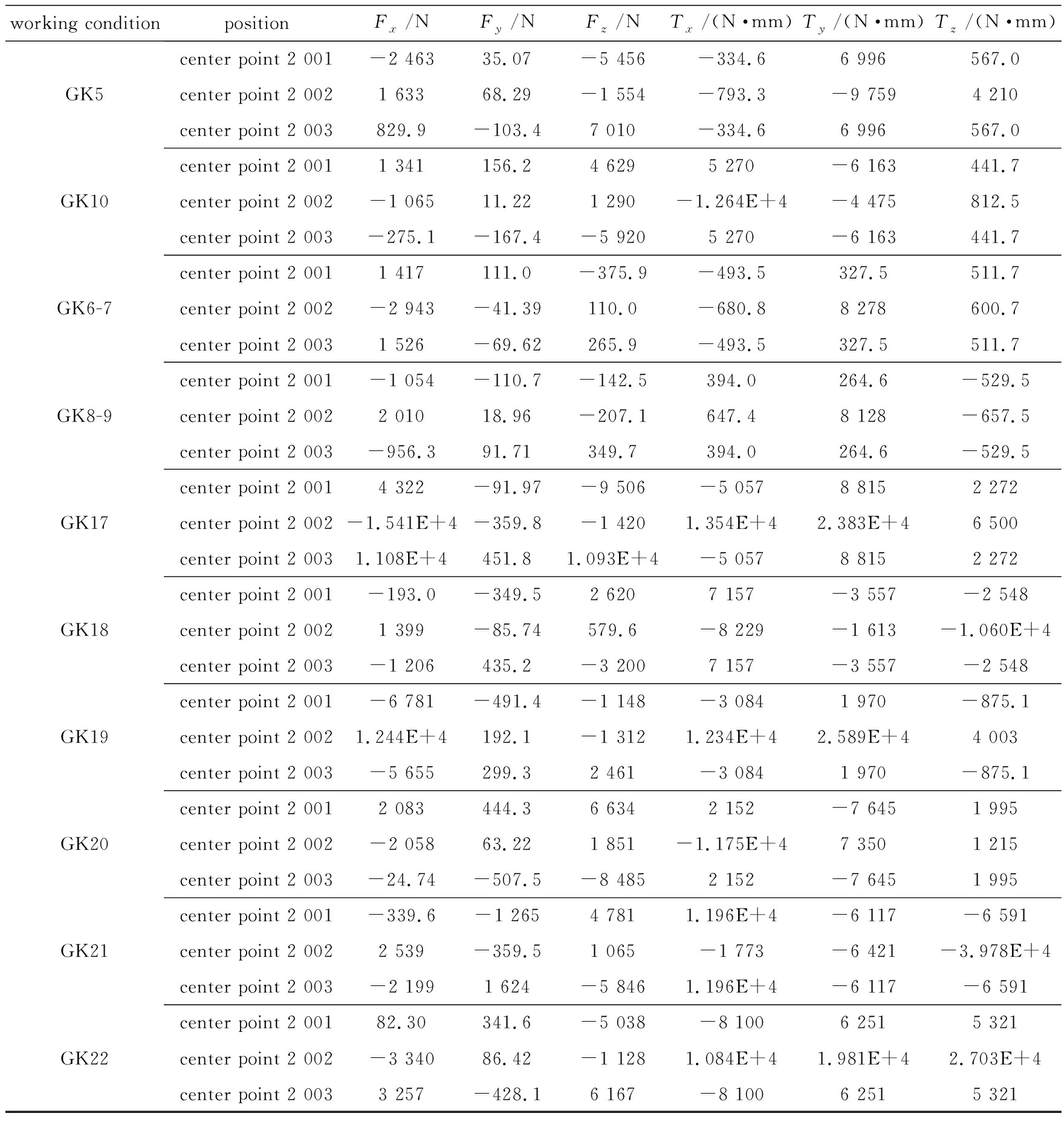
套管和纵臂臂身通过理想的共节点连接,套管中心点与套管表面上的各节点建立耦合约束,材料参数基于龚友坤等对T700碳纤维单向带的力学性能测试[10],载荷和边界条件施加在套管的中心点上,后纵臂各载荷点的载荷信息见表1.
表1后纵臂各载荷点的载荷信息
Table 1 Load information of each load point in the rear longitudinal arm
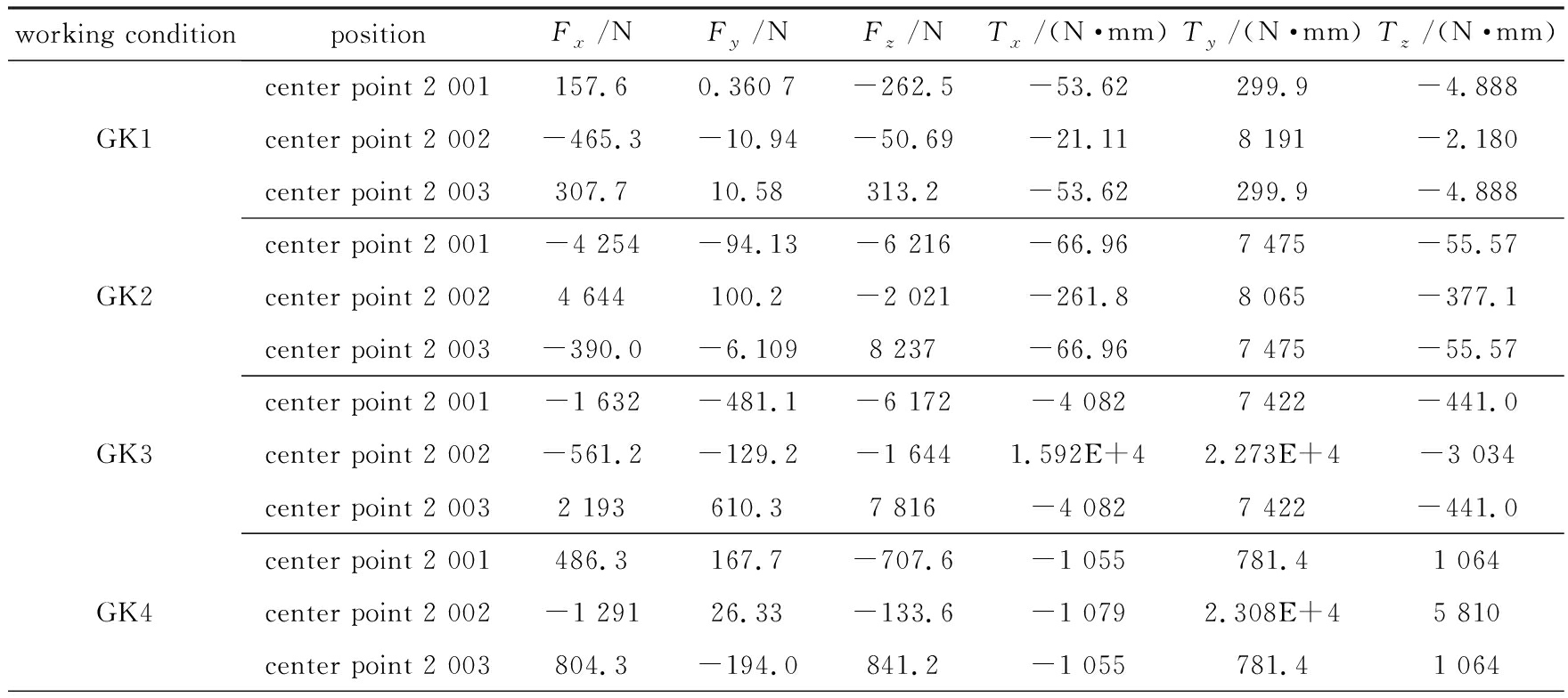
续表1
铺层角度只选取0°,45°,-45°,90°这4个值,铺层厚度是0.175 mm(单层碳纤维单向带预浸料厚度)的倍数值,均为离散性变量.各铺层角度占比如图2所示.
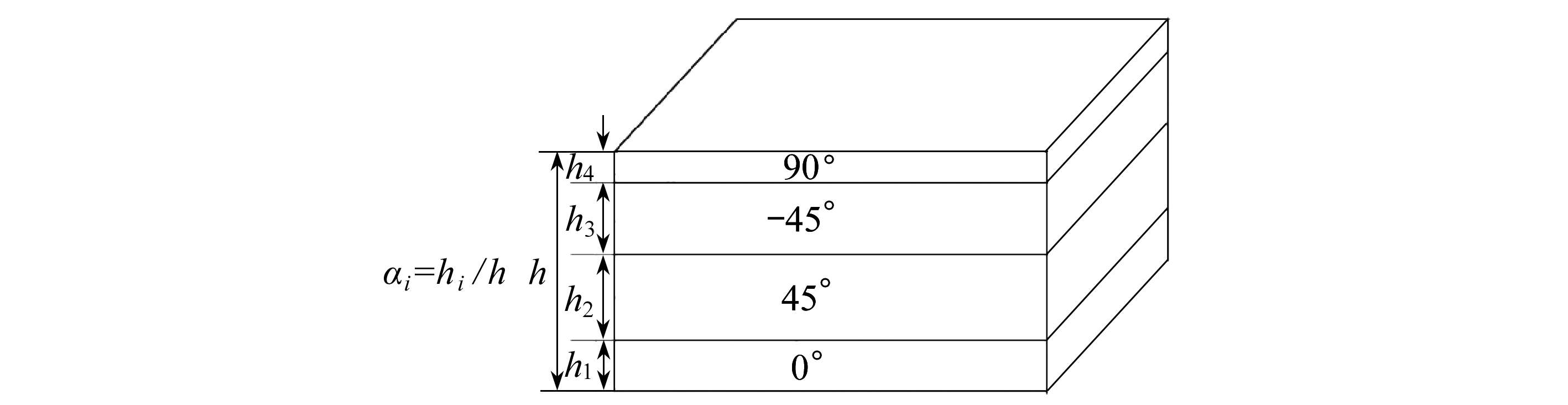
图2 各铺层角度占比示意图
Fig. 2 Schematic diagram of the proportion of different ply angles
碳纤维复合材料后纵臂CAE分析的要求是,在各个强度工况下强度达到标准并且变形小于2 mm.强度分析采用Tsai-Wu失效准则[9],当Tsai-Wu因子大于1时,碳纤维复合材料发生失效.
初步设定铺层数为21, 对不同工况下的0°铺层厚度占比(α1)、 45°铺层厚度占比(α2)、-45°铺层厚度占比(α3)、 90°铺层厚度占比(α4)进行遍历求解,读取Tsai-Wu因子和位移值.
具体流程如下:
1) 批量生成input文件.这里面包含两个子步,先生成一个input文件模板,后用Python将input模板修改成可以批量化输出input的文件.主要的工作是将模板文字查询关键字位置后插入需要修改的参数值,调用Python的循环语句,循环生成input文件.对于21层铺层下的所有αi的组合值与14种工况叠加生成28 336(2 024×14)个input文件.
2) 批量提交input文件进行计算.采用Windows批量处理文件,直接在DOS窗口提交.Windows批量处理文件有如下优势: ① 可以批量提交,实现全日夜工作,节省时间; ② 删掉不需要的结果文件,选择只存储ODB文件,节省磁盘空间.每个工况(2 024个job)平均计算时间为12.34 h,生成29.6 GB的海量数据.
3) 批量读取ODB文件目标数据.后处理ODB文件分为两步:第一步是根据ODB文件的数据结构,使用Python批量调取ODB文件.由于ODB文件的数据结构复杂,且每个分支的读取格式不完全相同,所以需要先确定读取的目标数据.第二步循环读取Tsai-Wu因子、最大位移值,并写出到文本文件中.每个工况(2 024个ODB文件)平均计算时间为11.35 h,生成约88 kB(约为总数据量的0.29%)的数据.
作为一类回归模型,基于树 (tree based) 的算法[11-12]增加了模型准确性和可靠性以及减小了解释的难度.和线性模型不同,它们对非线性关系也能进行很好的映射.常见的基于树的模型[12]有:决策树(decision tree)、随机森林(random forest) 和提升树(boosted tree).决策树[12]是最基础的算法,为了克服决策树的各种缺点,发展出了很多其他算法[13-14],比如袋装(bagging)[15]、随机森林[12]、XGBoost[16]、DART(dropouts meet multiple additive regression tree)[17-18].每种方法都包括生成多种树,如图3所示.这些树被联合起来,生成一个单一的一致性预测结果,并且经常带来预测精度的提升.
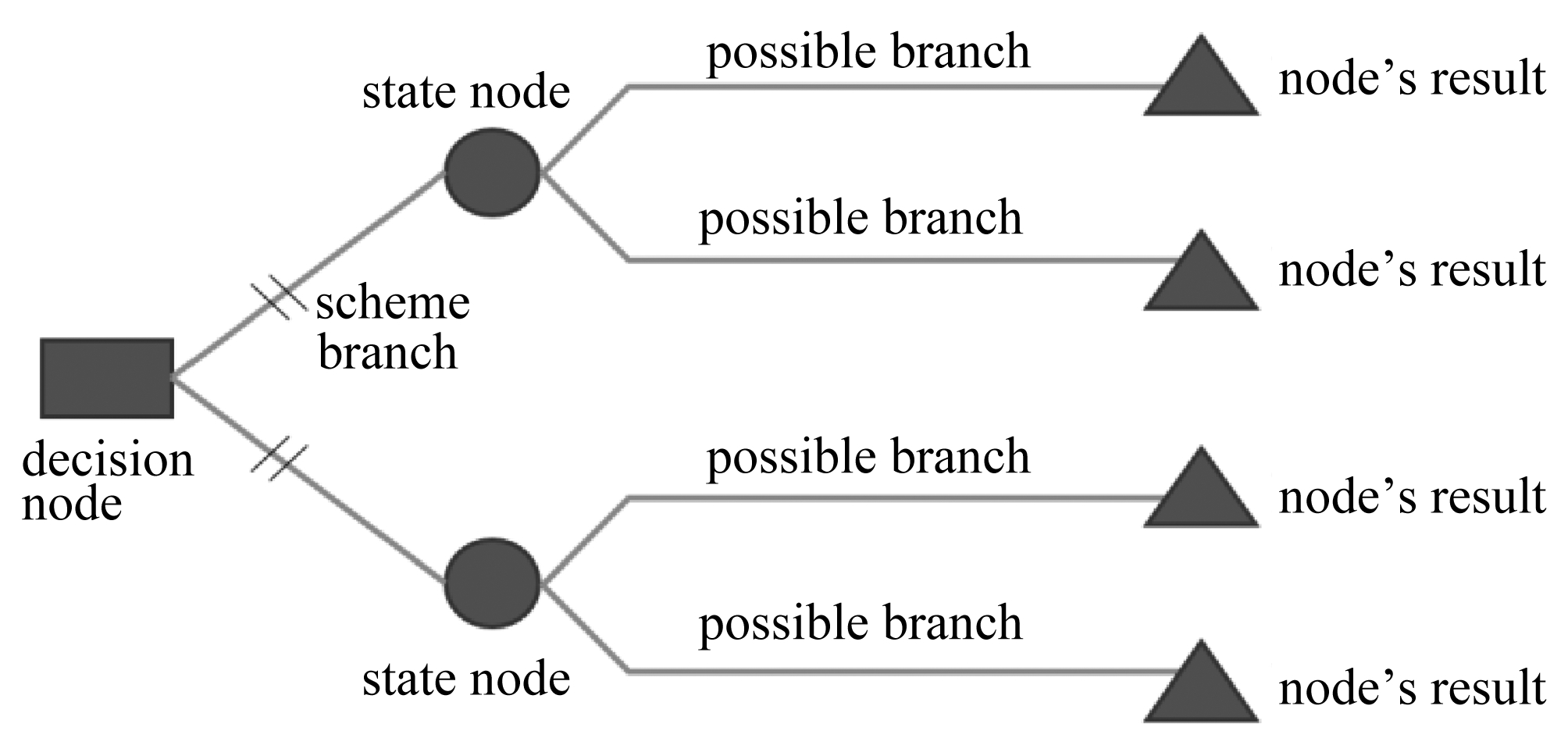
图3 决策树概念图
Fig. 3 Decision tree
对于新工况的计算,本文提出了采用基于树的算法解决计算量大、耗时长的问题.对新工况GK0进行了遍历性计算,GK0的载荷信息如表2所示,生成了2 024行数据.
从GK0取出i行和之前已有工况的28 336行数据共同组成训练集((i+28 336)行),而相应剩余的数据((2 024-i)行)作为测试集验证算法模型的准确性,新工况所需计算量与测试集占比的关系如表3.如若算法模型可靠,那么只计算i行数据,就可得到合理有效的解.可以将i看作新工况的所需计算量.
表2新工况GK0的载荷信息
Table 2 Load information of new working condition GK0

表3新工况所需计算量与测试集占比的关系表
Table 3 A relationship table for the ratio of the amount of calculation to the test set in the new working condition

Tsai-Wu因子是连续值且具有一定规律性的数据, 在数学建模中, 通常建立回归模型对其进行预测.而本文数据量只有3万左右, 建立基于树的模型对于这样的数据量来说是有效且合理的.
基于铺层和工况情况, 本节提取了各角度铺层占比αi(i=1,2,3,4)、力fjk(j=1,2,3分别对应套管2 001, 2 002, 2 003;k=1,2,3分别对应x,y,z三个坐标轴方向)、 力矩Tjk(参数设定同fjk).另外计算了不同套管的力的标量值fj(j=1,2,3分别对应套管2 001, 2 002, 2 003)和不同套管的力矩的标量值Tj(参数设定同fj).分析数据可以看出, 套筒2 003的扭矩情况与2 001相同, 所以剔除了套筒2 003的扭矩相关特征, 即T3和T3k(k=1,2,3).
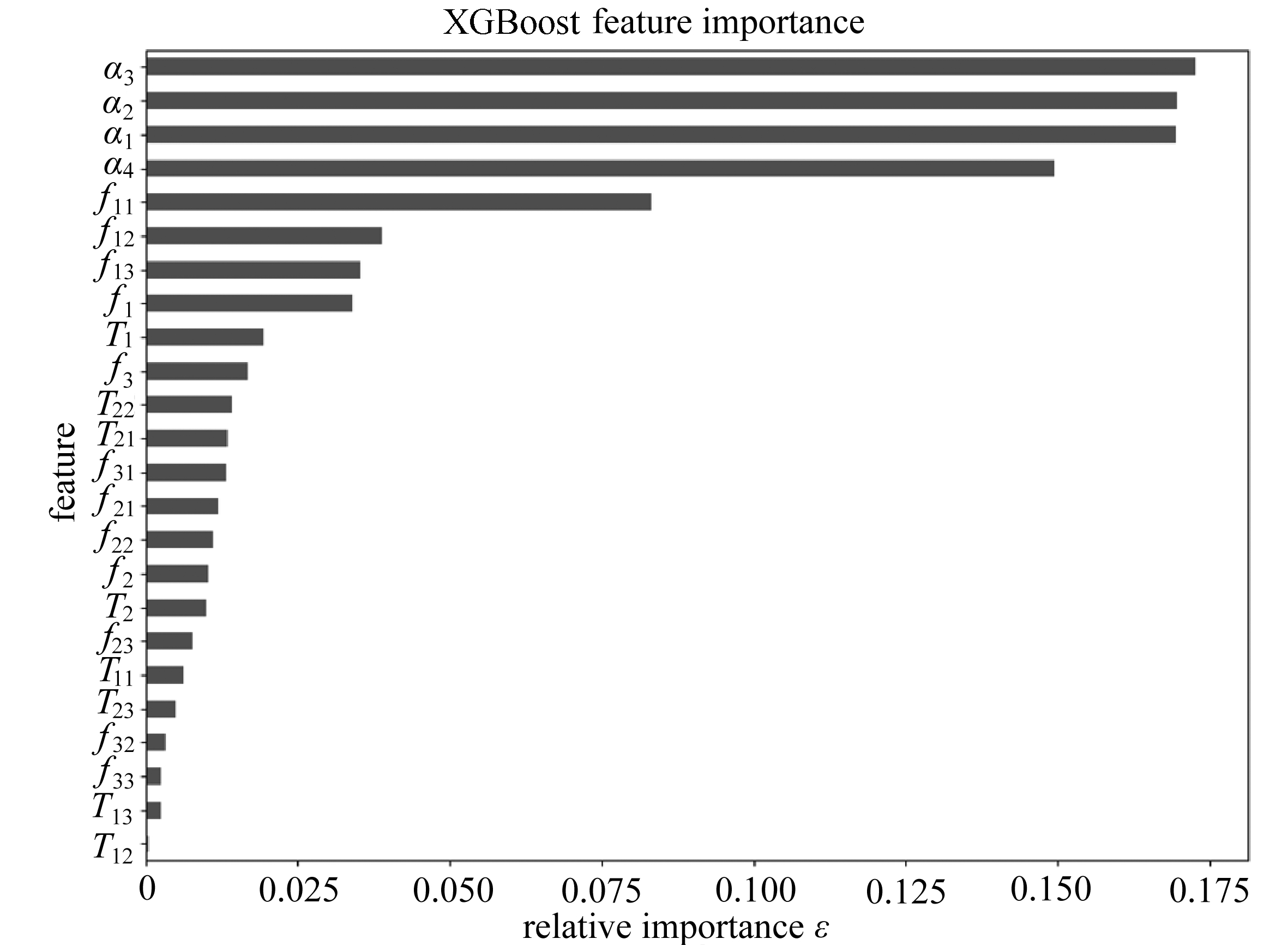
图4 XGBoost输出的Tsai-Wu特征重要性排序
Fig. 4 The sorting of characteristic importance of Tsai-Wu from the XGBoost output
现共有24维特征值,这些特征中可能存在冗余,易引起过拟合[19].采用了嵌入式的方法进行特征选择.因为模型部分采用了树模型XGBoost和随机森林,这两种模型在训练后可以直接得到特征的重要性,可以方便地进行排序,剔除重要性低的特征.采用1.1小节中计算出的数据进行了第一次XGBoost计算,得到了特征重要性排序,如下图4所示.可以看出,αi是最重要的因素,且影响远远大于其他特征.分别对于Tsai-Wu因子剔除重要性排名最后5位的因素进行后续计算.
模型方面,采用了数据挖掘领域广泛使用的XGBoost、不久之前发表的DART、以及经典的随机森林.
据以上研究发现均方根误差(RMSE)值很小,说明模型十分可靠,于是随机剔除一半工况的数据(GK4、GK8-9、GK10、GK17、GK19、GK20、GK21)进一步降低运算量,使用剩余数据和新工况的数据训练模型得出结论.
由于后续还需进行铺层顺序的优化,所以本文适当放宽了最大位移值的要求.有效解设定为Tsai-Wu因子小于1,最大位移值小于5 mm所对应的各角度铺层占比αi(i=1,2,3,4).而最优解采用简化处理,即为满足有效解要求的情况下,使得Tsai-Wu因子与最大位移值加和最小的αi(i=1,2,3,4).以工况横坐标,各角度铺层层数为纵坐标,作出不同角度下的最大层数、最小层数、最优层数的散点图,如图5所示.
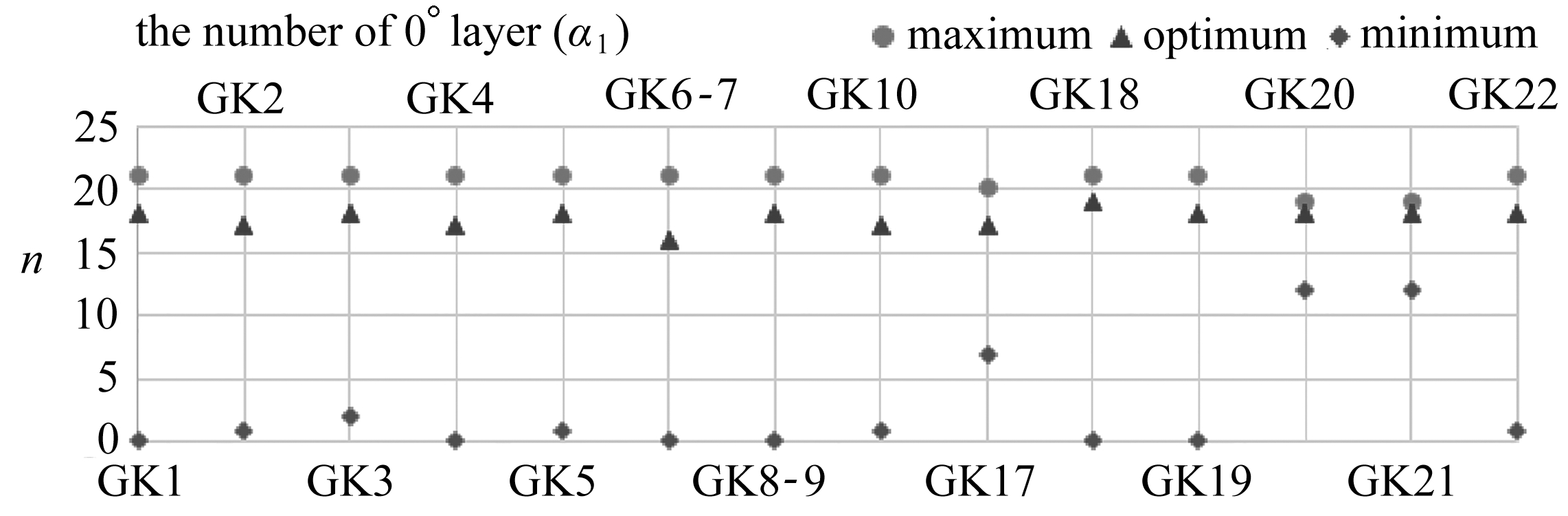
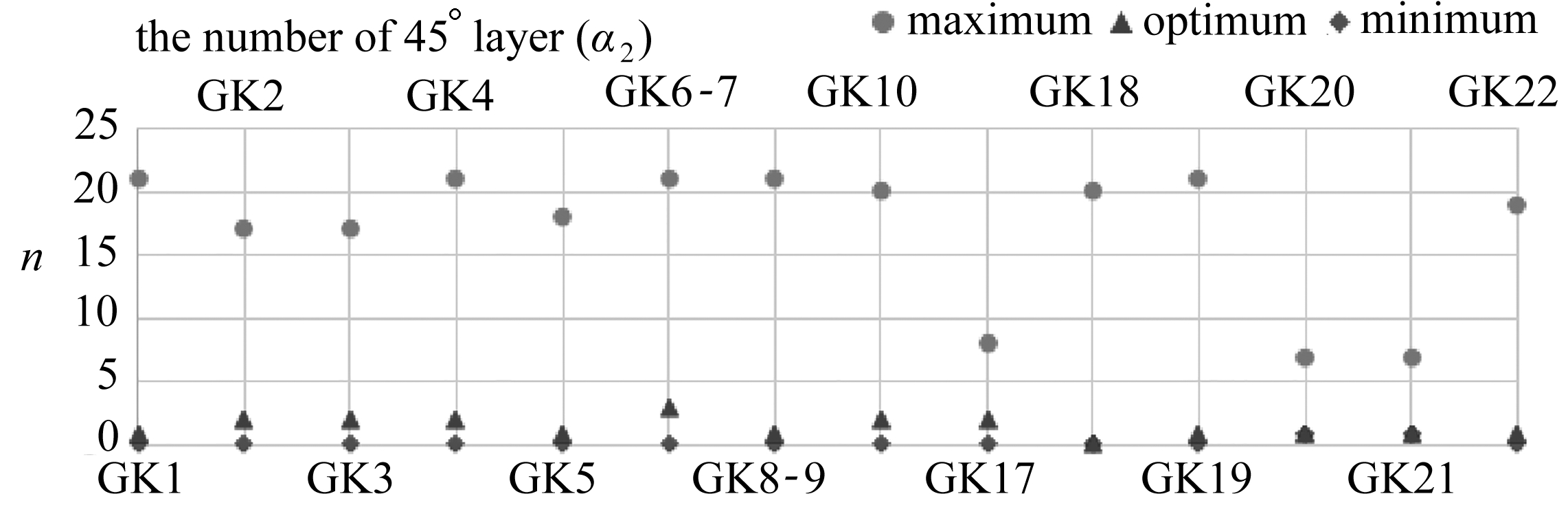
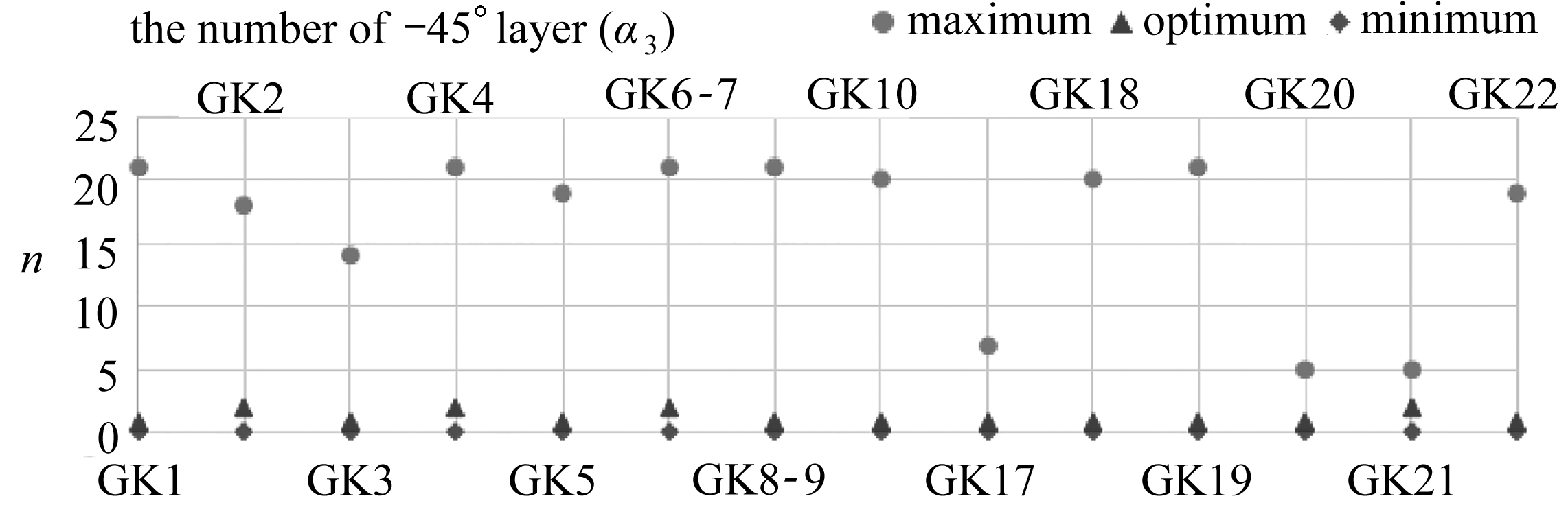
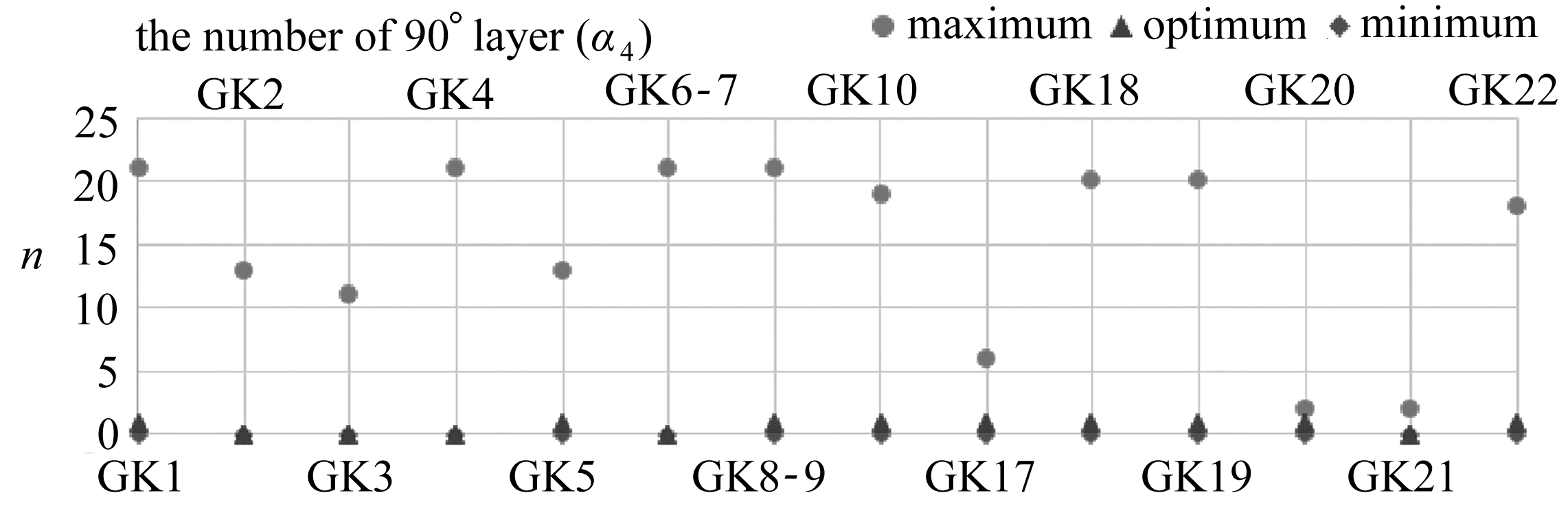
图5 各角度铺层的有效解与最优解
Fig. 5 The effective solution and optimal solution of the plys of each angle
从图5中可以看出,不同工况下有效解范围不尽相同,但是最优解的波动明显小很多.所以零件形状一旦确定,其受力会出现一定的相似性.
参数设定方面,本文采用的是回归模型,所以统一以RMSE作为检验数据的评价指标.另外,这三种树模型有一个共同并且重要的参数min-child-weight.对于回归问题来说,这个参数对应的就是每个叶子节点上最小的样本个数.这个参数值设置得越小,越容易过拟合.在本文中,min-child-weight设置为5,相比设置为1,RMSE会有不小的提升.对于不同的新工况所需计算量,分别训练了XGBoost、DART和随机森林模型,得出的Tsai-Wu因子的预测值与测试集中Tsai-Wu因子的真实值进行计算得到RMSE值,如表4中前3行所示.
模型融合方面,XGBoost、DART、随机森林这三种模型都是基于树的模型.XGBoost和DART是boosting算法,侧重于降低模型偏差.随机森林是bagging算法,偏重于降低模型方差[20].将这几种模型进行融合,可以进一步地提高模型的性能.常用的且效果比较好的融合方法是stacking或blending,但是由于数据量相对较小,做多层(multi level)的stacking/blending learning容易过拟合[21],所以最终只采用了简单的加权平均方法.而在本文模型中,3种模型融合效果并不理想,所以剔除随机森林的模型,做了不同比例的XGBoost和DART的融合,如表4后7行所示.计算量的不同,所对应的最优模型配比也不尽相同,但是0行数据量和10行数据量的最优模型同为0.2XGBoost+0.8DART,RMSE可以分别达到0.037 15和0.017 18,均比单独XGBoost和DART模型的RMSE值小.
表4不同模型的RMSE值IRMSE
Table 4 Different models and RMSE valueIRMSE
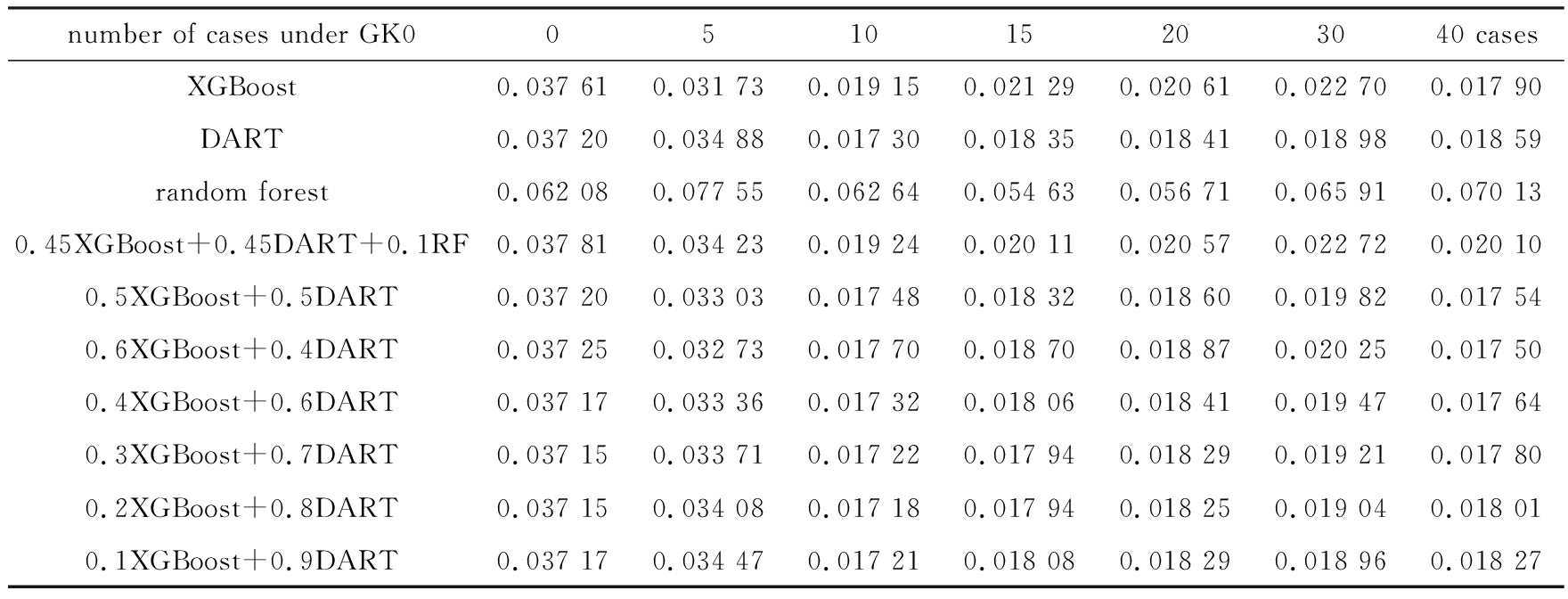
另作出XGBoost、DART模型的RMSE与数据量之间的关系图,如图6所示.从表4和图6中可以得出以下结论: 1) 对于出现的新工况不进行计算,直接通过已有数据获得的模型,RMSE就可达到0.037左右,对于Tsai-Wu准则判断临界值1来说是可以接受的,对于低精度要求的计算完全可用; 2) 对于XGBoost和DART模型以及融合模型,新工况计算10行数据是一个使得模型RMSE大幅度提升的途径.从5行计算量到10行数据量,XGBoost和DART模型的RMSE值均有大幅度下降.

图6 XGBoost、DART模型的RMSE与数据量之间的关系
Fig. 6 The relationship between the RMSE of XGBoost and DART models and the amount of data
减半工况后同样计算得到RMSE值,如表5所示.可以看出,减半工况后训练出的模型的RMSE是远远高于使用所有工况的情况,但是只需要将新工况计算量提高到40行数据,RMSE就可达到0.050 41,在精度要求不高的情况下,仍不失为一种快速有效的方法.
表5减半工况数据量后不同模型的RMSE值
Table 5 RMSE of different models with half of working conditions

训练一个XGBoost模型时间平均为21 min,训练一个DART模型的时间平均为12 min,对于新工况的计算时间为5 min,即使加上训练时间总和也仅为38 min,最大位移值的模型训练时间与计算时间与Tsai-Wu因子基本相同,两个值的总获取时长为76 min,远远短于采用路径input文件-提交job-爬取数据的时长23.70 h.
1) 将基于树的算法引入铺层计算中,采用了XGBoost、DART和随机森林以及其融合模型,分别在新工况计算量在0行和10行的情况下,Tsai-Wu因子的准确率可以达到96.3%和98.3%(与失效值1相比).在将已有工况数据量减少一半的情况下,如果提高新工况计算量到40行,准确率可以达到95.0%(与失效值1相比).
2) 作为一种通用的思路,对于复杂零部件铺层的计算,使用ABAQUS计算小部分数据,后采用回归的算法模型进行计算,可快速得到准确率较高的力学参数.
参考文献(References):
[1] 杨小平, 隋刚. 碳纤维复合材料在新能源产业中的应用进展[J]. 新材料产业, 2012(2): 20-24.(YANG Xiaoping, SUI Gang. Application of carbon fiber composite materials in new energy industry[J].Advanced Materials Industry, 2012(2): 20-24.(in Chinese))
[2] 冯美斌. 汽车轻量化技术中新材料的发展及应用[J]. 汽车工程, 2006,28(3): 213-220.(FENG Meibin. Development and application of new materials in automotive lightweighting technologies[J].Automotive Engineering, 2006,28(3): 213-220.(in Chinese))
[3] PARPINELLI R S, LOPES H S, FREITAS A A. Data mining with an ant colony optimization algorithm[J].IEEE Transactions on Evolutionary Computation, 2 002,6(4): 321-332.
[4] 肖书敏, 闫云聚, 姜波澜. 基于小波神经网络方法的桥梁结构损伤识别研究[J]. 应用数学和力学, 2016,37(2): 149-159.(XIAO Shumin, YAN Yunju, JIANG Bolan. Damage identification for bridge structures based on the wavelet neural network method[J].Applied Mathematics and Mechanics, 2016,37(2): 149-159.(in Chinese))
[5] DILEEP P N, KUMAR RR, RAO G V. A neural-genetic algorithm approach for evaluation of notched strength of laminate[J].Journal of the Institution of Engineers(India), 2 002.
[6] 刘振国, 胡杰, 胡龙. 基于遗传算法的层合板分级铺层全局优化[J]. 北京航空航天大学学报, 2013,39(4): 478-483.(LIU Zhenguo, HU Jie, HU Long. Global optimization of classified composite laminated structures based on genetic algorithms[J].Journal of Beijing University of Aeronautics and Astronautics, 2013,39(4): 478-483.(in Chinese))
[7] RAO A R M, LAKSHMI K. Optimal design of stiffened laminate composite cylinder using a hybrid SFL algorithm[J].Journal of Composite Materials, 2012,46(24): 3031-3055.
[8] SALAMAT A R, RAIESINEZHAD M. Optimum design ofantisymmetric cross-ply and angle-ply laminate with bees algorithm[Z]. 2012.
[9] YAO Y, WANG T, GONG Y, et al. Development of a carbon fiber reinforced composite chassis longitudinal arm[J].Science of Advanced Materials, 2016,8(11): 2133-2141.
[10] 龚友坤, 王韬, 姚远, 等. 汽车底盘碳纤维后纵臂成形实验与分析[J]. 汽车工程, 2016,38(2): 248-251.(GONG Youkun, WANG Tao, YAO Yuan, et al. Forming experiment and analysis of vehicle rear longitudinal arm of carbon fiber reinforced composite[J].Automotive Engineering, 2016,38(2): 248-251.(in Chinese))
[11] ROKACH L, MAIMON O.Data Mining With Decision Trees:Theory and Applications[M]. Singapore: World Scientific Publishing Company, 2008.
[12] KIM Y, PERRIG A, TSUDIK G. Tree-based group key agreement[J].Acm Transactions on Information&System Security, 2004,7(1): 60-96.
[13] LIANG X, QU F, YANG Y, et al. An improved ID3 decision tree algorithm based on attribute weighted[C]//International Conference on Civil,Materials and Environmental Sciences. Paris, France, 2015.
[14] LU G, KRISHNAMACHARI B, RAGHAVENDRA C S. An adaptive energy-efficient and low-latency MAC for tree-based data gathering in sensor networks: research articles[J].Wireless Communications&Mobile Computing, 2007,7(7): 863-875.
[15] QUINLAN J R. Induction on decision tree[J].Machine Learning, 1986,1(1): 81-106.
[16] CHEN T, GUESTRIN C. XGBoost: a scalable tree boosting system[C]//ACM Sigkdd International Conference on Knowledge Discovery and Data Mining. San Francisco, California, USA, 2016: 785-794.
[17] VINAYAK R K, GILAD-BACHRACH R. DART: Dropouts meet multiple additive regression trees[C]//Proceedings of the Eighteenth International Conference on Artificial Intelligence and Statistics. Vol38. San Diego, California, USA, 2015: 489-497.
[18] SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al. Dropout: a simple way to prevent neural networks fromoverfitting[J].Journal of Machine Learning Research, 2014,15(1): 1929-1958.
[19] GUYON I, ELISSEEFF A. An introduction to variable and feature selection[J].Journal of Machine Learning Research, 2 003,3(6): 1157-1182.
[20] ERNST D, GEURTS P, WEHENKEL L. Tree-based batch mode reinforcement learning[J].Journal of Machine Learning Research, 2005,6(2): 503-556.
[21] 史忠植. 知识发现[M]. 北京: 清华大学出版社, 2011.(SHI Zhongzhi.Knowledge Discovery[M]. Beijing: Tsinghua University Press, 2011.(in Chinese))
ZHU Di, YAO Yuan, PENG Xiongqi
(School of Materials Science and Engineering,Shanghai Jiao Tong University,Shanghai200030,P.R.China)
(Contributed by PENG Xiongqi, M. AMM Editorial Board)
Abstract:The rear longitudinal arm is one of the main structures of the automobile chassis. Design of the rear longitudinal arm with carbon fiber reinforced polymer (CFRP) can reduce its weight effectively. However, the application of composite materials also brings great challenges to the optimization design process, such as complex multiple conditions and a large number of design variables. The secondary development of ABAQUS was conducted with Python to fulfill the global ergodic search for thickness ratios of different ply angles to find the effective range and the optimum solution. In order to reduce the long running time under multi working conditions, the tree-based algorithms, such as XGBoost, DART and random forest, were introduced into the thickness ratio calculation. In view of both the running time and the computation accuracy, for 0 or 10 cases of calculation under the new condition, the accuracy rate of the Tsai-Wu factor can reach 96.3% and 98.3% (compared with failure value 1). If the number of cases under new working conditions increases to 40 while existing working conditions decreases by half, the accuracy rate can reach 95.0%. The developed algorithm provides a useful reference for reducing the running time of optimization design of composite parts under multi working conditions.
Key words:automobile chassis longitudinal arm; carbon fiber reinforced composite; secondary development of ABAQUS; tree based model; ply optimization
引用本文/Cite this paper: 朱迪, 姚远, 彭雄奇. 碳纤维汽车底盘后纵臂CAE设计的优化算法[J]. 应用数学和力学, 2018,39(8): 925-934.ZHU Di, YAO Yuan, PENG Xiongqi. An optimization algorithm for CAE design of carbon fiber reinforced composite chassis longitudinal arms[J].Applied Mathematics and Mechanics, 2018,39(8): 925-934.
文章编号:1000-0887(2018)08-0925-10
ⓒ 应用数学和力学编委会,ISSN 1000-0887
*收稿日期:2018-01-02;
修订日期:2018-01-14
作者简介:
朱迪(1993—),女,硕士生(E-mail: iriszhudi@163.com);
彭雄奇(1970—),男,教授,博士生导师(通讯作者. E-mail: xqpeng@sjtu.edu.cn).
摘要:后纵臂是汽车底盘的主要结构之一.采用碳纤维复合材料设计后纵臂可以有效减重.然而复合材料的应用也给其优化设计带来了很大的挑战,如复杂的多工况和大量的设计变量.使用Python语言对ABAQUS二次开发,对于各角度铺层占比进行全局遍历得出其有效解与最优解.为了解决多工况下运算时间长的问题,将基于树的算法模型,如XGBoost、DART、随机森林,引入到各铺层角度占比设计的计算中.同时考虑到计算量和计算准确率两者的关系,在新工况计算量在0条和10条的情况下,Tsai-Wu因子的准确率分别可以达到96.3%和98.3%(与失效值1相比).在将已有工况数据量减少一半的情况下,如果提高新工况计算量到40条,准确率可以达到95.0%.为多工况下碳纤维复合材料零件轻量化计算提供了有益的参考.
关 键 词:汽车底盘纵臂; 碳纤维复合材料; ABAQUS二次开发; 基于树的模型; 铺层优化
中图分类号:TB324
文献标志码:A
DOI:10.21656/1000-0887.390001