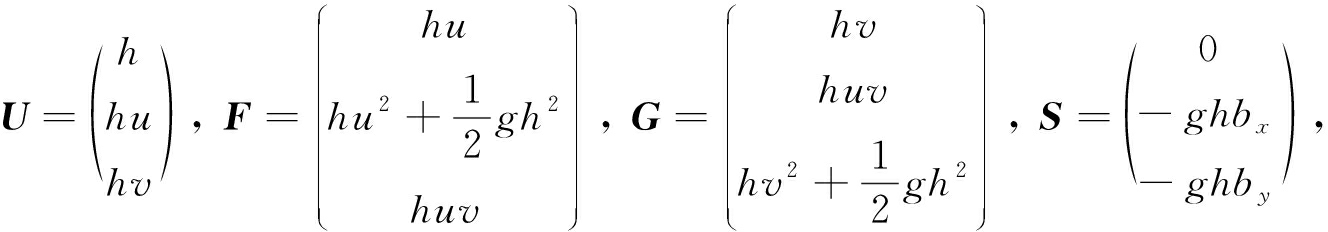
张海军, 封建湖, 程晓晗, 李 雪
(长安大学 理学院, 西安 710064)
浅水波方程是浅水环境下各类流体运动的一种数学描述,它是研究河流、灌溉和海洋等波动问题的一种重要模型.因此,对浅水波方程的数值求解越来越得到人们的重视.含源项浅水波方程具有形式[1]:
Ut+F(U)x+G(U)y=S(x,y,U),
(1)
其中
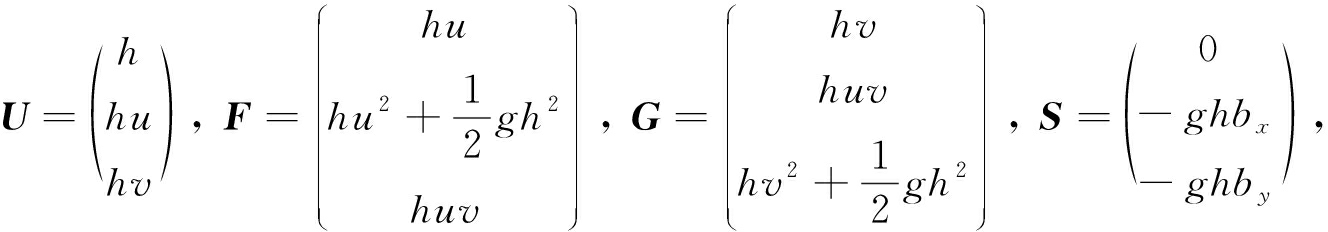
h为水深,u,v分别为x和y方向的水流速度,g为重力加速度,函数b=b(x,y)为底部地势.在没有源项的情况下,浅水波方程是一类非线性的双曲守恒律方程.非线性双曲守恒律方程有一个显著的特点是:不管初始条件是否光滑,其数值解都可能随时间的推移在某一时刻产生间断[2].这对求解浅水波方程的精确解带来了很大的困难.1954年,Lax针对双曲守恒律方程提出了弱解的概念[2],在弱意义下允许间断解的存在;但是弱解并不唯一.为了确定具有物理意义的唯一弱解,1973年Lax又提出了熵稳定条件[3].文献[1]把熵稳定条件推广到了带源项浅水波方程,即如果弱解U在弱意义下满足熵不等式:
E(U)t+(H(U)+J1)x+(K(U)+J2)y≤0,
则称U是式(1)的唯一弱解.其中E(U)是熵函数,且它的Hesse矩阵E″(U)是正定矩阵,H(U),K(U)和J=[J1(x,y,U),J2(x,y,U)]T是熵通量函数且满足等式:
∂UH=〈V,∂UF(U)〉, ∂UK=〈V,∂UG(U)〉, ∂xJ1+∂yJ2=〈V,S〉,
其中V为熵变量,定义为V=∂UE.
为了满足熵稳定条件,Tadmor在1987年通过引入熵势和熵变量的概念,定义了一类二阶的熵守恒格式,记为EC(entropy conservation)格式[4].该格式能够很好地捕捉到光滑解,但是由于该格式缺少熵耗散机制,在间断区域对解的捕捉会产生振荡.2006年,Roe在文献[5]中提出,在熵守恒格式的基础上加上Roe黏性项来获得熵稳定格式,记为ES(entropy stable)格式.该格式能够对激波的捕捉达到良好的效果,但是该格式是一阶精度格式.2009年,Ismail和Roe[6]通过进一步分析熵稳定格式中熵耗散的大小,得到了更稳定的熵相容格式,并应用于Euler方程的计算.2013年,Mohammed等[7]将熵相容格式推广应用于Navier-Stokes方程的计算.在Roe格式的基础上,Liu(刘友琼)和Feng(封建湖)等[8-11]通过限制器机制的方法构造了一些行之有效的高分辨率熵稳定/熵相容格式,并应用于双曲守恒律方程的计算.程晓晗等[12-13]、郑素佩等[14]通过结合熵稳定格式和重构方法,构造了高分辨率的熵稳定格式.
本文针对带源项浅水波方程,对于空间导数的离散,通过对数值通量函数嵌入限制器的方法,提出了一种高分辨率的熵稳定数值通量表达式;对源项的离散采用中心差分格式;并将该格式分别应用于一维和二维浅水波方程的数值算例中.将所得结果与熵守恒格式和带Roe黏性项的熵稳定格式的数值结果对比,表明该格式具有高分辨率和基本无振荡的特点,是模拟带源项浅水波方程的理想方法.本文在时间方向的推进采用文献[15]中提出的三阶Runge-Kutta方法:
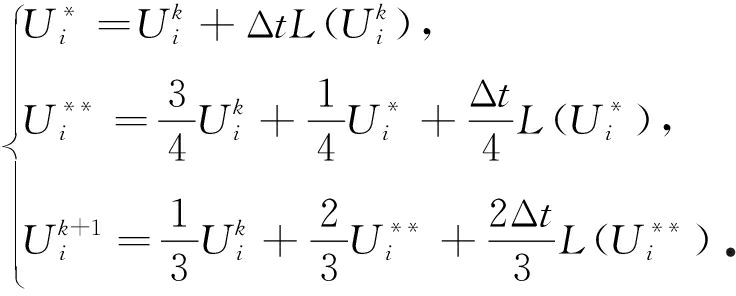
一维浅水波方程的初值问题为
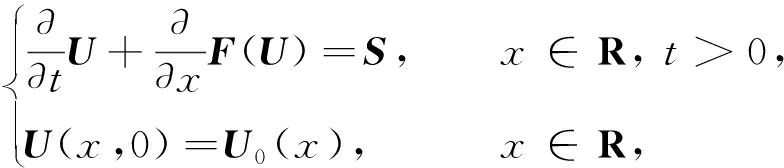
(2)
其中

考虑一维情况的高分辨率熵稳定格式.
考虑在均匀网格{xi}i下浅水波方程的熵守恒格式,熵守恒格式保持总熵不变,此时满足离散熵等式:
(3)
其中Ui是xi处的值,取势能与内能的和作为熵函数E(U),即E(U)=(hu2+gh2)/2+ghb,可得熵通量函数H(U)=guh2+hu3/2.熵守恒半离散格式定义为
(4)
其中
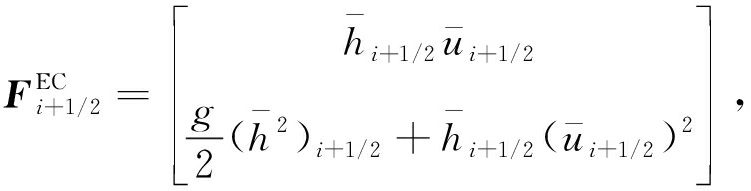
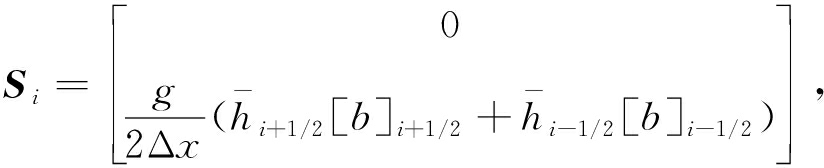
本文推广文献[16]中熵稳定的ERoe格式到带源项浅水波方程,具体形式为
(5)
其中R是F′(U)的特征向量矩阵且
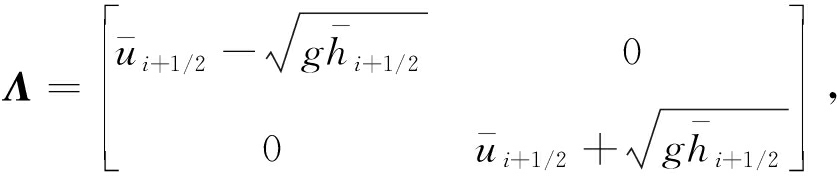
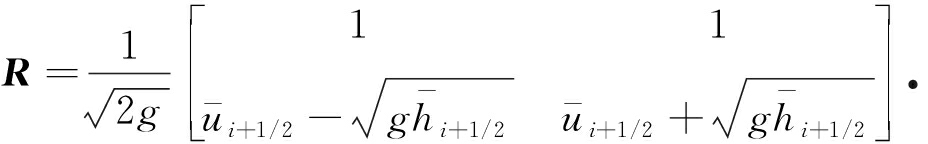
综上可知,带源项浅水波方程熵稳定格式的半离散格式为
(6)
采用在文献[9]中给出的限制器:
φ(θ)=max(0,min(1,2θ),min(1,θ)).
该限制器在Sweby给出的限制器的二阶TVD区域内[9],且显然有φ(1)=1,即限制器φ(θ)过(1,1)点,所以能满足二阶精度的要求.对于方程(2)而言,该限制器是一个矩阵形式:
ψ1=diag(φ(θ1),φ(θ2)),
其中
其中![]() 是方程(2)的Jacobi矩阵的第k个特征值在数值解Ui+1/2处的值,
是方程(2)的Jacobi矩阵的第k个特征值在数值解Ui+1/2处的值,![]() 是αi+1/2的第k个分量,αi+1/2=Li+1/2Δi+1/2U,Li+1/2是Ui+1/2处对应的左特征向量矩阵.时间步长Δt满足CFL条件c(Δt/Δx)≤1,其中c=maxi|λi+1/2|.
是αi+1/2的第k个分量,αi+1/2=Li+1/2Δi+1/2U,Li+1/2是Ui+1/2处对应的左特征向量矩阵.时间步长Δt满足CFL条件c(Δt/Δx)≤1,其中c=maxi|λi+1/2|.
通过添加限制器来充分运用熵守恒格式和熵稳定格式的优势, 即在解的光滑区域, 新格式自动选用熵守恒格式, 从而保持格式的二阶精度.在解的间断区域, 新格式自动选用熵稳定格式, 从而避免了伪振荡的发生.记新格式为ESL(entropy stable with limiters)格式,具体格式如下:
(7)
考虑二维带源项浅水波方程:
Ut+F(U)x+G(U)y=S,
取总能E(U)=(gh2+hu2+hv2+ghb)/2作为熵函数,其中g为重力加速度.则熵通量函数
H(U)=guh2+(hu3+huv2)/2,K(U)=gvh2+(hv3+hvu2)/2,J=ghb[u,v]T.
把一维熵守恒格式的数值通量推广到二维,可得二维浅水波方程的半离散熵守恒格式:
(8)
其中
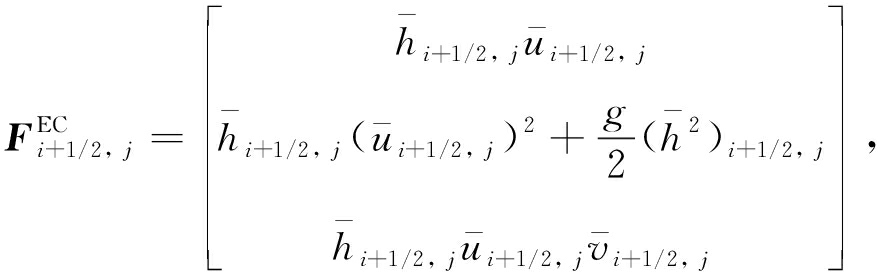
(9)
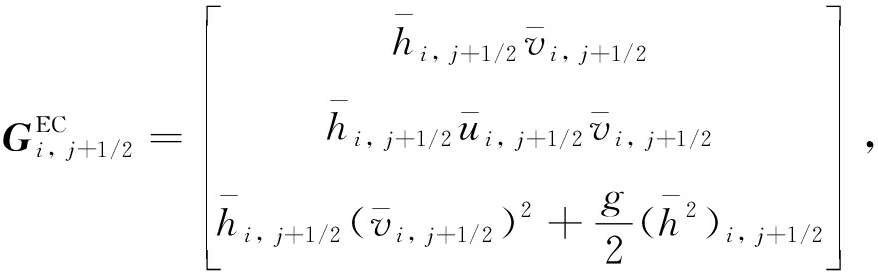
(10)
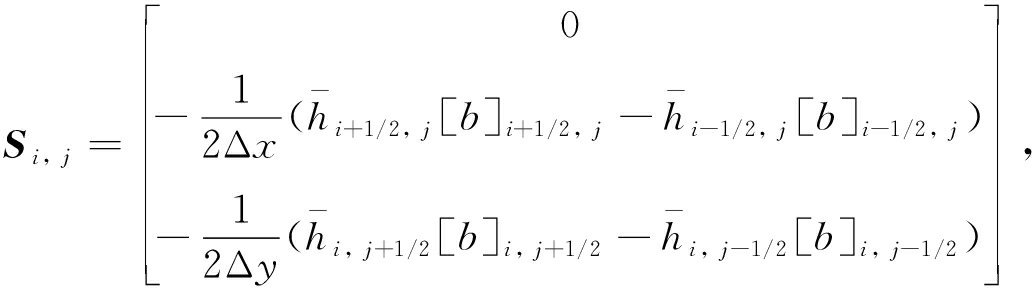
(11)
[a]i+1/2,j=ai+1,j-ai,j, [a]i,j+1/2=ai,j+1-ai,j.
用二维的熵守恒通量(9)和(10)代替式(5)中一维的熵守恒通量, 可得二维的熵稳定格式.记F′(U),G′(U)的特征向量和特征值矩阵分别为Rx,Λx和Ry,Λy,则数值通量为
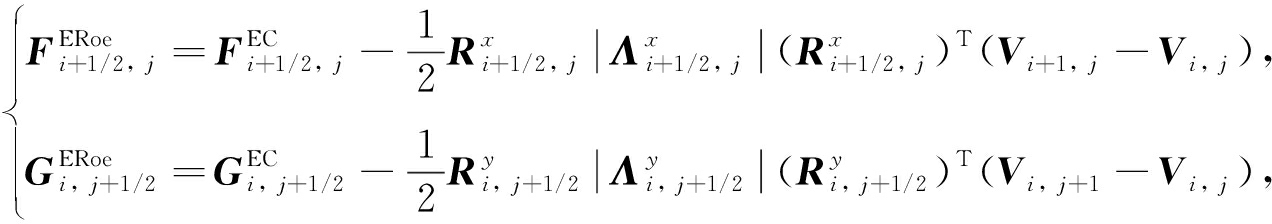
(12)
其中
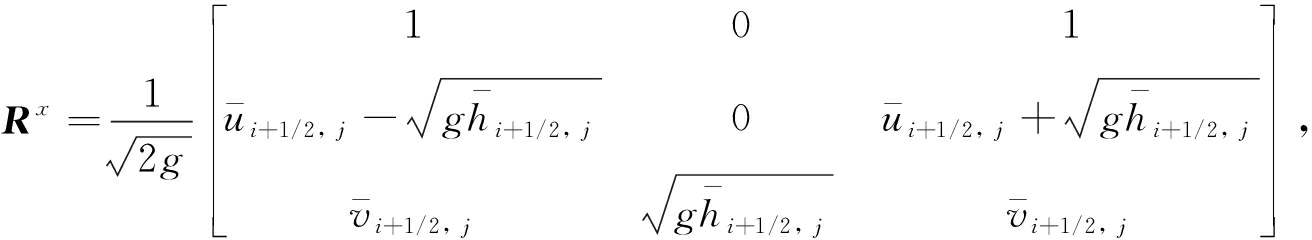
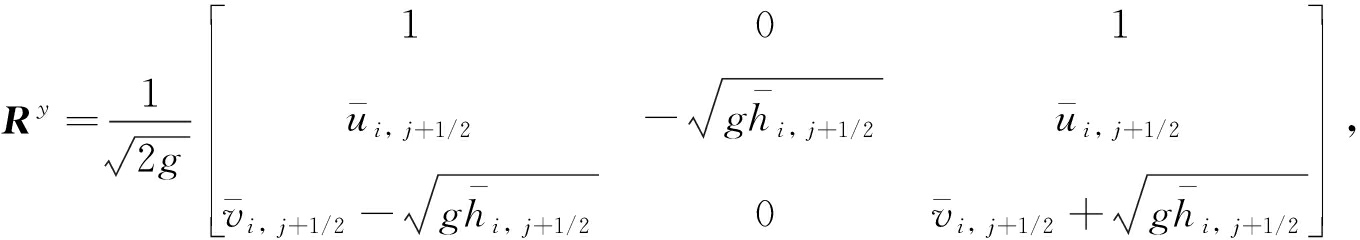
用二维的熵守恒通量(9)和(10)代替式(7)中一维的熵守恒通量,可得二维的高分辨率熵稳定格式,具体格式如下:

(13)
其中限制器ψ2=diag(φ(θ1),φ(θ2),φ(θ3)),φ(θk)(k=1,2,3)取二维情况下的值.
算例1考虑区间[-1,1]上连续的底部地势b(x)=1上的大型溃坝问题,初始条件取
取空间网格数为100, 计算到t=0.1,g=1, CFL条件数为0.1, 采用周期性边界条件.以1 200个加密网格点的熵相容格式[9]作为参考解,图1显示了高度h的变化情况,可以看出,熵稳定格式(6)和ESL格式(7)很好地捕捉到了解的结构,且熵稳定格式相比于ESL格式抹平现象严重.熵守恒格式(4)精确捕捉到了稀疏波,但是熵守恒格式在激波过度区域没有熵耗散,故在激波区域出现了强振荡现象.
算例2考虑区间[0,3]上的高度接近0的溃坝问题,底部地势和初始条件分别为
取空间网格数为200, 计算到t=0.1,g=1, CFL条件数取0.1, 采用周期性边界条件.以1 200个加密网格点的熵相容格式[9]作为参考解,图2显示了水部表面h的波动情况.熵守恒格式(4)的计算结果为NAN(出现了分母为0的情况),所以不能用于求解该问题.熵稳定格式(6)和ESL格式(7)都能保持波的非负性,且ESL格式相比于熵稳定格式更加精确,模拟效果更好.
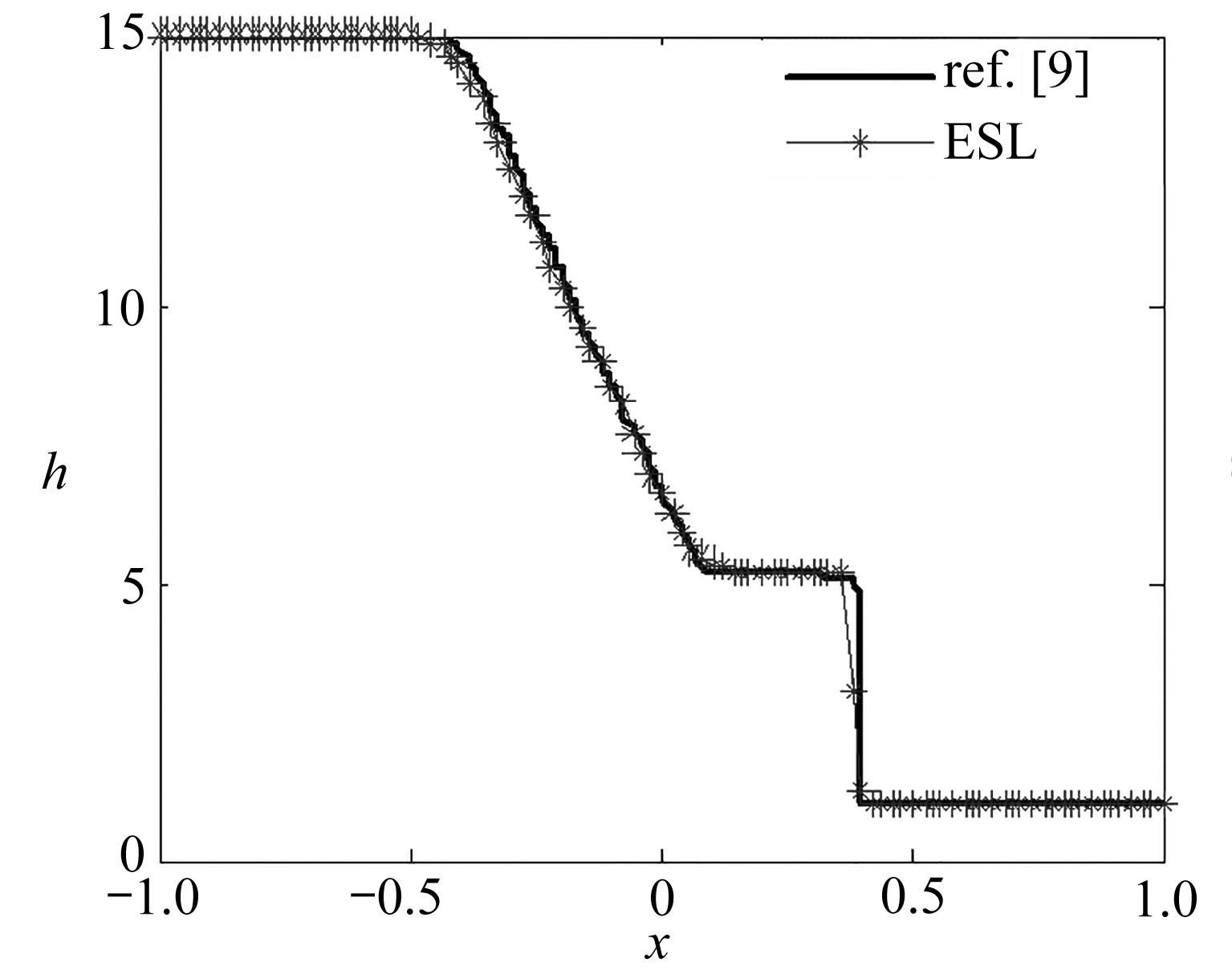
(a) ESL格式
(a) Results with the ESL scheme
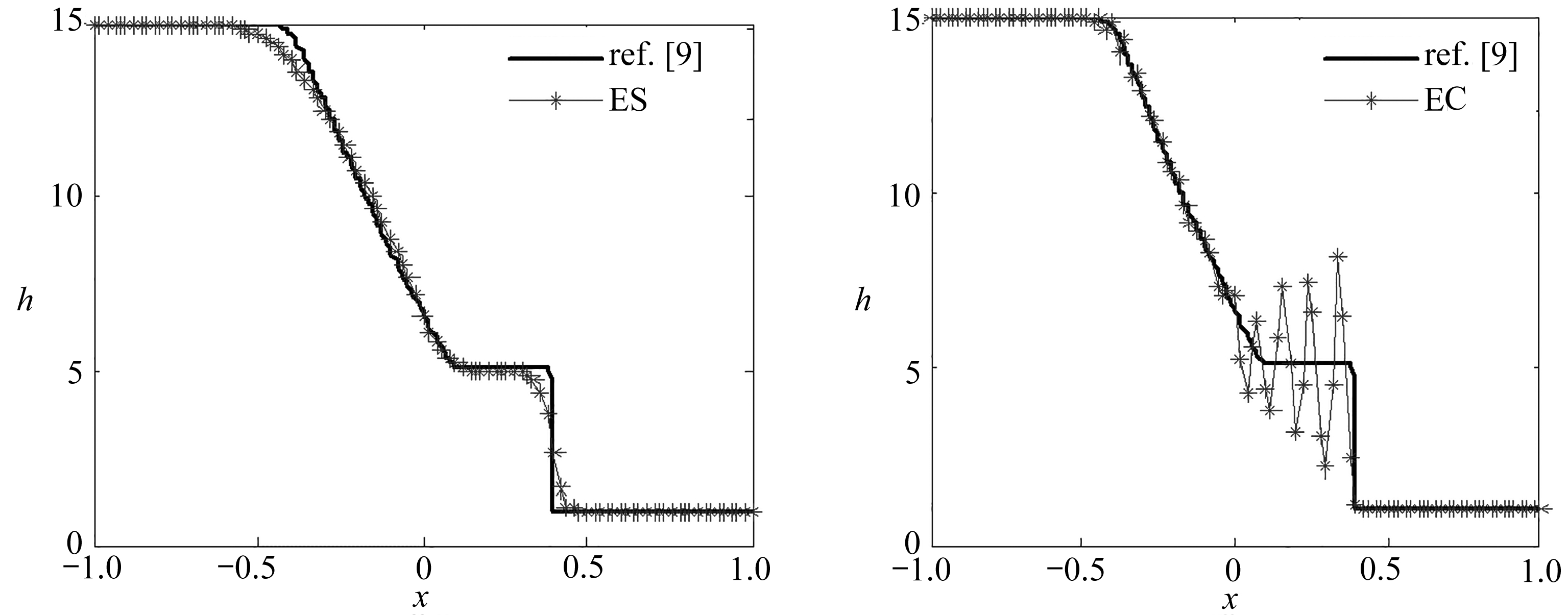
(b) 熵稳定格式 (c) 熵守恒格式 (b) Results with the ES scheme (c) Results with the EC scheme
图1 大型溃坝问题计算结果
Fig. 1 Numerical results of a large dam break problem
算例3考虑区间[0,150]上的溃坝问题,底部地势和初始条件分别为
取空间网格数为200,计算到t=4.5,CFL条件数为0.1,采用周期性边界条件.以1 200个加密网格点的熵相容格式[9]作为参考解,图3显示了h+b的变化情况.可以看出,3种格式都能精确捕捉到光滑解,但是熵守恒格式(4)在激波区域跳跃较大,振荡现象严重.熵稳定格式(6)在激波过度区域有较强的抹平现象,而ESL格式(7)能够在精确捕捉到激波的同时,抑制伪振荡的发生.
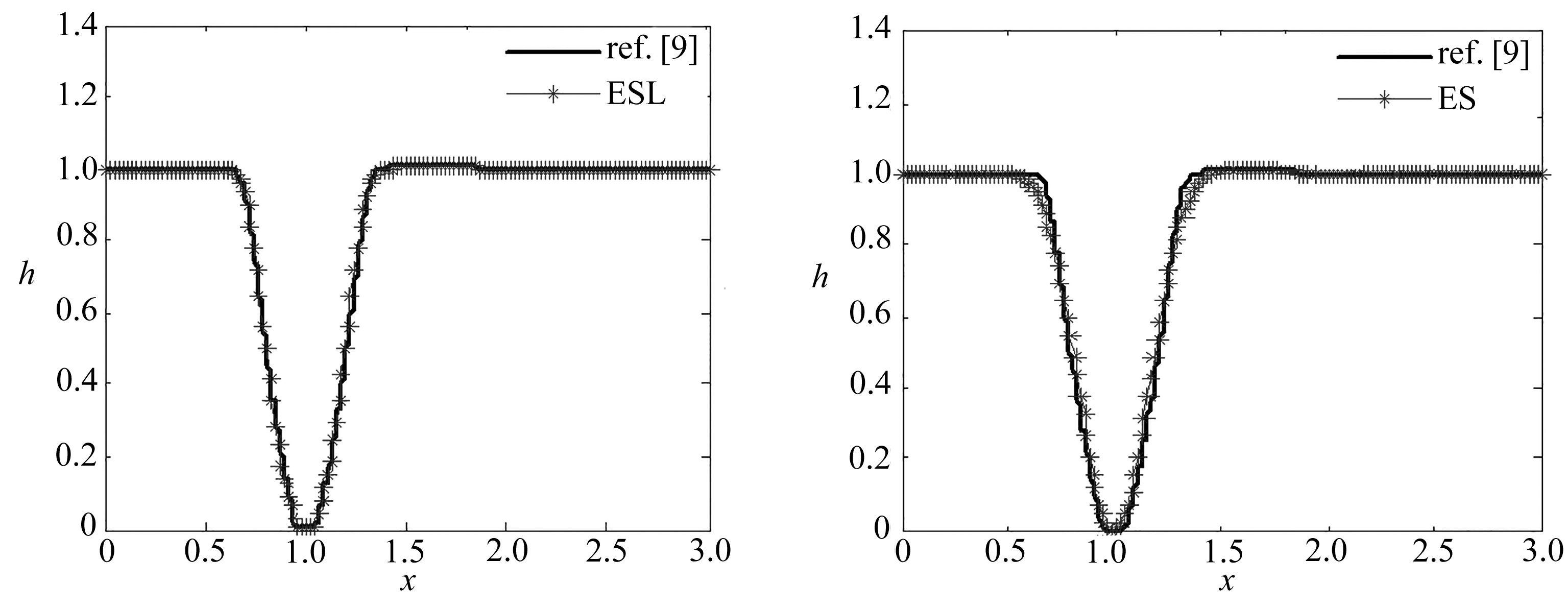
(a) ESL格式 (b) 熵稳定格式 (a) Results with the ESL scheme (b) Results with the ES scheme
图2 高度接近0的溃坝问题的计算结果
Fig. 2 Numerical results of a dam break problem of a near-zero height
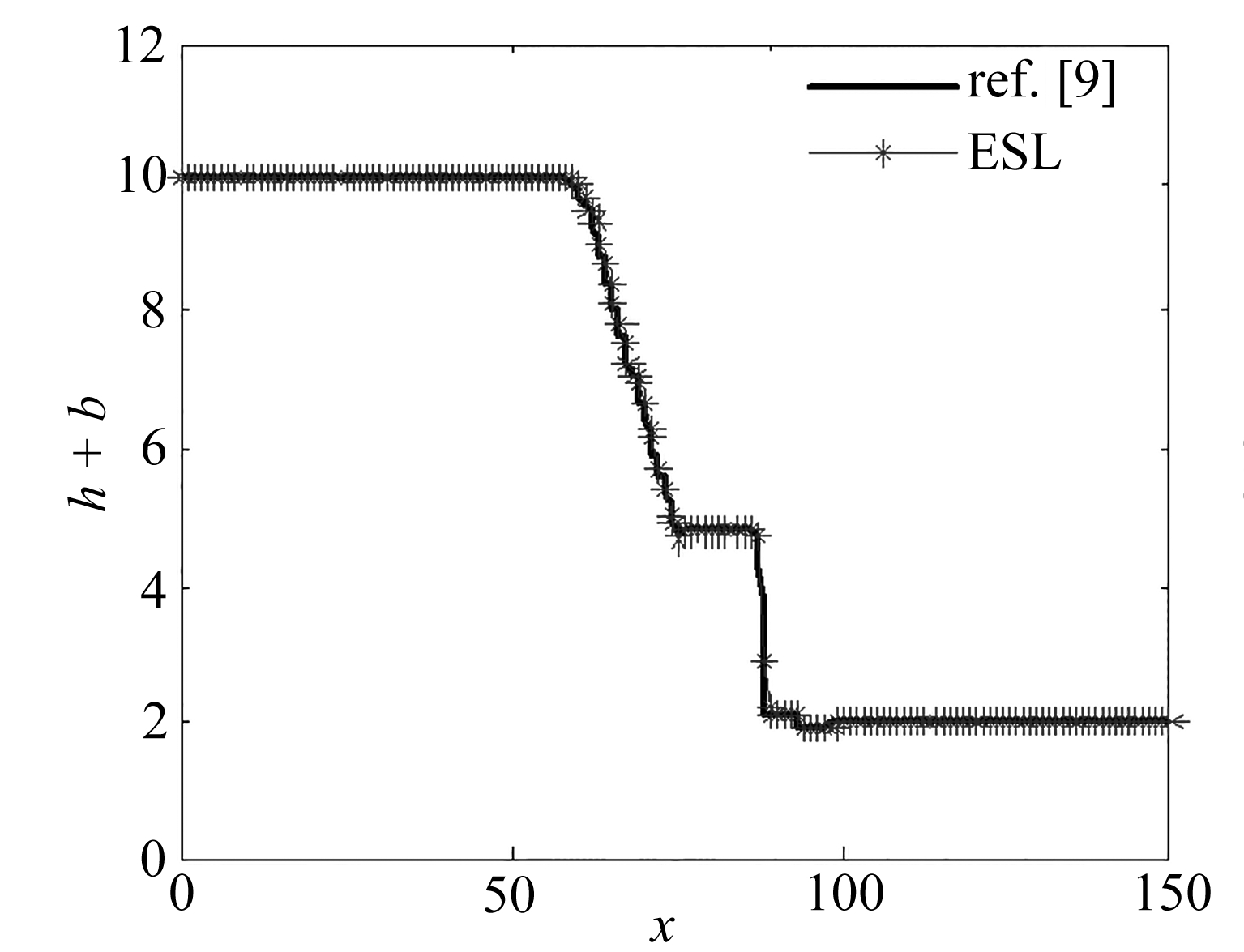
(a) ESL格式
(a) Results with the ESL scheme
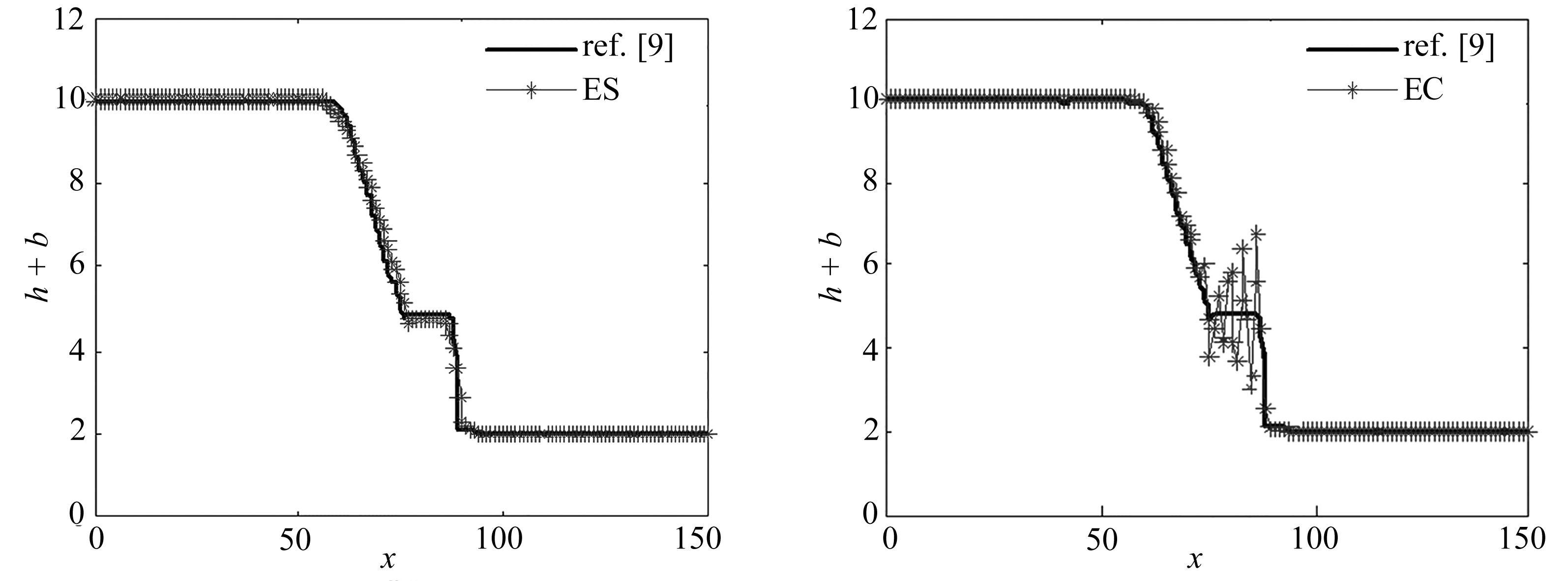
(b) 熵稳定格式 (c) 熵守恒格式 (b) Results with the ES scheme (c) Results with the EC scheme
图3 一维溃坝问题的计算结果
Fig. 3 Numerical results of the 1D dam break problem
算例4考虑[0,2]×[0,1]上的二维浅水波问题,其中底部地势和初始条件分别为
b(x,y)=0.8e-50(x-0.9)2-50(y-0.5)2,
u(x,y,0)=0,v(x,y,0)=0,h(x,y,0)=1-b(x,y).
取空间网格数为50×50,计算到t=0.1,g=1,CFL条件数为0.25,采用周期性边界条件.图4显示了ESL格式的运算结果,此时水平面保持稳定.表1和表2显示了不同网格下3种格式的L1误差与L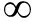 误差以及数值精度.从表中可以看出,熵守恒格式(8)的确是二阶方法,熵稳定格式(12)是一阶方法,但加入限制器的ESL格式(13)对于该问题也达到了二阶,且比熵守恒格式的精度更高;3种格式都保持了解的稳定性,但是熵稳定格式的结果产生的误差比其他两种格式都要大.其中L1误差为ΔxΔy∑i,j|hi,j+bi,j-1|,L
误差以及数值精度.从表中可以看出,熵守恒格式(8)的确是二阶方法,熵稳定格式(12)是一阶方法,但加入限制器的ESL格式(13)对于该问题也达到了二阶,且比熵守恒格式的精度更高;3种格式都保持了解的稳定性,但是熵稳定格式的结果产生的误差比其他两种格式都要大.其中L1误差为ΔxΔy∑i,j|hi,j+bi,j-1|,L 误差为maxi,j|hi,j+bi,j-1|.
误差为maxi,j|hi,j+bi,j-1|.
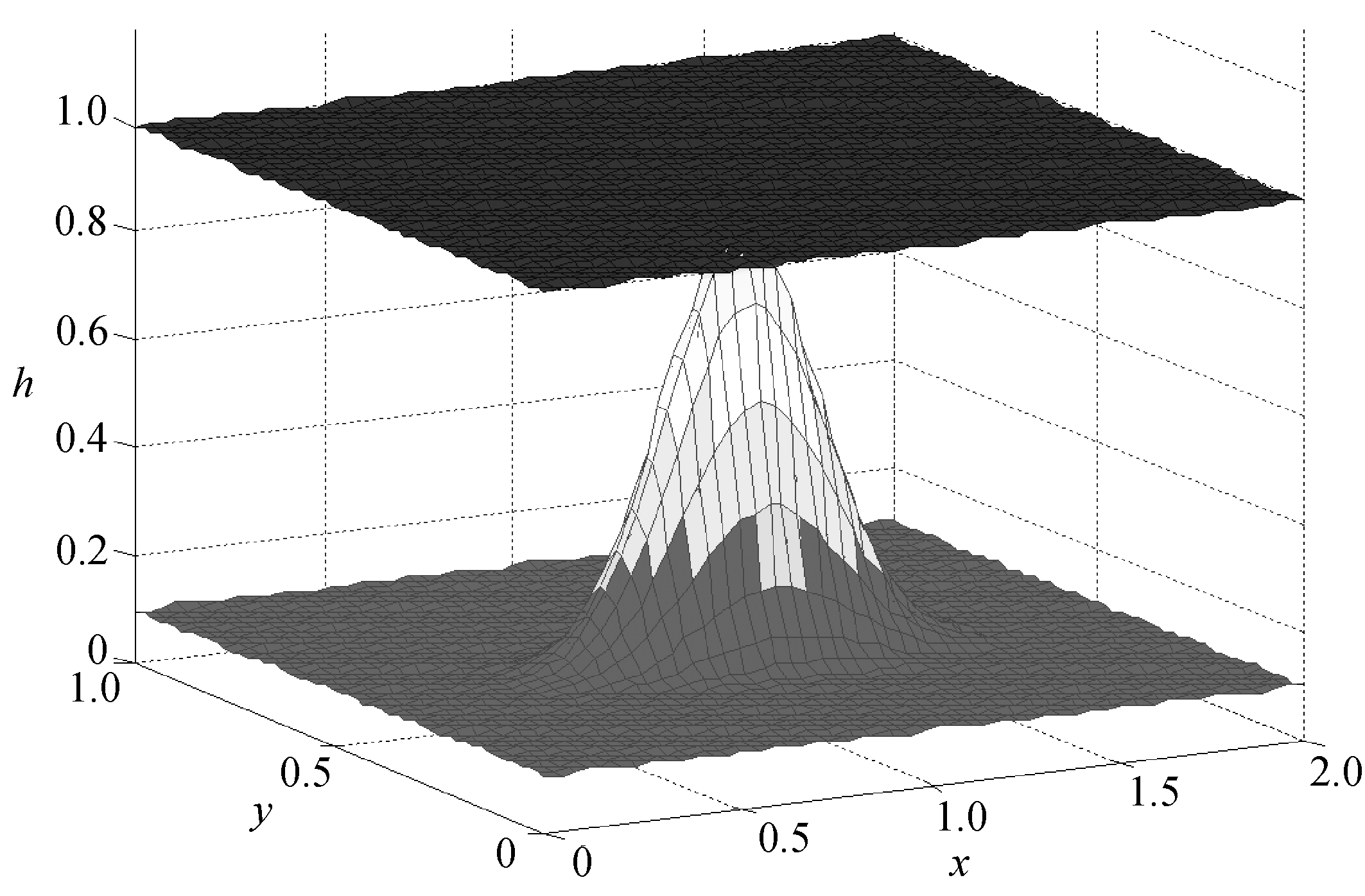
图4 ESL格式的计算结果
Fig. 4 Results with the ESL scheme
表1 L1误差与阶
Table 1L1errors and orders

表2 L 误差与阶
误差与阶
Table 2L errors and orders
errors and orders

算例5考虑[-2,2]×[-2,2]上的二维波动问题,其中底部地势和初始条件为
取空间网格数为40×40,计算到t=0.1,g=1,CFL条件数为0.1,采用周期性边界条件.图5显示了ESL格式的计算结果以及3种格式计算结果的y=x剖面图,以熵相容格式[9]作为参考解.可以看出,3种格式的计算结果都成功地模拟了水面的波动的情况,但是一阶的熵稳定格式(12)在波峰的捕捉上有明显的抹平现象,没有ESL格式(13)和熵守恒格式(8)计算结果锐利.而ESL格式和熵守恒格式都能很好地模拟波峰与波谷的形成,且ESL格式在峰值的捕捉上更加锐利,模拟效果相对于熵守恒格式要好.
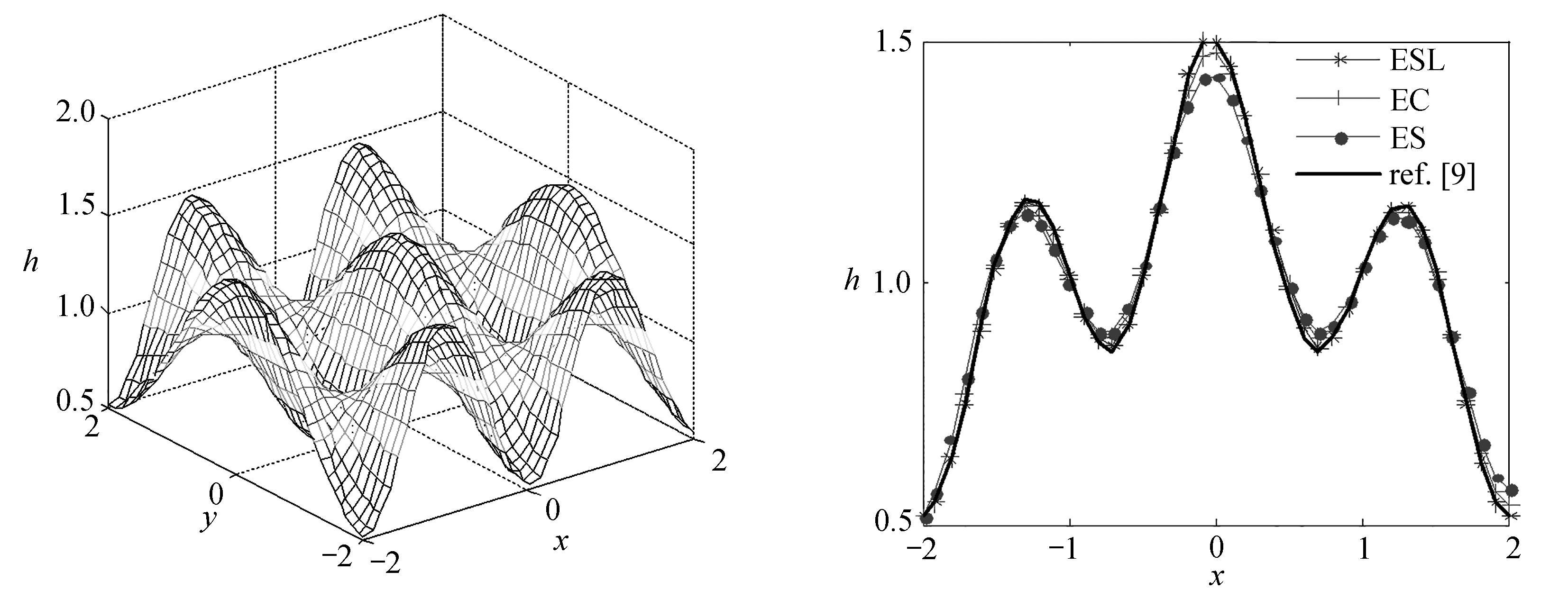
(a) ESL格式的数值结果 (b) 截面y=x的水深数值结果 (a) Numerical results with ESL scheme (b) Numerical results of the water height at y=x
图5 二维波动问题ESL格式和水深h的数值结果
Fig. 5 Numerical results with the ESL scheme and the water height for the 2D wave equation
本文针对带源项浅水波方程,通过添加限制器的方法构造了ESL格式.该格式能在解的光滑区域自动选用熵守恒格式,在解的间断区域自动选用熵稳定格式,从而在光滑区域保持二阶精度的同时避免了间断区域伪振荡的发生.利用该格式计算了一维和二维的算例,数值结果表明,ESL格式明显优于熵守恒格式和熵稳定格式.
参考文献(References):
[1] FJORDHOLM U S, MISHRA S, TADMOR E. Well-balanced and energy stable schemes for the shallow water equations with discontinuous topography[J].Journal of Computational Physics, 2011,230(14): 5587-5609.
[2] LAX P D. Weak solutions of nonlinear hyperbolic equations and their numerical computation[J].Communications on Pure and Applied Mathematics, 1954,7(1): 159-193.
[3] LAX P D. Hyperbolic systems of conservation laws and the mathematical theory of shock waves[C]//SIAM Regional Conference Lectures in Applied Mathematics. Vol11. Philadelphia, USA, 1973.
[4] TADMOR E. The numerical viscosity of entropy stable schemes for systems of conservation laws. I[J].Mathematics of Computation, 1987,49(179): 91-103.
[5] ROE P L. Entropy conservation schemes forthe Euler equations[R]. Talk at HYP 2006, Lyon, France, 2006.
[6] ISMAIL F, ROE P L. Affordable, entropy-consistent Euler flux functions Ⅱ: entropy production at shocks[J].Journal of Computational Physics, 2009,228(15): 5410-5436.
[7] MOHAMMED A N, ISMAIL F. Study of an entropy-consistent Navier-Stokes flux[J].International Journal of Computational Fluid Dynamics, 2013,27(1): 1-14.
[8] LIU Y, FENG J, REN J. High resolution, entropy-consistent scheme using flux limiter for hyperbolic systems of conservation laws[J].Journal of Scientific Computing, 2015,64(3): 914-937.
[9] 任炯, 封建湖, 刘友琼, 等. 求解双曲守恒律方程的高分辨率熵相容格式[J]. 计算物理, 2014,31(5): 539-551.(REN Jiong, FENG Jianhu, LIU Youqiong, et al. High resolution entropy consistent schemes for hyperbolic conservation laws[J].Chinese Journal of Computational Physics, 2014,31(5): 539-551.(in Chinese))
[10] 刘友琼, 封建湖, 梁楠, 等. 求解浅水波方程的熵相容格式[J]. 应用数学和力学, 2013,34(12): 1247-1257.(LIU Youqiong, FENG Jianhu, LIANG Nan, et al. An entropy-consistent flux scheme for shallow water equations[J].Applied Mathematics and Mechanics, 2013,34(12): 1247-1257.(in Chinese))
[11] 刘友琼, 封建湖, 任炯, 等. 求解多维Euler方程的二阶旋转混合型格式[J]. 应用数学和力学, 2014,35(5): 542-553.(LIU Youqiong, FENG Jianhu, REN Jiong, et al. A second-order rotated-hybrid scheme for solving multi-dimensional compressible Euler equations[J].Applied Mathematics and Mechanics, 2014,35(5): 542-553.(in Chinese))
[12] 程晓晗, 聂玉峰, 蔡力. 基于WENO重构的熵稳定格式求解浅水方程[J]. 计算物理, 2015,32(5): 523-528.(CHENG Xiaohan, NIE Yufeng, CAI Li. WENO based entropy stable scheme for shallow water equations[J].Chinese Journal of Computational Physics, 2015,32(5): 523-528.(in Chinese))
[13] 程晓晗, 封建湖, 聂玉峰. 求解双曲守恒律方程的WENO型熵相容格式[J]. 爆炸与冲击, 2014,34(4): 501-507.(CHENG Xiaohan, FENG Jianhu, NIE Yufeng. WENO type entropy consistent scheme for hyperbolic conservation laws[J].Explosion and Shock Waves, 2014,34(4): 501-507.(in Chinese))
[14] 郑素佩, 封建湖, 刘彩侠. 高分辨率熵相容算法在二维溃坝问题中的应用[J]. 水动力学研究与进展, 2013,28(5): 545-551.(ZHENG Supei, FENG Jianhu, LIU Caixia. High-resolution entropy consistent algorithm for the two-dimensional dam-break flows[J].Chinese Journal of Hydrodynamics, 2013,28(5): 545-551.(in Chinese))
[15] GOTTLIEB S, SHU C W. A survey of strong stability preserving high order time discretizations[J].SIAM Review, 2001,43(1): 89-112.
[16] FJORHOLM U S. Structure preserving finite volume methods for the shallow water equations[D]. Master Thesis. Norway: University of Oslo, 2009.
ZHANG Haijun, FENG Jianhu, CHENG Xiaohan, LI Xue
(School of Science,Chang’an University,Xi’an710064,P.R.China)
Abstract:An entropy stable scheme was developed for the shallow water equations with source terms, and a 1st-order entropy stable scheme and a high-order entropy conservation scheme were combined with a flux limiter function. The new entropy scheme preserves advantages of both the entropy conservation scheme and the entropy stable scheme, having higher accuracy in the regions of the smooth solutions and capturing shocks accurately while avoiding non-physical phenomena in the regions of the discontinuous solutions, thus achieves high resolution. The new scheme was successfully applied to calculate the classical 1D and 2D problems. The numerical results show that the new scheme does be an ideal method to simulate the shallow water equations with source terms.
Key words:shallow water equations; entropy conservation scheme; entropy stable scheme; high resolution
Foundation item:The National Natural Science Foundation of China(11601037;11401045;11171043)
引用本文/Cite this paper: 张海军, 封建湖, 程晓晗, 李雪. 带源项浅水波方程的高分辨率熵稳定格式[J]. 应用数学和力学, 2018,39(8): 935-945.ZHANG Haijun, FENG Jianhu, CHENG Xiaohan, LI Xue. An entropy stable scheme for shallow water equations with source terms[J].Applied Mathematics and Mechanics, 2018,39(8): 935-945.
文章编号:1000-0887(2018)08-0935-11
ⓒ 应用数学和力学编委会,ISSN 1000-0887
*收稿日期:2017-07-13;
修订日期:2017-12-07
基金项目:国家自然科学基金(11601037;11401045;11171043); 中央高校基本科研业务费(310812171002)
作者简介:张海军(1992—),男,硕士生(E-mail: 2397381704@qq.com); 封建湖(1960—),男,教授,博士,博士生导师(通讯作者. E-mail: jhfeng@chd.edu.cn).
摘要:提出了一种求解带源项浅水波方程的熵稳定格式.新格式利用通量限制函数将一阶熵稳定格式和高阶熵守恒格式结合,具有熵守恒格式和熵稳定格式的优点:在解的光滑区域具有高精度,在解的间断区域避免了非物理现象的产生,同时可以准确地捕捉激波,从而达到高分辨率的效果.利用新格式计算了一维和二维的经典算例,数值结果表明,新格式是模拟带源项浅水波方程的理想方法.
关 键 词:浅水波方程; 熵守恒格式; 熵稳定格式; 高分辨率
中图分类号:O354; O241.82
文献标志码:A
DOI:10.21656/1000-0887.380195