徐维铮1,2， 吴卫国1,2
(1. 武汉理工大学 高性能舰船技术教育部重点实验室， 武汉 430063； 2. 武汉理工大学 交通学院 船舶、海洋与结构工程系， 武汉 430063)
冲击波流场包含激波间断和光滑流场等复杂结构，对冲击波流场的模拟需要高精度、低耗散的激波捕捉格式．1994年，Liu等[1]在ENO格式[2]构造思想的基础上首次提出WENO格式(weighted essentially non-oscillatory scheme)的构造方法．紧接着，Jiang和Shu[3]在改进原始WENO格式光滑因子的基础上，提出了三阶、五阶WENO格式的构造框架．由于WENO格式作为一种典型的高精度激波捕捉格式，对流场内的激波间断具有较高的分辨率，适于求解包含激波、膨胀波以及接触间断等复杂结构的流场，因此被大量研究者用来进行相关的数值计算研究[4-7]．然而自从Henrick等[8]指出五阶WENO格式在连续解一阶极值点处会降为三阶的缺陷，基于映射函数的五阶WENO-M格式[8]以及采用线性组合低阶模板光滑因子构造高阶全局光滑因子的方法构造的五阶WENO-Z格式[9]先后被提出．文献[10-17]致力于改进高阶WENO格式(主要集中在五阶、七阶和九阶)在极值点处精度．针对WENO-JS3格式的改进，Yamaleev等[18]提出三阶能量稳定WENO格式(ESWENO)．Wu等[19]指出传统的WENO-Z3格式[20]在极值点处会降阶，并在Hu等[21]提出的加权组合局部和全局光滑因子构造思想的启发下，提出了WENO-N3格式，提高了格式的分辨率．之后，为了提高WENO-N3格式在极值点处的计算精度，其提出了非线性组合局部模板和全局模板光滑因子的方式，推导给出了WENO-NP3格式[22]．最近，Gande等[23]进一步发展了Wu等的思想，通过非线性组合局部模板和全局模板中一阶导数光滑因子的方式构造了另一种提高极值点处精度的WENO-F3格式．
在文献[19, 22-23]研究的基础上，首先推导WENO-JS3格式收敛精度的充分条件，采用Taylor级数展开的方法构造出一种改进的WENO-NZ3格式，致力于提高传统的WENO-Z3格式在极值点处的计算精度．选取Sod激波管、激波与熵波相互作用、Rayleigh-Taylor不稳定性等经典算例，考察了改进格式(WENO-NZ3格式)的计算性能．研究表明，改进格式不仅提高了极值点处的计算精度，还改善了对流场结构的分辨率．
含激波流场采用可压缩Euler(欧拉)方程进行描述，其具体形式如下：
Qt+Ex+Fy=0,
(1)
其中
(2)
(3)
p=(γ-1)ρe，
(4)
式中，ρ是密度，u,v是x,y方向上的速度分量，p为流体压力，E是单位体积流体的总能量，e是比内能，γ表示气体的绝热指数，本文中该参数取为1.4．
在方程(1)的每个方向上均可以看成是一个双曲守恒律方程：
(5)
例如，针对x方向，方程(5)的数值离散形式为
(6)
其中，
分别为单元在xi-1/2,xi+1/2的左、右界面处对流项数值通量，Δx为x方向的均匀网格间距，在本文的数值计算中，x，y两个方向的网格间距相同．控制方程的空间离散采用下一节中的数值方法，时间项离散采用三阶TVD Runge-Kutta(龙格-库塔)格式[24]．
2.1.1 数值重构过程
WENO-JS3格式的数值离散和推导过程如下[3](这里仅给出右界面通量
的重构过程)．对于该格式，的2种二阶精度通量重构方式分别为
(7)
利用上述两种二阶通量的凸组合计算最终具有三阶精度的数值通量
即
(8)
对于光滑情形，有ω0=d0=1/3，ω1=d1=2/3．式(8)所给出的形式既适合光滑流场也适合含间断流场，对于含激波间断流场，式中的非线性权函数ωk需要根据下式求得
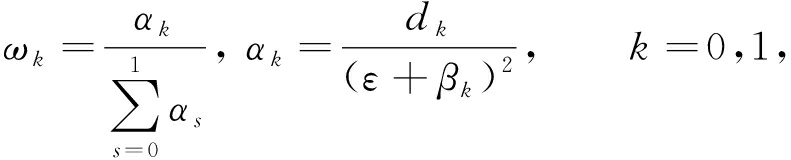
(9)
其中，在本文的数值计算中参数ε取值为10-6．光滑因子βk(k=0,1)的表达式如下：
β0=(fi-1-fi)2,β1=(fi-fi+1)2．
(10)
2.1.2 收敛精度的充分条件
本小节在文献[18, 23]研究的基础上，对WENO-JS3格式的收敛精度充分条件进行推导．
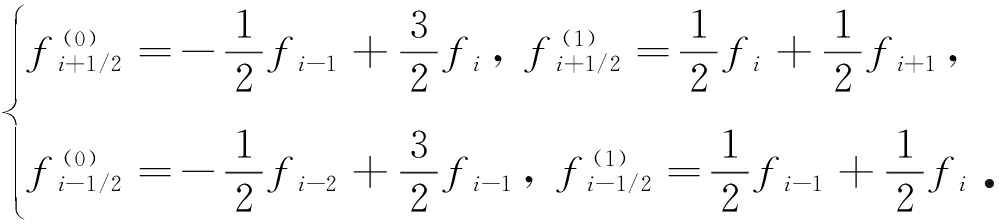
(11)
将式(11)在xi处进行Taylor级数展开可得
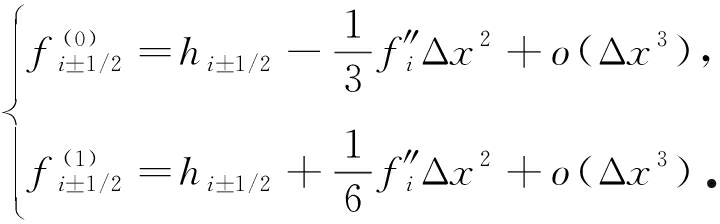
(12)
根据式(12)可得候选模板通量表达式为
fki±1/2=hi±1/2+AkΔx2+o(Δx3),k=0,1．
(13)
进一步可得WENO-JS3格式界面通量表达式为
(14)
式(14)中存在关系式
因此，根据式(6)、(14)，可以得到满足WENO-JS3格式收敛到设计精度的充分条件：
ωk-dk=o(Δx2)．
(15)
这里需要注意的是，式(15)中的ωk包含
其中，
对应右界面通量
的非线性权重，
对应左界面通量
的非线性权重．
WENO-Z3格式[20]的具体形式如下：
(16)
τ=|β0-β1|．
(17)
2.2.1 在非极值点处的精度
这里首先分析WENO-Z3格式在非极值点处(f′i≠0)的精度，式(10)中的光滑因子在xi处进行Taylor级数展开可得
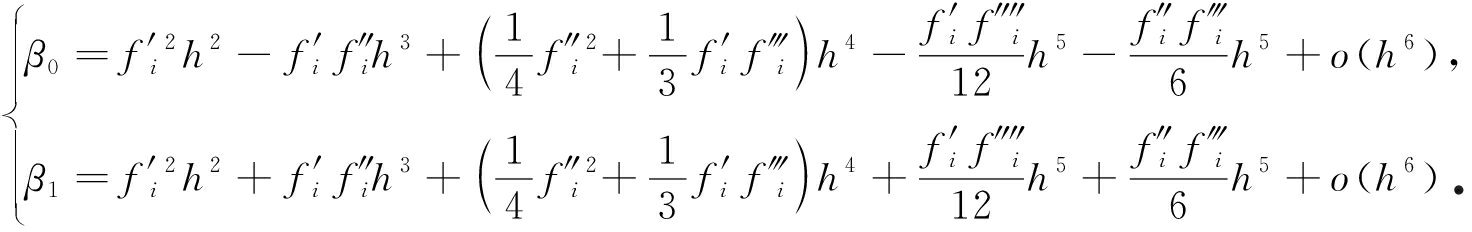
(18)
将式(17)、(18)代入式(16)可得
(19)
(20)
再根据式(9)中的加权法则可得右界面通量所对应权函数
(21)
(22)
同理可得
(23)
(24)
再根据式(9)中的加权法则可得左界面通量所对应权函数
(25)
(26)
根据式(21)、(22)、(25)、(26)可知，
满足式(15)中的充分条件，这也就证明了WENO-Z3格式在光滑流场非极值点处能满足三阶精度．
2.2.2 在极值点处的精度
下面紧接着探讨WENO-Z3格式在一阶极值点处(f′i=0,f″i≠0,f‴i≠0)的精度，在一阶极值点处，式(18)退化为如下关系：
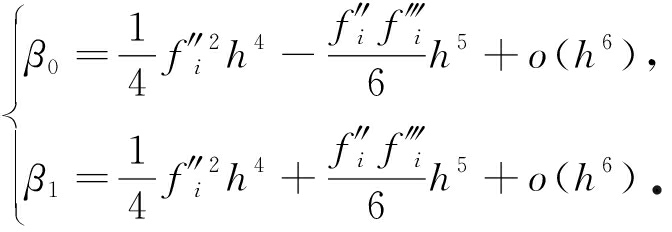
(27)
将式(17)、(27)代入式(16)可得
(28)
(29)
再根据式(9)中的加权法则可得右界面通量所对应权函数
(30)
(31)
同理可得
(32)
(33)
再根据式(9)中的加权法则可得左界面通量所对应权函数
(34)
(35)
从式(30)、(31)可知
从式(34)、(35)可知
因此可以预知，WENO-Z3格式在极值点处将降阶．文献[19]通过极值点算例证实了WENO-Z3格式在一阶极值点处会降低为一阶精度．
为了提高WENO-Z3格式在极值点处的计算精度，本文在WENO-NP3格式[22]构造思想启发下，将该构造思想直接推广应用到WENO-Z3，并采用Taylor级数展开的方式进行理论推导，给出最终的构造格式：
(36)
τNZ=
,ε=10-40．
(37)
2.3.1 改进格式在极值点处的精度
本小节将主要探讨改进格式在一阶极值点处的精度．首先给出右界面通量所对应权函数
的计算过程，将式(27)、(37)代入式(36)中可得
(38)
(39)
再根据式(9)中的加权法则可得右界面通量所对应权函数
(40)
(41)
同理可得
(42)
(43)
再根据式(9)中的加权法则可得左界面通量所对应权函数
(44)
(45)
根据式(40)、(41)、(44)、(45)可知
(46)
为了满足式(15)的充分条件，可得参数P的取值为
(47)
由于该参数的推导主要是基于精度的考虑，还需要进一步验证该参数在提高计算精度的条件下，是否能够满足数值计算无振荡的特性．针对该改进格式，在P=3/2附近还选取了如下3个参数P=2，4/3，6/5进行数值计算．这里选择经典的Sod激波管算例进行初步考察．该算例初始条件如式(48)所示[25]，计算网格数划分为200，计算结束时间取为0.18．图1给出该算例计算结束时刻密度曲线图及局部放大图．
(48)
通过对比分析发现：当采用参数P=2，3/2计算经典的激波管算例时，计算结果给出明显的虚假振荡，且随着P的增大，虚假振荡增强，因此可以推断虚假振荡的产生是由于格式的耗散性不足．当P=4/3时，格式能给出较优的计算结果．然而根据式(46)计算发现：
即参数P=4/3不能满足左数值通量对应非线性权重
的要求．但是为了得到一个合理的计算结果，参数P=4/3是一种权衡计算精度和计算稳定性的结果．因此，本文将该改进格式命名为WENO-NZ3格式(P=4/3)．
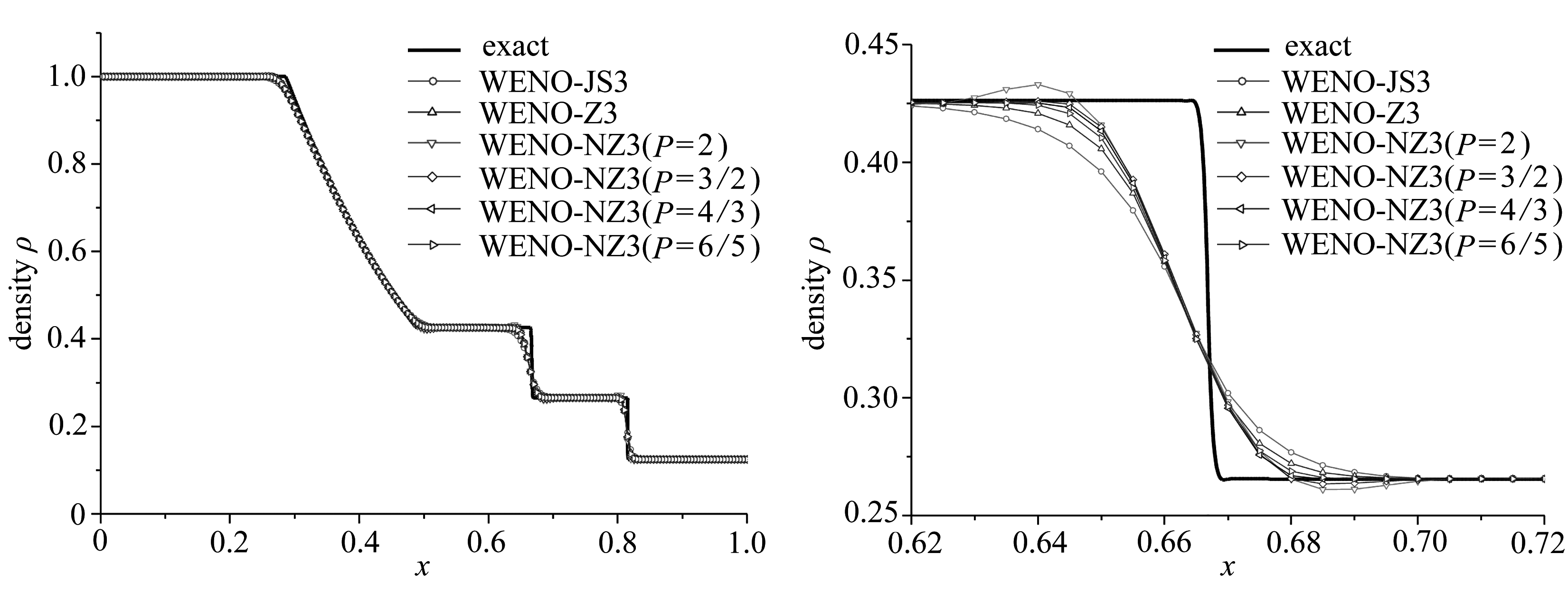
(a) 密度曲线图 (b) 密度曲线局部放大图 (a) Density curves (b) The partial enlarged detail of density curves
图1 Sod激波管计算结束后密度曲线及其局部放大图
Fig. 1 Density curves and the partial enlarged detail at the final time for the Sod problem
2.3.2 改进格式在非极值点处的精度
这里将进一步证明WENO-NZ3格式在光滑非极值点处同样能达到三阶精度．将式(18)、(37)代入式(36)可得
(49)
(50)
再根据式(9)中的加权法则可得右界面通量所对应权函数
(51)
(52)
同理可得
(53)
(54)
再根据式(9)中的加权法则可得左界面通量所对应权函数
(55)
(56)
根据式(51)、(52)、(55)、(56)可知
(57)
式(57)满足式(15)中的充分条件，这也就证明了改进WENO-NZ3格式(P=4/3)在光滑流场非极值点处能满足三阶精度．
为了进一步考察改进WENO-NZ3格式的计算性能，选取线性精度测试、一维Sod激波管、激波与熵波相互作用、Rayleigh-Taylor不稳定性等经典算例进行自主编程计算，并将该格式计算结果与WENO-JS3、WENO-Z3、WENO-N3格式进行对比．
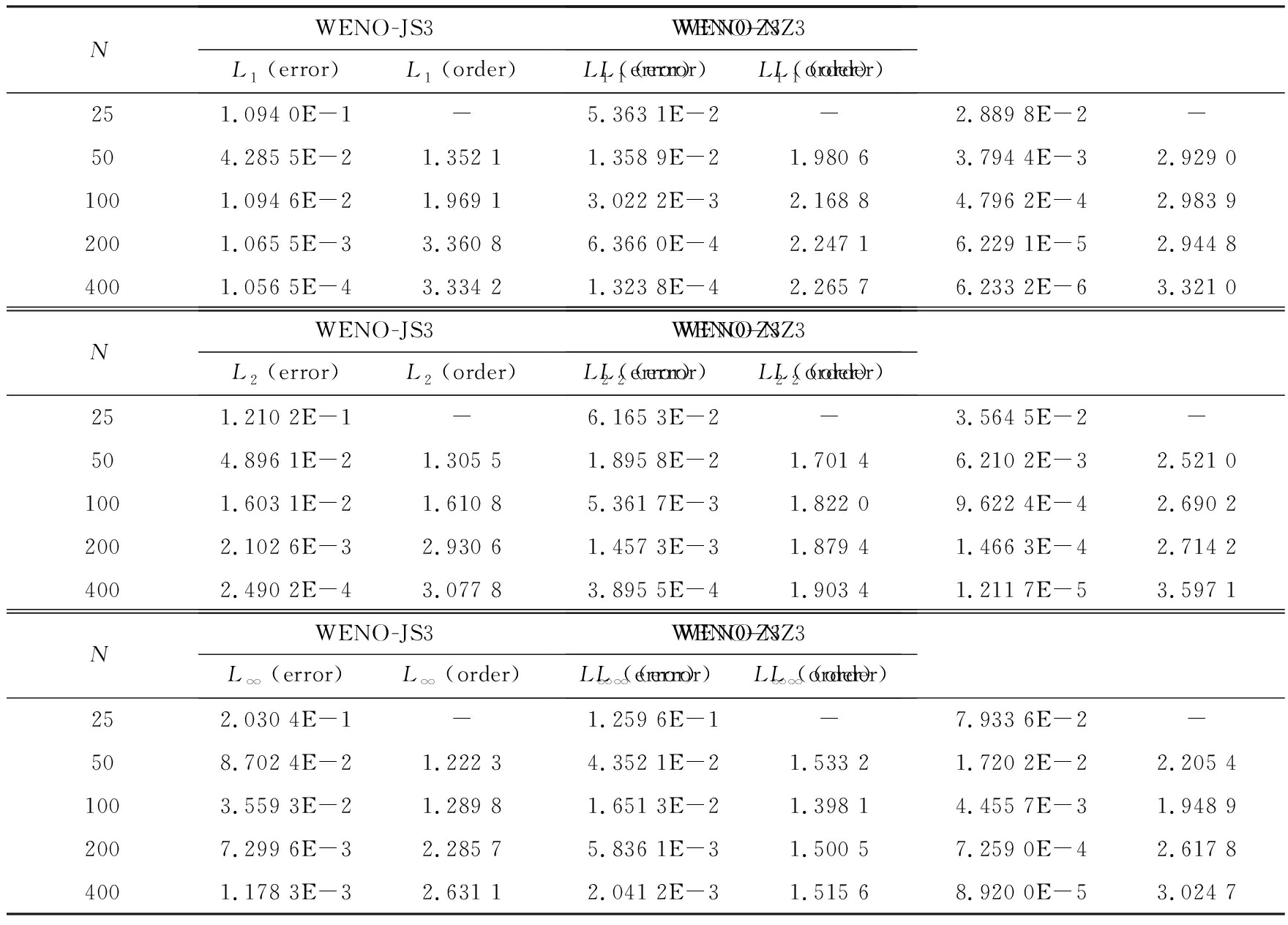
表1针对初始条件(58)，在t=2时不同数值计算格式L1,L2,L∞误差和精度比较
Table 1 Comparison ofL1,L2,L∞(error and order) for linear advection equations under initial condition (58) att=2 with different schemes
该算例选自文献[23]，计算初始条件为
u0(x)=sin(πx)，
(58)
其包含两个一阶极值点．表1给出了WENO-JS3、 WENO-Z3、 WENO-NZ3格式的L1，L2，L∞误差和精度， 其中各计算公式见式(59)～(61)．根据表1可知，WENO-NZ3格式的计算精度逼近三阶．
(59)
(60)
L
=max|ui-uexact,i|,
(61)
其中i=0,1,…,N．
该算例选自文献[8]，计算初始条件为
(62)
其包含两个一阶极值点．表2给出了WENO-JS3、WENO-Z3、WENO-NZ3格式的L1，L2，L∞误差和精度．根据表2可知，WENO-NZ3相较WENO-Z3格式提高了在极值点处的计算精度．
表2针对初始条件(62)，在t=2时不同数值计算格式L1,L2,L∞误差和精度比较
Table 2 Comparison ofL1,L2,L∞(error and order) for linear advection equations under initial condition (62) att=2 for different schemes
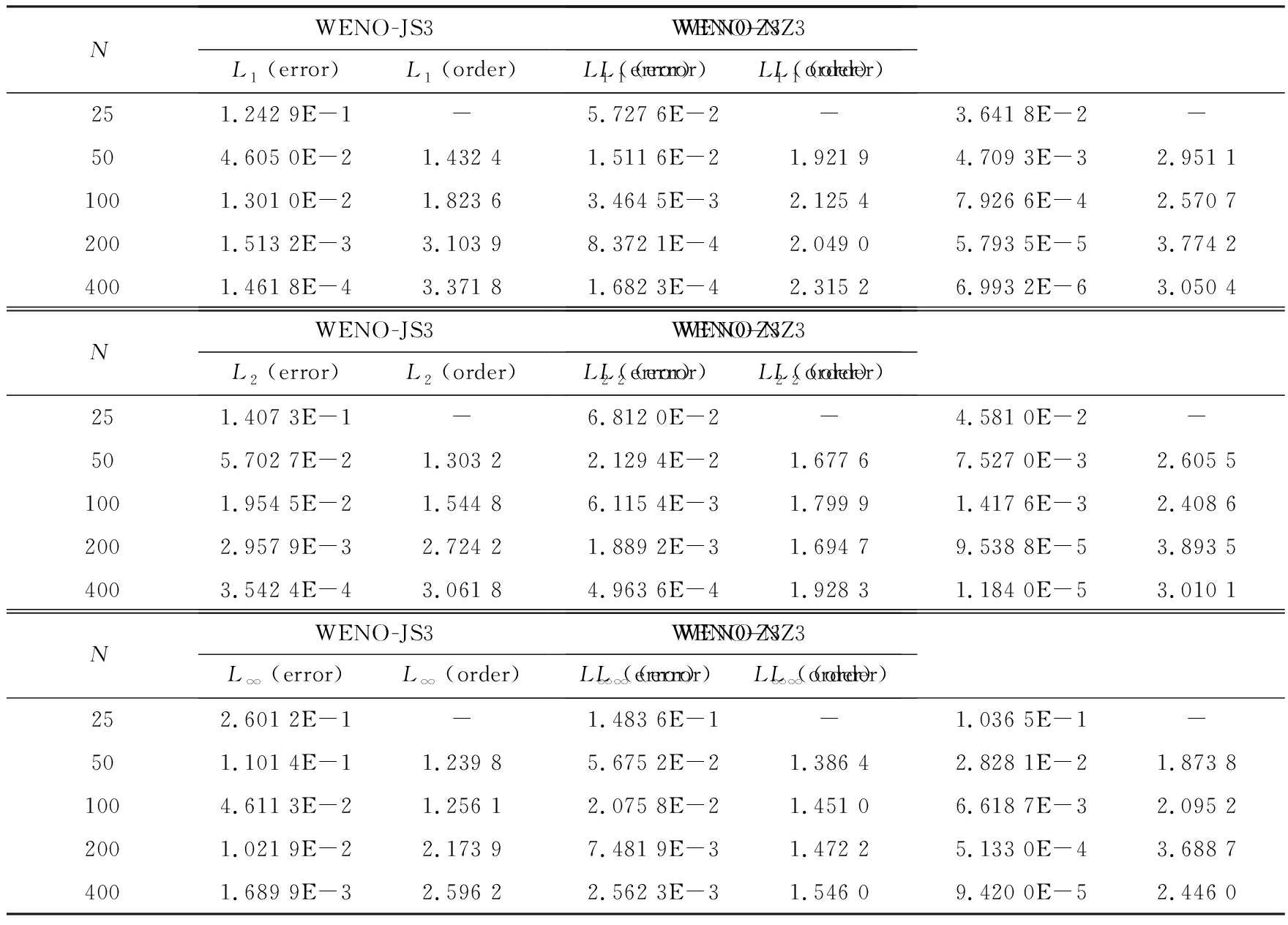
该算例选自文献[24]，式(63)给出计算的初始条件，该算例描述一个Mach(马赫)数为3的平面激波与局部密度扰动区的相互作用．网格数为800，计算结束时间为1.8，“精确解”的计算网格数为10 000．计算结束时刻密度曲线图及局部放大图见图2．
(63)
(a) 密度曲线图 (b) 密度曲线局部放大图 (a) Density curves (b) The partial enlarged detail of density curves
图2 Shu-Osher激波与熵波相互作用计算结束后密度曲线及其局部放大图
Fig. 2 Density curves and the partial enlarged detail at the final time for the Shu-Osher problem
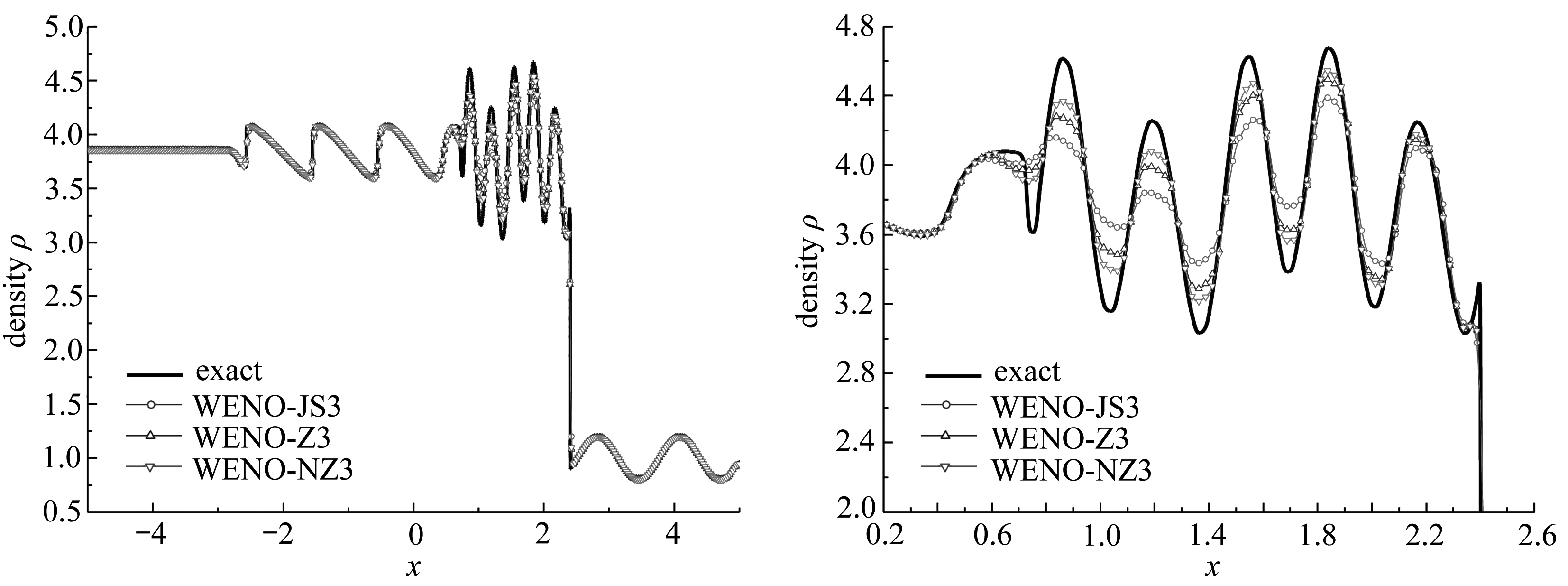
该算例选自文献[26]， 式(64)给出计算的初始条件， 网格数为4 000， 计算结束时间为5.0，“精确解”的计算网格数为6 000．计算结束时刻密度曲线图及局部放大图见图3．
(64)
(a) 密度曲线图 (b) 密度曲线局部放大图 (a) Density curves (b) The partial enlarged detail of density curves
图3 Titarev-Toro激波与熵波相互作用计算结束后密度曲线及其局部放大图
Fig. 3 Density curves and the partial enlarged detail at the final time for the Titarev-Toro problem
图2、图3的算例计算结果表明，WENO-NZ3格式相较于WENO-JS3、WENO-Z3格式不仅提高了在极值点处的计算精度，而且降低了格式的耗散．
该问题选自文献[21, 27-28]，主要描述重力场作用下，重流体加速进入轻流体界面失稳过程．利用该算例可以考察数值方法的分辨率特性．计算域设置为[0, 0.25]×[0, 1], 计算初始条件如下所示：
(65)
该算例中，绝热指数γ取值为5/3．为了考虑重力效应，在Euler方程的y方向的动量方程和能量方程的右端分别加入ρ，ρv作为源项．左右边界设置成反射边界条件，顶部和底部边界条件分别为
(ρ,u,v,p) = (1, 0, 0, 2.5)， (ρ,u,v,p) = (2, 0, 0, 1)．
网格数划分为240 × 960，计算结束时间为1.95．
图4给出不同格式(WENO-JS3、WENO-Z3、WENO-N3、WENO-NZ3)密度等值线图，共绘制15条等值线，其取值区间为[0.952 269， 2.145 89]．改进格式WENO-NZ3在接触间断附近具有更低的耗散性，给出分辨率更优的结果．
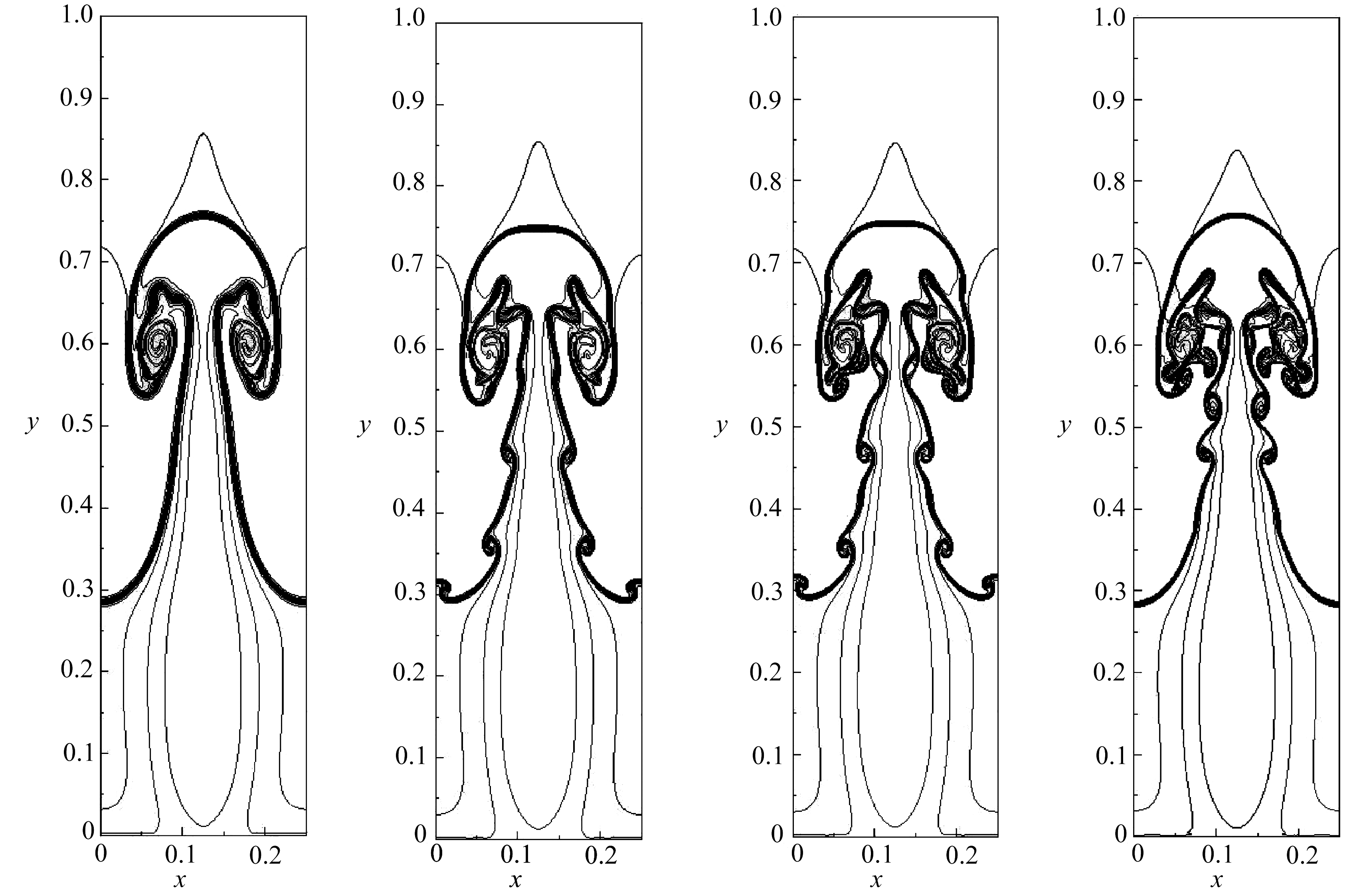
(a) WENO-JS3 (b) WENO-Z3 (c) WENO-N3 (d) WENO-NZ3
图4 Rayleigh-Taylor不稳定性问题不同格式(WENO-JS3、 WENO-Z3、 WENO-N3、 WENO-NZ3)密度曲线图
Fig. 4 Density contours of the Rayleigh-Taylor instability computed with the WENO-JS3, WENO-Z3, WENO-N3 and WENO-NZ3 schemes
该问题选自文献[29]，计算初始条件如下：
(66)
计算网格数选取为960×960，计算结束时间为t=0.8．图5给出计算结束时刻不同格式密度曲线等值线图，共绘制40条等值线，其取值区间为[0.14，1.7]．WENO-NZ3格式相较WENO-JS3、WENO-Z3、WENO-N3格式在滑移线附近给出分辨率较高的结果．
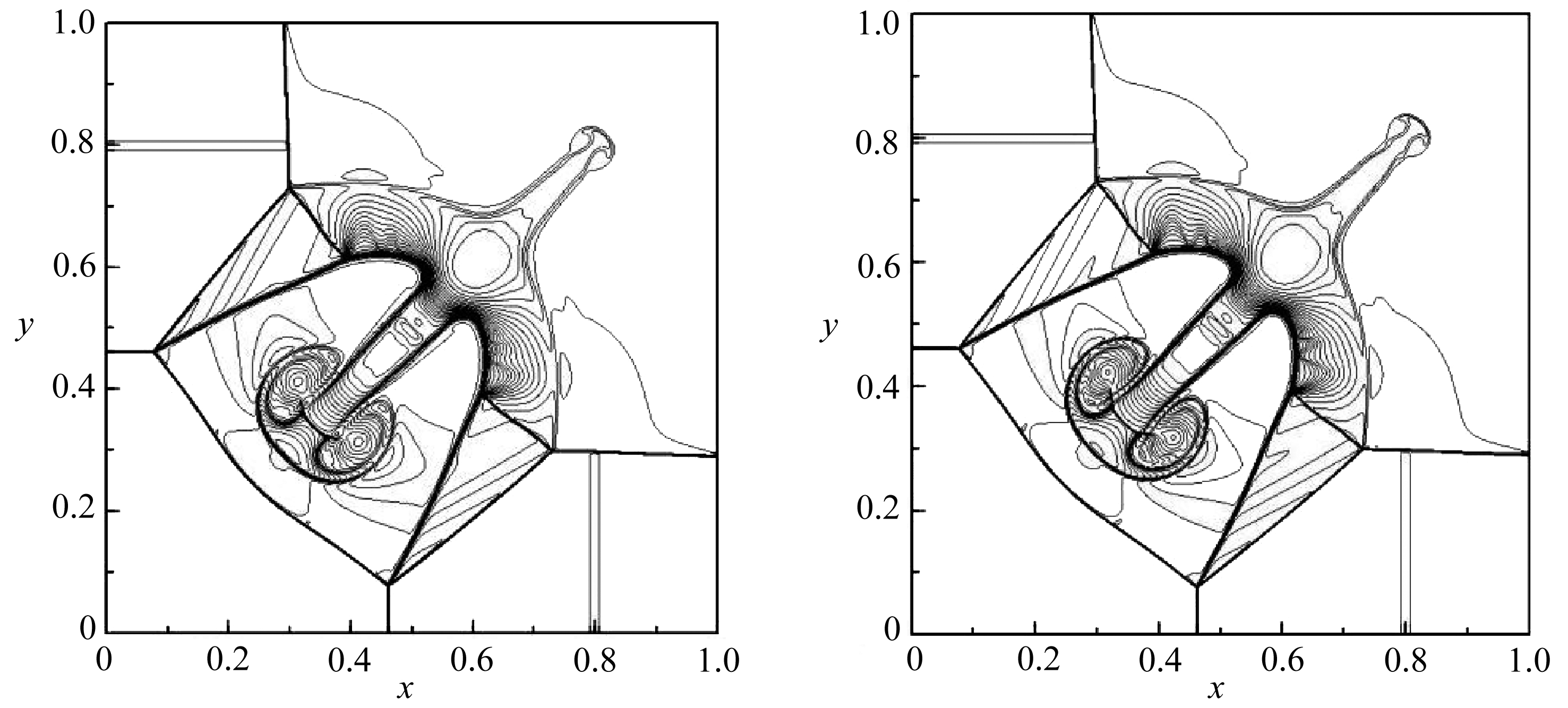
(a) WENO-JS3 (b) WENO-Z3
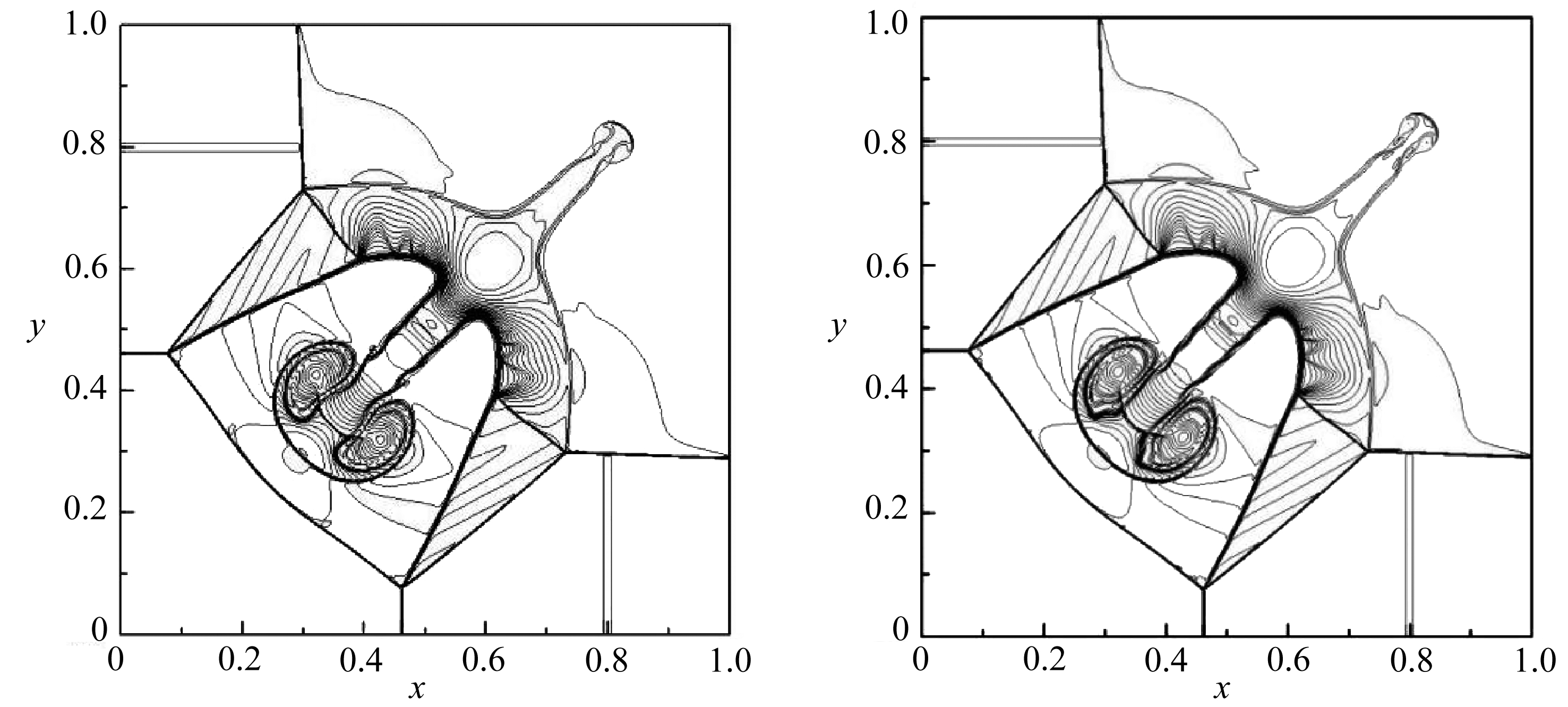
(c) WENO-N3 (d) WENO-NZ3
图5 二维Riemann问题不同格式(WENO-JS3、 WENO-Z3、 WENO-N3、 WENO-NZ3)密度曲线图
Fig. 5 Density contours of the 2D Riemann problem computed with the WENO-JS3, WENO-Z3, WENO-N3 and WENO-NZ3 schemes at t=0.8
本文采用Taylor级数展开的方式，构造出一种提高极值点计算精度的WENO-NZ3格式，并通过精度测试、Sod激波管等经典算例，从精度和耗散性(分辨率)两个角度考察了WENO-NZ3格式的计算性能．通过本文的研究主要得到以下两点结论：
1) WENO-NZ3格式综合权衡了计算精度和计算稳定性，其在极值点处逼近收敛精度，本文的构造方法可以进一步推广应用于五阶以上WENO格式；
2) WENO-NZ3格式相较其他格式(WENO-JS3、WENO-Z3、WENO-N3)不仅降低了格式的耗散，同时还提高了对复杂流场结构的分辨率．
参考文献(References)：
[1] LIU X D, OSHER S, CHAN T. Weighted essentially non-oscillatory schemes[J].Journal of Computational Physics, 1994,115(1): 200-212.
[2] HARTEN A, ENGQUIST B, OSHER S, et al.Uniformly High Order Accurate Essentially Non-Oscillatory Schemes,III[M]//HUSSAINI M Y, VAN LEER B, VAN ROSENDALE J, ed.Upwind and High-Resolution Schemes. Berlin, Heidelberg: Springer, 1987: 218-290.
[3] JIANG G S, SHU C W. Efficient implementation of weighted ENO schemes[J].Journal of Computational Physics, 1995,126(1): 202-228.
[4] HSIEH T J, WANG C H, YANG J Y. Numerical experiments with several variant WENO schemes for the Euler equations[J].International Journal for Numerical Methods in Fluids, 2008,58(9): 1017-1039.
[5] ZHAO S, LARDJANE N, FEDIOUN I. Comparison of improved finite-difference WENO schemes for the implicit large eddy simulation of turbulent non-reacting and reacting high-speed shear flows[J].Computes&Fluids, 2014,95(3): 74-87.
[6] WANG C, DING J X, SHU C W, et al. Three-dimensional ghost-fluid large-scale numerical investigation on air explosion[J].Computes&Fluids, 2016,137: 70-79.
[7] ZAGHI S, MASCIO A D, FAVINI B. Application of WENO-positivity-preserving schemes to highly under-expanded jets[J].Journal of Scientific Computing, 2016,69(3): 1-25.
[8] HENRICK A K, ASLAM T D, POWERS J M. Mapped weighted essentially non-oscillatory schemes: achieving optimal order near critical points[J].Journal of Computational Physics, 2005,207(2): 542-567.
[9] BORGES R, CARMONA M, COSTA B, et al. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws[J].Journal of Computational Physics, 2008,227(6): 3191-3211.
[10] YAMALEEV N K, CARPENTER M H. A systematic methodology for constructing high-order energy stable WENO schemes[J].Journal of Computational Physics, 2009,228(11): 4248-4272.
[11] FAN P. High order weighted essentially nonoscillatory WENO-ηschemes for hyperbolic conservation laws[J].Journal of Computational Physics, 2014,269(1): 355-385.
[12] FAN P, SHEN Y, TIAN B, et al. A new smoothness indicator for improving the weighted essentially non-oscillatory scheme[J].Journal of Computational Physics, 2014,269(10): 329-354.
[13] FENG H, HUANG C, WANG R. An improved mapped weighted essentially non-oscillatory scheme[J].Applied Mathematics&Computation, 2014,232(6): 453-468.
[14] SHEN Y, ZHA G. Improvement of weighted essentially non-oscillatory schemes near discontinuities[J].Computes&Fluids, 2014,96(12): 1-9.
[15] CHANG H K, HA Y, YOON J. Modified non-linear weights for fifth-order weighted essentially non-oscillatory schemes[J].Journal of Scientific Computing, 2016,67(1): 299-323.
[16] MA Y, YAN Z, ZHU H. Improvement of multistep WENO scheme and its extension to higher orders of accuracy[J].International Journal for Numerical Methods in Fluids, 2016,82(12): 818-838.
[17] WANG R, FENG H, HUANG C. A new mapped weighted essentially non-oscillatory method using rational mapping function[J].Journal of Scientific Computing, 2016,67(2): 540-580.
[18] YAMALEEV N K, CARPENTER M H. Third-order energy stable WENO scheme[J].Journal of Computational Physics, 2013,228(8): 3025-3047.
[19] WU Xiaoshuai, ZHAO Yuxin. A high-resolution hybrid scheme for hyperbolic conservation laws[J].International Journal for Numerical Methods in Fluids, 2015,78(3): 162-187.
[20] DON W S, BORGES R. Accuracy of the weighted essentially non-oscillatory conservative finite difference schemes[J].Journal of Computational Physics, 2013,250: 347-372.
[21] HU X Y, WANG Q, ADAMS N A. An adaptive central-upwind weighted essentially non-oscillatory scheme[J].Journal of Computational Physics, 2010,229(23): 8952-8965.
[22] WU X, LIANG J, ZHAO Y. A new smoothness indicator for third-order WENO scheme[J].International Journal for Numerical Methods in Fluids, 2016,81(7): 451-459.
[23] GANDE N R, RATHOD Y, RATHAN S. Third-order WENO scheme with a new smoothness indicator[J].International Journal for Numerical Methods in Fluids, 2017,85(2): 171-185.
[24] SHU C W, OSHER S. Efficient implementation of essentially non-oscillatory shock-capturing schemes, II[J].Journal of Computational Physics, 1989,83(1): 32-78.
[25] SOD G A. A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws[J].Journal of Computational Physics, 1978,27(1): 1-31.
[26] TITAREV V A, TORO E F. Finite-volume WENO schemes for three-dimensional conservation laws[J].Journal of Computational Physics, 2004,201(1): 238-260.
[27] SHI J, ZHANG Y T, SHU C W. Resolution of high order WENO schemes for complicated flow structures[J].Journal of Computational Physics, 2003,186(2): 690-696.
[28] ACKER F, BORGES R, COSTA B. An improved WENO-Z scheme[J].Journal of Computational Physics, 2016,313: 726-753.
[29] LAX P D, LIU X D. Solution of two-dimensional Riemann problems of gas dynamics by positive schemes[J].SIAM Journal on Scientific Computing, 1998,19(2): 319-340.
XU Weizheng1,2, WU Weiguo1,2
(1.Key Laboratory of High Performance Ship Technology of Ministry of Education,Wuhan University of Technology,Wuhan430063,P.R.China； 2.Department of Naval Architecture,Ocean and Structural Engineering,School of Transportation,Wuhan University of Technology,Wuhan430063,P.R.China)
Abstract:Firstly, the sufficient conditions for the 3rd-order WENO scheme satisfying the convergence precision were deduced. Based on the Taylor series method, the precision of the conventional 3rd-order WENO-Z scheme in the smooth flow field was analyzed. It was found that at the critical points, the 3rd-order WENO-Z scheme fails to achieve the convergence precision. In order to improve the precision near the critical points for the 3rd-order WENO-Z scheme, an improved 3rd-order WENO-Z scheme (WENO-NZ3) was constructed in view of the balance between precision and stability to finally determine the parameters. The improvement of the precision was verified through 2 typical numerical tests. What is more, the Sod shock wave tube, the shock-entropy wave interaction, the Rayleigh-Taylor instability and the 2D Riemann problem were calculated to confirm that the WENO-NZ3 scheme performs better than the conventional WENO schemes like WENO-JS3, WENO-Z3 and WENO-N3.
Key words:3rd-order WENO scheme; smoothness indicator; Taylor expansion; high precision; high resolution; hyperbolic conservation law
Foundation item:The National Natural Science Foundation of China(51409202)
引用本文/Cite this paper: 徐维铮, 吴卫国. 三阶WENO-Z格式精度分析及其改进格式[J]. 应用数学和力学, 2018,39(8): 946-960.XU Weizheng, WU Weiguo. Precision analysis of the 3rd-order WENO-Z scheme and its improved scheme[J].Applied Mathematics and Mechanics, 2018,39(8): 946-960.
文章编号：1000-0887(2018)08-0946-15
ⓒ 应用数学和力学编委会，ISSN 1000-0887
*收稿日期：2018-01-03；
修订日期：2018-01-29
基金项目：国防基础研究项目(B1420133057)；国家自然科学基金(51409202)；中央高校基本科研业务费(2016-YB-016)
作者简介：徐维铮(1991—)，男，博士生(E-mail: xuweizheng@whut.edu.cn); 吴卫国(1960—)，男，教授，博士生导师(通讯作者. E-mail: mailjt@163.com).
摘要：首先通过理论推导给出了三阶WENO格式(WENO-JS3格式)满足收敛精度的充分条件．采用Taylor(泰勒)级数展开的方法，分析发现传统的三阶WENO-Z格式(WENO-Z3格式)在光滑流场极值点处精度降低．为了提高WENO-Z3格式在极值点处的计算精度，根据收敛精度的充分条件构造一种改进的三阶WENO-Z格式(WENO-NZ3格式)，并综合权衡计算精度和计算稳定性确定所构造格式的参数．通过两个典型的精度测试，验证了WENO-NZ3格式在光滑流场极值点区域逼近三阶精度．选用Sod激波管、激波与熵波相互作用、Rayleigh-Taylor不稳定性、二维Riemann(黎曼)问题经典算例，进一步证实了本文提出的WENO-NZ3格式相较其他格式(WENO-JS3、WENO-Z3、WENO-N3)，不仅提高了计算精度，而且提高了对复杂流场结构的分辨率．
关 键 词：三阶WENO格式； 光滑因子； Taylor展开； 高精度； 高分辨率；双曲守恒律
中图分类号：O357.1
文献标志码：A
DOI:10.21656/1000-0887.390011