 )u+g
)u+g
 [
[
 (
( ·u),
·u),何郁波1, 董晓亮2, 林晓艳1
(1. 怀化学院 数学与计算科学学院, 湖南 怀化 418008; 2. 北方民族大学 数学与信息科学学院, 银川 750021)
Boussinesq方程也称为广义非线性二阶Benjamin-Ono方程,是一种能够描述规则波和不规则波在复杂地形上发生浅化、折射、绕射和反射效应相当有效的模型.
1872年,法国物理学家Boussinesq研究水波在平底传播的形态时,为了得到简化的传播方程,作出了适当的假设而得到了相应的数学模型——Boussinesq方程[1].文献[2]中介绍了不同形式的Boussinesq方程,并且证明了方程对应不同初边值条件的问题具有孤立子波.经典的Boussinesq方程为
utt=-αuxxxx+uxx+β(u2)xx,
(1)
其中宏观变量u(x,t)表示流体表面的自由运动,这里流动流体的深度和相应长波的特征速度决定了正常数α,β的值[2].文献[3-4]讨论了把Boussinesq方程中非线性和散射的影响考虑为线性波动方程的扰动.经典的Boussinesq方程的各种形式已在多方面得到了研究,如下面的Boussinesq方程[2]:
utt=-uxxxx+uxx+(f(u))xx.
(2)
针对问题(2),利用相应的变换方法,Tsutsumi等[5]将方程(2)转换为非线性Schrödinger方程组并证明了方程(2)的全局解和局部解的适定性及解的光滑特性[2].另外,方程(2)在特定的初边值条件下具有非线性稳定的孤立子[6],并且文献[6]也证明了如果给定的初值条件离孤立子不远,则所对应的局部解可拓展为方程的全局解.这个结论也符合文献[7-8]中关于Cauchy问题的解有限爆破的结论.其他方面的工作包括方程(2)的N-孤立子及系统宏观守恒律的验证[9],系统精确解更普遍的构造方法等[10].
在Boussinesq方程的其他数学模型研究方面,Peregrine于1967年在文献[11]中考虑了沿水深的积分方程,利用关于流速的摄动展开技术,推导了经典形式的Boussinesq方程.此时方程是一个水深可变的二维系统:
![]()
 )u+g
)u+g
![]()
 [
[
![]()
 (
( ·u),
·u),
(3)
其中的宏观变量u(x,t)表示流体横截面的流速.受一些特殊形式的要求,当水深较浅,一般要求h/L0≤0.12,此时Boussinesq方程(3)可比较精确地刻画出水波的传播.
在低阶的Boussinesq方程的数值研究方面,包括Wei,Kirby等[12]在内的学者们做了为数不多的有益工作.详细的关于低阶Boussinesq方程解的有限差分格式和有限元方法等的研究工作请参阅文献[12-14]及其中所提到的相关文献,这里不再作赘述.
格子Boltzmann方法(LBM)是基于微观模型和介观动理学模型之间的一种近年来用于模拟计算流体力学的数值仿真技术,LBM从诞生至今一直受到国内外学者的广泛关注.LBM将连续流体假想为离散粒子分布到Euler坐标系的格子上,采用固定的Euler网格代表流场,避免传统的有限体积法和有限元方法中移动网格的重建,降低计算成本,在多相流[15]、非Newton流体[16]、悬浮粒子流[17]、微流体[18-19]等复杂的流体系统中具有较大的优势.
据笔者所知,目前针对广义非线性四阶Boussinesq方程的数值研究较少,尤其是利用LBM对Boussinesq方程进行数值模拟的工作迄今为止没有发现.基于此,为了推广利用LBM新技术求解高阶的Boussinesq方程,考虑如下的一类具有初边值问题的广义非线性含源四阶Boussinesq方程:
(4)
满足的初始条件为
(5)
边界条件为
(6)
其中α,β为正常数,k为正整数,F(u)为源项.α的物理意义是控制非线性和水波特征速度的常系数,β是流体的深度,u(x,t)为流体自由表面的运动.
1) 当k=2,β>0,F(u)=0时,方程(4)称为“good” Boussinesq方程.由于此时系统所具有的线性稳定性,因此可以用来描述线性梁的小幅振动[20-21].
2) 当k=2,β<0,F(u)=0时,方程(4)称为“bad” Boussinesq方程.此种情形时,方程(4)具有某种线性不稳定性.此种情况下的方程起源于诸如非线性点阵波、具一致各向同性特征的等离子声波等的物理现象.同时,此种情形下的系统也可以用来刻画水深较浅的表面长波的传播[22-23].
由于方程(4)也可用来描述两个相反方向传播的KdV孤波,因此方程也可以刻画一维非线性晶格的振动[24].
本节将讨论方程(4)初边值问题的LBM的建立及误差分析.
用eα表示粒子速度,c=|eα|表示粒子的运动速率,eα=0表示静止的粒子.采用一维五速度(D1Q5)格子离散速度模型,定义粒子速度为
eα=[e0,e1,e2,e3,e4]=[0,c,-c,2c,-2c].
(7)
fα(x,t)定义为时刻t时,在点x处带有速度eα的单个粒子的分布函数,α=1,2,3,4代表运动粒子,α=0代表静止粒子.假定![]() 为局部平衡态分布函数,且满足如下的守恒律:
为局部平衡态分布函数,且满足如下的守恒律:
(8)
分布函数fα(x,t)满足如下带修正函数及源项的离散LBM:
fα(x+εeα,t+ε)-fα(x,t)=
(9)
其中Knudsen数小参数ε与时间步长Δt相等,定义其数值为ε=l/L,其中l表示分子的平均自由程,L表示系统的特征尺度.hα(x,t)为修正函数,F(u)是方程的源项,代表波所受到的外力项.为了能够恢复宏观方程(4),与标准的LBM有所不同,定义粒子的速度分布函数和局部平衡态分布函数及宏观变量u(x,t)满足如下的守恒律:
(10)
利用Taylor展开式对方程(9)左边进行展开,可得
(11)
将等式右边的展开式关于Knudsen数保留至O(ε6),有
(12)
对粒子的速度分布函数fα(x,t),运用Chapman-Enskog多尺度技术在局部平衡态分布函数![]() 附近关于小参数ε进行多尺度展开,展开到O(ε6)有
附近关于小参数ε进行多尺度展开,展开到O(ε6)有
(13)
同时,利用Chapman-Enskog多尺度技术,引入不同的时间尺度t0,t1,t2,t3,t4,t5,定义
ti=εit,i=0,1,2,3,4,5
(14)
和
(15)
将式(13)及(15)代入式(12),并比较方程(9)的两边小参数ε的同次幂系数就可以得到不同时间尺度上的系列偏微分方程:
(16)
(17)
(18)
(19)
(20)
由方程(16)可得
(21)
将方程(21)代入方程(17)得ε2尺度上的分布函数![]() 为
为
(22)
同时将方程(21)、(22)代入方程(18)可得ε3尺度上的分布函数![]() 满足
满足
(23)
联合方程(21)~(23),从而由方程(19)可得
(24)
由方程(24)可得ε4尺度上的分布函数![]()
(25)
将方程(21)~(23)及(25)代入方程(20)得
(26)
在方程(22)两边关于时间尺度t1求偏导数,可得
(27)
联合方程(22)~(24)、(26)及(27)可得截断误差项为
(28)
由方程(28)可知模型的截断误差与局部平衡态分布函数![]() 的一阶、二阶、三阶和五阶矩及修正函数的零阶、三阶矩有关,另外截断误差还与压力源项F(u)的零阶及二阶矩有关.
的一阶、二阶、三阶和五阶矩及修正函数的零阶、三阶矩有关,另外截断误差还与压力源项F(u)的零阶及二阶矩有关.
分别对方程(21)~(23)及(25)求一阶矩,得
(29)
(30)
(31)
(32)
为了恢复宏观方程(4),且满足可解性条件,基于保证截断误差(28)达到最小,可以确定所选择的局部平衡态分布函数![]() 及非平衡态分布函数
及非平衡态分布函数![]() 应满足如下的各阶矩条件:
应满足如下的各阶矩条件:
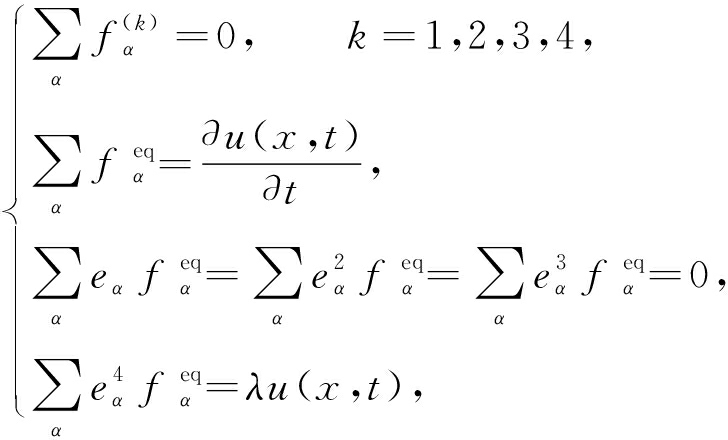
(33)
其中λ是待定常数.
同时,还选取修正函数hα(x,t)满足如下的各阶矩条件:
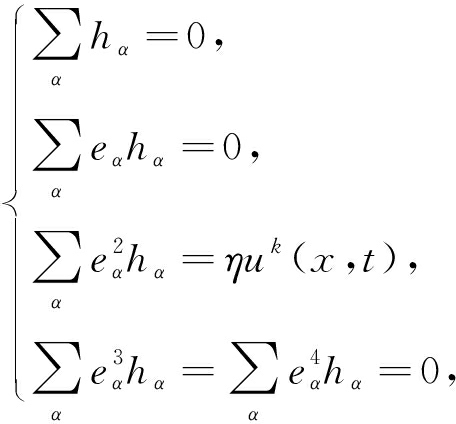
(34)
其中η是自由未知量.
利用矩条件(33)及(34),由方程(29)~(32)可得不同时间尺度上的偏微分方程:
(35)
(36)
(37)
(38)
由方程
eq.(35)+ε× eq.(36)+ε2× eq.(37)+ε3× eq.(38)
可得
5τεF(u)+O(ε6).
(39)
若要恢复宏观方程(4),只需令
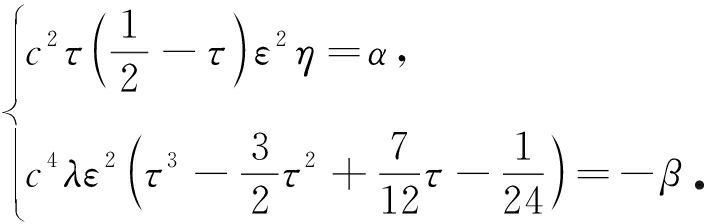
(40)
由方程(33)可解得各方向上局部平衡态分布函数![]() 为
为
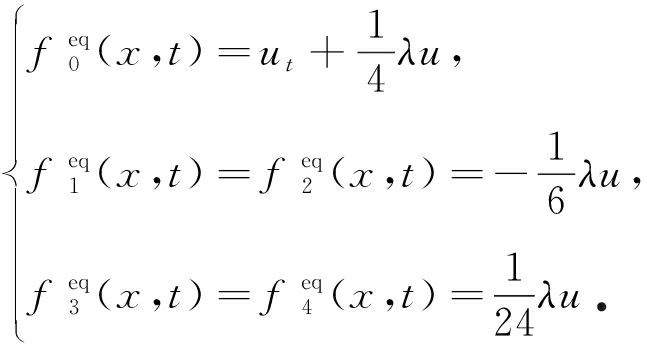
(41)
另外,解方程组(34)得各方向上的修正函数hα(x,t)为

(42)
根据演化方程(9),可得到各方向上迭代格式的经典差分形式:
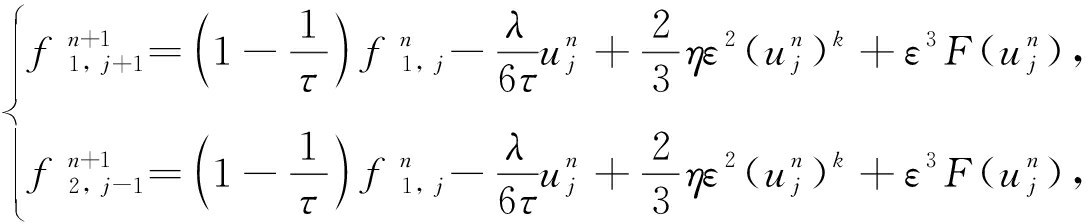
(43a)
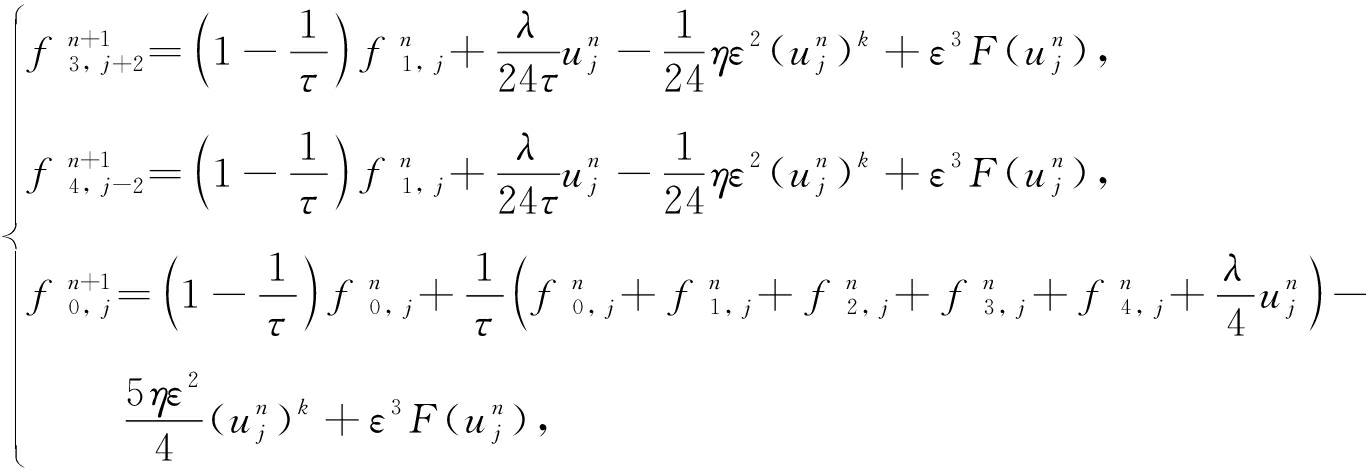
(43b)
其中
本节将选取3个算例来检验模型的有效性和稳定性.算例中有的具有精确解,有的精确解未知.为了验证模型(43)的有效性,将数值结果与算例的精确解进行对比;为了验证模型(43)的稳定性和正确性,将精确解未知时模型的数值解与MFDM进行对比.下面给出MFDM:包括宏观变量对时间的导数及对空间变量导数的差分格式.
1) 宏观变量u对时间t的一阶导数的差分格式采用如下的三阶全变差下降Runge-Kutta(TVD Runge-Kutta)显式时间推进格式[21,25]:
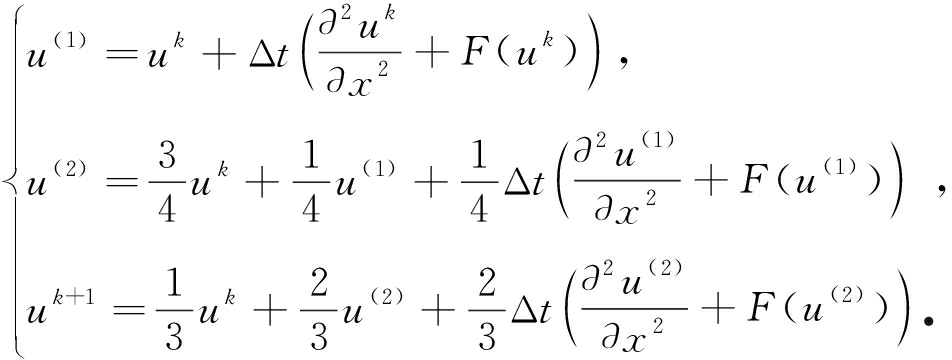
2) 宏观变量u(x,t)关于空间变量x的二阶导数的差分格式采用如下中心差分方法:
如果初始条件没有给出,则初始条件中所有网格点处的分布函数fi(x,0)的值近似地用局部平衡态分布函数![]() 的值代替.宏观变量u(x,t)满足初始化条件.若边界条件未知时,边界值则采用非平衡态外推格式[26].模型的误差精度由总体相对误差EGRE、L∞模误差和L2模误差来刻画.EGRE定义如下:
的值代替.宏观变量u(x,t)满足初始化条件.若边界条件未知时,边界值则采用非平衡态外推格式[26].模型的误差精度由总体相对误差EGRE、L∞模误差和L2模误差来刻画.EGRE定义如下:

式中u(xi,t),u*(xi,t)分别表示由模型所得到数值解的值和系统精确解的值在所有的网格点处进行求和.
算例1[27]在带边界条件和初始条件的Boussinesq系统中取α=-1,β=1,k=2,F(u)=0,则系统为如下的初边值问题:
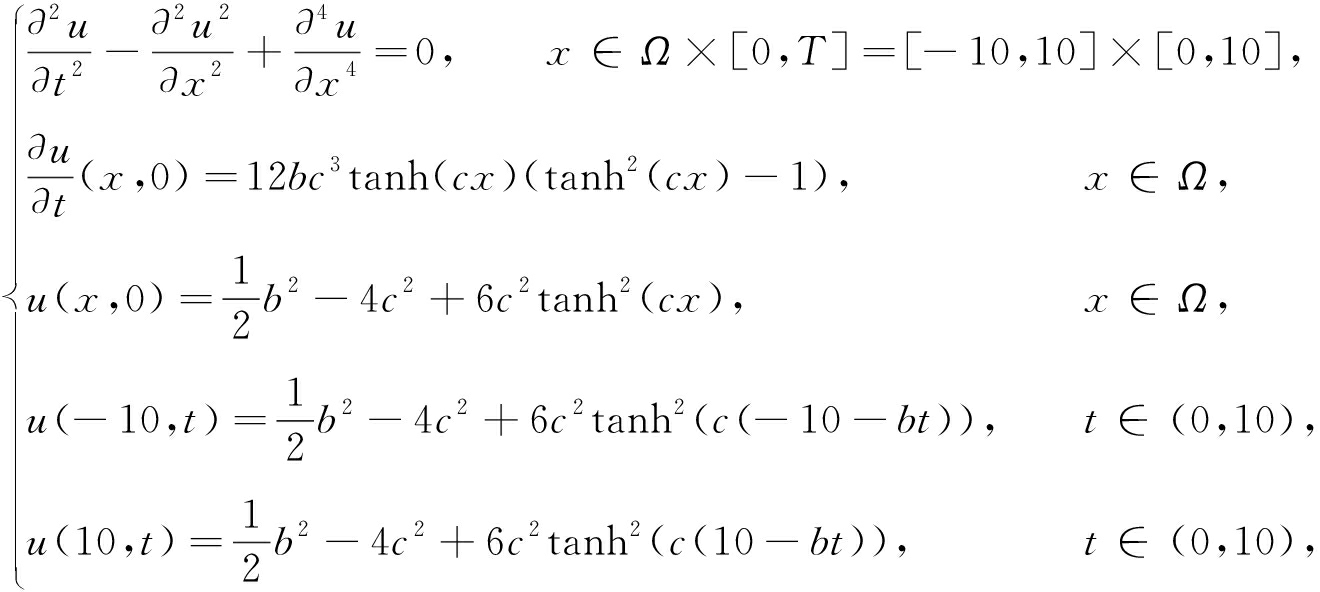
其中b,c为任意常数.此时系统具有解析解,且解析解的表达式为
针对算例1的数值模拟,在模型中取参数如下:α=-1,β=1,k=2,F(u)=0,b=0.01,c=0.3, Δx=0.1, Δt=0.01,Ω=[-10,10],格子数N=200.时刻t=1, 2, 3, 4时数值解与解析解u(x,t)的模拟对比结果见图1.同时,本文为了考虑本节所建立的LBM的精度,还给出了不同时刻数值解的全局相对误差,相对误差结果见表1.
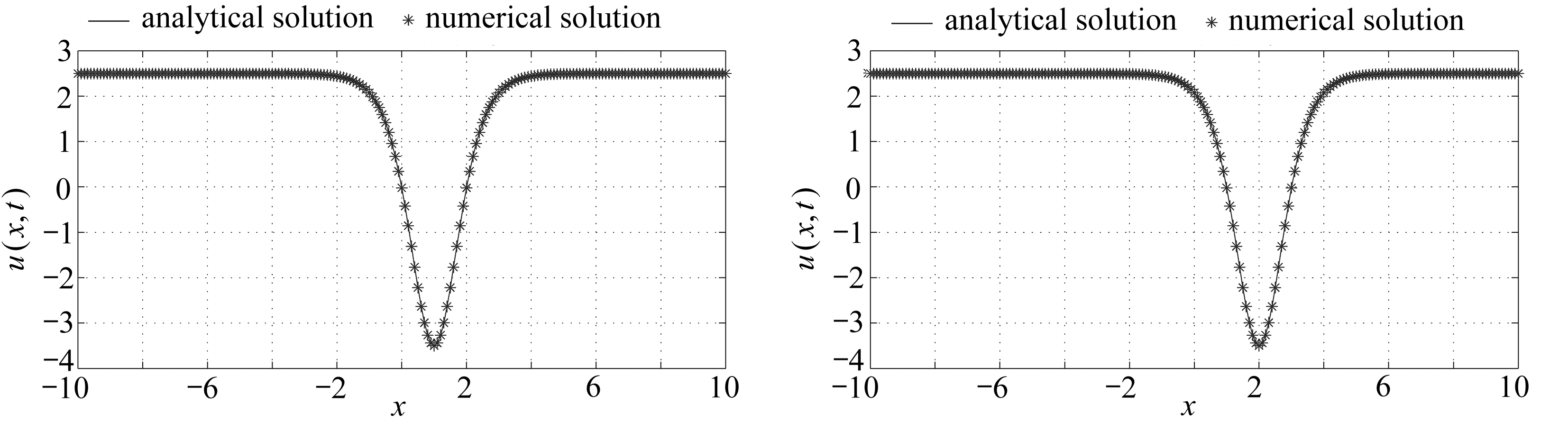
(a) t=1 (b) t=2
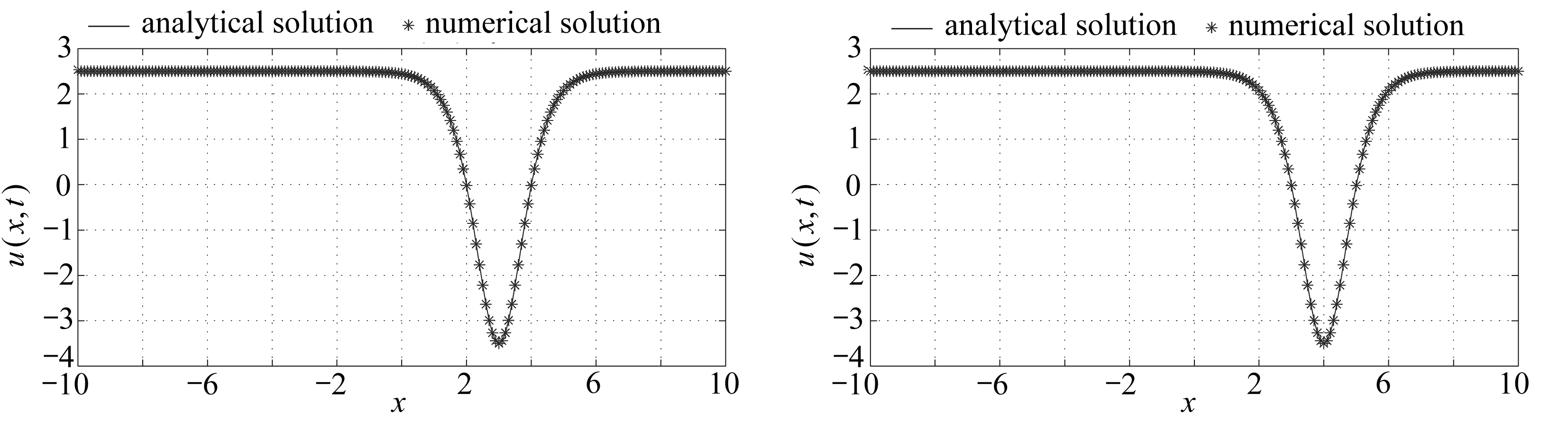
(c) t=3 (d) t=4
图1 算例1不同时刻解析解和LBM的数值解的比较
Fig. 1 Comparison between the numerical solutions and the analytical solutions of example 1
同时,在图2中给出了算例1中Boussinesq系统在对应的初边值条件下的LBM的数值解u(x,t)的时空演化图.由图2可以看出,波形呈倒钟形,并且随着时间的推移保持着振幅不变地往前传播.
图1和图2表明了本节所建立的LBM对于算例1具初边值条件的Boussinesq系统是有效的,数值解与解析解相吻合.另外,表1说明本节的LBM精度比较好,总体相对误差精度达到了时间步长的O(Δt2).
为了考察系统(4)中参数α,β的符号对波形、振幅及波的传播的影响,在算例2中讨论α,β均小于零的情形.
表1算例1中Boussinesq系统在不同时刻数值解与解析解的全局相对误差对比
Table 1 Comparison of the global relative errors between the LBM solutions and the analytical solutions at different moments in example 1

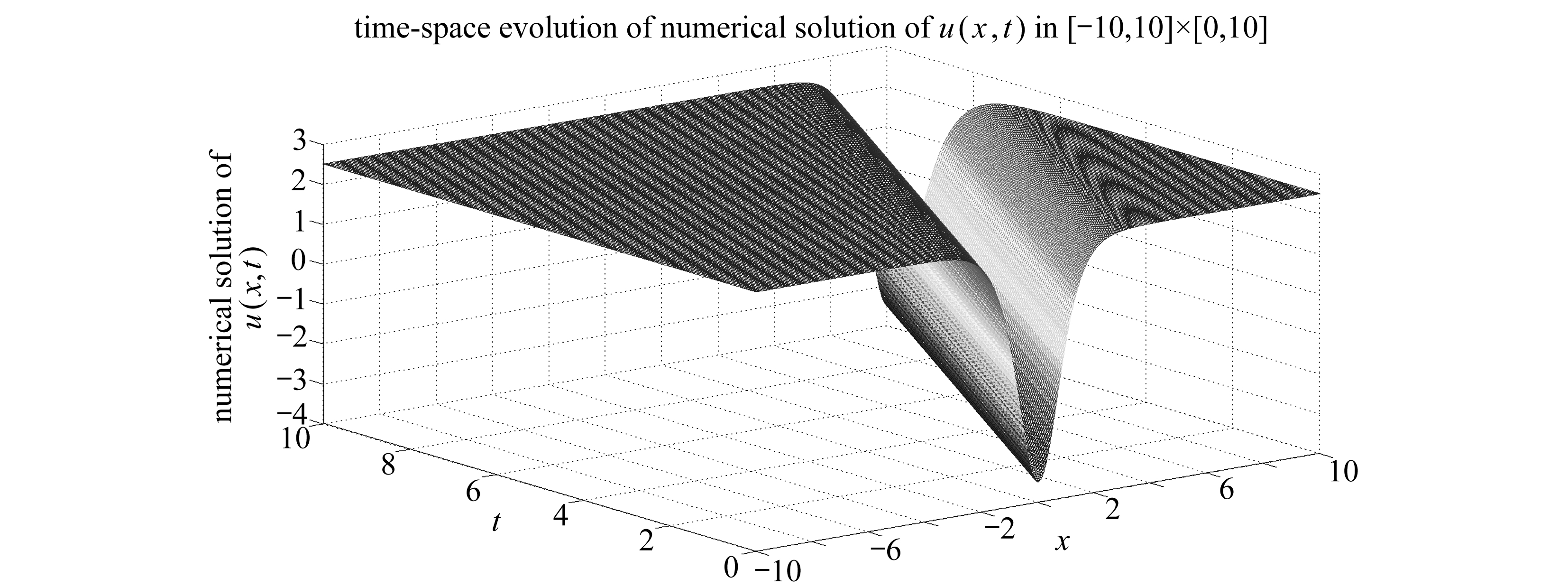
图2 算例1的数值解u(x,t)的时空演化图
Fig. 2 The time-space evolution graph of the numerical solutions of example 1 obtained with the LBM
算例2在Boussinesq系统中取α=β=-1,k=2,F(u)=0,则系统为
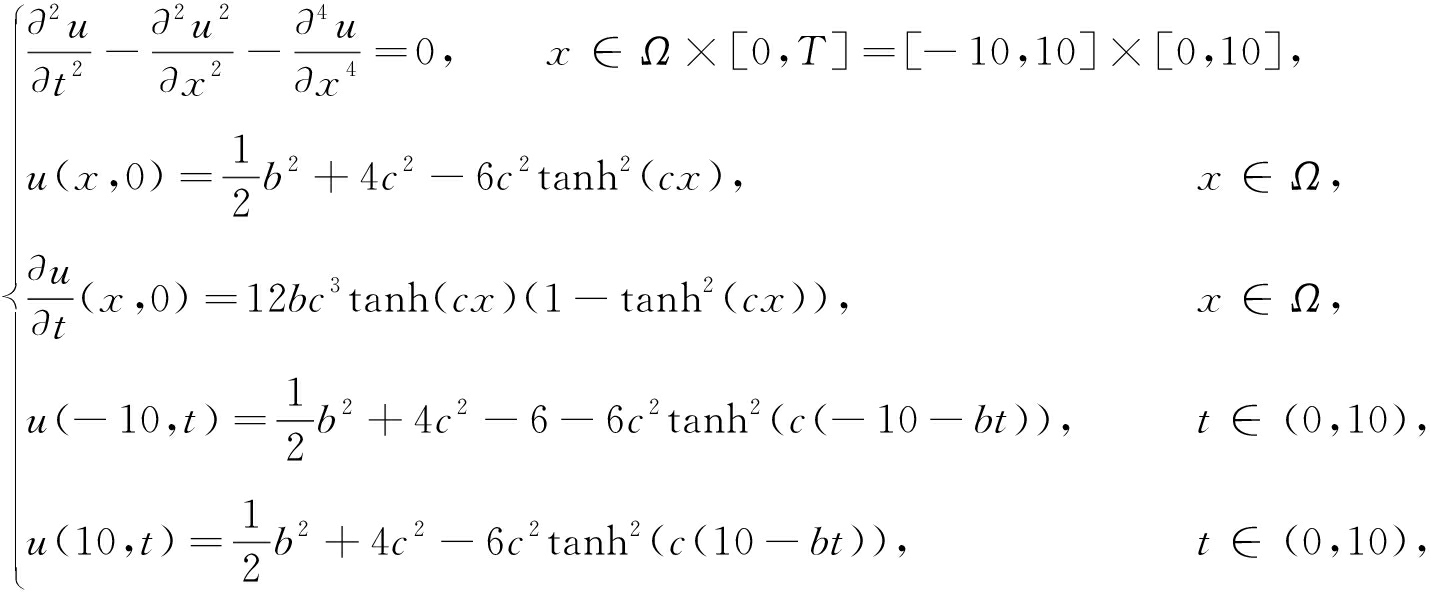
其中b,c为任意常数.此时,系统具有解析解[27]
对算例2,同样用来检验本节LBM的有效性,选取的参数同算例1,不同时刻t=1, 2, 3, 4时数值解与解析解的对比结果见图3.图1和图3表明,由本节所建立的LBM(43)得到的数值解与系统的精确解是一致的,几乎重合.这说明了LBM在模拟Boussinesq方程的初边值问题时,具有短时间演化的高精度和有效性,及较好的稳定性.
图4是算例2中系统的数值解u(x,t)在空间区域[-10,10]、时间区域[0,10]内的时空演化图,具体的参数选取见图4中所示.从图4可以看出,数值模拟结果显示的波为钟形,且波峰随着时间的推移往前传播,振幅保持不变.比较图2和图4的波形,发现系统中的高阶导数项的参数β控制着波峰的形状: 当β>0时, 波峰为倒立的钟形; 当β<0时, 波峰为正立的钟形.
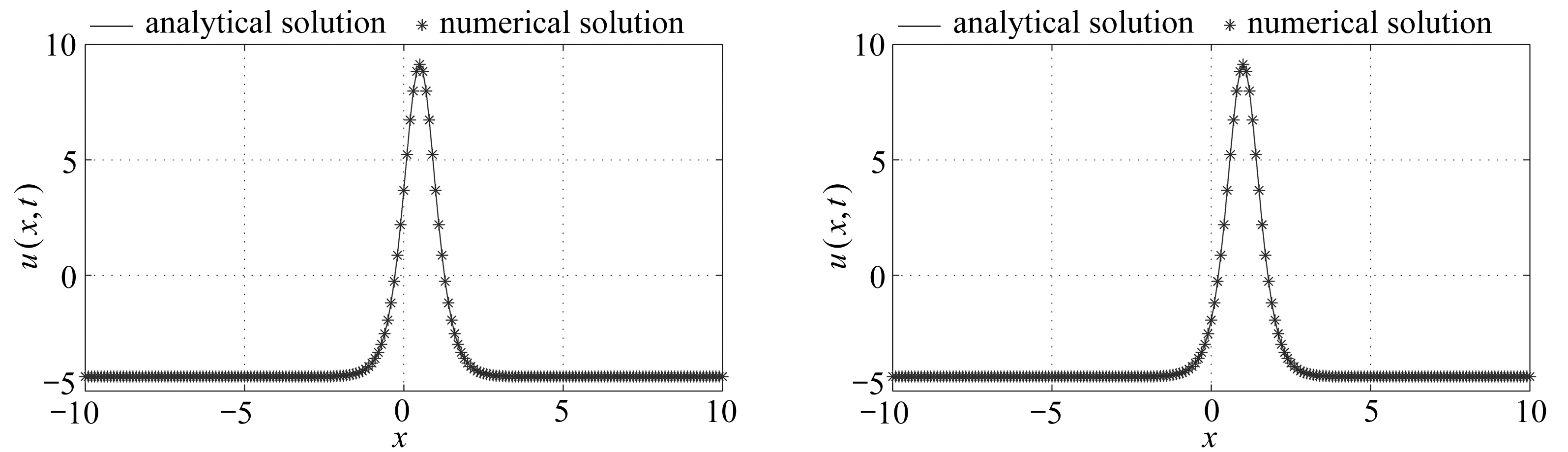
(a) t=1 (b) t=2

(c) t=3 (d) t=4
图3 算例2不同时刻解析解和LBM的数值解的比较
Fig. 3 Comparison between the numerical solutions and the analytical solutions of example 2

图4 算例2的数值解u(x,t)的时空演化图
Fig. 4 The time-space evolution of numerical solution of u(x,t) in [-10,10]×[0,10]
为了比较Boussinesq系统在两种不同参数的选取下,不同的初边值条件如何影响波的传播速度以及LBM的数值解和改进的有限差分格式的数值解,给出了小时间范围t=1,2,3,4个时间单位的对比图.对比图分别见图1和图5,由两图可知,当初边值条件中的参数b,c的取值为b=0.01,c=0.3 时, 孤立波的传播见图1.当时间变量为t=4个时间单位时, 波峰已经传播到空间变量x=4的位置; 当初边值条件中的参数取值为b=0.5,c=1.5时, 孤立波的传播见图5;当时间变量为t=4个时间单位时,孤立波峰到达空间变量x=2的位置,因此波速较小参数时慢.
由图1可知本文的LBM数值解拟合程度较高;另外由图5可知,两种数值格式拟合程度较高,这说明本文所建立的格式与MFDM在较短时间内演化过程的精度相当.
为了考察本文所构造的LBM在长时间演化的情形下误差精度,本文给出了长时间不同时刻下LBM和MFDM的数值解与解析解的误差对比情况.定义L∞模误差和L2模误差为
其中u(xi,t),u*(xi,t)分别为数值解和解析解.
针对算例2在解析解已知的情况下,将本文所构造的LBM与经典的MFDM进行误差对比分析.由表2的对比结果可知,当演化时间较短时,本文所构造的LBM与经典的MFDM得到的数值解与解析解的误差精度相当.当经过长时间的演化时,本文所构造的模型得到的数值解与解析解的相对误差明显优于由经典的MFDM得到的数值解与解析解的相对误差.特别是当演化时间达到t=30,50时,本文模型的L2模误差优于MFDM模型的L2模误差两个数量级.
表2算例2由本文所构造LBM的数值解和MFDM的数值解的误差对比
Table 2 Comparison of theL2andL∞errors of numerical solutions between the LBM and the MFDM

表3算例2在本文所构造LBM的数值解在不同空间网格数N下的误差情况和收敛阶数
Table 3 The errors and the convergence rates of the present method foru(x,t) with fixed time step
Δtand different space gridN

进一步,考察在相同的时间步长下,不同的空间网格数对LBM误差精度的影响.为了减少时间步长对精度的影响,尽量选取较小的时间步长Δt=0.001.重复模拟t=5.0时刻数值解u(x,t)与解析解的L∞模误差和L2模误差, 结果见表3.从表3的结果可以看出,当空间网格数较小即空间步长较大时,本文所构造的LBM的数值解与解析解的误差较大.随着空间网格的加密,空间步长变小时,两种模误差都相应变小.在指数坐标系下,L2模误差随着空间网格数变化在2.001 7到2.346 6之间变动. L∞模误差随着空间网格数变化在1.903 7到2.351 7之间变动.这两种误差的平均收敛阶都大于2.0,即说明本文所构造的LBM的空间精度不低于二阶,这优于经典的MFDM的超线性收敛阶.

(a) t=1 (b) t=2

(c) t=3 (d) t=4
图5 算例2由LBM得到的数值解和MFDM得到的数值解的比较
Fig. 5 Comparison of u(x,t) at different times between the numerical solutions of example 2 obtained with LBM and MFDM
算例3在Boussinesq系统中取α=-1,β=-1,k=2,F(u)=sin(u),则系统为
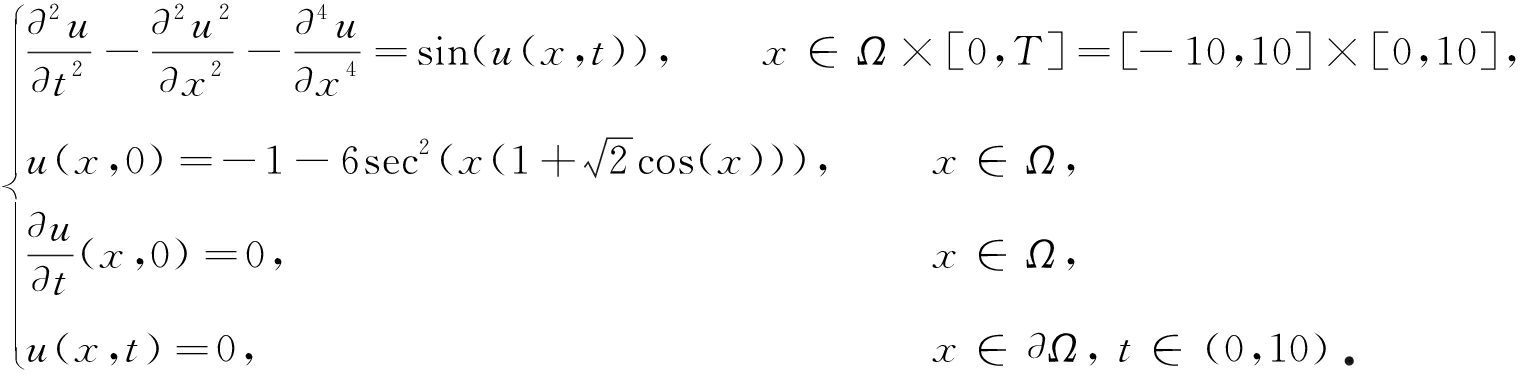
此时系统是否存在精确解未知,为了检验算例3系统解的存在性,本文借助于经典的MFDM来对系统进行数值模拟.同时将模拟的结果与LBM进行比较,从而检验LBM(43)的有效性.
考虑到数值对比的方便性,两种模型采用相同的时间步长和空间步长,同时在模型中也选取相同的初始条件和边界条件.所有的数值实验都在MATLAB 7.0系统上运行,试验中,空间步长和时间步长分别为Δx=0.1, Δt=0.01.LBM中格子数定为N=200,数值模拟的空间区域固定为[-10,10],数值模拟结果见图6.
图6表明,当Boussinesq系统中有周期压力源项F(u)=sin(u(x,t))时,系统会产生一个周期的孤波解.此时边界条件为零,初始条件也具有一定的周期性.从4组数值试验可以看出,本节所构造LBM的数值解与MFDM得到的数值解在演化的中期非常吻合,具有很好的一致性,表明所构造LBM的有效性和稳定性.但是在演化的早期和晚期,MFDM所得数值解与LBM所得解产生偏差.同时,本文也给出了在区域(x,t)∈[-10,10]×(0,10)里由LBM所得到数值解u(x,t)的时空演化图(图7).由图7可知,此时系统具有周期的孤波解.
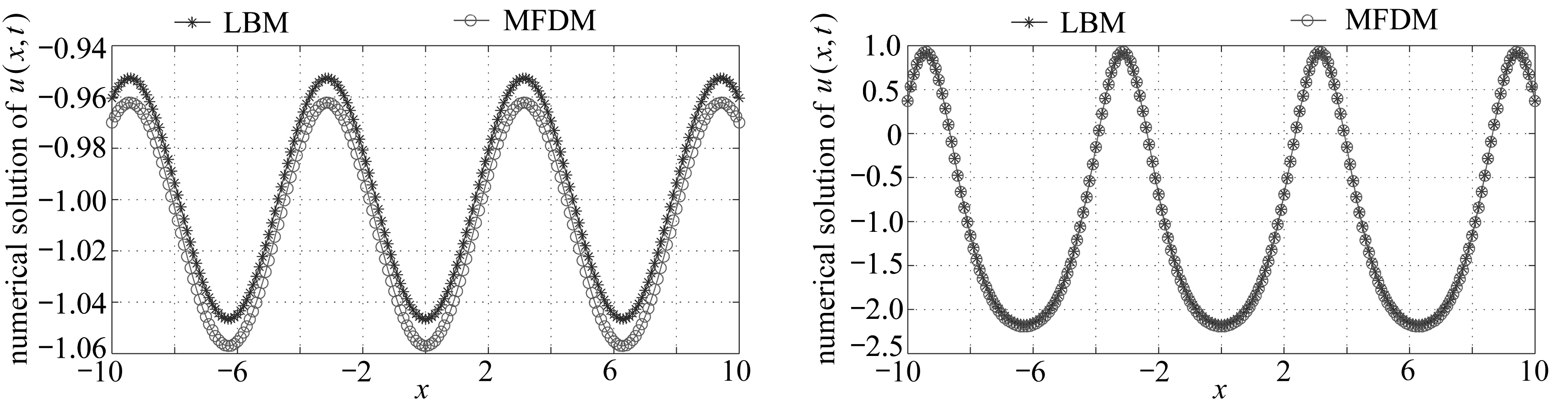
(a) t=2 (b) t=4
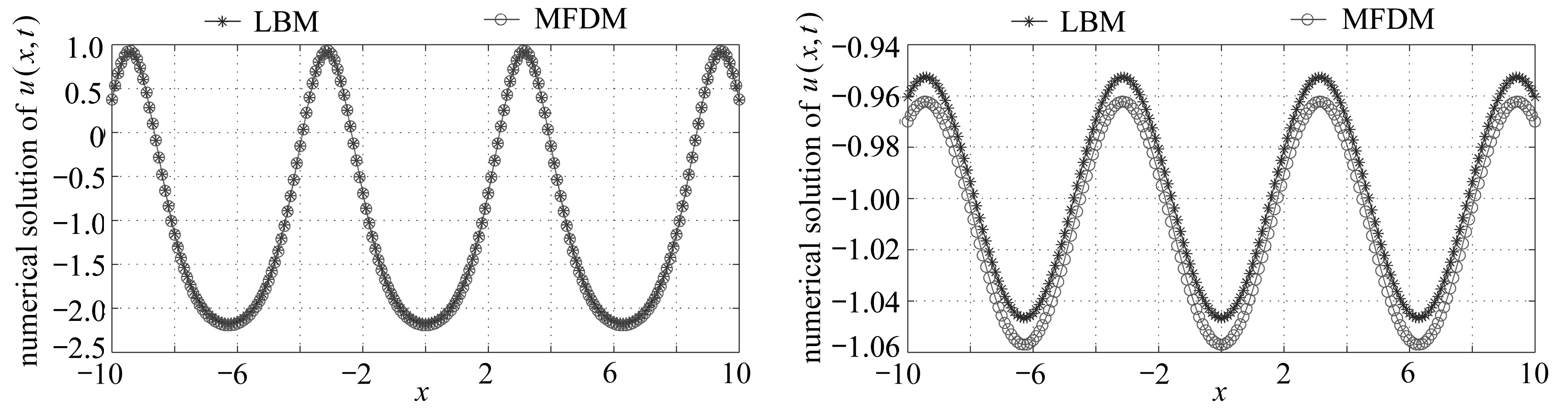
(c) t=6 (d) t=8
图6 算例3由LBM与MFDM所得数值解u(x,t)的对比
Fig. 6 Comparison of the numerical solution of u(x,t) obtained by the LBM and MFDM
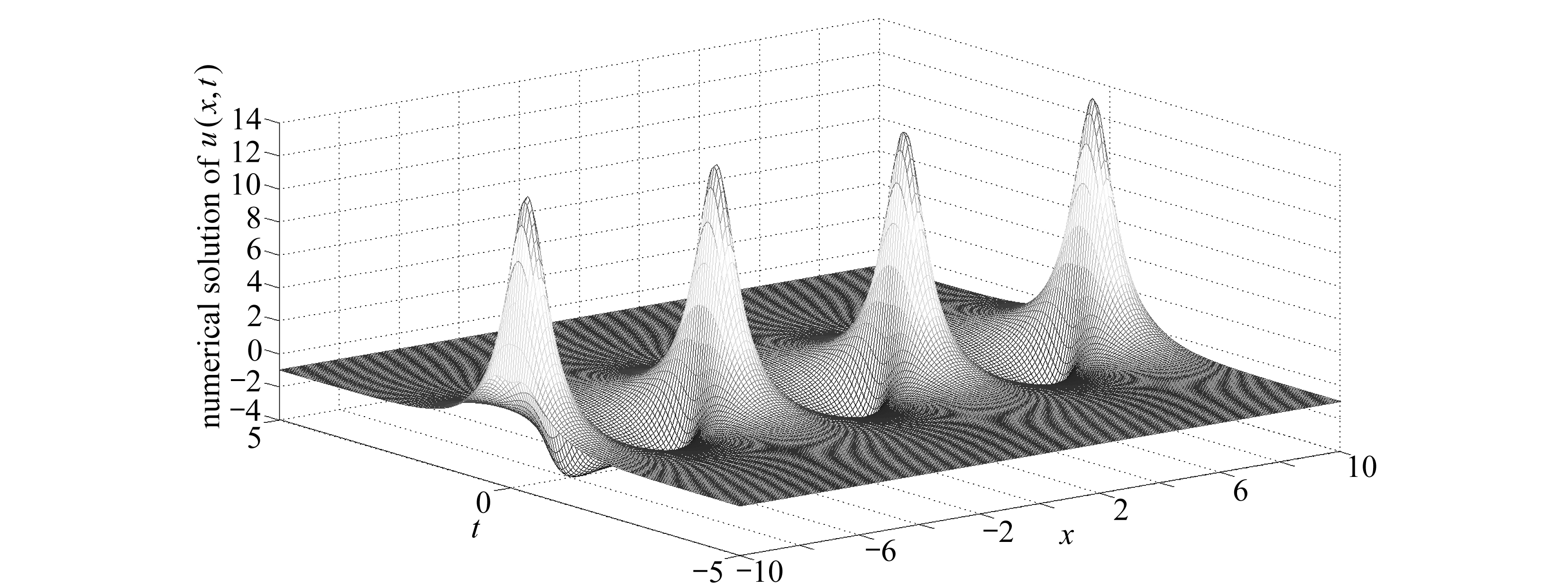
图7 算例3由LBM所得数值解u(x,t)的时空演化图
Fig. 7 The time-space evolution graph of the numerical solution of example 3 obtained with the LBM
为了检验压力源项F(u)对系统解的影响,取F(u)=sin(u(x,t))+cos(u(x,t)),其他参数同上.此时的精确解表达式仍未知,用LBM与MFDM 格式对问题进行数值模拟.由本文给出了此时系统两种数值解u(x,t)的对比图(图8)和数值解u(x,t)的时空演化图(图9).
由图8可观察到,此时两种格式所得到的数值解u(x,t)吻合得比较好.由图9可以表明,此时系统具有交叉的孤波解.以上算例都是在系统(4)中取k=2的情形,笔者将在以后的研究中,具体讨论当k≠2时系统解的存在性及其他一些解的性态.
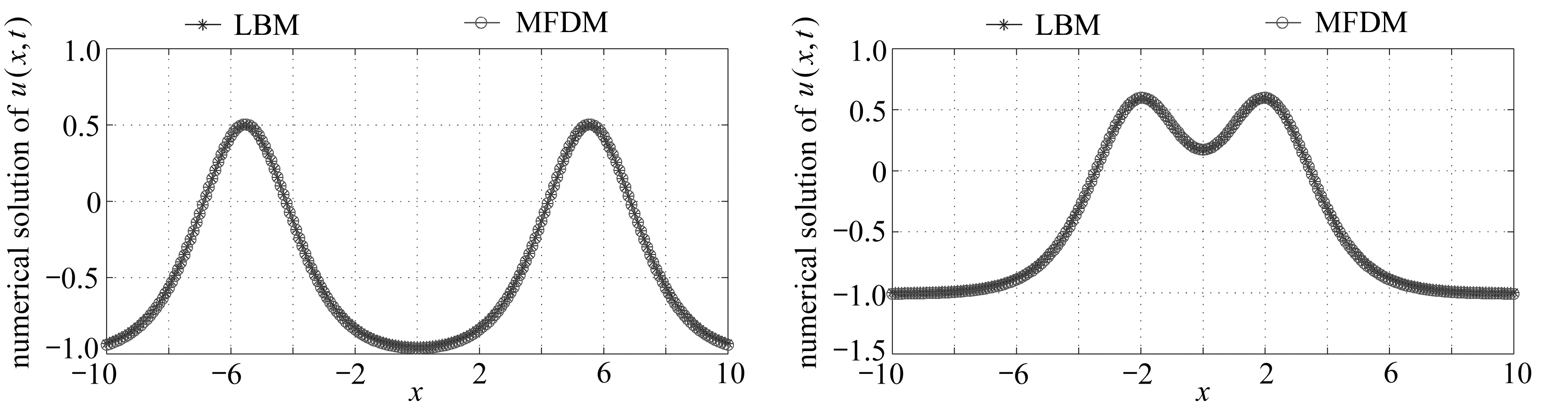
(a) t=2 (b) t=4
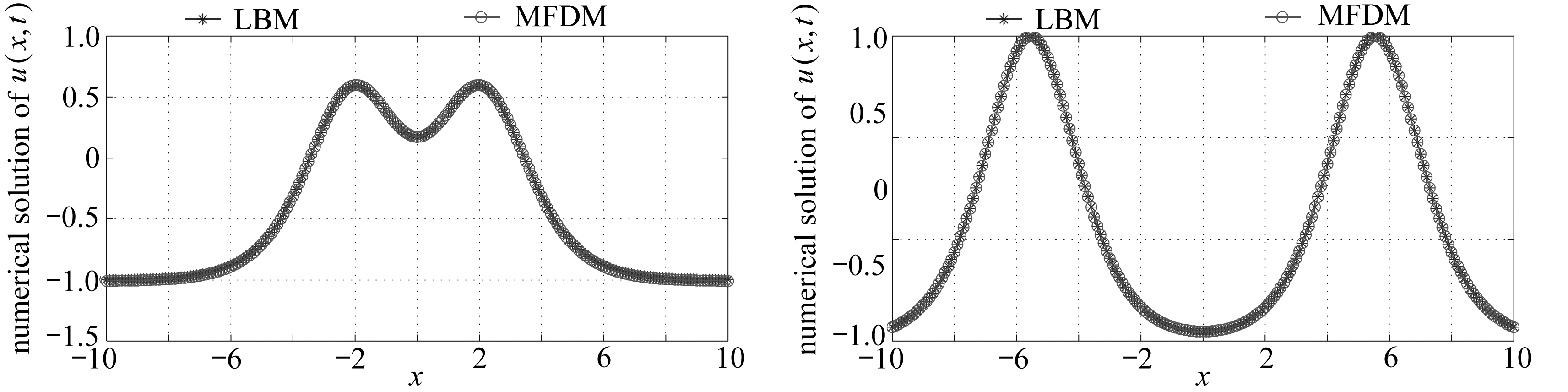
(c) t=6 (d) t=8
图8 算例3由LBM得到的数值解和MFDM得到的数值解的比较
Fig. 8 Comparison of the numerical solution of example 3 obtained with the LBM and MFDM
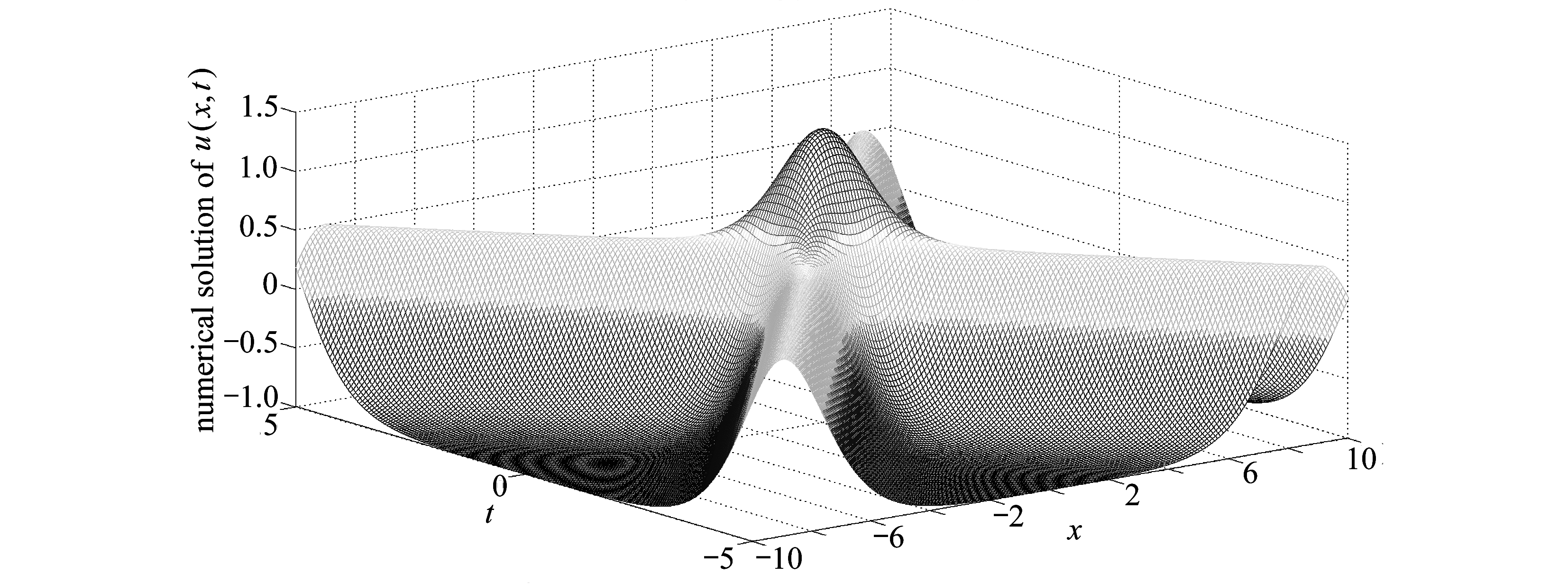
图9 算例3由LBM所得数值解u(x,t)的时空演化图
Fig. 9 The time-space evolution graph of the numerical solution of example 3 obtained with the LBM
本文针对一类初边值问题的含源Boussinesq方程,提出了一维五速度且带修正函数和源项的LBM.通过求解设计的分布函数必须满足宏观量守恒律的方程组及其他的各阶矩方程组,得到了满足宏观方程的平衡态分布函数以及附加的修正函数.本文模型的分析和建立中,得到了模型的截断误差.为了检验模型的有效性,选择了3类不同初边值条件的Boussinesq方程进行数值模拟,并将LBM的数值解与相应的精确解进行对比;若系统精确解未知时,利用修正的有限差分方法与本文所提模型进行数值对比.数值实验的结果表明,本文所构造的LBM的有效性、相容性和稳定性得到了保证.在相同的步长计算格式下,LBM的误差精度和收敛阶都优于经典的MFDM.
参考文献(References):
[1] 熊志强. Boussinesq方程模型的数值造波方法研究[D]. 硕士学位论文. 天津: 天津大学, 2007.(XIONG Zhiqiang. Numerical wave generation in Boussinesq equation models[D]. Master Thesis. Tianjin: Tianjin University, 2007.(in Chinese))
[2] 王颖. 几类Boussinesq方程的Cauchy问题[D]. 博士学位论文. 成都: 四川大学, 2007.(WANG Ying. The Cauchy problems for some classes of Boussinesq equations[D]. PhD Thesis. Chengdu: Sichuan University, 2007.(in Chinese))
[3] MILES J W. Solitary waves[J].Annual Review of Fluid Mechanics, 1980,12: 11-43.
[4] MILEWSKI P A, KELLER J B. Three-dimensional water waves[J].Studies in Applied Mathematics, 1996,97(2): 149-166.
[5] TSUTSUMI M, MATAHASHI T. On the Cauchy problem for the Boussinesq type equation[J].Mathematics Japonica, 1991,36: 371-379.
[6] BONA J, SACHS R. Global existence of smooth solution and stabilityof solitary waves for a generalized Boussinesq equation[J].Communications in Mathematical Physics, 1988,118(1): 12-29.
[7] KALANTAROV V K, LADYZHENSKAYA O A. The occurrence of collapse for quasilinear equations of parabolic and hyperbolic types[J].Journal of Mathematical Sciences, 1978,10(1): 53-70.
[8] LEVIN H A, SLEEMAN B D. A note on the nonexistence of global solutions of initial-boundary value problems for the Boussinesq equationutt=3uxxx+uxx-12(u2)xx[J].Journal of Mathematical Analysis and Applications, 1985,107(1): 206-210.
[9] HIROTA R. ExactN-solition solutions of the wave equation of long waves in shallow-water and in nonlinear lattices[J].Journal of Mathematical Physics, 1973,14(7): 810-814.
[10] CLARKSON P. New exact solution of the Boussinesq equation[J].European Journal of Applied Mathematics, 1990,1(3): 279-300.
[11] PEREGRINE D H. Long waves on a beach[J].Journal of Fluid Mechanics, 1967,27(4): 815-827.
[12] WEI G, KIRBY J T, GRILLI S T, et al. A fully nonlinear Boussinesq model for surface wave: part I, highly nonlinear unsteady waves[J].Journal of Fluid Mechanics, 1995,294: 71-92.
[13] 李春颖. 基于Boussinesq方程的海岸地区波浪数学模型研究[D]. 硕士学位论文. 天津: 天津大学, 2003.(LI Chunying. Research on numerical model for waves in coastal region based on Boussinesq equations[D]. Master Thesis. Tianjin: Tianjin University, 2003.(in Chinese))
[14] 王涛. 高阶Boussinesq方程的数值模型[D]. 硕士学位论文. 大连: 大连理工大学, 2002.(WANG Tao. The numerical model of the high order Boussinesq equation[D]. Master Thesis. Dalian: Dalian University of Technology, 2002.(in Chinese))
[15] OLLILA S, DENNISTON C, KARTTUNEN M, et al. Fluctuating Lattice-Boltzmann model for complex fluids[J].Journal of Chemical Physics, 2011,134(6): 549-197.
[16] FALLAH K, KHAYAT M, BORGHEI M H, et al. Multiple-relaxation-time lattice Boltzmann simulation of non-Newtonian flows past a rotating circular cylinder[J].Journal of Non-Newtonian Fluid Mechanics, 2012,177/178: 1-14.
[17] MAO W, GUO Z L, WANG L. Lattice Boltzmann simulation of the sedimentation of particles with thermal convection[J].Acta Physica Sinica, 2013,62(8): 786-790.
[18] YANG T Z, JI S, YANG X D, et al. Microfluid-induced nonlinear free vibration of microtubes[J].International Journal of Engineering Science, 2014,76(4): 47-55.
[19] HE Y B, TANG X H, LIN X Y. Numerical simulation of a class of Fitz Hugh-Nagumo systems based on the lattice Boltzmann method[J].Acta Physica Sinica, 2016,65(15): 133-142.
[20] VARLAMOV V V. Long-time asymptotics of solutions of the second initial-boundary value problem for the damped Boussinesq equation[J].Abstract and Applied Analysis, 1998,2(3/4): 281-289.
[21] 赖惠林. 几类非线性波方程的格子玻尔兹曼模型的数值分析及模拟[D]. 博士学位论文. 福州: 福建师范大学, 2012.(LAI Huilin. Numerical analysis and simulation of lattice Boltzmann models for some nonlinear wave equations[D]. PhD Thesis. Fuzhou: Fujian Normal University, 2012.(in Chinese))
[22] MAKHANKOV V G. Dynamics of classical solitons(in non-integrable systems)[J].Physics Reports, 1978,35(1): 1-128.
[23] CLARKSON P A, KRUSKAL M D. New similarity reductions of the Boussinesq equation[J].Journal of Mathematical Physics, 1989,30(10): 2201-2213.
[24] DEIFT P, TOMEI C, TRUBOWITZ E. Inverse settering and the Boussinesq equation[J].Pure and Applied Mathematics, 1982,35(5): 567-628.
[25] SHU C W, OSHER S. Efficient implementation of essentially non-oscillatory shock-capturing schemes[J].Journal of Computational Physics, 1998,77(2): 439-471.
[26] GUO Z L, ZHENG C G, SHI B C. Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method[J].Chinese Physics, 2002,11(4): 366-374.
[27] FU Z T, LIU S K, LIU S D, et al. The JEFE method and periodic solutions of two kinds of nonlinear wave equations[J].Communications in Nonlinear Science and Numerical Simulation, 2003,8(2): 67-75.
HE Yubo1, DONG Xiaoliang2, LIN Xiaoyan1
(1.School of Mathematics and Computation Science,Huaihua University,Huaihua,Hunan418008,P.R.China; 2.School of Mathematics and Information Science,North Minzu University,Yinchuan750021,P.R.China)
Abstract:For a class of initial value problems of the high-order Boussinesq systems with source terms, a D1Q5 nonstandard lattice Boltzmann model (LBM) with correction functions and source terms was proposed. Different local equilibrium distribution functions and correction functions were selected, and the nonlinear wave equation was recovered by means of the Chapman-Enskog multi-scale analysis and the Taylor expansion technique. Some initial boundary value problems of the Boussinesq systems with analytical solutions were simulated to verify the effectiveness of the LBM. The results show that the numerical solutions agree well with the analytical solutions and the norm errors obtained with the LBM are smaller than those with the modified finite difference method (MFDM). Furthermore, some problems without analytical solutions were numerically studied with the present method and the MFDM. The comparison shows that the numerical solutions from the LBM are in good agreement with those from the MFDM, which validates the effectiveness and stability of the proposed model.
Key words:lattice Boltzmann model; Boussinesq equation; Chapman-Enskog expansion; modified finite difference method
引用本文/Cite this paper: 何郁波, 董晓亮, 林晓艳. 一类含源Boussinesq系统解的数值分析及仿真[J]. 应用数学和力学, 2018,39(8): 961-978.HE Yubo, DONG Xiaoliang, LIN Xiaoyan. Numerical analysis and simulation of solutions to a class of boussinesq systems with source terms[J].Applied Mathematics and Mechanics, 2018,39(8): 961-978.
文章编号:1000-0887(2018)08-0961-18
ⓒ 应用数学和力学编委会,ISSN 1000-0887
*收稿日期:2017-05-08;
修订日期:2017-11-07
基金项目:国家自然科学基金(11471137;11501232;11601012);宁夏自然科学基金(NZ17103)
作者简介:何郁波(1979—),男,副教授,博士(通讯作者. E-mail: heyinprc@csu.edu.cn); 董晓亮(1981—),男,副教授,博士(E-mail: dongxl@stu.xidian.edu.cn).
摘要:对于一类含源的高阶非线性波动方程Boussinesq方程的初边值问题,利用D1Q5模型的格子Boltzmann方程,通过选取不同的演化方程和局部平衡态分布函数及修正函数,应用Chapman-Enskog多尺度技术和Taylor展开技术,提出了具有五阶高精度带修正函数的非标准格子Boltzmann模型.应用所提出的模型,仿真模拟了几个具有精确解的Boussinesq方程初边值系统,并与传统的修正有限差分法(MFDM)进行了对比,结果表明该文模型所得的数值解与精确解吻合,其模误差小于MFDM.此外,还针对精确解未知的Boussinesq方程初边值系统进行了数值仿真,并与MFDM进行了对比.数值结果表明,两种计算格式的数值解比较吻合,进一步证明了文中所构造模型的有效性和稳定性.
关 键 词:格子Boltzmann模型; Boussinesq方程; Chapman-Enskog展开;
修正有限差分法
中图分类号:TP301.6;O241.82
文献标志码:A
DOI:10.21656/1000-0887.380126