
图1 套管构件的边界条件 图2 内核与套筒的点接触
Fig. 1 Boundary conditions of a sleeved column Fig. 2 Point contact between the inner core and the sleeve
赵啸峰 1,2 , 申 波 1,2 , 马克俭 1,2 , 刘盼盼 1,2 ,王 惠 1,2 , 吴骏杨 1,2 , 杨 磊 1,2
(1. 贵州大学 空间结构研究中心, 贵阳 550003;2. 贵州省结构工程重点实验室, 贵阳 550025)
摘要 : 针对轴向压力作用下具有内核伸出段的套管构件,理论研究了初弯曲内核与柔性套筒的点接触变形过程 . 采用小挠度二阶平衡微分方程,推导了内核处于点接触状态时套管构件的挠度、剪力、弯矩、接触力等物理量的计算公式 . 理论的对比结果表明:1)内核伸出段会显著增大套管构件的弯曲轴向位移,降低套管构件的非线性轴向刚度;2)内核伸出段使内核与套筒端部的接触反力有显著的增加,随着轴向压力的增大,该接触反力的增加更大;3)内核伸出段使内核的剪力、弯矩均有显著的提高,尤其在内核与套筒抗弯刚度比值较大时,弯矩的提高更显著 . 该文的研究可为套管构件及内核与套筒端部连接的设计提供依据 .
关 键 词 : 内核伸出段; 套管构件; 力学模型; 点接触; 屈曲
针对杆系结构中受压构件容易出现失稳的现象,研究者提出了相应的限制失稳构件 . 限制失稳构件被应用于大量的工程实践中,并且取得了不错的效果 [1-3] . 套管构件是一种限制失稳构件,它由内核与套筒组成,两者之间有间隙;套管构件具有稳定控制、滞回性能优良等特点;内核与套筒各司其职——内核承受压力而套筒则抵抗内核的弯曲,套筒约束内核的屈曲变形,显著提高内核的承载力;在受到意外荷载作用时,能够利用内核屈曲消耗瞬时荷载所产生的能量,减少结构的动力响应,减轻整体结构的破坏程度 [4-6] .
套管构件在受力过程中,内核与套筒呈现不同的接触状态 . 在这些接触状态中,套筒约束内核的弯曲变形 . 当内核首先发生屈曲时,内核外壁与套筒内壁之间接触,它们处于点接触的状态 . 文献[7]试验研究了内核与刚性套筒发生点接触时内核的轴压承载力 . 文献[8-10]理论与试验研究了弹性柱与刚性墙之间的点接触 . 文献[11-14]理论研究了内核与柔性套筒的点接触,认为内核与套筒等长,并推导出相关物理量的计算公式 . 文献[15]在理论研究的基础上,试验研究了内核与套筒的点接触,其内核试件外伸出套筒试件;通过试验研究发现,在轴向荷载作用下内核伸出段容易出现屈曲,极大降低内核的承载力 .
有鉴于此,需要研究内核伸出段对套管构件的变形、内力的影响,以便合理设计套管构件,加强内核与套筒端部的连接构造 . 本文提出考虑内核伸出段的内核与柔性套筒点接触的力学模型,采用线弹性小挠度理论研究了轴压初弯曲内核的变形,推导了内核与套筒挠度、剪力、弯矩、接触力等物理量的计算公式 . 通过本文理论与文献[15]中理论、试验的算例对比,表明内核伸出段对套管构件的变形、受力有显著影响 .
为了便于套管构件的安装及使用,套管构件中的内核需要外伸出套筒,如图1所示的内核伸出段 . 内核两端与结构的其他构件铰接,内核与套筒端部采用“限位连接”,使内核与套筒在两端连接处具有相同的挠度,二者允许相对转动,连接的一侧允许轴向相对滑动,类似活动铰接的构造 . 根据图1所示,内核与套筒处于点接触时的力学模型如图2所示,图中给出了内核轴线、套筒轴线及其内壁的变形 .

图1 套管构件的边界条件 图2 内核与套筒的点接触
Fig. 1 Boundary conditions of a sleeved column Fig. 2 Point contact between the inner core and the sleeve
在推导内核与套筒点接触的方程时,给出无量纲量的图、推导、算例 . 采用了以下基本假定:内核有一阶、二阶混合屈曲模态初弯曲,套筒无初弯曲;它们的材料为线弹性,且变形为小变形;忽略内核与套筒之间的摩擦力 .
在本文中符号约定如下:字母上带横线的表示有量纲量,相应字母上不带横线的表示相应的无量纲量;用下标i表示内核的相应物理量,而下标e表示套筒的相应物理量 . 如图2所示, ![]() 表示轴向坐标,
表示轴向坐标, ![]() 表示横向坐标,
表示横向坐标, ![]() 表示内核长度,
表示内核长度, ![]() 表示内核伸出套筒的长度,
表示内核伸出套筒的长度, ![]() 表示内核与套筒净间隙,
表示内核与套筒净间隙, ![]() 表示内核与套筒接触点的轴向坐标;
表示内核与套筒接触点的轴向坐标; ![]() 表示轴向压力,
表示轴向压力, ![]() 分别为内核与套筒的抗弯刚度,
分别为内核与套筒的抗弯刚度, ![]() 分别为内核与套筒的挠度,
分别为内核与套筒的挠度, ![]() 表示在接触点处内核的挠度 . 其他物理量采用常用习惯,
表示在接触点处内核的挠度 . 其他物理量采用常用习惯, ![]() 为内核弯曲产生的轴向位移,
为内核弯曲产生的轴向位移, ![]() 为内核的总轴向位移,
为内核的总轴向位移, ![]() 为内核弯矩,
为内核弯矩, ![]() 为内核剪力 . 如图3所示,
为内核剪力 . 如图3所示, ![]() 分别为内核与套筒端部的接触反力,
分别为内核与套筒端部的接触反力, ![]() 为内核与套筒点接触处的集中接触力 .
为内核与套筒点接触处的集中接触力 .
![]() 为内核的初弯曲,右端第一项表示内核具有一阶屈曲模态的初弯曲,右端第二项表示内核具有二阶屈曲模态的初弯曲,
为内核的初弯曲,右端第一项表示内核具有一阶屈曲模态的初弯曲,右端第二项表示内核具有二阶屈曲模态的初弯曲, ![]() 分别为它们的相应幅值且均大于零 . 设
分别为它们的相应幅值且均大于零 . 设 ![]() 定义无量纲量:
定义无量纲量:
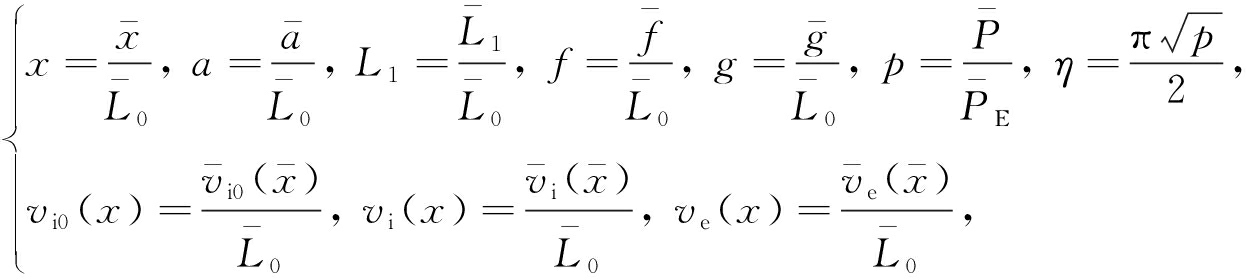
(1)
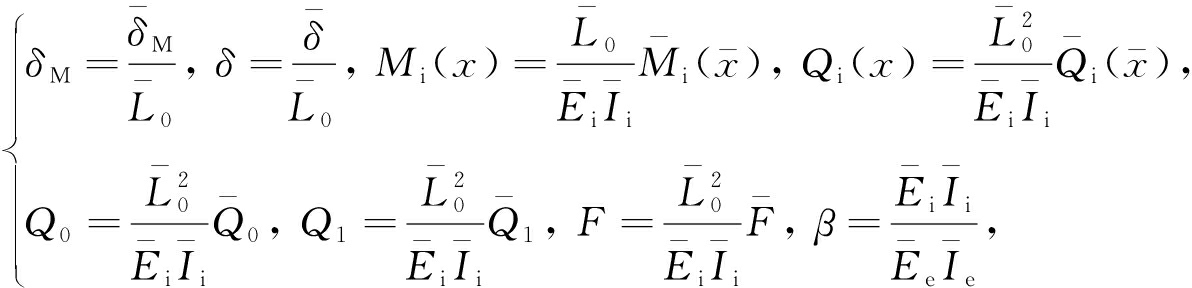
(2)
(3)
根据无量纲量的定义及内核微元体的本构方程、几何关系、平衡方程 [16-17] 推导出如下关系式:
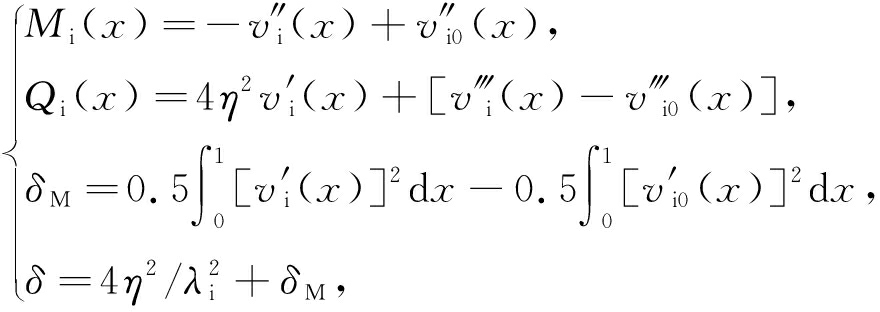
(4)
其中 λ i 为内核的长细比,( · )′表示对 x 求一阶导数 .
随着轴向压力 p 增加,初弯曲内核发生弯曲变形,直到其外壁与套筒内壁刚好接触,此时内核与套筒刚好出现点接触,套筒未发生弯曲变形 . 随着轴向压力 p 持续增加,内核变形继续加大,套筒开始产生弯曲变形 . 内核受力如图3(a)所示,其中内核挠度 v i ( x )为分段函数,分别为 v i1 ( x ), v i2 ( x ), v i3 ( x ), v i4 ( x );套筒受力如图3(b)所示,其中套筒挠度 v e ( x )为分段函数,分别为 v e1 ( x ), v e2 ( x ) . 当轴压内核与套筒在接触点 A 曲率相等时,点接触状态结束,此时的轴向压力 p 即为点接触的结束荷载 .
根据内核的平衡方程有
F = Q 0 (1-2 L 1 )/(1- L 1 - a ), Q 1 = Q 0 ( a - L 1 )/(1- L 1 - a ) .
(5)

(a) 内核点接触受力图 (b) 套筒点接触受力图
(a) The force diagram of the point contact in the inner core (b) The force diagram of the point contact in the sleeve
图3 内核与套筒点接触时的受力图
Fig. 3 Diagrams of load and point contact reactions between the inner core and the sleeve
根据小挠度理论 [16-17] 、无量纲变量定义,关于 v i1 ( x ), v i2 ( x ), v i3 ( x ), v i4 ( x )的二阶微分方程为
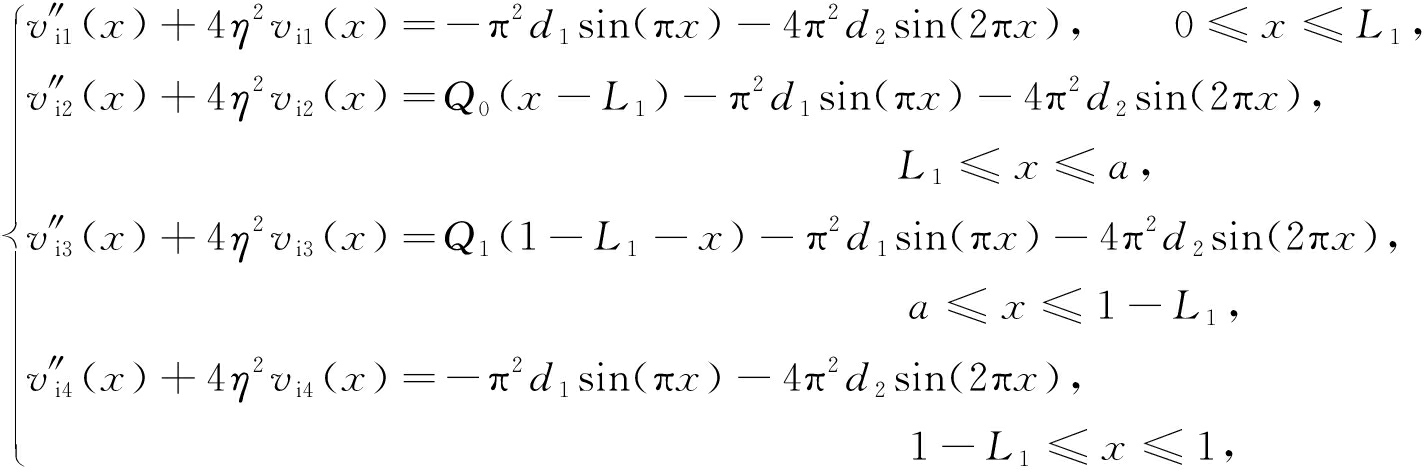
(6)
边界及变形连续条件为
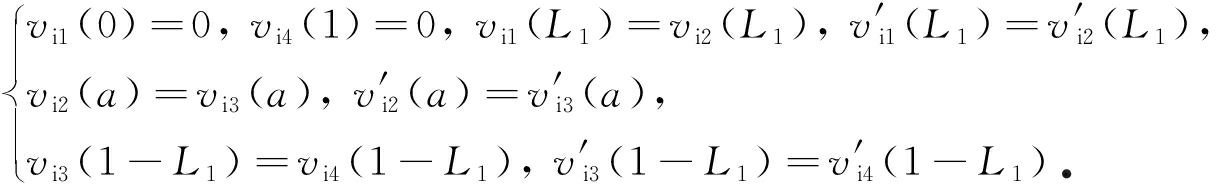
(7)
根据小挠度理论 [16-17] 、无量纲变量定义,关于 v e1 ( x ), v e2 ( x )的二阶微分方程为
(8)
变形连续条件为
(9)
内核与套筒的变形协调条件为
v e1 ( L 1 )= v i1 ( L 1 ), v e2 (1- L 1 )= v i4 (1- L 1 ),
(10)
v i2 ( a )- g = v e1 ( a ),
(11)
(12)
由内核的平衡微分方程(6)、边界及变形连续条件(7)得
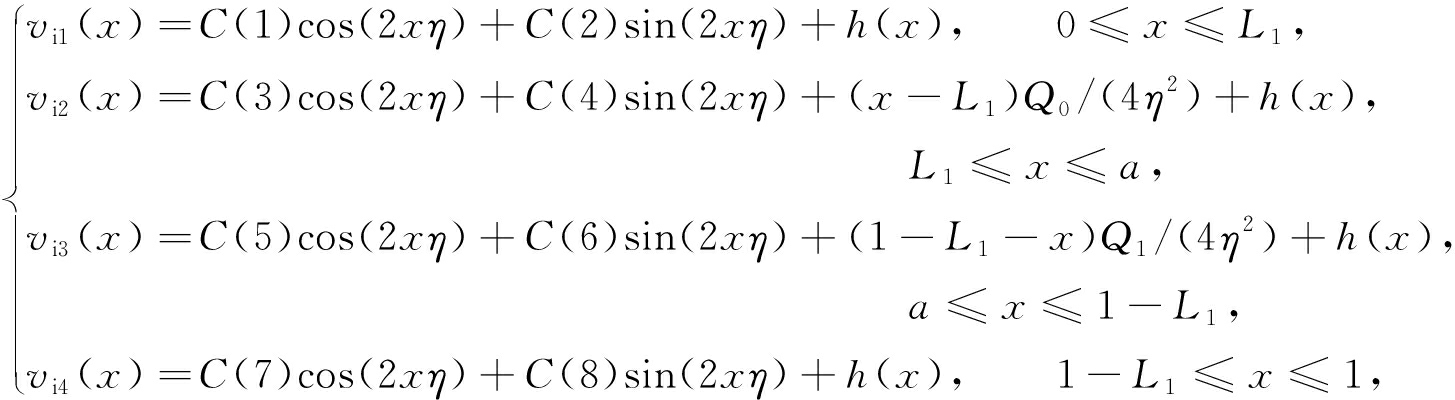
(13)
其中
h ( x )=π 2 [ d 1 sin(π x )/(π 2 -4 η 2 )+ d 2 sin(2π x )/(π 2 - η 2 )],
相应的系数 C (1) ~ C (8)为
C (1)=0, C (3)= Q 0 sin(2 L 1 η )/(8 η 3 ),
(14)
C (2)=csc(2 η ){-2[( a - L 1 ) Q 0 +(-1+ a + L 1 ) Q 1 ] η cos[2(-1+ a ) η ]+
Q 1 sin(2 L 1 η )-( Q 0 + Q 1 )sin(2 η -2 aη )+ Q 0 sin(2 η -2 L 1 η )}/(8 η 3 ),
(15)
C (4)=csc( η )sec( η ){-4[( a - L 1 ) Q 0 +
(-1+ a + L 1 ) Q 1 η cos[2(-1+ a ) η ]]+
2 Q 1 [sin(2 L 1 η )-sin(2 η -2 aη )]+ Q 0 [-sin[2(1+ L 1 ) η ]-
2sin(2 η -2 aη )+sin(2 η -2 L 1 η )]}/(32 η 3 ),
(16)
C (5)={2[( a - L 1 ) Q 0 +(-1+ a + L 1 ) Q 1 ] η cos(2 aη )-
( Q 0 + Q 1 )sin(2 aη )+ Q 0 sin(2 L 1 η )}/(8 η 3 ),
(17)
C (6)=csc(2 η ){-2[( a - L 1 ) Q 0 +(-1+ a + L 1 ) Q 1 ] η cos[2(-1+ a ) η ]-
2[( a - L 1 ) Q 0 +(-1+ a + L 1 ) Q 1 ] η cos[2(1+ a ) η ]+ Q 0 sin[2(1+ a ) η ]+
Q 1 sin[2(1+ a ) η ]+2 Q 1 sin(2 L 1 η )- Q 0 sin[2(1+ L 1 ) η ]-
Q 0 sin(2 η -2 aη )- Q 1 sin(2 η -2 aη )+ Q 0 sin(2 η -2 L 1 η )}/(16 η 3 ),
(18)
C (7)= Q 0 {2[( a - L 1 ) Q 0 +(-1+ a + L 1 ) Q 1 ] η cos(2 aη )-
( Q 0 + Q 1 )sin(2 aη )+ Q 1 sin[2(1- L 1 ) η ]+ Q 0 sin(2 L 1 η )}/(8 η 3 ),
(19)
C (8)=-cot(2 η ){2[( a - L 1 ) Q 0 +(-1+ a + L 1 ) Q 1 ] η cos(2 aη )-
( Q 0 + Q 1 )sin(2 aη )+ Q 1 sin[2(1- L 1 ) η ]+ Q 0 sin(2 L 1 η )}/(8 η 3 ) .
(20)
由套筒的平衡微分方程(8)、变形连续条件(9)、变形协调条件(10)得
(21)
相应的系数 C (9) ~ C (12)为
C (9)=-{- C (7)cos[2(-1+ L 1 ) η ]+2 d 2 π 2 sin(2 L 1 π)/(π 2 - η 2 )+
2(-1+ a + L 1 ) 3 Q 1 ] β -6 C (8)sin[2(1- L 1 ) η ]+
6 C (2)sin(2 L 1 η )}/6}/(1-2 L 1 ),
(22)
2(-1+ a + L 1 ) 3 Q 1 ] β }/(-6+12 L 1 )-{ C (7) L 1 cos[2(-1+ L 1 ) η ]+
d 1 (-1+2 L 1 )π 2 sin( L 1 π)/(π 2 -4 η 2 )- d 2 π 2 sin(2 L 1 π)/(π 2 - η 2 )+
C (2)(-1+ L 1 )sin(2 L 1 η )+ C (8) L 1 sin(2 η -2 L 1 η )}/(-1+2 L 1 ),
(23)
C (11)={6 C (7)(-π 2 + η 2 )cos[2(-1+ L 1 ) η ]+12 d 2 π 2 sin(2 L 1 π)+
(π- η )(π+ η )×[[2( a - L 1 ) 3 Q 0 +[-3 a 2 +2 a 3 +2(-1+ L 1 ) 3 -
6 a (-1+ L 1 ) L 1 ] Q 1 ] β +6 C (8)sin[2(-1+ L 1 ) η ]+
6 C (2)sin(2 L 1 η )]}/[6(-1+2 L 1 )(π- η )(π+ η )],
(24)
6 d 1 π 2 sin( L 1 π)/(π 2 -4 η 2 )+[-6 d 2 π 2 sin(2 L 1 π)+
(π- η )(π+ η )[6 C (8) L 1 sin[2(1- L 1 ) η ]+(-1+ L 1 )×
[[2( a - L 1 ) 3 Q 0 +[-3 a 2 +2 a 3 -6 a (-1+ L 1 ) L 1 -
2(-1+ L 1 ) 2 L 1 ] Q 1 ] β +
6 C (2)sin(2 L 1 η )]]]/[(-1+2 L 1 )(π- η )(π+ η )]} .
(25)
当内核与套筒发生点接触时,满足内核与套筒的变形协调条件(11),将 v i2 ( x ), v e1 ( x )代入该式中,化简可得 Q 0 :
Q 0 ={96(-1+ a + L 1 ) η 3 cos( η )[(-1+2 L 1 )[ d 1 π 2 (-π 2 + η 2 )sin( a π)+
(π 2 -4 η 2 )[ g (π- η )(π+ η )- d 2 π 2 sin(2 a π)]+
d 1 π 2 (π- η )(π+ η )sin( L 1 π)]+
(-1+2 a ) d 2 π 2 (π 2 -4 η 2 )sin(2 L 1 π)]sin( η )}/{(π 4 -5π 2 η 2 +4 η 4 )×
[6( a - L 1 )(-1+ a + L 1 )+6[1+(-1+ a ) a +3(-1+ L 1 ) L 1 ]cos(2 η )-
3(1-2 L 1 ) 2 ×cos[(2-4 a ) η ]-6(-1+ a + L 1 )(-1+2 L 1 )×
cos[2(1- a + L 1 ) η ]+6(-1+ a + L 1 )×
(-1+2 L 1 )cos[2(-1+ a + L 1 ) η ]+
6( a - L 1 )(-1+2 L 1 )cos[2( a + L 1 ) η ]+
4( a - L 1 )(-1+ a + L 1 )(-1+2 L 1 ) η [3+4( a - L 1 )×
(-1+ a + L 1 ) βη 2 ]sin(2 η )]} .
(26)
利用式(4)可以得到内核的以下物理量:
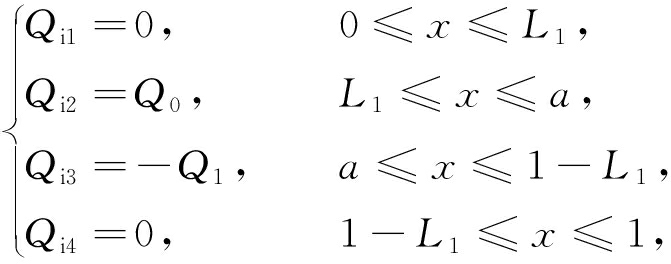
(27)
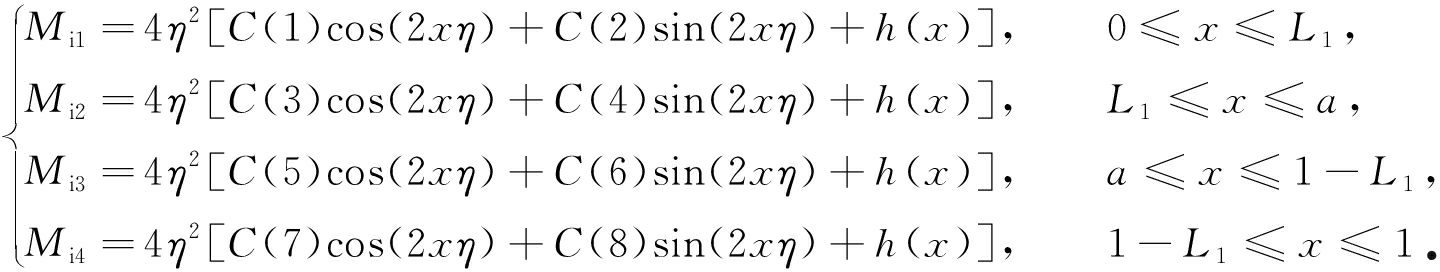
(28)
由内核与套筒的受力(图3),在内核与套筒接触点 A 处,内核与套筒的转角相等,满足内核与套筒的变形协调条件(12),将 v i2 ( x ), v e1 ( x )代入该式中,经过整理、化简后,确定 a 的方程为
Q 0 /(4 η 2 )+ h ′( a )-2 ηC (3)sin(2 aη )+2 ηC (4)cos(2 aη )=
βQ 1 (6 L 1 a +3 a 2 -6 a )/6+ C (11) .
(29)
当内核与套筒在接触点 A 曲率相等时,即 ![]() 点接触状态结束,此时 p = p M =4( η M /π) 2 , η M 的控制方程为
点接触状态结束,此时 p = p M =4( η M /π) 2 , η M 的控制方程为
(30)
文献[15]理论研究的轴压套管构件,其内核与套筒等长;在以下的对比算例中,文献[15]的内核长度、套筒长度均取算例中的内核长度,即 ![]() 除此以外,文献[15]采用与本文相同的参数 . 在对比图中,
除此以外,文献[15]采用与本文相同的参数 . 在对比图中, ![]() 分别表示文献[15]相应于本文 Q 0 , Q i , M i 的理论解答 . 内核与套筒均采用圆钢管,它们的弹性模量均为
分别表示文献[15]相应于本文 Q 0 , Q i , M i 的理论解答 . 内核与套筒均采用圆钢管,它们的弹性模量均为 ![]() 内核一阶、二阶屈曲模态初弯曲的无量纲幅值分别为 d 1 =1/1 000, d 2 =1/1 000 .
内核一阶、二阶屈曲模态初弯曲的无量纲幅值分别为 d 1 =1/1 000, d 2 =1/1 000 .
本算例具体参数为,内核直径 ![]() 壁厚
壁厚 ![]() 套筒直径
套筒直径 ![]() 壁厚
壁厚 ![]() 内核长度
内核长度 ![]() 内核伸出套筒长度
内核伸出套筒长度 ![]() 内核与套筒之间的净间隙
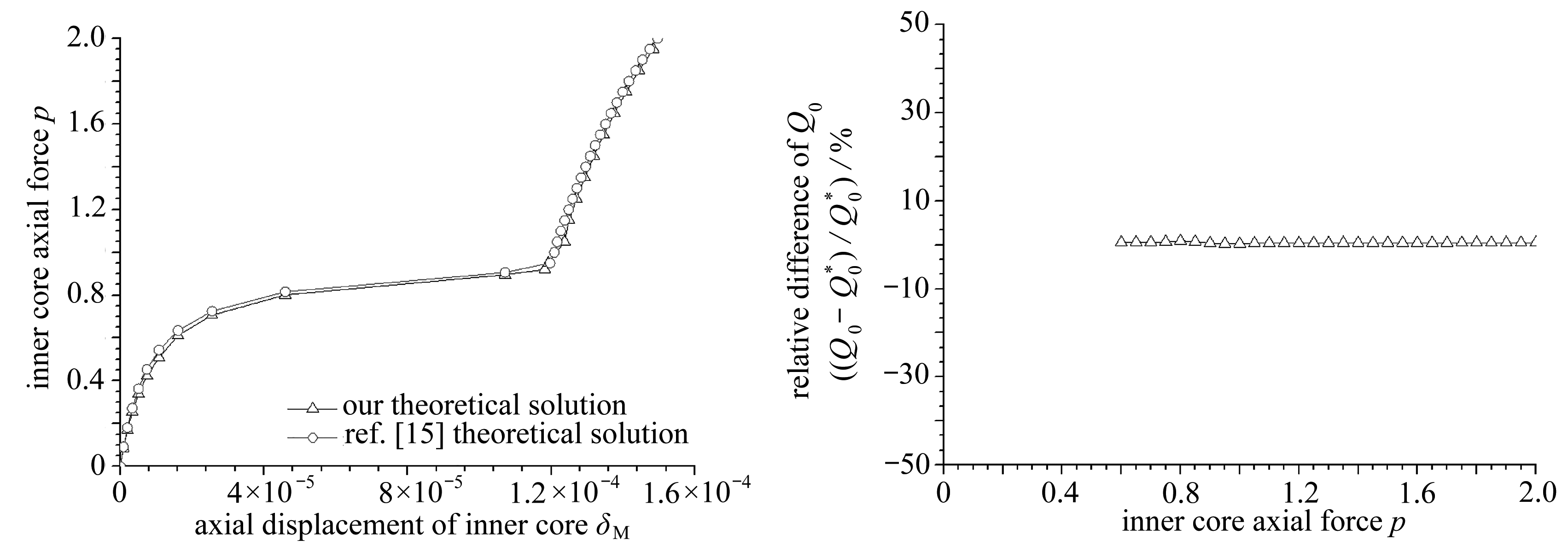
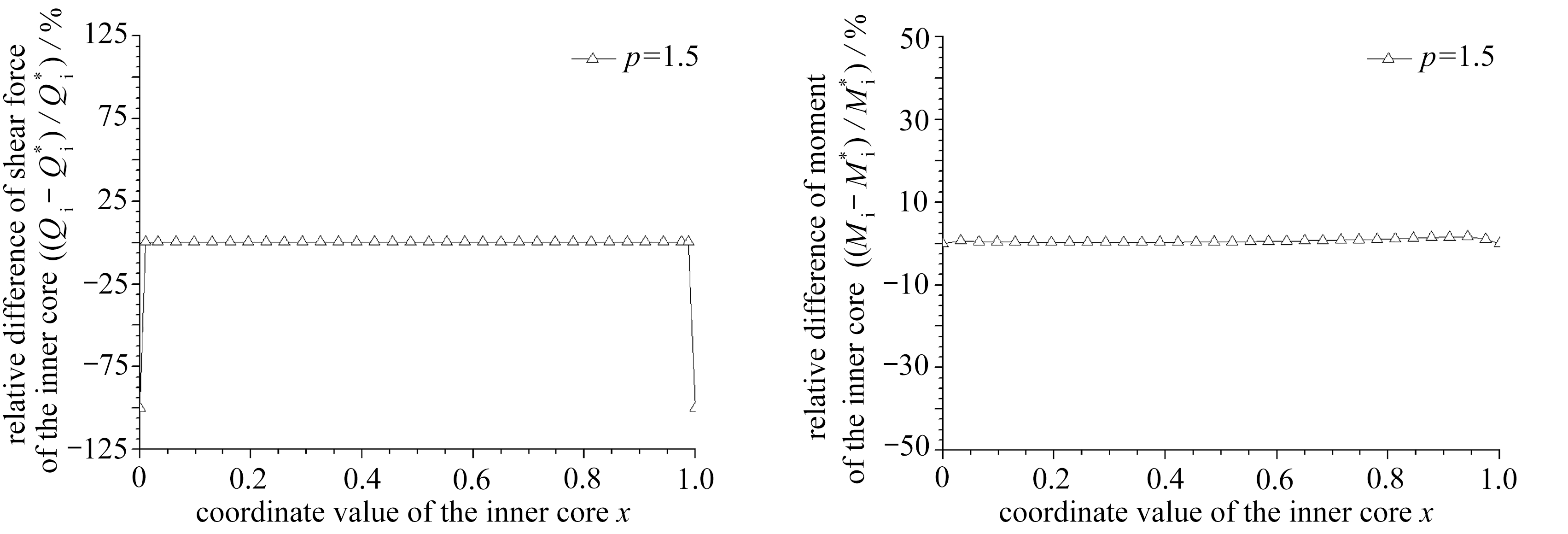
内核与套筒之间的净间隙 ![]() 相应的无量纲量为: g =6.911×10 -3 , β =0.028 5 . 本文与文献[15]的理论解答对比如图4所示,其中内核的轴向压力 p -轴向位移 δ M 曲线对比如图4(a);图4(b)给出点接触阶段 Q 0 的相对差值;图4(c)、4(d)给出点接触阶段内核剪力 Q i 及内核弯矩 M i 的相对差值 .
相应的无量纲量为: g =6.911×10 -3 , β =0.028 5 . 本文与文献[15]的理论解答对比如图4所示,其中内核的轴向压力 p -轴向位移 δ M 曲线对比如图4(a);图4(b)给出点接触阶段 Q 0 的相对差值;图4(c)、4(d)给出点接触阶段内核剪力 Q i 及内核弯矩 M i 的相对差值 .
通过算例对比可知,由于内核伸出套筒长度非常小,在点接触阶段,图4(a)、4(b)、4(d)中本文与文献[15]的结果吻合较好;在图4(c)中,内核中部的剪力吻合较好;验证了本文的理论推导和计算的正确性 . 在图4(c)中,内核伸出段的剪力差别大,这是由于在文献[15]中,内核与套筒等长,内核受到支座反力的作用而产生剪力;由本文的内核受力图3可知,内核在伸出段的剪力为0;因而这种差别是模型本身所固有的差别,这也说明了本文推导的正确性 .
(a) 内核p-δ M 曲线 (b) Q 0 相对差值
(a) The p-δ M curve of the inner core (b) The relative difference of Q 0
(c) 内核剪力相对差值 (d) 内核弯矩相对差值
(c) The relative difference of shear force of the inner core (d) The relative difference of moment of the inner core
图4 算例的两种力学模型理论结果对比
Fig. 4 Comparison of the theoretical results from 2 mechanical models for the example
本算例中内核与套筒的抗弯刚度比值较小 . 具体参数为, 内核直径 ![]() 壁厚
壁厚 ![]() 套筒直径
套筒直径 ![]() 壁厚
壁厚 ![]() 内核长度
内核长度 ![]() 内核伸出套筒长度
内核伸出套筒长度 ![]() 内核与套筒之间的净间隙
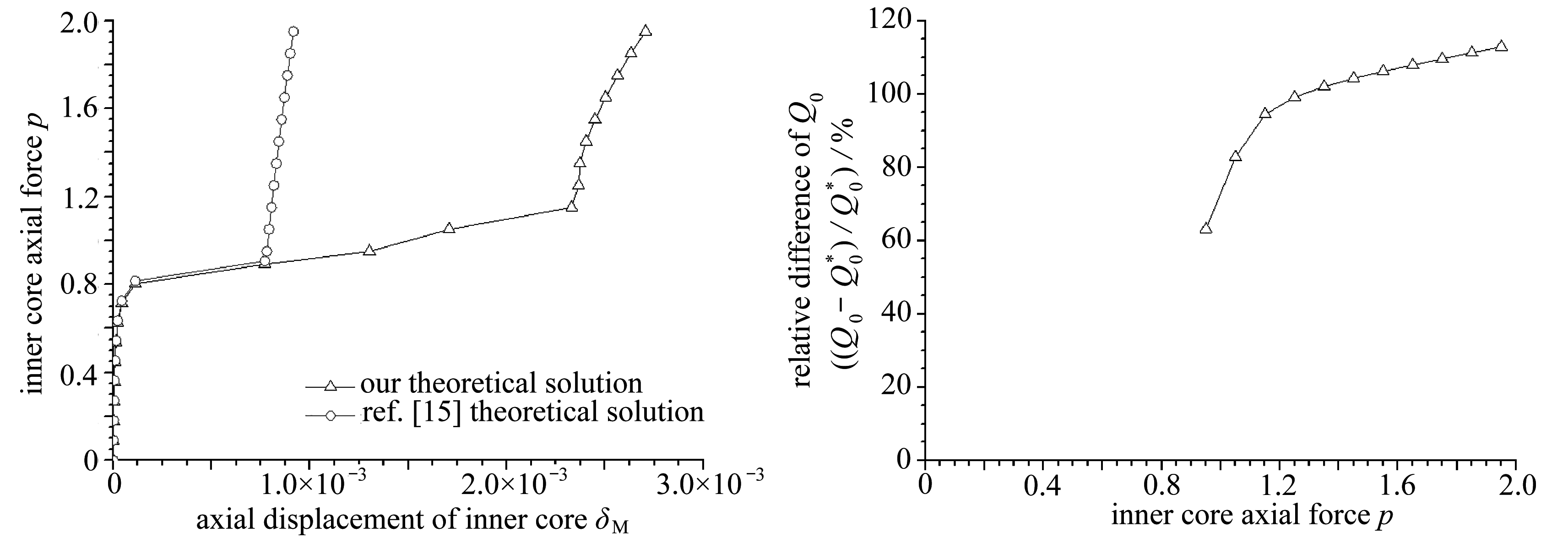
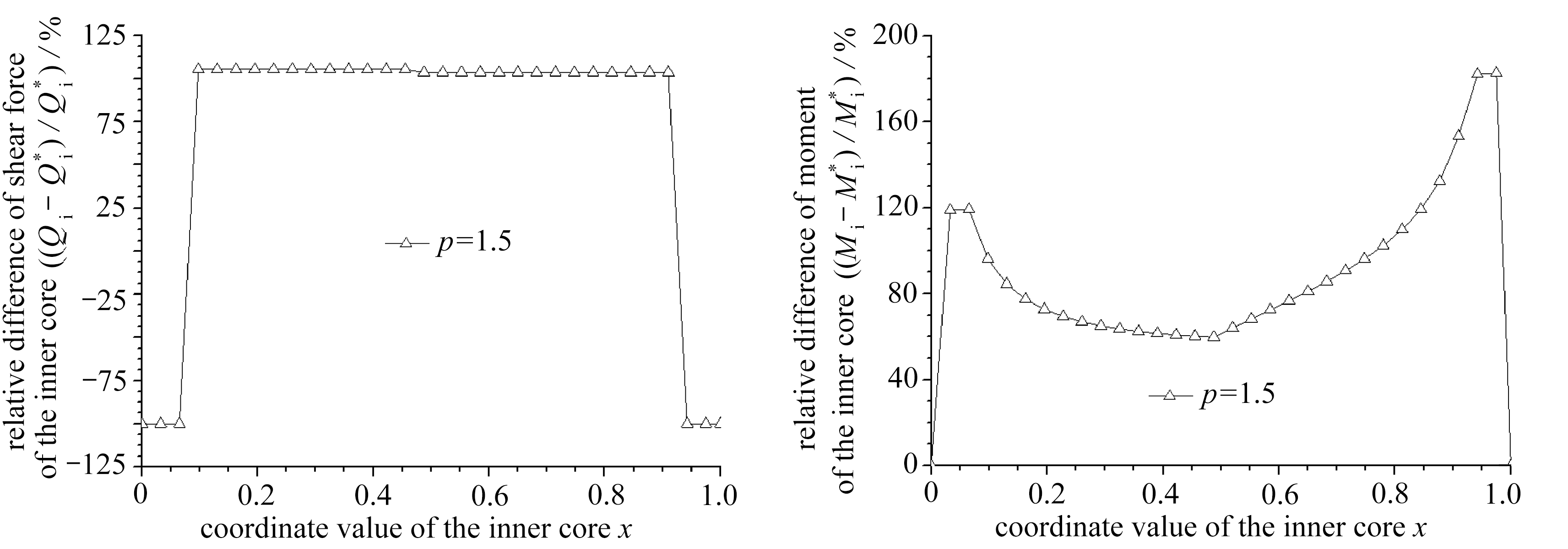
内核与套筒之间的净间隙 ![]() 相应的无量纲量为: g =0.018, β =0.053 . 本文与文献[15]的理论解答对比如图5所示 .
相应的无量纲量为: g =0.018, β =0.053 . 本文与文献[15]的理论解答对比如图5所示 .
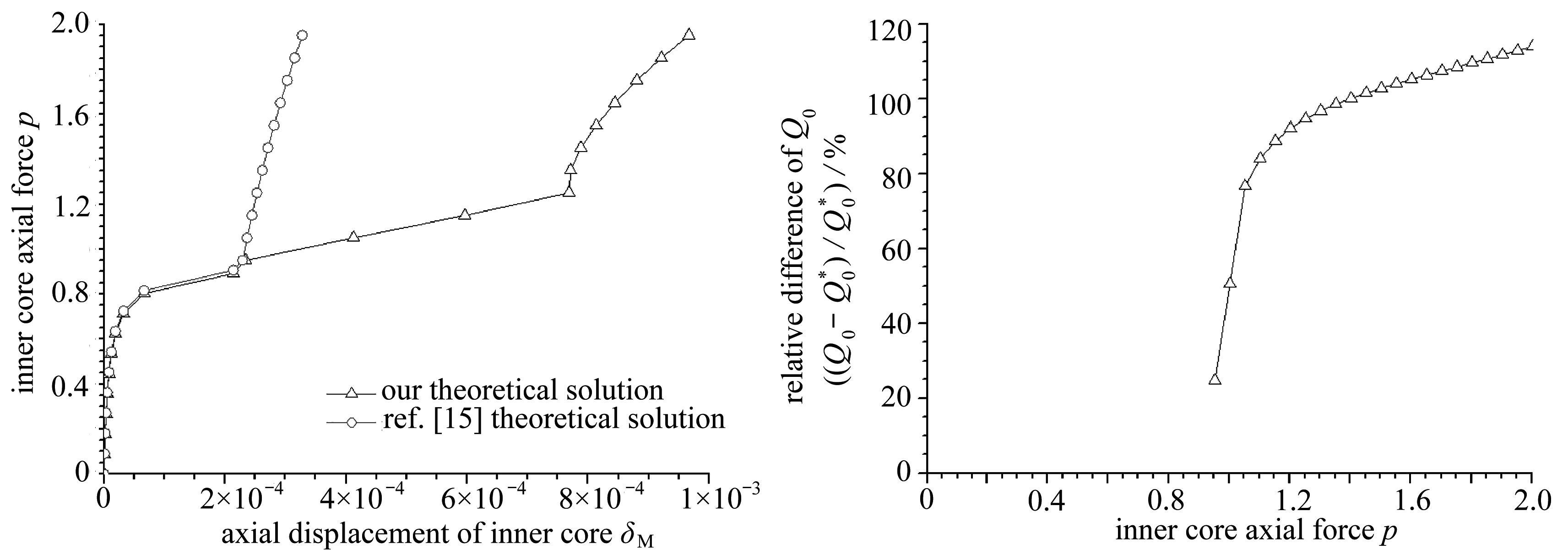
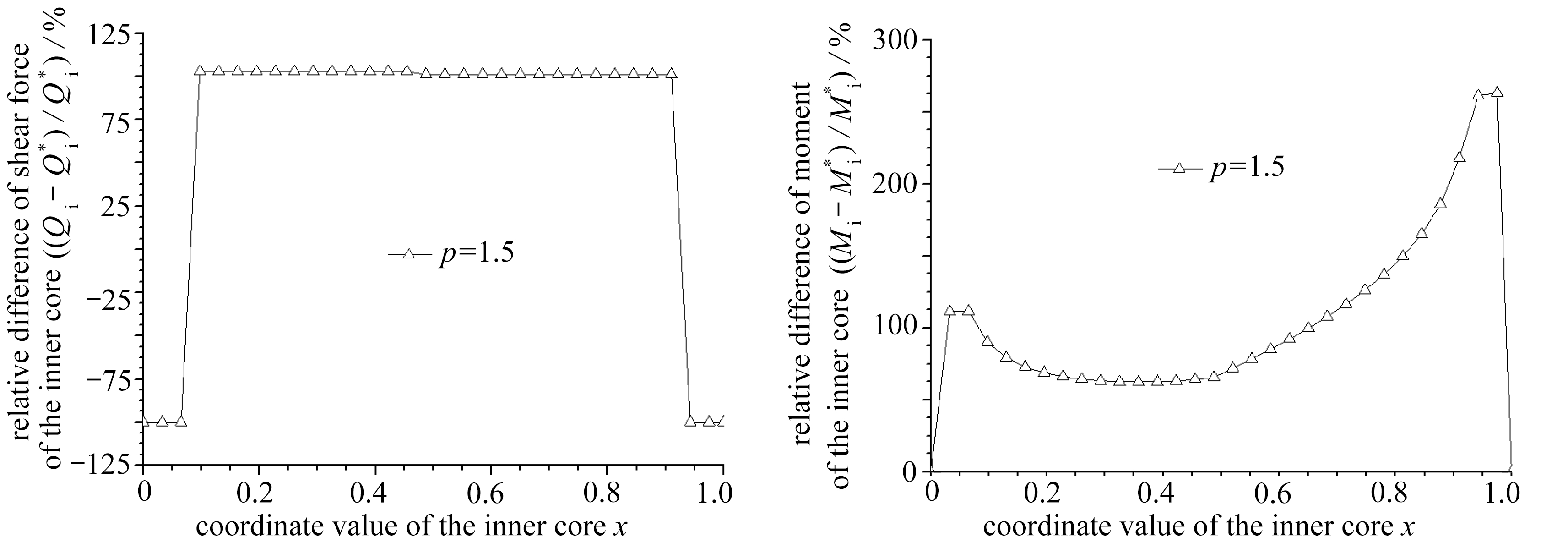
本算例中内核与套筒的抗弯刚度比值为中等 . 具体参数为, 内核直径 ![]() 壁厚
壁厚 ![]() 套筒直径
套筒直径 ![]() 壁厚
壁厚 ![]() 内核长度
内核长度 ![]() 内核伸出套筒长度
内核伸出套筒长度 ![]() 内核与套筒之间的净间隙
内核与套筒之间的净间隙 ![]() 相应的无量纲量为: g =9.565×10 -3 , β =0.129 . 本文与文献[15]的理论解答对比如图6所示 .
相应的无量纲量为: g =9.565×10 -3 , β =0.129 . 本文与文献[15]的理论解答对比如图6所示 .
(a) 内核p-δ M 曲线 (b) Q 0 相对差值
(a) The p-δ M curve of the inner core (b) The relative difference of Q 0
(c) 内核剪力相对差值 (d) 内核弯矩相对差值
(c) The relative difference of shear force of the inner core (d) The relative difference of moment of the inner core
图5 算例1的两种力学模型理论结果对比
Fig. 5 Comparison of the theoretical results from 2 mechanical models for example 1
(a) 内核p-δ M 曲线 (b) Q 0 相对差值
(a) The p-δ M curve of the inner core (b) The relative difference of Q 0
(c) 内核剪力相对差值 (d) 内核弯矩相对差值
(c) The relative difference of shear force of the inner core (d) The relative difference of moment of the inner core
图6 算例2的两种力学模型理论结果对比
Fig. 6 Comparison of the theoretical results from 2 mechanical models for example 2
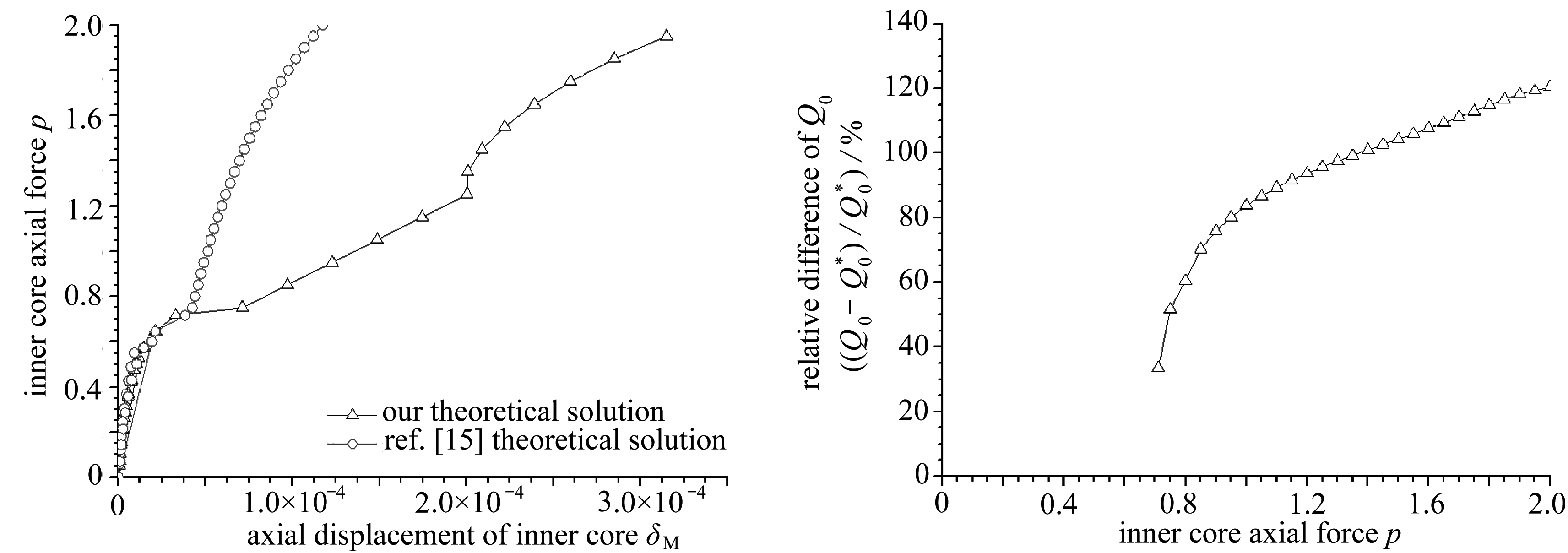
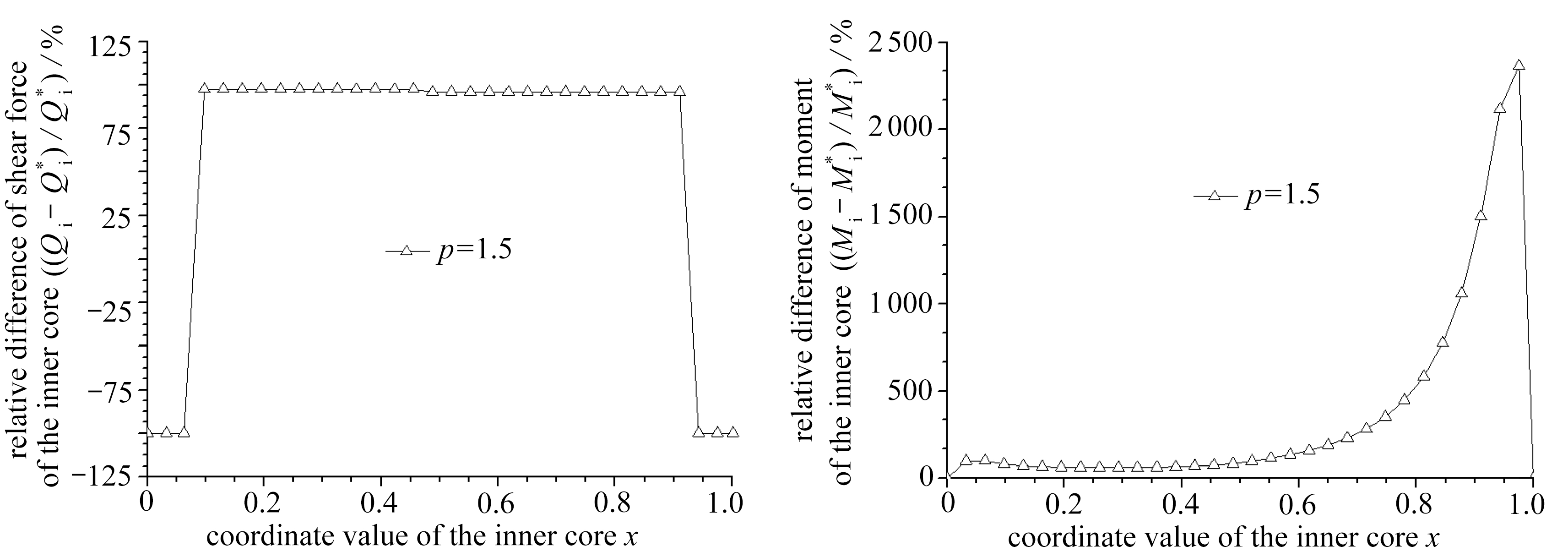
本算例中,内核与套筒的抗弯刚度比值较大 . 具体参数为, 内核直径 ![]() 壁厚
壁厚 ![]() 套筒直径
套筒直径 ![]() 壁厚
壁厚 ![]() 内核长度
内核长度 ![]() 内核伸出套筒长度
内核伸出套筒长度 ![]() 内核与套筒之间的净间隙
内核与套筒之间的净间隙 ![]() 相应的无量纲量为: g =4.13×10 -3 , β =0.282 . 本文与文献[15]的理论解答对比如图7所示 .
相应的无量纲量为: g =4.13×10 -3 , β =0.282 . 本文与文献[15]的理论解答对比如图7所示 .
由以上算例1~3的对比可知,在点接触阶段,随着内核与套筒抗弯刚度比值的增大,本文与文献[15]的轴向压力 p -轴向位移 δ M 曲线差别逐渐减小;当轴向压力 p 一定时,具有内核伸出段的套管构件有较大的弯曲轴向位移,这会显著降低套管构件的非线性轴向刚度 . 在内核与套筒抗弯刚度比值为较小、中等、较大时,本文内核与套筒端部的接触反力解答显著大于文献[15]的解答,且随着轴向压力 p 的增加,这种差别越大,可见内核伸出段对该接触反力有较大影响 . 本文内核的剪力、弯矩解答均显著大于文献[15]的解答,剪力的相对差值基本在100%左右;尤其在内核与套筒抗弯刚度比值为较大时,弯矩的相对差值达到了异常大的值 .
(a) 内核p-δ M 曲线 (b) Q 0 相对差值
(a) The p-δ M curve of the inner core (b) The relative difference of Q 0
(c) 内核剪力相对差值 (d) 内核弯矩相对差值
(c) The relative difference of shear force of the inner core (d) The relative difference of moment of the inner core
图7 算例3的两种力学模型理论结果对比
Fig. 7 Comparison of the theoretical results from 2 mechanical models for example 3
综上可见,内核伸出段对套管构件的受力性能有显著影响 . 与文献[15]的理论研究相比较,具有内核伸出段的套管构件力学模型能较准确模拟实际的套管构件,可以较准确地得到内核的变形、受力性能,为套管构件及内核与套筒端部连接构造的设计提供依据 .
本文针对轴压套管构件,提出了考虑内核伸出段的套管构件点接触力学模型,推导了点接触变形过程中,内核挠度、剪力、弯矩、接触力等物理量的计算公式,并与文献[15]的理论结果进行对比,得出了如下结论:
1) 当轴向压力 p 一定时,具有内核伸出段的套管构件有较大的弯曲轴向位移,会显著降低套管构件的非线性轴向刚度;
2) 内核伸出段使内核与套筒端部的接触反力有显著的增加,随着轴向压力 p 的增大,该接触反力增大更为显著;
3) 内核伸出段使内核的剪力、弯矩均有显著的提高,尤其在内核与套筒抗弯刚度比值较大时,弯矩的提高更显著 .
参考文献 ( References ):
[1] XIE Q. State of the art of buckling-restrained braces in Asia[J]. Journal of Constructional Steel Research , 2005, 61 (6): 727-748.
[2] 郭彦林, 江磊鑫. 双矩管带肋约束型装配式防屈曲支撑的设计方法[J]. 建筑科学与工程学报, 2010, 27 (2): 67-74.(GUO Yanlin, JIANG Leixin. Design method of buckling-restrained braces assembled with dual ribbed rectangular hollow[J]. Journal of Architecture and Civil Engineering , 2010, 27 (2): 67-74.(in Chinese))
[3] 马宁, 吴斌, 赵俊贤, 等. 十字形内芯全钢防屈曲支撑构件及子系统足尺试验[J]. 土木工程学报, 2010, 43 (4): 1-7.(MA Ning, WU Bin, ZHAO Junxian, et al. Full scale uniaxial and subassemblage tests on the seismic behavior of all-steel buckling-resistant brace[J]. China Civil Engineering Journal , 2010, 43 (4): 1-7.(in Chinese))
[4] HU L, SHEN B, MA K J, et al. A mechanical model and experimental investigations for axially compressed sleeved column[J]. Journal of Constructional Steel Research , 2013, 89 (5): 107-120.
[5] 殷占忠, 陈伟, 陈生林, 等. 改进型双钢管约束屈曲支撑试验研究[J]. 建筑结构学报, 2014, 35 (9): 90-97.(YIN Zhanzhong, CHEN Wei, CHEN Shenglin, et al. Experimental study of improved double-tube buckling restrained braces[J]. Journal of Building Structures , 2014, 35 (9): 90-97.(in Chinese))
[6] 殷占忠, 王秀丽. 带接触环的双钢管约束屈曲支撑的恢复力特征分析[J]. 兰州理工大学学报, 2010, 36 (2): 93-97.(YIN Zhanzhong , WANG Xiuli. Analysis of force restoring characteristics of buckling restraining braces formed with double-tube with contact ring[J]. Journal of Lanzhou University of Technology , 2010, 36 (2): 93-97.(in Chinese))
[7] PRASAD B K. Experimental investigation of sleeved column[C]//33 rd Structures , Structural Dynamics and Materials Conference . Dallas, Texas, USA, 1992.
[8] DOMOKOS G, HOLMES P, ROYCE B. Constrained Euler buckling[J]. Journal of Nonlinear Science , 1997, 7 (3): 281-314.
[9] CHAI H. The post-buckling response of a bi-laterally constrained column[J]. Journal of the Mechanics and Physics of Solids , 1998, 46 (7): 1155-1181.
[10] POCHEAU A, ROMAN B. Uniqueness of solutions for constrained elastica[J]. Physica D : Nonlinear Phenomena , 2004, 192 (3/4): 161-186.
[11] SRIDHARA B N. Sleeved compression member: United States Patent 5175972[P]. 1993-01-05.
[12] 申波, 邓长根. 柔性套管约束下轴心受压杆件的屈曲分析[J]. 力学与实践, 2006, 28 (5): 43-46.(SHEN Bo, DENG Changgen. Buckling analysis of an axially compressed strut constrained by a flexible sleeve[J]. Mechanics in Engineering , 2006, 28 (5): 43-46.(in Chinese))
[13] 申波, 邓长根. 双钢管构件由点接触到线接触的连续过渡[J]. 工程力学, 2007, 24 (2): 154-160.(SHEN Bo, DENG Changgen. Continuous transition from point contact to linecontact between the axially compressed inner core and the flexible sleeve in a sleeved column[J]. Engineering Mechanics , 2007, 24 (2): 154-160.(in Chinese))
[14] 申波, 邓长根. 套管构件中轴压内核与柔性套筒线接触的屈曲[J]. 工程力学, 2007, 24 (11): 63-69.(SHEN Bo, DENG Changgen. Buckling of the line-contact segment between axially compressed inner core and the flexible sleeve in a sleeved column[J]. Engineering Mechanics , 2007, 24 (11): 63-69.(in Chinese))
[15] 申波, 马克俭, 邓长根. 轴压套管构件静力稳定的理论与试验研究[J]. 工程力学,2013, 30 (3): 8-16, 23.(SHEN Bo, MA Kejian, DENG Changgen. Theoretical and experimental investigations on the static stability of a sleeved column[J]. Engineering Mechanics , 2013, 30 (3): 8-16, 23.(in Chinese))
[16] 刘鸿文. 材料力学[M]. 北京: 高等教育出版社, 1992.(LIU Hongwen. Mechanics of Materials [M]. Beijing: Higher Education Press, 1992.(in Chinese))
[17] 费志中. 弹性稳定[M]. 北京: 煤炭工业出版社, 1989.(FEI Zhizhong. Theory of Elastic Stability [M]. Beijing: China Coal Industry Publishing House, 1989.(in Chinese))
ZHAO Xiaofeng 1,2 , SHEN Bo 1,2 , MA Kejian 1,2 , LIU Panpan 1,2 , WANG Hui 1,2 , WU Junyang 1,2 , YANG Lei 1,2 ①
(1. Space Structures Research Center , Guizhou University , Guiyang 550003, P . R . China ,2. Key Lab of Structure Engineering of Guizhou Province , Guiyang 550025, P . R . China )
Abstract : To study the sleeved column with inner core over-hang lengths under axial compression, the deformation process of point contact between the initially bending inner core and the flexible sleeve was studied theoretically. The 2nd-order differential equilibrium equations of small deflection were used to deduce the formulas for the physical quantities including the deflection, the moment, the shear force and the contact reaction of the inner core and the sleeve, etc. The comparison of the theoretical results shows: 1) for the inner core with over-hang lengths, the contact process significantly increases the bending axial displacement of the sleeved column under axial compression, and reduces its nonlinear axial stiffness; 2) the contact process dramatically raises the reaction forces between the inner core and the sleeve ends, even more sharply with the increase of the axial compression; 3) the contact process remarkably magnifies the shear force and the bending moment of the inner core, and the moment increases faster especially in the case of a larger flexural rigidity ratio of the inner core to the sleeve. This research provides a basis for the design of sleeved columns and the end connection between the inner core and the sleeve.
Key words: over-hang length of the inner core; sleeved column; mechanical model; point contact; buckling
Foundation item: The National Natural Science Foundation of China(51468007)
ⓒ 应用数学和力学编委会,ISSN 1000-0887
文章编号 : 1000-0887(2018)09-1009-12
赵啸峰(1993—),男,硕士生(E-mail: xfzhao0923@163.com);
申波(1970—),男,教授,博士,硕士生导师(通讯作者. E-mail: gy-shenbo@sohu.com).
基金项目 : 国家自然科学基金(51468007);贵州省优秀科技教育人才省长专项资金(黔省专合字(2012)67号)
作者简介 :
* 收稿日期 : 2017-11-16;
修订日期: 2017-12-27
文献标志码: A
DOI: 10.21656/1000-0887.380288
中图分类号 : TU311.4 ; TU398
①引用本文 / Cite this paper: 赵啸峰, 申波, 马克俭, 刘盼盼, 王惠, 吴骏杨, 杨磊. 具有内核伸出段的套管构件点接触力学模型研究[J]. 应用数学和力学, 2018, 39 (9): 1009-1020.ZHAO Xiaofeng, SHEN Bo, MA Kejian, LIU Panpan, WANG Hui, WU Junyang, YANG Lei. Mechanical model research on point contact between the sleeve and the inner core with over-hang lengths for sleeved columns[J]. Applied Mathematics and Mechanics , 2018, 39 (9): 1009-1020.