汪明武, 董 昊, 叶 晖, 周天龙, 金菊良
(合肥工业大学 土木与水利工程学院, 合肥 230009)
摘要 : 岩爆机理复杂影响因素众多且呈现多种不确定性,应用云模型预测岩爆问题虽能刻画指标的随机性和模糊性,但很难模拟非正态分布的评价指标及存在冲突数据融合失真问题 . 为克服这些缺陷,探讨了岩爆烈度的联系云-证据预测模型 . 该模型首先基于联系数定量表达评价指标,通过联系云构建评价矩阵,并应用D-S证据理论得到基本概率赋值,进而基于距离函数的组合权重与融合均值证据预测样本的岩爆等级 . 实例应用及与其他方法对比结果表明, 该模型应用于岩爆预测是有效可行的, 且克服了传统云模型和证据理论的不足, 为岩爆烈度分级预测提供了一种新的途径 .
关 键 词 : 联系云; 证据理论; 岩爆; 预测; 组合权重
岩爆是在高地应力环境地下工程常见的地质灾害之一 [1] ,它对施工人员以及施工设备的安全造成严重威胁,因此准确和有效预测岩爆对确保实际工程安全极其重要和必要 . 目前,国内外众多研究者基于现场调查和试验结果,应用了各种理论提出了各种预测方法,如案例推理方法 [2] 、功效系数法 [3] 、集对分析方法 [4] 、可拓综合评价方法 [5] 、加权距离判别法 [6] 、支持向量机法 [7] 、理想点法 [8] 和智能识别方法 [9-10] ,这些方法促进了岩爆预测的研究与发展,但它们不能或很难同时处理指标信息冲突性和指标的随机模糊性 . 而近些年来发展的云模型和证据理论,则为此提供了思路,为了克服单一信息处理方法的局限性和片面性 [11] ,人们将正态云模型和证据理论引入岩爆分级研究 [12-13] ,取得了一定的成果,然而传统正态云模型是建立在评价指标服从于正态分布的基础之上,而证据理论在处理强冲突问题易发生失真 . 显然,简单直接将它们应用于复杂岩爆预测问题时,可能导致评价结果同实际情况存在差异 . 为此,本文将有限区间非对称联系云和改进D-S证据理论耦合,提出岩爆烈度预测模型,以减少评价指标间的冲突程度和真实再现指标的实际分布特征,提高岩爆烈度预测的可靠性和准确性 .
联系云是云模型与联系数理论耦合改进的有限区间云模型 [14] . 云模型最早由中国的Li(李德毅)提出 [15] ,其在处理不确定及模糊性问题方面具有显著的优势,但要求指标分布服从正态分布,故应用存在一定局限性,而近期发展起来的联系云则能模拟有限区间内的随机模糊性,克服了传统云模型的缺陷 . 相应的定义如下:若研究对象评价等级共有 s ( i =1,2,…, s )类,对应的评价指标有 d ( j =1,2,…, d )个,则评价指标 j 属第 i 等级的云,可基于非对称联系云的数字特征( E x , E n , H e , a , k )和云滴数 N 产生,相应云滴 x i 的确定度 μ i 为
(1)
(2)
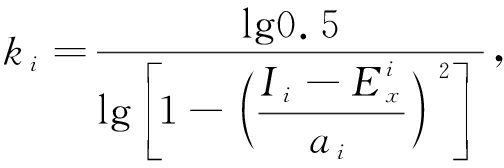
(3)
(4)
(5)
(6)
式中, a i 为等级 i 联系云半区间长 ![]() 为修正后的研究对象某等级 i 半区间长度,当
为修正后的研究对象某等级 i 半区间长度,当 ![]() 为左半区间长度修正值时,
为左半区间长度修正值时, ![]() 当
当 ![]() 为右半区间长度修正值时,
为右半区间长度修正值时, ![]() 其中
其中 ![]() 为等级 i 联系云左、右半区间的分布函数阶数;
为等级 i 联系云左、右半区间的分布函数阶数; ![]() 分别为等级 i 左半支或右半支非对称联系云的期望值和超熵, I i 为等级 i 区间的上限
分别为等级 i 左半支或右半支非对称联系云的期望值和超熵, I i 为等级 i 区间的上限 ![]() 或下限
或下限 ![]() 为等级 i 左半支或右半支非对称联系云的熵; γ 为常数,可根据具体指标的模糊性和随机性由经验值获得 . 可见,联系云模型可实现刻画有限区间内分布的定性与定量之间的映射关系,并能克服传统云模型对正态分布指标要求的缺陷 .
为等级 i 左半支或右半支非对称联系云的熵; γ 为常数,可根据具体指标的模糊性和随机性由经验值获得 . 可见,联系云模型可实现刻画有限区间内分布的定性与定量之间的映射关系,并能克服传统云模型对正态分布指标要求的缺陷 .
证据理论是基于决策者知识、经验与数据的决策方法,可随决策者对事物的知识和经验不断动态调整,故其描述不确定性问题更符合人类思维习惯 [16] . D-S证据理论则是基于两个相互独立的信息源证据提出的融合法则的证据理论 . 它可在不需任何先验信息的情况下对样本进行概率赋值分析,实现随机模糊性的处理,并能未知性区分认知中的“不知道”和“未知性”,即通过定义域在(0, 1)的信度函数和似然函数不确定地描述可能产生的判决结果,通过合成规则合成不同的证据,以及获得不同证据之间不确定关联的合成结果 . 但D-S证据理论对于强冲突证据融合存在比较大的缺陷 [16] ,相应的定义如下 .
若识别框架 Θ 为全部评价结果的论域集合,且 Θ 中各元素互斥,则当集函数 m :2 Θ →[0,1](2 Θ 为 Θ 的所有子集)满足 m (∅)=0,∑ A ∈ Θ m ( A )=1,则称 m 函数为识别框架 Θ 的基本信任函数,表示事件 A 发生的概率,为估计数据,故可以通过联系云模型计算获取,其中 A 为识别框架的任意元素(焦元) . 若两个评价指标的基本概率赋值函数为 m 1 和 m 2 ,令 m 12 为融合后的基本概率赋值,据证据理论 A ∈ Θ 的融合规则可知 [16]
(7)
(8)
其中, K 表示证据之间的冲突程度; B , C 为任意两个证据源,其焦元分别为 B j 1 , B j 2 ,…, B js 和 C j 1 , C j 2 ,…, C js ; A 为 B , C 的某个共域,其焦元为 A j 1 , A j 2 ,…, A js .
基于证据理论的岩爆联系云预测原理为:首先根据研究问题的评价指标求得各等级的左、右半区间长度;进而求得左半支和右半支联系云的数字特征( E x , E n , H e , a , k );再根据数字特征对应的联系云发生器,模拟评价指标隶属于某级别的非对称云模型;最后,将样本指标实测值代入联系云模型求得确定度,并转换为基本概率赋值,运用改进的D-S证据理论求得其属于各岩爆等级的融合基本概率,利用“最大隶属度原则”综合预测样本评价等级 . 具体流程如图1所示 .
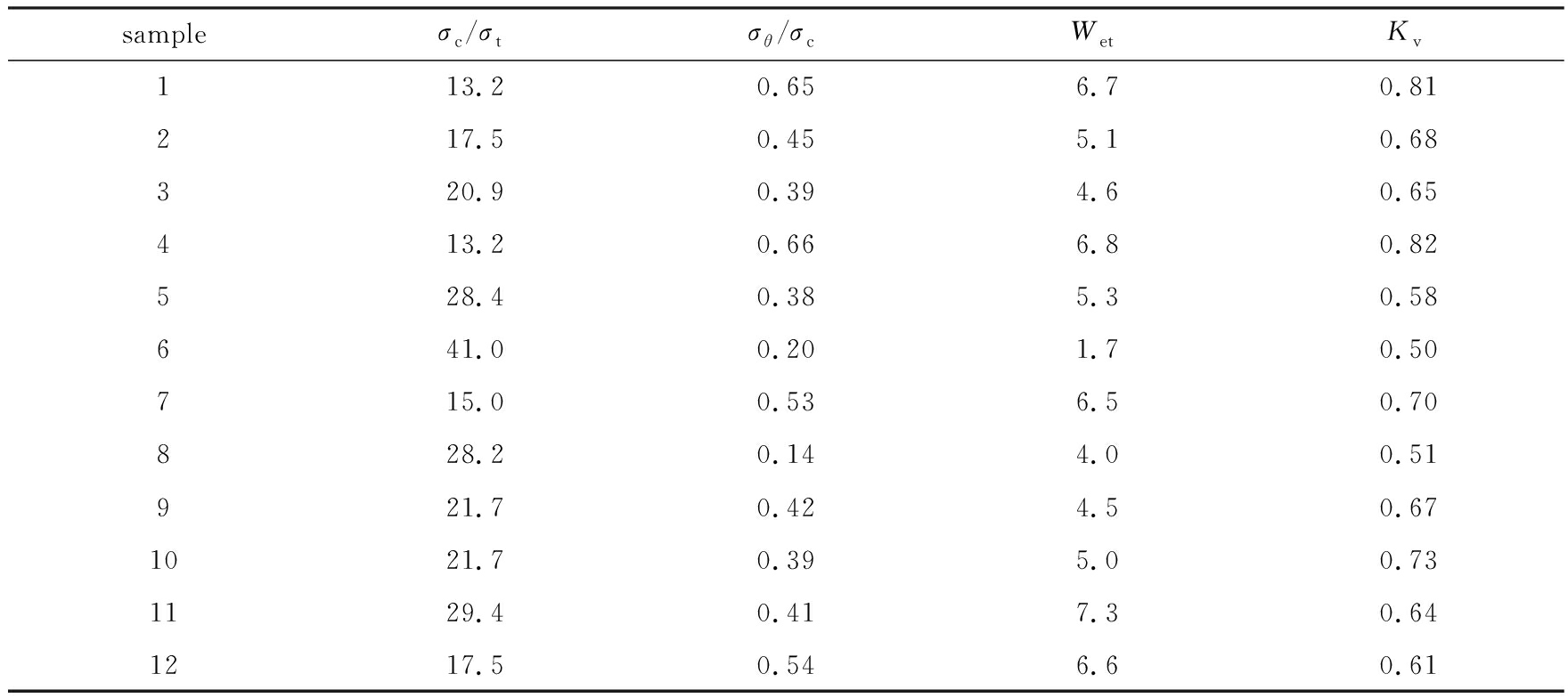
影响岩爆的指标很多,基于已有资料和经验 [1-12] ,本文选取岩石单轴抗压强度与抗拉强度比 σ c / σ t 、岩石切向应力与岩石单轴抗压强度比 σ θ / σ c 、弹性变形能指数 W et 和岩体完整性系数 K v 作为应变型岩爆评价指标,相应的评价标准见表1 .
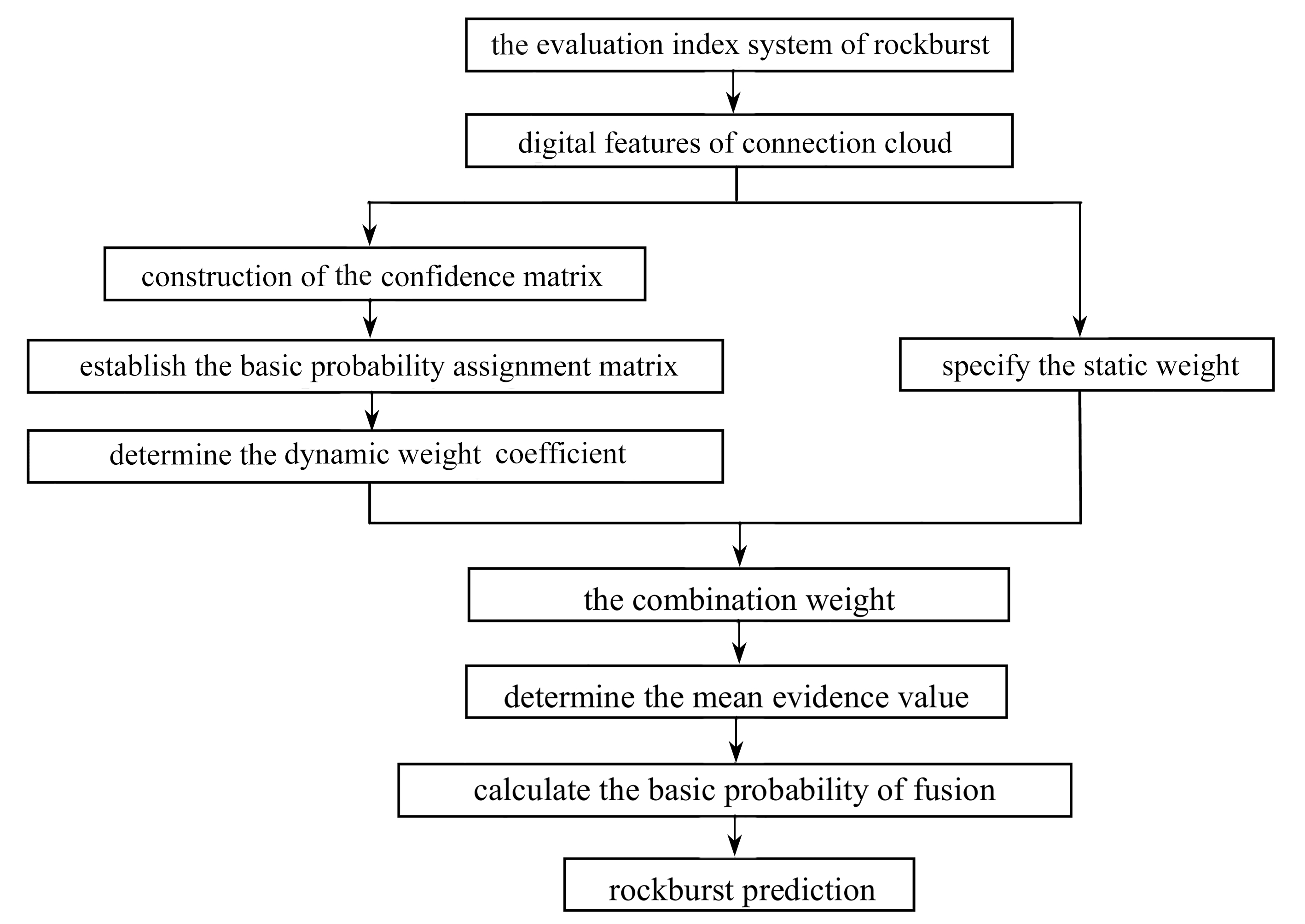
图1 岩爆预测流程
Fig. 1 The flowchart of forecast procedure based on the connection cloud model and the evidence theory for rockburst intensity
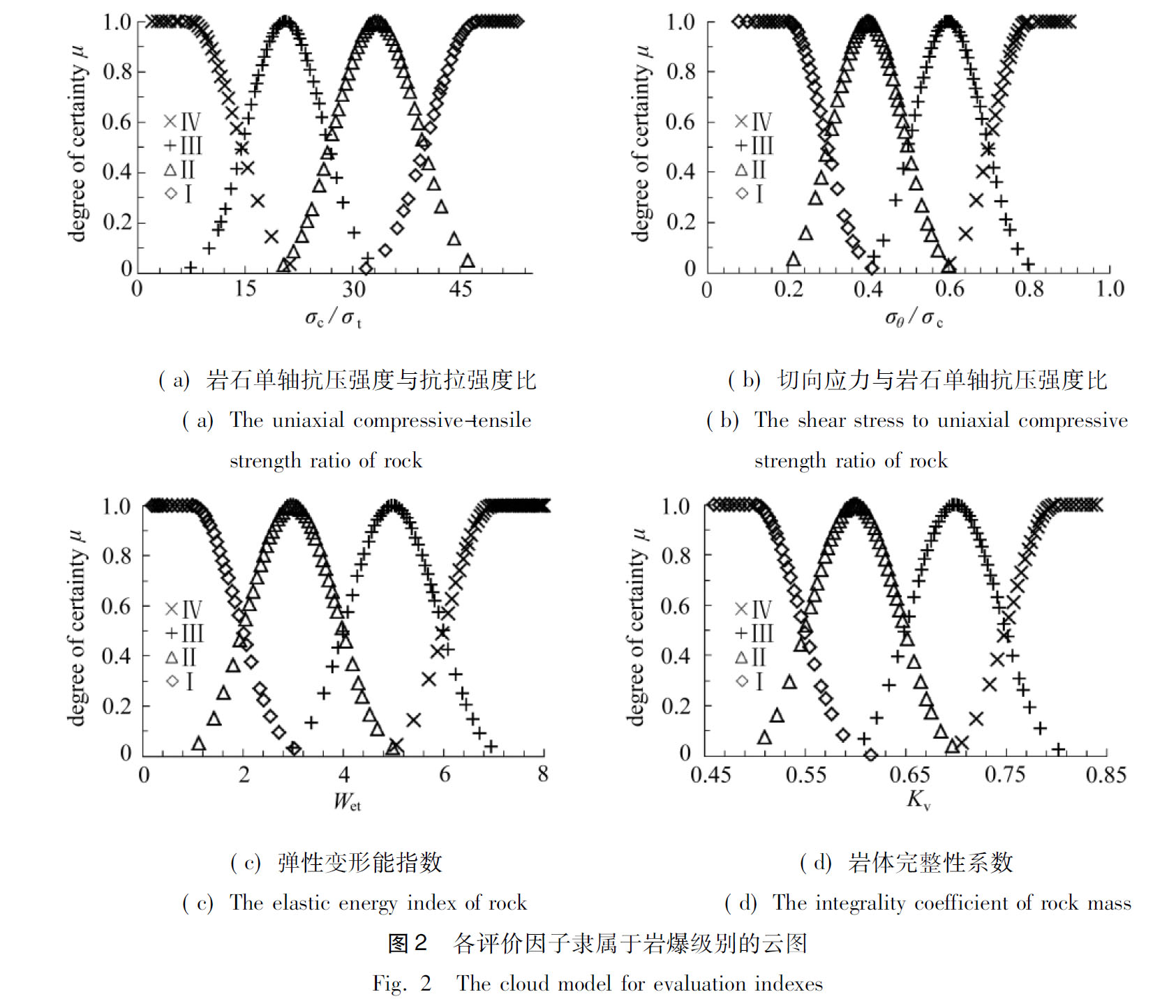
基于上述的联系云模型,根据表1的预测指标分级标准,按式(2)~(6)可求得各预测指标对应相应等级的联系云数字特征( E x , E n , H e , a , k );再根据式(1)可模拟指标 j 属于等级 i 左半区间和右半区间的各1 000的云滴,即可构成评价指标 j 对应等级 i 联系云, 结果如图2所示 . 其中横坐标代表评价指标值,纵坐标代表相应的确定度 . 图2(a)从左到右分别代表指标等级Ⅳ~等级Ⅰ对应的联系云,而图2(b)、(c)和(d)从左到右则为指标等级Ⅰ~等级Ⅳ的联系云 .
表1 岩爆预测指标及分级标准 [12]
Table 1 Rockburst prediction indexes and classification standards [12]

在证据框架中,信度函数获取是证据理论决策方法的关键 . 为使联系云模型生成的确定度 μ ji 满足概率赋值的定义,需进行相应的转换,计算模型如下:
(9)
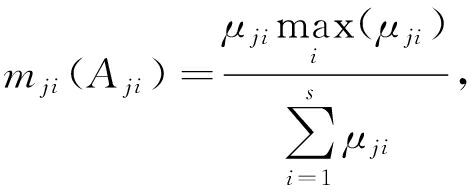
(10)
式中, m ji ( A ji )为相应 μ ji 的基本概率赋值; m j ( A j ( s +1) )表示第 j 个指标因素相应的不确定度 θ j 的基本概率赋值 . 由它们可得基本概率赋值矩阵:

(11)
合理确定组合权重对评价结果至关重要,本文为最优求解静态和动态权重的组合系数,采用两类权重差异程度与其相应的分配系数差异一致原理,相应模型如下:
η j = ξω 1 j + ζω 2 j ,
(12)
(13)
ξ + ζ =1,
(14)
式中, η j 为组合权重; ξ 和 ζ 为动、静态权重系数权重的分配系数; d ( ω 1 j , ω 2 j )为第 j 个评价指标的动态权重 ω 1 j 和静态权重 ω 2 j 的距离函数,权重相应的确定方法如下 .
动态权重求解中为避免指标强冲突而造成失真问题,本文采用证据理论进行融合确定 . 若任意证据向量表示为 q j ={ m j 1 ( A j 1 ), m j 2 ( A j 2 ),…, m js ( A js ), m j ( A j ( s +1) )} T ( j , k =1,2,…, d ),则任意两个证据向量 q j 和 q k 间的相容系数 R jk 为
(15)
由上式可知,两证据向量的余弦值越大,表示两证据间的相容系数越大,故某条证据 m j 绝对相容度为 ![]() 由于可信度随着证据的变化而发生变化,故可将绝对相容度归一化后的证据可信度作为动态权重,即
由于可信度随着证据的变化而发生变化,故可将绝对相容度归一化后的证据可信度作为动态权重,即
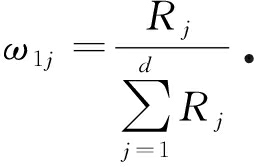
(16)
本文采用熵权法确定指标静态权重 . 设 x jp 为 p ( p =1,2,…, P )样本第 j 个评价指标的实测值, y jp 为 x jp 归一化后的值,则第 j 个指标的静态权重为
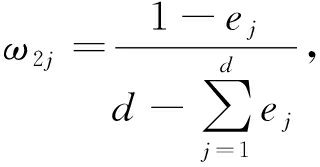
(17)
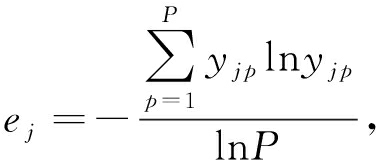
(18)
式中, ω 2 j 为第 j 个评价指标的静态权重 .
基于组合权重 η j ,通过对证据体 m ji 进行均值加权可求得均值证据 [17] :
(19)
式中, M a, p 为样本 p 的均值证据 . 则利用D-S证据理论融合式(7)和(8),对 M a, p 进行4次合成,即可得 p 样本的融合基本概率 F p .
为检验构建模型的合理性和有效性,实例选取了文献[8]岩爆数据进行应用和对比分析,实例数据见表2 .
表2 评价指标值实例 [8]
Table 2 Values of evaluation indexes for example [8]
现以表2数据中样本1为例,来说明本文模型预测评级的计算过程 . 将表2数据代入联系云模型中,由式(1)计算得到 μ 1,1 =0, μ 1,2 =0, μ 1,3 =0.352 2, μ 1,4 =0.634 3,表明样本1的指标 σ c / σ t 隶属于岩爆等级Ⅳ的程度最大,其次隶属于岩爆等级Ⅲ,不可能隶属于岩爆等级Ⅰ,Ⅱ . 同理可求出其他指标属于各个等级的确定度,则样本1的隶属度矩阵为

利用式(9)和(10)可将隶属度矩阵转化为基本概率赋值矩阵:

同样,按式(15)和(16)可求得样本1的动态权重系数 ω 1,1 =(0.289 0, 0.162 1, 0.285 1, 0.263 8),据式(17)和(18)可计算静态权重为 ω 2,1 =(0.333 0,0.215 0,0.259 0,0.193 0) . 由式(13)和(14)可得 ξ =0.34, ζ =0.66和 ξ =0.66, ζ =0.34 . 但实际证据间支持程度较指标重要性对最终评价的影响小,故应取 ξ =0.34, ζ =0.66,相应可求得综合权重 η 1 =(0.318 0, 0.197 0,0.267 9,0.217 1),均值证据为 M a,1 =(0.000 0,0.000 1,0.236 1,0.596 4, 0.167 4) . 利用D-S证据理论融合规则进行4次融合,可得最终融合概率为 F 1 =(0.000 0,0.000 2,0.091 9, 0.907 5, 0.000 5) . 由结果可知,改进后的证据理论将不确知的基本概率降到了0.000 5,依“最大隶属度原则”可知样本1岩爆等级为强烈岩爆Ⅳ级 . 同理,可得其他样本的融合基本概率和判别等级,详见表3 .
表3 岩爆烈度预测结果及对比
Table 3 Prediction results and comparison of rockburst intensity
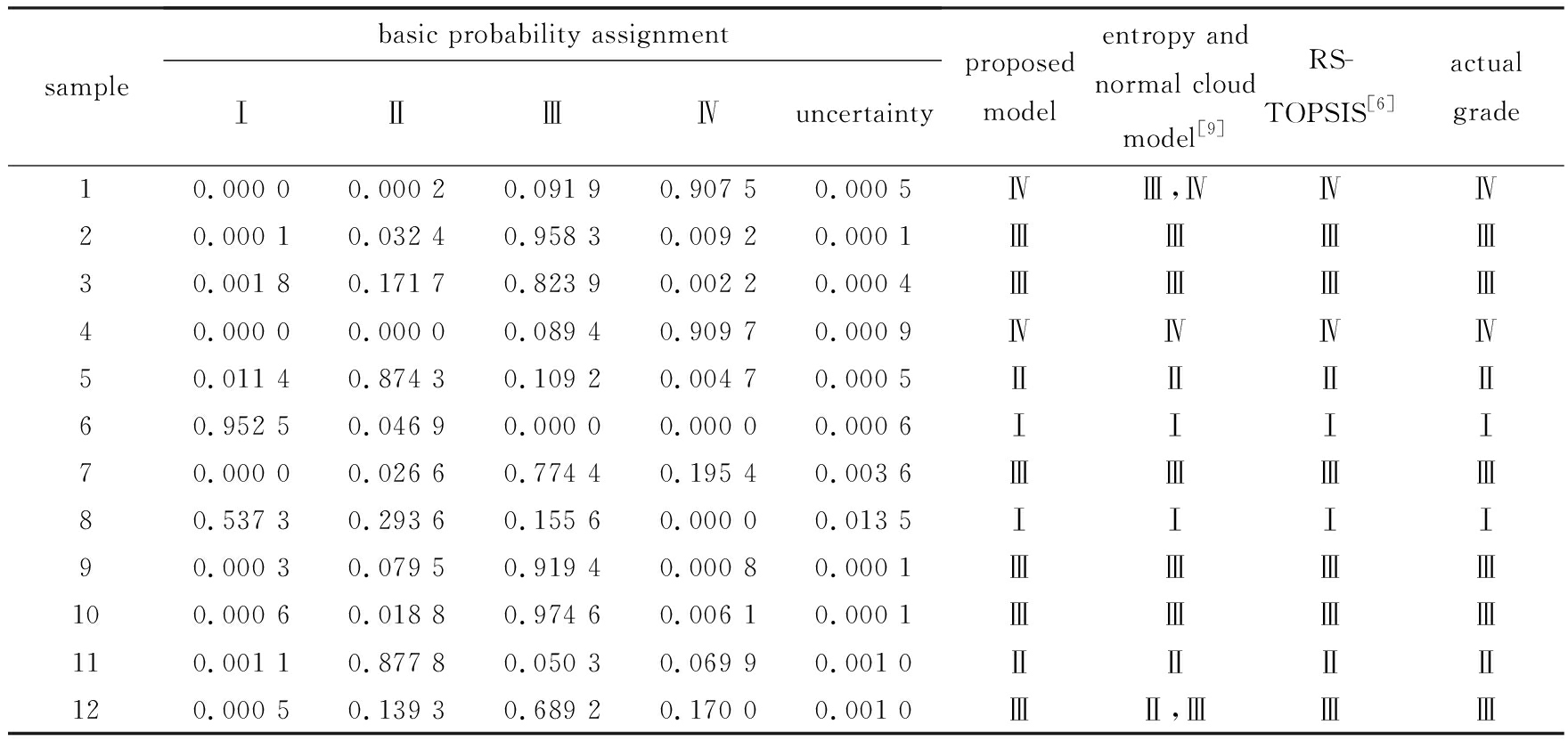
由表3结果可知,样本6、8属于无岩爆Ⅰ级,样本5属于弱岩爆Ⅱ级,样本1、4属于强烈岩爆Ⅳ级,其余样本均属于中等岩爆Ⅲ级 . 结果表明本文模型预测结果与RS-TOPSIS模型结果及实际现场情况完全一致,表明本文模型应用于岩爆预测是有效可行的 . 同时,基于联系云-证据理论的岩爆预测模型还综合考虑了有限区间分布评价指标的不确定性与随机模糊性,较传统云模型更接近指标实际分布形态和特征,并能体现预测等级的模糊不确定性转换特征,以及能有效克服不同指标冲突引起的不利影响,从而可使模型预测结果更加接近实际情况和体现决策者认识岩爆的不确定性 .
岩爆评价指标一般为有限区间分布的,且具有随机模糊性和信息冲突性,本文将联系云和D-S证据理论耦合提出岩爆烈度的预测新模型,实例应用及对比分析,可得如下主要结论:
1) 通过联系云描述岩爆评价指标体系,可统一定量描述等级模糊转换状态和指标的确定性与不确定性,并能同时处理指标信息的冲突性和随机模糊性 . 同时实现模拟能真实再现评价指标实际分布特征, 并可解决传统正态云模型应用局限问题, 使评价结果更加符合工程实际情况 .
2) 基于距离函数确定组合权重确定中,引入D-S证据理论进行数据融合,可实现比概率函数更恰当地刻画信息中的不确定性,在避免权重确定主观缺陷同时,可降低强冲突指标引起结果失真的问题 . 特别是可避免结果出现与实际情况不符的、不同等级而隶属度相似的评价结果,达到有效提高岩爆预测结果的可靠性和准确性 .
3) 实例应用及对比结果表明,表明基于联系云-证据理论模型预测岩爆烈度级的结果,符合现场实际情况,是有效可行的,也为类似工程评价提供了参考 .
参考文献 ( References ):
[1] 许迎年, 徐文胜, 王元汉, 等. 岩爆模拟试验及岩爆机制研究[J]. 岩石力学与工程学报, 2002, 21 (10): 1462-1466.(XU Yingnian, XU Wensheng, WANG Yuanhan, et al. Simulation testing and mechanism studies on rockburst[J]. Chinese Journal of Rock Mechanics and Engineering , 2002, 21 (10): 1462-1466.(in Chinese))
[2] 苏国韶, 张小飞, 燕柳斌. 基于案例推理的岩爆预测方法[J]. 采矿与安全工程学报, 2008, 25 (1): 63-67.(SU Guoshao, ZHANG Xiaofei, YAN Liubin. Rockburst prediction method based on case reasoning pattern recognition[J]. Journal of Mining and Safety Engineering , 2008, 25 (1): 63-67.(in Chinese))
[3] 王迎超, 尚岳全, 孙红月, 等. 基于功效系数法的岩爆烈度分级预测研究[J]. 岩土力学, 2010, 31 (2): 529-534.(WANG Yingchao, SHANG Yuequan, SUN Hongyue, et al. Study of prediction of rockburst intensity based on efficacy coefficient method[J]. Rock and Soil Mechanics ,2010, 31 (2): 529-534.(in Chinese))
[4] 汪明武, 李丽, 金菊良. 岩爆预测的改进集对分析模型[J]. 岩土力学, 2008, 28 (S1): 511-518.(WANG Mingwu, LI Li, JIN Juliang. An improved set pair analysis model for the prediction of rockburst[J]. Rock and Soil Mechanics , 2008, 28 (S1): 511-518.(in Chinese))
[5] 陈祥, 祈小博, 蔡新滨, 等. 可拓综合评价方法在岩爆判别中的应用[J]. 北京交通大学学报, 2009, 33 (1): 99-108.(CHEN Xiang, QI Xiaobo, CAI Xinbin, et al. Extensional evaluation method and its application in the judgments of rockburst[J]. Journal of Beijing Jiaotong University , 2009, 33 (1): 99-108.(in Chinese))
[6] 罗磊, 曹平. 深部巷道岩爆加权距离判别法模型的分析和应用[J]. 中南大学学报(自然科学版), 2012, 43 (10): 222-226.(LUO Lei, CAO Ping. Model of weighted distance discriminant analysis and application for deep roadway[J]. Journal of Central South University ( Science and Technology ), 2012, 43 (10): 222-226.(in Chinese))
[7] 李宁, 王李管, 贾明涛. 基于粗糙集理论和支持向量机的岩爆预测[J]. 中南大学学报(自然科学版), 2017, 48 (5):1268-1275.(LI Ning, WANG Liguan, JIA Mingtao. Rockburst prediction based on rough set theory and support vector machine[J]. Journal of Central South University ( Science and Technology ), 2017, 48 (5): 1268-1275.(in Chinese))
[8] 徐琛, 刘晓丽, 王恩志, 等. 基于组合权重-理想点法的应变型岩爆五因素预测分级[J]. 岩土工程学报, 2017, 39 (12): 2245-2252.(XU Chen, LIU Xiaoli, WANG Enzhi, et al. Prediction and classification of strain mode rockburst based on five-factor criterion and combined weight-ideal point method[J]. Chinese Journal of Rock Mechanics and Engineering , 2017, 39 (12): 2245-2252.(in Chinese))
[9] 高玮. 基于蚁群聚类算法的岩爆预测研究[J]. 岩土工程学报, 2010, 32 (6): 874-880.(GAO Wei. Prediction of rock burst based on ant colony clustering algorithm[J]. Chinese Journal of Geotechnical Engineering , 2010, 32 (6): 874-880.(in Chinese))
[10] 张乐文, 张德永, 李术才, 等. 基于粗糙集理论的遗传-RBF神经网络在岩爆预测中的应用[J]. 岩土力学, 2012, 33 (S1): 270-276.(ZHANG Lewen, ZHANG Deyong, LI Shucai, et al. Application of RBF neural network to rockburst prediction based on rough set theory[J]. Rock and Soil Mechanics , 2012, 33 (S1): 270-276.(in Chinese))
[11] 汪明武, 魏东方, 周欣玮, 等. 基于联系矩阵的围岩稳定性组合评价模型[J]. 应用数学和力学, 2015, 36 (3): 294-302.(WANG Mingwu, WEI Dongfang, ZHOU Xinwei, et al. Connectional matrix-based combination evaluation method for surrounding rock stability[J]. Applied Mathematics and Mechanics , 2015, 36 (3): 294-302.(in Chinese))
[12] 周科平, 林允, 胡建华, 等. 基于熵权-正态云模型的岩爆烈度分级预测研究[J]. 岩土力学, 2016, 37 (S1): 596-602.(ZHOU Keiping, LIN Yun, HU Jianhua, et al. Grading prediction of rockburst intensity based on entropy and normal cloud model[J]. Rock and Soil Mechanics , 2016, 37 (S1): 596-602.(in Chinese))
[13] 贾义鹏, 吕庆, 尚岳全, 等. 基于证据理论的岩爆预测[J]. 岩土工程学报, 2014, 36 (6): 1079-1086.(JIA Yipeng, LÜ Qing, SHANG Yuequan, et al. Rockburst prediction based on evidence theory[J]. Chinese Journal of Geotechnical Engineering , 2014, 36 (6): 1079-1086.(in Chinese))
[14] 汪明武, 金菊良. 联系数理论与应用[M]. 北京: 科学出版社, 2017.(WANG Mingwu, JIN Juliang. The Theory and Applications of Connection Numbers [M]. Beijing: Science Press, 2017.(in Chinese))
[15] LI D Y, HAN J W, SHI X Mi, et al. Knowledge representation and discovery based on linguistic atoms[J]. Knowledge - Based Systems , 1988, 10 (7): 431-440.
[16] YAN S D, XIAN N T. Damage identification of offshore platform based on D-S evidence theory[J]. Advanced Materials Research , 2011, 255 : 314-318.
[17] DENG Y, SHI W K, ZHU Z F, et al. Combining belief functions based on distance of evidence[J]. Decision Support Systems , 2004, 38 (3): 489-493.
WANG Mingwu, DONG Hao, YE Hui, ZHOU Tianlong, JIN Juliang ①
( School of Civil and Hydraulic Engineering , Hefei University of Technology , Hefei 230009, P . R . China )
Abstract : Rockburst mechanism is a complex problem involving various uncertain factors. Although the cloud model can deal with the randomness and fuzziness of indicators for prediction of rockburst intensity, it cannot simulate the state of evaluation indicators in a finite distribution interval and address the distortion of data fusion. Herein, a connection cloud-evidence theory coupling model was built to remedy these defects. In this model, evaluation indicators were firstly expressed quantitatively by connection numbers. Then the evaluation matrix was constructed with the connection cloud model and the basic probability assignment based on the evidence theory was obtained. Finally, with the combination weight obtained from a distance function, classification of the rockburst intensity was determined according to the mean evidence value. The case study and comparison with other methods show that, the proposed model is effective and feasible for the prediction of rockburst intensity. It can overcome the shortcomings of the normal cloud model and the evidence theory, making a novel method for comprehensive prediction of rockburst intensity.
Key words: connection cloud; evidence theory; rockburst; prediction; combination weight
Foundation item: The National Key R&D Plan(2016YFC0401303); The National Natural Science Foundation of China(41172274; 51579059)
ⓒ 应用数学和力学编委会,ISSN 1000-0887
文章编号 : 1000-0887(2018)09-1021-09
基金项目 : 国家重点研发计划(2016YFC0401303);国家自然科学基金(41172274;51579059)
作者简介 : 汪明武(1972—),男,教授,博士,博士生导师(通讯作者. E-mail: wanglab307@foxmail.com).
* 收稿日期 : 2017-11-13;
修订日期: 2018-01-31
文献标志码: A
DOI: 10.21656/1000-0887.380286
中图分类号 : TU457
①引用本文 / Cite this paper: 汪明武, 董昊, 叶晖, 周天龙, 金菊良. 基于联系云-证据理论的岩爆烈度预测模型[J]. 应用数学和力学, 2018, 39 (9): 1021-1029.WANG Mingwu, DONG Hao, YE Hui, ZHOU Tianlong, JIN Juliang. A connection cloud-evidence theory coupling model for prediction of rockburst intensity[J]. Applied Mathematics and Mechanics , 2018, 39 (9): 1021-1029.