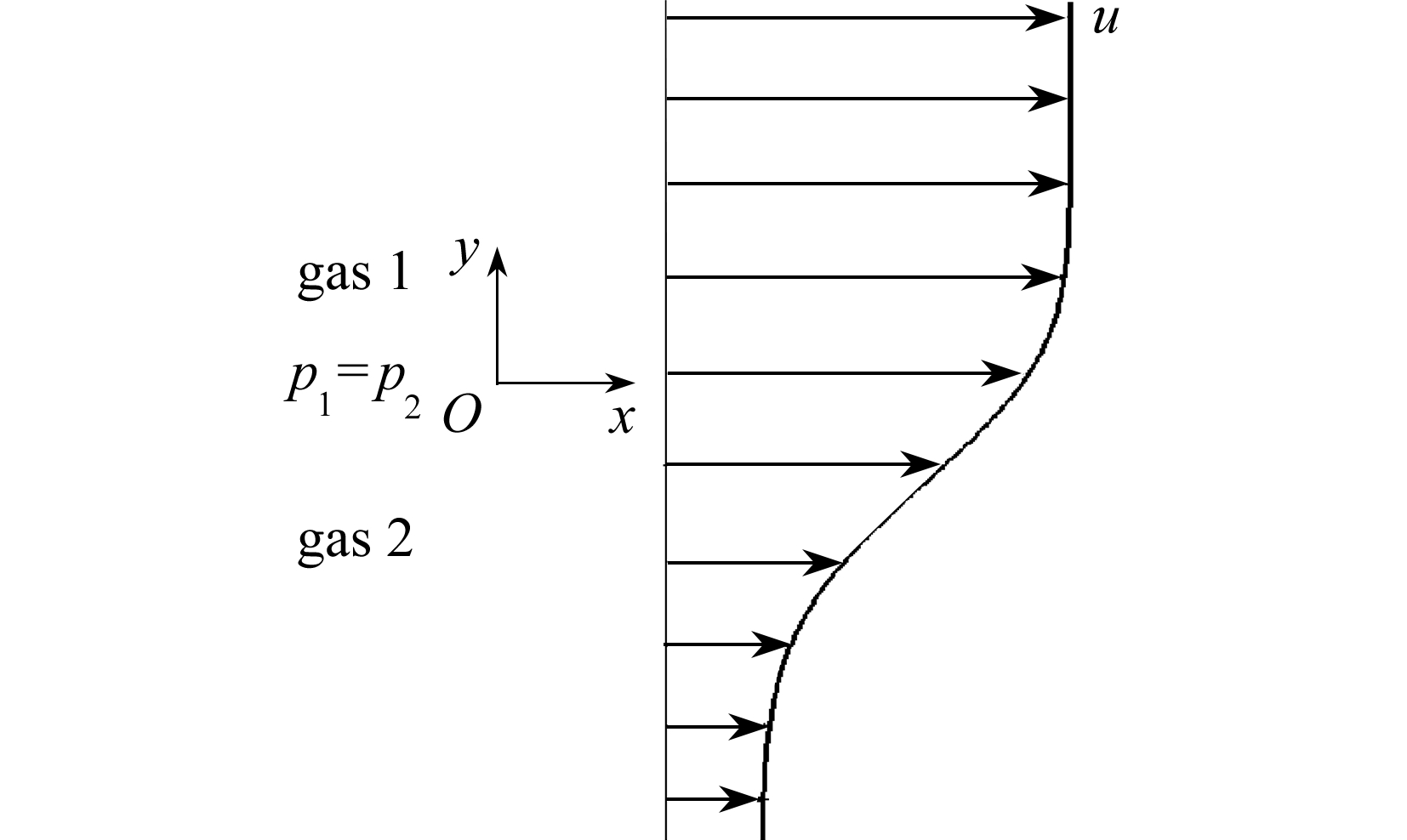
图1 二元气体混合层示意图
Fig. 1 Schematic diagram of binary gas mixing layers
高 军 1 , 李 佳 2 , 刘凤君 3 , 时晓天 1 , 袁湘江 1
(1. 中国航天空气动力技术研究院,北京 100074; 2. 唐山学院 基础教学部, 河北 唐山 063000; 3. 北京动力机械研究所, 北京 100074)
摘要 : 针对氧气和氮气构成的两组分气体混合层流动,采用线性稳定性理论分析了流动的线性失稳特性 . 两组分气体混合层的基本流剖面由相似性解给出 . 首先研究了对流Mach(马赫)数对相似性解剖面的影响;然后重点考察了对流Mach数、二维和三维扰动对稳定性的影响 . 线性稳定性理论的结果表明,第一模态最不稳定波的最大增长率始终大于第二模态波 . 随着对流Mach数的增加,混合层中的第一模态和第二模态的最大增长率都受到抑制 .
关 键 词 : 线性稳定性; 混合层; 二元气体; 对流Mach数; 相似性解
混合层流动在航空航天实际工程中具有广泛的应用 . 增强或抑制两股气流的掺混对整个系统性能的提高起到关键的作用 . 在冲压发动机内,喷注燃料和空气形成了超声速混合层 . 为了获得更高的推力需要提高燃烧室内燃料与空气的混合效率 [1] . 在气动光学领域 [2-3] ,为了降低光学窗口上的热流,通常采用喷流的办法将主流与光学窗口隔开,喷流和主流形成了超声速混合层;为了准确制导需要降低两股气流掺混 . 因此,研究混合层的稳定性特征对揭示流动机理和进行流动控制具有重要的应用意义和研究价值 .
混合层的混合程度取决于混合层的不稳定性特征 . 混合层中扰动的增长率可以使用线性稳定性理论进行预测 . 目前对于自然转捩的预测,工程上通常采用的还是基于线性稳定性理论的e N 方法 [4] . 线性稳定性理论的研究始于Rayleigh、Orr和Sommerfeld的研究工作 . Rayleigh的无黏线性稳定性理论指出对于无黏流动速度剖面存在拐点是流动不稳定性的必要条件 . Michalke [5] 利用双曲剖面进行无黏线性稳定性分析得到了不可压缩时间发展混合层中的最不稳定波数和空间发展混合层中的最不稳定频率 . Blumen等 [6] 采用时间模式研究了混合层的不稳定特性,研究发现当对流Mach数 Ma c >1时,出现第二模态并且是最不稳定的 . Jackson等在无黏空间模式的稳定性分析中发现了两个超声速不稳定波,按照相速度大小分为快模态和慢模态,其中一个相对慢速流体是超声速的,而另一个相对于快速流体也是超声速的 [7] . 罗纪生等 [8] 研究发现当 Ma c 接近1时二维扰动的增长率很小,对混合层的混合影响很小,三维扰动虽然有较大的增长率但是法向速度较小,也不能使混合层有效混合 . 王强等 [9] 对时间发展的混合层做了稳定性分析,研究了二维波、三维波及黏性对增长率的影响 . 杨武兵、沈清等 [10-11] 回顾了近十年来混合层的研究进展 . 以上介绍的混合层的稳定性分析都基于单一组分气体,基本流模型大都采用了双曲函数 . 近些年来人们开始研究多组分气体组成的混合层的稳定性 . Kozusko等 [12] 利用二元气体可压缩混合层的相似性解剖面分析了混合层的稳定性特征,研究发现二组分气体摩尔质量比是影响稳定性的一个重要因素 . Leonardo等 [13] 研究了Prandtl(普朗特)数和Lewis(李维斯)数对O 2 -N 2 混合层的稳定性的影响 . Okong等 [14] 研究了真实气体效应对二元气体混合层的稳定性的影响 . Fedioun等 [15] 对三维可压缩混合层做了时间模式的稳定性分析和数值模拟 . Mendonca [16] 研究了喷流和尾迹流对O 2 -H 2 混合层稳定性的影响,研究发现当尾迹流的温度较低时,混合层变得更不稳定 . Shin等 [17] 和Day等 [18] 研究了带化学反应的混合层的稳定性,研究发现释热使混合层变得更加稳定 .
本文考虑两种组分气体构成的混合层,首先通过相似性变换得到二元气体混合层的相似性解,然后研究了对流Mach数对混合层剖面及稳定性的影响 .
线性稳定性分析需要基本流场的信息, 本节

图1 二元气体混合层示意图
Fig. 1 Schematic diagram of binary gas mixing layers
将首先建立二元气体的基本流模型,作为开展流动稳定性研究的前提条件,然后给出二元气体的线性稳定性方程 .
考虑两股气流以不同的速度流过分离板而产生的平面混合层,并忽略分离板后缘产生的尾迹,在下游混合层的速度 u 的剖面示意图如图1所示 . 图中下标1表示上层流体,下标2表示下层流体,上下两层流体是等压的,即 p 1 = p 2 . 流动满足可压缩边界层控制方程:
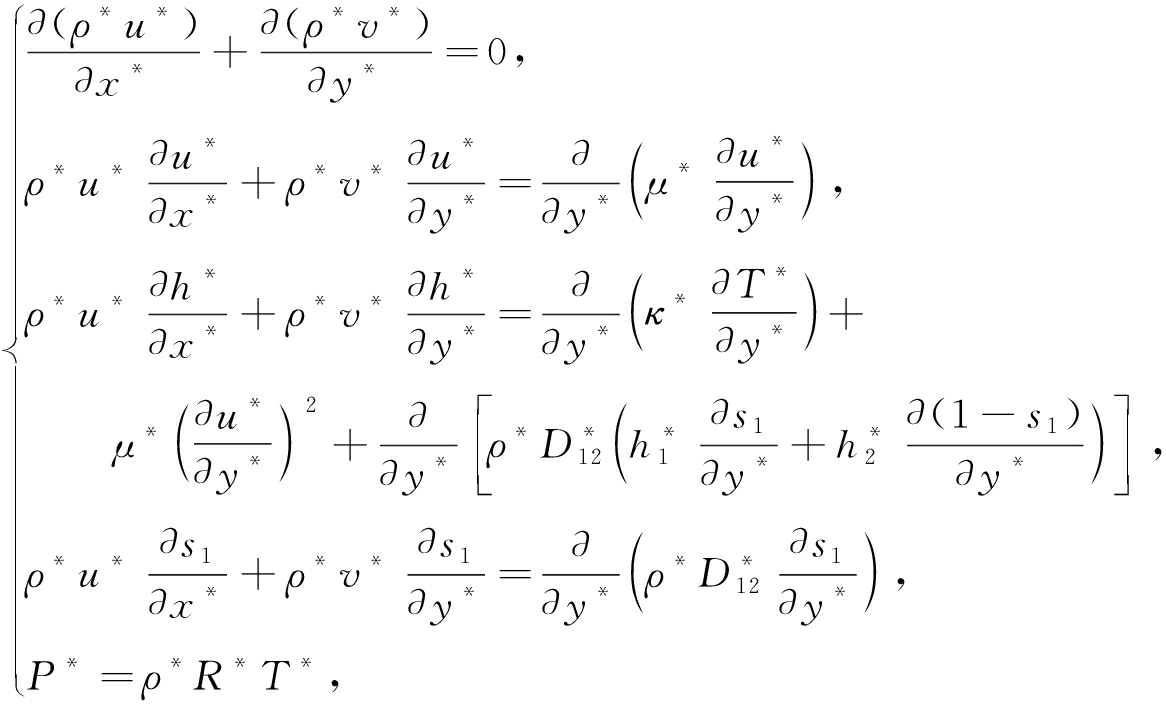
(1)
其中,上标*表示有量纲的量, s 1 表示上层流体的质量分数, h 1 表示上层流体的焓, h 2 表示下层流体的焓, h 表示混合气体的焓, R 为混合气体的气体常数, D 12 为扩散系数 . 以上层流体在无穷远(+∞)的值 ![]() 作为密度、速度、温度和黏性系数在无量纲化时的参数;以涡量厚度作为长度在无量纲化时的参数:
作为密度、速度、温度和黏性系数在无量纲化时的参数;以涡量厚度作为长度在无量纲化时的参数:
(2)
对流Mach数表示为
其中 ![]() 为上层流体的声速,
为上层流体的声速, ![]() 为下层流体的声速 .
为下层流体的声速 .
定义流函数 ψ * ( x * , y * ):
(3)
引入Lees-Dorodnitsyn变换:
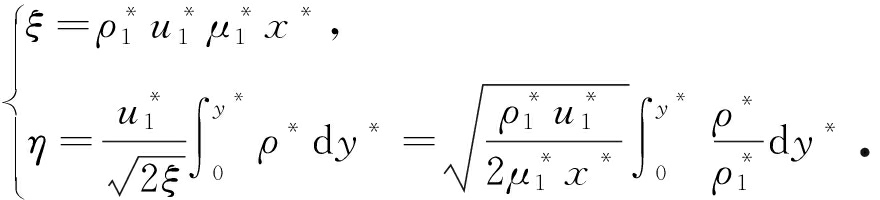
(4)
设无量纲流函数及焓为
(5)
可得相似性解满足的常微分方程
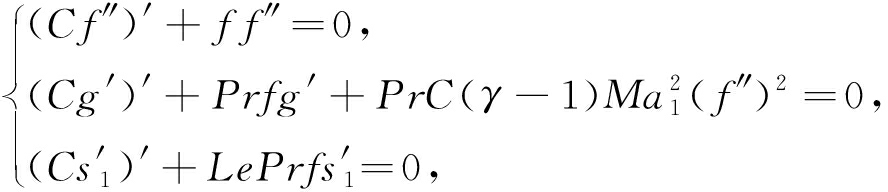
(6)
其中, C 为Chapman-Rubesin因子:
(7)
Le 为Lewis数:
(8)
每种组分的比定容热容和比定压热容为
(9)
c p ,1 = γ 1 c V ,1 , c p ,2 = γ 2 c V ,2 ,
(10)
其中 ![]() 分别表示两个气体的摩尔质量 .
分别表示两个气体的摩尔质量 .
混合气体比热容为
(11)
边界条件满足
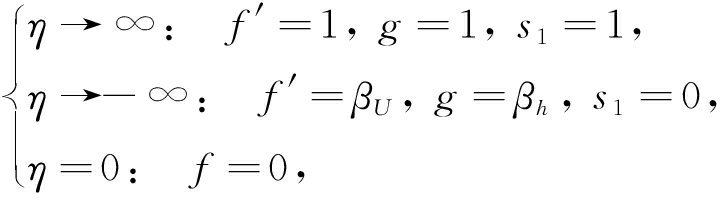
(12)
其中, β U 为下层流体与上层流体的速度比, β h 为下层流体与上层流体的焓比 . 由Lees-Dorodnitsyn反变换有
(13)
y * 无量纲化后有
(14)
将 η 坐标下的物理量转换到 y 坐标下,可以得到用相似性解表示的基本流 .
瞬时流动可表示为基本流和小扰动的和的形式,即
φ = φ 0 + φ ′ .
(15)
将瞬时流动满足的方程减去基本流满足的方程,并略去扰动的二阶及以上高阶项及黏性项可以得到无黏线性扰动方程 . 为了推导方便,用算子L表示:
L(∂ t ,∂ x ,∂ y ,∂ z ) φ ′=0 .
(16)
将扰动表示为行进波的形式:
(17)
其中 α , β , ω 分别为流向波数、展向波数及频率 .
将扰动量代入无黏线性扰动方程,消去变量 ![]() 可以得到用
可以得到用 ![]() 表示的无黏线性稳定性方程:
表示的无黏线性稳定性方程:
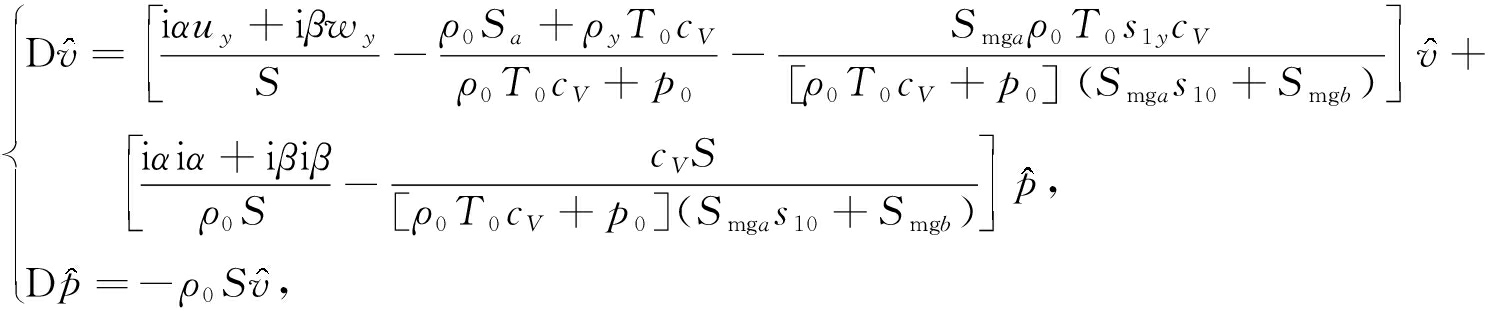
(18)
其中
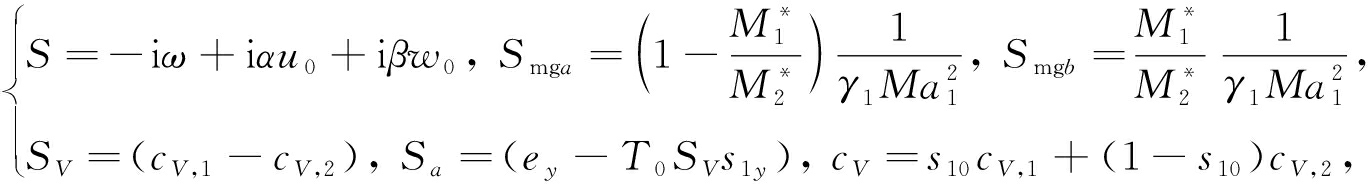
(19)
e y 为气体内能 e 关于 y 的导数 .
采用直接数值模拟的方法验证了程序的正确性 . l atm(1 atm=101.325 kPa)下,温度为300 K时氧气、氢气和氮气的热物性参数见表1 . 考虑等压等温的氧气-氢气混合层,上层流体为氧气,下层流体为氢气,记为O 2 -H 2 . 上层氧气的来流Mach数为4,下层氢气的速度为氧气的一半 . O 2 -H 2 混合层的涡量厚度为0.398 mm . 图2给出了O 2 -H 2 混合层的速度和温度剖面 .
表1 1 atm,300 K时氧气、氢气和氮气的热物性参数
Table 1 Thermal properties of O 2 , H 2 and N 2 at 1 atm and 300 K


(a) 速度和温度剖面 (b) 氧气的质量分数剖面
(a) The profile of the velocity and the temperature (b) The profile of the O 2 mass fraction
图2 混合层的相似性解
Fig. 2 Similar solutions of mixing layers
将相似性解剖面作为基本流,入口处Reynolds(雷诺)数 Re =3.295×10 4 ,在计算域入口添加由稳定性分析给出的特征模态,计算扰动的线性演化 . 图3给出了直接数值模拟的结果与线性稳定性理论的结果的比较,由图可见,它们吻合很好,这也验证了本文计算程序的正确性 .
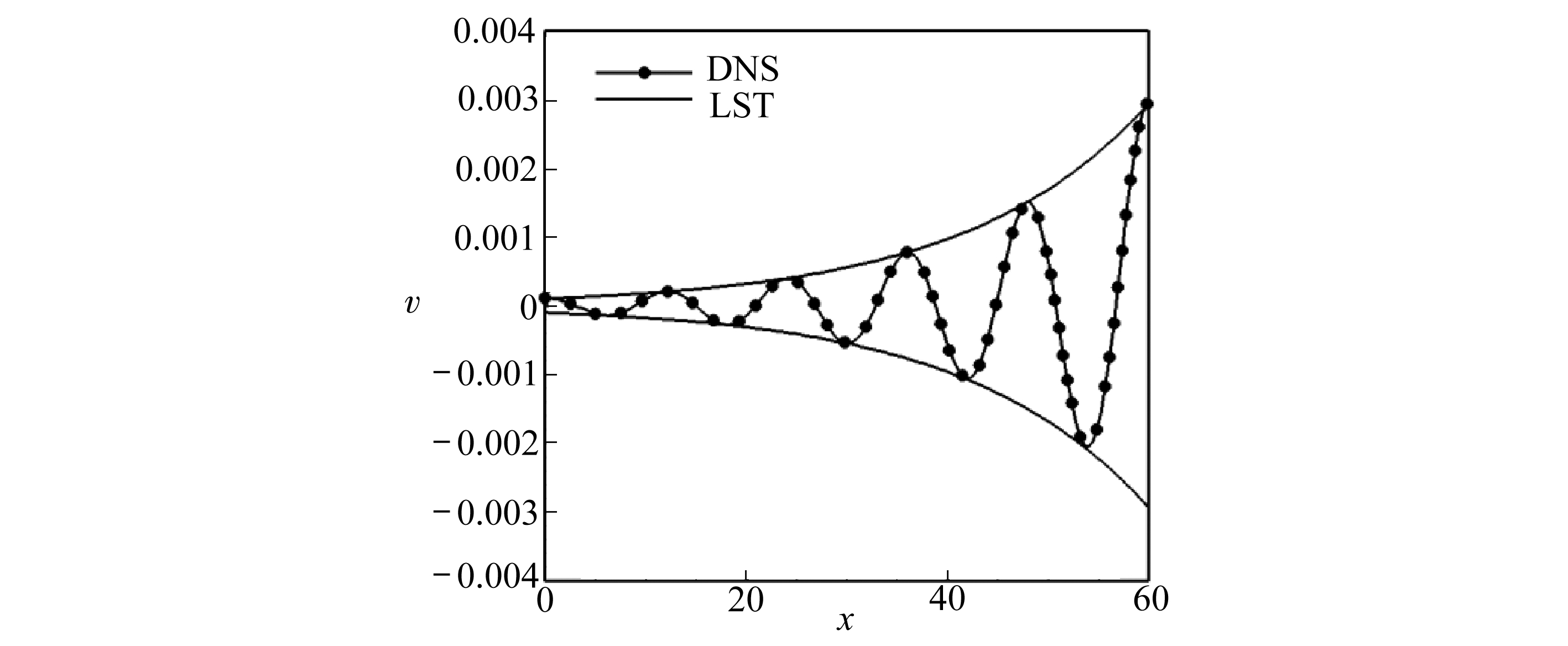
图3 直接数值模拟的结果与线性稳定性理论的比较
Fig. 3 Comparison of the results of DNS and LST
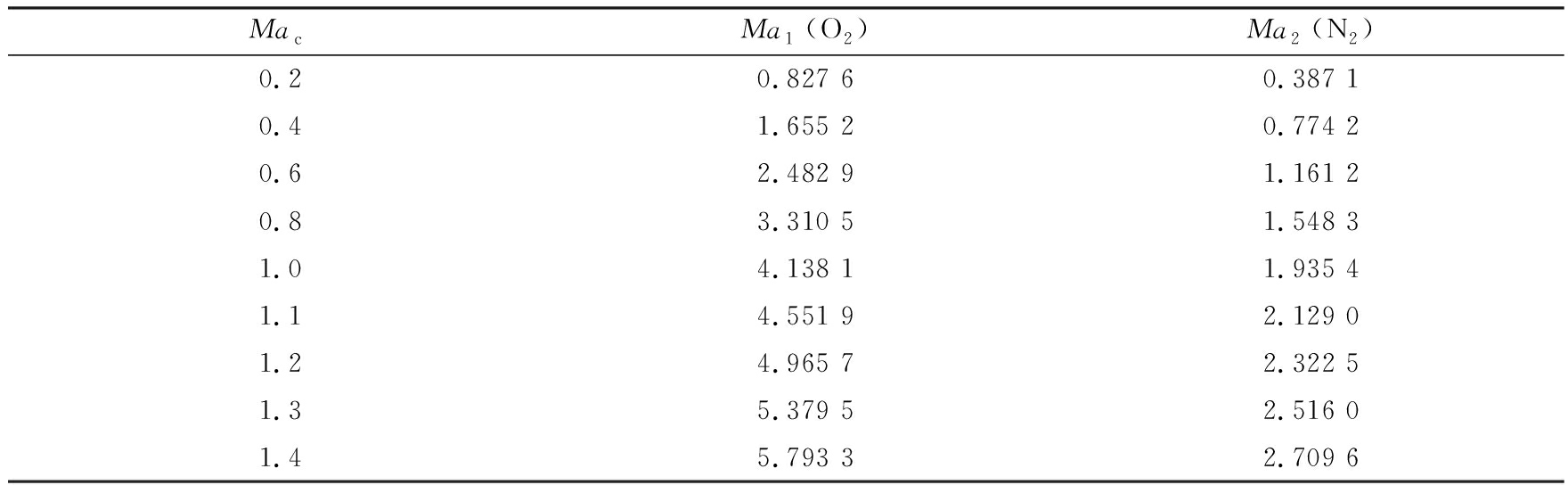
考虑1 atm, 温度300 K时O 2 -N 2 的混合层, N 2 的速度为O 2 速度的一半, 不同对流Mach数 Ma c 下O 2 和N 2 的来流Mach数见表2 . 图4(a)、 (b)分别给出了对流Mach数 Ma c =0.2~1.4时速度和O 2 的质量分数剖面 . 图中箭头所指的方向表示对流Mach数增加 . 可以看出速度和质量分数基本上不随对流Mach数改变 . 图4(c)、(d)分别给出了密度和温度的剖面,随着对流Mach数的增加混合层中心的密度在减小,而温度在增加 . 这是由于随着对流Mach数增加,流体间的剪切增加,导致流体间的黏性耗散增加,耗散的能量使流体的内能增加,从而使温度升高;同时由于上下两层流体是等压的,则密度随着对流Mach数减小 .
表2 O 2 -N 2 混合层对流Mach数及相应的来流Mach数
Table 2 Convective Mach numbers and corresponding Mach numbers of O 2 -N 2 mixing layers
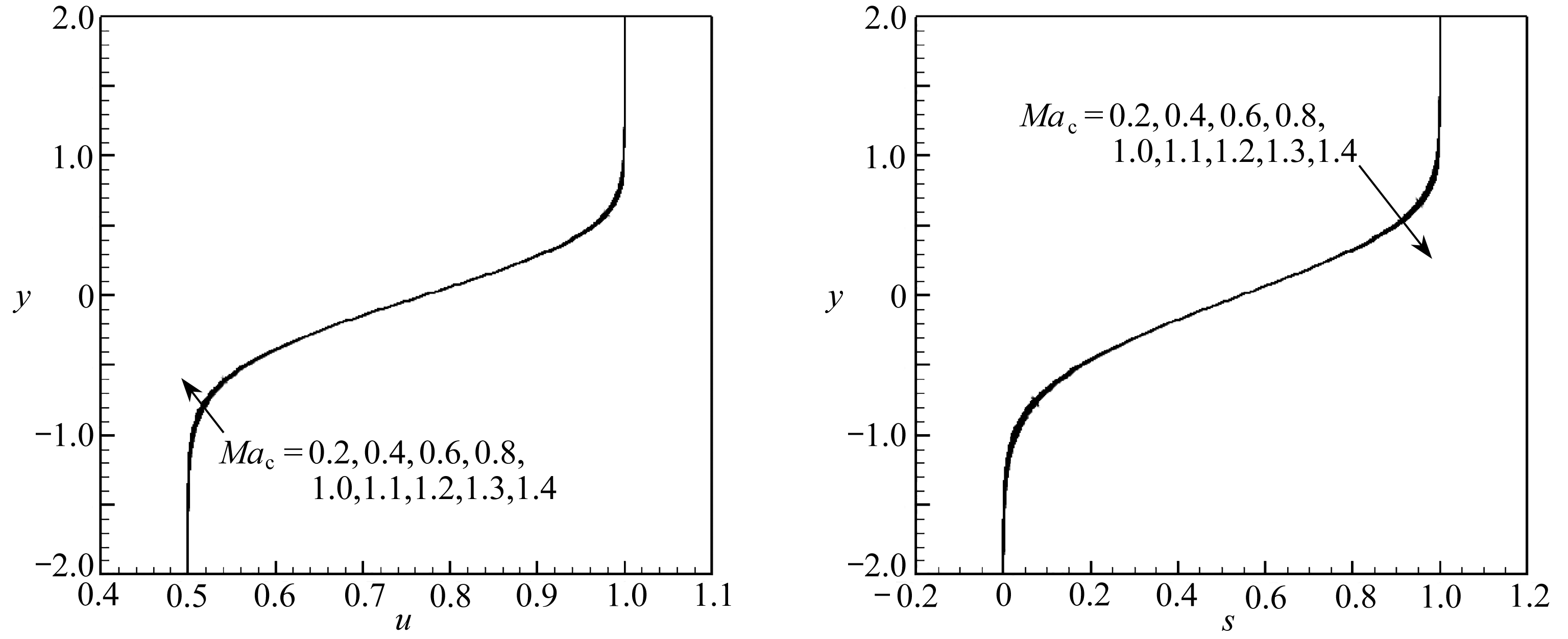
(a) 速度 (b) O 2 的质量分数
(a) Velocity (b) The mass fraction of O 2
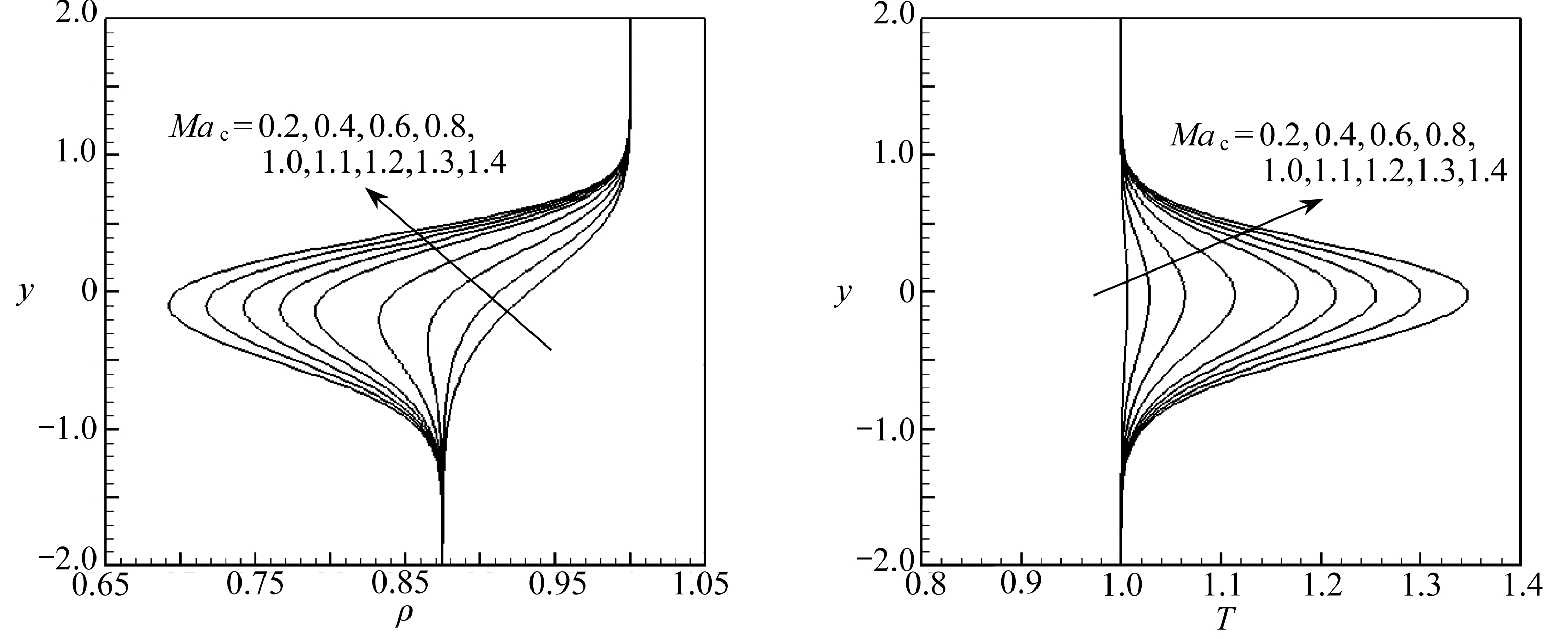
(c)密度 (d)温度
(c) Density (d) Temperature
图4 不同对流Mach数下的相似性解剖面
Fig. 4 Similar solution profile with different convective Mach number
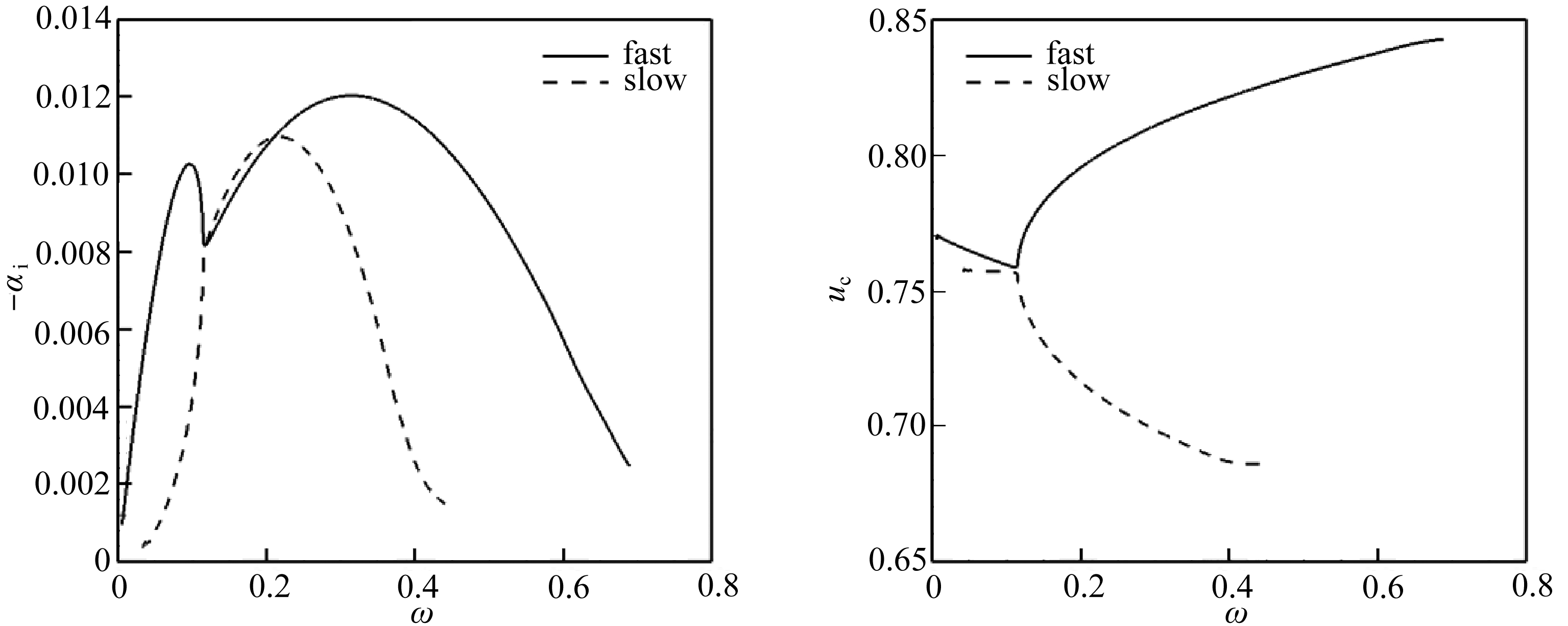
在系统分析O 2 -N 2 混合层稳定性之前,首先对混合层中可能出现的模态进行分类 . 在这里以 Ma c =0.8和 Ma c =1.1说明混合层中存在的扰动模态 . 图5(a)、(b)给出了 Ma c =0.8二维波的增长率和相速度随频率的变化曲线 . 在 Ma c =0.8时,增长率曲线只有一个峰值,这一支模态称为第一模态 . 图6给出了 Ma c =1.1时二维波的增长率随频率的变化 . 在 Ma c =1.1时,同一个频率下存在两个不稳定波,它们的相速度如图6(b)所示 . 相速度较大的一支称为快模态;相速度较小的一支称为慢模态 . 对于快模态,它的增长率曲线存在两个峰值 . 第一个峰值称为第一模态,它对应着 Ma c =0.8时的第一模态;第二个峰值称为第二模态,这是在 Ma c >1时新出现的模态 .
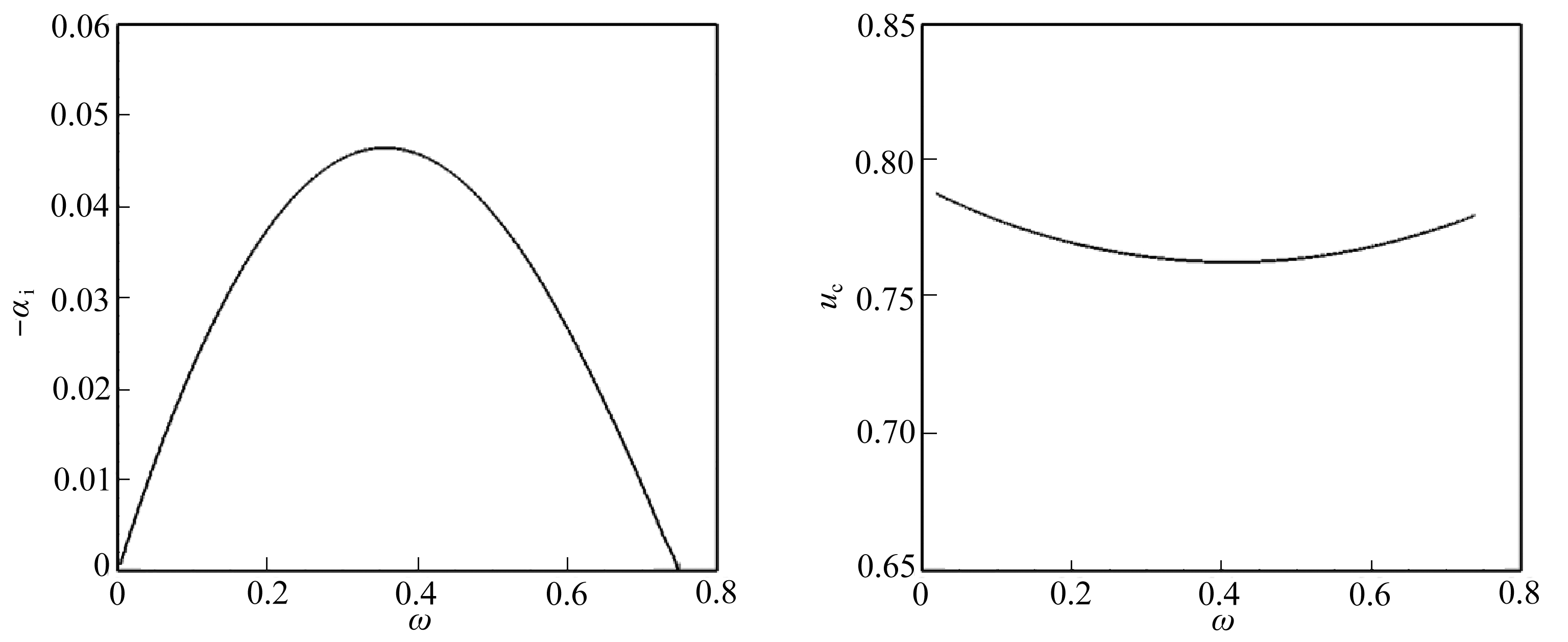
(a) 增长率 (b) 相速度
(a) The growth rate (b) The phase speed
图5 Ma c =0.8,二维波的增长率和相速度曲线
Fig. 5 The growth rate and the phase speed vs. the frequency for 2D disturbance at Ma c =0.8
(a) 增长率 (b) 相速度
(a) The growth rate (b) The phase speed
图6 Ma c =1.1快模态和慢模态的增长率和相速度曲线
Fig. 6 The growth rate and the phase speed vs. the frequency for fast and slow modes at Ma c =1.1
表3给出了 Ma c =0.8, Ma c =1.1频率分别为 ω =0.355, ω =0.095的二维波的特征值 . 这两个频率对应的都是第一模态波,它们的特征函数如图7所示 . 表4给出了 Ma c =1.1时,频率为 ω =0.25时快模态和慢模态二维波的特征值 . 频率 ω =0.25对应着第二模态波,特征函数如图8所示 . 与第一模态相比,第二模态波的特征函数具有辐射特性,其中快模态在慢速流一侧衰减振荡;慢模态在快速流一侧衰减振荡 .
表3 Ma c =0.8,1.1时第一模态的特征值
Table 3 Eigenvalues of the 1st mode at Ma c =0.8,1.1

表4 Ma c =1.1时快模态、慢模态的特征值
Table 4 Eigenvalues of fast and slow modes at Ma c =1.1


(a) Ma c =0.8 (b) Ma c =1.1
图7 不同对流Mach数下扰动压力的特征函数剖面
Fig. 7 Eigenfunction profiles of the disturbance pressure at different convective Mach numbers
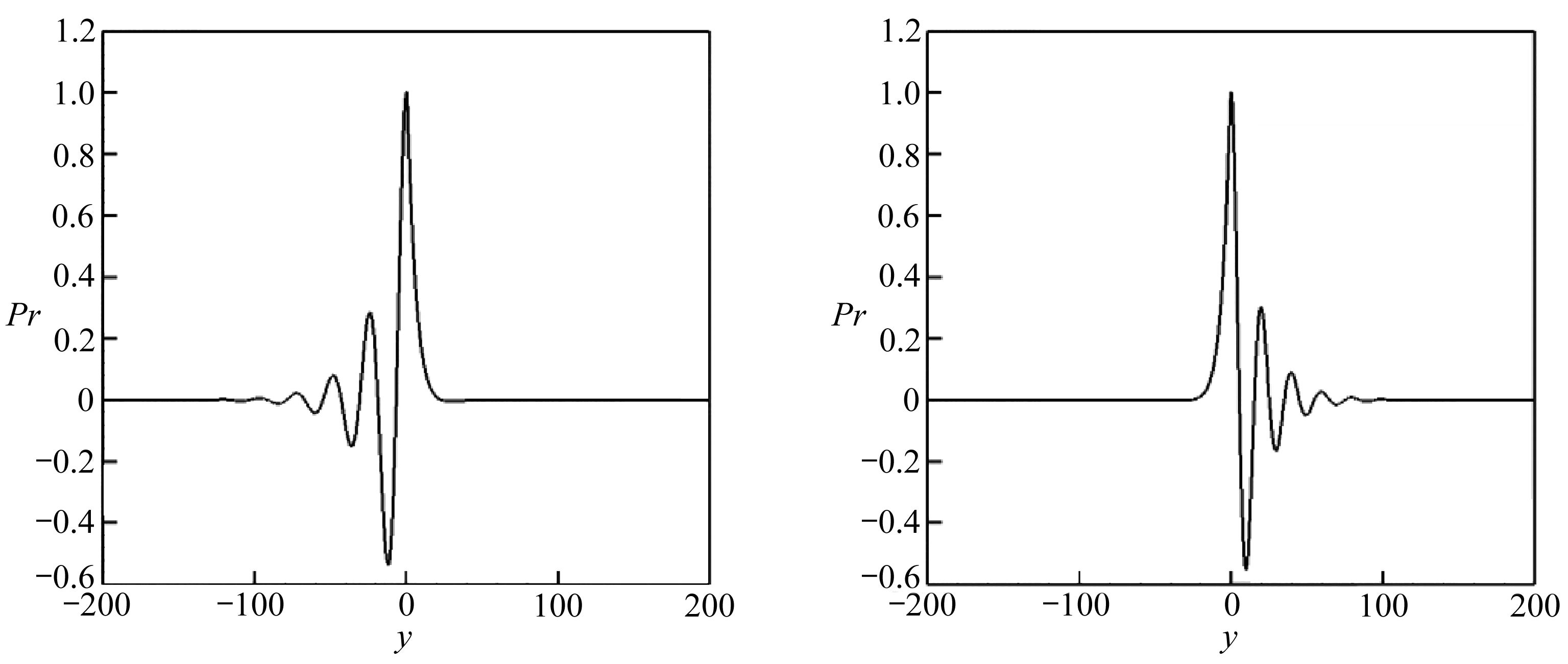
(a) 快模态 (b) 慢模态
(a) The fast mode (b) The slow mode
图8 Ma c =1.1快模态和模态扰动压力的特征函数
Fig. 8 Eigenfunction profiles of the disturbance pressure of fast and slow modes at Ma c =1.1
考虑二维扰动波,即展向波数 β =0 . 图9给出了 Ma c =0.2~0.8时增长率随频率的变化曲线 . 可以看出随对流Mach数增加,可压缩效应增强,第一模态的增长率逐渐减小,频率范围也逐渐减小并向低频段移动 . 图10(a)、(b)给出了 Ma c =1.0~1.4时快模态和慢模态增长率随频率的变化曲线 . 对于快模态,随着可压缩性增强增长率都逐渐减小 . 对于慢模态, Ma c =1.0, Ma c =1.1时,在低频段内的增长率较小,高频段内仍然体现出可压缩效应增强增长率减小的趋势;在 Ma c >1.2时,在整个频率范围内增长率随 Ma c 增加而减小 . 在 Ma c =1.0时,增长率最大的为第一模态,即第一模态占主导地位 . 在 Ma c =1.1时第二模态的增长率超过第一模态的 . 特别地,在 Ma c =1.2的时候第一模态在慢模态这一支模态上,如图10(b)所示 . 在 Ma c =1.3, Ma c =1.4时只有第二模态,第一模态消失 .
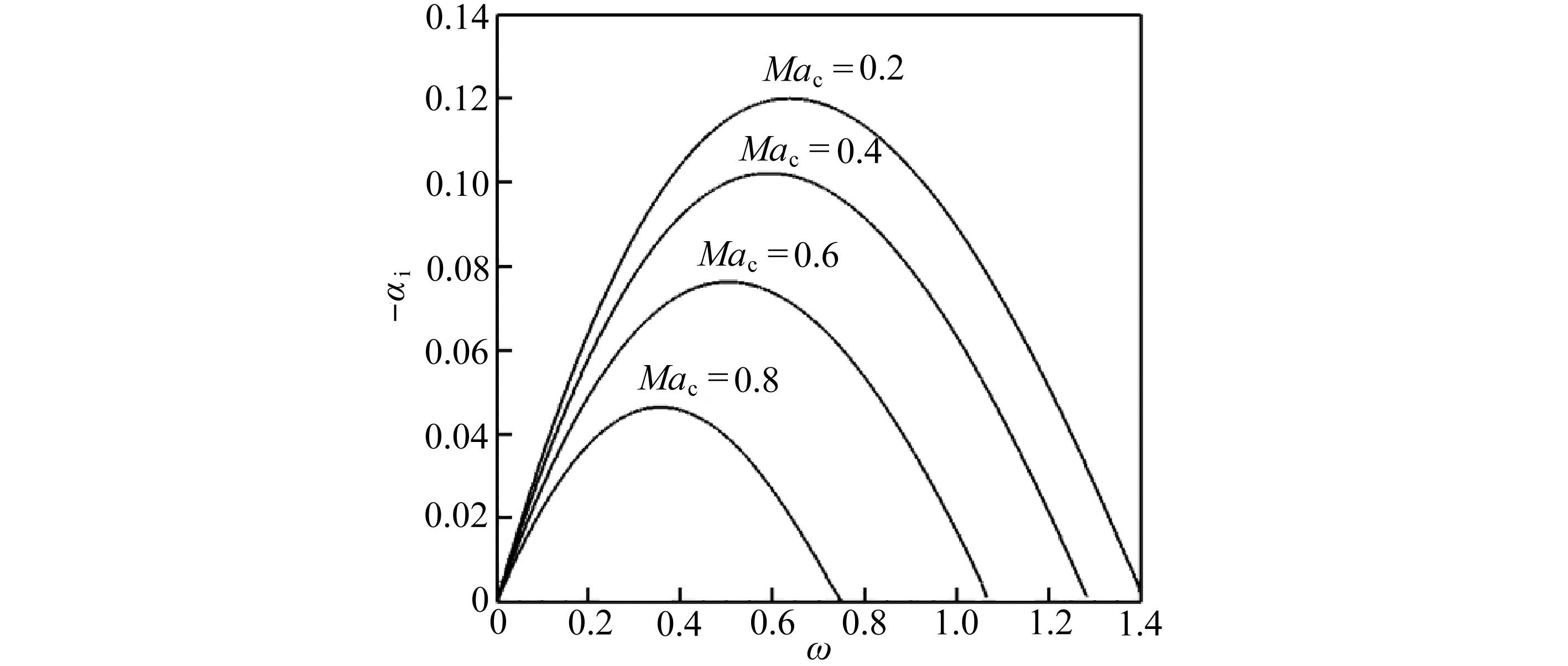
图9 Ma c <1时,不同对流Mach数下的增长率的曲线
Fig. 9 The growth rate at different convective Mach numbers, Ma c <1
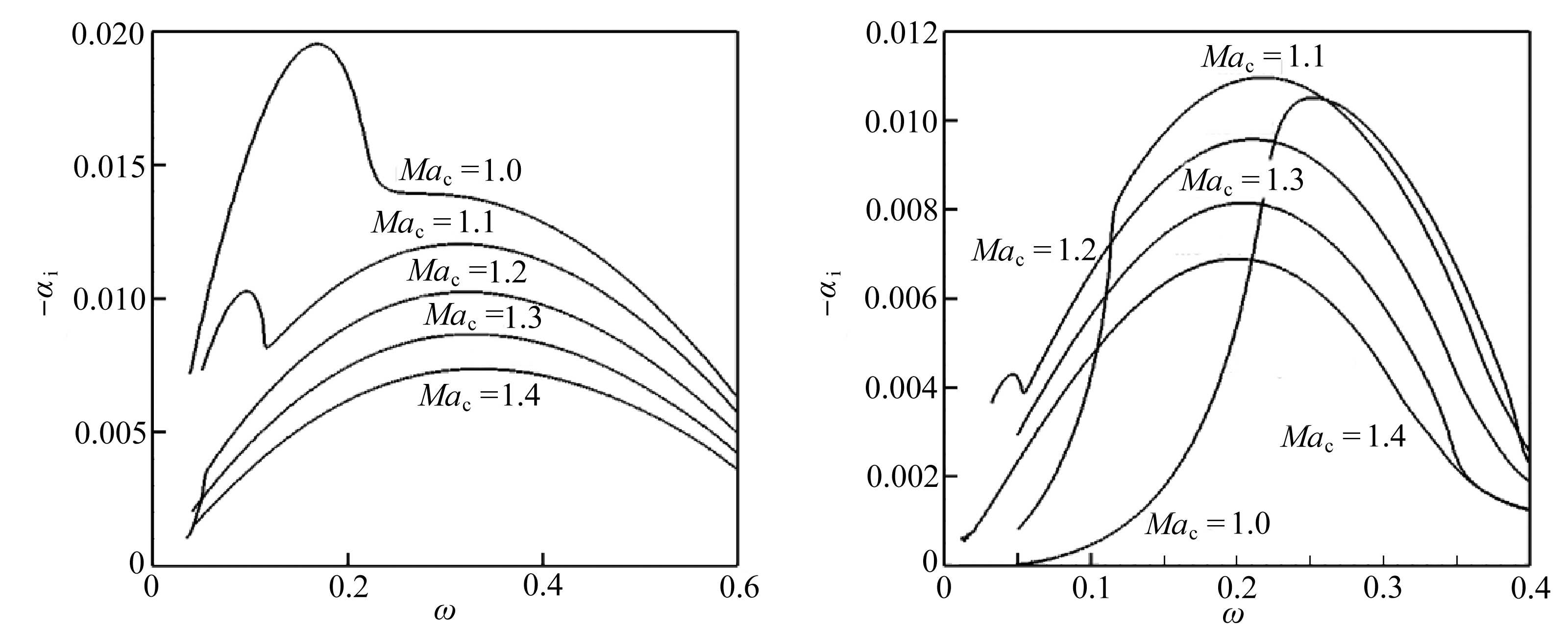
(a) 快模态 (b) 慢模态
(a) The fast mode (b) The slow mode
图10 Ma c ≥1时,不同对流Mach数下快模态和慢模态的增长率的曲线
Fig. 10 The growth rates of fast and slow modes at different convective Mach numbers, Ma c ≥1
为了寻找最不稳定的扰动, 将三维扰动波对增长率的影响考虑进来 . 图11给出了 Ma c =0.2~1.4时第一模态最不稳定波随频率的变化曲线 . 可以看出最大增长率随着对流Mach数增加而减小,并且频率向低频方向移动 . 上文分析中指出只考虑二维波时第一模态在 Ma c >1.2时消失,计算发现在高对流Mach数下第一模态以三维波的形式出现 . 图12给出了不同对流Mach数下最不稳定波的波角随频率的变化曲线 . 可以看出,在 Ma c ≤0.6时,在低频范围内三维波比二维波更不稳定,在高频范围内二维波比三维波更不稳定;在 Ma c >0.6时,在整个频率范围内三维波比二维波更不稳定 . 图13给出了最不稳定波的波角随 Ma c 的变化 . 可以看出,以 Ma c ≈0.6为分界线,在 Ma c <0.6时,最不稳定的扰动波为二维波;在 Ma c >0.6时最不稳定的扰动波是三维波 .

图11 不同对流Mach数下第一模态最大 图12 不同对流Mach数下第一模态波
增长率随频率的变化 最不稳定波的波角随频率的变化
Fig. 11 The maximum growth rates of the 1st mode Fig. 12 The wave angles of the most unstable wave vs. the frequency at different convective of the 1st mode vs. the frequency at Mach numbers different Mach numbers
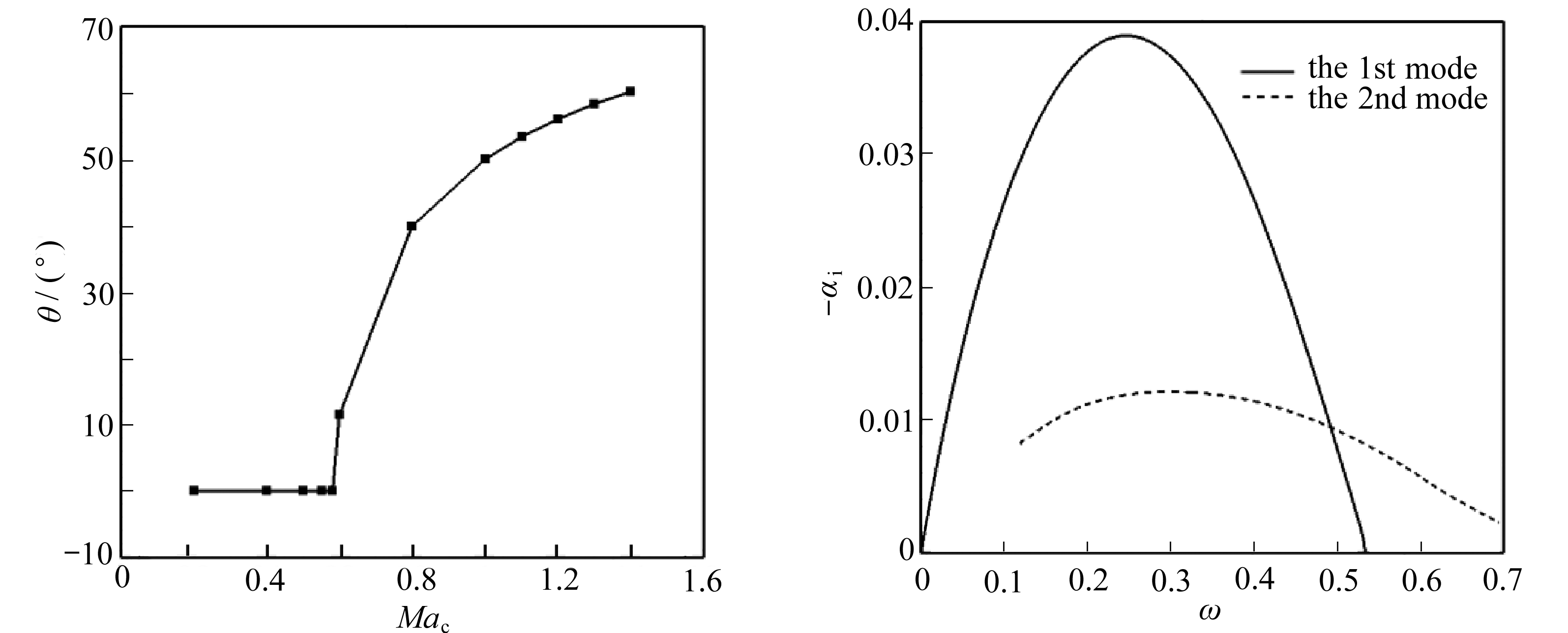
图13 第一模态最不稳定波的波角 图14 Ma c =1.1时第一模态、第二模态最不
随对流Mach数的变化 稳定波增长率随频率的变化
Fig. 13 The wave angle of the most unstable Fig. 14 The growth rates of the most unstable wave of the 1st mode changing with wave of the 1st and 2nd modes at the convective Mach number Ma c =1.1
图14给出了第一模态、第二模态最不稳定波增长率随频率的变化曲线 . 可以看出,第一模态波的最大增长率大于第二模态波的,第二模态波的不稳定频率范围更大 . 图15给出了 Ma c =1.1~1.4时第二模态最大增长率随频率的变化曲线,计算表明随对流Mach数增加,第二模态的增长率在减小 . 图16 给出了不同对流Mach数下第二模态波最不稳定波的波角随频率的变化 . 可以看出,第二模态波在低频范围内三维波是更不稳定的,在高频范围内二维波是更不稳定的 . 图17给出了最不稳定波的波角随 Ma c 的变化 . 在 Ma c >1是最不稳定的扰动波为三维波,且波角随对流Mach数增加而增加 . 第一模态、第二模态最不稳定波的增长率随对流Mach数的变化如图18所示,可以看出在所计算的对流Mach数范围内第一模态的最大增长率始终大于第二模态波的最大增长率 .

图15 不同对流Mach数下第二模态 图16 不同对流Mach数下第二模态波
最大增长率随频率的变化 最不稳定波的波角随频率的变化
Fig. 15 The maximum growth rates of the 2nd Fig. 16 The wave angles of the most unstable wave mode vs. the frequency at different of the 2nd mode vs. the frequency convective Mach numbers at different Mach numbers
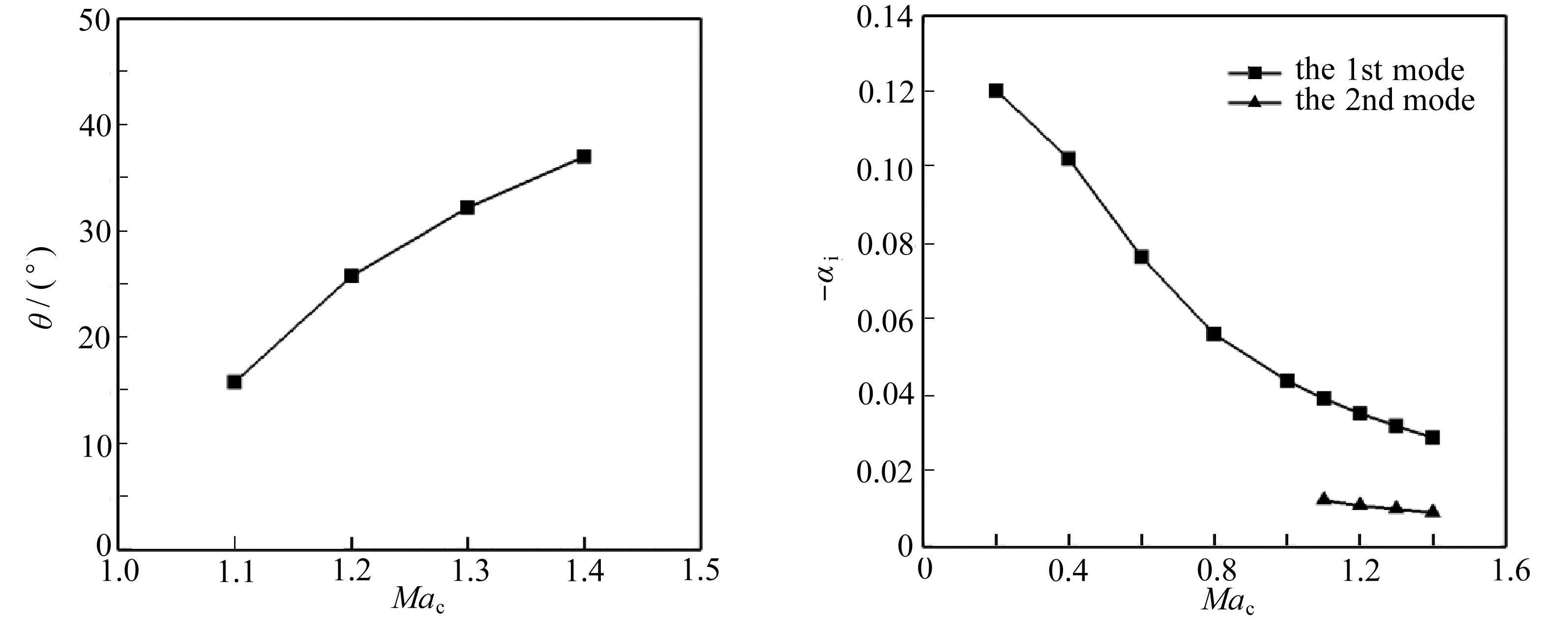
图17 第二模态最不稳定波的波角 图18 第一模态、第二模态最大增长率
随对流Mach数的变化 随对流Mach数的变化
Fig. 17 The wave angle of the most unstable wave Fig. 18 The maximum growth rates of the 1st and of the 2nd mode changing with the 2nd modes at different convective convective Mach number Mach numbers
本文针对O 2 和N 2 组成的混合层流动,给出了二元气体混合层流动的相似性解 . 混合层的速度和质量分数基本不随对流Mach数改变 . 对流Mach数主要影响混合层的密度和温度 . 随着对流Mach数的增加混合层中心的密度逐渐减小,而温度逐渐增加 . 利用线性稳定性理论研究了对流Mach数,二维和三维扰动波对稳定性的影响 . 研究发现在 Ma c >1时出现第二模态,并且同一频率下存在两个不稳定波,按照其相速度大小分别称为快模态和慢模态 . 第二模态扰动波的特征函数具有辐射的特征 . 二维波情况下,在 Ma c >1.2时二维波形式的第一模态消失,第一模态扰动波以三维波的形式出现 . 随着对流Mach数增加第一模态和第二模态的最大增长率逐渐减小,第一模态始终是最不稳定的 . 第一模态在 Ma c <0.6时二维波是最不稳定的,在 Ma c >0.6时三维波是最不稳定的,且随对流Mach数增加波角变大;第二模态最不稳定的扰动波均为三维波 .
参考文献 ( References ):
[1] 何国强, 秦飞, 魏祥庚, 等. 火箭冲压组合发动机燃烧的若干基础问题研究[J]. 实验流体力学, 2016, 30 (1): 1-14.(HE Guoqiang, QIN Fei, WEi Xianggeng, et al. Investigation of several fundamental combustion problems in rocket-based combined-cycle engines[J]. Journal of Experiments in Fluid Mechanics , 2016, 30 (1): 1-14.(in Chinese))
[2] 李睿劬, 马汉东. 高超声速边界层气动光学研究综述[J]. 气体物理, 2015, 10 (2): 17-28.(LI Ruiqu, MA Handong. Summary on hypersonic boundary-layer aero-optical investigations[J]. Physics of Gases , 2015, 10 (2): 17-28.(in Chinese))
[3] 甘才俊, 熊红亮, 马汉东. 可压缩混合层气动光学效应研究[J]. 计算物理, 2010, 27 (1): 65-72.(GAN Caijun, XIONG Hongliang, MA Handong. Aero-optical effect in compressible mixing layer[J]. Chinese Journal of Computational Physics , 2010, 27 (1): 65-72.(in Chinese))
[4] 杨志洋, 赵磊, 罗纪生. 超音速后掠椭圆柱横流定常涡的不稳定特性及转捩预测[J]. 应用数学和力学, 2017, 38 (8): 853-862.(YANG Zhiyang, ZHAO Lei, LUO Jisheng. Instability and transition prediction of stationary crossflow vortices over supersonic swept elliptic cylinders[J]. Applied Mathematics and Mechanics , 2017, 38 (8): 853-862.(in Chinese))
[5] MICHALKE A. On spatially growing disturbances in aninviscid shear layer[J]. Journal of Fluid Mechanics , 1965, 23 (3): 521-544.
[6] BLUMEN W, DRAZIN P G, BILLINGS D F. Shear layer instability of an inviscid compressible fluid: part 2[J]. Journal of Fluid Mechanics , 1975, 71 (2): 305-316.
[7] JACKSON T L, GROSCH C E. Inviscid spatial stability of a compressible mixing layer[J]. Journal of Fluid Mechanics , 1989, 217 : 609-637.
[8] 罗纪生, 吕祥翠. 超音速混合层稳定性分析及增强混合的研究[J]. 力学学报, 2004, 36 (2): 202-207.(LUO Jisheng, LÜ Xiangcui. Investigation on stability of 3-D supersonic mixing layer and method of enhancing the mixing[J]. ACTA Mechanica Sinica , 2004, 36 (2): 202-207.(in Chinese))
[9] 王强, 傅德薰, 马延文. 可压缩平面混合层稳定性数值计算[J]. 计算物理, 1997, 14 (4/5): 413-416.(WANG Qiang, FU Dexun, MA Yanwen. A numerical investigation of the stability of compressible plane mixing layers[J]. Chinese Journal of Computational Physics , 1997, 14 (4/5): 413-416.(in Chinese))
[10] 杨武兵, 庄逢甘, 沈清. 可压缩混合层流动近十年研究进展[J]. 力学进展, 2008, 38 (1): 62-76.(YANG Wubing, ZHUANG Fenggan, SHEN Qing. Advances in the study of compressible mixing layer in recent ten years[J]. Advances in Mechanics , 2008, 38 (1): 62-76.(in Chinese))
[11] 沈清, 袁湘江, 王强, 等. 可压缩边界层与混合层失稳结构的研究进展及其工程应用[J]. 力学进展, 2012, 42 (3): 252-261.(SHEN Qing, YUAN Xiangjiang, WANG Qiang, et al. Review on the instability structure in compressible boundary layers and mixing layers and its application[J]. Advances in Mechanics , 2012, 42 (3): 252-261.(in Chinese))
[12] KOZUSKO F, LASSEIGNE D G, GROSH C E, et al. The stability of compressible mixing layers in binary gases[J]. Physics of Fluids , 1996, 8 (7): 1954-1963.
[13] LEONARDO S, MARCIO T M. Spatial and temporal linear stability analysis of binary compressible shear layer[C]// AIAA 38 th Fluid Dynamics Conference and Exhibit . Seattle, Washington, USA, 2008.
[14] OKONG N A, BELLAN J. Real gas effects on mean flow and temporal stability of binary-species mixing layers[J]. AIAA Journal , 2003, 41 (12): 2429-2443.
[15] FEDIOUN I, LARDJANE N. Temporal linear stability analysis of three-dimensional compressible binary shear layers[J]. AIAA Journal , 2005, 43 (1): 111-123.
[16] MENDONCA M T. Linear stability analysis of binary compressible mixing layers modified by a jet or a wake deficit[C]//52 nd Aerospace Sciences Meeting . 2014: 1444. DOI: 10.2514/6.2014-1444.
[17] SHIN D S, FERZIGER J H. Linear stability of the reacting mixing layer[J]. AIAA Journal , 1991, 29 (10): 1634-1642.
[18] DAY M J, REYNOLDS W C, MANSOUR N N. The structure of the compressible reacting mixing layer: Insights from linear stability analysis[J]. Physics of Fluid , 1998, 10 (4): 993-1007.
GAO Jun 1 , LI Jia 2 , LIU Fengjun 3 ,SHI Xiaotian 1 , YUAN Xiangjiang 1 ①
(1. China Academy of Aerospace Aerodynamics , Beijing 100074, P . R . China ,2. Foundation Department , Tangshan College , Tangshan , Hebei 063000, P . R . China ; 3. Beijing Power Machinery Institute , Beijing 100074, P . R . China )
Abstract : For the mixing layer flow composed of oxygen and nitrogen, the linear stability analysis was utilized to investigate the stability characteristics. The basic flow profile of the binary gas mixing layers was obtained from the similar solution. The effects of the convective Mach number on the similar solution were firstly investigated. Then, the influences of the convective Mach number, 2D and 3D waves on the stability were studied. The results of linear stability indicate that, the maximum growth rate of the 1st mode is always larger than that of the 2nd mode, and the maximum growth rates of the 1st and 2nd modes are suppressed with the increasing convective Mach number.
Key words: linear stability; mixing layer; binary gas; convective Mach number; similar solution
Foundation item: The National Natural Science Foundation of China(51476152; 11302213)
ⓒ 应用数学和力学编委会,ISSN 1000-0887
文章编号 : 1000-0887(2018)09-1030-13
高军(1985—),男,工程师,博士(E-mail: gaojun856@163.com);
时晓天(1981—),男,研究员,博士(通讯作者. E-mail: xxtshi@163.com).
基金项目 : 国家自然科学基金(51476152;11302213)
作者简介 :
* 收稿日期 : 2018-02-27;
修订日期: 2018-05-16
文献标志码: A
DOI: 10.21656/1000-0887.390064
中图分类号 : O357.4
①引用本文 / Cite this paper: 高军, 李佳, 刘凤君, 时晓天, 袁湘江. 二元气体混合层的稳定性分析[J]. 应用数学和力学, 2018, 39 (9): 1030-1042.GAO Jun, LI Jia, LIU Fengjun, SHI Xiaotian, YUAN Xiangjiang. Stability analysis of binary gas mixing layers[J]. Applied Mathematics and Mechanics , 2018, 39 (9): 1030-1042.