杨 墨, 富 娜
(西南交通大学 数学学院, 成都 610031)
摘要 : 研究了一类动态边界上的随机波动方程 . 通过建立一种分解技术,证明了方程随机吸引子的存在性 . 分解同时表明,该吸引子上的点(或者解)一定满足某种稳定的边界条件 . 最后,证明了吸引子的结构与分解所得的静态边界上波动方程的随机吸引子相同 .
关 键 词 : 动态边界条件; 波动方程; 随机吸引子
设( Ω ,F, P )是概率空间,{ W ( t ), t ∈ R }是一维的标准Brown(布朗)运动 . 考虑如下动态边界上的随机波动方程:
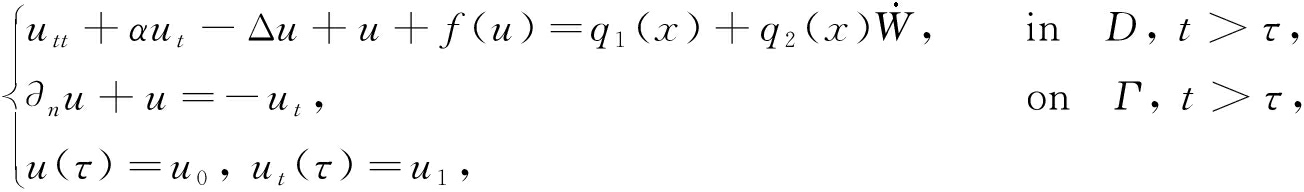
(1)
其中 ![]() 是Brown运动的衍生物
是Brown运动的衍生物 ![]() 为白噪声), D 是 R 3 上的一个具有光滑边界 Γ 的有界区域,∂ n 表示边界 Γ 上的单位外法向量, αu t 为阻尼项 .
为白噪声), D 是 R 3 上的一个具有光滑边界 Γ 的有界区域,∂ n 表示边界 Γ 上的单位外法向量, αu t 为阻尼项 .
设 f : R → R , F ( s )= ![]() f ( η )d η ,且 f , F 满足如下条件:
f ( η )d η ,且 f , F 满足如下条件:
(2)
并且存在 c 1 , c 2 >0,使得
(3)
| f ′( s )|≤ c 2 (1+| s | 2 ) .
(4)
为不失一般性,假设 q i ∈ L 2 ( D )( i =1,2), q 2 | Γ =0 .
吸引子可以描述方程解的长时间行为并且刻画系统的最终状态,其本身具有不变性与吸收性,Temam在文献[1]中详细地介绍了吸引子的定义与性质 . 对于静态边界条件的许多偏微分方程,其解的渐近行为已经得到了很多学者的深入研究,详见文献[2-5] . 当系统边界为动态时,文献[6-7]中分别研究了抛物型方程与Cahn-Hilliard方程的全局吸引子 . 但对于动态边界上的波动方程来说,是否可以找到一种普遍的方法来研究吸引子的存在性呢?事实上,由于吸引子本身的性质就意味着稳定性,某种意义上说明动态边界条件下吸引子中的点(或者解)也应该是稳定的,而不是动态的 . 于是认为,如果方程(1)的随机吸引子存在,那么吸引子上的点也应当满足如下静态边界上的随机波动方程:
(5)
这个想法给予我们处理动态边界问题一种新的方法,即将方程(1)分解为两个方程,其中一个带有静态边界条件,另一个则带有动态边界条件 . 同时,也将揭示方程(1)和(5)两个系统吸引子之间的关系 .
本文结构安排如下:在第1节,证明方程(1)确定了一个随机动力系统(以后简写为RDS)以及解的存在唯一性 . 在第2节,得到解的有界性 . 在第3节,证明随机吸引子的存在性 . 最后,给出随机吸引子的结构 .
在本节,将证明系统(1)可以确定一个随机动力系统 .
记 L 2 ( D )空间中的内积和范数分别为(·,·) 0 和‖ · ‖ 0 ,且对∀ u , v ∈ L 2 ( D ),有
对∀ u , v ∈ L 2 ( Γ ),定义 L 2 ( Γ )上的内积和范数如下:
记Sobolev空间 H 1 ( D )上的内积和范数为(·,·) 1 和‖ · ‖ 1 ,且对∀ u , v ∈ H 1 ( D ),有
( u , v ) 1 =( u , v ) 0 +(  u ,
u ,  v )
v ) ![]()
下面引入空间:
E = H 1 ( D )× L 2 ( D ),
并且对 E ,赋予其内积和范数分别为
对∀ ![]() 成立 .
成立 .
设 v = u t ,那么方程(1)等价于如下的一阶方程组:
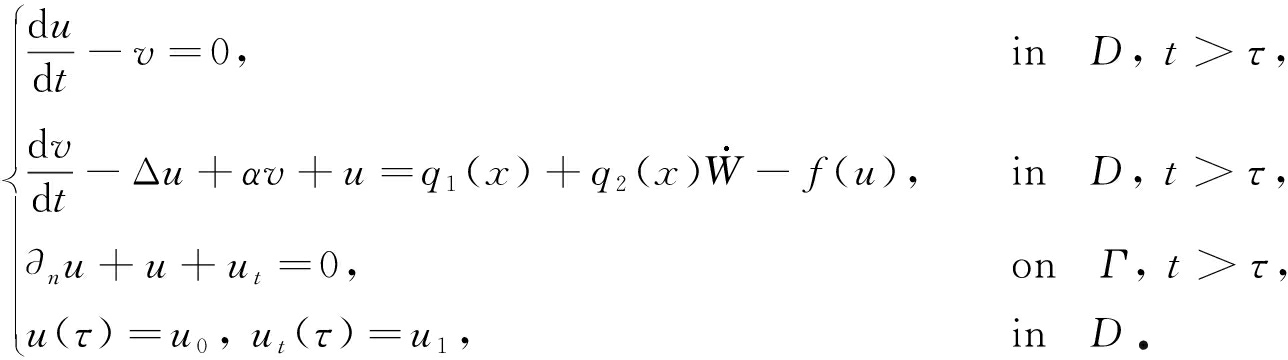
(6)
定义算子 L : D ( L )⊂ E ![]() E ,其中
E ,其中
D ( L )={( u , v ):Δ u ∈ L 2 ( D ), ∂ n u + v + u | Γ =0},
则有
记
ϑ ![]() ϑ
ϑ ![]()
那么方程(6)可以写成下面的形式:
![]() ϑ= G (ϑ
ϑ= G (ϑ ![]()
(7)
通过保测度变换 ![]() 则式(7)等价于如下系统:
则式(7)等价于如下系统:
(8)
其中
接下来研究算子 L 的性质 .
引理1 算子 L 满足
(a) 对任意的 θ ∈ D ( L ),有( L ( θ ), θ ) E ≥0;
(b) I + L 的值域为 E ,其中 I 为恒等算子;
(c) - L 的预解集包含 R + =[0,+∞);
(d) 对任意 λ ≥0,有 ![]()
证明 由
可得(a)和(c) .
对 λ ≥0以及 φ =( u , v ) T ∈ D ( L ),有
可知
‖( λI + L ) φ ‖ E ≥ λ ‖ φ ‖ E ,
故(d)成立 .
结论(b)可参见文献[8-10] .
由文献[11]中的性质3.6以及引理1的(a)、(b)可知,式(8)中的算子 L 是稠密的(即 ![]() 又由引理1的(c)、(d)以及Hille-Yosida定理,容易验证知- L 生成 E 上的 C 0 半群e - Lt , t ≥0 . 由条件(2)~(4),不难验证
又由引理1的(c)、(d)以及Hille-Yosida定理,容易验证知- L 生成 E 上的 C 0 半群e - Lt , t ≥0 . 由条件(2)~(4),不难验证 ![]() 是关于
是关于 ![]() 局部Lipschitz(利普希茨)连续的 . 由发展方程解的局部存在唯一性理论 [12] ,对任意的
局部Lipschitz(利普希茨)连续的 . 由发展方程解的局部存在唯一性理论 [12] ,对任意的 ![]() 式(8)都存在唯一的柔和解:
式(8)都存在唯一的柔和解:
这里只得到解的局部存在性,对于解的整体存在性可由下一节中的引理3得到 . 于是映射
![]()
![]()
![]()
![]() E
E
定义了一个关于式(8)的随机动力系统 .
由等价关系可知
S ( t , θ τ ω ): ϑ( τ ) ![]() ϑ( t ), E
ϑ( t ), E ![]() E
E
是由式(7)所确定的一个连续的随机动力系统 .
在本节,将给出RDS S ( t , θ τ w )在 E 上的吸收性 .
令
φ 1 = u , φ 2 = u t + εu - q 2 W ,
其中
那么方程(1)可改写为
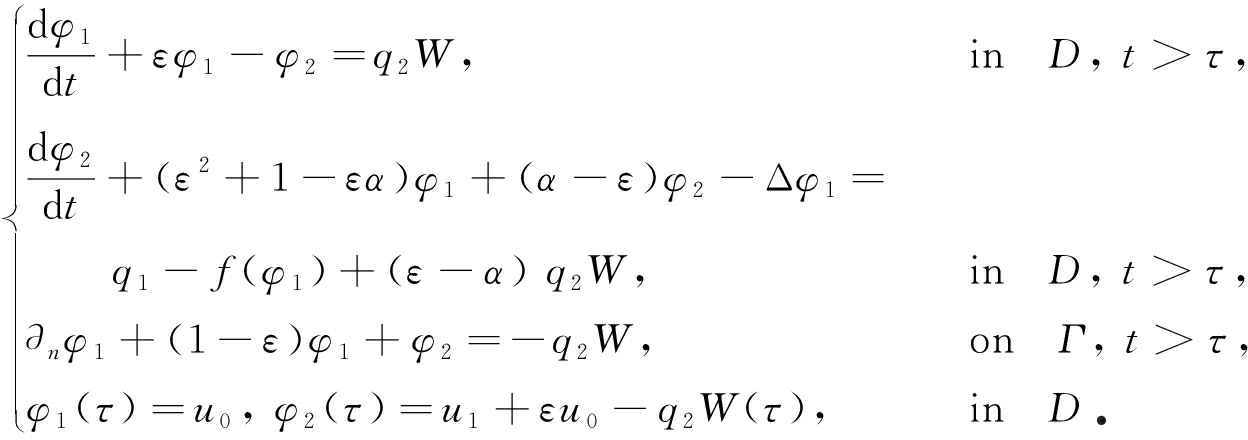
(9)
设
则方程(9)可写成
(10)
容易验证映射
![]()
![]()
![]()
![]() E
E
是由式(10)所生成的RDS .
由于
其中 R ε :( u , z ) T ![]() ( u , z + εu ) T 是 E 上的一个同构,所以 S ε ( t , θ τ ω )是
( u , z + εu ) T 是 E 上的一个同构,所以 S ε ( t , θ τ ω )是 ![]() 的一个同构 . 同时由于式(8)和式(7)的等价关系,只研究式(7)的等价系统(10)以及它的RDS S ε ( t , θ τ ω ) . 为了后面的计算方便,先介绍下面的引理 .
的一个同构 . 同时由于式(8)和式(7)的等价关系,只研究式(7)的等价系统(10)以及它的RDS S ε ( t , θ τ ω ) . 为了后面的计算方便,先介绍下面的引理 .
引理2 对于任意的 ![]() 有
有
证明 由
![]()
 φ 1 ,
φ 1 ,  φ 2 ) 0 -〈 φ 1 , φ 2 〉+
φ 2 ) 0 -〈 φ 1 , φ 2 〉+
![]()
 φ 1 ,
φ 1 ,  φ 2 ) 0 +( ε 2 - εα )( φ 1 , φ 2 ) 0 -〈 φ 1 , φ 2 〉-
φ 2 ) 0 +( ε 2 - εα )( φ 1 , φ 2 ) 0 -〈 φ 1 , φ 2 〉-
以及Green(格林)第二公式,可知
那么
ε ‖ φ 1 ‖ ∂ ‖ φ 2 ‖ ∂ - ε ( α - ε )‖ φ 1 ‖ 0 ‖ φ 2 ‖ 0 ≥
由于
ε 2 ≤2 ε , ε 2 α 2 ≤ ε ( α -3 ε ),
于是有
以及
证毕 .
引理3 对于 E 中任意的有界集 B ,都存在一个缓增的随机变量 C 1 ( ω )>0和 T 0 ( B , ω ),对 τ ≥ T 0 ( ω )以及ϑ(- τ )∈ B ,有
‖ S ε (0, θ - τ ω )ϑ(- τ )‖ E ≤ C 1 ( ω ) .
证明 对式(10)的两边分别乘以 ![]() 并作内积,得
并作内积,得
(11)
由引理2,可知
(12)
通过对式(12)进行整理,得到
( q 2 W , φ 1 ) 1 +( q 1 , φ 2 ) 0 -( α - ε )( q 2 W , φ 2 ) 0 .
由条件(2)和(3),存在某个常数 k >0使得
(13)
(14)
通过条件(4)、Hölder不等式以及Young不等式,可知
(15)
再利用式(13)、(15)以及Cauchy-Schwartz不等式,可得
εk + C ( ε )(| W | 4 +| W |),
也就是说
C ( ε )(| W | 4 +| W |),
其中 κ =min{1, c 1 } .
由Gronwall不等式,得到
C ( ε )(| W | 4 +| W |)
)e - εκ ( t - s )/2 d s ,
由式(14),可知
设 ![]() 由式(3)以及Sobolev嵌入定理,必定存在 K ( r )>0使得
由式(3)以及Sobolev嵌入定理,必定存在 K ( r )>0使得
故
C ( ε )(| W | 4 +| W |)
)e - εκ ( t - s )/2 d s , t ≥- τ .
选取
C ( ε )(| W | 4 +| W |)
)e - εκ ( t - s )/2 d s ,
不难验证 C 1 ( θ t ω )关于时间 t 是缓增的 . 证毕 .
由引理3,可知存在一个关于RDS S ε (0, θ τ ω )的半径为 r 0 的吸收集 B 0 ,使得
S ε ( t , θ - τ ω ) B 0 ⊆ B 0 , t ≥ τ ,
其中 ![]()
本节将证明RDS S ε ( t , θ τ ω )的随机吸引子存在性 .
设 u = v + w ,则式(1)可分解为如下两个系统:
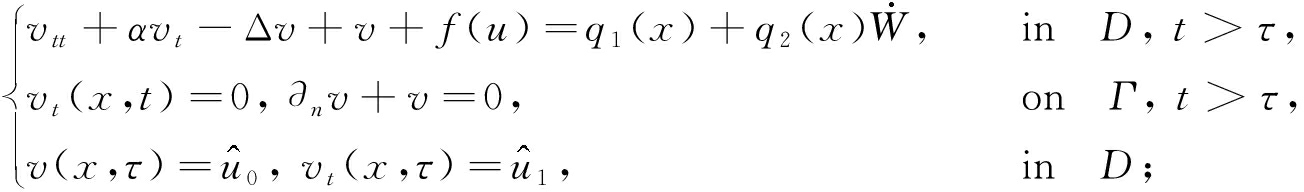
(16)
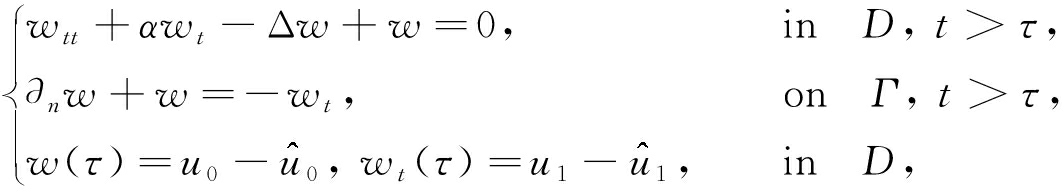
(17)
其中 ![]() 且
且 ![]()
令
ϑ ![]()
![]() ϑ
ϑ ![]()
于是可以将式(17)改写为
![]() ϑ b )=0 .
ϑ b )=0 .
(18)
类似地,不难验证对任意的ϑ b ( τ )∈ E ,式(18)存在唯一的解ϑ b ( t )∈ E ,且
![]() ϑ b ( τ )
ϑ b ( τ ) ![]() ϑ b ( t ), t ≥ τ
ϑ b ( t ), t ≥ τ
是由式(18)所确定的连续RDS .
引理4 对 E 中的任意有界集 B ,有
证明 对式(18)两边分别乘以ϑ b ,且由于
![]() ϑ b ),ϑ
ϑ b ),ϑ ![]()
![]() ϑ
ϑ ![]()
![]() ϑ
ϑ ![]()
不难得出
![]() ϑ
ϑ ![]() ϑ
ϑ ![]()
再利用Gronwall引理,可知
‖ϑ ![]() ϑ
ϑ ![]()
证毕 .
记
ϑ ![]()
![]() ϑ
ϑ ![]()
可将式(16)改写为
![]() ϑ
ϑ ![]()
(19)
易知映射
![]() ϑ a ( τ )
ϑ a ( τ ) ![]() ϑ a ( t ), t ≥ τ
ϑ a ( t ), t ≥ τ
是一个连续的RDS .
接下来将给出紧性的证明 .
引理5 对于任意的 ![]() ⊆
⊆ ![]() 在 E 中预紧 .
在 E 中预紧 .
证明 做变换 ![]()
设
映射
![]()
![]() θ a ( t ), E
θ a ( t ), E ![]() E .
E .
因为 ![]() 其中 R α /2- ε :( v , z ) T
其中 R α /2- ε :( v , z ) T ![]() ( v , z +( α /2- ε ) v ) 是 E 上的同构,则
( v , z +( α /2- ε ) v ) 是 E 上的同构,则 ![]() 等价于
等价于 ![]() 于是只需要证明
于是只需要证明 ![]() 的渐近紧性 .
的渐近紧性 .
设 ![]() 为 B 0 中的一族序列,且 t j →∞ . 下面将证明序
为 B 0 中的一族序列,且 t j →∞ . 下面将证明序 ![]() 在 E 中是预紧的 .
在 E 中是预紧的 .
由于证明需要,引入如下的辅助函数:
![]()

![]()
通过简单的计算,可得
令
于是有
(20)
由引理3以及引理4可知, ![]() 在 E 中是有界的 . 又由于
在 E 中是有界的 . 又由于 ![]() 与
与 ![]() 之间具有等价性,于是
之间具有等价性,于是
![]() ⇀ θ * .
⇀ θ * .
(21)
类似地,对于每个 T ∈ N ,序 ![]() 有弱收敛子列,且
有弱收敛子列,且
![]() ⇀
⇀ ![]()
(22)
其中 ![]() 再由式(21)和(22),可得
再由式(21)和(22),可得 ![]()
对式(20)乘以e αt ,以 ![]() 为初值进行积分,有
为初值进行积分,有
(23)
这里取
对于每个 ![]() 在 E 中都弱收敛于
在 E 中都弱收敛于 ![]() 这就意味着
这就意味着 ![]() 在 H 1 ( D )中弱收敛于
在 H 1 ( D )中弱收敛于 ![]() 设
设 ![]()
因此,
对 t ≥0成立 .
强收敛性允许我们利用控制收敛定理,得到(见文献[13]中的命题4.2)
类似地,有
由引理4,不难得到映射
R 1 : u ∈ H 1 ( D ) ![]()
![]()
的序列弱连续性(见文献[14]中的定理3.6),于是有
由式(23),可知
(24)
另一方面,对式(20)以 ![]() 为初值进行积分,有
为初值进行积分,有
I (ϑ ![]()
(25)
通过式(24)和(25)可以发现
且当 T →+∞,可知 ![]() 又因为范数的弱下半连续性,容易得出
又因为范数的弱下半连续性,容易得出 ![]() 因此
因此 ![]() 再考虑到式(21)中的弱收敛性,可知
再考虑到式(21)中的弱收敛性,可知 ![]() 在 E 中强收敛于 θ * . 证毕 .
在 E 中强收敛于 θ * . 证毕 .
由引理4以及引理5,可得RDS S ( t , θ τ ω )随机吸引子的存在性 .
定理1 RDS S ( t , θ τ ω ) 在 E 中有一个紧的随机吸引子A( ω ),且满足
S ( t , θ τ ω )A( θ τ ω )=A( θ t ω ), t ≥ τ .
由于RDS S ( t , θ τ ω )与RDS S ε ( t , θ τ ω )之间的等价关系,RDS S ε ( t , θ τ ω )存在一个紧的随机吸引子A ε ( ω ),且满足
S ε ( t , θ τ ω )A ε ( θ τ ω )=A ε ( θ t ω ), t ≥ τ .
本节将讨论RDS S ( t , θ τ ω )的吸引子的结构 .
设 ![]() 对于固定的 t ,存在 t j 以及 θ j (- t j )⊂ B 0 ,使得
对于固定的 t ,存在 t j 以及 θ j (- t j )⊂ B 0 ,使得
![]() ϑ j (- t j )=ϑ( t ) .
ϑ j (- t j )=ϑ( t ) .
设
S ε ( t , θ τ ω )ϑ j (- t j )=(ϑ a ) ( j ) ( t )+(ϑ b ) ( j ) ( t ),
其中(ϑ a ) ( j ) ( t ),(ϑ b ) ( j ) ( t )分别满足系统(16)和(17) .
由引理4,
![]() ϑ b ) ( j ) ( t )=0,
ϑ b ) ( j ) ( t )=0,
这意味着
![]() ϑ
ϑ ![]()
因此,对随机吸引子中任意的ϑ=( u , u t + εu - q 2 W ) T ,有
(26)
定义算子 A =-Δ: D ( A )→ L 2 ( D ),其中 D ( A )={ u :-Δ u ∈ L 2 ( D ),∂ u + u | Γ =0} . 则算子 ![]() = I + A 是 L 2 ( D )中的自共轭、正定、线性紧算子 .
= I + A 是 L 2 ( D )中的自共轭、正定、线性紧算子 .
对每个 s ∈ R ,Sobolev空间 ![]() 的内积和范数记为(·,·) s , ‖ · ‖ s ,且满足
的内积和范数记为(·,·) s , ‖ · ‖ s ,且满足
记 ![]() 容易验证
容易验证
P ( t , θ τ ω ):( u ( τ ), u t ( τ )) T ∈ E 0 ![]() ( u ( t ), u t ( t )) T ∈ E 0 , t ≥ τ
( u ( t ), u t ( t )) T ∈ E 0 , t ≥ τ
是关于系统(26)的连续RDS .
下面的定理将给出随机吸引子A( ω )的结构 .
定理2 RDS P ( t , θ τ ω )在 ![]() 中拥有一个随机吸引子A 0 ( ω ),并且
中拥有一个随机吸引子A 0 ( ω ),并且
A( ω )=A 0 ( ω ) .
证明 类似于引理3以及引理5的证明,可知RDS P ( t , θ τ ω )在 E 0 中的吸收性和紧性 . 则 P ( t , θ τ ω )在 ![]() 中有一个随机吸引子A 0 ( ω ),使得
中有一个随机吸引子A 0 ( ω ),使得
P ( t , θ τ ω )A 0 ( θ τ ω )=A 0 ( θ t ω ) .
因为
S ( t , θ τ ω )A( θ τ ω )=A( θ τ ω ),
并且A( ω )中的点均满足方程(26),于是
P ( t , θ τ ω )A( θ τ ω )=A( θ τ ω ),
这意味着
A 0 ( ω )=A( ω ) .
证毕 .
本文研究了动态边界上随机波动方程吸引子,主要有以下几点结论:
1) 证明了 ![]() 将随着时间而消失,而
将随着时间而消失,而 ![]() 在 E 上是渐近紧的,从而完成动态边界上随机波动方程吸引子存在性的证明 .
在 E 上是渐近紧的,从而完成动态边界上随机波动方程吸引子存在性的证明 .
2) 进一步研究了静态边界上的波动方程随机吸引子A 0 的性质,并指出其结构和原波动方程的随机吸引子A结构是一致的 .
同时,本文研究的是带线性阻尼的随机波动方程吸引子存在性 . 未来,还可以从以下几个方面进行研究:
1) 进一步对本文中的波动方程吸引子Hausdorff维数进行研究,对维数上界进行估计,从而展示吸引子的复杂程度 .
2) 考虑如下带非线性阻尼的随机波动方程吸引子存在性:
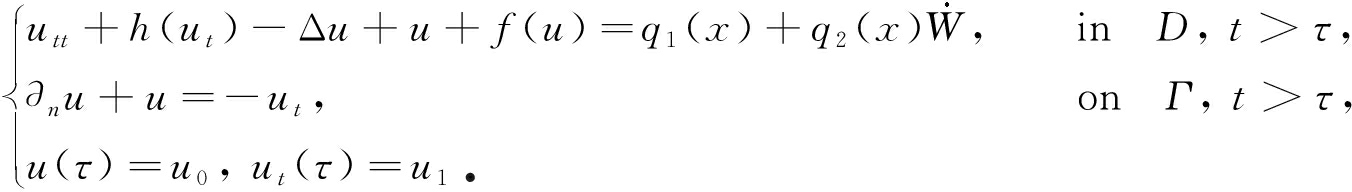
在阻尼为非线性条件时,找到合适的能量不等式将变得困难,且 f 为临界指数时,紧嵌入定理也不再适用,因此需要考虑 h , f , q 1 , q 2 满足什么条件随机吸引子存在,且吸引子的Hausdorff 维数有限 .
参考文献 ( References ):
[1] TEMAM R. Infinite - Dimensional Dynamical Systems in Mechanics and Physics [M]. New York: Springer-Verlag, 1988.
[2] FAN X. Random attractor for a damped stochastic wave equation with multiplicative noise[J]. International Journal of Mathematics , 2008, 19 (4): 421-437.
[3] WANG Z, ZHOU S, GU A. Random attractor for a stochastic damped wave equation with multiplicative noise on unbounded domains[J]. Nonlinear Analysis Real World Applications , 2011, 12 (6): 3468-3482.
[4] ZHANG W. Maximal attractors for the m -dimensional Cahn-Hilliard system[J]. Acta Mathematica Sinica , 2004, 20 (2): 233-246.
[5] ZHANG W N. Dimension of maximal attractors for the m -dimensional Cahn-Hilliard system[J]. Acta Mathematica Sinica , 2005, 21 (6): 1487-1494.
[6] FAN Z H, ZHONG C K. Attractors for parabolic equations with dynamic boundary conditions[J]. Nonlinear Analysis Theory Methods and Applications , 2008, 68 (6): 1723-1732.
[7] MIRANVILLE A, ZELIK S. Exponential attractors for the Cahn-Hilliard equation with dynamic boundary conditions[J]. Mathematical Methods in the Applied Sciences , 2005, 28 (6): 709-735.
[8] CHUESHOV I, ELLER M, LASIECKA I. On the attractor for a semilinear wave equation with critical exponent and nonlinear boundary dissipation[J]. Communications in Partial Differential Equations , 2002, 27 (9): 1901-1951.
[9] WU H, ZHENG S. Convergence to equilibrium for the damped semilinear wave equation with critical exponent and dissipative boundary condition[J]. Quarterly of Applied Mathematics , 2006, 64 (1): 167-188.
[10] YASSINE H. Existence and asymptotic behavior of solutions to semilinear wave equations with nonlinear damping and dynamical boundary condition[J]. Journal of Dynamics & Differential Equations , 2012, 24 (3): 645-661.
[11] BARBU V. Nonlinear Semigroups and Differential Equations in Banach Spaces [M]. New York: Springer-Verlag, 2010.
[12] PAZY A. Semigroups of Linear Operators and Applications to Partial Differential Equations [M]. New York: Springer-Verlag, 1983.
[13] FRIGERI S. Attractors for semilinear damped wave equations with an acoustic boundary condition[J]. Journal of Evolution Equations , 2010, 10 (1): 29-58.
[14] BALL J M. Global attractors for damped semilinear wave equations[J]. Discrete & Continuous Dynamical Systems , 2004, 10 (1): 31-52.
YANG Mo, FU Na ①
(School of Mathematics, Southwest Jiaotong University, Chengdu 610031, P.R.China)
Abstract : A class of wave equations with dynamic boundary conditions were studied. Through suitable decomposition, the existence of the stochastic attractor was proved. The decomposition shows that the point (or solution) of the attractor satisfies some stationary boundary condition. Finally, the attractor also exists in the stochastic dynamic system determined by the stochastic wave equation with the static boundary condition developed in decomposition.
Key words: dynamic boundary condition; wave equation; stochastic attractor
Foundation item: The National Natural Science Foundation of China(71273214)
ⓒ 应用数学和力学编委会,ISSN 1000-0887
文章编号 : 1000-0887(2018)09-1068-13
基金项目 : 国家自然科学基金(71273214);中央高校基本科研业务费(SWJTU12ZT13)
作者简介 : 杨墨(1991—), 男,硕士生(通讯作者. E-mail: 251160504@qq.com).
* 收稿日期 : 2017-09-08;
修订日期: 2017-11-14
文献标志码: A
DOI: 10.21656/1000-0887.380254
中图分类号 : O175; O19
①引用本文 / Cite this paper: 杨墨, 富娜. 动态边界上随机波动方程的吸引子[J]. 应用数学和力学, 2018, 39 (9): 1068-1080.YANG Mo, FU Na. Attractors of stochastic wave equations with nonlinear damping and dynamic boundary conditions[J]. Applied Mathematics and Mechanics , 2018, 39 (9): 1068-1080.