刘俊卿, 韩 晶
(西安建筑科技大学 理学院, 西安 710055)
摘要 : 在分析沥青路面结构可靠度时,为了更符合路面实际工况,将模糊数学理论纳入可靠度分析中 . 首先给出沥青路面结构的失效隶属函数;然后将路表弯沉值作为控制指标;从而推导出沥青路面结构模糊可靠度计算模式;并结合西咸新区二级沥青路段进行了相关的验证 . 结果表明:在一模糊事件中,模糊可靠度与传统可靠度相比总是低于传统可靠度 . 基于此,在对路面结构进行可靠性设计时采用模糊可靠度能更加巩固路面的使用性能,延长了路面的使用年限 . 在使用过程当中,外界因素对路面的损害程度相较于采用传统可靠度设计的路面结构小,从而使得路面的维修次数减少,节省了后期路面维护的人力和财力 . 所选取的隶属函数中 k 的取值和模糊临界区间均对模糊可靠度的大小起直接影响作用,通过对不同路面组合,不同 k 值的计算发现,当 k 值取作 ![]() 较为合理 . 在具体的工程实践中,应该根据实际情况来确定临界区间的范围,以保证结构的安全性 .
较为合理 . 在具体的工程实践中,应该根据实际情况来确定临界区间的范围,以保证结构的安全性 .
关 键 词 : 道路工程; 结构可靠度; 模糊数学理论; 沥青路面结构; 隶属函数;路表弯沉
20世纪40年代,有关的道路学者开始将概率论方法贯穿到结构的设计与分析当中,并逐步发展成了有关结构可靠度的传统性理论 . 结合沥青路面结构的特点,其结构可靠度可定义为 [1-3] :对于正常设计、正常施工和正常使用的路面结构,在路面达到规定的设计累计标准轴载作用次数的时间内,路面表面弯沉 [4] 和层底弯拉应力 [5] 分别不超过其容许值的概率 .
美国自动控制学家Zadeh教授于20世纪60年代提出“模糊集合”概念,模糊数学 [6-8] 从此宣告诞生,之后模糊理论及方法得到了迅速发展 . 在路面结构领域中,涉及到模糊性的概念十分常见,如路面结构的可靠度定义的模糊性、实际模型和计算模型之间的差异模糊性等 . 在进行相关课题的探析中发现,模糊数学理论与经典理论相较而言,模糊数学具有明显的优越性 . 近年来,我国的相关道路工作者在进行沥青路面设计所出现的不确定性以及随机性的研究时,总结并归纳出多种涉及到路面结构可靠度的计算研究途径,比如Monte-Carlo(蒙特-卡罗)法和极值理论,近似求导的J-C法等,但要作为比较合理的可靠度计算方法,应同时考虑随机性以及模糊性对结构可靠度可能产生的影响 . 由于沥青路面结构的可靠度不仅具备随机性,同时也具备模糊性,因而沥青路面结构可靠度是一个模糊随机可靠度 . 在路面的模糊可靠性研究方面,娄峰 [9] 将模糊理论运用到沥青路面结构的可靠性分析当中,并编制了沥青路面结构模糊可靠度的计算程序,但没有针对具体的工程实例进行分析,也未能凸显出模糊可靠度相较于传统可靠度的优越之处 . 贾致荣等 [10] 将模糊理论运用到一高速公路沥青路面中,该路面共有沥青面层、水泥稳定碎石基层、石灰土底基层以及土基四种结构,在标准轴载累计作用1×10 7 下进行计算 . 结果表明,模糊可靠度低于传统的可靠度,该高速公路传统的可靠度和可靠度指标满足目标可靠度95%~99%及可靠度指标1.645~2.327的要求,而模糊可靠度的弯沉及底基层弯拉应力不满足要求 . 这表明有的设计指标仍存在导致路面损坏的缺陷,而取值较低的模糊可靠度更客观地表现了结构的实际可靠度,能够更多地暴露结构的安全隐患 .
本文以沥青路面结构为研究对象并从沥青路面结构极限状态方程具有的模糊性角度出发,把路表弯沉作为控制指标得到由其表达的极限函数,继而应用模糊数学理论对其进行可靠度分析 .
在传统的可靠度理论分析方法中,把沥青路面结构的极限状态(即结构由安全到破坏的状态) [11-12] 用结构抗力 R 和荷载效应 S 之间的关系加以描述,则结构的功能函数可表示为 Z = R - S ,相应的极限状态方程为
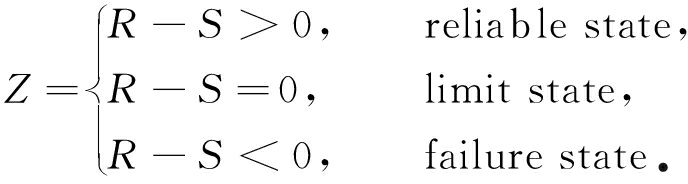
本文是以路表弯沉为控制指标的,故得到沥青路面结构可靠度计算的极限函数为
Z = l d - l s ,
(1)
式中, l d 为路表的设计弯沉值, l s 为交通荷载作用下产生的路表弯沉值(即实际弯沉值) .
已知沥青路面结构的设计弯沉 l d 和实际弯沉 l s 相互独立且均服从正态分布,观察式(1)可知结构的功能函数 Z 是由设计弯沉 l d 和实际弯沉 l s 两个独立的随机变量所组成的一个新函数 . 按照概率论中的随机变量运算法则,若随机变量 X 1 和 X 2 均服从正态分布,则 X 1 和 X 2 的差值所组成的新随机变量也是服从正态分布的,即 Z 服从正态分布 ![]() 其中 μ Z 为 Z 的均值, σ Z 为 Z 的标准差,且由概率论中随机变量的运算法则可知
其中 μ Z 为 Z 的均值, σ Z 为 Z 的标准差,且由概率论中随机变量的运算法则可知
(2)
Z 是服从正态分布的,则 Z 的概率密度函数为正态分布概率密度函数,即
(3)
20世纪60年代,Zadeh按如下定义提出了模糊集合的概念:给定一论域 U , U 上的一个模糊子集 A ,指的是从 U 到[0,1]区间的一个映射
μ A : U →[0,1], u → μ A ( u ),
其中 μ A 称为 A 的隶属函数, μ A ( A )称为 u 对 A 的隶属度 .
在模糊数学理论中,隶属函数 [13-16] 的确定和选择尤为重要,隶属函数 μ ( Z )的形式多种多样 . 对于本文中的沥青路面结构,由于降半正态隶属函数能够较好地反映以路表弯沉为控制指标的沥青路面结构模糊失效区的特点 [9] ,因此选用了降半正态分布形式的隶属函数,其数学表达式为
(4)
其函数图形如图1所示 .

图1 降半正态函数分布图
Fig. 1 The reduced semi-normal function distribution map
需要注意的是,在确定了以路表弯沉为控制指标的隶属函数式(4)中,参数 k 的选取尚未确定 . 根据文献[9]中关于 k 值选取原则的研究,首先通过选取典型沥青路面结构形式进行模糊可靠度的计算分析,结果表明 k 值的选取范围在 ![]() 由于典型路面具有特殊性而不具有普遍性,因此又反复计算大量不同路面结构类型、不同路面结构形式,从而确定当 k 值取作
由于典型路面具有特殊性而不具有普遍性,因此又反复计算大量不同路面结构类型、不同路面结构形式,从而确定当 k 值取作 ![]() 时较为合理,同时亦符合沥青路面结构的实际工况 . 通过计算发现,在此区间当 k 值选取为
时较为合理,同时亦符合沥青路面结构的实际工况 . 通过计算发现,在此区间当 k 值选取为 ![]() 时,其结果较为明显且具有代表性,故本文选取这4个值进行分析 .
时,其结果较为明显且具有代表性,故本文选取这4个值进行分析 .
考虑到沥青路面结构传统可靠度计算模式及模糊数学的方法,且在已确定了的基本隶属函数下,则可得到沥青路面结构破坏的概率 P f 为
P f = ![]() μ ( Z ) f Z ( Z )d Z .
μ ( Z ) f Z ( Z )d Z .
(5)
继而可得其模糊可靠度为
P S =1- P f ,
(6)
模糊可靠度指标为
β = φ -1 ( P S ) .
(7)
式(5)~(7)中, P f 为沥青路面结构的模糊失效概率; μ ( Z )为结构失效的隶属函数; f Z ( Z )为沥青路面结构模糊事件的概率密度函数; P S 为沥青路面结构的模糊可靠度; β 为沥青路面结构的模糊可靠度指标; φ -1 为标准正态分布函数的反函数 .
本文已经得到了沥青路面结构可靠度计算的极限函数(1),且知道了 Z 的概率密度函数式(3),结合上文的沥青路面结构可靠度的计算方法,则可得沥青路面的模糊可靠度为
本文选取的隶属函数为降半正态分布隶属函数,已知其函数表达式(4),代入展开可得
进一步展开可得
(8)
式中
式(8)即为沥青路面结构模糊可靠度的计算表达式 . 观察该计算表达式有:当取模糊数 a =0时,将 a =0和 k 的对应取值分别代入式(8),则式(8)可近似简化为
(9)
显然,上式与传统可靠度的表达式相同 . 由此可得该模糊可靠度计算模型在取模糊数 a =0时和传统的可靠度计算方法是一致的 .
以上,本文得出了当控制指标为路表弯沉值时的沥青路面结构可靠度计算极限函数 Z 是服从正态分布的,且知道了 Z 的概率密度函数,并在相关的计算表达式下可以得到沥青路面结构的模糊失效概率图 [9] 如图2所示,黑色区域即为模糊区失效概率 .
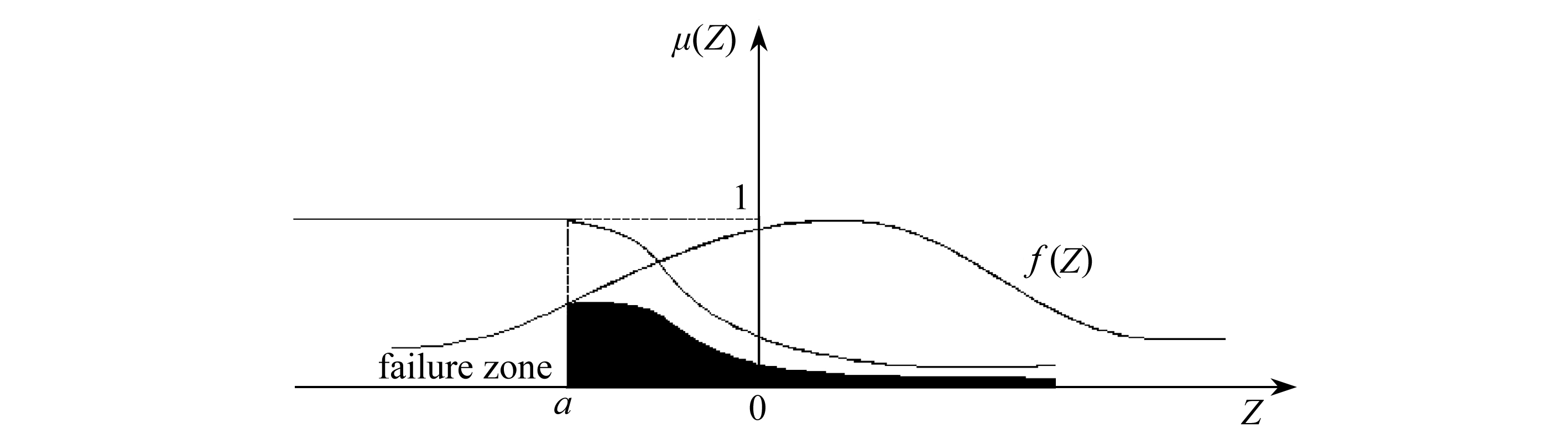
图2 沥青路面结构模糊失效概率图
Fig. 2 The fuzzy failure probability map of the asphalt pavement structure
为了确保理论公式推导对实际工程具有一定指导意义,本文根据“西咸新区秦汉新城同文路(统一路—永平路)”项目的二级沥青路面面层弯沉检测试验结果进行分析计算 . 根据《公路路基路面现场测试规程》(JTG E60—2008)中的T0951-2008 Beckmann(贝克曼)梁测定路基路面回弹弯沉试验方法进行测定 . 按照每公里选取80~100个点进行弯沉测试,并将测点进行可靠度算例验证,其中该沥青路面弯沉数据如表1所示 .
表1 沥青路面弯沉数据
Table 1 Deflection data of the asphalt pavement

已知此沥青路面的设计弯沉值为 l d =25 mm,由以上所给弯沉数据通过数学计算可得该沥青路面路表弯沉的均值为15.15 mm,标准差为7.50 mm . 则由概率论中的运算法则即式(2)可得模糊极限状态变量 Z 的均值为 μ Z = E ( Z )= E ( l d )- E ( l s )=25-15.15=9.85 mm;标准差为 ![]() mm .
mm .
本文采用一次二阶矩法对沥青路面结构进行传统可靠度计算,由所给数据可求得该段公路的传统可靠度为
将所得结果与模糊可靠度计算结果进行比较,如表2所示 .
在进行模糊可靠度的相关分析时,模糊区的大小应该遵循“3 σ ”规则 [9] ,即对于正态分布函数,在区间[ μ -3 σ , μ +3 σ ]上的概率为99.73%,接近于1,这说明落在该区间外的概率大小仅为0.27%,概率很小 . 根据概率统计原理,对于小概率事件在一次试验中几乎是不可能发生的,这就是所谓的“3 σ ”规则 . 因而在对沥青路面结构进行模糊可靠性分析时,模糊区的大小应该遵循该原则,以保证路面结构的失效模糊区间合理(即只要对模糊区间的估计误差不过大,那么模糊可靠度的计算结果是合理的) . 模糊数首先按照一倍标准差原则取值,即就是 a = μ Z - σ Z ,应用沥青路面结构模糊可靠度的计算式(8)可求得该沥青路面结构在不同 k 值下的以弯沉为控制目标的模糊可靠度 P S 的对应值 .
如果模糊数按照 N 倍标准差来取值,即就是 a = μ Z - Nσ Z ,按照“3 σ ”规则,本文选定 N 的取值范围在[0,1.5]之间来进行分析 . 同理,应用沥青路面结构模糊可靠度的计算式(8)可得到在不同 N 值的情况下,以路表弯沉为控制指标的沥青路面结构模糊可靠度计算结果如表2所示 .
表2 模糊区界限对模糊可靠度 P S 的影响
Table 2 The influence of fuzzy zone boundaries on fuzzy reliability degree P S
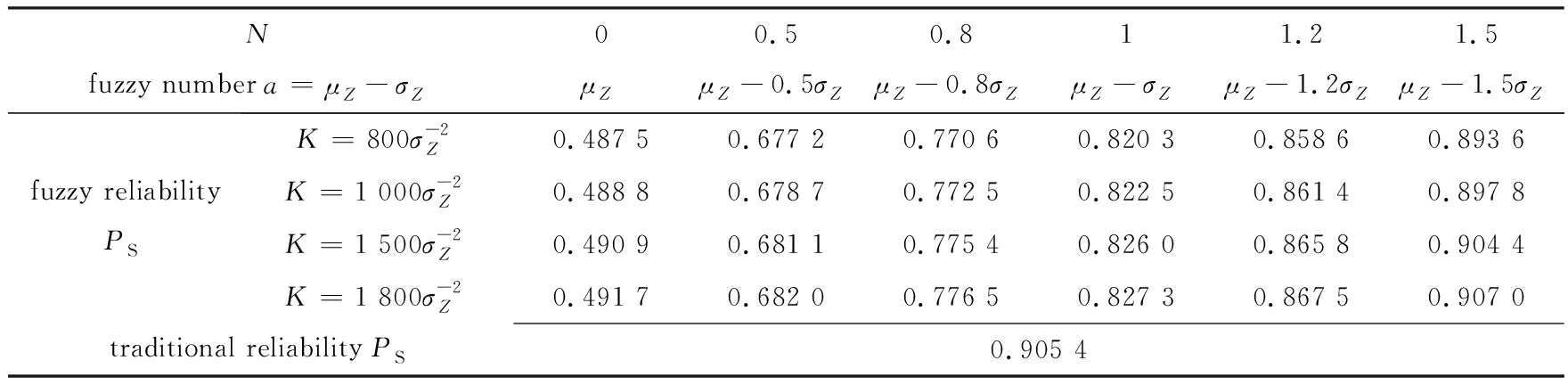
由表2中的数据可绘制出模糊可靠度与模糊区大小的关系(如图3所示) .
表2和图3均表明了以路表弯沉为控制指标的沥青路面结构模糊可靠度 P S 与其模糊临界区间范围的关系 . 通过对表2和图3的观察可得:
① 当选定确定的 N 值时,模糊可靠度 P S 随着 k 值的增大而增大 . 这表明了隶属函数中 k 的取值对模糊可靠度的大小具有直接影响 .
② 当 ![]() 时,取 N =0.5,有 P S =67.87%;而取 N =1.5,有 P S =89.78% . 当 k 取其他值时亦然 . 这表明了模糊临界区间同样对模糊可靠度的大小具有直接影响 .
时,取 N =0.5,有 P S =67.87%;而取 N =1.5,有 P S =89.78% . 当 k 取其他值时亦然 . 这表明了模糊临界区间同样对模糊可靠度的大小具有直接影响 .
③ 结合表2和图3可以发现传统可靠度的计算结果过于单一,无法进行类比判断且传统可靠度的计算结果未能表明路面结构可靠度的变化情况,模糊可靠度则相应地给出了确切的模糊临界区间,同时表明了沥青路面结构随模糊临界范围变化的趋势,对实际工程更具有指导作用 . 在遵循概率论中“3 σ 规则”的情况下,模糊可靠度总是低于传统可靠度(当 ![]() 且取 N =1.5时,有 P S =90.70%>90.54%,但其结果仍在误差的允许范围内) . 这是因为,其一,对比模糊可靠度的计算表达式与传统可靠度的不同,可以发现,由于隶属函数的分布问题(降半正态函数的取值≤1),导致模糊可靠度的计算表达式中的被积函数小于传统可靠度,由概率论的运算法则可知,模糊可靠度的最终计算结果小于传统可靠度;其二,由结构的状态函数中加入的模糊区可知,结构由完全安全到完全破坏中间存在着不完全安全、临界状态及不完全破坏等状态,这些状态的存在导致了沥青路面结构可靠度的降低,而传统可靠度仅由完全安全到完全破坏,即理论上模糊可靠度也是小于传统可靠度的 . 同时存在工程实践证明,沥青路面结构在基本满足传统可靠度的要求下,有的设计指标仍会导致路面的损坏 . 此时,取值较低的模糊可靠度更加客观地表明了路面结构的实际可靠度,且能更多地暴露出路面结构的安全隐患 .
且取 N =1.5时,有 P S =90.70%>90.54%,但其结果仍在误差的允许范围内) . 这是因为,其一,对比模糊可靠度的计算表达式与传统可靠度的不同,可以发现,由于隶属函数的分布问题(降半正态函数的取值≤1),导致模糊可靠度的计算表达式中的被积函数小于传统可靠度,由概率论的运算法则可知,模糊可靠度的最终计算结果小于传统可靠度;其二,由结构的状态函数中加入的模糊区可知,结构由完全安全到完全破坏中间存在着不完全安全、临界状态及不完全破坏等状态,这些状态的存在导致了沥青路面结构可靠度的降低,而传统可靠度仅由完全安全到完全破坏,即理论上模糊可靠度也是小于传统可靠度的 . 同时存在工程实践证明,沥青路面结构在基本满足传统可靠度的要求下,有的设计指标仍会导致路面的损坏 . 此时,取值较低的模糊可靠度更加客观地表明了路面结构的实际可靠度,且能更多地暴露出路面结构的安全隐患 .
④ 由图3可以直接观察到在每一条确定的 k 值图线和本文所选定的 N 的范围中, N 与 P S 成正比例关系 . 这是因为本文所选取的隶属函数为降半正态隶属函数 . 结合图2和图3可发现随着 N 值的增大,失效模糊区范围减小,即模糊失效概率减小,则结构的模糊可靠度增大 . 在具体的工程实践中,应该根据实际情况来确定临界区间的范围,以保证结构的安全性 .
⑤ 当取模糊数 a =0时,沥青路面结构的模糊可靠度近似地等于传统可靠度,即传统可靠度可视为模糊可靠度的一种特殊形式 .

图3 沥青路面结构模糊可靠度和模糊临界区间范围的关系
Fig. 3 Relationship between the fuzzy reliability degree and the fuzzy critical interval range of the asphalt pavement structure
本文将模糊数学理论引入到沥青路面结构的可靠度分析中, 确定了以路表弯沉为控制指标时的隶属函数(即降半正态分布隶属函数), 并得到了在此隶属函数下的沥青路面结构的模糊可靠度计算表达式(8) . 对西咸新区二级沥青路面进行了模糊可靠度分析和计算, 其结果表明:
1) 模糊数学理论相对于经典理论对路面结构进行分析是具有优越性和实际工程意义的 .
2) 在一模糊事件中,模糊可靠度与传统可靠度相比总是低于传统可靠度 . 隶属函数中 k 的取值和模糊临界区间均对模糊可靠度的大小起直接影响作用 . 在具体的工程实践中,应该根据实际情况来确定临界区间的范围(对于工程中的实际情况,若已知其沥青路面结构功能函数的统计量(均值 μ Z 和标准差 σ Z ),可初步限定路面结构的失效模糊区间,再结合沥青路面结构模糊失效概率图的分布情况,进一步限定沥青路面结构的临界区间的范围),以保证结构的安全性 .
3) 本文中的模糊可靠度分析模型和传统的可靠度计算方法在取模糊数 a =0时所求结果是一致的,即传统的可靠度可以视作是一种特殊形式的模糊可靠度 .
4) 正确的模糊可靠度依靠正确的隶属函数,但隶属函数的确定尚有待进一步研究 . 在通过模糊数学理论对沥青路面结构进行可靠度分析的过程中,沥青路面的结构失效(或者结构破坏)问题就是一个模糊事件,沥青路面结构失效隶属函数的选择和确定是对沥青路面结构进行可靠度分析的基础 . 在对沥青路面结构的可靠度分析当中,隶属函数仍然有很多问题需要解决,但不可以任意选择函数形式 . 因此,如何选取和确定合适的隶属函数尚有待研究 .
参考文献 ( References ):
[1] 赵安龙, 李洪双. 基于概率支持向量机的可靠性分析与设计方法[J]. 应用力学学报, 2017, 34 (1): 50-56.(ZHAO Anlong, LI Hongshuang. Reliability analysis and optimization design based on probabilistic support vector machine[J]. Chinese Journal of Applied Mechanics , 2017, 34 (1): 50-56.(in Chinese))
[2] 李刚, 孟增. 基于RBF神经网络模型的结构可靠度优化方法[J]. 应用数学和力学, 2014, 35 (11): 1272-1279.(LI Gang, MENG Zeng. Reliability-based design optimization with the RBF neural nerwork model[J]. Applied Mathematics and Mechanics , 2014, 35 (11): 1272-1279.(in Chinese))
[3] 刘杰, 卿启湘, 张青春, 等. 结构模糊可靠性分析方法的泛灰求解[J]. 应用数学和力学, 2015, 36 (3): 285-293.(LIU Jie, QING Qixiang, ZHANG Qingchun, et al. Solving of the structural fuzzy reliability analysis method with universal grey numbers[J]. Applied Mathematics and Mechanics , 2015, 36 (3): 285-293.(in Chinese))
[4] 郑健龙. 基于状态设计法的沥青路面弯沉设计标准[J]. 中国公路学报, 2012, 25 (4): 1-9.(ZHENG Jianlong. Deflection design standards of asphalt pavement based on state design method[J]. China Journal of Highway and Transport , 2012, 25 (4): 1-9.(in Chinese))
[5] 吁新华, 谈至明. 沥青路面结构层弯拉应力与应变的近似计算[J]. 同济大学学报(自然科学版), 2012, 40 (6): 849-853.(YU Xinhua, TAN Zhiming. Approximate calculation of flexural stresses and tensile strains in asphalt pavements[J]. Journal of Tongji University ( Natural Science ), 2012, 40 (6): 849-853.(in Chinese))
[6] 龚文慧, 王元汉, 郑俊杰. 基于模糊理论的膨胀土路基沉降的可靠度分析[J]. 华中科技大学学报(自然科学版), 2008, 36 (3): 50-53.(GONG Wenhui, WANG Yuanhan, ZHENG Junjie. Reliability analysis on settlement of expansive soil roadbed based on fuzzy theory[J]. Journal of Huazhong University ( Natural Science Edition ), 2008, 36 (3): 50-53.(in Chinese))
[7] 凌建明, 官盛飞, 赵鸿铎, 等. 公路沥青路面预养护多层次模糊决策模型[J]. 公路交通科技, 2008, 25 (6): 25-34.(LING Jianming, GUAN Shengfei, ZHAO Hongduo, et al. Multi-hierarchy fuzzy decision-making medol for PPM treatment selection of highway asphalt pavement[J]. Journal of Highway and Transport Research and Development , 2008, 25 (6): 25-34.(in Chinese))
[8] 颜可珍, 周志雄. 基于非线性模糊法的水泥路面性能评价[J]. 浙江大学学报(工学版), 2013, 47 (8): 1379-1392.(YAN Kezhen, ZHOU Zhixiong. Cement pavement performance evaluation based on nonlinear fuzzy method[J]. Zhejiang University ( Engineering Science ), 2013, 47 (8): 1379-1392.(in Chinese))
[9] 娄峰. 基于模糊理论的沥青路面可靠度分析[D]. 硕士学位论文. 长沙: 湖南大学, 2004.(LOU Feng. Reliability analysis for asphalt pavement based on fuzzy theory[D]. Master Thesis. Changsha: Hunan University, 2004.(in Chinese))
[10] 贾致荣, 樊克恭, 赵成泉. 沥青路面结构的模糊可靠度分析[J]. 中外公路, 2001, 21 (4): 15-18.(JIA Zhirong, FAN Kegong, ZHAO Chengquan. Fuzzy reliability degree analysis of asphalt pavement structure[J]. Journal of Foreign Highway , 2001, 21 (4): 15-18.(in Chinese))
[11] 张文. 沥青路面极限承载力与使用寿命预估研究[D]. 硕士学位论文. 长沙: 湖南大学, 2004.(ZHANG Wen. Prediction of ultimate bearing capacity and life-span of asphalt pavement[D]. Master Thesis. Changsha: Hunan University, 2004.(in Chinese))
[12] 习宇. 沥青路面结构极限承载力分析与应用研究[D]. 硕士学位论文. 长沙: 湖南大学, 2006.(XI Yu. Research on analysis and application of ultimate bearing capacity for asphalt pavement[D]. Master Thesis. Changsha: Hunan University, 2006.(in Chinese))
[13] 于少伟. 基于区间数的模糊隶属函数构建[J]. 山东大学学报(工学版), 2010, 40 (6): 32-36.(YU Shaowei. Construction of a fuzzy membership function based on interval number[J]. Shandong University ( Engineering Science ), 2010, 40 (6): 32-36.(in Chinese))
[14] 李鑫, 杨锡武, 黄金. 基于模糊数学的水泥路面使用性能综合评价体系研究[J]. 兰州大学学报(自然科学版), 2009, 45 (S1): 88-92.(LI Xin, YANG Xiwu, HUANG Jin. Comprehensive evaluation system of cement pavement performance based on fuzzy mathematics[J]. Journal of Lanzhou University ( Natural Sciences ), 2009, 45 (S1): 88-92.(in Chinese))
[15] 战高峰, 王洪范. 模糊数学理论在确定水泥混凝土路面目标可靠度时的应用[J]. 公路交通科技, 2000, 17 (S1): 2-7.(ZHAN Gaofeng, WANG Hongfan. Application of fuzzy mathematic theory in determining the objective for the cement concrete pavement[J]. Journal of Highway and Transport Research and Development , 2000, 17 (S1): 2-7.(in Chinese))
[16] 丁晓丽. 基于模糊数学理论下高速公路隧道路面选型评定[J]. 公路工程, 2017, 42 (5): 262-266.(DING Xiaoli. The selection of highway tunnel pavement evaluation based on the fuzzy mathematics theory under[J]. Highway Engineering , 2017, 42 (5): 262-266.(in Chinese))
LIU Junqing, HAN Jing ①
( School of Science , Xi ’ an University of Architecture and Technology , Xi ’ an 710055, P . R . China )
Abstract : The fuzzy mathematics theory was introduced into the analysis of asphalt pavement structure reliability, to better fit the actual condition of pavement. The failure membership function was first given for asphalt pavement structure, then with the road surface deflection value as the control index, the asphalt pavement structure fuzzy reliability calculation model was built and verified with 2 asphalt roads in the Xixian New Area. The results show that, in a fuzzy event, the fuzzy reliability is always lower than the traditional reliability. Based on this, the reliability design of the pavement structure with the fuzzy reliability can strengthen the pavement performance and prolong the service life of pavement. In service, under the fuzzy reliability the pavement damage degree due to environmental factors is less than that under the traditional reliability, thus reducing the amount of pavement maintenance and saving manpower and maintenance cost. The values of k and fuzzy critical intervals of the selected membership functions play a direct role in the magnitude of the fuzzy reliability. Through the calculation of different road combinations and different k values, it is found that the reasonable value of k is within ![]()
![]() In the real engineering practice, the critical interval shall be determined according to the actual situation, so as to ensure the safety of the structure.
In the real engineering practice, the critical interval shall be determined according to the actual situation, so as to ensure the safety of the structure.
Key words: road engineering; structural reliability degree; fuzzy mathematics theory; asphalt pavement structure; membership function; pavement deflection
Foundation item: The National Natural Science Foundation of China(51178387)
ⓒ 应用数学和力学编委会,ISSN 1000-0887
文章编号 : 1000-0887(2018)09-1081-10
刘俊卿(1957—),男,教授,博士生导师(E-mail: liujunqingjd@126.com);
韩晶(1992—),女,硕士生(通讯作者. E-mail: 1623944726@qq.com).
基金项目 : 国家自然科学基金(51178387);陕西省教育厅自然科学基金(14JK1414)
作者简介 :
* 收稿日期 : 2017-10-31;
修订日期: 2017-12-15
文献标志码: A
DOI: 10.21656/1000-0887.380278
中图分类号 : U416.2
①引用本文 / Cite this paper: 刘俊卿, 韩晶. 基于模糊数学理论的沥青路面结构可靠度分析[J]. 应用数学和力学, 2018, 39 (9): 1081-1090.LIU Junqing, HAN Jing. Reliability analysis of asphalt pavement structure based on the fuzzy mathematics theory[J]. Applied Mathematics and Mechanics , 2018, 39 (9): 1081-1090.