朴思扬 1 , 祁 峰 2 , 张亚辉 1
(1. 工业装备结构分析国家重点实验室(大连理工大学), 辽宁 大连 116024;2. 北京宇航系统工程研究所, 北京 100076)
关 键 词 : 有限元理论; 模型修正; 动力子结构法; 模态综合法
大型复杂结构整体动力学特性的获得往往是比较困难的,主要有试验和仿真两类途径 . 进行大型结构整体试验对试验条件、试验技术要求很高,试验成本随之增加,试验设施的后期利用率也是需要考虑的问题 . 仿真分析虽然在成本和效率方面具有优势,但其结果的可信程度备受关注,实际应用当中又常常需要佐以试验验证 . 资料表明 [1] ,在大型运载火箭研究方面,美国和欧洲逐渐通过缩比模型试验和部段级试验取代整箭试验获取全箭动特性,并且已有成功发射的案例 . 我国在CZ-2E和CZ-2F运载火箭研制中,在进行实尺全箭振动试验的同时,还曾进行过缩比模型试验和子结构试验建模综合技术的尝试,取得了较好的效果 [2-4] .
子结构试验建模综合技术是实现“用部件试验代替全结构试验” [5] 的两种途径之一 . 另一种途径称为子结构试验模态综合 [3-4] ,即完全通过子结构试验的方法获取全结构的减缩模型,虽然理论上避免了仿真模型分析结果与实测结果之间的误差,但由于其在子结构模态参数获取的可行性和实现精度等方面仍存在困难,目前距离实际应用还有一段距离 .
子结构试验建模综合技术主要包含动力子结构法和有限元模型修正技术 . 首先,将整体结构划分成若干子结构,对子结构进行试验分析 . 然后,应用有限元模型修正技术缩小子结构仿真模型与实际的差距 . 最终,将修正好的子结构模型组装起来代表整体结构 .
在实际应用方面,文献[2-4]介绍了子结构试验建模综合技术在CZ-2E和CZ-2F运载火箭全箭模态试验仿真预示中的应用,整体结构仿真分析结果与实测基本吻合,但局部偏差较大 . 文献[6]应用这项技术进行了火箭发动机结构动力分析,取得了比较好的效果 . 然而在实际操作中,由于子结构模型的规模仍然很大,对子结构进行模型修正十分耗时 .
在上述研究工作的基础上,本文对子结构试验建模综合技术进行了改进 . 在子结构模型修正阶段,应用固定交界面模态综合法,对子结构模型进一步进行减缩,提高了每个子结构模型修正的计算效率,从而提高了子结构试验建模综合技术的整体计算效率 . 本文详细推导了基于减缩模型的模型修正设计参数法的计算公式,给出了具体的子结构试验建模综合技术执行步骤,并基于商业软件ANSYS进行二次开发,以一个运载火箭模型为算例,验证了本文方法的有效性 .
模态综合法是对大型结构施行Ritz法的一类子结构方法 [7] ,常用的模态综合法包括固定交界面法、自由交界面法和混合交界面法等 . 这些方法的实施过程大体上是一致的 . 首先,将整体结构划分成若干子结构,每个子结构包含内部和交界面自由度两部分 . 然后,对每个子结构进行独立的模态分析,获得该子结构的减缩基底 . 最后,通过子结构组装,获得整体结构减缩基底,进而应用Ritz法计算整体结构的固有频率,并经过复原获得整体结构的振型 .
最早的模态综合方法由Hurty提出 [8] ,随后Craig和Bampton [9] 对其进行了改进,形成了现今广泛使用的固定交界面模态综合法(C-B法) . C-B法的减缩基底包含主模态和约束模态两部分,主模态由交界面完全约束条件下的子结构模态分析得到;约束模态是通过依次释放子结构交界面自由度而得到的内部自由度的静位移 . C-B法的优点是理论简单,计算精度也比较高,但存在减缩后模型的自由度数量一定会大于子结构交界面自由度数量的缺点 . 由此,Castanier等 [10] 、Simon和Cost [11] 提出了用特征约束模态进行交界面减缩的方法 . 自由交界面法最早由Hou [12] 和Goldman [13] 提出,是一种只使用子结构自由模态形成减缩基底的方法,但计算精度较差 . Macneal [14] 和Rubin [15] 先后通过引入剩余柔度和剩余惯性的概念,近似地将截去的高阶模态影响重新引入,提高了计算精度 . 随后,王文亮等对剩余柔度进行了深入研究,提出了双协调自由界面模态综合法 [16] . Benfield和Hruda [17] 提出了一种混合界面模态综合方法(B-H法),可以解决自由界面子结构与固定界面子结构混合连接的情况 . 由于忽略了从子结构对主子结构的自由界面主模态的影响,所以B-H法计算精度不高 . 此后,长松昭男通过将从子结构凝聚到界面自由度上,提高了B-H法的低阶频率计算精度,但高阶精度有所降低 [18] . 为了进一步提高模态综合法计算精度,许多学者又在上述经典方法的基础上进行了大量研究 [19-21] .
有限元模型修正是一项试验 [22-23] 和仿真相结合,用于缩小分析模型与实际结构差异的理论方法 [24-25] . 应用这一方法不仅可以提升仿真模型的精度,还可以指导试验设计,减少非必要的试验 . 文献[24-26]对常用的有限元模型修正的方法进行了综述,主要有最优矩阵法、设计参数法、频响函数法、智能算法及统计学方法等 . 基于模态测试数据的设计参数法具有物理意义明确、修正理论简单、适用范围广等特点,可以满足实际工程需要 . 应用设计参数法进行模型修正包括模型误差参数化、确定设计参数、灵敏度分析和构造迭代关系四个环节 [25] . 模型误差参数化的目的是引入设计参数, 常见的是基于Taylor级数展开至一阶导数, 将模型参数进行参数化的方法 [27] . 设计参数包括模型的物理、 几何等参数, 需要依据模型误差关于设计参数的灵敏度进行选择 . 对于大型复杂结构, 直接求解灵敏度是比较困难的, 通常可以通过数值微分的方法获得 . 使用设计参数灵敏度构造迭代关系, 通过求解线性代数方程组可以获得设计参数更新 .
模态综合法减缩模型通过设计参数法进行修正,比较理想的方式是完全针对减缩模型进行修正 . 修正开始时,对模型进行减缩,修正过程中,完全对减缩模型进行操作,修正结束时,对模型进行复原,全部修正过程只经历一次模型减缩和复原 . 这种方式由于模型规模小,所以计算效率高,但在实际操作中需要对减缩基进行更新,因此会引入较大误差,且不容易在商业软件上进行二次开发 . 本文方法不需要对减缩基进行更新,但需要在每次修正迭代时生成新的减缩基 . 这种方法虽然需要多次模型减缩和复原,但避免了减缩基更新误差,且易于通过商用有限元程序实现 .
将整体结构划分为 N 个子结构 s i ( i =1,2,…, N ),由于每一个子结构的规模仍然很大,本文为了提高模型修正的计算效率,应用固定交界面模态综合法对每一个子结构进一步进行减缩 . 将子结构 s i 划分成 n i 个子结构 s i , r ( r =1,2,…, n i ),建立模态矩阵 Φ s i , r ,对子结构 s i , r 的质量矩阵 M s i , r 和刚度矩阵 K s i , r 进行减缩,得到减缩质量矩阵 ![]() 和刚度矩阵
和刚度矩阵 ![]() 即
即
(1)
(2)
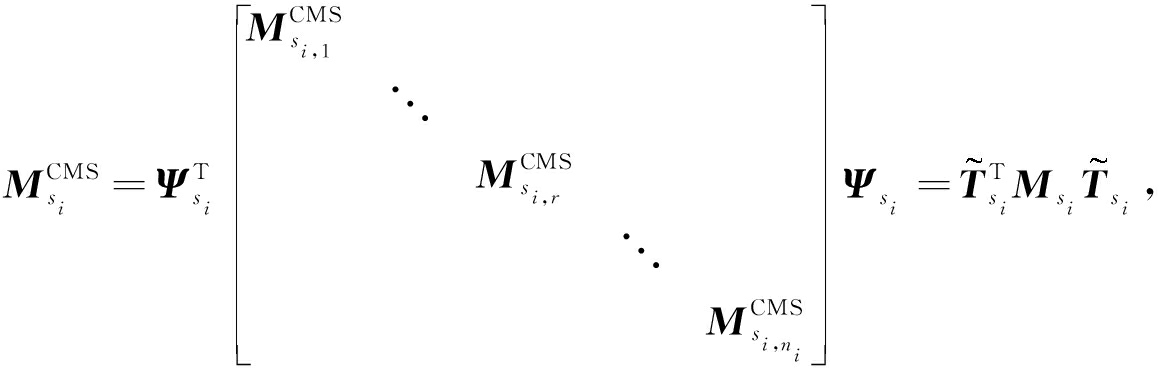
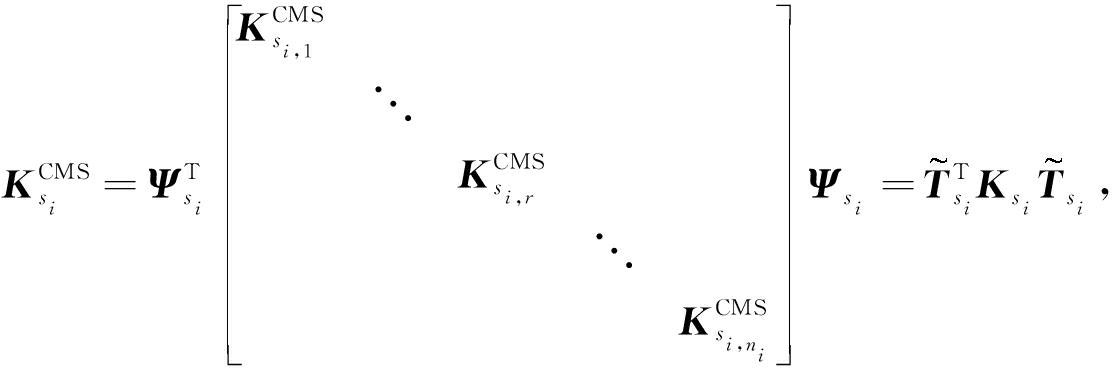
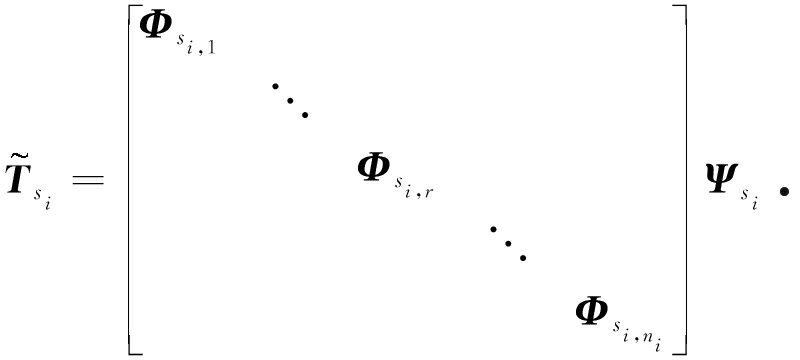
根据子结构交界面连接条件,建立子结构组装坐标变换矩阵 Ψ s i ,对 n i 个子结构 s i , r 进行组装,得到子结构 s i 的减缩质量矩阵 ![]() 和刚度矩阵
和刚度矩阵 ![]() 即
即
(3)
(4)
其中, M s i 和 K s i 分别为子结构 s i 的质量阵和刚度阵 . 需要注意的是,在模型修正阶段并不需要形成 M s i 和 K s i .
(5)
基于减缩模型进行模型修正,首先需要对子结构 s i 进行误差定位,选取设计参数 θ ={ θ 1 , θ 2 ,…, θ l },进行误差参数化,将设计参数引入到子结构模型矩阵中 . 将减缩质量矩阵 ![]() 和刚度矩阵
和刚度矩阵 ![]() 在初始设计参数处关于设计参数进行一阶Taylor展开:
在初始设计参数处关于设计参数进行一阶Taylor展开:
(6)
(7)
其中,下标(0)表示初始设计参数状态,δ θ j 代表设计参数的增量 . 减缩模型 s i 的第 k 阶特征值 ![]() 和特征向量 q k 满足
和特征向量 q k 满足
(8)
对式(8)等号两端关于设计参数 θ j 求导,整理可得
(9)
式(9)两边左乘 ![]() 应用振型正交性,可以得到特征值
应用振型正交性,可以得到特征值 ![]() 关于设计参数 θ j 的灵敏度:
关于设计参数 θ j 的灵敏度:
(10)
联立式(9)和(10),可得
(11)
其中
(12)
特征向量 q k 关于设计参数 θ j 的灵敏度∂ q k /∂ θ j 可表达为由全部 W 阶特征向量线性组合的形式 [28] ,即
(13)
特征向量 q k 满足质量归一化条件:
(14)
对式(14)关于设计参数 θ j 求导,应用式(13)并根据 ![]() 的对称性,可确定式(13)中系数 c k :
的对称性,可确定式(13)中系数 c k :
(15)
将式(13)代入式(11)中可求得向量 v k ,但由于 ![]() 所以直接求解存在困难 . 一种解决办法是把向量 v k 中第 α 个元素 v kα 置零( α 是向量 q k 中绝对值最大的元素所对应的位置),将求解向量 v k 的方程化为如下分块形式 [28] :
所以直接求解存在困难 . 一种解决办法是把向量 v k 中第 α 个元素 v kα 置零( α 是向量 q k 中绝对值最大的元素所对应的位置),将求解向量 v k 的方程化为如下分块形式 [28] :
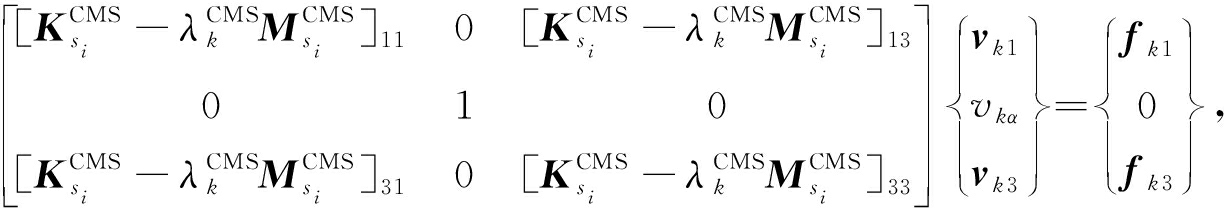
(16)
其中,下标1和3分别对应向量 v k 中的前 α -1个元素和后 W - α 个元素 .
使用特征值和特征向量关于设计参数灵敏度的计算结果,应用罚函数法可以构造设计参数 θ 的迭代关系,用下标 n 和 n +1分别代表第 n 次和第 n +1次迭代 . 修正参数向量 z 由模型的特征值和特征向量的仿真结果组成,这些特征值和特征向量的实测数据构成修正目标向量 z m . 修正参数 z n 和修正目标 z m 之间的关系可表示为
z n + S ( θ n +1 - θ n )= z m ,
(17)
其中, S 是修正参数向量 z n 关于设计参数向量 θ 的灵敏度矩阵 .
对式(17)进行整理,可以得到设计参数显式迭代更新关系:
(18)
其中, ![]() 是灵敏度逆矩阵 . 由于式(17)构成的线性代数方程组往往是过定义的或欠定义的,因此矩阵
是灵敏度逆矩阵 . 由于式(17)构成的线性代数方程组往往是过定义的或欠定义的,因此矩阵 ![]() 常常不是矩阵 S 的简单求逆,二者关系如下:
常常不是矩阵 S 的简单求逆,二者关系如下:

(19)
本文联合使用ANSYS和MATLAB软件,通过子结构试验建模综合技术,对整体结构模型的自振频率进行修正 . 子结构模型修正环节,应用固定交界面法获取减缩模型,通过罚函数法构造设计参数迭代关系 . 在子结构组装环节,分别使用了固定交界面法和自由交界面法对修正后的子结构进行组装,并与直接组装得到的全自由度模型的仿真分析结果进行了比较 . 具体实施流程如下:
(a) 将复杂结构划分为若干子结构 s i ,分别进行振动测试实验 . 在ANSYS软件中建立有限元模型,进行仿真分析,得到子结构自振频率分析结果,并与测试数据进行比对,确定设计参数 . 本文算例部分用设计参数的一组摄动值构造有限元模型,将仿真分析结果作为振动测试数据进行模型修正 .
(b) 将每一个子结构 s i 再划分为若干子结构 s i , r ,根据式(1)~(4)对子结构 s i 进行减缩,获得减缩质量矩阵 ![]() 和刚度矩阵
和刚度矩阵 ![]() 本文应用ANSYS软件实现模型减缩并将减缩后的质量矩阵和刚度矩阵导出 .
本文应用ANSYS软件实现模型减缩并将减缩后的质量矩阵和刚度矩阵导出 .
(c) 根据式(10)和(13)计算子结构自振频率关于设计参数的灵敏度,生成灵敏度矩阵 S ,构造设计参数迭代格式,即式(18),进行设计参数更新 . 本文通过MATLAB软件编制程序,使用差分法对灵敏度进行分析,实现设计参数更新 .
(d) 使用新的设计参数,生成新的子结构模型,通过步骤(b)得到的减缩基进行模型减缩,并求解修正参数 . 如果修正参数的减缩模型仿真结果与试验数据误差超过预设范围,则进行步骤(c) . 如果仿真结果误差小于预设范围,则分析修正参数的未减缩模型仿真结果误差 . 如果小于预设范围,则部件模型修正结束,反之回到步骤(b),重新生成减缩基 . 此外,如果修正参数仿真结果波动比较剧烈,或者出现收敛值大于预设范围的情况,需要重新选取设计参数进行模型修正 .
(e) 对每一个子结构 s i ( i =1,2,…, N )重复上述步骤,直至所有子结构模型均达到精度要求 . 然后在ANSYS软件中实现子结构的组装 . 本文分别采用固定交界面法、自由交界面法和直接组装3种方式对子结构模型进行了组装 .
为了提高分析效率,本文将所有ANSYS软件操作环节整理成Apdl命令,通过MATLAB软件编程实现参数修改,并自动调用ANSYS软件执行 . 步骤(b)~(d)是子结构模型修正环节,模型之间没有数据交互,本文通过编制程序实现并行求解,节省了计算时间 .
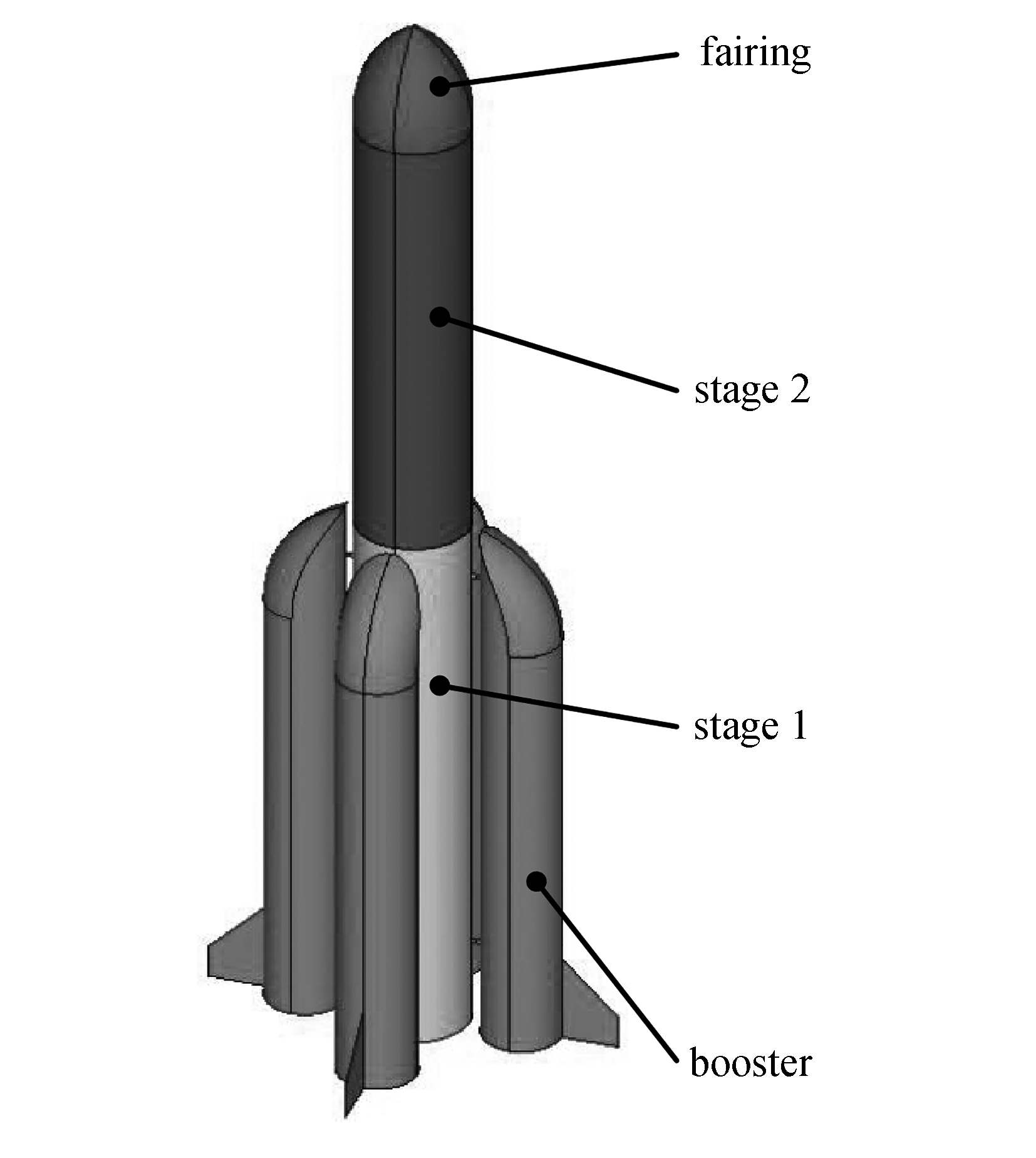
图1 运载火箭模型
Fig. 1 A launch vehicle model
图1是一个运载火箭形结构,总高50 m,最大宽度18 m . 由1个直径5 m高25 m的圆柱形芯一级,1个直径5 m高20 m的圆柱形芯二级,1个底部直径5 m高5 m的钟形整流罩和4个直径3.5 m高25 m尾翼宽2.5 m的助推器组成 . 助推器与芯一级间距为0.5 m .
本文将全箭结构划分为芯一级、芯二级、整流罩和4个助推器共7个功能部件子结构,分别使用Shell181单元建立初始有限元模型,并使用前述方法得到全箭前10阶固有频率 . 在部件模型修正中,第 k 阶固有频率的仿真结果 λ k 相对试验固有频率 ![]() 的误差 ε k 定义为
的误差 ε k 定义为
(20)
相对误差的修正目标为低于1% .
初始模型和修正后模型的参数与预设试验模型参数的误差如表1所示 . 由表1可见,经过模型修正,模型参数更趋近于预设试验模型参数 . 各部件模型在修正时的减缩比约为1%,如表2所示,这极大减小了模型规模,提高了计算效率 .
表1 功能部件模型参数误差
Table 1 The model parameter errors of each component
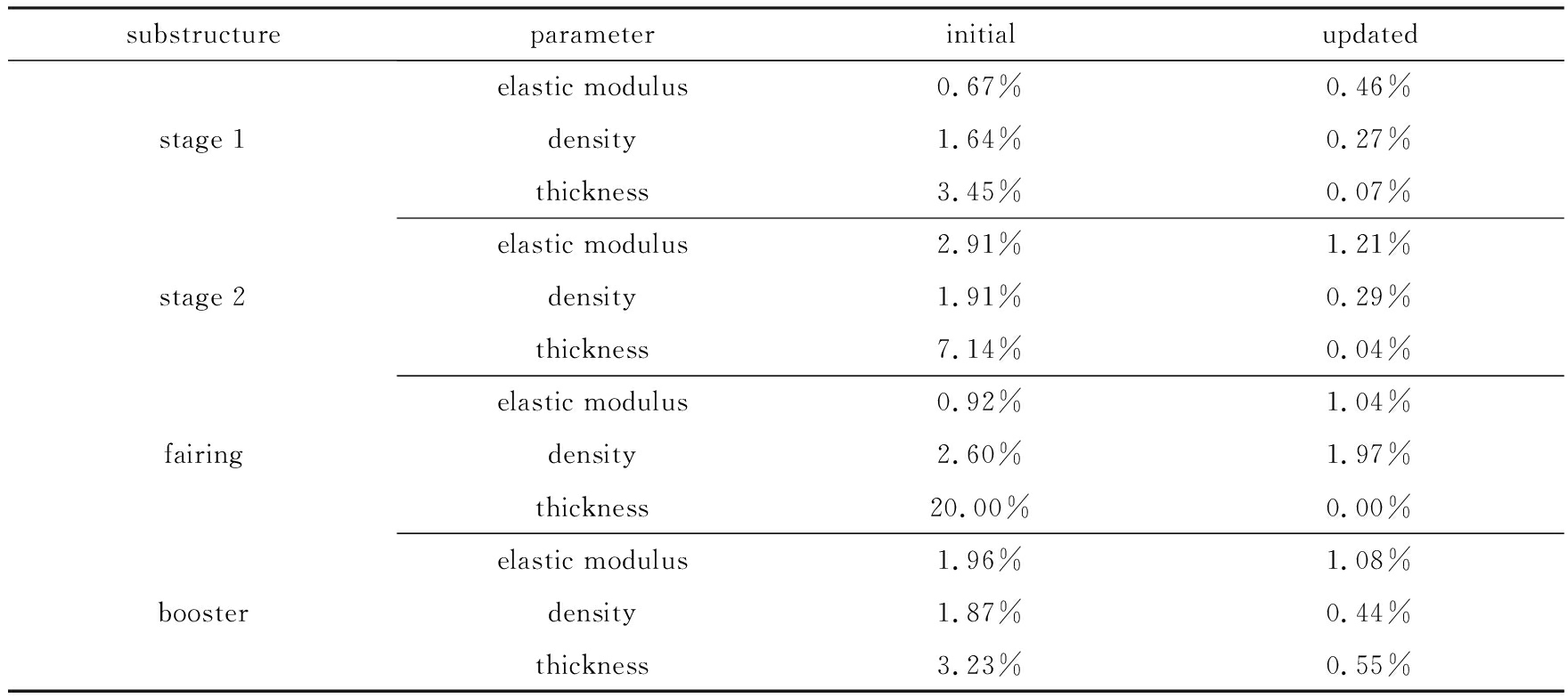
表2 功能部件原始模型与减缩模型自由度数
Table 2 The original/reduced model DOFs of each component


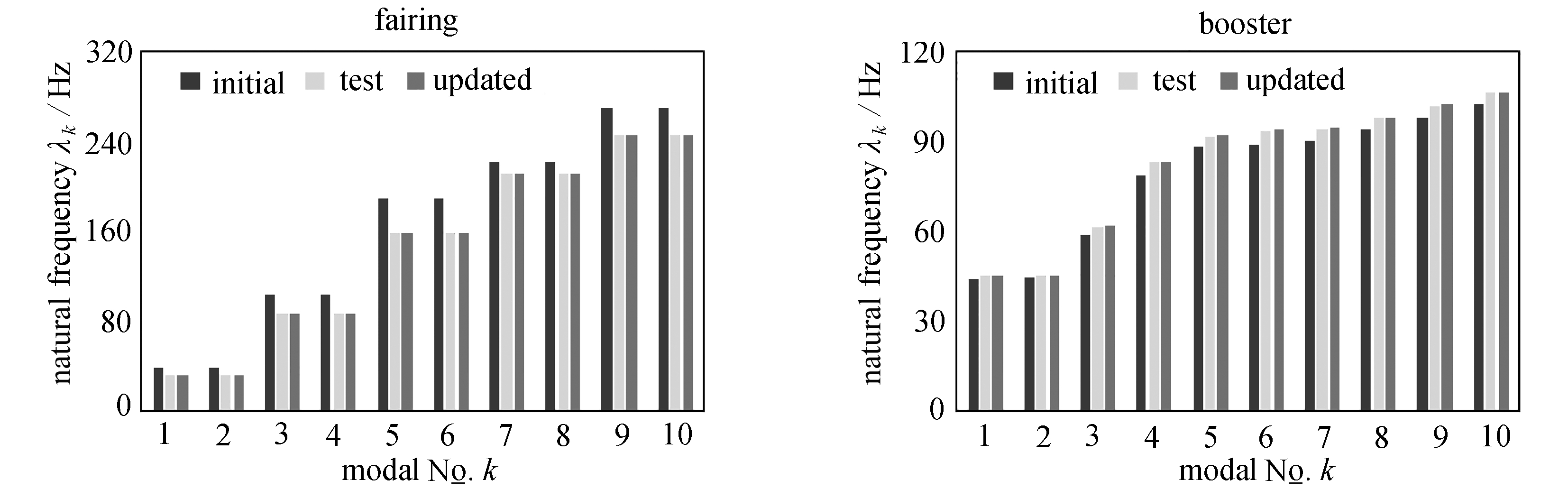
图2 功能部件前10阶固有频率
Fig. 2 First 10 natural frequencies of each component
表3 全箭前10阶固有频率
Table 3 First 10 natural frequencies of the whole launch vehicle
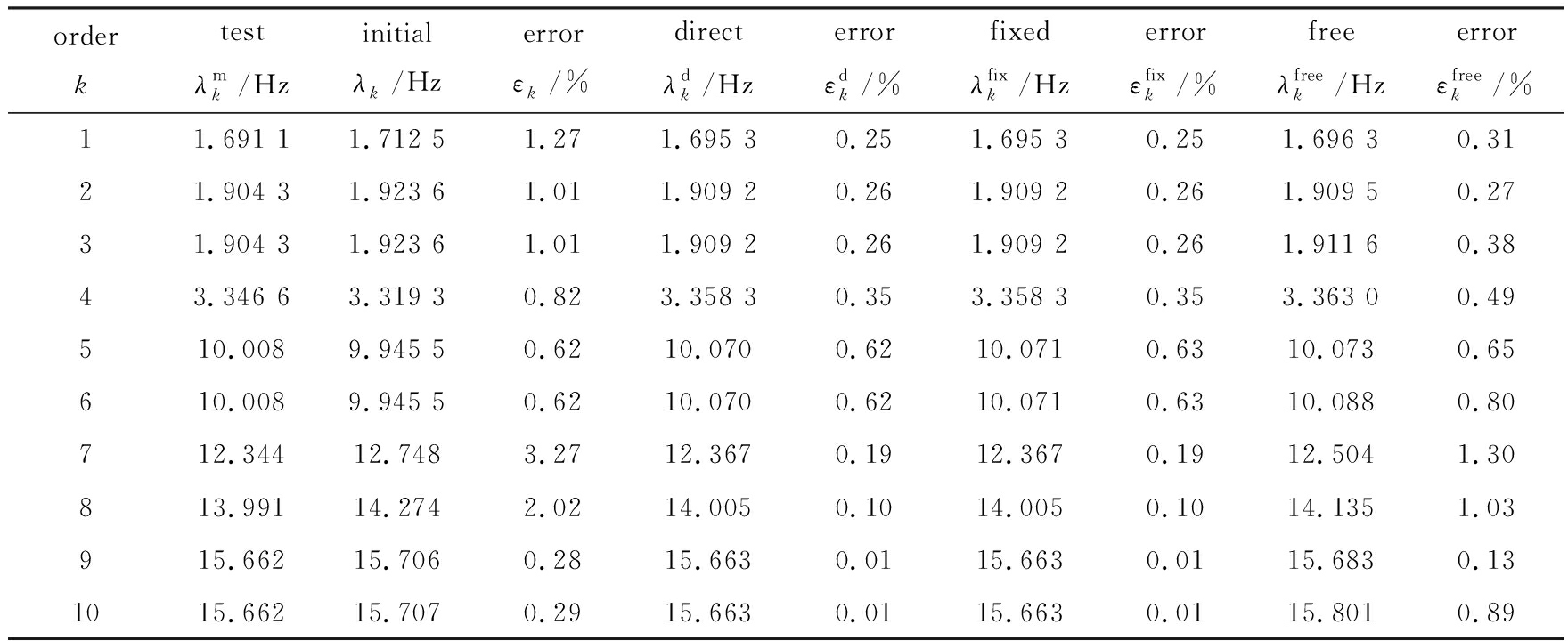
各功能部件原始模型和修正后模型的前10阶固有频率的计算结果与预设试验数据的比较如图2所示 . 可以看出,本文方法显著提高了修正后模型固有频率的精度 . 表3给出了直接组装、固定交界面法和自由交界面法3种方式获得的全箭前10阶固有频率与预设试验结果的比较 . 其中,在固定交界面法和自由交界面法中,芯一级、芯二级、整流罩和4个助推器7个功能部件各保留了前100阶主模态 . 直接组装方式的仿真结果相对误差低于1%,固定交界面法结果与直接组装方式几乎一致,自由交界面法结果存在一定误差,第7、8阶固有频率相对误差高于1% .
本文改进的子结构试验建模综合方法能够明显降低模型修正的规模,有效提高建模精度 . 应用本文方法,子结构仿真模型可以精细化建立,不必考虑模型规模对模型修正效率的影响,降低了由于模型简化不合理而引入的模型误差 . 另外,使用本文推导的理论公式,按照执行步骤操作,通过MATLAB编程对ANSYS进行二次开发,可以基于商业软件对大型复杂结构整体动力学模型进行修正,并得到与试验结果偏差较小的动力学模型,文中通过某运载火箭的算例验证了该方法的有效性 .
本文方法为子结构试验建模综合技术工程应用提供了一条有效实现途径 . 在此基础上,可以对模型误差定位、振动测试技术、模型不确定性估计、结构动力学行为预测等领域进行深入研究,最终形成标准化操作流程,供工程技术人员使用 . 另外,数字建模、生产制造、试验测试、实际工作过程中的不确定性因素对结构的力学行为影响很大,对结构的不确定性影响进行评估并通过仿真技术进行预测是十分有必要的 . 因此,将参数化和非参数化的不确定性因素考虑到子结构试验建模综合技术中,可以进一步提升大型复杂结构模型的可信度 .
参考文献 ( References ):
[1] 王毅, 朱礼文, 王明宇, 等. 大型运载火箭动力学关键技术及其进展综述[J]. 导弹与航天运载技术, 2000(1): 29-37.(WANG Yi, ZHU Liwen, WANG Mingyu, et al. Summary of some key technologies on dynamics of large launch vehicle[J]. Missiles and Space Vehicles , 2000(1): 29-37.(in Chinese))
[2] 邱吉宝, 王建民. 运载火箭模态试验仿真技术研究新进展[J]. 宇航学报, 2007, 28 (3): 515-521.(QIU Jibao, WANG Jianmin. The recent progresses on research into modal test simulation techniques for launch vehicles[J]. Journal of Astronautics , 2007, 28 (3): 515-521.(in Chinese))
[3] 邱吉宝, 王建民. 航天器虚拟动态试验技术研究及展望[J]. 航天器环境工程, 2007, 24 (1): 1-14.(QIU Jibao, WANG Jianmin. A review on virtual dynamic test techniques for space vehicles[J]. Spacecraft Environmental Engineering , 2007, 24 (1): 1-14.(in Chinese))
[4] 张正平, 邱吉宝, 王建民, 等. 航天器结构虚拟动态试验技术新进展[J]. 振动工程学报, 2008, 21 (3): 209-222.(ZHANG Zhengping, QIU Jibao, WANG Jianmin, et al. Progresses on virtual dynamic test techniques for space vehicles[J]. Journal of Vibration Engineering , 2008, 21 (3): 209-222.(in Chinese))
[5] 张德文. 未来大型复杂结构分析模型与试验状态的展望: 模型修正与模态综合技术的发展[J]. 强度与环境, 1988, 15 (6): 35-48, 53.(ZHANG Dewen. A review on analytical model and experimental state of large complex structures: development of model updating and modal synthesis techniques[J]. Structure & Environment Engineering , 1988, 15 (6):35-48, 53.(in Chinese))
[6] 杜飞平, 谭永华, 陈建华. 基于子结构试验建模综合的火箭发动机结构动力分析[J]. 推进技术, 2015, 36 (10): 1547-1553.(DU Feiping, TAN Yonghua, CHEN Jianhua. Structural dynamic analysis of rocket engine based on synthetic technology for substructure test model[J]. Journal of Propulsion Technology , 2015, 36 (10): 1547-1553.(in Chinese))
[7] 张亚辉, 林家浩. 结构动力学基础[M]. 大连: 大连理工大学出版社, 2007. (ZHANG Yahui, LIN Jiahao. Fundamentals of Structural Dynamics [M]. Dalian: Dalian University of Technology Press, 2007.(in Chinese))
[8] HURTY W C. Vibrations of structural systems by component mode synthesis[J]. Journal of Engineering Mechanics Division , 1960, 86 (4): 51-69.
[9] CRAIG R R, BAMPTON M. Coupling of substructures for dynamic analysis[J]. AIAA Journal , 1968, 6 (7): 1313-1319.
[10] CASTANIER M P, TAN Y C, PIERRE C. Characteristic constraint modes for component mode synthesis[J]. AIAA Journal , 2001, 39 (6): 1182-1187.
[11] SIMON D, COST T. Selection of characteristic constraint modes for component mode synthesis using a modification of effective interface mass[J]. AIAA Journal , 2006, 92 (1): 248-263.
[12] HOU S N. Review of modal synthesis techniques and a new approach[J]. Shock and Vibration Bulletin , 1969, 40 (4): 25-30.
[13] GOLDMAN R L. Vibration analysis by dynamic partitioning[J]. AIAA Journal , 1969, 7 (6):1152-1154.
[14] MACNEAL R H. A hybrid method of component mode synthesis[J]. Computers & Structures , 1971, 1 (4): 581-601.
[15] RUBIN S. Improved component-mode representation for structural dynamic analysis[J]. AIAA Journal , 1975, 13 (8): 995-1006.
[16] 向树红, 邱吉宝, 王大钧. 模态分析与动态子结构方法新进展[J]. 力学进展, 2004, 34 (3): 289-303.(XIANG Shuhong, QIU Jibao, WANG Dajun. The resent progresses on modal analysis and dynamic sub-structure methods[J]. Advances in Mechanics , 2004, 34 (3): 289-303.(in Chinese))
[17] BENFIELD W A, HRUDA R F. Vibration analysis of structures by component mode substitution[J]. AIAA Journal , 1971, 9 (7): 1255-1261.
[18] 楼梦麟. 结构动力分析的子结构方法[M]. 上海: 同济大学出版社, 1997.(LOU Menglin. Substructure Methods of Structural Vibration Analysis [M]. Shanghai: Tongji University Press, 1997.(in Chinese))
[19] SUAREZ L E, SINGH M P. Improved fixed interface method for modal synthesis[J]. AIAA Journal , 1992, 30 (12): 2952-2958.
[20] QIU J B, YINGZ G, WILLIAMS F W. Exact modal synthesis techniques using residual constraint modes[J]. International Journal for Numerical Methods in Engineering , 1997, 40 (13): 2475-2492.
[21] 张德文, 张欧骐. 关于固定界面法的一个附注: 精确固定界面法[J]. 振动与冲击, 1994, 52 (4): 15-22.(ZHANG Dewen, ZHANG Ouqi. Annotations on fixed-interface method: an accurate fixed-interface method[J]. Journal of Vibration and Shock , 1994, 52 (4): 15-22.(in Chinese))
[22] EWINS D J. Modal Testing : Theory and Practice [M]. Baldock: Research Studies Press, 2000.
[23] ALLEMANG R J, BROWN D L, ROST R W. Experimental modal analysis and dynamic component synthesis, measurement techniques for experimental modal analysis: AFWAL TR 87-3069 volume 2[R]. Flight Dynamics Laboratory, 1987.
[24] MOTTERSHEAD J E, LINK M, FRISWELL M I. The sensitivity method in finite element model updating: a tutorial[J]. Mechanical Systems and Signal Processing , 2011, 25 (7): 2275-2296.
[25] FRISWELL M I, MOTTERSHEAD J E. Finite Element Model Updating in Structural Dynamics [M]. Dordrecht: Kluwer Academic Publishers, 1995.
[26] 袁爱民. 基于灵敏度分析的有限元模型修正技术若干关键问题研究[D]. 博士学位论文. 南京: 东南大学, 2006.(YUAN Aimin. Studies on several key problems of finite element model updating based on the sensitivity analysis[D]. PhD Thesis. Nanjing: Southeast University, 2006.(in Chinese))
[27] FRISWELL M I. Candidate reduced order models for structural parameter estimation[J]. Journal of Vibration and Acoustics , 1990, 112 (1): 93-97.
[28] NELSON R B. Simplified calculation of eigenvector derivatives[J]. AIAA Journal , 1976, 14 (9): 1201-1205.
PIAO Siyang 1 , QI Feng 2 , ZHANG Yahui 1 ①
(1. State Key Laboratory of Structural Analysis for Industrial Equipment ( Dalian University of Technology ), Dalian , Liaoning 116024, P . R . China ; 2. Beijing Institute of Astronautical Systems Engineering , Beijing 100076, P . R . China ) (Contributed by ZHANG Yahui, M. AMM Editorial Board)
Abstract : A synthetic technology for substructure test modeling was developed based on the finite element model updating theory and the modal synthesis method. During the substructure model updating, the fixed interface component modal synthesis method was adopted to reduce the substructure model, improve the computational efficiency and thereby promote the overall efficiency of the substructure test modeling. The steps of the design parameter method in model updating and the corresponding formulas based on the reduced model were given. With a launch vehicle model as the example, and by means of the secondary development of ANSYS, the present method gets verification of effectiveness.
Key words: finite element method; model updating;dynamic substructure method;modal synthesis method
Foundation item: The National Natural Science Foundation of China(11672060)
ⓒ 应用数学和力学编委会,ISSN 1000-0887
文章编号 : 1000-0887(2018)09-0989-10
祁峰(1985—),男,高级工程师(E-mail: qifeng04@tsinghua.org.cn);
张亚辉(1972—),男,教授,博士生导师(通讯作者. E-mail: zhangyh@dlut.edu.cn).
作者简介 :
朴思扬(1992—),男,博士生(E-mail: siyang_piao@mail.dlut.edu.cn);
* 收稿日期 : 2018-02-27
基金项目 : 国家自然科学基金(11672060)
文献标志码: A
DOI: 10.21656/1000-0887.390065
(我刊编委张亚辉来稿)
中图分类号 : O342
摘要 : 基于有限元模型修正理论和模态综合法,改进了子结构试验建模综合方法 . 在子结构模型修正阶段,应用固定交界面模态综合法,对子结构模型实施减缩,提高子结构模型的计算和修正效率,从而提高了子结构试验建模综合技术整体计算效率 . 在减缩模型的基础上,推导模型修正设计参数法的计算公式,详细列出此方法的执行步骤,并以某运载火箭模型为算例,结合商业软件ANSYS二次开发,验证了该文方法的有效性 .
①引用本文 / Cite this paper: 朴思扬, 祁峰, 张亚辉. 基于模态综合法的大型结构模型修正技术[J]. 应用数学和力学, 2018, 39 (9): 989-998.PIAO Siyang, QI Feng, ZHANG Yahui. Model updating for large structures based on the modal synthesis method[J]. Applied Mathematics and Mechanics , 2018, 39 (9): 989-998.