沈暗明 1 , 陈 锐 2 , 杜丘美 1
(1. 重庆大学 航空航天学院, 重庆 400044;2. 机械传动国家重点实验室(重庆大学), 重庆 400044)
摘要 : 经典弹性理论在近代工程技术中得到广泛应用,但其本构关系中不包含任何与尺寸相关的参数,因此不适用于微观结构,不能预测和解释尺寸效应 . 广义弹性理论增加了偶应力及其对应的曲率张量,完善了对小变形的几何描述,适用于微结构的尺寸效应研究 . 该文采用广义弹性理论,并结合Hamilton变分原理推导了悬臂微梁的振动微分方程,对微梁的固有频率及其模态进行了分析 . 结果表明,随着微梁厚度的不断减小,固有频率的尺寸效应与其对应的模态密切相关 . 扭转和弯曲模态包含了旋转变形,其对应的固有频率显著提高,表现出了显著的尺寸效应;而拉压模态不涉及旋转变形,固有频率未产生明显变化,没有尺寸效应 .
关 键 词 : 尺寸效应; 广义弹性理论; Hamilton原理; 固有频率; 模态; 悬臂微梁
经典弹性理论建立在材料连续性、均匀性的基本假设上,当材料的本征长度远小于结构的几何尺寸时,该理论并不引起显著误差,即在宏观尺度下可以忽略材料的不均匀性以简化计算并确保计算的准确性 [1] . 但在微观尺度下,实际材料通常是由若干非连续甚至不均匀的粒子构成,结构内部表现有较强的非均匀性 . Fleck等 [2] 开展了不同直径的细铜丝扭转试验,结果显示当细铜丝的直径为12 μm时,无量纲的扭转硬化增加至直径为170 μm时的3倍,此现象并不出现在拉伸试验中 . Stölken和Evans [3] 在开展镍薄梁弯曲试验中发现当梁的厚度从50 μm减小到12.5 μm时,其无量纲的弯曲硬度明显增加 . 一系列的微观试验 [2-5] 表明,当结构的几何尺寸缩小到微米或亚微米量级,可以与材料的本征长度相比较时,其力学特性将出现显著变化,即表现出显著的尺寸效应 . 此时,经典弹性理论由于其本构关系不包含任何本征长度参数,便无法很好地预测和解释材料微观力学行为与尺寸效应 .
现阶段已有多种微观弹性理论可用以解释材料的微观尺寸效应 . Cosserat等 [6] 最早针对非理想流体,系统地提出了偶应力理论 . 在其基础上,Mindlin和Tiersten [7] ,Toupin [8] 以及Koiter [9] 提出了含偶应力的线弹性理论,但其理论给出的本构关系中存在较多参数 . Fleck和Hutchinson [10-11] 从位错理论出发建立了应变梯度理论,对很多尺寸效应现象做出了较为合理的解释,但由于应变梯度的引入,以及定义的高阶应力,使得本构关系以及边界条件都比较复杂 . 在此期间,还有不少理论成果发表,可参见文献[12-14] . Liu等 [15] 在Mindlin和Tiersten的含偶应力的线弹性理论基础上 [7] ,发展了广义弹性理论,从变形的几何描述出发,以应变张量描述平动变形,曲率张量描述旋转变形,二者功共轭于对称应力和偶应力,质点满足动量和动量矩方程 . 广义弹性理论涉及3个材料参数,其中两个为经典的Lamé(拉梅)常数,另一个附加材料参数为旋转模量 . 由于考虑了旋转变形的影响,使得广义弹性理论对微结构进行静力学和动力学的分析成为可能 [16] .
本文采用Liu等的广义弹性理论 [15] ,着眼于解决在航空航天、信息通讯和环境监测等领域具有广泛应用的微电子机械系统(MEMS)中的微结构,如微型压力传感器(AFM原子力显微镜)、微型陀螺仪等的微观力学行为 [17] . 相比传统机电系统,这些微结构具有微型化、智能化、多功能化等突出优点 [18] ,因此研究其微观尺度的力学行为具有重要意义 . 悬臂微梁是MEMS器件中的常见结构,目前国内外已有不少学者对微梁力学性能和尺寸效应进行了研究 [19-22] ,但仍主要侧重于分析微梁固有频率的尺寸效应问题,而未见结合微梁固有频率及对应的模态对尺寸效应做进一步的分析研究 .
本文首先简要介绍了广义弹性理论,然后利用Hamilton变分原理推导了悬臂微梁振动微分方程,并根据微分方程得到对应的微梁固有频率,将引入的旋转变形的广义弹性模型结果与经典弹性理论模型比较,分析了不同模态对应的微梁固有频率的尺寸效应 .
广义弹性理论模型将变形分解为平动变形和旋转变形,分别由应变张量和曲率张量表达,二者共轭于对称应力和偶应力,质点的运动满足动量方程和动量矩方程 . 考虑无限小变形范围, u i 为弹性体变形的位移矢量, u i , j 为二阶非对称张量,用以描述弹性体变形的位移空间梯度 . 对位移梯度进行和分解:
u i , j = ε ij + Ω ij ,
(1)
式中 ε ij 为二阶对称应变张量, Ω ij 为二阶反对称旋转张量,二者相互独立,可分别表述为
(2)
(3)
对于旋转张量,其反偶矢量为位移的旋度,即旋转矢量 ω i ,它与旋转张量的关系可通过置换张量 ε ijk 表示为
(4)
经典弹性理论仅考虑了应变张量 ε ij ,用以描述变形体的平动变形,而忽略了弹性体的旋转变形 . 旋转矢量 Ω ij 描述了变形体内一点的旋转变形程度,但不足以描述固体的旋转变形,为此需要引入曲率张量 χ ij ,用以表征变形体内任意一点的旋转变形:
(5)
式中曲率张量为二阶非对称张量,是位移的二阶导数,随着尺寸的变小,其对弹性体的影响也不断增加 . 容易验证曲率张量为无迹的二阶张量,即
χ ii = ω i , i =0 .
(6)
在连续介质力学的基础上,考虑某变形体中的任意微元体,质点受到质点邻域作用在其表面的应力和偶应力作用,考虑了含偶应力的动量方程和动量矩方程可表述为
(7)
m ji , j + ρc i + t jk ε ijk =0,
(8)
式中 b i 和 c i 分别为体力和体力偶, t ij 和 m ij 分别表示非对称应力和偶应力 .
偶应力 m ij 定义为单位面积上的力偶,它的存在导致应力张量 t ij 不再对称,可将应力张量分解为对称的Cauchy(柯西)应力 σ ij 和反对称应力 τ ij :
t ij = σ ij + τ ij .
(9)
由式(9)容易建立偶应力与反对称应力的关系:
(10)
由式(7)和式(10)可得到考虑了Cauchy应力和偶应力作用的质点动力学方程:
(11)
广义弹性理论中,考虑了变形体的平动变形和旋转变形,因此,应该分别建立平动变形和旋转变形的两种本构关系 . 平动变形下对称应力 σ ij 与对称应变 ε ij 的本构关系由广义Hooke(胡克)定律提供:
σ ij =2 με ij + λε kk δ ij .
(12)
旋转变形对应的本构关系可通过虚功原理建立 . 在静力平衡条件下,力边界条件和位移边界条件可分别写为
(13)
取虚位移δ u i 和虚旋转矢量δ ω i ,同时考虑体力和体力矩,面力和面力偶所做的虚功为
![]()
(14)
由上式可得到内力虚功的变分形式:
(15)
由式(15)可知,平动变形的对称应力与应变张量以及旋转变形的偶应力与曲率张量均分别互为功共轭,同时注意到曲率张量和偶应力均为无迹的二阶张量,由此,关于线弹性体旋转变形的本构关系可表述为
m ij =4 η χ ij ,
(16)
式中, η 为反映材料旋转变形特性的材料参数,可称之为旋转模量 . 通常定义 η = μl 2 ,材料特征尺度参数 l 为微米量级 [2] .
广义弹性理论考虑了弹性体的转动变形,增加了与之相对应的偶应力以及动量矩守恒方程 . 其模型涉及了3个材料参数,其中两个为经典的Lamé常数,另外附加的材料参数为旋转模量,用以反映材料变形特性 . 旋转模量的引入,考虑了材料的尺寸参数,为研究结构的尺寸效应提供了可能,使得整个理论模型相比于经典弹性理论更加完备 .
为分析悬臂微梁的尺寸效应,考虑匀质等截面细直梁的扭转振动,如图1所示 . 将悬臂微梁的扭转问题处理为圆截面柱形杆的扭转,由此,将坐标原点取在一端截面内,于是可求得截面的转动位移 [23] :
u 1 =- θ ( z , t ) y , u 2 = θ ( z , t ) x , u 3 =0 .
(17)
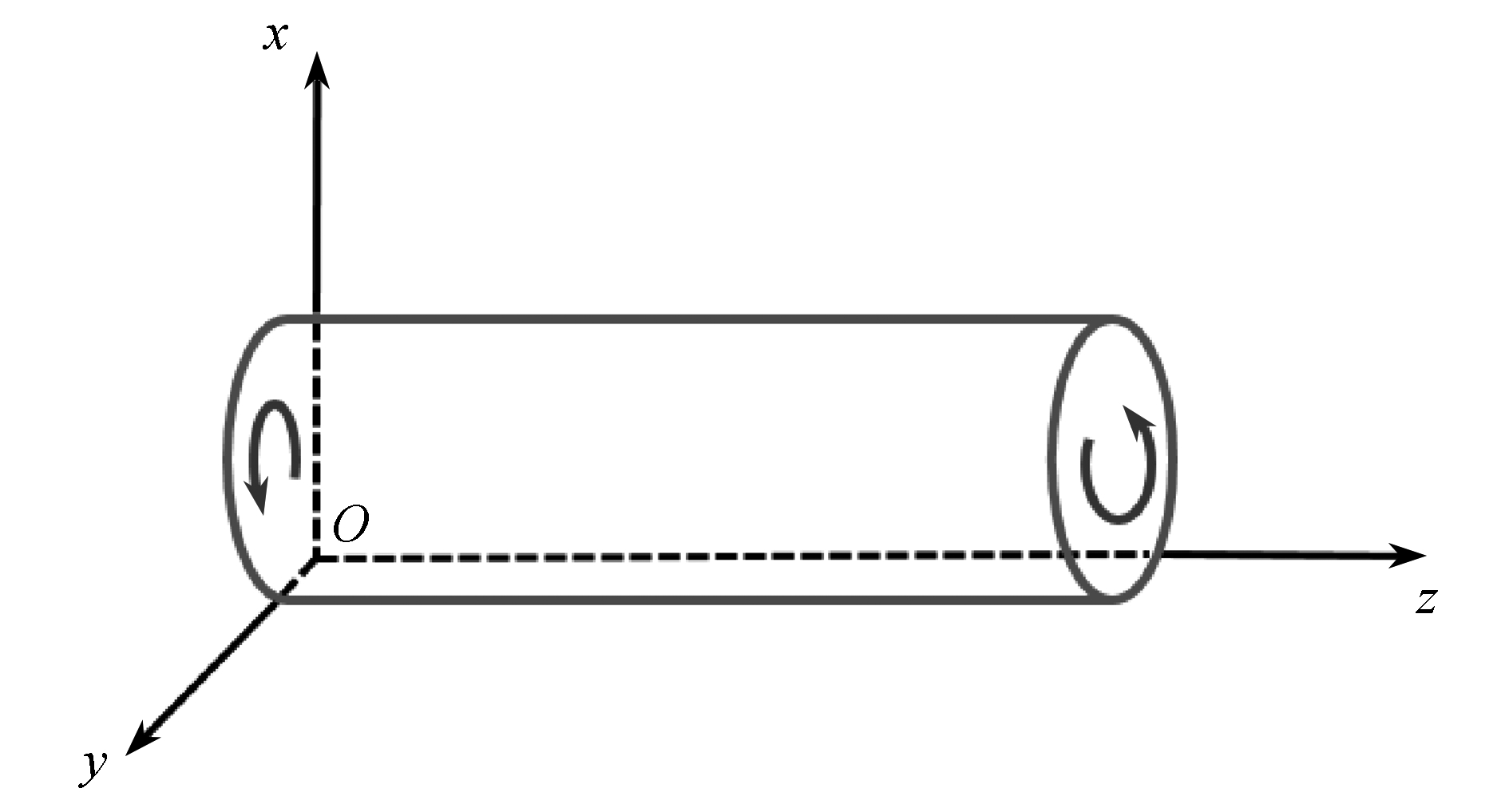
图1 匀质微杆的扭转
Fig. 1 Torsion of a micro cylinder
对于广义弹性理论,增加旋转变形及其本构关系,由式(4)可得旋转矢量为
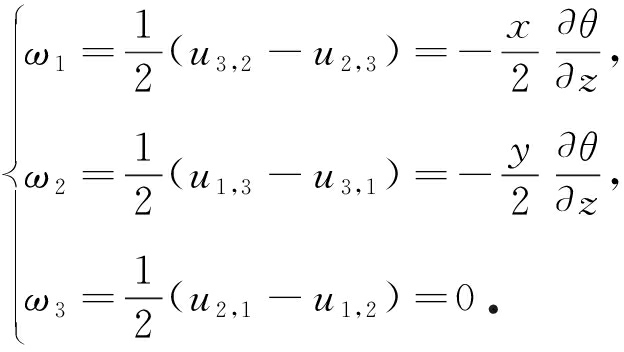
(18)
非零的曲率张量可由式(5)得
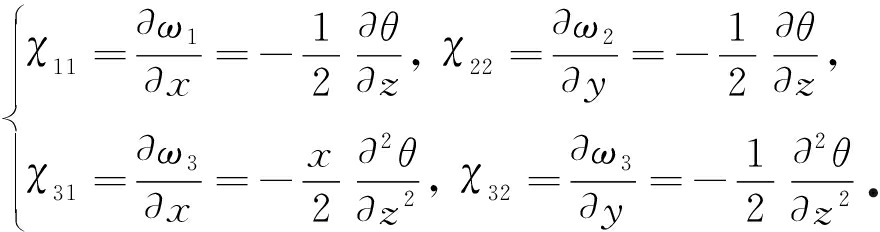
(19)
由式(16)代入可求得本构关系:
(20)
由上述非零的应变分量、应力分量、旋转矢量以及对应的曲率张量,可得到微杆扭转的应变能为
(21)
微杆扭转时其动能可表述为
(22)
考虑自由扭转问题无外力做功,由Hamilton原理可得
δ S = ![]() (δ U -δ T )dt=0 .
(δ U -δ T )dt=0 .
(23)
将式(20)、(21)代入Hamilton原理并分部积分,可得到场方程:
(24)
则其运动微分方程为
(25)
上式运动微分方程中略去高次项,有
(26)
同理,经典弹性理论中均质等截面杆扭转的运动微分方程为
(27)
如图2所示,考虑匀质等截面细直梁的横向弯曲振动,忽略剪切变形和转动惯量的影响,取固定端的形心为坐标原点,梁上任意一点的位移分量可表述为 [23]
(28)
同上扭转变形,其非零的旋转矢量以及对应的曲率张量为
(29)

图2 悬臂微梁的弯曲
Fig. 2 Bending of the micro cantilever beam
将式(29)代入式(16)可求得本构关系:
(30)
由此可以得到微梁弯曲的应变能、动能分别为
(31a)
(31b)
将式(31a)、(31b)代入Hamilton原理可得到引入了广义弹性理论的悬臂梁的弯曲方程:
(32)
经典弹性理论中均质等截面梁弯曲的运动微分方程为
(33)
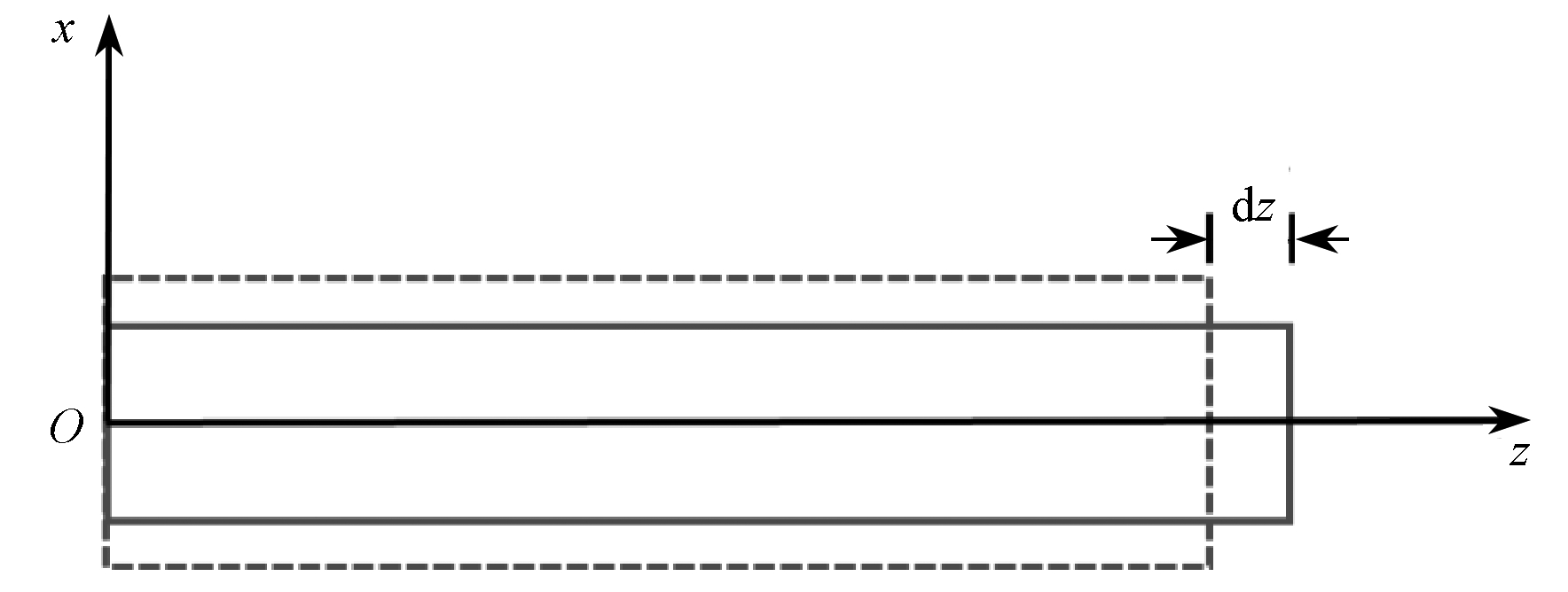
图3 悬臂微梁的拉伸
Fig. 3 Tension of the micro cantilever beam
如图3所示,匀质等截面细梁的拉伸,设梁长为 L ,单位体积的质量为 ρ . 忽略梁的纵向伸缩引起的横向变形,Poisson(泊松)比 υ 为零 . 同一横截面上各点仅在 z 方向产生相等的位移,则任意一点的位移分量为 [23]
u 1 =0, u 2 =0, u 3 = Z ( z , t ) .
(34)
引入广义弹性理论,增加旋转变形及其本构关系,可发现悬臂微梁的拉伸中无旋转变形,其旋转矢量均为零:
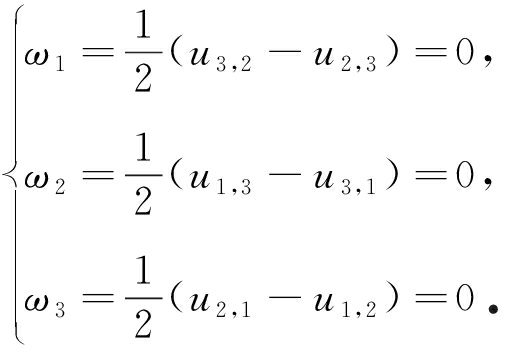
(35)
其对应的曲率张量以及偶应力也均为零,微梁拉伸的应变能、动能不发生变化 .
二者的运动微分方程均为
(36)
定义无量纲频率为广义弹性理论与经典弹性理论模型计算所得的固有频率之比 . 根据式(27)、(33)、(36)可分别得到扭转、弯曲和拉伸所对应的无量纲频率方程:
(37a)
(37b)
(37c)
式中 f , f 0 分别为广义弹性理论模型与经典弹性理论模型所计算的固有频率 .
考虑等截面匀质悬臂梁,左端固定,梁长度为 L ,梁截面高度为 H ,柱形杆的扭转截面直径为 H . 取弹性模量 E =209 GPa,Poisson比 υ =0.31,旋转模量 η =2.84 Pa · m 2 .
图4考察了悬臂微梁截面高度对无量纲频率的影响 . 由图4可知,不断减小悬臂梁的截面高度, 广义弹性理论与经典弹性理论模型计算的结果开始出现较大的偏差, 随着微梁结构尺寸的不断减小, 旋转变形的动力特性效应不断加大,无量纲频率明显增加, 微梁尺寸效应显著增强 .
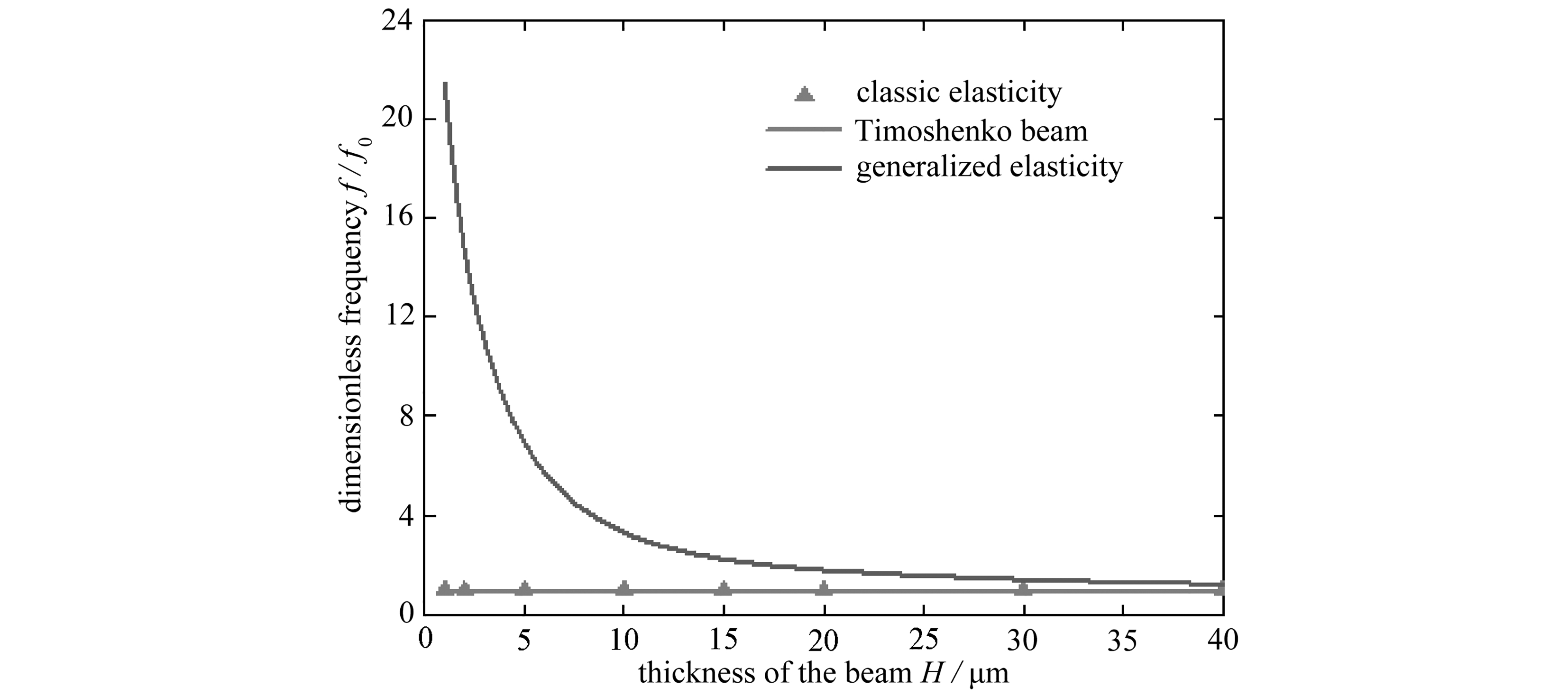
图4 不同微梁截面高度下无量纲频率的变化
Fig. 4 Dimensionless frequencies under different section heights of the micro cantilever beam

图5 Hamilton原理预测3种模态下的微梁无量纲频率的变化
Fig. 5 Dimensionless frequencies of 3 modes of the micro beam predicted by Hamilton’s principle
图5是基于广义弹性理论下,利用Hamilton原理推导的无量纲频率,反映了3种模态下微梁截面高度对无量纲频率的影响 . 图6给出了采用广义弹性理论建立三维有限元动力学方程, 使用MATLAB编制仿真程序得到微梁的无量纲频率 . 图中横坐标为微梁截面高度的对数,纵坐标为无量纲频率 . 随着微梁截面高度的降低,弯曲和扭转模态所对应的无量纲频率出现不同程度的增幅 . 悬臂梁结构尺寸较大时,由两种理论预测的扭转、弯曲和拉压状态所对应的一阶固有频率基本保持一致;随着微梁尺寸的不断减小,广义弹性理论计算所得到的扭转和弯曲模态所对应的一阶固有频率相比经典弹性理论所得到的结果出现较明显的增幅,其中扭转与弯曲模态包含了旋转变形,所对应的无量纲频率有显著提高,而拉伸模态不存在旋转变形,故其所对应的频率并未产生明显变化 .
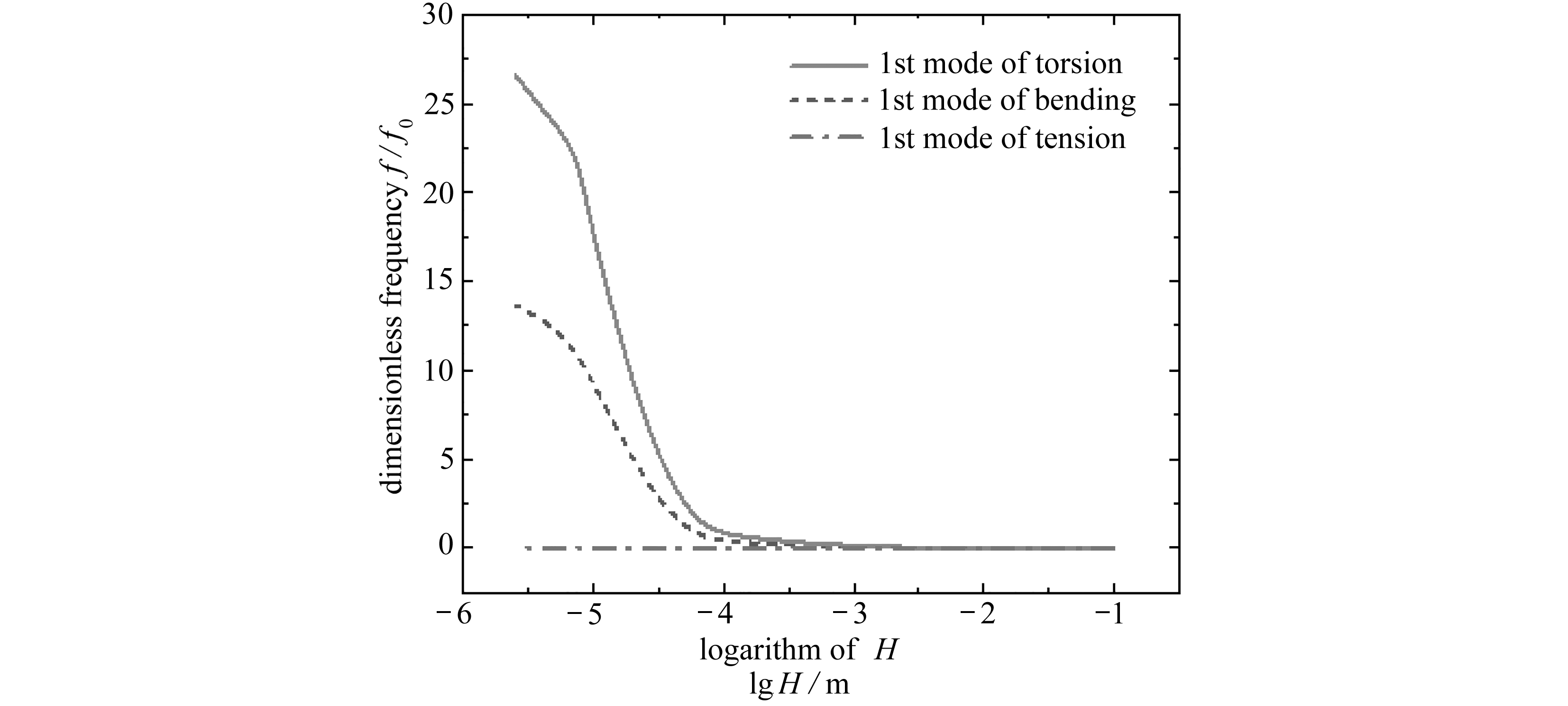
图6 MATLAB仿真程序预测3种模态下微梁无量纲频率的变化
Fig. 6 Dimensionless frequencies of 3 modes of the micro beam predicted by MATLAB
本文基于广义弹性理论,利用Hamilton原理建立了不同模态下的悬臂微梁振动微分方程,对微梁固有频率的尺寸效应进行了分析,分析结果表明,不同模态显示出了对结构的尺寸效应敏感性的差异 . 由于扭转和弯曲模态包含了旋转变形,随着微梁截面厚度的不断减小,二者对应的固有频率显著提高,表现出显著的尺寸效应;而拉压模态不包含旋转变形,微梁厚度的减小对其固有频率未产生明显影响,其固有频率不存在尺寸效应 . 本文通过引入连续旋转变形的广义弹性理论,弥补了经典弹性理论无法分析解释尺寸效应的缺陷,分析了微纳米结构广泛存在的悬臂微梁结构在不同运动状态下的尺寸效应,对MEMS等微纳米结构的材料力学响应分析以及结构设计具有指导意义 .
参考文献 ( References ):
[1] 吴家龙. 弹性力学[M]. 北京: 高等教育出版社, 2010.(WU Jialong. Elasticity [M]. Beijing: Higher Education Press, 2010.(in Chinese))
[2] FLECK N A, MULLER G M, ASHBY M F, et al. Strain gradient plasticity: theory and experiment[J]. Acta Metallurgica et Materialia , 1994, 42 (2): 475-487.
[3] STÖLKEN J S, EVANS A G. A microbend test method for measuring the plasticity length scale[J]. Acta Materialia , 1998, 46 (14): 5109-5115.
[4] LAM D C C, YANG F, CHONG A C M, et al. Experiments and theory in strain gradient elasticity[J]. Journal of the Mechanics and Physics of Solids , 2003, 51 (8): 1477-1508.
[5] CHEN X X, NGAN A H W. Specimen size and grain size effects on tensile strength of Ag microwires[J]. Scripta Materialia , 2011, 64 (8):717-720.
[6] COSSERAT E, COSSERAT F. Th é orie des Corps D é formatbles [M]. Paris: Hermann & Fils, 1909.
[7] MINDLIN R D, TIERSTEN H F. Effects of couple-stresses in linear elasticity[J]. Archive for Rational Mechanics & Analysis , 1962, 11 (1): 415-448.
[8] TOUPIN R A. Elastic materials with couple-stresses[J]. Archive for Rational Mechanics & Analysis , 1962, 11 (1): 385-414.
[9] KOITER W T. Couple-stresses in the theory of elasticity, I and II[J]. Koninklijke Nederlandse Akademie van Weteschappen : Series B , 1964, 67 : 17-44.
[10] FLECK N A, HUTCHINSON J W. A phenomenological theory for strain gradient effects in plasticity[J]. Journal of the Mechanics and Physics of Solids , 1993, 41 (12): 1825-1857.
[11] FLECK N A, HUTCHINSON J W. Strain gradient plasticity[J]. Advances in Applied Mechanics , 1997, 33 : 295-361.
[12] YANG F, CHONG A C M, LAM D C C, et al. Couple stress based strain gradient theory for elasticity[J]. International Journal of Solids and Structures , 2002, 39 (10): 2731-2743.
[13] CHEN S H, WANG T C. A new hardening law for strain gradient plasticity[J]. Acta Materialia , 2000, 48 (16): 3997-4005.
[14] 黄克智, 邱信明, 姜汉卿. 应变梯度理论的新进展(一): 偶应力理论和SG理论[J]. 机械强度, 1999, 21 (2): 81-87.(HUANG Kezhi, QIU Xinming, JIANG Hanqing. Recent advances in strain gradient plasticity, I: couple stress theory and SG theory[J]. Journal of Mechanical Strength , 1999, 21 (2): 81-87.(in Chinese))
[15] LIU Z F, FU Z. Scale effects of the stress symmetry in generalized elasticity[J]. International Journal of Aerospace and Lightweight Structures , 2012, 2 (4): 509-521.
[16] 颜世军, 刘占芳. 修正的偶应力线弹性理论及广义线弹性体的有限元方法[J]. 固体力学学报, 2012, 33 (3): 279-286.(YAN Shijun, LIU Zhanfang. A modified couple stress linear elasticity and finite element method for generalized elastic bodies[J]. Chinese Journal of Solid Mechanics , 2012, 33 (3): 279-286.(in Chinese))
[17] 张威, 张大成, 王阳元. MEMS概况及发展趋势[J]. 微纳电子技术, 2002, 39 (1): 22-27. (ZHANG Wei, ZHANG Dacheng, WANG Yangyuan. Survey and development of MEMS[J]. Micronanoelectronic Technology , 2002, 39 (1): 22-27.(in Chinese))
[18] 孙圣和. 现代传感器发展方向[J]. 电子测量与仪器学报, 2009, 23 (1): 1-10. (SUN Shenghe. Development trend of modern sensor[J]. Journal of Electronic Measurement and Instrument , 2009, 23 (1): 1-10.(in Chinese))
[19] PARK S K, GAO X L. Bernoulli Euler beam model based on a modified couple stress theory[J]. Journal of Micromechanics and Microengineering , 2006, 16 (11): 2355-2359.
[20] MA H M, GAO X L, REDDY J N. A microstructure-dependent Timoshenko beam model based on a modified couple stress theory[J]. Journal of the Mechanics and Physics of Solids , 2008, 56 (12): 3379-3391.
[21] 康新, 席占稳. 基于Cosserat理论的微梁振动特性的尺度效应[J]. 机械强度, 2007, 29 (l): l-4.(KANG Xin, XI Zhanwen. Size effect on the dynamic characteristic of a micro beam based on Cosserat theory[J]. Journal of Mechanical Strength , 2007, 29 (l): l-4.(in Chinese))
[22] 徐晓建, 邓子辰. 多层简化应变梯度Timoshenko梁的变分原理分析[J]. 应用数学和力学, 2016, 37 (3): 235-244.(XU Xiaojian, DENG Zichen. The variational principle for multi-layer Timoshenko beam systems based on the simplified strain gradient theory[J]. Applied Mathematics and Mechanics , 2016, 37 (3): 235-244.(in Chinese))
[23] 铁摩辛柯 S P, 古地尔 J N. 弹性理论[M]. 徐芝纶, 译. 3版. 北京: 高等教育出版社, 2013: 267-343.(TIMOSHENKO S P, GOODIER J N. Theory of Elasticity [M]. XU Zhilun, transl. 3rd ed. Beijing: Higher Education Press, 2013: 267-343.(Chinese version))
SHEN Anming 1 , CHEN Rui 2 , DU Qiumei 1 ①
(1. College of Aerospace Engineering , Chongqing University , Chongqing 400044, P . R . China ; 2. State Key Laboratory of Mechanical Transmissions ( Chongqing University ), Chongqing 400044, P . R . China )
Abstract : Classical elasticity has been widely applied in engineering technologies. But the length scale parameter is not included in the classical elasticity, which leads to the scale effects on mechanical characteristics and no longer satisfies the micro scale. Generalized elasticity is especially applicable to microstructures with scale effects, where both the rotational deformation and the couple stress are taken into account, and the measurement of deformation is improved. By means of Hamilton’s variation principle and generalized elasticity, the vibration differential equations for the micro cantilever beam in different motion states were derived. Then natural frequencies and vibration modes of the micro cantilever beam were analyzed. The results show that, with the decreasing of the micro beam height, the scale effect on the natural frequency is closely related to the mode. The corresponding natural frequencies of torsional and bending modes have significant increment and scale effect compared with those according to the classical elasticity, for the rotational deformation is considered. However, little variation of the natural frequency of the tensile mode is found because there is no rotational deformation involved.
Key words: scale effect; generalized elasticity; Hamilton’ s principle; natural frequency; mode; micro cantilever beam
Foundation item: The National Natural Science Foundation of China(51505044)
ⓒ 应用数学和力学编委会,ISSN 1000-0887
文章编号 : 1000-0887(2018)09-0999-10
基金项目 : 国家自然科学基金(51505044)
作者简介 : 沈暗明(1991—),男,硕士(通讯作者. E-mail: sam@cqu.edu.cn).
* 收稿日期 : 2017-12-05;
修订日期: 2018-01-09
文献标志码: A
DOI: 10.21656/1000-0887.380301
中图分类号 : O343
①引用本文 / Cite this paper: 沈暗明, 陈锐, 杜丘美. 基于广义弹性理论的微梁固有频率及模态的尺寸效应[J]. 应用数学和力学, 2018, 39 (9): 999-1008.SHEN Anming, CHEN Rui, DU Qiumei. Scale effects on natural frequencies and vibration modes of micro cantilever beams based on generalized elasticity[J]. Applied Mathematics and Mechanics , 2018, 39 (9): 999-1008.