应用数学和力学编委会,ISSN 1000-0887
水波问题是许多工程领域的共性问题,其分析通常在Euler表示下进行[1],以流速为基本未知量,但往往忽视水波的动力学属性.水波问题也可以位移为基本未知量,通过分析力学的Hamilton变分原理来建立水波方程[2-7],其特点是能够保辛.最近,文献[8]提出了基于位移表示的水波动力学理论,并给出了线性水波、 浅水波的位移周期行波解.针对一般水深周期行波解, 文献[8]提出了保辛摄动法, 可以直接给出质点粒子的轨迹, 模拟出水面尖锐的周期行波解.
文献[8]提出保辛水波动力学的基本理论,并基于流函数给出了计算质点粒子轨迹的保辛摄动法,而没有涉及到压强的计算.压强是工程师特别关心的物理量,是工程结构安全分析的重要基础.本文将在文献[8]的基础上,研究计算压强的保辛摄动方法.为方便论述,本文所采用的基本符号、变量等均与文献[8]相同,部分公式则直接采用文献[8]中的公式.
本文采用位移描述水波的运动,在水平方向和竖直方向的坐标分别记为(x,z),时间记为t,水深设为常数,记为h,水底为z=-h.静止水面记为z=0,变形后的水面记为z=w(x,0,t)=η(x,t).波幅记为η0,即为水面波η(x)的最大值.另外将波高记为A,表示水波波峰与波谷之见的相对高度,即为η(x)的最大值和最小值之差.波长记为L.
以变量u(x,z,t)为例,为表示方便,u(x,z,t)对某个自变量求偏导时,以下标表示.如u(x,z,t)对x和z的偏导分别记为ux和uz.但u(x,z,t)对时间t的偏导记为![]() 其余变量的偏导采用相同标记方法.
其余变量的偏导采用相同标记方法.
根据文献[8],二维无黏水波问题的动能和势能分别为
(1)
和
(2)
其中ρ为水密度,u(x,z,t)和w(x,z,t)分别为水平方向和竖向方向的位移,g为重力加速度.再考虑不可压缩条件,有修正项:
(3)
其中p是压强,也是Lagrange参数,与约束条件为对偶变量.再根据最小作用量原理,推得水波动力学方程可以写为
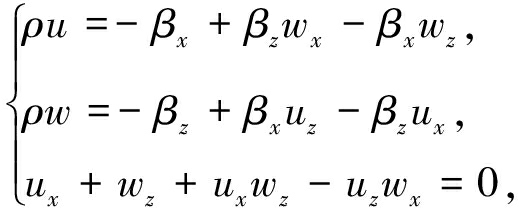
(4)
其中
(5)
即将压强p分解为重力压强-ρg(z+w)和波动产生的动压强β(x,z,t)之和.水面要求压强为零,则
(6)
如果要分析周期行波解,则令
(7)
于是有
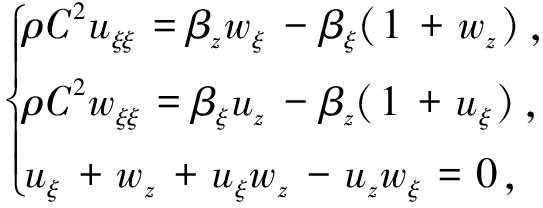
(8)
及边界条件
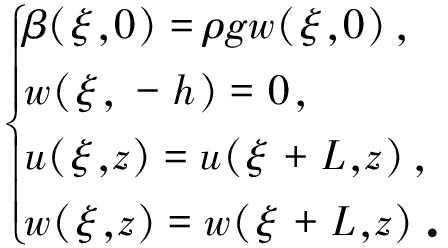
(9)
假设水是连续的,没有破碎,位移和动压强也是小量,则式(4)中

(10)
显然是比u,w,β高一阶的小量.如果水的晃动很小, 可以视为线性变形的话, 则式(4)可近似为
(11)
以上是线性水波的控制方程,可以精确求解.如果考虑非线性,则可以线性解为零阶近似解,代入fi(i=1,2,3),于是形成如下的迭代格式:
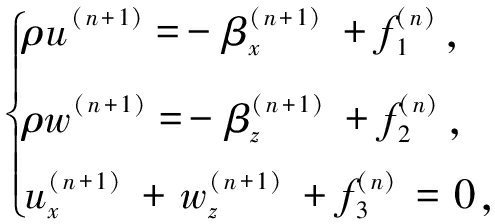
(12)
其中
(13)
其实式(12)也可以从最小作用量变分原理导出,对应的作用量为
(14)
这表明该迭代是保辛的乘法摄动.每步迭代计算中,都可以通过对式(14)进行离散,然后变分导出线性的微分-代数方程,并采用保辛的祖冲之类算法求解该方程.本文采用线性水波晃荡的振型作为空间离散的基函数,因此相当于在波数域进行离散.对于水底平坦问题的水波晃荡解可参考文献[7].
分析行波解也可采用乘法迭代方法,此时有
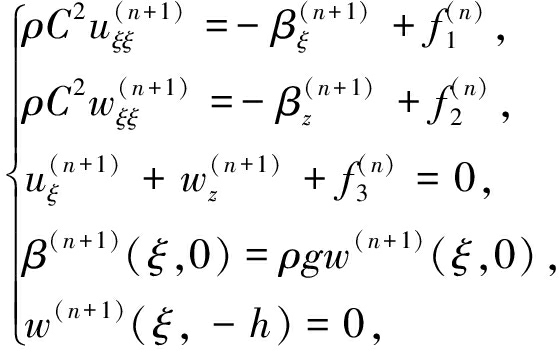
(15)
其中

(16)
式(15)对应于一种变分原理:
(17)
根据变分原理可以推出式(15).每步迭代计算中,都可以通过对式(15)进行离散,然后变分导出线性方程进行求解.本文采用线性水波的行波解作为空间离散的基函数,因此相当于在波数域进行离散.线性水波的行波解可参考文献[8].
考虑L=50 m和h=1 m的矩形水池,水密度为ρ=1 000 kg/m3,重力加速度为g=10 m/s2,初始水面形状为
(18)
其中,ξ=x+u(x,0),α和A为两个形状参数,通过调节α和A可以改变初始水面形状.α或者A越小,初始水面越平坦.该算例在文献[6]中采用浅水方程SWE-DP和祖冲之算法分析过,这里用乘法迭代计算,并与文献[6]中的结果进行比较,以测算本文方法的可靠性,计算时参数选择α=0.1和0.3,A=0.8.用本文方法计算时,空间场取40个水波晃荡的振型进行近似,采用保辛迭代法分析,时间步长取Δt=0.01 s,每次迭代时均采用2阶的保辛算法计算,迭代时要求两次迭代之间的位移差小于10-5.
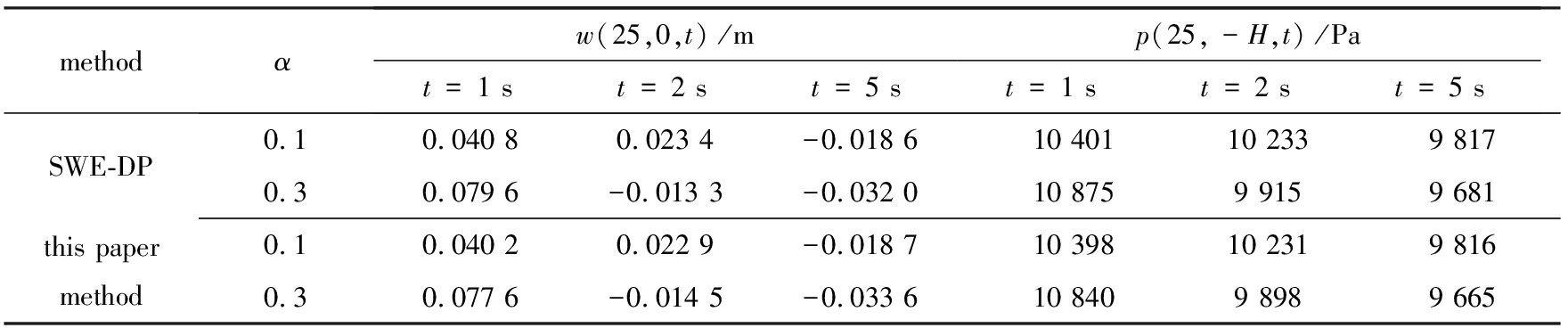
表1给出了SWE-DP与本文方法计算得到的表面x=25 m处的竖向位移w(25,0,t)和水底x=25 m处的压强p(25,-H,t)在t=1,2,5 s时的计算结果.图1和图2给出了不同参数下,水波在不同时间的形态,以及相应的压强分布.表1中,SWE-DP的计算结果取自文献[6].本文是完全非线性模型,而SWE-DP采用了浅水假定,两种模型之间存在一定差异,也必然导致在计算浅水波时的结果存在一定的微小差异.由表1可见,两种模型的计算结果差异很小:比较两种模型计算的不同时间竖直方向的位移,最大差异为8%;比较压强,两者之间的最大差异为0.3%.两种模型的计算结果基本吻合,显示了本文方法的正确性.
表1 SWE-DP与本文方法的计算结果对比
Table 1 Comparisons between results computed with the SWE-DP and the proposed method
methodαw(25,0,t)/mt=1 st=2 st=5 sp(25,-H,t)/Pat=1 st=2 st=5 sSWE-DP0.10.040 80.023 4-0.018 610 40110 2339 8170.30.079 6-0.013 3-0.032 010 8759 9159 681this paper method0.10.040 20.022 9-0.018 710 39810 2319 8160.30.077 6-0.014 5-0.033 610 8409 8989 665
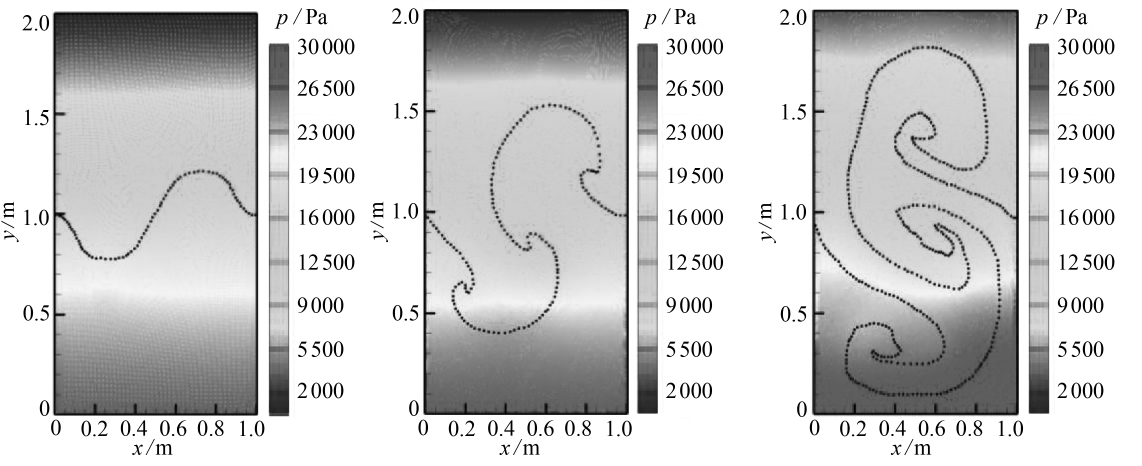
(a)t=3 s(b)t=6 s
图1 不同时刻压强分布,α=0.1
Fig. 1 The pressure distributions at different moments,α=0.1
计算行波,取h=1 m.以线性水波的行波解作为空间离散的基函数进行迭代计算,初始迭代时波幅均取为η0=0.1h,波长取L=0.65,1,2,10,15,20 m分别进行计算.当波长由小变大,对应的水波从深水波渐变为浅水波.图3绘制了不同波长下行波的形态, 以及相对应的压强分布.
由图3可见, 本文方法可以统一地给出深水和浅水行波的位移、 形态以及压强分布.L=0.65 m对应的行波很特别,其水波表明存在尖锐的波峰,这实际上是一种涌波(swell wave).随着波长的增加,水波逐渐从涌波演变为孤立波.当波长相对于水深较小时,水波属于深水波,如图3(a)~3(c);当波长相对于深水较大时,水波属于浅水波,如图3(d)~3(f).从压强分布可见:对于深水波,水表面的形态对水底压强分布的影响很小;对于浅水波,水表面的形态对水底压强的影响很大.
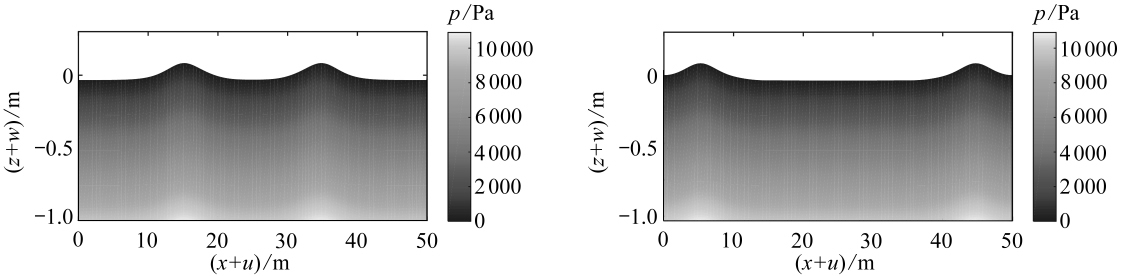
(a)t=3 s(b)t=6 s
图2 不同时刻压强分布,α=0.3
Fig. 2 The pressure distributions at different moments,α=0.3
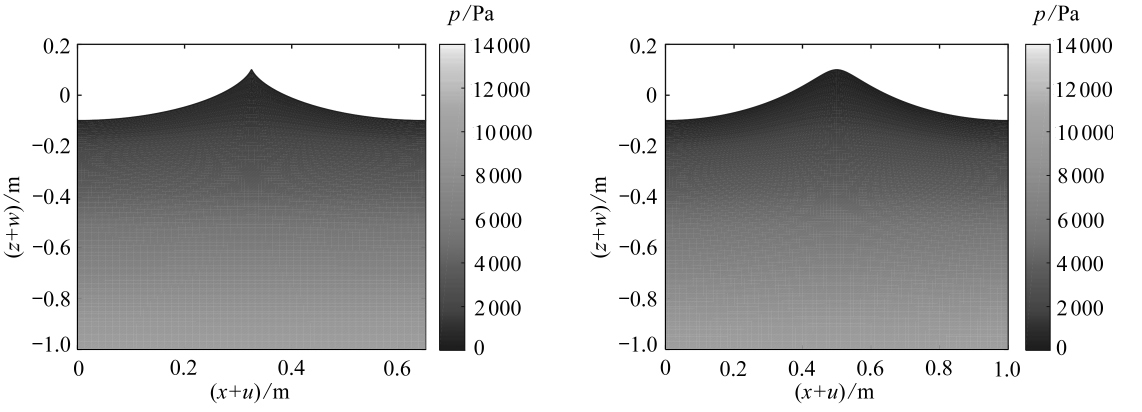
(a)L=0.65 m(b)L=1 m

(c)L=2 m(d)L=10 m
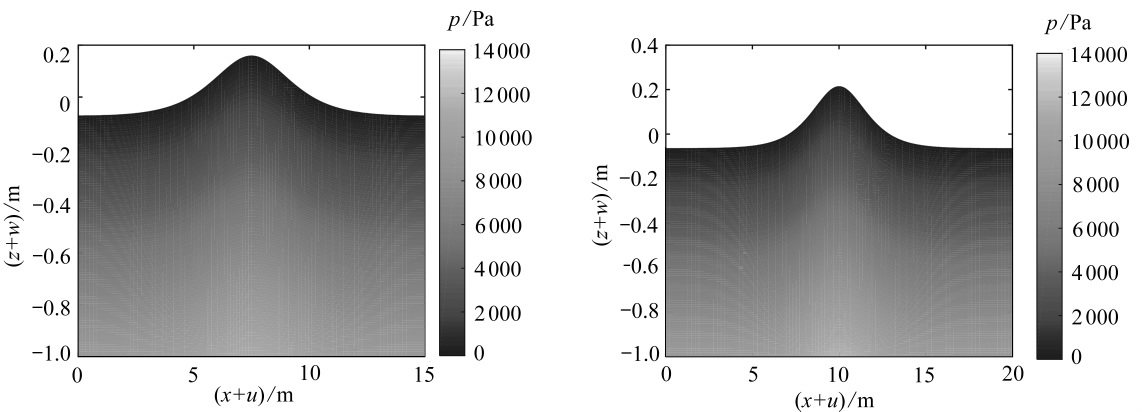
(e)L=15 m(f)L=20 m
图3 不同波长对应的波的形态及压强分布
Fig. 3 The wave shapes and pressure distributions for different wave lengths
对于工程中涉及到的水波问题,压强是需要特别关注的物理量.本文在《保辛水波动力学》一文的基础上,研究了同时考虑位移和压强的保辛摄动方法,该方法以线性水波解作为初试迭代解,然后在每个迭代过程中均通过最小作用量变分原理进行离散,保证每个迭代过程均保辛,由此建立保辛的迭代格式.与《保辛水波动力学》中的不同之处在于,本文方法可以同时计算出位移和压强.具体的数值算例表明,本文方法适用于水波的非线性演化分析,也适用于孤立波、尖锐的涌波等自然界中出现的非线性波的模拟.
[1] 梅强中. 水波动力学[M]. 北京: 科学出版社, 1984.(MEI Qiangzhong.Water Wave Dynamics[M]. Beijing: Science Press, 1984.(in Chinese))
[2] 钟万勰, 姚征. 位移法浅水孤立波[J]. 大连理工大学学报, 2006,46(1): 151-156.(ZHONG Wanxie, YAO Zheng. Shallow water solitary waves based on displacement method[J].Journal of Dalian University of Technology, 2006,46(1): 151-156.(in Chinese))
[3] 钟万勰. 应用力学的辛数学方法[M]. 北京: 高等教育出版社, 2006.(ZHONG Wanxie.Symplectic Method in Applied Mechanics[M]. Beijing: High Education Press, 2006.(in Chinese))
[4] 钟万勰, 陈晓辉. 浅水波的位移法求解[J]. 水动力学研究与进展, 2006,21(4): 486-493.(ZHONG Wanxie, CHEN Xiaohui. Solving shallow water waves with the displacement method[J].Journal of Hydrodynamics, 2006,21(4): 486-493.(in Chinese))
[5] 钟万勰, 吴锋. 力-功-能-辛-离散: 祖冲之方法论[M]. 大连: 大连理工大学出版社, 2016. (ZHONG Wanxie, WU Feng.Force-Work-Energy-Symplecticity-Discretization:ZU Chongzhi’s Methodology[M]. Dalian: Dalian University of Technology Press, 2016.(in Chinese))
[6] 吴锋, 钟万勰. 浅水问题的约束Hamilton变分原理及祖冲之类保辛算法[J]. 应用数学和力学, 2016,37(1): 1-13.(WU Feng, ZHONG Wanxie. The constrained Hamilton variational principle for shallow water problems and the Zu-type symplectic algorithm[J].Applied Mathematics and Mechanics, 2016,37(1): 1-13.(in Chinese))
[7] 吴锋. 基于位移的水波数值模拟: 辛方法[M]. 大连: 大连理工大学, 2017. (WU Feng.Numerical Modeling of Water Waves Based on Displacement:Symplectic Method[M]. Dalian: Dalian University of Technology Press, 2017.(in Chinese))
[8] 钟万勰, 吴锋, 孙雁, 等. 保辛水波动力学[J]. 应用数学和力学, 2018,39(8): 855-874.(ZHONG Wanxie, WU Feng, SUN Yan, et al. Symplectic water wave dynamics[J].Applied Mathematics and Mechanics, 2018,39(8): 855-874.(in Chinese))