ⓒ 应用数学和力学编委会,ISSN 1000-0887
最优化问题是应用数学的一个重要研究领域,它在金融决策、工程设计、经济管理、交通规划、国防科学等重要领域都有广泛的应用,人们对它的研究已经取得了许多重要的成果.其中分裂可行问题(SFP)是一类非常重要的最优化问题,它在医学、信号处理、图像重建都有着广泛的应用[1-4].1994年,Censor和Elfving[5] 根据医学中有关强放射治疗的实践经验和理论最早提出了SFP. 它是这样一个问题:设C,Q分别是Hilbert空间H1,H2上的非空闭凸子集,A:H1→H2是一个有界线性算子.SFP(见文献[5])就是要找一点x,满足
(1)
近年来,很多学者关注SFP,并提出了许多算法(详见文献[6-9]).其中部分学者用多重投影的方法得到了求解该问题的迭代算法,但这些算法在迭代中需要计算矩阵的逆,而矩阵逆的计算需要花费大量的时间且不容易求解,从而影响算法的迭代效率.为了克服这一点,Byrne[10]提出了解决分裂可行问题的CQ算法,其迭代公式为
其中λ∈(0,2/ρ(A*A)),ρ(A*A)是自伴算子A*A的谱半径,PC表示到集合C的投影.
在Hilbert空间中,CQ算法一般不具备强收敛性. 2010年,Xu[11]利用CQ算法构造了平均算子的Mann迭代序列,但仅得到弱收敛性. 此前,Xu[12]应用Halpern迭代得到了强收敛性. 之后,Wang和Xu[13]利用一族压缩算子去逼近一个非扩张算子,构造了如下序列:
且得到算法的强收敛. 本文受文献[13]的启发,主要研究改进的Halpern迭代,提出了下列算法: 对于任意的初始值u∈H1,定义迭代序列为
其中系数αk,βk,γk⊂(0,1),并证明了该算法的强收敛性,推广了Wang和Xu的结果.
本文中假设SFP是有解的,用Γ表示它的解集,即Γ=x∈C;Ax∈Q=C∩A-1(Q),设H是Hilbert空间,〈·,·〉表示内积,‖·‖表示对应的范数,I表示Hilbert空间上的单位算子,Fix(T)=xx=T(x)表示算子T的不动点集合. 全文用“![]() ”表示弱收敛,“→”表示强收敛.下面给出本文所用到的一些定义和引理.
”表示弱收敛,“→”表示强收敛.下面给出本文所用到的一些定义和引理.
定义1 设C是H中的一个非空闭凸子集,令F:C→H为非线性算子,称
1)F是非扩张算子,如果
(2)
2)F是固定非扩张算子,如果
(3)
3)F是α-平均算子,如果
(4)
其中α∈(0,1),I是单位算子,S:H→H是非扩张算子.
定义2 设C是H的非空闭凸子集,定义
为x到C的正交投影.
关于正交投影,有如下性质.
引理1 设C是H的一个非空闭凸子集,则对于任意的x,y∈H,有
(5)
(6)
(7)
引理2[14](demi-closed principle) 设C是H的一个非空闭凸子集,T:C→C是一个非扩张映象,如果![]() 并且xk-Txk→0,则x=T(x).
并且xk-Txk→0,则x=T(x).
引理3[15] 假设αk是一个非负序列,满足
其中γk⊂(0,1),δk满足下列条件:
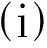

则有![]()
算法1 设C,Q分别是Hilbert空间H1,H2上的非空闭凸子集,对任意选取的初始点x0∈H1,令x0=u,定义迭代序列xk为
(8)
其中U=I-λA*(I-PQ)A,系数列αk,βk,γk⊂(0,1).
引理4[9] 如果C∩A-1(Q)≠∅,设T(x)=PCU(x),其中U=I-λA*(I-PQ)A,那么
1)U是平均算子,即U=(1-β)I+βV,其中β∈(0,1)是一个常数,V是非扩张映象.
2) Fix(U)=A-1(Q),且Fix(T)=Fix(PC)∩Fix(U)=C∩A-1(Q).
引理5 设U=I-λA*(I-PQ)A,则U是非扩张映象.
证明 因为U平均算子,对于任意的x,y∈H1,有
所以U是非扩张映象.
定理1 假设SFP的解集非空,非负序列αk,βk,γk⊂(0,1)且满足下列条件
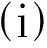 αk+βk+γk=1,∀k≥0;
αk+βk+γk=1,∀k≥0;
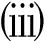
则由迭代序列(8)生成的序列xk强收敛到![]() 其中
其中![]()
证明 令T(x)=PCU(x),其中U=I-λA*(I-PQ)A.接下来分5步完成证明.
第1步 证明序列xk和Uxk是有界的.
对于任意的x*∈Fix(T)=C∩A-1(Q),有x*∈C且Ax*∈Q,于是PC(x*)=x*,Ux*=x*,Tx*=x*.由引理5知U是非扩张映象,即
从而
所以序列xk和Uxk是有界的.
第2步 证明limk→∞‖xk+1-xk‖=0.
由于U是非扩张映象,于是
由于前面所证序列xk和Uxk有界,令M=supk≥0‖u‖,‖xk‖,‖Uxk‖>0,从而
由定理1的条件 、
、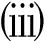 和引理3得到
和引理3得到
(9)
第3步 令Txk=PCUxk,证明limk→∞‖xk-Txk‖=0.
由第1步所证序列xk,Uxk的有界性及定理1的条件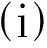 得
得
进一步,由式(9)及定理1的条件 得
得
(10)
第4步 设![]() 证明
证明
(11)
由于
先证明![]() 取xk的子列xki使得
取xk的子列xki使得
(12)
由于xk有界,不失一般性,假定![]() 则由式(12)和引理1,可得
则由式(12)和引理1,可得
(13)
下面证明
(14)
由引理4知U是平均算子,所以可以表示为U=(1-β)I+βV,其中β∈(0,1),V是非扩张映象,任取z∈Fix(T)=Fix(PCU),有
由于xk有界,取正数N使得‖xk-z‖<N,于是
结合定理1的条件 和式(9)得
和式(9)得
(15)
又因为U=(1-β)I+βV,所以上式说明式(14)成立 ,故式(11)成立.
第5步 证明![]()
(16)
式(16)即是
(17)
其中![]() 结合定理1的条件
结合定理1的条件 和式(11),得到lim supk→∞δk≤0.由引理3可得
和式(11),得到lim supk→∞δk≤0.由引理3可得![]() 故xk强收敛到
故xk强收敛到![]()
定理1中取βk=0和αk,βk=0将得到如下两个推论.
推论1 假设SFP的解集非空 ,对任意选取的初始点x0∈H1,令x0=u,序列定义为
(18)
其中αk⊂(0,1)且满足下列条件:
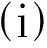

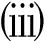
则由迭代序列(18)生成的序列xk强收敛到SFP的解集.
推论2 假设SFP的解集非空 ,对任意选取的初始点x0∈H1,序列定义为
(19)
其中αk⊂(0,1)且满足下列条件:
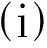

则由迭代序列(19)生成的序列xk强收敛到SFP的解集.
在Hilbert空间中,求解分裂可行问题的CQ算法一般不具备强收敛性. 为了得到其强收敛性,本文引入3个参数,利用改进的Halpern迭代,构造了求解分裂可行问题的新算法,并证明了在较弱的条件下该算法强收敛到分裂可行问题的一个解,推广了相关结果.
[1] BYRNE C. A unified treatment of some iterative algorithms in signal processing and image reconstruction[J].Inverse Problems, 2004,20(1): 103-120.
[2] CENSOR Y, ELFVING T, KOPF N, et al. The multiple-sets split feasibility problem and its applications for inverse problems[J].Inverse Problems, 2005,21(6): 2017-2084.
[3] CENSOR Y, BORTFELD T, MARTIN B, et al. A unified approach for inversion problems intensity-modulated radiation therapy[J].Physics in Medicine and Biology, 2006,51(10): 2353-2365.
[4] CENSOR Y, MOTOVA A, SEGAL A. Perturbed projections and subgradient projections for the multiple-sets split feasibility problem[J].Journal of Mathematical Analysis and Applications, 2007,327(2): 1244-1256.
[5] CENSOR Y, ELFVING T. A multiprojection algorithm using Bregman projections in a product space[J].Numerical Algorithms, 1994,8(2): 221-239.
[6] YANG Q Z. The relaxed CQ algorithm solving the split feasibility problem[J].Inverse Problems, 2004,20(4): 1261-1266.
[7] QU B, XIU N H. A note on the CQ algorithm for the split feasibility problem[J].Inverse Problems, 2005,21(5): 1655-1665.
[8] DANG Y Z,GAO Y. The strong convergence of a KM-CQ-like algorithm for split feasibility problem[J].Inverse Problems, 2011,27(1): 1-9.
[9] 杨丽, 李军. Hilbert空间中分裂可行性问题的改进Halpern 迭代和黏性逼近算法[J]. 应用数学和力学, 2017,38(9): 1072-1080.(YANG Li, LI Jun. Modified Halpern iteration and viscosity approximation methods for split feasibility problems in Hilbert spaces[J].Applied Mathematics and Mechanics, 2017,38(9): 1072-1080.(in Chinese))
[10] BYRNE C. Iterative oblique projection onto convex sets and the split feasibility problem[J].Inverse Problems, 2002,18(2): 441-453.
[11] XU H K. Iterative methods for the split feasibility problem in infinite-dimensional Hilbert spaces[J].Inverse Problems, 2010,26(10): 1-17.
[12] XU H K. A variable Krasnosel’skii-Mann algorithm and the multiple-set split feasibility problem[J].Inverse Problems, 2006,22(6): 2021-2034.
[13] WANG F H, XU H K. Approximating curve and strong convergence of the CQ algorithm for the split feasibility problem[J].Journal of Inequalities and Application, 2010,2010(1): 1-13.
[14] GOEBEL K, KIRK W A.Topics in Metric Fixed Point Theory[M]. Cambridge: Cambridge University Press, 1990.
[15] XU H K. Viscosity approximation methods for nonexpansive mappings[J].Journal of Mathematical Analysis and Applications, 2004,298(1): 279-291.