 ·v,
·v,ⓒ 应用数学和力学编委会,ISSN 1000-0887
大密度比界面流动[1]有重要工程应用背景[2-3].高精度界面捕捉方法和界面边界条件处理也是计算流体力学和计算数学难题之一.Lagrange方法可直接捕捉变形界面,特别是无网格Lagrange方法更有优势,如SPH[4-5]和耗散粒子动力学(DPD)[6]等.SPH方法最初用于计算天体物理问题[7],后被推广到计算力学领域并取得成功[8-10].SPH在界面和计算域边界条件、人工黏性项、粒子近似、光滑函数和算法精度等方面仍有待改进,近年来主要体现在单相SPH方法推广到多相SPH方法,用于计算难度较大的大密度比界面流动问题[11-13].
标准SPH方法不能计算大密度比(高密度与低密度相比约为1 000)界面流场.主要修正包括:① 在界面施加排斥力[14];② 采用数密度代替质量密度[15];③ 采用速度光滑、人工表面张力和密度重新初始化[11,16];④ 界面处采用补偿函数.Colagrossi等[11]计算了不同密度比溃坝流场,认为必须修正标准SPH方法.采用新的粒子近似,可增加数值稳定性和去掉伪表面张力,修正低密度流体状态方程可提高界面尖锐性(sharpness).其他修正还包括周期性密度重新初始化和人工黏性项、速度等.基于耗散粒子类方法(DPD方法)[17],Hu和Adams[18]提出了可计算宏观和细观界面流场SPH方法.采用不同的粒子近似函数,即粒子光滑函数是针对邻近点体积而不是密度.其他修正还包括动量方程压力梯度项近似、黏性力、表面张力和密度重新初始化、边界布置镜像对称虚粒子等,但未计算大密度比复杂界面流场.在此基础上,Hu和Adams [15]还提出“零密度变化”和“速度散度限制”、新的密度和速度梯度算子投影公式等,计算了Rayleigh-Taylor界面不稳定性问题.Chen等[12]发现Hu和Adams[18]提出的SPH方法不能计算大密度比界面流场.Chen等[12]考虑界面两侧压强连续,采用了光滑函数和水弱可压缩模型,修正粒子近似,每隔20步重新初始化密度,固壁边界采用耦合动力学方法处理,基于GFM(ghost fluid method)思想给界面虚粒子赋值,限制了密度最大值以避免出现压力为负和保持数值稳定性.但他们未修正速度和人工表面张力,分别计算了Rayleigh-Taylor界面不稳定性、非Boussinesq锁定交换和溃坝流场.鉴于Chen等[12]修正Hu和Adams[18]压力梯度项近似方法不满足对称性,且捕捉界面不够光滑,本文提出修正压力梯度项近似,使其满足对称性,并在界面处施加排列力[19],计算了Rayleigh-Taylor界面不稳定性[12]、非Boussinesq锁定交换[12]、溃坝[11-12]和气泡上升[11,13]等问题,验证了本文方法计算大密度比界面流场时的有效性.
Lagrange形式流动控制方程为
 ·v,
·v,(1)
 p+Θ-g,
p+Θ-g,(2)
(3)
其中,ρ,v,p,g,r,t和Θ分别表示密度、速度、压强、重力加速度、位移、时间和黏性项.
采用微可压缩假设描述不可压缩流体,采用如下状态方程[12]:
(4)
其中,c,ρref和pref分别表示数值声速、参考密度和参考压强.pref保证方程(4)不出现负值p;c表征水压缩性,![]() 对应单位Δρ产生的p;为保证水满足Δρ/ρ<1%,对密度相差较大的多相流,低密度流体可压缩性大,通常选取高密度流体声速作为参考速度,以保证其微可压缩性.
对应单位Δρ产生的p;为保证水满足Δρ/ρ<1%,对密度相差较大的多相流,低密度流体可压缩性大,通常选取高密度流体声速作为参考速度,以保证其微可压缩性.
函数f(r)和导数 f(r)的SPH核近似和粒子近似写为[21]
f(r)的SPH核近似和粒子近似写为[21]
(5)


 W(r-rj,h),
W(r-rj,h),(6)
其中,脚标j表示j粒子,h表示光滑长度,本文取h=1.33Δx,Δx表示粒子初始间距,W表示光滑函数,本文取Gauss函数[11]形式.
基于方程(6),方程(1)采用SPH粒子近似为
 iWij,
iWij,(7)
其中,Vj表示j粒子体积,Vj=mj/ρj, iWij表示
iWij表示 W(r-rj,h)|r=ri.
W(r-rj,h)|r=ri.
要说明的是,当t=0时,粒子均匀分布且粒子Vj相同.在相界面,支持域包含mj值量级相差大的不同相流体粒子.选用方程(8)加权求和mj,可保证不同相mj值偏差较小.
考虑流体层流黏性,方程(2)黏性项形式为
 2v,
2v,(8)
其中,υ表示运动黏性系数.
本文采用文献[22]提出的黏性项近似表达式,即
(9)
其中rij=ri-rj,vij=vi-vj,μi=υiρi.
当SPH计算不考虑黏性项,就需要采用人工黏性,以避免激波附近出现非物理震荡,本文采用Monaghan人工黏性项形式[23]:
 iWij,
iWij,(10)
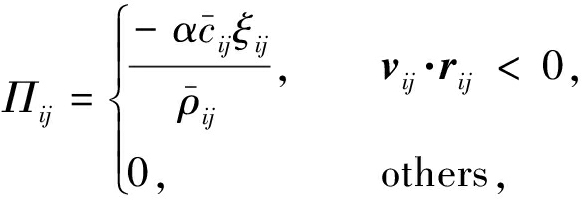
(11)
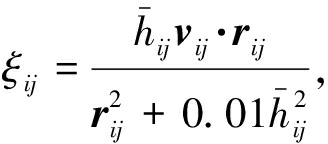
(12)
其中,avisc表示人工黏性项,α为人工黏性系数,![]() 脚标i表示粒子i.
脚标i表示粒子i.
当界面两侧流体密度相差较大(ρ1/ρ2≈1 000)时,在方程(1)的计算中,即使密度出现较小误差(如Δρ/ρ≈1%)也会引起方程(4)的压力计算出现较大误差.因此,方程(2)在界面附近的离散和界面边界条件的恰当处理是SPH计算的关键.Hu和Adams[18]对方程(2)压力梯度项采用离散形式如下:
 iWij.
iWij.(13)
Chen等[12]指出方程(13)不能处理大密度比界面问题.界面两侧流体满足pi≈pj.当ρi≪ρj时,有ρipj≪ρjpi.方程(13) 右端项简化为
(14)
方程(14)表明界面的高密度流体对低密度流体几乎无影响,这和实际不符合.本文修改方程(13)为如下形式:
 iWij.
iWij.(15)
方程(15)不会出现Chen等[12]指出的问题.当t=0时,粒子分布均匀且密度变化率不大,在界面处,有pi=pj和![]() (N表示界面法线).尽管粒子i支持域包含不同相流体粒子j,但在同一量级加权方程(15)右端项,这说明采用方程(15)离散压强梯度项是合理的.方程(15)保持了对称性,方程(2)粒子i受粒子j作用力为
(N表示界面法线).尽管粒子i支持域包含不同相流体粒子j,但在同一量级加权方程(15)右端项,这说明采用方程(15)离散压强梯度项是合理的.方程(15)保持了对称性,方程(2)粒子i受粒子j作用力为
 iWij.
iWij.(16)
同样地,粒子j受粒子i作用力为
 jWji.
jWji.(17)
考虑到 jWji=-
jWji=- iWij,方程(17)改写为
iWij,方程(17)改写为
 iWij.
iWij.(18)
比较方程(17)和(18)可知,粒子i和粒子j作用力大小相等、方向相反,自动满足Newton第二定律.
为避免界面出现多相粒子混合并影响界面光滑性,借鉴Monaghan等[19]的思想,在界面施加排斥力条件,方程(15)压力梯度项修正最终形式如下:
(19)
其中,ρref,j表示粒子j参考密度,ε表示小正数,不同算例ε取不同值.
从方程(19)知,当粒子i远离界面,粒子i支持域仅包含同相流体,有
(20)
于是方程(19)退化为方程(15),因此,选择方程(19)计算远离界面的粒子是合理的,不会引入误差.当粒子i位于界面,粒子i支持域包含不同相粒子j,有
(21)
粒子j对粒子i加速度为
(22)
与方程(15)相比,粒子j对粒子i加速度多出如下部分:
(23)
方程(23)避免了不同相粒子在界面出现混合现象,并保持界面光滑性.这与物理上的相斥流体界面现象相对应,即当流体与另外一种与其不相容的流体相互接触的时候,交界面上的力会保持界面的光滑性与清晰性.
根据1.3小节的分析,本文对动量方程(2)采用如下粒子近似:
(24)
对常微分方程
(25)
采用二阶预估校正格式[24],具体为
(26)
(27)
(28)
其中,φ和L分别表示方程(7)和(24)的左侧变量(ρi,vi)和右侧算子,n表示时间步.
使用连续性方程求解密度时,不能保证密度的光滑性,所以为了保持密度的光滑性,每20步计算对密度重新初始化[25],具体如下:
(29)
其中,粒子j和粒子i为同相流体,Wij=W(ri-rj,h).
界面和计算域边界均布置镜像对称虚粒子.当流体粒子和边界距离小于3h,在边界镜像布置虚粒子(见图1),即rg=2rw-ri,虚粒子密度、质量、压强和流体粒子相等,即fg=fi(f=ρ,m,p),脚标g和i分别表示虚粒子和实粒子,w表示壁面.对黏性壁面,取虚粒子和流体粒子速度方向相反、大小相等,即vg,t=-vi,t,vg,n=-vi,n;对无黏壁面,虚粒子和流体粒子切向速度相等,但法向速度大小相等、方向相反,即vg,t=vi,t且vg,n=-vi,n,其中,脚标“g,t”和“i,t”表示虚粒子和流体粒子切向,“g,n”和“i,n”表示虚粒子和流体粒子法向.
图1 边界和界面附近流体粒子和虚粒子示意图
Fig. 1 Schematic of fluid and ghost particles close to walls and interfaces
对靠近边界和界面的流体粒子,虚粒子排斥力表达式[26]为
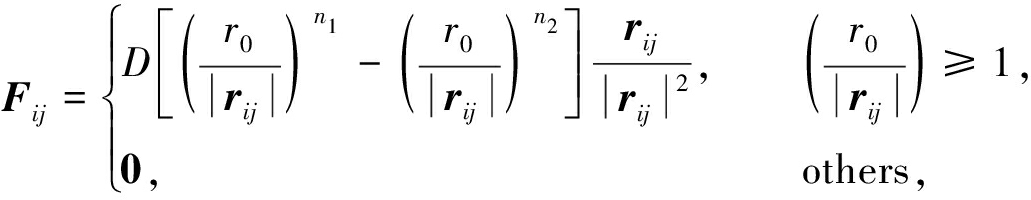
(30)
其中,Fij为排斥力,n1和n2分别取4和2,r0表示截止距离,D为Fij依赖的常数,和流体粒子最大速度平方同一量级[26].
选择4个算例验证本文方法计算不同密度比多相流场的有效性.包括Rayleigh-Taylor界面不稳定性(算例1)、非Boussinesq锁定交换(算例2)、溃坝(算例3)和气泡(算例4).其中,算例1和2的密度比小于2,算例3和4的密度比大于800.
采用SPH方法,Hu和Adams[15]、Cummins和Rudman[27]、Monaghan和Rafiee [19]、Chen等[12]都计算过算例1两种流体界面,但密度等参数取法不同.参见图2(a),当t=0时,密度为1 800 kg/m3流体(红色)置于密度1 000 kg/m3流体(蓝色)上方,界面形状为y=1.0-0.15sin(2πx).矩形容器截面尺寸为1 m×2 m, 流体粒子数取150×300.不考虑黏性,α取0.05,Δt取30 μs,ε取0.01,无量纲时间![]() 取为
取为![]() (L=1 m).
(L=1 m).
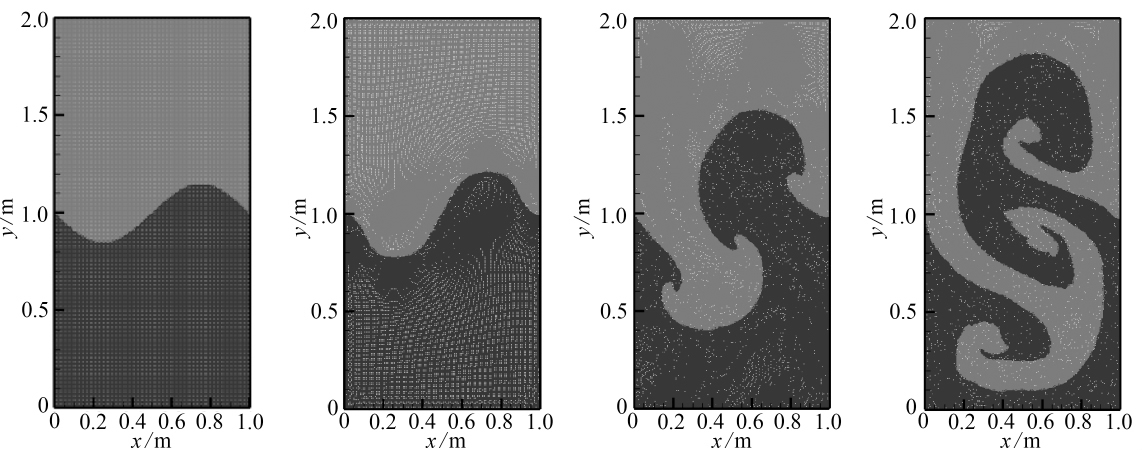
![]()
图2 不同时刻粒子分布(算例1)
Fig. 2 Particle distributions at different moments(case1)
注 为了解释图中的颜色,读者可以参考本文的电子网页版本,后同.
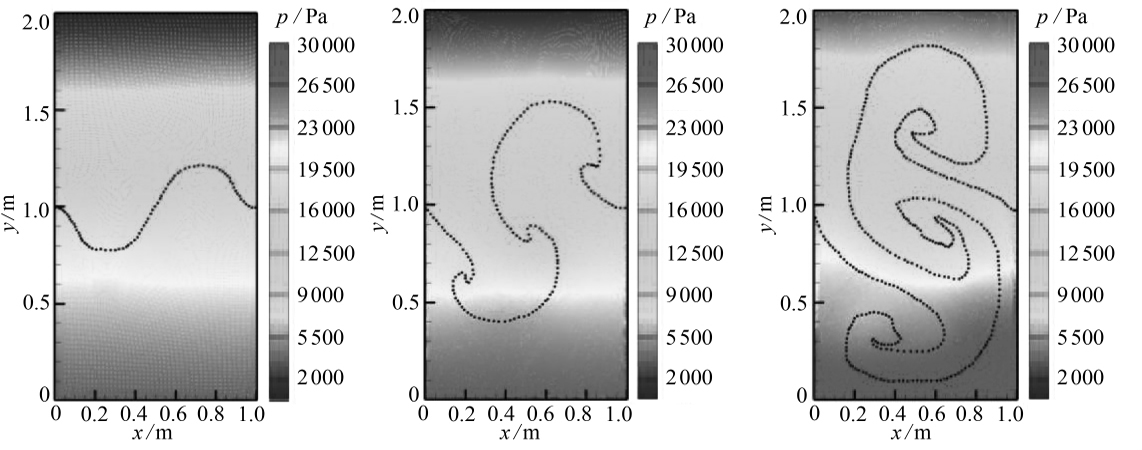
![]()
图3 不同时刻压强分布(算例1)
Fig. 3 Pressure contours at different moments(case1)
图2给出了不同时刻流体粒子分布.从图2看出,本文清晰地捕捉到不同时刻两种流体界面,界面未呈现明显扰动.轻重流体分别在对方区域产生斜入的蘑菇状射流,即尖钉(spike,重流体进入轻流体)和气泡(bubble,轻流体进入重流体).这和初始水平界面产生的沿法向、近似对称的蘑菇状射流(尖钉和气泡)是类似的[28],但正弦函数分布的初始界面是产生斜入射流的原因.压力梯度和密度梯度不共线,导致蘑菇状界面失稳并产生“滚卷(roll-up)”涡结构.这和Grenier和Antuono等[29]采用高精度level-set方法得到的计算结果是相近的.与Chen等[12]、Monaghan和Rafiee [19]计算结果相比,本文捕捉的界面光滑性更好(图2).和图2对应,图3给出了不同时刻流场压强云图,流场压强呈连续变化,这表明本文压力梯度修正适合界面附近流场计算,界面光滑,压力场连续性也较好.计算未出现“粒子集聚”现象,避免了虚假压力场(人工表面张力)导致界面曲率变大、界面之间出现很小的“狭缝”(gap).
为定量验证计算结果,图4给出了低密度流体界面最高点位移y随![]() 变化曲线,Chen和Zong等[12]也给出了对应的计算结果.从图4看出,当
变化曲线,Chen和Zong等[12]也给出了对应的计算结果.从图4看出,当![]() 较小时,本文y计算值略低于Dalziel[30]简化得到的Layzer理论值,当
较小时,本文y计算值略低于Dalziel[30]简化得到的Layzer理论值,当![]() 较大时,y逐渐趋近Layzer理论值,最后和Layzer理论值重合.和Chen等[12]的结果相比,在
较大时,y逐渐趋近Layzer理论值,最后和Layzer理论值重合.和Chen等[12]的结果相比,在![]() 范围内,本文得到的
范围内,本文得到的![]() 曲线与Layzer理论值符合更好.
曲线与Layzer理论值符合更好.
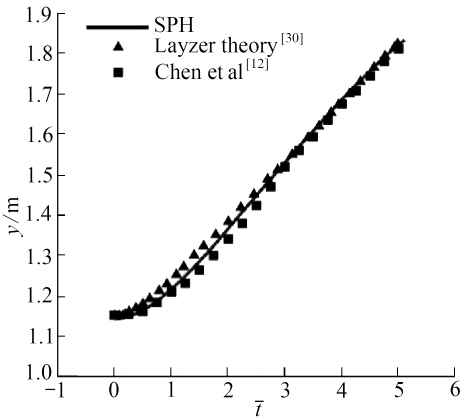
图4 低密度流体![]() 曲线(算例1)
曲线(算例1)
Fig. 4 The![]() for light fluid(case1)
for light fluid(case1)

(a) 粒子分布
(a) Particles distribution

(b) 压强分布
(b) Pressure contours
图5 流体粒子和压强分布(t=0,算例2)
Fig. 5 Distribution of particles and pressure contours att=0(case2)
挡板隔开矩形截面水平管两侧不同密度流体(图5),当瞬时抽去无质量隔板后,两种流体发生相对运动.密度相差大的情况称为非Boussinesq锁定交换问题(算例2),反之称为Boussinesq锁定交换问题.算例2已有多篇文献进行了计算,如Chen和Zong等[12]、Monaghan和Rafiee[19]采用SPH方法,Birman和Martin等[31]采用高精度谱Galerkin方法离散空间导数和三阶Runge-Kutta方法离散时间导数.取矩形管道长L和高H分别为1.82 m和0.2 m,保证流动达到定常状态.挡板左侧为高密度(红色)流体、右侧为低密度流体(蓝色),表1给出各变量列表,脚标1和2分别代表挡板左、右侧状态.密度比r1=ρr1/ρr2约为0.681.假设两种流体运动黏性系数均为10-6 m2·s-1,不采用人工黏性项.当t=0时,流体粒子数取80×728,粒子均匀分布且Δx为2.5 mm,c取![]() 取为20 μs,ε=0.01,无量纲时间
取为20 μs,ε=0.01,无量纲时间![]() 取为
取为![]()
表1 挡板左右两侧流体参数
Table 1 Parameters on left and right sides of the baffle

reference densitypressuredensityleft fluidρr1=1 466 kg/m3 p1=ρr1gyρ1=ρr1+p1/c2right fluidρr2=1 000 kg/m3p2=ρr2gyρ2=ρr2+p2/c2
![]()
图6 本文计算界面和文献[32]实验照片
Fig. 6 The computed interfaces and experimental pictures in ref. [32]

图7 重流体计算界面锋面的局部放大图![]() 算例2)
算例2)
Fig. 7 The enlarged interface front for the heavy fluid at![]() (case 2)
(case 2)
当![]() 为2.4和4.2时,图6给出了流体粒子分布.图6(a)和6(b)给出的流体粒子分布显示了计算界面;图6(c)和6(d)为文献[32]的实验照片.从图6看出,轻重流体分别沿水平管上、下壁面自右至左和自左至右运动,形成了剪切界面.随计算时间增大,左右相对运动的界面存在切向速度剪切或速度差,出现了界面失稳或表面波(Kelvin-Helmholtz界面不稳定性).图6(a)和6(b)界面形状与图6(c)和6(d)实验照片定性相符,如表面波及其形状等,但下壁面附近的界面锋面位置有明显差异.其原因是,Kelvin-Helmholtz界面失稳产生剪切混合并发展为湍流.在界面处,表面波峰和波谷的光散射导致界面附近出现消光,导致实验照片出现黑色区域.和Chen等[12]的计算结果相比,本文计算界面和实验图像更接近.图7为图6(b)界面锋面局部放大图.从图7看出,自水平管下壁的界面锋面下游(左侧),界面出现了两种流体卷吸,轻流体被卷入重流体,表面波导致了湍流混合,但Chen等[12]未给出这些细致的计算结果.他们认为误差主要原因是实验采用可混溶的两种流体(淡水和氯化钠溶液)[32],水平管下壁面为密度大的流体,对应的压强也高,加速了流体运动并促进两者混合.本文与Chen等[12]流场计算均采用Euler方程描述,但方程(1)忽略由Fick定律控制的流体扩散效应.本文与Chen等[12]对方程(2)压力梯度粒子近似的修正是不同,本文在界面增加了排斥力,减小了计算界面和实验照片之间的偏差.
为2.4和4.2时,图6给出了流体粒子分布.图6(a)和6(b)给出的流体粒子分布显示了计算界面;图6(c)和6(d)为文献[32]的实验照片.从图6看出,轻重流体分别沿水平管上、下壁面自右至左和自左至右运动,形成了剪切界面.随计算时间增大,左右相对运动的界面存在切向速度剪切或速度差,出现了界面失稳或表面波(Kelvin-Helmholtz界面不稳定性).图6(a)和6(b)界面形状与图6(c)和6(d)实验照片定性相符,如表面波及其形状等,但下壁面附近的界面锋面位置有明显差异.其原因是,Kelvin-Helmholtz界面失稳产生剪切混合并发展为湍流.在界面处,表面波峰和波谷的光散射导致界面附近出现消光,导致实验照片出现黑色区域.和Chen等[12]的计算结果相比,本文计算界面和实验图像更接近.图7为图6(b)界面锋面局部放大图.从图7看出,自水平管下壁的界面锋面下游(左侧),界面出现了两种流体卷吸,轻流体被卷入重流体,表面波导致了湍流混合,但Chen等[12]未给出这些细致的计算结果.他们认为误差主要原因是实验采用可混溶的两种流体(淡水和氯化钠溶液)[32],水平管下壁面为密度大的流体,对应的压强也高,加速了流体运动并促进两者混合.本文与Chen等[12]流场计算均采用Euler方程描述,但方程(1)忽略由Fick定律控制的流体扩散效应.本文与Chen等[12]对方程(2)压力梯度粒子近似的修正是不同,本文在界面增加了排斥力,减小了计算界面和实验照片之间的偏差.
和图6对应,图8给出了流场压强云图分布.图8表明,流场压强变化是连续的.当高度相同,尽管不同流体初始压强相差较大(图5(b)),但不同流体压强差随计算时间增大而逐渐缩小.其原因是,特征时间小的流场压差是以波形式传播,达到压力平衡所需时间短.这和实际也是定性相符的.

![]()
图8 不同时刻流场压强分布(算例2)
Fig. 8 Pressure contours at different moments(case 2)
图9给出轻重流体界面锋面和挡板无量纲距离x/H随![]() 变化曲线.从图9看出,轻重流体x/H随
变化曲线.从图9看出,轻重流体x/H随![]() 变化曲线和测量值变化趋势相同,两者近似呈线性变化,与文献计算和实验结果[19,31-32]相符合.对重流体,
变化曲线和测量值变化趋势相同,两者近似呈线性变化,与文献计算和实验结果[19,31-32]相符合.对重流体,![]() 曲线的测量值略高于计算值.初始误差较小,误差随
曲线的测量值略高于计算值.初始误差较小,误差随![]() 增大而增大并趋于恒定值 (图9(a)).对轻流体,
增大而增大并趋于恒定值 (图9(a)).对轻流体,![]() 曲线的计算值和测量值误差在初始时较大,随计算时间增大,误差趋近于0(图9(b)).这表明本文修正方法、界面和计算域边界处理是合理的.
曲线的计算值和测量值误差在初始时较大,随计算时间增大,误差趋近于0(图9(b)).这表明本文修正方法、界面和计算域边界处理是合理的.
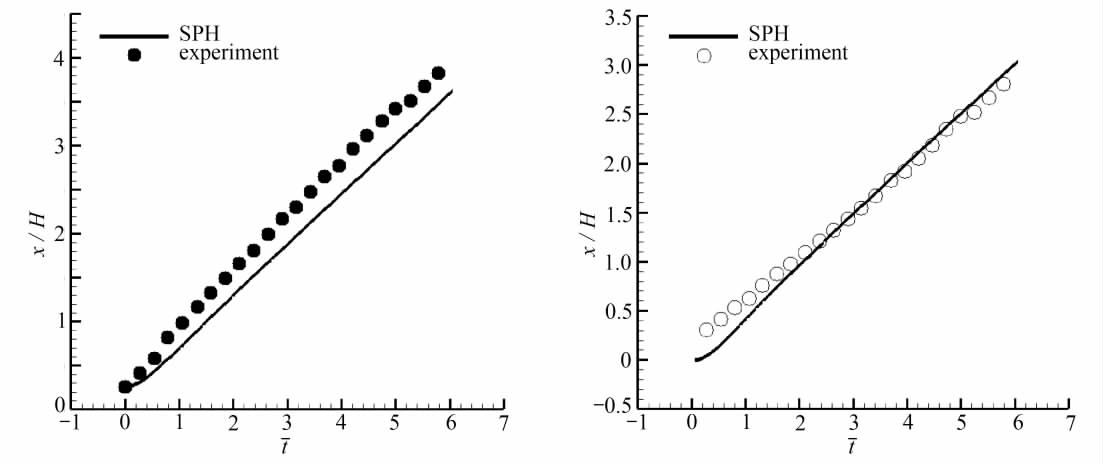
(a) 重流体(b) 轻流体
(a) The heavy fluid(b) The light fluid
图9 轻重流体![]() 曲线 (算例2)
曲线 (算例2)
Fig. 9 Curvex/H vs.![]() for light and heavy fluids respectively(case 2)
for light and heavy fluids respectively(case 2)
分别采用水单相、空气和水两相流模型,Colagrossi等[11]、Chen等[12]、沈雁鸣和陈坚强[13]计算了算例3,目的是验证算法对大变形和破碎界面或自由面、界面流动的适应性.由于所取计算域和水域等参数均不相同,因此,无法比较这些文献的算例结果.参照文献[11-13], 图10(a)给出了算例3计算域(1.6 m×0.9 m)示意图, 计算域左下角(红色)的水域尺寸为0.6 m× 0.3 m,其他区域为空气(蓝色),垂直挡墙位于右侧x=1.6 m.水和空气参考密度ρrw取1 000 kg/m3,ρrg取1.29 kg/m3.采用两相SPH方法分别计算空气和水流场(两相流界面),水和空气密度取其参考密度.当t=0时,Δx取5 mm,流体粒子数取320×180.忽略流体黏性,α取0.05,c取![]() 为水高度(H=0.3 m),Δt取2.5 μs,ε=0.08,无量纲时间
为水高度(H=0.3 m),Δt取2.5 μs,ε=0.08,无量纲时间![]() 取为
取为![]() 固壁速度取滑移条件,水和空气的初始压强皆为100 Pa.
固壁速度取滑移条件,水和空气的初始压强皆为100 Pa.


![]()
图10 不同时刻流体粒子位置和自由面(算例3)
Fig. 10 Particle positions and free surfaces at different moments(case 3)
当![]() 取3.2,4.8,5.6,6.4和7.0时,图10(b)~10(f)给出不同时刻流体粒子位置.从图10看出,受重力作用,初始静止的水沿下壁面向右加速流动(图10(a)),水自由面高度自左向右逐渐降低,但水速度逐渐增大.和挡墙撞击后,水沿x轴被滞止,水动能急剧减小但压力增大,左侧水仍继续高速向右运动(惯性大).在挡墙和下壁面交线处,水自由面锋面沿挡墙垂直向上爬升(图10(b)),随着时间增大,重力导致水沿挡墙壁面速度逐渐减小.当水到达挡墙最高点(ymax≈0.9 m)且速度降为零后,重力又使水沿挡墙反向加速运动.上行和下行水流在挡墙(y≈0.6 m)汇集,形成图10(c)“鼓包”(滞止区),沿挡墙下行水流速度减小但压力增大,上行水继续冲击“鼓包”底部,水从“鼓包”顶部继续下落,受挤压的“鼓包”形成了图10(d)向左下角弯曲的“水射流”.“水射流”包裹部分空气并形成气泡.重力和“鼓包”导致“水射流”左下方下落,形成类似“水射流”冲击底面的水自由面,“水射流”撞击近似水平的自由面并向右上方再次反射为“水射流”,反射的“水射流”出现自由面破碎或飞溅,水沿挡墙壁面逐渐分离 “水舌”(图10 (e)).随着时间增大,水沿下壁面的自由面高度逐渐降低并逐渐达到平衡、沿挡墙壁面的水速度不断减小,水自挡墙壁面分离且分离点不断下移,在自由面再次反射的“水射流”沿左上方变长,下壁面的水自由面高度也基本不变(图10 (f)).和文献[11-13]相比,图10表明气水界面较光滑且计算结果定性相符,但各算例所取参数不同,流场细节仍有差别,较单相SPH计算的界面更光滑[12].和图10对应,图11给出了不同时刻流场压强云图.图11表明,流场压强呈连续变化且未出现明显压强震荡.
取3.2,4.8,5.6,6.4和7.0时,图10(b)~10(f)给出不同时刻流体粒子位置.从图10看出,受重力作用,初始静止的水沿下壁面向右加速流动(图10(a)),水自由面高度自左向右逐渐降低,但水速度逐渐增大.和挡墙撞击后,水沿x轴被滞止,水动能急剧减小但压力增大,左侧水仍继续高速向右运动(惯性大).在挡墙和下壁面交线处,水自由面锋面沿挡墙垂直向上爬升(图10(b)),随着时间增大,重力导致水沿挡墙壁面速度逐渐减小.当水到达挡墙最高点(ymax≈0.9 m)且速度降为零后,重力又使水沿挡墙反向加速运动.上行和下行水流在挡墙(y≈0.6 m)汇集,形成图10(c)“鼓包”(滞止区),沿挡墙下行水流速度减小但压力增大,上行水继续冲击“鼓包”底部,水从“鼓包”顶部继续下落,受挤压的“鼓包”形成了图10(d)向左下角弯曲的“水射流”.“水射流”包裹部分空气并形成气泡.重力和“鼓包”导致“水射流”左下方下落,形成类似“水射流”冲击底面的水自由面,“水射流”撞击近似水平的自由面并向右上方再次反射为“水射流”,反射的“水射流”出现自由面破碎或飞溅,水沿挡墙壁面逐渐分离 “水舌”(图10 (e)).随着时间增大,水沿下壁面的自由面高度逐渐降低并逐渐达到平衡、沿挡墙壁面的水速度不断减小,水自挡墙壁面分离且分离点不断下移,在自由面再次反射的“水射流”沿左上方变长,下壁面的水自由面高度也基本不变(图10 (f)).和文献[11-13]相比,图10表明气水界面较光滑且计算结果定性相符,但各算例所取参数不同,流场细节仍有差别,较单相SPH计算的界面更光滑[12].和图10对应,图11给出了不同时刻流场压强云图.图11表明,流场压强呈连续变化且未出现明显压强震荡.


![]()
图11 不同时刻流场压强云图(算例3)
Fig. 11 Pressure contours at different moments(case 3)
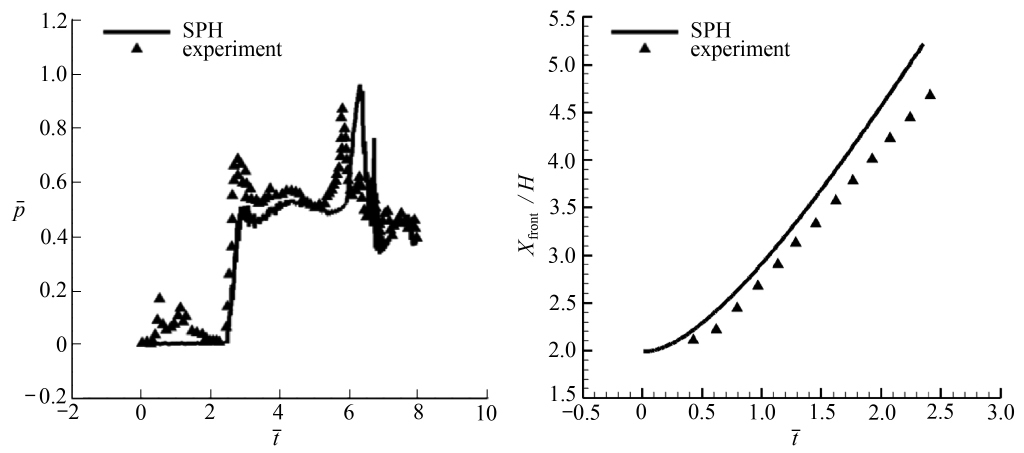
图12 实验和计算得到![]() 曲线(算例3)图13 水前端与时间关系
曲线(算例3)图13 水前端与时间关系
Fig. 12 The computed![]() compared Fig. 13 The relationship between the
compared Fig. 13 The relationship between the
with measurement(case 3) water front and the time
图12给出图10挡墙壁面A点(yA=50 mm)无量纲压强![]() 随
随![]() 变化曲线.其中,
变化曲线.其中,![]() 为水参考压强.由图12知,本文计算和实验数据[11-12]吻合较好.对照图10,当
为水参考压强.由图12知,本文计算和实验数据[11-12]吻合较好.对照图10,当![]() 时,水沿下壁面流动但未到达挡墙,在A点
时,水沿下壁面流动但未到达挡墙,在A点![]() 为零.当
为零.当![]() 时,水到达挡墙A点,
时,水到达挡墙A点,![]() 开始急剧增大,表明了水自由面冲击效应.水随后沿挡墙壁面继续向上运动,
开始急剧增大,表明了水自由面冲击效应.水随后沿挡墙壁面继续向上运动,![]() 出现波动但变化不大.当
出现波动但变化不大.当![]() 时,
时,![]() 曲线出现第二次上升,这和水沿挡墙壁面A点出现“鼓包”是对应的,水受惯性力沿挡墙壁面自下而上运动,但顶部水受重力自上而下坠落,导致A点压力再次急剧上升,但
曲线出现第二次上升,这和水沿挡墙壁面A点出现“鼓包”是对应的,水受惯性力沿挡墙壁面自下而上运动,但顶部水受重力自上而下坠落,导致A点压力再次急剧上升,但![]() 二次峰实验值低于计算值且到达时刻也晚.文献[12]将二次压力上升解释为“水射流”包裹“空气泡”受压上升的观点是不正确的,原因是水表面张力和压力相比很小.水逐渐离开挡墙壁面,导致
二次峰实验值低于计算值且到达时刻也晚.文献[12]将二次压力上升解释为“水射流”包裹“空气泡”受压上升的观点是不正确的,原因是水表面张力和压力相比很小.水逐渐离开挡墙壁面,导致![]() 开始也缓慢下降.总体上看,本文
开始也缓慢下降.总体上看,本文![]() 曲线计算和实验结果符合较好.
曲线计算和实验结果符合较好.
图13给出了水前端离左侧壁面距离随时间的变化趋势,以及实验值[13].从图中可以看出,SPH数值结果比实验结果稍微大一些,但是整体而言,数值计算结果与实验结果是一致的.造成误差的原因有,在实验中,水沿着壁面流动是会受到摩擦力的作用,而在数值计算中并没有考虑摩擦力的影响.同时,数值计算是针对二维情况,而实验是三维情况,这也是不能忽略的影响因子.
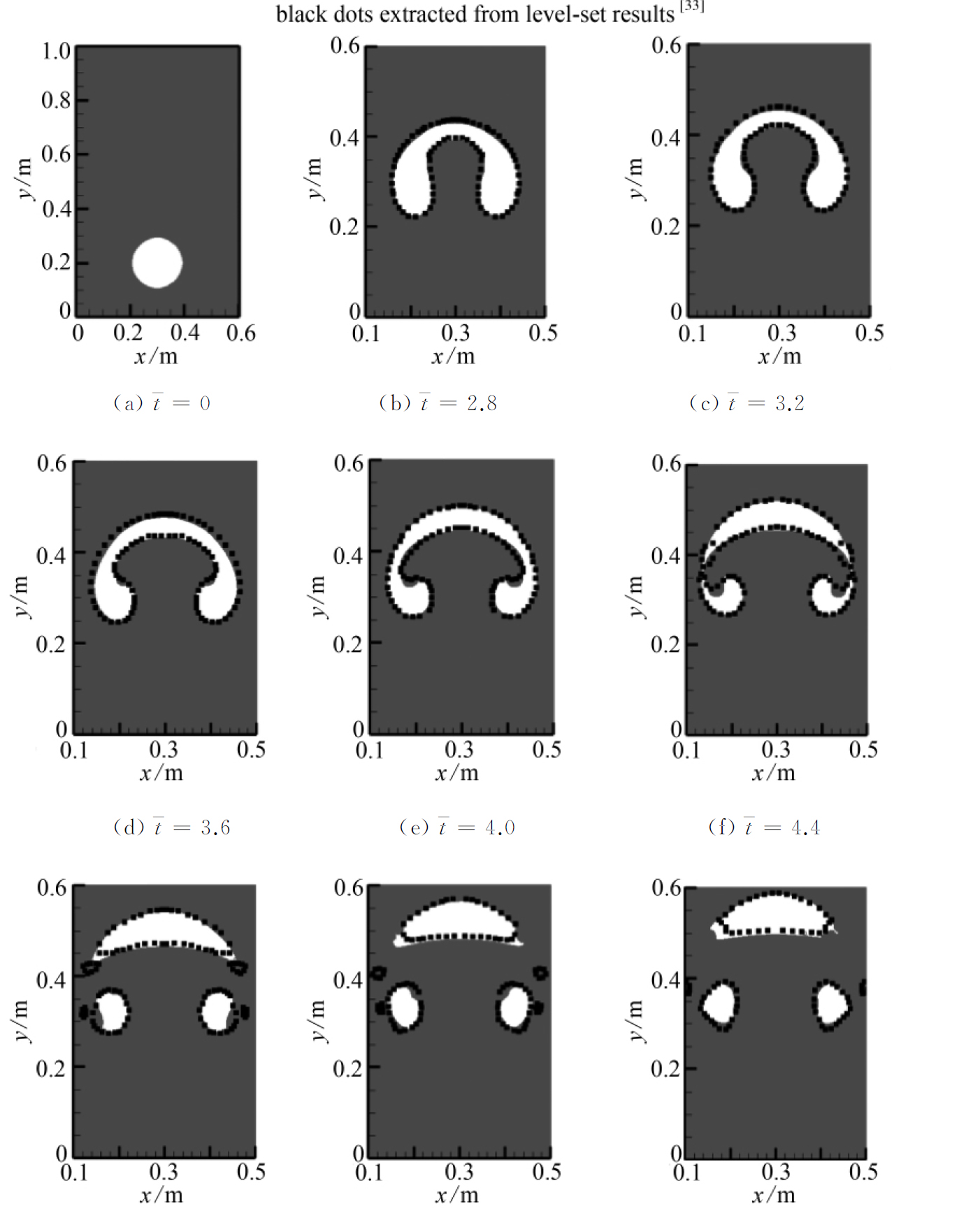
![]()
图14 不同时刻气泡和水粒子位置(算例4)
Fig. 14 Particle positions and interfaces at different moments(case 4)
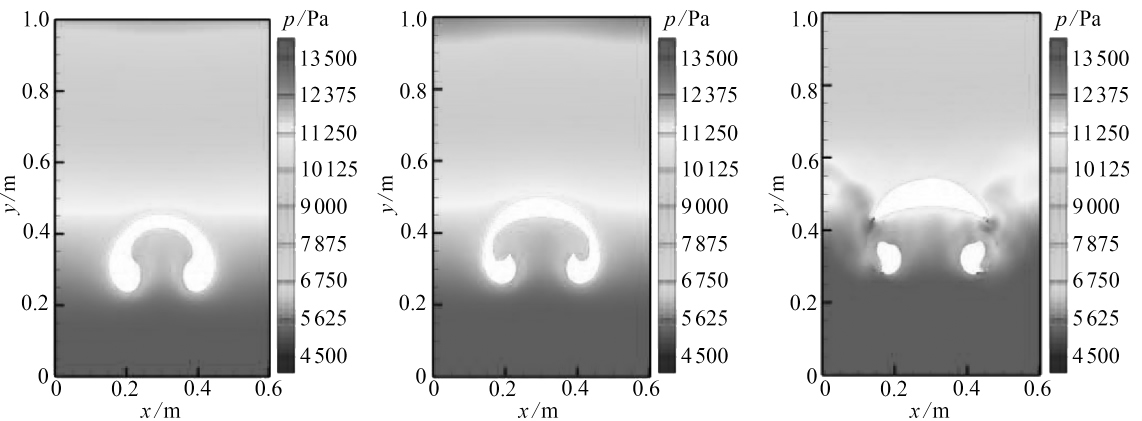
![]()
图15 流场压强云图 (算例4)
Fig. 15 Pressure contours(case 4)
算例4是大密度比和大变形界面验证算例[11,13](图14).主要参数设定:当t=0,在矩形(6R×10R,R=0.1 m)容器充满水(红色),半径为R气泡(白色)圆心位于点(3R,2R).水和空气层流动力黏性系数分别取10-6 m2·s-1和10-5 m2·s-1,不考虑人工黏性项.水和空气参考密度分别取ρr1=1 000 kg/m3,ρr2=1 kg/m3.记流体粒子位置为r=(x,y),水初始密度取为ρwater=ρr1+ρr1g(10R-y)/c2,气泡初始密度取为ρair=ρr2+2Rρr1g/c2,其中,声速![]() 均布的流体粒子数为480×800,Δt取2 μs,ε=0.08,无量纲时间
均布的流体粒子数为480×800,Δt取2 μs,ε=0.08,无量纲时间![]() 取为
取为![]()
图14给出了不同时刻粒子气泡和水粒子分布(黑点为level-set计算结果[33]).图14表明,圆形气泡受浮力作用而向上运动(图14(a)~14(e)),然后由于较大阻力导致气泡头部变得扁平,气泡左右侧面受到拉伸,界面向下内凹大变形并呈左右对称的“蘑菇状”,这和算例1的Rayleigh-Taylor界面不稳定性的形成机理是类似的.随着时间推进,气泡两侧断裂直至产生小气泡(图14(f)).原气泡分裂为左右两个小气泡和上部单个“月牙状”气泡,“月牙状”气泡沿水平方向收缩(图14(g)~14(i)).文献[11,13]的计算结果和本文定性相符合.未破碎前的气泡形状,本文和level-set方法[33]计算的气泡位置和形状几乎重合.当气泡破碎后,level-set计算的小气泡数目更多.文献[11]也做了两种方法计算结果差别的对比,但两者差别的原因需作进一步分析,不能简单地归结为所用方法不同.和图14对应,图15给出了不同时刻流场压强云图.图15表明,流场压强呈连续变化,未出现明显的压力震荡.
本文修正了动量方程压强梯度项SPH粒子近似公式,在界面施加排斥力.采用Rayleigh-Taylor界面不稳定性、非Boussinesq锁定交换、溃坝和水中气泡上升等进行算例验证.结果表明:针对密度比较大范围变化、大变形和破碎的两相界面流动问题,修正压力梯度项的粒子近似,本文的单相和多相SPH方法捕捉大变形和破碎界面光滑性好,界面附近压力场未出现明显震荡,和文献计算或实验结果符合较好,表明了本文方法的适应性和健壮性.
致谢 本文作者衷心感谢中国运载火箭技术研究院基金(CALT201601)和清华大学自主课题(20161080102)对本文的资助.
[1] 徐志敏, 宋思远, 辛锋先, 等. 小Reynolds数下粗糙圆管中黏性流场的理论解[J]. 应用数学和力学, 2018,39(2): 123-136.(XU Zhimin, SONG Siyuan, XIN Fengxian, et al. Analytical solution for the viscous flow of small Reynolds numbers in rough pipes[J].Applied Mathematics and Mechanics, 2018,39(2): 123-136.(in Chinese))
[2] BRACKBILL J, KOTHE D B, ZEMACH C. A continuum method for modeling surface tension[J].Journal of Computational Physics, 1992,100(2): 335-354.
[3] BALACHANDAR S, EATON J K. Turbulent dispersed multiphase flow[J].Annual Review of Fluid Mechanics, 2010,42: 111-133.
[4] ZHENG Jun, YU Kaiping, WANG Junfeng,et al. SPH for developing super cavity induced by high speed underwater body[J].Chinese Journal of Computational Physics, 2014,31(1): 27-32.
[5] 上官子柠, 周秀丽, 宋鑫, 等. 典型自由面流动问题的SPH-ALE数值模拟[J].计算物理, 2017,34(6): 641-650.(SHANGGUAN Zining, ZHOU Xiuli, SONG Xin, et al. Numerical simulation of typical free surface flow with SPH-ALE[J].Chinese Journal of Computational Physics, 2017,34(6): 641-650.(in Chinese))
[6] ESPANOL P, WARREN P. Statistical mechanics of dissipative particle dynamics[J].Europhysics Letters, 1995,30(4): 191-196.
[7] GINGOLD R A, MONAGHAN J J. Smoothed particle hydrodynamics: theory and application to non-spherical stars[J].Monthly Notices of the Royal Astronomical Society, 1977,181(3): 375-389.
[8] 韩亚伟, 强洪夫. 改进的物理粘性SPH方法及其在溃坝问题中的应用[J]. 计算物理, 2012,29(5): 693-699.(HAN Yawei, QIANG Hongfu. An improved SPH method with physical viscosity and application in dam-break problem[J].Chinese Journal of Computational Physics, 2012,29(5): 693-699.(in Chinese))
[9] 王安文, 徐绯, 张岳青. SPH方法在液固撞击数值模拟中的应用[J]. 计算物理, 2012,29(4): 525-533.(WANG Anwen, XU Fei, ZHANG Yueqing. SPH method in numerical simulation of liquid-solid impact[J].Chinese Journal of Computational Physics, 2012,29(4): 525-533.(in Chinese))
[10] 卞梁, 王肖钧, 章杰, 等. 高速碰撞数值计算中的SPH分区算法[J]. 计算物理, 2011,28(2): 207-212.(BIAN Liang, WANG Xiaojun, ZHANG Jie, et al. Numerical simulation of hypervelocity impact with subdomains in SPH computation[J].Chinese Journal of Computational Physics, 2011,28(2): 207-212.(in Chinese))
[11] COLAGROSSI A, LANDRINI M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics[J].Journal of Computational Physics, 2003,191(2): 448-475.
[12] CHEN Z, ZONG Z, LIU M B, et al. An SPH model for multiphase flows with complex interfaces and large density differences[J].Journal of Computational Physics, 2015,283: 169-188.
[13] 沈雁鸣, 陈坚强. SPH方法对气液两相流自由界面运动的追踪模拟[J]. 空气动力学学报, 2012,30(2): 157-161, 168.(SHEN Yanming, CHEN Jianqiang. Numerical tracking of interface in multiphase flows with smoothed particle hydrodynamics[J].Acta Aerodynamica Sinica, 2012,30(2): 157-161, 168.(in Chinese))
[14] MONAGHAN J J. SPH without a tensile instability[J].Journal of Computational Physics, 2000,159(2): 290-311.
[15] HU X Y, ADAMS N A. An incompressible multi-phase SPH method[J].Journal of Computational Physics, 2007,227(1): 264-278.
[16] COLAGROSSI A. A meshless Lagrangian method for free-surface and interface flows with fragmentation[D]. PhD Thesis. Rome: University of Rome, 2005
[17] HOOGERBRRUGGE P J, KOELMAN J M V A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics[J].Europhys Letter, 1992,19(3): 155-160.
[18] HU X Y, ADAMS N A. A multi-phase SPH method for macroscopic and mesoscopic flows[J].Journal of Computational Physics, 2006,213(2): 844-861.
[19] MONAGHAN J J, RAFIEE A. A simple SPH algorithm for multi-fluid flow with high density ratios[J].International Journal for Numerical Methods in Fluids, 2013,71(5): 537-561.
[20] MONAGHAN J J. Simulating free surface flows with SPH[J].Journal of Computational Physics, 1994,110(2): 399-406.
[21] LIU M B, LIU G R. Smoothed particle hydrodynamics (SPH): an overview and recent developments[J].Archives of Computational Methods in Engineering, 2010,17(1): 25-76
[22] EDMOND Y M, SHAO S D. Simulation of near-shore solitary wave mechanics by an incompressible SPH method[J].Applied Ocean Research, 2002,24(5): 275-286.
[23] MONAGHAN J J. Shock simulation by the particle method SPH[J].Journal of Computational Physics, 1983,52(2): 374-389.
[24] 沈雁鸣. 基于SPH方法的物体入水冲击问题数值模拟研究[D]. 博士学位论文. 绵阳: 中国空气动力研究与发展中心研究生部, 2016: 24-26.(SHEN Yanming. A numerical study of water entry problems based on smoothed particle hydrodynamics (SPH) method[D]. PhD Thesis. Mianyang: The Graduate Faculty of China Aerodynamics Research and Development Center, 2016: 24-26.(in Chinese))
[25] 陈臻. SPH算法改进及在晃荡与入水中的应用[D]. 硕士学位论文. 大连: 大连理工大学, 2014.(CHEN Zhen.Improving SPH methodology with its application to sloshing and water entry[D]. Master Thesis. Dalian: Dalian University of Technology, 2014.(in Chinese))
[26] LIU M B, SHAO J R, CHANG J Z. On the treatment of solid boundary in smoothed particle hydrodynamics[J].Science China Technological Sciences, 2012,55(1): 244-254.
[27] CUMMINS S J, RUDMAN M. An SPH projection method[J].Journal of Computational Physics, 1999,152(2): 584-607.
[28] LEE H G, KIM J. Numerical simulation of the three-dimensional Rayleigh-Taylor instability[J].Computers and Mathematics With Applications, 2013,66(8): 1466-1474.
[29] GRENIER N, ANTUONO M, COLAGROSSI A, et al. An Hamiltonian interface SPH formulation for multi-fluid and free surface flows[J].Journal of Computational Physics, 2009,228(22): 8380-8393.
[30] DALZIEL S. Toy models for Rayleigh Taylor instability[C]//8th International Workshop on the Physics of Compressible Turbulent Mixing. Lawrence Livermore National Laboratory: UCRL-MI-146350, 2001.
[31] BIRMAN V K, MARTIN J E, MEIBURG E. The non-Boussinesq lock-exchange problem, part 2: high-resolution simulations[J].Journal of Fluid Mechanics, 2005,537: 125-144.
[32] LOWE R J, ROTTMAN J W,LINDEN P F. The non-Boussinesq lock-exchange problem, part 1: theory and experiments[J].Journal of Fluid Mechanics, 2005,537: 101-124.
[33] SUSSMAN M, SMEREKA P, OSHER S. A level set approach for computing solutions to incompressible two-phase flow[J].Journal of Computational Physics, 1994,114(1): 146-159.