ⓒ 应用数学和力学编委会,ISSN 1000-0887
自Iijima[1]发现碳纳米管以来,其特殊的力学性能及其在纳米器件领域的潜在应用,引起了国内外众多科研工作者的兴趣.其中,有关纳米结构的动力学问题也是近年来的重点研究课题.大量的实验结果表明[2-3],纳米结构展现出了一些与宏观尺度下的理论预测完全不同的力学行为,经典力学已无法直接应用于纳米结构中.因此,许多学者致力于对连续介质力学进行改进以适用于纳米结构,非局部理论应运而生.
由Eringen等[4-5]提出的非局部理论将分子间作用力是长程力的思想,通过非局部核函数,直接引入到传统连续介质力学的本构方程.该理论认为,连续体内某一点的应力不只是该点应变的函数,而是连续体内所有点的应变及变形历史的函数.已有大量文献[6-22]报道,非局部理论在碳纳米管、石墨烯等纳米材料的力学性能研究中扮演重要角色.对于碳纳米管,研究者将其考虑为纳米杆、纳米梁及壳体等多种模型,进行了大量的研究工作.杨武等[6]基于经典弹性理论和非局部弹性理论分析了锥形纳米管纵向振动的固有频率;黄伟国等[7]研究了非局部效应下的压杆稳定性问题,小尺度效应使压杆更易失稳及引起低频共振;Li等[8]讨论了传统非局部纳米杆模型与等效非局部纳米杆模型的差异并解释了二者结论相反的原因;Narendar等[9]分析了非局部效应下纳米管纵波传播的特性及与经典力学的差别等.
最近,Xu等[23-24]发现在-196~1 000 ℃范围下碳纳米管存在黏弹性.Pang等[10]研究了在非局部效应和表面效应的作用下,黏弹性碳纳米管弯曲波的传播特性.此外,利用非局部理论研究纳米梁、纳米板及压电纳米板力学特性的文献也很多[16-22].目前,在众多碳纳米管的文献中,考虑材料黏弹性的文章较为少见,其中关于黏弹性纳米管的轴向动力学问题还没有被详细讨论.本文考虑纳米杆模型,研究碳纳米管的轴向动力学问题,基于非局部理论和Kelvin黏弹性理论,分别讨论了黏弹性纳米杆的轴向自由振动和波传播行为,通过数值算例重点考察非局部效应和材料的黏性系数对固有频率、纵波的波速及阻尼比的影响规律.
根据Eringen非局部弹性理论,在不计体力、线弹性、均匀和各向同性材料情况下非局部弹性问题的基本方程为[4-5]
(1a)
(1b)
(1c)
其中,σij,εij,ui和Cijkl分别表示非局部应力、应变、位移和四阶弹性张量.根据方程(1b),σij(x)在x处的值不仅取决于该点的应变,还取决于整个区域中所有点的应变的加权平均.其权重系数由非局部模量χ(x-x′,Γ)决定,x-x′是欧氏距离,Γ是非局部核函数.由方程(1a)和(1c)知,非局部理论下平衡方程和几何方程与经典理论是一致的,而方程(1b)能够表达成如下微分形式[4]:
 2]σ=σ′,
2]σ=σ′,(2a)
其中,σ是非局部应力张量,σ′是经典的应力张量, 2是Laplace(拉普拉斯)算子,e0是非局部的材料常数,a是内特征长度,比如晶格常数、碳碳单键键长等.
2是Laplace(拉普拉斯)算子,e0是非局部的材料常数,a是内特征长度,比如晶格常数、碳碳单键键长等.
本文考虑一个长度为L,质量密度为ρ,横截面积为A的均匀、各向同性的黏弹性纳米杆.对于直角坐标系下的一维纳米杆模型,Laplace算子 2=∂2/∂x2,代入式(2a)得
2=∂2/∂x2,代入式(2a)得
(2b)
其中,σx是非局部正应力,![]() 是经典力学沿x方向的正应力.
是经典力学沿x方向的正应力.
另一方面,Kelvin-Voigt经典黏弹性理论的本构关系[25]为
(3)
其中,E为材料的弹性模量,τd为黏性系数,![]() 为应变率.
为应变率.
结合式(2)、(3),可得一维非局部黏弹性应力应变关系:
(4)
仅考虑x方向的轴向振动,由d’Alembert(达朗贝尔)原理,可得长度为dx的黏弹性纳米杆微元在x方向的平衡方程为
(5)
其中,u为纳米杆的轴向位移,x为轴向坐标,t为时间,N为轴向力,![]()
由方程(1c)可得到纳米杆轴向位移与应变关系为
(6)
将式(6)代入式(4),并在式(4)两边对横截面积A积分得
(7)
对式(7)中关于x求一次偏导数,得
(8)
由式(5)和式(8)可得黏弹性纳米杆的轴向动力学控制方程为
(9)
式(9)是以轴向位移为未知量表示的动力学控制方程,涉及到弹性系数、黏性系数、小尺度参数等.下面将通过分离变量法对该方程进行求解,并分析各参数对频率的影响规律.
为研究纳米杆的轴向自由振动问题,引入以下无量纲量:
(10)
将式(9)控制方程无量纲化,得
(11)
由式(11)知,无量纲位移U是时间变量T和空间变量X的函数,为了方便求解利用分离变量法设其解为
(12)
其中,![]() 表示纳米杆的第n阶无量纲固有频率.
表示纳米杆的第n阶无量纲固有频率.
将式(12)代入式(11)得
(13)
不难求得其解为
(14)
则式(11)的解可表达为
(15)
其中,c1,c2为任意常数,由边界条件确定.
工程中常见的固定、固支、可移简支和自由边界条件,在只考虑轴向位移情况下固定和固支等同,可移简支和自由等同,因此只有固支和自由两种边界条件.它们可以组成3种类型的杆,分别为两端固支、一端固支一端自由和两端自由杆.本节将分别讨论3种边界类型黏弹性纳米杆的轴向振动情况,考察小尺度参数和黏弹性对轴向振动固有频率的影响.
考虑两端固支黏弹性纳米杆,此时杆两端没有轴向位移,即[26]
(16)
将式(15)代入式(16),根据要求得到非平凡解可求解得频率为
(17)
事实上![]() 的实部是黏弹性纳米杆轴向振动的固有频率,虚部是衰减系数.当α=0,τ=0时,固有频率表达式回归到经典力学下弹性杆轴向振动的结果.考虑受到无量纲非局部参数α、黏性系数τ的共同作用下,两端固支黏弹性纳米杆轴向振动的前三阶无量纲固有频率如图1所示.由图1的前两阶模态图可以发现,当非局部参数α增大或者黏性系数τ增大时,固有频率持续减小,即出现杆件结构的刚度削弱现象;而且一阶频率的减小速度比二阶要小.第三阶模态图中,若黏性系数较大(比如τ=0.2时),随着非局部效应的增强,固有频率先增大后减小(在大约α=0.1处达到峰值),且最小值仍大于经典理论(α=0)下的频率值,即表现出刚度增强现象.这就表明,随着非局部效应的增强,黏弹性纳米结构可能会出现刚度增强和削弱两种趋势.这个现象与Li等[8]对纳米材料和结构的非局部力学性能的研究结论一致,验证了文献[8]工作的同时,也说明了本文理论模型的有效性.
的实部是黏弹性纳米杆轴向振动的固有频率,虚部是衰减系数.当α=0,τ=0时,固有频率表达式回归到经典力学下弹性杆轴向振动的结果.考虑受到无量纲非局部参数α、黏性系数τ的共同作用下,两端固支黏弹性纳米杆轴向振动的前三阶无量纲固有频率如图1所示.由图1的前两阶模态图可以发现,当非局部参数α增大或者黏性系数τ增大时,固有频率持续减小,即出现杆件结构的刚度削弱现象;而且一阶频率的减小速度比二阶要小.第三阶模态图中,若黏性系数较大(比如τ=0.2时),随着非局部效应的增强,固有频率先增大后减小(在大约α=0.1处达到峰值),且最小值仍大于经典理论(α=0)下的频率值,即表现出刚度增强现象.这就表明,随着非局部效应的增强,黏弹性纳米结构可能会出现刚度增强和削弱两种趋势.这个现象与Li等[8]对纳米材料和结构的非局部力学性能的研究结论一致,验证了文献[8]工作的同时,也说明了本文理论模型的有效性.
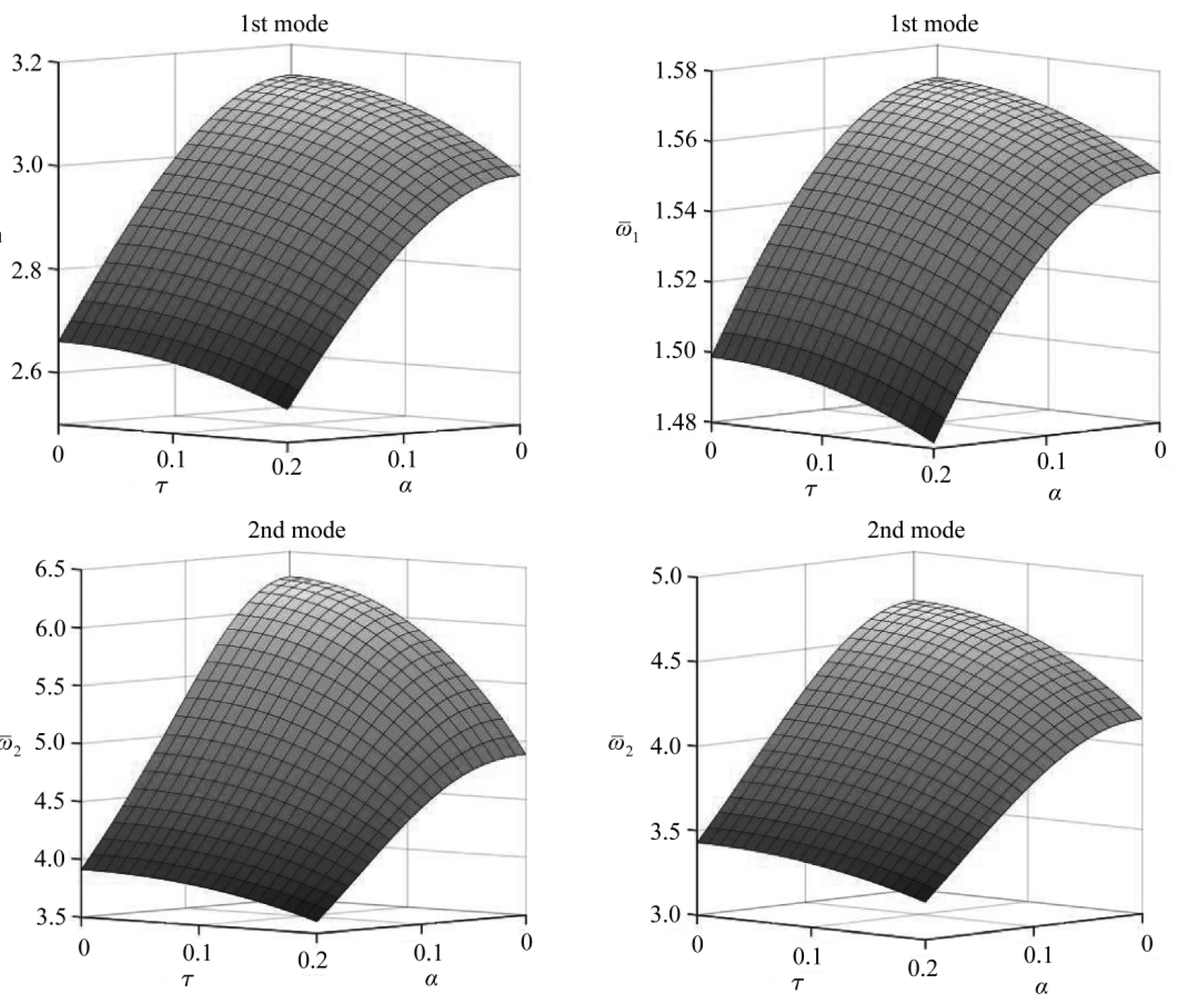

图1 两端固支前三阶无量纲固有频率图2 一端固支一端自由前三阶无量纲固有频率
Fig. 1 The 1st 3 dimensionless natural frequenciesFig. 2 The 1st 3 dimensionless natural frequencies
under fixed-fixed supporting condition under fixed-free supporting condition
考虑一端固支一端自由黏弹性纳米杆,其边界条件为
(18)
将式(15)代入式(18),同理可得
(19)
一端固支一端自由边界条件下的前三阶无量纲固有频率如图2所示.对比图1与图2,可以发现,两种边界条件下的频率变化规律基本保持一致;但受边界条件的影响,图2中第三阶固有频率变化趋势没有图1的明显,前3阶模态下均表现出刚度削弱的现象.另外,相同模态下,一端固支一端自由杆件的固有频率略小于两端固支情况.
考虑两端自由黏弹性纳米杆,此时杆的自由端轴向力为0,即
(20)
将式(15)代入式(20),可求得频率为
(21)
对比式(21)和式(17)可知,两端自由边界下固有频率表达式与两端固支情形相同,其频率变化规律在此不再赘述.值得说明的是,由于n的取值范围不同,两端自由边界下多出零频率情况,这是由没有限制刚体位移引起的.对比上文3种边界条件,可以得到:对于黏弹性纳米杆件,相同条件下,两端自由边界条件下固有频率最低,一端固支一端自由次之,两端固支边界下固有频率最高.这一点也与经典理论3种边界条件下固有频率大小排序一致.
考虑一端固支一端自由的特例,自由端带有集中质量m的情况,这种杆件在微机械系统中非常常见.此时,要求固定一端轴向位移为0,带有集中质量的自由端满足自由端的轴向力等于集中质量轴向振动的惯性力,即
(22)
其中,M=m/(ρAL).将式(15)代入式(22),求解可得
(23)
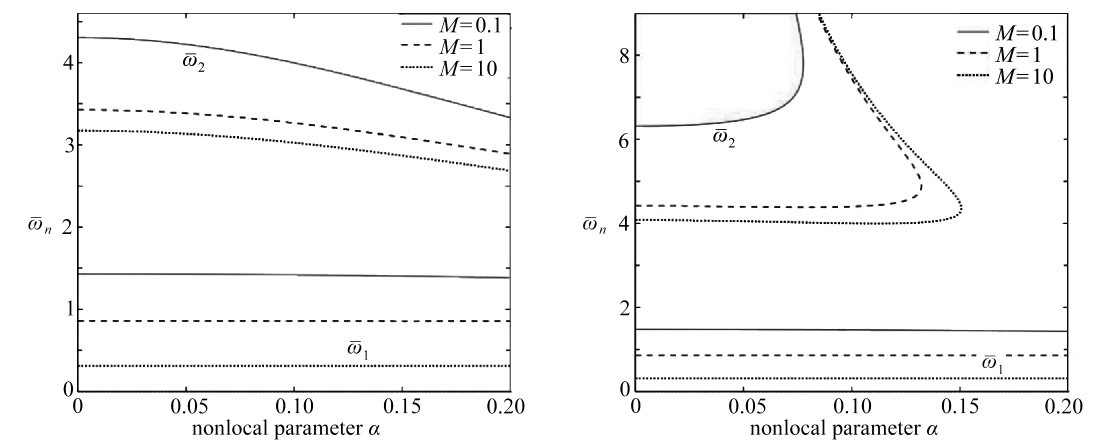
通过数值方法,可以获得不同集中质量下杆件前两阶无量纲固有频率的变化情况.对于弹性纳米杆(τ=0)和黏弹性纳米杆(τ=0.2),自由端带有的集中质量越大,其固有频率越小,如图3所示.由图3可以看到,非局部效应对第一阶固有频率的影响非常小,对第二阶频率的影响较大.对比黏性系数τ=0,0.2两种情况,若黏性系数较大(与非局部参数相当),第二阶固有频率会迅速增大,并出现多值的情况,容易造成结构失稳.
(a)τ=0(b)τ=0.2
图3 不同黏性系数下自由端带有集中质量纳米杆的固有频率
Fig. 3 The natural frequencies in the case of a free end with a concentrated mass
for different viscoelastic coefficients
为了研究纳米杆纵向波的传播问题,轴向动力学控制方程(9)的解可设为[9]
(24)
其中,k为波数,ω为圆频率,U0为波的振幅.
将式(24)代入式(9),得到色散关系:
(25)
其中,![]() 为经典理论下杆件纵波传播的波速[14].
为经典理论下杆件纵波传播的波速[14].
由式(25)可得圆频率ω的复数解为
(26)
对于黏弹性纳米杆纵向波传播问题,圆频率ω与波数k的关系由式(26)的实部Re(ωc)得到
(27)
则纵波传播的波速为
(28)
其虚部由材料的阻尼效应引起.阻尼比ζ由圆频率的虚部和实部之比定义:
(29)
以下算例中,首先选取扶手椅型单壁碳纳米管(10,10)来检验本文模型,由文献[15]提供其相关参数如下:有效厚度h=0.34 nm,弹性模量E=0.45 TPa,密度ρ=2.237 g/cm3.为验证本文模型的有效性,取黏性系数τd=0,图4给出了圆频率ω与波数k分别在经典弹性理论(CET)和非局部弹性理论下的关系,其中非局部参数e0a分别取0.1,0.5,1.0,2.0 nm.图4显示,在经典弹性理论下,圆频率与波数呈线性关系,其斜率为c0;在非局部理论下,圆频率随波数的增大而增大,且逐渐趋于稳定值,称为逃逸频率;非局部效应越强,逃逸频率越小,该结论与王碧蓉等[12]、Narendar等[9]的研究结论相符.图5为黏性系数τd=100 fs(10-13 s)时黏弹性纳米杆的圆频率ω与波数k之间的关系图.在经典理论下,随着波数增大,圆频率先增大然后迅速减小至0;当非局部参数e0a取0.1 nm和0.5 nm时,圆频率变化趋势不变,但衰减速度明显变慢;当e0a取1.0 nm和2.0 nm时,随着波数增大,圆频率逐渐增大并趋于稳定值,即再次出现逃逸频率.

图4τd=0时不同非局部参数下的频率 图5τd=100 fs时不同非局部参数下的频率
Fig. 4 Frequencies for different nonlocal Fig. 5 Frequencies for different nonlocal
parameters,τd=0 parameters,τd=100 fs
图6和图7给出了纵波传播的波速c与波数k的关系曲线图,其中图6侧重研究黏性系数τd的影响,而图7则考虑非局部参数e0a的影响情况.如图6所示,在经典弹性理论下,纵波波速为常数c0;非局部弹性理论下,当波数较小时(k<108m-1)波速约为常数c0,之后随着波数的增大而快速减小,渐渐趋于0;在非局部黏弹性理论下,分别取黏性系数τd=100,200,300 fs,波速快速衰减至0,衰减速度随黏性系数增大而增大.在图7中,取黏性系数τd=100 fs,由于黏性阻尼的作用,经典理论下波速随波数的增加而急剧减小至0;在非局部黏弹性理论下,非局部参数e0a分别取0.1 nm和0.5 nm,波速依旧快速减小至0,而此时截止的波数明显增大;当e0a分别取1.0 nm和2.0 nm时,波速随波数的增加减小缓慢,阻尼效应明显减弱,纵波能够在高波数段传播.对比以上结果可知,非局部效应的增强可弱化材料的阻尼效应,有利于纵波在黏弹性纳米杆件中的传播.

图6e0a=1.0 nm时不同黏性系数下的波速 图7τd=100 fs时不同非局部参数下的波速
Fig. 6 Wave velocities for different viscoelasticFig.7 Wave velocities for different nonlocal
coefficients,e0a=1.0 nm coefficients,τd=100 fs
图8反映了阻尼比ζ随着波数k的变化情况.由图8可知,当波数较小时(k<3×107m-1),对阻尼比影响微弱,可忽略不计.当波数k∈[3×107,3×109] m-1时,阻尼比随波数的增大而增大,且受其影响显著;若波数继续增大,阻尼比渐趋于定值.另外,在相同条件下,黏性系数越大阻尼比越大,且受波数影响的范围越大.

图8 不同黏性系数下的阻尼比
Fig. 8 Damping ratios for different viscoelastic coefficients
本文基于非局部黏弹性理论建立了黏弹性纳米杆的轴向动力学模型,分析了纳米杆轴向自由振动问题和纵波传播问题,并基于扶手椅型单壁碳纳米管的算例分析,得到如下结论:
1) 对于黏弹性纳米杆轴向自由振动问题,固有频率随黏性系数的增大而减小,且频率阶数越高,减小幅度越大.
2) 随着非局部参数增大,低阶模态的固有频率持续减小,而高阶频率先增大后减小,出现纳米结构非局部刚度削弱或增强现象.
3) 自由端带有集中质量情形,高阶固有频率出现多值情况,易导致杆件失稳.
4) 波传播问题中,黏性阻尼效应使圆频率和波速快速衰减为0.非局部效应增强后,出现逃逸频率,实现纵波在高波数段传播.阻尼比随黏性系数增大而增大,低波数段下其影响可忽略不计.
[1] IIJIMA S. Helical microtubules of graphitic carbon[J].Nature, 1991,354: 56-58.
[2] ERINGEN A C, KIM B S. Stress concentration at the tip of the crack[J].Mechanics Research Communications, 1974,1(4): 233-237.
[3] TREACY M M J, EBBESEN T W, GIBSON J M. Exceptionally high Young’s modulus observed for individual carbon nanotubes[J].Nature, 1996,381: 678-680.
[4] ERINGEN A C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves[J].Journal of Applied Physics, 1983,54(9): 4703-4710.
[5] ERINGEN A C, EDELEN D G B. On nonlocal elasticity[J].International Journal of Engineering Science, 1972,10(3): 233-248.
[6] 杨武, 彭旭龙, 李显方. 锥形纳米管纵向振动固有频率[J]. 振动与冲击, 2014,33(2): 158-162.(YANG Wu, PENG Xulong, LI Xianfang. Natural frequencies of longitudinal vibration of cone-shaped nanotubes[J].Journal of Vibration and Shock, 2014,33(2): 158-162.(in Chinese))
[7] 黄伟国, 李成, 朱忠奎. 基于非局部理论的压杆稳定性及轴向振动研究[J]. 振动与冲击, 2013,32(5): 154-156.(HUANG Weiguo, LI Cheng, ZHU Zhongkui. On the stability and axial vibration of compressive bars based on nonlocal elasticity theory[J].Journal of Vibration and Shock, 2013,32(5): 154-156.(in Chinese))
[8] LI C, LI S, YAO L Q. Nonlocal theoretical approaches and atomistic simulations for longitudinal free vibration of nanorods/nanotubes and verification of different nonlocal models[J].Applied Mathematical Modelling, 2015,39(15): 4570-4585.
[9] NARENDAR S, GOPALAKRISHNAN S. Nonlocal scale effects on ultrasonic wave characteristics of nanorods[J].Physica E:Low-Dimensional Systems and Nanostructures, 2010,42(5): 1601-1604.
[10] PANG M, ZHANG Y Q, CHEN W Q. Transverse wave propagation in viscoelastic single-walled carbon nanotubes with small scale and surface effects[J].Journal of Applied Physics, 2015,117(2): 024305.
[11] WANG L F, HU H Y. Flexural wave propagation in single-walled carbon nanotubes[J].Journal of Computational &Theoretical Nanoscience, 2008,5(4): 581-586.
[12] 王碧蓉, 邓子辰, 徐晓建. 基于梯度理论的碳纳米管弯曲波传播规律的研究[J]. 西北工业大学学报, 2013,31(5): 774-778.(WANG Birong, DENG Zichen, XU Xiaojian. Modified Timoshenko beam models for flexural wave dispersion in carbon nanotubes with shear deformation considered[J].Journal of Northwestern Polytechnical University, 2013,31(5): 774-778.(in Chinese))
[13] 张宇, 邓子辰, 赵鹏. 辛体系下碳纳米管阵列中太赫兹波传播特性研究[J]. 应用数学和力学, 2016,37(9): 889-900.(ZHANG Yu, DENG Zichen, ZHAO Peng. Study of terahertz wave propagation in carbon nanotube arrays based on the symplectic formulation[J].Applied Mathematics and Mechanics, 2016,37(9): 889-900.(in Chinese))
[14] 尹春松, 杨洋. 考虑非局部剪切效应的碳纳米管弯曲特性研究[J]. 应用数学和力学, 2015,36(6): 600-606.(YIN Chunsong, YANG Yang. Shear deformable bending of carbon nanotubes based on a new analytical nonlocal Timoshenko beam model[J].Applied Mathematics and Mechanics, 2015,36(6): 600-606.(in Chinese))
[15] 徐晓建, 邓子辰. 非局部因子和表面效应对微纳米材料振动特性的影响[J]. 应用数学和力学, 2013,34(1): 10-17.(XU Xiaojian, DENG Zichen. Surface effects of adsorption-induced resonance analysis of micro/nanobeams via nonlocal elasticity[J].Applied Mathematics and Mechanics, 2013,34(1): 10-17.(in Chinese))
[16] LI C, LIU J J, CHENG M, et al. Nonlocal vibrations and stabilities in parametric resonance of axially moving viscoelastic piezoelectric nanoplate subjected to thermo-electro-mechanical forces[J].Composites Part B:Engineering, 2017,116: 153-169.
[17] LI C. Nonlocal thermo-electro-mechanical coupling vibrations of axially moving piezoelectric nanobeams[J].Mechanics Based Design of Structures &Machines, 2017,45(4): 463-478.
[18] SHEN J P, LI C, FAN X L, et al. Dynamics of silicon nanobeams with axial motion subjected to transverse and longitudinal loads considering nonlocal and surface effects[J].Smart Structures and Systems, 2017,19(1): 105-113.
[19] LIU J J, LI C, FAN X, et al. Transverse free vibration and stability of axially moving nanoplates based on nonlocal elasticity theory[J].Applied Mathematical Modelling, 2017,45: 65-84.
[20] LIU J J, LI C, YANG C J, et al. Dynamical responses and stabilities of axially moving nanoscale beams with time-dependent velocity using a nonlocal stress gradient theory[J].Journal of Vibration and Control, 2017,23(20): 3327-3344.
[21] KARAMI B, SHAHSAVARI D, LI L. Hygrothermal wave propagation in viscoelastic graphene under in-plane magnetic field based on nonlocal strain gradient theory[J].Physica E:Low-Dimensional Systems and Nanostructures, 2018,97: 317-327.
[22] EL-BORGI S, RAJENDRAN P, FRISWELL M I, et al. Torsional vibration of size-dependent viscoelastic rods using nonlocal strain and velocity gradient theory[J].Composite Structures, 2018,186: 274-292.
[23] XU M, FUTABA D N, YAMADA T, et al. Carbon nanotubes with temperature-invariant viscoelasticity from -196 ℃ to 1 000 ℃[J].Science, 2010,330(6009):1364-1368.
[24] XU M, FUTABA D N, YUMURA M, et al. Tailoring temperature invariant viscoelasticity of carbon nanotube material[J].Nano Letters, 2011,11(8): 3279-3284.
[25] 杨挺青. 黏弹性理论与应用[M]. 北京: 科学出版社, 2004.(YANG Tingqing.Viscoelastic Theory and Application[M]. Beijing: Science Press, 2004.(in Chinese))
[26] 谢官模. 振动力学[M]. 北京: 国防工业出版社, 2007.(XIE Guanmo.Vibration Mechanics[M]. Beijing: National Defense Industry Press, 2007.(in Chinese))