ⓒ 应用数学和力学编委会,ISSN 1000-0887
动力学问题的经典算法非常丰富,如中心差分法、Runge-Kutta(龙格-库塔)法、Wilsonθ方法和Newmarkβ方法等,但这些方法本身会耗散系统的能量,其长期跟踪能力不够理想.在数值计算方面,学者们正在关注和研究两大类算法:能量守恒算法和辛算法,它们都是非常优秀的算法,其中能量守恒算法能够保持系统的能量,而辛算法能够保持系统的辛结构.在数值算法应尽可能多地保持原问题的本质特征指导原则下,冯康先生等首先提出辛算法的思想,他和他的研究团队取得了一系列重大成果,并且引起国内外学者的极大兴趣,产生了许多重要的后继成果[1-5].计算试验已经表明,辛算法具有优异的稳定性和长时间跟踪能力.对于具体的一个守恒系统而言,用能量守恒算法积分还是用辛算法积分一般认为是比较两难的问题.近年来,这一难点在一定程度上也已得到解决,由钟万勰先生及其研究团队创新性地提出了保辛-保能的算法[6].
在研究非线性动力学问题时,能保持系统能量的能量守恒算法比传统的数值算法有更大的优越性.守恒系统的能量守恒格式的研究仍是现在国际前沿课题[2,7].除了经典的离散梯度法外,近来发展的平均向量场方法[8-9]就是一种构造能量守恒格式的方法(下文简称“均向量场法”).均向量场法适合于Hamilton(哈密尔顿)系统,是一种有效的离散梯度法.人们对数值积分首次积分研究后发现,对于一些特殊的微分方程其数值方法的误差可以得到控制,即能够使数值方法的误差随着时间的增长而保持在很小的范围内.
有一类单步法是基于B级数构造而成的,即幂级数在每一时间步长处都是向量场基本差分的和式.B级数法可以保线性不变量.在这一背景下,产生了保系统能量的平均向量场方法,它是一类特殊的B级数方法,可以保持所有向量场的能量.
均向量场法[10-11]令人关注之处在于能够保持所有Hamilton系统的能量.而自然界中的许多物理现象都可以看作Hamilton系统,其微分方程一般可表示为Hamilton微分系统.国内外也有多位学者进行了相关研究,如文献[12]给出AVF方法两种局部精确和保能量的修正形式,并应用于求解Coulomb-Kepler问题;Cai等[13]给出了AVF方法在三维时域Maxwell方程中的数值分析;李昊辰等[14]研究了非线性Schrödinger(薛定谔)方程的平均向量场方法.本文首先以线性微分方程为例介绍二阶精度的AVF方法,然后讨论其在两个非线性问题中的应用:单摆问题和Kepler问题.针对被积函数的不同形式,给出均向量场法中具体的映射迭代格式,从而便于应用该方法.
均向量场法的优势在于使用时不需要知道系统具体的能量函数,即可建立迭代格式,并能保持系统的Hamilton能量,然后通过求解代数方程得到迭代解,从而在保证精度的前提下大大方便了应用.
对一般的常微分方程组
(1)
建立如下映射xn→xn+1:
(2)
其中h是积分步长[15].
运用内积运算和微积分中值定理等,可证明均向量场法是能够保能量的,具体参见文献[16]中的证明.
式(2)是二阶精度的,也是本文所采用的格式.高阶的均向量场法具有更复杂的映射形式,本文不做讨论.
对于微分方程或微分方程组,应用均向量场法的一般步骤可分为如下3步:
1) 引入若干状态变量(往往是一些导数项),把原微分方程(组)写成向量方程组的形式;
2) 基于均向量场法写出具体的映射迭代格式;
3) 结合初值条件,迭代求解得到不同时刻的振动响应.
在执行第2)步时,迭代格式右端积分项需要针对被积函数的具体形式进行化简.如式(2)中,当被积函数g(x)取常见的若干函数形式时,所得积分结果分别罗列如下:
① 线性项g(u)=u,代入积分得
② 幂次项g(u)=um,积分得
③ 对正、余弦函数,积分得
④ 两个向量函数u和v的乘积,积分结果为
在第2)步中,所得迭代格式一般是隐式的.但在一些情况下可通过代数方程求解得到显式格式,需视具体问题而定.
首先以一个线性系统为例.弹簧谐振子的振动是一个线性系统,其振动方程![]() 可化为
可化为
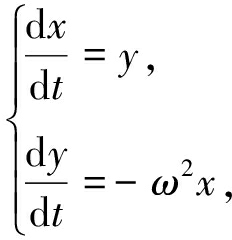
(3)
其中x表示振动位移,y表示速度.给定初始位移和速度条件x(0)=x0,y(0)=y0.
由均向量场法的一般步骤,得到对应的迭代格式如下:
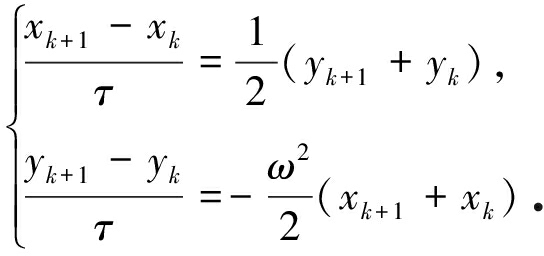
(4)
对式(4)进一步化简,得到一般的迭代公式:
(5)
其中z=[x,y]′,矩阵A为Jacobi(雅可比)矩阵,形式为
其中τ为积分步长,且
对比后发现,此形式与Euler(欧拉)中点格式[17]完全相同.对于Euler中点格式,文献[16-17]已经指出其在保守系统中的保辛特性及高精度.由第2节中的具体映射格式知,对于线性Hamilton系统,均向量场法的迭代格式可退化为Euler-中点格式.
另外,由式(4)中两式相除可得
(6)
此式恰好反映了弹簧谐振子振动过程中的能量变化情况,故该算法是保能量的.
选取![]() 为计算方便,此处数值均选为量纲一.图1给出该线性系统式(3)的数值模拟结果,所对比的精确解为
为计算方便,此处数值均选为量纲一.图1给出该线性系统式(3)的数值模拟结果,所对比的精确解为
在数值离散方程组时时间步长的引入会导致一定的误差.可选较小的时间步长τ,以减少误差.实际上相对于经典算法,采用同样的时间步长时,均向量场法的误差,即使在长时间后,也是非常小的[16,18-20].

图1 一个线性微分系统的数值解与精确解的比较
Fig. 1 Comparison between the numerical solution and the exact solution for a linear differential system

图2 运动过程的相图
Fig. 2 The phase diagram of the motion
图2为τ =0.2时运动过程的相图,时间取t≤30 s.由图2可知,均向量场法所得的相图始终在精确解附近的一定范围内,从而说明了均向量场法具有长时间求解的能力.如果时间步长取得更小,则误差也变小.
考虑无阻尼单摆的自由振动系统[21-22],取角位移变量x,振动方程可写成

(7)
其中![]() 为单摆微幅振动固有频率的平方,l为摆长,g为重力加速度,A是初始摆角.
为单摆微幅振动固有频率的平方,l为摆长,g为重力加速度,A是初始摆角.
引入新变量q=x和角速度变量![]() 方程(7)可化为
方程(7)可化为
(8)
初始条件为![]() 其Hamilton函数(即系统能量)为
其Hamilton函数(即系统能量)为![]() 按第2节中的方法,可写出保能量的二阶均向量场法计算公式:
按第2节中的方法,可写出保能量的二阶均向量场法计算公式:
(9a)
(9b)
由式(9b)/(9a),并化简得
(10)
离散时间段τ在式(10)中被消去了.按单摆的力学知识,式(10)易于由动能定理得到,且其正确性与离散时间段τ的大小无关.由式(10)得
(11)
式(11)中正负号根据单摆摆动方向确定,即顺时针运动取负号,而逆时针运动时为正.
基于式(11)和(9b),选取![]() 若直接按固定时间步长,求解变量q和p,会出现超越方程,难以求解.故这里固定摆角步长dq,求出对应的不同时间间隔,从而可得动态响应(如位移、速度和加速度等).
若直接按固定时间步长,求解变量q和p,会出现超越方程,难以求解.故这里固定摆角步长dq,求出对应的不同时间间隔,从而可得动态响应(如位移、速度和加速度等).
由于单摆模型的解析解很难给出,以Runge-Kutta方法的数值解为参考比较各方法的误差.图3~图6是初始摆角A为120°时的摆角-时间曲线、角速度-时间曲线,并且与ODE数值积分方法的结果(图中为实线条所示)比较,两者吻合得很好.还可得出,在摆角位移随时间变化图中,接近极值点时,宜选择更小的dq,以反映真实的摆角变化.
表1给出不同初始摆角时的固有频率参数T0/T的值,其中T0是线性单摆振动的周期,即![]() 由表1看出,当A=135°时,本文解(取dq=0.01 rad)与精确解的误差为0.17%;2阶摄动解的误差为6.1%;DQ法误差为0.24%.而当A=150°时,本文解(取dq=0.01 rad)与精确解的误差为2.02%;2阶摄动解的误差为15.85%;DQ法误差为1.25%.
由表1看出,当A=135°时,本文解(取dq=0.01 rad)与精确解的误差为0.17%;2阶摄动解的误差为6.1%;DQ法误差为0.24%.而当A=150°时,本文解(取dq=0.01 rad)与精确解的误差为2.02%;2阶摄动解的误差为15.85%;DQ法误差为1.25%.

图3 当dq=0.1 rad时的摆角-时间曲线 图4 当dq=0.1 rad时的角速度-时间曲线
(初摆角A=120°) (初摆角A=120°)
Fig. 3 The swing angle-time curve for Fig. 4 The angular velocity-time curve for
dq=0.1 rad (A=120°) dq=0.1 rad (A=120°)
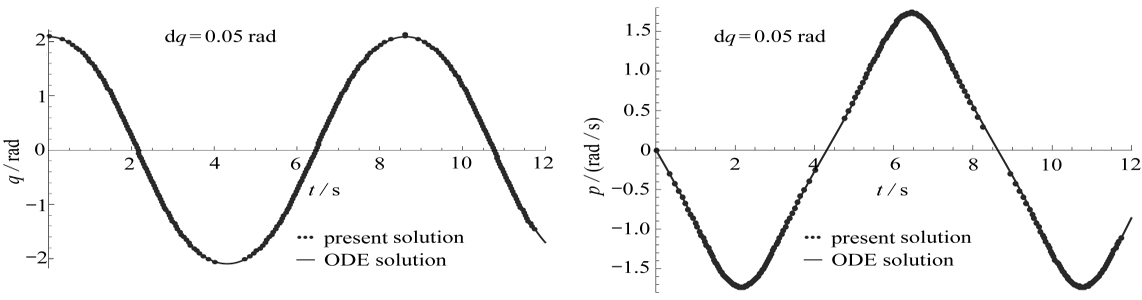
图5 当dq=0.05 rad时的摆角-时间曲线图6 当dq=0.05 rad时的角速度-时间曲线
(初摆角A=120°) (初摆角A=120°)
Fig. 5 The swing angle-time curve for Fig. 6 The angular velocity-time curve for
dq=0.05 rad (A=120°) dq=0.05 rad (A=120°)
表1 不同初始摆角时的固有频率参数T0/T的值(dq=0.01 rad)
Table 1 Values of the natural frequency parameterT0/T with different initial swing angles(dq=0.01 rad)

含耦合项的非线性问题有很多种,如旋转梁引起的耦合问题,又如非线性耦合振子等.为简便计,这里讨论经典力学中的微分方程组模型:Kepler问题[12,19].其对应的微分方程组为
(12a)
(12b)
其中q1,q2的物理意义是质点位置的横、纵坐标.式(12)可写成如下方程组:

(13)
其Hamilton函数![]() 是守恒量,而且,角动量Θ=q1p2-q2p1也是守恒量.
是守恒量,而且,角动量Θ=q1p2-q2p1也是守恒量.
基于二阶均向量场法的步骤,得Kepler问题中式(13)的等效数值格式如下:
(14a)
(14b)
(14c)
(14d)
分别运算式(14a)/(14b)和式(14c)/(14d),可消去τ,得
(15a)
(15b)
由式(15a)+(15b),化简得
(16)
式(16)即对应于原系统的Hamilton量(能量)守恒.这也间接地验证了均向量场法格式是保能量的.
图7给出时间步长取不同值(0.03 s和0.07 s)时的轨道图形. 当dt取0.07 s时,所得结果在图7(a)上显示有一定的进动,这对于数值积分而言误差是难免的;而小步长0.03 s时,在长时间内几乎没有出现进动.图8是积分时间为18 s时,本文解与精确解的比较.由图8可知,取大步长0.07 s时,轨道图的初始误差较小,然后逐步增大.但步长取0.02 s时,本文解与真实椭圆轨道解基本重合,长时间内的误差也很小.
图9给出dt=0.07 s时的角动量误差随时间的变化, 其中初始角动量为Θ0=0.8, 此处的误差定义为(Θ-Θ0)/Θ0,不同时刻的误差均在10-2以内.图10给出了系统能量随时间的变化, 其中初始Hamilton函数H0=0.5,能量误差定义为(H-H0)/H0,不同时刻的误差均在10-5以内.
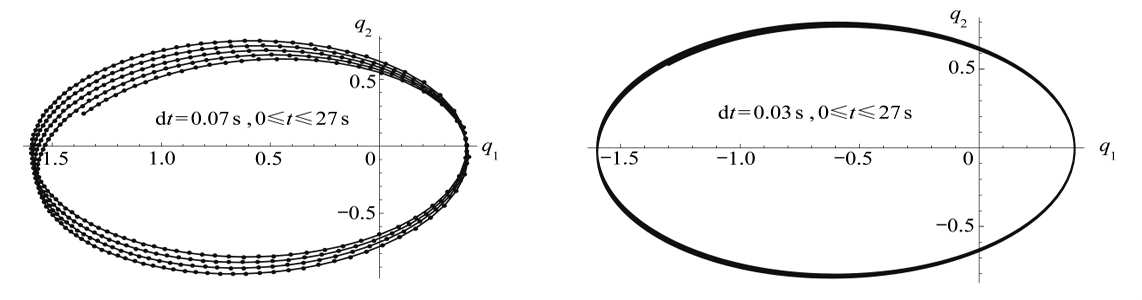
(a) dt=0.07 s(b) dt=0.03 s
图7 不同dt时的轨道图
Fig. 7 The orbit diagrams with different dt values

(a) dt=0.07 s(b) dt=0.02 s
图8 本文解与轨道真实解[24]间的比较
Fig. 8 Comparison of orbit diagrams between the present solution and the exact solution[24]
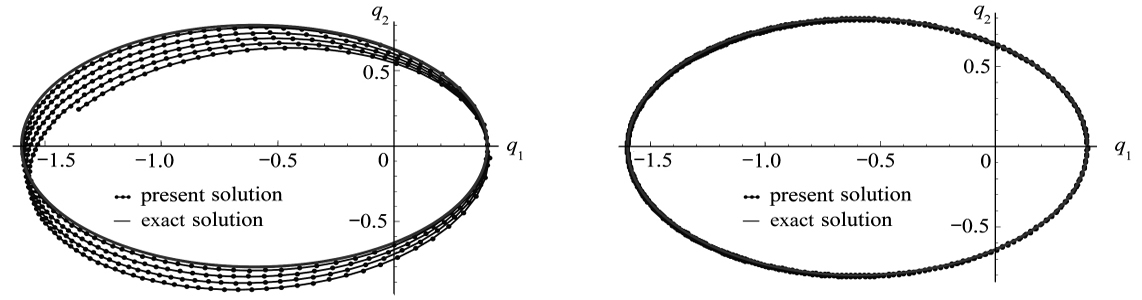
图9 当dt=0.07 s时的角动量误差图10 当dt=0.07 s时Hamilton守恒量误差
随时间的变化 随时间的变化
Fig. 9 The angular momentum error varying Fig. 10 The Hamiltonian conserved quantity error
with time, dt=0.07 s varying with time, dt=0.07 s
1) 采用保能量的均向量场法研究非线性振动方程,需先转为状态空间的一阶微分方程组,利用映射格式建立迭代方程组,该方法能够保持Hamilton系统的能量.
2) 本文给出了常见函数在均向量场格式中积分后的转化形式,便于直接应用该法.
3) 对于非线性程度较高的单摆振动,甚至含耦合项的微分振动系统,算例结果说明本文方法在积分步长相对较大时精度较二阶摄动法高,与微分求积法精度接近.如果减少积分步长,精度会更好.
4) 在解决线性振动系统时,均向量场法可退化为经典的Euler-中点法.
[1] 冯康, 秦孟兆. 哈密尔顿系统的辛几何算法[M]. 杭州: 浙江科学技术出版社, 2003.(FENG Kang, QIN Mengzhao.Symplectic Geometric Algorithm for Hamilton System[M]. Hangzhou: Zhejiang Science and Technolog Press. 2003.(in Chinese))
[2] 秦孟兆, 王雨顺. 偏微分方程中的保结构算法[M]. 杭州: 浙江科技出版社, 2010.(QIN Mengzhao, WANG Yushun.Structure-Preserving Algorithms for Partial Differential Equation[M]. Hangzhou: Zhejiang Science and Technolog Press, 2010.(in Chinese))
[3] FENG K. Difference schemes for Hamiltonian formalism and symplectic geometry[J].Journal of Computational Mathematics, 1986,4(3): 279-289.
[4] 胡伟鹏, 邓子辰. 无限维动力学系统的保结构分析方法[M]. 西安: 西北工业大学出版社, 2015.(HU Weipeng, DENG Zichen.The Infinite Dimensional Dynamical System Structure Analysis Method[M]. Xi’an: Northwestern Polytechnical University Press, 2015.(in Chinese))
[5] HU W P, DENG Z C, ZHANG Y. Multi-symplectic method for peakon-antipeakon collision of quasi-Degasperis-Procesi equation[J].Computer Physics Communications, 2014,185(7): 2020-2028.
[6] 高强, 钟万勰. Hamilton系统的保辛-守恒积分算法[J]. 动力学与控制学报, 2009,7(3): 193-199.(GAO Qiang, ZHONG Wanxie. The symplectic and energy preserving method for the integration of Hamilton system[J].Journal of Dynamics and Control, 2009,7(3): 193-199.(in Chinese))
[7] BRUGNANO L, IAVERNARO F, TRGIANTE D. A two-step, fourth-order method with energy preserving properties[J].Computer Physics Communications, 2012,183(9): 1860-1868.
[8] 陈璐, 王雨顺. 保结构算法的相位误差分析及其修正[J]. 计算数学, 2014,36(3): 271-290.(CHEN Lu, WANG Yushun. Phase error analysis and correction of structure preserving algorithms[J].Mathematica Numerica Sinica, 2014,36(3): 271-290.(in Chinese))
[9] 叶霄霄. 基于平均向量场方法的暂态稳定计算[D]. 硕士学位论文. 宜昌: 三峡大学, 2015.(YE Xiaoxiao. Transient stability calculation based on the average vector field method[D]. Master Thesis. Yichang: China Three Gorges University, 2015.(in Chinese))
[10] QUISPEL G R W, MCLACHLAN D I. A new class of energy-preserving numerical integration methods[J].Journal of Physics A:Mathematical and Theoretical, 2008,41(4): 045206. DOI: 10.1088/1751-8113/41/4/045206.
[11] CELLEDONI E, MCLACHLAND I, OWREN B, et al. Energy-preserving integrators and the structure of B-series[J].Foundations of Computational Mathematics, 2010,10(6): 673-693.
[12]![]() J L. Improving the accuracy of the AVF method[J].Journal of Computational and Applied Mathematics, 2014,259: 233-243.
J L. Improving the accuracy of the AVF method[J].Journal of Computational and Applied Mathematics, 2014,259: 233-243.
[13] CAI J X, WANG Y S, GONG Y Z. Numerical analysis of AVF methods for three-dimensional time-domain Maxwell’s equations[J].Journal of Scientific Computing, 2016,66(1): 141-176.
[14] 李昊辰, 孙建强, 骆思宇. 非线性薛定谔方程的平均向量场方法[J]. 计算数学, 2013,35(1): 60-66.(LI Haochen, SUN Jianqiang, LUO Siyu. An averaged vector field method for the nonlinear Schrödinger equation[J].Mathematica Numerica Sinica, 2013,35(1): 60-66.(in Chinese))
[15] HAIRER E, LUBICH C, WANNER G.Geometric Numerical Integration:Structure-Preserving Algorithms for Ordinary Differential Equations[M]. Berlin: Springer, 2006.
[16] 陈璐. 保结构算法的相位误差分析及其修正[D]. 硕士学位论文. 南京: 南京师范大学, 2014.(CHEN Lu. Phase error analysis and correction of structure preserving algorithms[D]. Master Thesis. Nanjing: Nanjing Normal University, 2014.(in Chinese))
[17] 邢誉峰, 杨蓉. 动力学平衡方程的中点辛差分求解格式[J]. 力学学报, 2007,39(1): 100-105.(XING Yufeng, YANG Rong. Application of Euler midpoint symplectic integration method for the solution of dynamic equilibrium equations[J].Chinese Journal of Theoretical and Applied Mechanics, 2007,39(1): 100-105.(in Chinese))
[18] 刘晓梅, 周钢, 王永泓, 等. 辛算法的纠飘研究[J]. 北京航空航天大学学报, 2013,39(1): 22-26.(LIU Xiaomei, ZHOU Gang, WANG Yonghong, et al. Rectifying drifts of symplectic algorithm[J].Journal of Beijing University of Aeronautics and Astronautics, 2013,39(1): 22-26.(in Chinese))
[19] 邢誉峰, 杨蓉. 单步辛算法的相位误差分析及修正[J]. 力学学报, 2007,39(5): 668-671.(XING Yufeng, YANG Rong. Phase errors and their correction in symplectic implicit single-step algorithm[J].Chinese Journal of Theoretical and Applied Mechanics, 2007,39(5): 668-671.(in Chinese))
[20] 秦于越, 邓子辰, 胡伟鹏. 谐振子的辛欧拉分析方法[J]. 动力学与控制学报, 2014,12(1): 9-12.(QIN Yuyue, DENG Zichen, HU Weipeng. Symplectic Euler method for harmonic oscillator[J].Journal of Dynamics and Control, 2014,12(1): 9-12.(in Chinese))
[21] 李鹏松, 孙维鹏, 吴柏生. 单摆大振幅振动的解析逼近解[J]. 振动与冲击, 2008,27(2): 72-74.(LI Pengsong, SUN Weipeng, WU Baisheng. Analytical approximate solutions to large amplitude oscillation of a simple pendulum[J].Journal of Vibration and Shock, 2008,27(2): 72-74.(in Chinese))
[22] 吕中荣, 刘济科. 摆的振动分析[J]. 暨南大学学报(自然科学版), 1999,20(1): 42-45.(LÜ Zhongrong, LIU Jike. Vibration analysis of a pendulum[J].Journal of Jinan University(Natural Science), 1999,20(1): 42-45.
[23] 周凯红, 王元勋, 李春植. 微分求积法在单摆非线性振动分析中的应用[J]. 力学与实践, 2003,25(3): 50-52.(ZHOU Kaihong, WANG Yuanxun, LI Chunzhi. The application of differential quadrature method in nonlinear vibration analysis of simple pendulum[J].Mechanics in Engineering, 2003,25(3): 50-52.(in Chinese))
[24] 李文博, 赵定柏. 开普勒问题的一种简单处理[J]. 大学物理, 2000,19(1): 45-47.(LI Wenbo, ZHAO Dingbai. A simple treatment of the Kepler problem[J].College Physics, 2000,19(1): 45-47.(in Chinese))